Examining the challenges of simulating surface water–groundwater interactions in a post-glacial environment

Abstract

Although integrated models are increasingly used for water management purposes, detailed applications of these models under different conditions are necessary to guide their implementation. The objective of this study was to examine some of the challenges encountered when simulating surface water–groundwater interactions in a post-glacial geological environment. The integrated Mike SHE model was used to simulate transient-state heads and flows in the Raquette River watershed in the Vaudreuil-Soulanges region of southwestern Quebec (Canada) over a 2-year period. This application benefited from a detailed hydrogeological database recently developed for the region. Overall, flows, heads and groundwater inputs to the river were adequately simulated. A sensitivity analysis has shown that many hydrogeologic and surface flow parameters have an impact on both flow rates and heads, thus underlining the importance of using an integrated model to study watershed-scale water issues. Additional flow rate measurements to improve the quality of rating curves and continuous flow measurements in tributaries could improve model calibration. An explicit simulation of unsaturated zone infiltration processes, including soil flow, plant and evaporation processes, as well as the inclusion of the agricultural tile drainage system, could reduce simulation errors. Extending the model calibration over a longer period, including contrasting hydrological conditions, would make the model more robust in view of its use for water management under land use and climate change conditions. Nevertheless, this work demonstrated that, using data readily available for southern Québec aquifers, it is possible to build an integrated model that is representative of actual hydrological conditions. The maintenance and improvement of this model for long-term use is recommended.

Les modèles entièrement couplés sont de plus en plus utilisés pour réaliser la gestion intégrée des ressources en eau, mais les exemples détaillés d’applications sont encore peu nombreux. L’objectif de cette recherche était d’examiner les défis posés par la simulation des interactions eaux de surface–eaux souterraines dans un environnement géologique post-glaciaire. Le modèle couplé Mike SHE a été utilisé pour simuler les charges et les débits sur le bassin de la rivière à la Raquette dans la région de Vaudreuil-Soulanges (Québec, Canada), sur une période de 2 années. Ce travail a bénéficié d’une base de données hydrogéologiques récemment développée pour la région. Les résultats montrent que les débits, les charges et les flux échangés entre l’aquifère et la rivière sont relativement bien simulés, ce qui indique que le modèle est utile dans son état actuel, malgré le fait que certaines incertitudes et limitations aient été identifiés. L’analyse de sensibilité a montré que plusieurs paramètres hydrogéologiques et d’écoulement superficiel ont un impact à la fois sur les débits et les charges, ce qui met en évidence l’importance d’utiliser un modèle couplé pour la gestion intégrée de l’eau. Des mesures de débits aux tributaires pour toute l’année ainsi que des courbes de tarages basées sur une plus large gamme de débits pourraient améliorer le calage du modèle. Une représentation explicite de la zone non saturée, incluant les processus d’écoulement dans le sol, le prélèvement par les plantes et l’évaporation, de même que l’inclusion du réseau de drains agricoles, pourraient contribuer à réduire les erreurs de simulation. Le prolongement de la période de calibration pour inclure des conditions hydrologiques contrastées contribuerait à rendre le modèle plus robuste pour des applications liées à la gestion de l’eau en conditions de changement dans l’utilisation du territoire et de changements climatiques. Néanmoins, cette recherche a montré que les données utilisées, qui correspondent à celles généralement disponibles dans le sud du Québec, permettent de construire un modèle couplé qui représente bien les conditions hydrologiques actuelles. Il est recommandé de poursuivre le développement du modèle pour des applications à long terme.

Introduction

Over the last two decades, surface water and groundwater reservoirs have increasingly been studied as two expressions of a single resource, a paradigm described by Winter et al. (1998). In humid climates, aquifers sustain water inflow to rivers, maintaining riparian ecosystems (Brunke and Gonser 1997; Hayashi and Rosenberry 2002) and thermal refuges for fish species (Kurylyk et al. 2015), especially during low-flow periods. Increasing groundwater pumping (Konikow and Kendy 2005), and the resulting water table drawdown, can reduce groundwater inflow into rivers (McCallum et al. 2013) and induce river water infiltration into the riverbed (Chen and Shu 2002). Poor groundwater quality can also affect river water quality (Rozemeijer and Broers 2007).

As a result of the growing recognition of their coupled nature, surface water–groundwater interactions have been monitored and simulated in a large range of geological and climatic conditions throughout the world. Reviews of related processes and methods are reported in Fleckenstein et al. (2010) and Kalbus et al. (2006). Integrated model applications are increasingly used to understand the complex interactions between different water reservoirs, and are increasingly used as tools to guide integrated water management by consultants and regulatory agencies. However, applications of integrated models are not yet routine, due to either the lack of available data, or the lack of human and computer resources to develop the models. A thorough analysis of integrated flow conditions, including a sensitivity analysis and an examination of the areas needing improvement to build a more robust model, is usually reserved to academic contexts. As a result, integrated models that are used and improved upon over the long term to guide integrated water management are still rare. Such models are necessary to address low flow, as well as flooding conditions, while allowing the different water users to perform their various activities.

The challenge of simulating surface and groundwater flows together is heightened when studying complex three-dimensional (3D) geological environments, where topography, stratigraphy and hydraulic parameters of the media can vary substantially over short distances. Topography and geology have large effects on surface water–groundwater interactions (e.g. Gleeson and Manning 2008). Complex post-glacial environments are especially difficult to assess, due to the high horizontal and vertical spatial heterogeneity of the geological units that typically comprise them. In addition, the unconsolidated sediments often lie on fractured bedrock, where the spatial heterogeneity of hydraulic properties can be very large. These difficulties can be exacerbated in small agricultural rivers that are prone to large variations in flow rates as a result of the flashy behavior due to the limited extent of permeable areas that allow infiltration relative to the large clayey areas, where tile drainage is pervasive. Such conditions are particularly difficult to simulate using integrated flow models, because they require a good characterization of both runoff and groundwater flow processes to represent the full range of rapidly changing flow conditions.

The objective of this study was to examine some of the challenges encountered when simulating surface water–groundwater interactions in a post-glacial environment. It is intended to contribute to the development of models that will become truly useful water management tools. This study makes use of recently updated geological, hydrogeological and hydrological data for the Vaudreuil-Soulanges region of southern Quebec, Canada (Larocque et al. 2015), obtained through a detailed regional aquifer characterization project. This watershed is an example of post-glacial geological conditions in which surface water–groundwater interactions are not easily assessed, and as such is an excellent case study area for which to build an integrated model.

Study area

Physiography and land use

The Raquette River watershed (133 km²) is located in the St. Lawrence Lowlands, 50 km west of Montreal, in the province of Quebec (Canada; Figure 1). Approximately 75% of the area is covered by light detection and ranging (LiDAR) data (GéoMont 2011) with a vertical accuracy of 15 cm on a horizontal grid of 1 m². Over the rest of the study area, topographic data are derived from a digital elevation model with a vertical precision of 3 m and a spatial resolution of 10 m. The watershed has a marked topography over short distances, with elevations ranging from 23 m (all elevations stated as meters above sea level) near the Outaouais River to 228 m at the peak of Mount Rigaud. Between the Saint-Lazare Hill and Mount Rigaud, a northeast–southwest-aligned bedrock depression corresponds to the Sainte-Marthe corridor. At the base of Mount Rigaud, the agricultural plain ranges from 60 to 75 m in elevation at the southern boundary of the Raquette watershed. At the northern boundary, topography ranges from 23 to 35 m. The sandy Hudson Hill is located along the northeast boundary, reaches 80 m, and corresponds to the Raquette River water divide (Larocque et al. 2015).

Figure 1. Location of the Raquette River watershed in the Vaudreuil-Soulanges region of southern Quebec (Canada), including topography and monitoring stations.

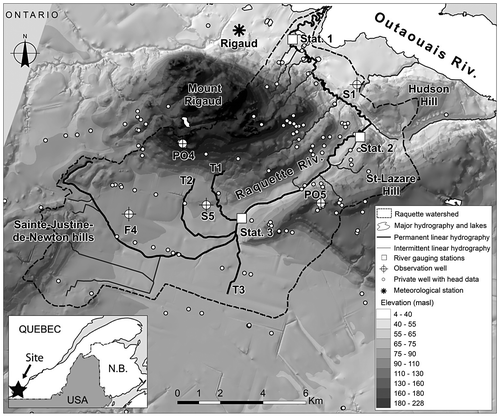
Land use is classified as agricultural for more than half of the watershed (53%; Larocque et al. 2015). Agricultural fields are mainly located upgradient in the watershed, south of Mount Rigaud. Forest covers 41% of the watershed, mostly on Mount Rigaud, and on the Saint-Lazare and Sainte-Justine-de-Newton hills. Urban or residential areas cover 5% of the watershed, and the remaining 2% is occupied by power lines. There are very few wetlands and no lakes capable of water retention in the watershed.

Geology

Bedrock geology in the study area is composed of a sedimentary sequence of Paleozoic age with low deformation. It overlays the Precambrian bedrock and corresponds to the Grenville Province (Hofmann 1972). This sedimentary bedrock is located at the base of the sedimentary sequence of the St. Lawrence Lowlands.

The bottom of the sedimentary sequence is composed of sandstone of the Upper Cambrian Potsdam Group, with a total thickness of up to 450 m (Williams et al. 2010). The two formations of the Potsdam Group, Covey Hill and Cairnside, are composed of fossil-free feldspar sandstone and fossiliferous quartzite sandstone. The Lower Ordovician Beekmantown Group overlies the Potsdam sandstone, and is composed of dolomites, limestones and calcareous sandstones, approximately 250 m thick, including the Theresa and Beauharnois formations (Hofmann 1972). The Chazy Group rests on the Beekmantown Group, and is marked by a contribution of detrital elements during the Middle Ordovician. The Chazy Group is 100 m thick, and includes the members of the Ste-Thérèse Formation and of the Laval Formation.

The higher topography of Mount Rigaud results from an intrusion in the Grenville bedrock, which occurred at the end of the Cambrian and the beginning of the Ordovician (Greig 1968). The sedimentary sandstone bedrock outcrops in certain locations along the Raquette River bed, over a few hundred meters.

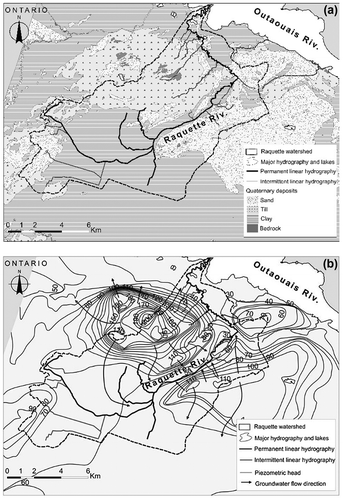
Surface deposits mapped in the study area were emplaced during the last glacial age, the late Wisconsinan (Roy and Godbout 2014; Figure 2(a)). They show contrasting conditions, with the top of Mount Rigaud covered by thin and discontinuous till, and the flanks of Mount Rigaud having till deposits of up to 15 m thick. Some till deposits are also visible to the southwest of Mount Rigaud. The Champlain Sea clay deposits are found everywhere in the plain and can reach 45 m in thickness. Major sand deposits are also present in the Raquette River watershed on the Hudson and Saint-Lazare hills, as well as in the area of Sainte-Justine-de-Newton. Between Mount Rigaud and the Hudson Hill, the Raquette River meanders on silty sand deposits. Littoral sands of glacio-marine origin are found in the Saint-Lazare area and on the slopes of Mount Rigaud. Available drilling data (Technorem 2005; MDDELCC [Ministère du Développement durable, de l’Environnement et de la Lutte contre les changements climatiques] 2013) and seismic information (Hobson and Tremblay 1962) provide evidence that buried channels of sand and gravel could locally reach 40 m thick below 20 to 30 m of Champlain Sea clay deposits. No storage coefficients or specific storage values were available for the study area.

Figure 2. Geological and hydrogeological conditions in the Raquette River watershed: (a) Quaternary deposits (modified from Roy and Godbout 2014), and (b) piezometric map (modified from Larocque et al. 2015).

Hydrology

The Raquette River is a fourth-order river, which drains surface water and groundwater over a distance of 34 km. Upstream, it begins on the till crests located southwest of Mount Rigaud. It drains eastward through the agricultural plain, contours Mount Rigaud on its eastern flank, and discharges into the Outaouais River. The watershed has three additional tributaries, which join the Raquette River upstream of the Sainte-Marthe valley, as well as other small streams also flowing from Mount Rigaud into the river. In the agricultural area of the watershed, a substantial drainage network is in place (ditches and drains).

Water levels were monitored at three locations on the Raquette River between March 2013 and fall 2014 by Larocque et al. (2015; see Figure 1 for the locations of gauging stations). Station 1 was installed in mid-March 2013, and water levels were measured throughout the year (water level measured at 30-min intervals with an ultrasonic Hobo Onset logger). However, winter values were discarded because of ice cover between January and early April 2014). Stations 2 and 3 were installed in mid-July and mid-May 2013, respectively (water level measured at 30-min intervals with Solinst Leveloggers in perforated plastic tubes at the river bed). These probes were removed between December 2013 and mid-May 2014 to prevent damage from ice. Water levels were transformed into flow rates using rating curves and velocities measured at different times during the study period (with an HACH portable Doppler flow meter [GENEQ] for low flows, and a StreamPro Acoustic Doppler Current Profiler [DASCO] for high flows). Two rating curves were constructed for station 3, due to equipment failure in December 2013. Twenty-three flow rate measurements were taken at station 1, between May 2013 and August 2014 (RMSE_stat1 = 2.3 m³s⁻¹; RMSE - root mean square error); 18 measurements were taken at station 2, between August 2013 and August 2014 (RMSE_stat2 = 0.2 m³ s⁻¹); and 26 measurements were taken at station 3, between April 2013 and August 2014 (RMSE_stat3 = 0.1 m³ s⁻¹ in 2013 and 0.2 m³ s⁻¹ in 2014). For all three stations, and particularly for station 1, the uncertainty is greatest for high flow rates. Detailed river cross-sections at the three gauging stations were obtained using a differential global positioning system (GPS). The average daily flow rates at gauging station 1, located downgradient in the study area, closest to the Raquette River outlet, varied between 0.4 and 88 m³ s⁻¹. It is clear from the rating curve RMSE at this station that a large error is associated with the high flow value. Flow rates at gauging station 2 varied between 0.1 and 17.4 m³ s⁻¹, while those at gauging station 3 varied between 0.03 and 24.3 m³ s⁻¹.

The evolution of flow rates along the Raquette River flow path was measured twice in August 2014 (12 and 25 August; no precipitation for five consecutive days prior to measurements; see Figure 3) at 23 locations between stations 1 and 3 using the velocity and cross-section method. The flow rates at the outlet of the three main tributaries of the Raquette River were measured in the same way on each occasion. The measured flow rates for the two dates were very similar, with differences within the uncertainty usually associated with this type of flow measurement (from 2 to 20%; Carter and Anderson 1963; Pelletier 1988; Sauer and Meyer 1992; Harmel et al. 2006), and varied between 0.008 and 0.220 m³ s⁻¹. Upgradient, where the river flows on clay deposits in an agricultural setting (between points 1 and 8), the flow rate is low and increases slowly. The Raquette River occasionally runs dry in this area. In the Sainte-Marthe Valley (between points 8 and 9), there is a marked increase in flow rates, even though the river flows on clay deposits. The increase in flow rates is smaller, but relatively constant, for these two dates between points 9 and 19. There is a drop in flow rates on both dates between points 19 and 20, a further increase between points 20 and 22, and a decrease in flow rates in the lowest reaches of the river.

Figure 3. Measured flow rates at 23 locations along the Raquette River on 12 and 25 August 2015. The black arrows indicate tributaries 1 (T1), 2 (T2) and 3 (T3). The grey arrows indicate the main streams. The dashed vertical lines indicate the locations of gauging stations 1, 2 and 3.

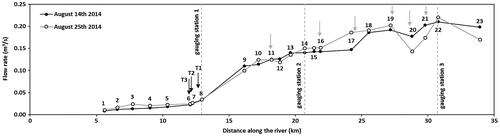
The three main tributaries reach the Raquette River between measurement points 6 and 8. In August 2014, the flow rates were very low for all three tributaries. At their outlets, the flow rates (1) were constant, at 0.008 m³ s⁻¹, for tributary 1 (T1); (2) varied between 0.002 and 0.003 m³ s⁻¹ for tributary 2 (T2); and (3) varied between 0.002 and 0.004 m³ s⁻¹ for tributary 3 (T3).

Hydrogeology

Available hydraulic conductivities were reported in Larocque et al. (2015), and are derived from three observation wells (150-mm open boreholes) drilled into the fractured bedrock (F4: 32.9 m, confined sedimentary bedrock; PO4: 50 m, unconfined crystalline bedrock; PO5: 60.9 m, unconfined sedimentary bedrock), and two observation wells (2” PVC piezometers) in the Quaternary sediment (S1: 8.2 m, confined; and S5: 16.8 m, semi-confined, with screen lengths of 3 and 1.5 m, respectively). Larocque et al. (2015) performed pumping tests in observation wells F4, PO4 and PO5, and slug tests in observation wells S1 and S5. They also compiled hydraulic conductivities (K) available from different consulting firms (see Table 1). K values for the crystalline bedrock vary between 1.0 × 10⁻⁶ and 8.3 × 10⁻⁵ m s⁻¹. These values are higher than those from the literature, which can range from 8.0 × 10⁻⁹ to 3.0 × 10⁻⁴ m s⁻¹ (Domenico and Schwartz 1990). K values for the sedimentary bedrock were highly variable spatially, and reported values range between 1.1 × 10⁻⁷ m s⁻¹, for wells in the Covey Hill and the Potsdam Formation, to 9.0 × 10⁻⁴ m s⁻¹, for a well in the Beekmantown Group. Reported sand K values vary between 7.0 × 10⁻⁶ and 7.4 × 10⁻³ m s⁻¹. Measured till K values were between 3.5 × 10⁻⁷ and 1.1 × 10⁻⁴ m s⁻¹. The few measured K values for clay deposits range between 1.6 × 10⁻¹⁰ and 9.7 × 10⁻⁸ m s⁻¹.

Table 1. Measured and calibrated parameters.

	Calibrated	Range of measured values
Hydraulic conductivity^a (K) (m s^−1)
Sand	3.0 × 10^−5	7.0 × 10^−6–7.4 × 10^−3
Till	1.0 × 10^−6	3.5 × 10^−7–1.1 × 10^−4
Clay	5.0 × 10^−8	1.6 × 10^−10–9.7 × 10^−8
Crystalline bedrock	1.6 × 10^−7	1.0 × 10^−6–8.3 × 10^−5
Sedimentary bedrock	1.4 × 10^−4	1.1 × 10^−7–9.0 × 10^−4
Storage coefficient^b (S) (−)
Sand	0.25	0.10–0.35
Till	0.15	0.06–0.16
Clay	0.025	0.00–0.05
Crystalline bedrock	0.01	0.01–0.05
Sedimentary bedrock	0.05	0.18–0.30
Specific storage^c (Ss) (m^−1)
Sand	3.0 × 10^−4	1.0 × 10^−5–1.0 × 10^−4
Till	1.0 × 10^−4	1.0 × 10^−5–1.0 × 10^−3
Clay	1.0 × 10^−4	1.0 × 10^−4–1.0 × 10^−2
Crystalline bedrock	1.0 × 10^−5	1.0 × 10^−7–1.0 × 10^−5
Sedimentary bedrock	1.0 × 10^−6	1.0 × 10^−7–1.0 × 10^−5
River leakage coefficient^d (rl) (s^−1)
Raquette River and main tributaries	7 × 10^−7	3.9 × 10^−7–1.4 × 10^−3
Drainage constant^e (Cd) (s^−1)
Small streams	5 × 10^−6	2.0 × 10^−8–4.9 × 10^−4
Manning coefficient^f (n) (m^1/3 s^−1)
Agricultural area (clay)	15	1.7–83.3
Infiltration fraction^g (fI)
Sand	0.70	0.44–0.66
Till	0.42	0.33–0.51
Clay	0.05	0.03–0.07
Undifferentiated bedrock	0.60	0.66–0.89

^a Measured values reported in Larocque et al. (2015).

^b Johnson (1967); Todd (1980).

^c Domenico and Mifflin (1965); Rutqvist et al. (1998).

^d Doppler et al. (2007); Spanoudaki et al. (2009); Irvine et al. (2012); Teloglou and Bansal (2012).

^e Al-Khudhairy et al. (1999); DHI (2007); Zhou et al. (2013).

^f McCuen (2004).

^g Croteau et al. (2010).

Groundwater levels measured once in private wells between July and August 2013 are also reported in Larocque et al. (2015) for 149 locations within the Raquette River watershed and 35 locations in the surrounding area (see Figure 1). Heads are also available from the five monitored observation wells, and have amplitudes (maximum minus minimum value during the study period) of 0.52, 6.39 and 0.80 m for bedrock wells F4, PO4 and PO5 (well PO4 is located at the highest altitude on Mount Rigaud), and amplitudes of 0.28 and 0.95 m for observation wells CPT1 and CPT5 in the Quaternary sediments. A piezometric map of the bedrock aquifer was interpolated (co-kriging with topopography data in ArcGIS; see Larocque et al. 2015 for details) using all available head data from the private wells and average heads from the observation wells, in addition to control points, where hydraulic connections between the surface and the bedrock aquifer were clear (e.g. where the bedrock outcrops in the Raquette riverbed, at ponds located on Mount Rigaud, and along the Outaouais River).

The piezometric map (Figure 2b) shows that groundwater flow is radial, with high hydraulic gradients (0.2 m m⁻¹) on Mount Rigaud. Hydraulic gradients are small in the clay plain (0.003 m m⁻¹), where artesian conditions were observed. The piezometric map is not modified by the river channel, indicating that there is no hydraulic connection between the Raquette River and the confined bedrock aquifer in this area. North of Mount Rigaud, groundwater flows toward the Outaouais River, with a low hydraulic gradient (0.004 m m⁻¹). Groundwater flow directions between Mount Rigaud and the Saint-Lazare Hill converge toward the Raquette River (no head forcing at this location). Flow rate measurements at different locations in this area, made in August 2014, show a marked increase in river flow. Between the Saint-Lazare and Hudson hills, head control points equal to river water levels were used in the interpolation to compensate for the small number of measured heads (see Figure 1) and to reproduce the drainage effect of the river in the piezometric map. On Hudson Hill, Technorem (2005) showed the presence of two distinct aquifers, the top granular aquifer and the fractured aquifer, confined by till and clay horizons. Head values suggest the presence of a local vertical gradient between the two aquifers, but this is not confirmed at some locations.

Meteorological conditions

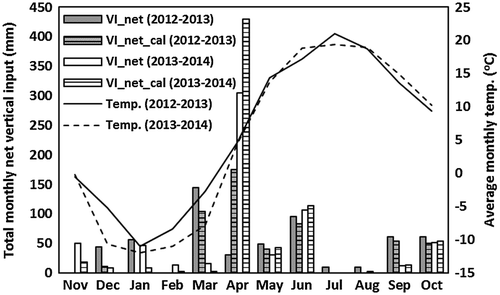
Long-term data for the 1981–2010 period from the Mount Rigaud weather station (MDDELCC 2014) show that total annual precipitation is 999 mm, of which 16% falls as snow between mid-November and mid-April. Total annual precipitation was 1049 mm between November 2012 and October 2013, and 1119 mm between November 2013 and October 2014. November 2012 was particularly dry, with only 7 mm of rain, while April 2014 was very wet, with 163 mm of rain. During both years of the study period, June was the month with the highest precipitation, and snowmelt occurred in April. The monthly average air temperature was lowest in February (−8.4°C in 2013 and −11.9°C in 2014), and highest in July (21°C in 2013 and 19.4°C in 2014; see Figure 4). The 2013–2014 hydrological year was hotter (5.9°C) on average than the 2012–2013 hydrological year (4.9°C). It is important to note that, in the current work, winter precipitation occurring as snow was not adjusted for wind-induced undercatch and snow sublimation. These processes typically reduce the water equivalent of the snow available at the time of snowmelt.

Figure 4. Net monthly vertical inflows (VI_net) and air temperature (Temp.) in the Raquette River watershed for the two hydrological years studied (November 2012–October 2013 and November 2013–October 2014). Vertical inflows (VI) correspond to the sum of precipitation occurring as rain when air temperature exceeds the freezing point and snowmelt occurring during the winter and in the spring snowmelt period. VI_net corresponds to VI values from which evapotranspiration has been substracted. VI_{net_cal} corresponds to the calibrated VI_net values.

Methods

Vertical inflows, and hydrological and hydrogeological monitoring

In a cold region, estimating the amount of water that can potentially infiltrate or run off is crucial. Vertical inflows (VI) are defined as the sum of liquid precipitation and snowmelt available daily for runoff, percolation or evaporation. In the absence of snow on the ground and when the precipitation is liquid, VI and precipitation data are equal. In the Raquette River watershed, monthly VI was estimated from November 2012 to October 2014 (see Figure 4) using the MOHYSE model (Fortin and Turcotte 2007), which uses daily air temperature and accumulated snow to calculate snowmelt using a degree-days approach. MOHYSE is a conceptual hydrological model that is not spatially discretized, designed to reproduce river flows at the watershed scale. After calibration on flow rates, the model provides an estimate of actual evapotranspiration (ETR), runoff, and infiltration (see Larocque et al. 2015 for details on the MOHYSE model application for the Raquette River watershed). During the study period, annual ETR was equal to 581 mm (2012–2013) and 459 mm (2013–2014). Subtracting monthly ETR from monthly VI values provides a VI_net time series, considered to be the volume of water that can potentially run off or infiltrate in a given month. For the two years of the study period, VI_net values were 518 and 686 mm. The daily VI_net values necessary for the flow model were calculated using a different VI/VI_net ratio for each month.

Groundwater levels in the five observation wells that were equipped with automated Solinst level loggers were monitored continuously at an hourly time step by Larocque et al. (2015) from June (F4), August (PO4 and PO5) and September (S1 and S5) 2013, until October 2014 (all wells except PO5, for which monitoring ended in July 2014).

Groundwater flow model

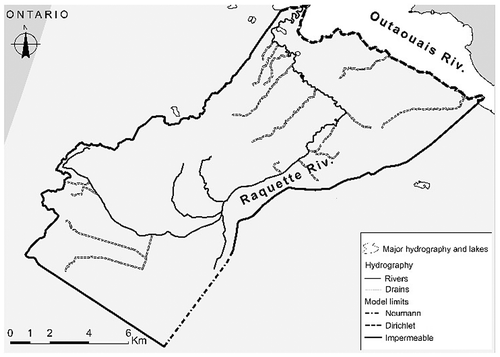
The integrated model was developed with Mike SHE (DHI 2007). The simulated domain (see Figure 5) covers an area of 118 km². It is similar to that of the Raquette River watershed, but slightly different in the northeast area to allow for the representation of groundwater outflow to the Outaouais River. It is also different in the southwest portion of the study area, where the simulated domain was based on the groundwater flow divide estimated from the piezometric map. The simulated domain was discretized horizontally into 100 m × 100 m cells to provide a refined representation of the Raquette River. This fine spatial resolution allows river entrenchment to be adequately described (Refsgaard 1997), but significantly increases calculation times (Vázquez et al. 2002). Surface topography was described using a single LiDAR datum for each cell. Topography in the model varies between 23 m close to the Outaouais River and 225 m at the top of Mount Rigaud. Vertically, the numerical model simulates a porous media aquifer to a uniform depth of −100 m. The model is divided into 10 layers of variable thicknesses. Layer depth increases gradually, from 2.5% of the total model thickness at any given location to 20% of the total model thickness. In total, 165,870 cells were used to horizontally and vertically discretize the study area.

Figure 5. Boundary conditions used to represent the Raquette River study area in the integrated Mike SHE model.

Representing the aquifer and the surface flow network

In the model, littoral sands and sand and gravel were simplified into a single sand unit. The bedrock was divided into crystalline and sedimentary (essentially Potsdam sandstone) bedrock, since the two formations have different hydraulic properties. Because the thickness of the sandstone above the crystalline bedrock is unknown, the crystalline bedrock was gradually reduced in thickness over a 2-km distance, starting from the sandstone–crystalline bedrock interface. Data available to constrain the conductivity calibration for the five different lithologies (i.e. sand, till, clay, crystalline bedrock, and sandstone bedrock) are reported in Table 1. For each geological unit, vertical hydraulic conductivity was set as 10% of the horizontal value, as is typically done when no measured K_v/K_h ratio is available.

The Raquette River and its three main tributaries were simulated using the Mike11 model. A cross-section was used at each significant change in bed slope to represent changes in river flow dynamics. Given the lack of precise field data, aquifer–river exchanges were set as occurring at the river bed. Two parameters characterize flow in the river channel, the Manning roughness coefficient (n) and the river leakage coefficient (r_l). Although n affects water level in the river, and thus aquifer–river interactions, the exchange coefficient has a larger influence on the exchanged fluxes (Refsgaard 1997). The n for the Raquette River and its main tributaries was set as 20 m^1/3 s⁻¹, and their exchange coefficient was a calibrated parameter. The small streams were represented using fixed head drains (see Figure 5) to evacuate water when heads are above the drain elevation. The elevation of these draining cells was determined using the LiDAR data. The drainage constant (C_d), which is known to have a considerable effect on the form of the hydrograph (Vázquez et al. 2002), was a calibrated parameter. DHI (2007) suggest using C_d values of between 1.0 × 10⁻⁷ and 1.0 × 10⁻⁶ s⁻¹, although values as low as 2.0 × 10⁻⁸ s⁻¹ (Al-Khudhairy et al. 1999) and as high as 4.9 × 0⁻⁴ s⁻¹ (Zhou et al. 2013) have been used elsewhere.

The detention storage was set to the Mike SHE default value of 25.4 mm (Frana 2012) to represent the water depth above which runoff occurs. Manning roughness coefficients (n) associated with surface runoff were attributed spatially as a function of the geological unit and land use in the top numerical layer. On the Raquette River, till, sand and bedrock zones are generally associated with wooded areas, while clay is associated with agricultural areas. The Manning roughness coefficient was fixed at 1.7 m^1/3 s⁻¹ for wooded areas (McCuen 2004). The agricultural areas are characterized by a complex drainage network of tile drainage (drains and agricultural ditches), which plays an important role in the watershed hydrology and rapidly evacuates water from the agricultural areas toward the Raquette River, shortening the hydrograph curve (Feyen et al. 2000). The Manning roughness coefficient influences river flow rates similarly to a tile drainage network.

Boundary conditions

The simulated domain does not correspond exactly to the Raquette River watershed (Figure 5). Rather, the boundary conditions were set to correspond to groundwater flow conditions. In the clay plain south of Mount Rigaud, a Neuman-type boundary condition was set at a right angle to groundwater flow, with a hydraulic gradient of 0.003 m m⁻¹. To the north of Mount Rigaud, the Outaouais River was used as a Dirichlet-type constant head condition. Water-level data from gauging stations located below the Carillon dam (Hydro-Québec 2014) and at the Deux-Montagne Lake (HYDAT 2014) were used to set a time-varying head. These time-varying head conditions were attributed to the top four numerical layers, equivalent to approximately 25 m below the surface, because the Outaouais River reaches approximately this depth at its center (Québec-Pêche 2011). A no-flow boundary was attributed to the lowest six layers. The other limits were flow boundaries, coinciding with either the watershed boundary (no flow) or with boundaries imposed by groundwater flow directions (imposed flux).

Unsaturated flow and evapotranspiration were not simulated in the model so as to reduce the number of unknown parameters and the simulation time. Alternatively, a simple algebraic representation of recharge was used (adapted from DHI 2007):(1)

where Rec is recharge (mm d⁻¹), VI_net is the water available for runoff or infiltration (mm d⁻¹), and f_I is the fraction of available water that can infiltrate (unitless). f_I is constant in time but varies spatially with the surface geology (bedrock, till, clay and sand).

Simulated conditions

The transient-state simulation spanned two hydrological years, from 1 November 2012 to 31 October 2014. A 10-year spin-up period, in which the meteorological data for the two years of the study period were repeated five times, was used to ensure that initial conditions were stable prior to simulating the actual conditions. Simulated flow rates and heads for over these two years were compared to measured values, and the model was calibrated manually. The time step was one day.

The model was calibrated through manual trial and error using the available head measurements for the modeled domain and using the hourly groundwater levels that were measured at the five observation wells. The flow rate data are from the three gauging stations. All these data were reported in Larocque et al. (2015). The relatively large number of calibrated parameters (22; Table 1) makes it plausible that the combinations of parameters that satisfy the minimization criteria could be numerous. Using an automatic calibration procedure might have alleviated this situation, but would not have eliminated it. The calibrated parameters are thus considered to represent one set of possible values.

The model was calibrated using a total of 22 parameters: five hydraulic conductivities (K) and five storage coefficients (S_s and S_y) of the different geological units (sand, till, clay, sandstone, and crystalline bedrock); the river leakage coefficient (r_l); the drainage constant for the small streams (C_d); the Manning roughness coefficient for runoff (n) (clay); and the infiltration fractions (f_I) for the sand, till, clay, and bedrock outcrops. Calibration intervals are described in Table 1, and are either measured values for the study area or from the scientific literature. The calibration of hydraulic heads was done to minimize the mean error (ME), the mean absolute error (MAE), the root mean square error (RMSE), and the normalized root mean square error (NRMSE).(2) (3) (4) (5)

where N is the number of head measurements, h_si is the simulated head (m), h_mi is the measured head (m), h_max is the highest measured head (m) and h_min is the lowest measured head (m).

The model performance for surface flow was evaluated using the following criteria:(6) (7) (8) (9)

where N_Q is the number of measured flow rates, Q_m is the measured flow rate (m³ s⁻¹), Q_s is the simulated flow rate (m³ s⁻¹), Q_{m_bar} is the average measured flow rate (m³ s⁻¹) and Q_{s_bar} is the average simulated flow rate (m³ s⁻¹).

The general quality of the simulated flow rates was estimated using the Nash–Sutcliffe model efficiency coefficient (NSE; Nash and Sutcliffe 1970). Because the NSE is particularly sensitive to high flow rates (Güntner et al. 1999), the NSE calculated on log-transformed flow rates (NSElog) was used to evaluate model performance during low-flow periods (Güntner et al. 1999). The ability of the model to simulate the average and maximum flood flow rates at each gauging station was estimated using the Fbal criteria (Henriksen et al. 2003) and the percent error in peak (PEP; Green and Stephenson 1986) respectively. To evaluate the general ability of the model to simulate flood events, the PEP criteria were averaged, with the PEP calculated for the five largest flow rates measured. Ideally, Fbal and PEP should tend toward 0, while NSE, NSElog and NSEcomb should tend toward 1. Fbal is positive when a simulated flow rate is smaller than the observed value, and vice versa. Similarly, a negative PEP indicates that the simulated flow rate is larger than the measured flow rate, and vice versa.

The model sensitivity coefficients were calculated for each parameter using a perturbation of 5% applied to the calibrated parameter values listed in Table 1. To facilitate the process, the four f_I values (infiltration fraction) were modified simultaneously, resulting in a total of 19 tested parameters. The calculations were done using the AUTOCAL module in Mike SHE:(10) (11)

where S_i,j is the sensitivity of model result j to parameter θ_i. Subscript j varies from 1 to 3 (k) in this case for flow rates (three flow rate measuring stations), and from 1 to 5 (k) for heads (five observation wells). The variable n corresponds to the total number of tested parameters (n = 19), Δθ_i is the 5% perturbation imposed on a parameter θ_i, and S_{i_TOT} is the total sensitivity of the model to this parameter. The sensitivity calculations were done for flow rates and heads separately, leading to S values for each of these two types of results. Prior to the sensitivity calculations, logarithmic transformations were applied to parameters with ranges spanning two or more orders of magnitude (i.e. K, S_s, n and r_l).

Results

Calibrated parameters

The hydraulic conductivities calibrated for sand, till and sedimentary bedrock are within the ranges of measured values (Table 1). Calibrated clay K was slightly higher than the measured range, while calibrated crystalline bedrock K is one order of magnitude lower than the measured range. The hydraulic conductivity of the sedimentary bedrock is significantly higher than that of the crystalline bedrock, as expected for this more productive formation.

Storage coefficients and specific storage values for all of the geological units are within the range of available literature values, with the exception of the sedimentary bedrock S and the sand S_s. Although there are unconfined areas in the study area, storage coefficients represent average values over the watershed, since geological units have been greatly simplified.

Although the river–aquifer exchange coefficient is known to vary spatially and temporally due to erosion and sedimentation processes, as well as water temperature and water levels in the river (Doppler et al. 2007), a single value of 7.0 × 10⁻⁷ s⁻¹ was calibrated for the entire length of the river. The drainage constant affects the high flows and controls the speed with which the small streams drain groundwater (Sahoo et al. 2006). In the study area, the calibrated drainage constant was 5.0 × 10⁻⁶ s⁻¹, within the range of measured values.

For sand, till and bedrock units associated with wooded areas, the Manning roughness coefficient (n) was not calibrated. It was calibrated for clay areas to reproduce the maximum flow rates encountered during flood events. A high value was necessary to evacuate water rapidly through runoff from clay-covered areas. It is hypothesized that this rapid mobilization of water at the surface has a similar impact on river flow rates as that of the agricultural tile drainage system, which was not otherwise represented in the model. The calibrated value of 15 m^1/3 s⁻¹ appears to be realistic, since it is higher than that used for the wooded areas (1.7 m^/3 s⁻¹), and lower than that proposed for river flow (20.0 m^1/3 s⁻¹).

The infiltration fractions were also distributed spatially as a function of the geology of the top numerical layer. The values were calibrated to best represent the simulated heads. The infiltration fractions calibrated for the sand, till, clay and undifferentiated bedrock were 0.70, 0.42, 0.05 and 0.60, respectively (Table 1). These values are comparable to those obtained by Croteau et al. (2010) over a 39-year simulation of the Chateauguay River watershed. The infiltration fraction obtained here for the undifferentiated bedrock is slightly lower than that of Croteau et al. (2010).

The calibrated model was fine-tuned by modifying the monthly VI_net data to provide a better adjustment for spring flow rates. This was done by reducing the readily available rain that occurred during the winter months (November to March) by half. The other half was considered to be stored in the snowpack, to the made available during the spring snowmelt (April). This proportion of winter-available precipitation that was transferred instead to water available in the spring resulted from a manual trial-and-error process. This volume represents water that falls on snow and freezes without reaching the river. Considering that there is limited recharge over frozen soil, the snowmelt associated with winter thawing is thus redistributed to the spring flood.

The flow rates show limited sensitivity (<1 and > 0.1) to sand K (S_TOT  = −0.66), crystalline bedrock K (S_TOT  = −0.49), sedimentary bedrock S_y (S_TOT  = −0.32), clay K (S_TOT  = 0.26), sedimentary bedrock K (S_TOT  = 0.14), till K (S_TOT  = −0.14), the C_d coefficient (S_TOT  = 0.13), the r_l coefficient (S_TOT  = 0.10) and the n coefficient (S_TOT  = −0.10). The model shows almost no sensitivity to the other 10 parameters (S_TOT < 0.1 in all cases; Figure 6a). The heads are most sensitive to crystalline bedrock K (S_TOT  = 73) and sedimentary bedrock K (S_TOT  = −23), and, to a more limited extent, to sand K (S_TOT = −6.5) and clay K (S_TOT  = −1.3). The heads show limited sensitivity (<1 and > 0.1) to crystalline bedrock S_s (S_TOT  = −0.85), clay S_y (S_TOT  = 0.41), the n coefficient (S_TOT = 0.18), till K (S_TOT  = −0.17) and sand S_y (S_TOT  = −0.11). The model shows almost no sensitivity to the other 10 parameters (S_TOT < 0.1; Figure 6b). The apparently higher total sensitivity of heads to parameter variation, compared with the less sensitive flow rates, could be related to the fact that S_TOT is the sum of S_i values for five observation wells, whereas it is the sum of S_i values for only three flow rate measuring stations.

Figure 6. Absolute values of total sensitivity coefficients (S_TOT) with respect to (a) flow rates and (b) heads, corresponding to 5% parameter variation. Plus signs indicate a positive sensitivity, whereas no sign indicates a negative sensitivity.

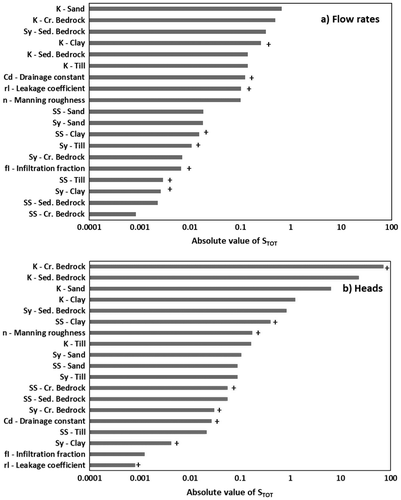
Positive total sensitivity values indicate a dominance of positive sensitivities (i.e. the head or flow rate increases when a parameter increases), whereas negative total sensitivity values indicate a dominance of negative sensitivities (i.e. the resulting head or flow rate increases when a parameter decreases). Interestingly, the total sensitivity can be positive for flow rates while being negative for heads (e.g. in the case of clay K). Again, this could be related to the fact that there are fewer flow rate measuring stations than observation wells.

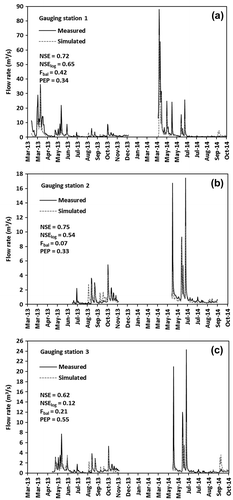
Simulated flow rates

The integrated model simulated measured flow rates at the three gauging stations relatively well, with NSE values of 0.72, 0.75 and 0.62 for stations 1, 2 and 3 respectively (Figure 7). The NSElog values of 0.65, 0.53, and 0.12 indicate that the low flows are well simulated at stations 1 and 2, but that they are less well reproduced at station 3. The minimum simulated flow rates at stations 1, 2 and 3 are 0.34, 0.21 and 0.04 m³ s⁻¹, respectively, compared to measured low flows of 0.40, 0.10 and 0.03 m³ s⁻¹. Although the minimum flow rate is underestimated at station 2, these simulated flow rates are of the correct order of magnitude.

Figure 7. Measured and simulated flow rates at gauging stations (a) 1, (b) 2 and (c) 3.

Positive Fbal values, 0.34, 0.07 and 0.21, for gauging stations 1, 2 and 3 respectively, indicate that the average flow rates are underestimated by the model at all three stations. The larger Fbal at station 1 is due to the significant underestimation of the spring flow rates in 2013 and 2014, which were measured only at this station. The PEP calibration criterion, which evaluates the quality of the flood simulation, was 0.42, 0.33 and 0.55 for stations 1, 2 and 3, respectively. This indicates that, on average, the five highest flow rates measured were underestimated at the three stations, and particularly at station 3.

During summer months when VI_net values are not equal to zero (i.e. VI ≤ ETR), the model does not simulate small flow-rate variations, such as those observed at the end of July 2013. The model also overestimates the flow observed in September 2013, while flows increase markedly between March and July of both years, as well as between September and November 2013, and in October 2014.

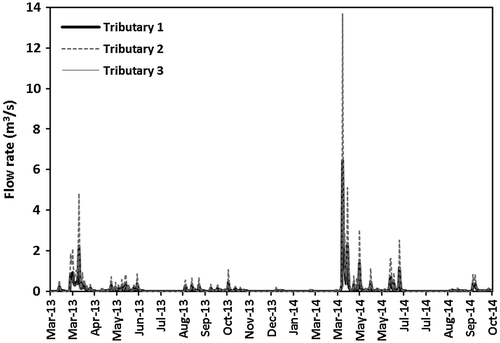
Flow rates at the outlets of the three tributaries were simulated in the same way as those in the Raquette River (Figure 8). They were found to vary significantly over the study period, between 0.002 and 6.46 m³ s⁻¹ for tributary 1, between 0.001 and 13.70 m³ s⁻¹ for tributary 2, and between 0.001 and 4.48 m³ s⁻¹ for tributary 3. Tributaries 1 and 3 have similar flow rates, while the peak flow rates are higher for tributary 2. All three tributaries have very low flows in July and August 2013 and 2014. The values simulated for August 2014 are of the same order of magnitude as the corresponding measured values: an average simulated flow rate of 0.002 m³ s⁻¹ compared to a measured value of 0.008 m³ s⁻¹ for tributary 1, an average simulated flow rate of 0.004 m³ s⁻¹ compared to measured values of 0.002 and 0.003 m³ s⁻¹ for tributary 2, and an average simulated flow rate of 0.001 m³ s⁻¹ compared to measured values of 0.002 and 0.004 m³ s⁻¹ for tributary 3. No flow rates were measured at the tributaries’ outlets at other times.

Figure 8. Simulated flow rates at the outlets of tributaries 1, 2 and 3.

Simulated heads

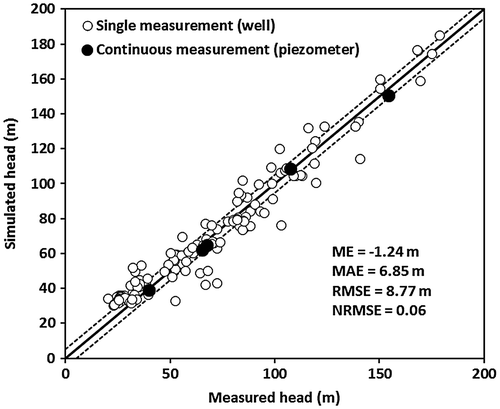
The average heads simulated with the calibrated model for the two years were found to adequately represent the 149 one-time measured heads in the Raquette watershed, and the average heads measured in the five observation wells (Figure 9). The ME of −1.24 m indicates no systematic over- or underestimation of heads, and the MAE of 6.85 m is of the same order of magnitude as the maximum head amplitude in the monitored observation wells (6.39 m at the crystalline bedrock well, PO4, on Mount Rigaud). The RMSE is 8.77 m and the NRMSE is 0.06, a value smaller than the 0.1 target value (Gallardo et al. 2005; Lutz et al. 2007). However, the largest simulated errors were not located in the crystalline bedrock of Mount Rigaud, but were found for Hudson Hill (−29.54 m) and for the eastern and northern extents of Mount Rigaud (−26.70 and −19.10 m, respectively). Some heads simulated for the plain north of Mount Rigaud, close to the Outaouais River boundary, are overestimated by approximately 12 m.

Figure 9. Measured and simulated steady-state heads. The thick black line is the 1:1 line and the dotted lines represent a +/− 5 m error envelope. ME - mean error, MAE - mean absolute error, RMSE - root mean square error, and NRMSE - normalized root mean square error.

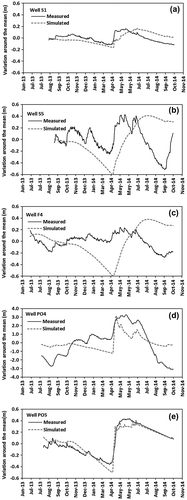
The transient heads simulated for the five observation wells were plotted relative to surface elevation to remove any errors related to topographical inaccuracies (Figure10). Head variations (timing and amplitude) at wells S1 and PO5 (unconfined conditions in sand deposits and in the sedimentary bedrock) were correctly simulated. The transient-state head simulations were of lower quality for wells S5 and PO4 (semi-confined conditions in the clay plain and unconfined condition in the crystalline bedrock), and were even poorer for well F4 (confined conditions in the clay plain). The low VI_net values used to simulate the winter seasons, followed by the large VI_net values at snowmelt, have a visible effect on the heads simulated at the five observation wells. This effect is apparent from the measured head time series at two unconfined wells, S1 and PO5. The F4 well tapping the confined aquifer in the clay plain south of Mount Rigaud does not exhibit either a winter decrease or a spring increase in heads. The semi-confined S5 well shows a winter decrease and a spring increase, which are well simulated in terms of timing, but overestimated in terms of amplitude. The simulated heads at the PO4 well in the crystalline bedrock of Mount Rigaud decrease slowly over the winter, compared with almost no measured head decrease, and increase more sharply at snowmelt than was measured in reality.

Figure 10. Measured and simulated transient-state heads at the five observation wells. Note that the vertical scale of the PO4 crystalline bedrock well is larger than that of the other wells.

Simulated groundwater discharge

The draining cells representing the streams in the model (see Figure 4 for locations) respond to the VI_net time series with maximal groundwater discharge during the spring melt and gradually decreasing discharge for the months with limited or no VI_net, corresponding to the gradually decreasing groundwater levels (Figure 11(a)). The streams located in the lower portion of the study area (between gauging stations 1 and 2) have the highest flow rates, with monthly values ranging between 0.052 m³ s⁻¹ (March 2014) and 0.136 m³ s⁻¹ (April 2014). Drained flow rates in the middle portion (between gauging stations 2 and 3) are much lower, ranging from 0.010 to 0.030 m³ s⁻¹. Above gauging station 3, the drained flow rates are very low throughout the year, except between snowmelt and early summer, when they vary between 0.001 and 0.015 m³ s⁻¹ in 2014. The very low drained flow rates in the higher portion of the study area reproduce the intermittent flow conditions observed in the small streams. Elsewhere in the study area, the draining cells remain active throughout the simulation period, indicating that the water table is generally higher than the drains.

Figure 11. Monthly simulated net vertical inflows (VI_net) and flows between gauging stations 1 and 2, between gauging stations 2 and 3, and above gauging station 3 for (a) drained flows and (b) baseflows.

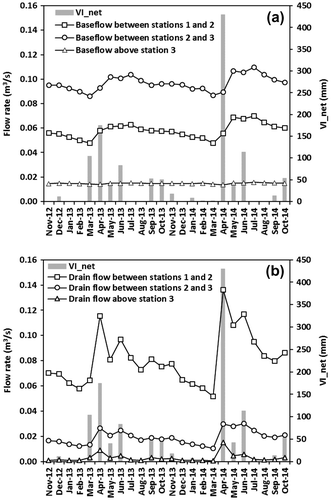
The groundwater flow contribution to the Raquette River reacted to VI_net similarly to the drained flows, albeit with a lower amplitude (Figure 11(b)). The central and lower portions of the simulated area responded similarly to VI_net, with reductions extending from mid-summer (August) to the end of winter (March) in the two simulated years. The rate of base flow reduction is relatively constant through time, notwithstanding positive VI_net months. The base flows increase in April and May, following the spring snowmelt, and are constant in June and July. In the lower portion of the watershed, the aquifer contributes with average monthly inflows of between 0.048 m³ s⁻¹ (March 2013 and 2014) and 0.070 m³ s⁻¹ (July 2014). The central portion of the river, between gauging stations 2 and 3, is where the aquifer contributes most to the river in the Sainte-Marthe Valley, with average monthly groundwater inflows of between 0.086 and 0.110 m³ s⁻¹. The aquifer contribution to the river upstream of gauging station 3 is relatively constant throughout the simulated period, on average 0.015 m³ s⁻¹.

Discussion

Model sensitivity

This work has shown that, for both flow rates and heads (see Figure 6), the model is less sensitive to S_s and S_y for sand, till, clay and bedrock than it is to K values for the same geological formations. This suggests that data acquisition aimed at developing an integrated flow model should prioritize the quantification of hydraulic conductivities, through pumping tests for example. The following calibration could be divided into a sequential process, starting with the calibration of K values to reproduce flow rates and heads, followed by a subsequent fine-tuning with calibration of S_s, S_y, r_l, C_d and n coefficients. It is important to highlight that the latter three parameters are rarely measured in the field, and are instead usually estimated from the scientific literature.

Interestingly, the sensitivity analysis showed that river flow rates are influenced by both hydraulic properties (K and S_y had S_TOT > 0.1) and surface flow parameters (r_l, C_d and n had S_TOT > 0.1). Heads are influenced mainly by hydrogeologic properties (K, S_s and S_y had S_TOT > 0.1), but are also influenced by the surface flow parameter, n (S_TOT > 0.1). This underlines the importance of using an integrated model (coupling surface flow and groundwater flow) that considers the hydraulic properties of the surrounding aquifers and the surface flow parameters when representing the water flow dynamics over the entire watershed.

The parameters to which flow rates and heads show almost no sensitivity (S_TOT < 0.1) represent more than half of all the calibrated parameters. As could be expected, these parameters of lesser importance include S_s and S_y values for some geological formations for the flow rates, and include the r_l and C_d coefficients, as well as the S_s and S_y values for some geological formations for heads. Interestingly, the f_I coefficient (infiltration fraction) had almost no effect on either flow rates (S_TOT = −0.0067) or heads (S_TOT = 0.0013). This indicates that this parameter, which should control the volume of water that infiltrates and flows through runoff, does not adequately represent the partition between these two processes. This is not to say that this partitioning is not important in integrated flow modeling, but a complete representation would probably reveal a greater impact of this process on flow rates and heads.

It is important to note that the model calibration was performed using a trial-and-error approach. Although this method can provide a reasonably well-calibrated model, using an automatic calibration approach might have identified a different parameter combination that would have provided a similar or even improved flow rate and head calibration.

Simulated flow rates and heads

Overall, the simulated flows were lower than the measured flows. For the frost-free period, from 1 April to 31 October 2013, the simulated total flow at station 1 was 256 mm, while the measured value was 380 mm. For the same period in 2014, the simulated and measured total flows were 385 and 557 mm, respectively. These discrepancies might be explained by the simplified representation of evapotranspiration and infiltration processes, which might have underestimated the available water in the model. They could also have been caused by the uncertainty of the rating curve for high flows at station 1. The high flows occur only during a short period of time in the March-to-May spring snowmelt and during large summer rain events. However, because they are much larger than the baseflows, they can result in an overestimation of the total annual flow. The maximum flow rate at station 3 (furthest up gradient) may have been higher than that at station 2 (middle) due to errors in the rating curves at these two gauging stations. Performing a simulation over a longer time period would also allow the model to be verified under a wider range of hydrological conditions.

Part of these simulation errors can be attributed to the simplified representation of VI_net. Because evapotranspiration is not simulated explicitly, the available water every month has been reduced using an evapotranspiration fraction. This results in large and intense rain vents being distributed uniformly over a month, which causes an underestimation of runoff and flow rate during and after precipitation events. This problem was noted by Jones et al. (2008), who reduced precipitation using a constant evapotranspiration fraction. In reality, during rain events, the evapotranspiration rate is one or many orders of magnitude smaller than the precipitation rate (Camporese et al. 2010). Moreover, the spatial variability of interception and evapotranspiration processes are overly simplified in the Raquette River model, and are not a function of land-use cover. Using the VI_net artifact to estimate available water for runoff and infiltration thus appears to be sound regionally, but is not entirely satisfactory. However, the alternative of using detailed information to represent different land-use covers would have added an unwarranted level of complexity to the model.

According to Furman (2008), using an infiltration fraction that is constant in time is less precise than explicitly simulating infiltration in the unsaturated zone, which produces a delay between infiltration and actual groundwater recharge, and considers soil water content in estimating the volume of water to runoff and infiltrate for each rain event. The simple approach used in this work instantaneously transfers a fraction of the rain to the saturated aquifer, not considering soil water content. During intensive rain events, this approach can significantly reduce the amount of runoff, which can lead to an underestimation of simulated peak flow rates in the river. Again, a complete representation of the infiltration processes might prove to more effectively fine-tune river flow rates and heads.

In the model, accelerated runoff with a low roughness coefficient has been used to mimic the role of agricultural drains (not represented explicitly in the model) that quickly discharge water following rain events. However, natural runoff is influenced by the topography, and is therefore not directly routed to streams, as would be the case for agricultural drains that are usually connected directly to streams and rivers. This may be another explanation for the underestimation of simulated flows, particularly in the clay plain upstream of the study area, where the slopes are very low.

The differences between measured and simulated flows could also be explained in part by differences between the estimated watershed boundary and the position of the model boundary (see Figures 1 and 4), as the actual catchment at station 1 covers an area of 133 km², while the simulated basin covers 118 km². However, this is expected to have a more limited effect on simulated flows than the above-mentioned causes. Longer time series over many years would provide further insight into what causes the differences between simulated and measured flow rates.

The adequacy of simulated flow rates at the outlets of tributaries 1, 2 and 3 could not be verified, because measurements were only available for the low-flow conditions encountered in August 2014. These low-flow conditions appear to be reasonable, and there is no indication that peak flows are over- or underestimated. In the absence of more measured flow rates, using a different numerical representation for these three tributaries (rivers with exchanged flows) compared to other, smaller streams (drains) might not be justified.

The simulated errors on the average simulated heads associated for the plain north of Mound Rigaud and close to the Outaouais River could be related to the use of a no-flow condition for the six lower layers of the aquifer. The impact of boundary conditions on simulated heads is a commonly reported problem (e.g. Sulis et al. 2011). For the Raquette River, this overestimation of heads in this part of the aquifer might have induced simulated baseflows that are higher than actual values, but this was not evidenced with available flow rate measurements. In the Raquette River model, tests performed with a constant head boundary condition on all 10 layers resulted in a lower error on heads in the vicinity of the Outaouais River. However, because there is no indication that groundwater enters the river below a 25-m depth, using a no-flow lower boundary appeared to be more realistic. In other areas, the overall error on the average simulated heads, especially for those above 75 m, which are exclusively from the crystalline bedrock, indicates that the spatially homogeneous hydraulic properties used in the porous equivalent model represent average values that do not reflect locally higher or lower values, due to the presence of flow in the fractured media.

The transient heads simulated at well F4, and to a lesser extent at well S5, decrease more rapidly and markedly than heads measured during the 2013–2014 winter months (November to March), indicating that the simulated aquifer releases too much water in this area during the snow-covered period. The overly simplified spatial distribution of storage coefficients may be the cause of this discrepancy, but this could not be overcome in the model without over-parameterizing, due to the availability of only five continuously measured piezometers. The simulated and measured heads at the PO4 crystalline bedrock well on Mount Rigaud vary much more in amplitude than those of the PO5 sedimentary bedrock well, located on the Saint-Lazare Hill. This is probably due to the fact that the storage coefficient of the crystalline bedrock (PO4 well) is smaller than that of the sedimentary bedrock (PO5 well). The use of a porous medium to represent the fractured (crystalline or sedimentary) bedrock aquifer could also explain part of the difference between measured and simulated transient-state heads. The complex geological setting of the study area, including low-K crystalline bedrock, highly transmissive sedimentary bedrock, high-K sand deposits and substantial clay deposits, contributes to the challenge of simulating transient-state heads.

Groundwater flow contribution to the Raquette River

Because they were obtained after a few days without precipitation events, the flow rates measured during the August 2014 low-flow conditions provide relevant information about the groundwater flow contribution to the Raquette River. The sharp increase in flow rates after station 8 could be due to a contribution from the aquifer through relatively permeable and heterogeneous materials within the clayey river bed deposits. That this inflow was contributed by the aquifer instead of drain flows was confirmed by the high ²²²Rn activities in surface water found in this portion of the river (Moreira 2016). In the Sainte-Marthe Valley, between stations 9 and 19, the relatively constant rate of flow increase indicates a similar level of connectivity between the river and the sand and bedrock aquifer, which outcrops along the reach where the river has eroded the clay deposits. The decrease in river flow between stations 19 and 20, and between stations 21 and 23, indicates that the river discharges water to the fluvio-glacial sand deposits in these areas.

The relatively limited variation in baseflow contributions to the river through time indicates that the simulated groundwater fluxes to the Raquette River are highly dependent on storage in the saturated aquifer, which apparently contributes a relatively constant groundwater flux to the river through the seasons. The absence of baseflow variation upgradient from station 3 reflects the limited aquifer connectivity in this area.

The simulated baseflows to the Raquette River are greatest between stations 2 and 3 (Figure 11(b)), corresponding with measured values. In August 2014, the measured baseflows in this reach varied between 0.03 and 0.15 m³ s⁻¹, while simulated values in the area are 0.10 m³ s⁻¹. Between stations 1 and 2, the simulated baseflows are 0.065 m³ s⁻¹, while measured values range between 0.15 and 0.21 m³ s⁻¹. This difference could be explained by the inflow of water from six streams flowing from Mount Rigaud to the Raquette River. Although their flow rates were not measured in the field, it is in this reach that the streams have the largest simulated contribution to the river (Figure 11(a)). In particular, this contribution could explain the increase in the measured river baseflows between stations 20 and 22, after the river has fed the aquifer over 1–2 km. Between stations 2 and 3, the model simulates very limited groundwater inflow to the river, which corresponds well with the measured values of August 2014. In light of these results, the spatial distribution of simulated groundwater contribution to the river appears reasonable along the Raquette River. The river leakage coefficient and the drainage constant can thus be considered well calibrated in their representation of measured values. However, it is possible that spatially variable river leakage coefficients and drainage constants would have provided more representative results. These parameters are known to vary in time and space following erosion and sedimentation processes, as well as with water temperature and levels (Blaschke et al. 2003; Doppler et al. 2007). In this study, not enough calibration data were available to make this fine-tuning relevant. At all three gauging stations, the model shows only limited changes in baseflows throughout the year (no variations at gauging station 3), but this could not be compared to measured baseflow values. Additional flow rate measurements during low flow at all streams would be useful to further validate the model.

Recommendations

This work has shown that some hydraulic and surface flow parameters have an impact on both simulated flow rates and simulated heads, highlighting the importance of using integrated models to study water flow at the watershed scale and to address issues related to integrated water management. Although this interconnected influence of processes on flows may not be universal, it is particularly important when a connectivity between rivers and unconsolidated aquifers exists in post-glacial environments, such as those found in the St. Lawrence Lowlands, elsewhere in southern Canada, and at similar latitudes around the world.

This work has also emphasized the importance of including a representation of unsaturated zone infiltration processes. This representation is available in models such as Mike SHE, but requires more parameterization efforts in order to describe soil and plant parameters, and evaporation processes. The results from this study point to the fact that these additional parameters are necessary to provide the fine-tuning needed to better represent the watershed reactions to rain events and snowmelt.

Including artificial drainage might also improve flow rate simulations. Tile drainage is widely used in the St. Lawrence Lowlands, even where soils are permeable. These drains are known to export significant volumes of water toward the streams, thus accelerating water transit time within a watershed. Although this still needs to be demonstrated more generally and beyond the local scale, tile drainage could also reduce groundwater recharge under given conditions at the regional scale. However, a rigorous simulation of artificial drainage would require additional exported drain flux measurements.

The relatively good simulation results indicate that the model is useful in is current state, even though uncertainties and limitations have been identified. However, if water managers are to use the model to estimate the impacts of land use and climate change, it needs to be calibrated and validated over a wider variety of hydrological and meteorological conditions. In this study, the model was calibrated over two relatively similar hydrological years. It is therefore recommended to revisit model calibration in a few years to refine its parameterization over extended conditions, making it more robust for management applications. Further model developments could also be considered, for example the simulation of nutrient transport through runoff, infiltration and tile drainage.

Conclusion

The objective of this work was to examine the challenges encountered when simulating surface water–groundwater interactions in a post-glacial environment, in order to guide their wider use for integrated water management. An available database was used to build an integrated 3D flow model for the Raquette River drainage area in the Vaudreuil-Soulanges region of southern Quebec (Canada). Simulated flows were compared to measured flow rates and heads from two hydrological years.

This work has shown that an integrated model based on data that are relatively easily available for southern Québec aquifers can provide reasonable estimates of current conditions. Some discrepancies were observed between observations and simulated results, with simulated total flows being lower than measured values, average heads having non-negligible errors in some areas, and simulated transient-state heads with amplitudes different from measured values at some wells. Possible improvements to the model include basing the model calibration on a longer period, including long-term calibrated rating curves and reducing the uncertainty in the rating curves, and including flow measurements of the tributaries from throughout the year. Using a complete representation of unsaturated zone processes and including the simulation of the agricultural tile drainage system could also contribute to reducing simulation errors.

The sensitivity analysis has underlined the importance of using an integrated model to simulate groundwater–surface water exchanges for integrated water management. Using the Raquette River integrated model to its full potential will require further development and long-term maintenance, which will necessitate new data. This would provide watershed managers with a robust model to assess the long-term implications of water-use and land-use planning under changing climate conditions.

Funding

This work was supported by the Ministère du Développement durable, de l’Environnement et de la Lutte contre les changements climatiques.

Acknowledgements

The authors would like to thank the Quebec Ministère du Développement durable, de l’Environnement et de la Lutte contre les changements climatiques (Quebec Ministry of Environment), the Vaudreuil-Soulanges regional county municipality, and the COBAVER-VS watershed agency, who contributed funding to this research. The authors also thank the private owners who allowed access to their land for water monitoring and water sampling.