Equifinality and automatic calibration: What is the impact of hypothesizing an optimal parameter set on modelled hydrological processes?

Abstract

Accepting the concept of equifinality may result in larger uncertainty associated with model predictions than that of the optimal parameter set paradigm. Despite the existence of uncertainty characterization methods, the semi-distributed hydrological model HYDROTEL has been used within the latter paradigm. What is the impact of hypothesizing an optimal parameter set? This paper focuses on the assesment of the impact of equifinality of calibration parameters with respect to modelled hydrological variables and indices, namely: (1) daily flows; (2) seasonal 7- and 30-day low flows, and maximum flow; (3) snow water equivalent (SWE); (4) shallow ground water variations; and (5) actual evapotranspiration. This assessment is presented for 10 southern Québec watersheds of the St. Lawrence River. The watershed models were calibrated and validated for 1982–1991 and 1991–2002, respectively. Automatic calibration was performed using the dynamically dimensioned search (DDS) algorithm based on the maximization of two objective functions (OFs): (1) the Kling–Gupta efficiency and (2) the Nash-log. DDS was executed to calibrate 12 hydrological parameters for one optimization trial for each watershed and each OF with a budget of 5000 model runs. To analyze parameter uncertainty and resulting equifinality, 250 sets of parameters were extracted from each trial run. Calibration performances for both OFs were between 0.75 and 0.95, while the selected 250 best sets of parameters had OF values differing by less than 1%. Results showed that the overall OF uncertainty was larger than the parameter uncertainty for all modelled processes except the SWE. Nevertheless, seasonal results suggested parameter uncertainty could be greater than OF uncertainty for specific seasons or years, although it was not possible to make a general outcome stand out. In particular for impact studies where the variables of interest are not daily flows but rather hydrological indices or variables, parameter uncertainty will need to be accounted for.

Accepter l’existence du concept d’équifinalité c’est reconnaître l’incertitude liée à l’existence d’une famille de solutions donnant des résultats de qualité similaire obtenus avec la même fonction objectif. Malgré l’existence de méthodes de caractérisations de cette incertitude, le modèle hydrologique HYDROTEL a été principalement utilisé jusqu’à maintenant selon le paradigme du calage optimal unique sans évaluer a posteriori les conséquences de ce choix. Cette étude propose d’évaluer l’impact du choix du jeu de paramètres optimisés sur certaines variables et indicateurs hydrologiques simulés, à savoir: (1) les débits journaliers; (2) les débits d’étiage à 7 et 30 jours et les débits maximum; (3) l’équivalent en eau de la neige (EEN); (4) les variations du contenu en eau du sol peu profond; et (5) l’évapotranspiration réelle. Dans ce contexte, HYDROTEL est mis en place sur 10 bassins versant du Québec méridional entre 1982 et 2002. Pour chacune des fonctions objectif (FO; Kling–Gupta efficiency et Nash-log) et chacun des bassins, l’algorithme dynamically dimensioned search (DDS) dispose d’un budget de 5000 répétitions pour optimiser les 12 paramètres de calage d’HYDROTEL sur 1981–1991. Ainsi, 250 jeux de paramètres sont conservés pour évaluer l’incertitude paramétrique et l’équifinalité résultante. Les résultats de calage indiquent des fonctions objectif comprises entre 0.75 et 0.95, tandis que pour chaque modèle les 250 meilleures répétitions présentent des fonctions objectif égales à 1% près. Globalement, pour tous les processus simulés excepté pour l’EEN, l’incertitude relative aux FO était plus importante que celle relative aux jeux de paramètres. Cependant, les résultats saisonniers suggèrent que l’incertitude paramétrique peut dépasser celle due aux FO dans certaines conditions particulières. Elle devra donc être prise en compte, en particulier pour les études d’impacts et de risque hydrologique dont les variables d’intérêt sont principalement des indicateurs hydrologiques simulés et non pas les débits journaliers.

Introduction

The equifinality concept refers to the existence of many parameter sets (and multiple model structures) associated with the same ‘optimal’ measure of efficiency (Beven and Freer 2001; Beven 2006a). Within a realistic parameter space, for a given mechanistic model of a complex environmental system, many local optima may exist. Despite the computational costs, equifinality has been revealed for many types of models and especially for rainfall-runoff models (Beven and Binley 1992; Duan et al. 1992; Beven 1993; Romanowicz et al. 1994; Li et al. 2012; Zhang et al. 2012; Linhoss et al. 2013; Fu et al. 2015; Futter et al. 2015; Prada et al. 2016; Zeng et al. 2016).

The main consequence of accepting the concept of equifinality is that the uncertainty associated with model predictions might be larger than that assessed within the optimal parameter set paradigm. Different types of approaches allow researchers to deal with such uncertainty (Vrugt et al. 2009a). Some approaches have their roots within a formal statistical (Bayesian) framework, but require in-depth understanding of mathematics and statistics as well as experience in implementing (Fisher and Beven 1996; Freer et al. 1996) these methods on computers (Vrugt et al. 2009b). This probably explains the success of the generalized likelihood uncertainty estimation (GLUE) method of Beven and Binley (1992). It operates within the context of Monte Carlo analysis coupled with Bayesian or fuzzy estimation and propagation of uncertainty. It is relativley easy to implement and requires no modifications to existing codes of simulation models. More recently, Tolson and Shoemaker (2007) presented how the dynamically dimensioned search (DDS) optimization algorithm coud replace random sampling in typical applications of GLUE. They also introduced a more efficent uncertainty analysis methodology called DDS-approximation of uncertainty (DDS-AU) that differs from the automatic calibration and uncertainty assessment using response surfaces (ACUARS) methods (Mugunthan and Shoemaker 2006). The former approach requires many optimization trials while the latter approach uses only one trial coupled with a declustering technique.

The idea of an optimal parameter set remains strong in environmental sciences and even stronger in hydrological modelling. For a physcically based, semi-distributed model such as HYDROTEL (Fortin et al. 2001b; Turcotte et al. 2003; Turcotte et al. 2007a; Bouda et al. 2012; Bouda et al. 2014), this frame of mind is rooted in two perceptions: (1) multiple feasible descriptions of reality lead to ambiguity and are possibly viewed as a failure of the modelling exercise (Beven 2006a); and (2) a manual search for an ‘optimum’ is already computationally expensive (Turcotte et al. 2003) while an automatic search may provide only a slight increase in model efficiency in comparison with the latter manual calibration (Bouda et al. 2014). This is why in the last decade, at the risk of avoiding important issues of model acceptability and uncertainty (Beven 2006a), HYDROTEL has almost always been applied within the optimal parameter set paradigm.

For example, in several studies (Fortin et al. 2001a; Quilbé et al. 2008; Minville et al. 2009; Khalili et al. 2011; Aissia et al. 2012; Rousseau et al. 2013; Fossey et al. 2015; Fossey and Rousseau 2016a, 2016b; Fossey et al. 2016; Oreiller et al. 2013), HYDROTEL has been manually calibrated following the four-step, trial-and-error, process-oriented, multiple-objective calibration strategy introduced by Turcotte et al. (2003). It has also been calibrated using the shuffled complex evolution algorithm (SCE-UA) designed by Duan et al. (1993) to find the optimal set of parameters while avoiding local optima (Ludwig et al. 2009; Ricard et al. 2013; Bouda et al. 2014; Gaborit et al. 2015; Trudel et al. 2016). But two exceptions emerge from the literature: Bouda et al. (2012) and Poulin et al. (2011) both used the SCE-UA algorithm to generate multiple parameter sets and assesed the uncertainty of hydrological modelling under the equifinality assumption. Poulin et al. (2011), based on one snow-dominated watershed, concluded that model uncertainty (conceptual models vs. more physically based models, for example) can be more significant than parameter uncertainty. Meanwhile, Bouda et al. (2012), from their work on two watersheds, stressed the need for further research that may lead to the implementation of a systematic uncertainty analysis in an operational hydrological forecasting system. Nevertheless, they both highlighted the need for additional validation of their results on additional watersheds.

It is important to mention that the technico-philosophical debate that began in 2006 (Beven 2006b, 2008) about the methods that should or should not be used to estimate the uncertainties associated with hydrological forecasting is beyond the scope of this paper. Indeed, the debate is still ongoing about the relative performances of formal (differential evolution adaptive metropolis [DREAM]) and informal (GLUE) Bayesian approaches in estimating the consequences of equifinality (Beven 2009; Vrugt et al. 2009b, 2009c), and about the multiple sources of uncertainty and non-stationarity in the analysis and modelling of hydrological systems (Beven 2016; Nearing et al. 2016). In this paper, equifinality is simply explored through the implementation of the automatic calibration algorithm DDS (Tolson and Shoemaker 2007), which has been reported to be superior to SCE-UA (Arsenault et al. 2014; Yen et al. 2016). This contribution builds on the work carried out on hydrological uncertainty to show in practical terms why equifinality needs to be taken into account, by answering one simple question taken out of the technico-philosophical debate: What are the consequences of not accounting for equifinality while calibrating HYDROTEL for an environmental impact study? Here, hydrological uncertainty (defined by the spread resulting from multiple calibrations) is assessed for five modelled hydrological variables and indices: (1) daily flows; (2) seasonal hydrological indices such as the 7-day low flow (7-d Qmin), 30-day low flow (30-d Qmin), and maximum flow (Qmax); (3) snow water equivalent (SWE); (4) shallow ground water content (GWC) variations; and (5) actual evapotranspiration (AET). Innovation resides in three elements. A calibration strategy close to that of manual calibration was used in order to demonstrate the need to account for equifinality in impact assessment studies aside from the technico-philosophical debate started in 2006. Moreover, using 10 watersheds across Québec avoided limiting the significance of the results to a specific region. Last, the relative importance of objective function (OF) uncertainty and parameter uncertainty was differentiated according to the variable being considered and its temporal scale (yearly or seasonal).

The next two sections of this paper introduce the modelled watersheds and the methods, the results and ensuing discussions. Throughout the paper, readers should keep in mind that the results do not aim at assessing the formal statistical uncertainty associated with the hydrological processes, but rather aim at showing the concrete consequences of equifinality on modelled hydrological processes.

Study area and data

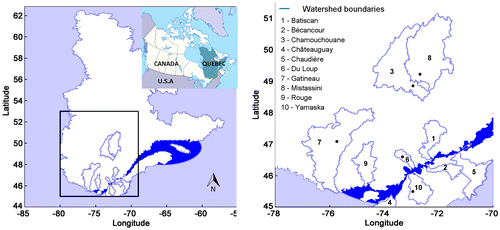
This study was carried out in southern Québec (Canada) on 10 watersheds spread out over five hydrographic regions of the St. Lawrence River (Figure 1). These 10 watersheds, namely (1) Batiscan, (2) Bécancour, (3) Chamouchouane, (4) Châteauguay, (5) Chaudière, (6) Du Loup, (7) Gatineau, (8) Mistassini, (9) Rouge, and (10) Yamaska, have modelled drainage areas ranging from 855 to 15,042 km², and various land cover patterns. Table 1 indicates that all of the watersheds but Yamaska have a forested (evergreen+deciduous trees) area covering more than 90% of the modelled land cover. Yamaska is the only watershed with a significant portion of urban area. Batiscan has over 40% evergreen while Gatineau, Chaudière, Rouge and Du Loup have 17, 21.5, 25.6 and 28.4% evergreen, respectively, and the remaining five watersheds have an evergreen area representing less than 10% of their total land cover. It is also noteworthy that Yamaska, Châteauguay, Bécancour and Chaudière have 21.1, 17.0, 8.2 and 3.9% cropland while the remaining six watershedshave less than 2%.

Figure 1. Location of the study watersheds in Québec, Canada, and around the St. Lawrence River.

Table 1. Land cover of the 10 studied watersheds in southern Québec, Canada.

Watershed	Evergreen		Dedicuous trees		Water		Urban		Cropland		Total
	km²	%	km²	%	km²	%	km²	%	km²	%
Batiscan	1816	41.9	2264	52.3	187	4.3	0	0	67	1.6	4334
Bécancour	255	9.7	2144	81.6	16	0.6	0	0	214	8.2	2629
Chamouchouane	817	5.4	13,156	87.5	1040	6.9	0	0	29	0.2	15,042
Châteauguay	112	5.0	1722	77.4	13	0.6	0	0	379	17.0	2227
Chaudière	1229	21.5	4206	73.4	71	1.2	0	0	223	3.9	5728
Du Loup	243	28.4	557	65.1	55	6.4	0	0	1	0.1	855
Gatineau	1159	17.0	5298	77.8	353	5.2	0	0	0	0	6810
Mistassini	569	6.1	8341	89.7	384	4.1	0	0	1	0	9295
Rouge	1401	25.6	3791	69.2	285	5.2	0	0	2	0	5480
Yamaska	23	1.7	2050	76.7	2	0.2	5	0.4	289	21.1	1389

According to available meteorological data (1981–2002, 1995 and 1996 being unavailable) from National Resources Canada, the region surrounding the St. Lawrence River delineated in Figure 1 is characterized by a mean annual temperature of 1.8°C and mean annual total precipitation of 940 mm. All watersheds are snow-dominated with peak flow occurring in spring. A summary of the hydroclimatic characteristics of the watersheds is provided in Tables 2 and 3 for two hydrological seasons, summer (1 June to 30 November) and winter (1 December to 31 May). While the mean summer rainfall is 545 mm and quite homogeneous among the watersheds (standard deviation of 30 mm), mean winter rainfall is more heterogeneous with a mean of 208 mm and a standard deviation of 64 mm. Meanwhile, mean snowfall is 271 mm with a standard deviation of 52 mm. Mean summer (10.8°C) and winter (−4.8°C) temperatures are also quite variable, with respective standard deviations of 1.8 and 2.8°C. This shows that in terms of climate characteristics, the studied watersheds are quite heterogeneous. In terms of hydrological characteristics, mean summer and winter daily flows are 1.2 and 1.9 mm, respectively, with standard deviations of 0.44 and 0.23. Winter flows are higher than summer flows on average because winter includes the snow melt and thus the spring peak flows. Higher variability in the summer flows is attributed to summer rainfall and convective storms that are more variable than snowfalls. The hydrological index mean values indicate that the watersheds, despite being located somewhat along the St. Lawrence River, have heterogeneous characteristics, with mean 7-d Qmin ranging from 2 to 156 m³ s⁻¹ for summer and from 4 to 120 m³ s⁻¹ for winter. Heterogeneity is even higher for mean Qmax, which ranges from 29 to 595 m³ s⁻¹ for summer and from 84 to 1350 m³ s⁻¹ for winter.

Table 2. Summary (1982–2002) of the climate characteristics of the study watersheds.

Watershed	Rain (mm)						Snow (mm)			Mean temp. (°C)
	Summer			Winter			Annual			Summer			Winter
	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max
Batiscan	337	558	645	97	180	403	286	356	416	8.4	10.3	11.5	−7.7	−5.4	−3.1
Bécancour	392	585	809	129	260	490	169	260	372	10.3	11.9	13.3	−5.0	−2.9	−1.0
Chamouchouane	293	518	690	85	131	248	219	290	383	6.4	8.6	10.0	−11.4	−8.7	−5.6
Chateauguay	402	512	620	174	269	429	137	193	252	12.4	13.8	15.2	−3.8	−1.1	0.9
Chaudière	421	590	794	179	253	392	216	266	316	9.5	11.2	12.5	−5.4	−3.3	−1.5
Du Loup	423	547	643	154	233	480	178	224	247	8.5	10.2	11.5	−7.5	−5.3	−3.0
Gatineau	324	519	671	86	145	242	224	290	350	7.9	9.7	11.4	−8.8	−6.4	−3.6
Mistassini	278	515	729	81	126	236	224	300	384	5.9	8.2	9.7	−12.0	−9.2	−6.1
Rouge	372	529	613	100	175	333	248	327	368	9.2	10.8	11.9	−6.9	−4.4	−2.0
Yamaska	476	577	743	180	305	526	122	204	294	11.6	13.1	14.5	−3.9	−1.5	0.6

Table 3. Summary (1982–2002) of the hydrological characteristics of the study watersheds.

Watershed	Q (mm/day)						Qmax (m^3/s)						7-d Qmin (m3/s)						30-d Qmin (m^3/s)
	Summer			Winter			Summer			Winter			Summer			Winter			Summer			Winter
	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max
Batiscan	0.9	1.6	2.4	1.4	2.1	3.1	140	265	528	349	558	837	17	31	57	18	24	35	22	37	72	19	26	43
Bécancour	0.6	1.1	1.9	1.5	2.1	2.9	69	203	402	296	494	848	2	7	21	7	120	402	3	10	32	8	13	21
Chamouchouane	1.1	1.8	2.6	1.2	1.5	1.9	404	781	1370	610	1350	2159	112	156	199	60	78	102	128	184	245	61	81	116
Chateauguay	0.3	0.6	1.3	1.1	1.8	2.6	27	168	623	193	460	1091	2	4	10	6	10	18	2	6	17	7	12	32
Chaudière	0.5	1.1	2.1	1.6	2.2	3.0	236	646	1318	847	1339	2140	4	10	26	12	19	32	5	17	45	14	23	47
Du Loup	0.3	0.8	1.3	1.0	1.6	2.3	12	29	79	55	84	130	1	2	6	3	4	5	1	3	7	3	4	6
Gatineau	1.0	1.5	2.4	1.1	1.7	2.5	202	425	1200	413	731	1500	19	38	56	20	32	46	21	50	92	22	34	48
Mistassini	1.2	1.9	2.7	1.3	1.7	2.3	314	595	959	604	1257	2050	58	92	129	27	39	67	70	119	159	28	41	76
Rouge	0.8	1.2	1.7	1.3	2.0	2.9	118	243	376	381	588	914	11	27	45	24	36	50	6	32	61	25	39	59
Yamaska	0.4	0.8	1.7	1.2	2.0	2.7	44	142	239	182	320	559	1	1	3	2	4	7	1	2	6	2	6	13

Material and methods

Hydrological model

HYDROTEL is a process-based, continuous, semi-distributed hydrological model (Fortin et al. 2001b; Turcotte et al. 2003, 2007a; Bouda et al. 2012; Bouda et al. 2014) that is currently used for inflow forecasting by Hydro-Quebec, Quebec’s major power utility, and the Quebec Hydrological Expertise Centre (CEHQ) which is in charge of the management and safety of publicly owned dams (Turcotte et al. 2004). It was designed to use available remote sensing and geographic information system (GIS) data and to use either a 3-h or a daily time step. It is based on the spatial segmentation of a watershed into relatively homogeneous hydrological units (RHHUs, elementary subwatersheds or hillslopes as desired) and interconnected river segments (RSs) draining the aforementioned units. A semi-automatic, GIS-based framework called PHYSITEL (Turcotte et al. 2001; Rousseau et al. 2011; Noël et al. 2014) allows easy watershed segmentation and parameterization of the hydrological objects (RHHUs and RSs). The model is composed of seven computational modules, which run in successive steps. Each module simulates a specific process (meteorological data interpolation, snowpack dynamics, soil temperature and freezing depth, potential evapotranspiration, vertical water budget, overland water routing, channel routing). Readers are referred to Fortin et al. (2001b) and Turcotte et al. (2007a) for more details on these aspects of HYDROTEL.

The main parameters of HYDROTEL can be subdivided into three groups (see Table 4). The first group includes the snow parameters and the second group includes the soil parameters. The last three individual parameters are related to the interpolations of temperature and precipitation according to the average of the three nearest meteorological stations weighed in by the square of the inverse distances between the RHHU and the three stations (also known as the reciprocal distance squared method).

Table 4. HYDROTEL key parameters.

Type	Parameters	Units
Snow parameters^a	MFEF – Melt factor for evergreen forests*	mm/d.°C
	MFDF – Melt factor for deciduous forests*	mm/d.°C
	MFOA – Melt factor for open areas*	mm/d.°C
	TEF – Threshold air temperature for melt in evergreen forests*	°C
	TDF – Threshold air temperature for melt in deciduous forests*	°C
	TOA – Threshold air temperature for melt in open areas*	°C
	Melt rate at the snow–soil interface	mm/d
	Compaction coefficient	–
Soil parameters^b	PETF – Potential evapotranspiration multiplication factor*	–
	z1 – Depth of the lower boundary of soil layer #1*	m
	z2 – Depth of the lower boundary of soil layer #2*	m
	z3 – Depth of the lower boundary of soil layer #3*	m
	RC – Recession coefficient*	m/h
	Extinction coefficient	–
	Maximum variation of soil moisture content	–
Interpolation coefficients	TSL – Threshold air temperature for partitioning solid and liquid precipitation*	°C
	Precipitation vertical gradient	mm/100 m
	Temperature vertical gradient	°C/100 m

^* Parameter calibrated in this paper.

^a For a complete description of snow parameters, the reader is referred to Turcotte et al. (2007a).

^b For a complete description of soil parameters, the reader is referred to Fortin et al. (2001b).

Data acquisition

Observed climate data for 1981–2002 were computed on a 0.75° × 0.75° grid by isotropic kriging following the method described in Poirier et al. (2012), using meteorological data provided by National Resources Canada. Each grid-point served as a meteorological station in HYDROTEL. Flow data were extracted from the CEHQ database, which operates around 230 hydrometric stations (CEHQ 2012). Stations were selected for their data availability and proximity to the outlets of the watersheds. For Batiscan (#050304 [−72.4° long., 46.6° lat.]), Bécancour (#024007 [−72.3° long., 46.2° lat.]), Châteauguay (#030905 [−73.8° long., 45.3° lat.]) and Rouge (#040204 [−74.7° long., 45.7° lat.]), stations were located at the outlet of each watershed, while for Chamouchouane (#061901 [−72.5° long., 48.7° lat.]), Chaudière (#023402 [−71.2° long., 46.6° lat.]), Du Loup (#052805 [−73.2° long., 46.6° lat.]), Gatineau (#040830 [−75.8° long., 47.1° lat.]), Mistassini (#062102 [−72.3° long., 48.9° lat.]) and Yamaska (#030304 [−72.9° long., 45.5° lat.]), the nearest stations were selected (see Figure 1).

Calibration/validation and parameter set generation

Model calibration on each watershed was carried out using a global optimization algorithm, DDS (presented in Tolson and Shoemaker 2007). It allows systematic and impartial calibration of HYDROTEL through all the watersheds using a fixed methodology. The shuffled complex evolution (SCE) algorithm (Duan et al. 1992, 1993, 1994) was also considered; it was viewed as the dominant optimization algorithm before 2007, with more than 300 different applications referring to the original set of SCE papers. However, it has since been proved that DDS is better suited for distributed watershed models requiring extensive computational time (Tolson and Shoemaker 2007; Arsenault et al. 2014; Yen et al. 2016). DDS performs a low number of model evaluations before converging to a good calibration solution. According to Yen et al. (2016), DDS outperforms other optimization techniques in both convergence speed and searching ability for parameter sets that satisfy statistical guidelines while requiring only one algorithm parameter (perturbation factor, default value 0.2) in the optimization process. This default value was used in this paper.

Automatic calibration was performed based on the maximization of four objective functions (OFs) computed from observed flow data: (1) Kling–Gupta efficiency (KGE); (2) Nash-log (that is, the Nash–Sutcliffe efficiency [NSE] calculated on log-transformed flows); (3) NSE_Q; and (4) NSE_√Q computed on root squared flows. DDS was executed for one optimization trial for each watershed and each OF with a budget of 5000 model runs – the trial was initiated from the same random set of parameter values for every watershed. To analyze parameter uncertainty and resulting equifinality, the 250 sets of parameters resulting in the best OF values were extracted from each trial run. Then each model was run over a validation period using the corresponding 250 sets of parameters (10 models × 4 OFs). However, this paper solely focused on two of the four OFs studied, namely KGE and Nash-log, because including the two other functions would not help in distinguishing the dominant type of uncertainty. Indeed, overall results for NSE are close to KGE results except around peak flows (Gupta et al. 2009), while NSE_√Q represents a tradeoff between KGE and Nash-log. Using the combination of KGE and Nash-log provides a contrasted calibration procedure that in turn favors high flows and low flows.(1)

where r is the linear correlation coefficient between simulated and observed values; α is a measure of relative variability in the simulated and observed values – that is, the ratio between simulated and observed standard deviations; and β stands for the bias – that is, the ratio between the mean simulated and mean observed flows.(2)

where α_log and r_log are the linear correlation coefficient and measure of relative variability between the log-transformed simulated and observed flows, respectively; and stands for the ratio between the bias of log-transformed simulated and observed flows, normalized by the standard deviation of observed values.

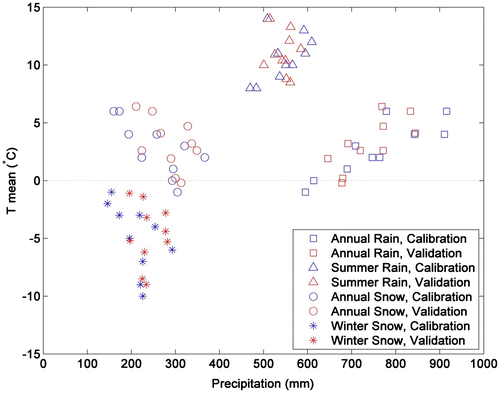
The calibration period extended from 1 December 1982 to 30 November 1991, i.e. 9 entire hydrological years. The validation period started on 1 December 1991 and ended on 30 November 2002; remembering that the 1995–1996 meteorological data series were unavailable (i.e. hydrological years 1994 – 1 December 1994 to 30 November 1995, and 1995 – 1 December 1995 to 30 November 1996 were unavailable), that is 8 complete hydrological years corresponding to nine summers and eight winters (January to the end of May 1997 is used as a spin-up to make sure that the model is on the right track). In each case, a 1-year spin-up period was used to minimize initialization errors. During the 1995–1996 meteorological data gap, the model was fed with data from 1993–1994 to prevent the rivers from drying out. These simulation periods (calibration and validation) followed the split-sample strategy applied to the available meteorological and hydrological data. The length of the calibration period was not so long as to increase computational costs too much, but not so short as to have issues related to the interannual variability of climate data compared with the validation period. Figure 2 illustrates the appropriateness of this approach in terms of mean annual and seasonal temperature and precipitation. For the calibration and validation, the simulation periods were relatively similar: precipitation and temperature are within [614, 911 mm] and [−1,+6 °C], and [646, 845 mm] and [−0.2, 6.4 °C], respectively.

Figure 2. Relationship between mean annual and seasonal temperatures and precipitation for the calibration and validation periods.

Out of the 18 key calibration parameters (Table 4), 12 were actually adjusted in this study: six snow parameters, five soil parameters, and one interpolation coefficient. Sensitivity analyses were not formally carried out for any of the watersheds beforehand, but these calibrated parameters are amongst the model’s most sensitive parameters (Turcotte et al. 2003). This selection of parameters was based on: (1) information provided by previous analyses (Ben Nasr 2014; Bouda et al. 2014); (2) knowledge built through the operational use of HYDROTEL (Turcotte et al. 2004); and (3) experience gained during the development of a Hydroclimatic Atlas conveying the potential impact of climate change on water resources for the 2050 horizon over Southern Québec (CEHQ 2013, 2015). The remaining parameters were fixed according to: (1) a regionalization study (Turcotte et al. 2007b); (2) results from the application of a global calibration strategy (Ricard et al. 2013) used in CEHQ (2013, 2015); and (3) previous manual calibration exercises.

Results

As previously mentioned, model uncertainty related to parameters used for the calibration of HYDROTEL and to the choice of the OF was assessed through five modelled hydrological variables and indices: (1) modelled streamflows, (2) hydrological indices computed from (1), and three internal variables, namely (3) SWE, (4) AET and (5) GWC variations. In this paper, parameter equifinality refers to the range that each calibration parameter covers within the predefined physical limits attributed to each parameter. Meanwhile, parameter uncertainty refers to the consequences of parameter equifinality with respect to the model outputs. Finally, OF uncertainty refers to the effects of using two different functions on the model outputs. For each subsection, a different watershed is used as a showcase; the other nine (and their related figures) are referred to as alternate watersheds (and alternate figures) and are available upon request from the corresponding author. This choice was made to focus on the global picture conveyed by this paper instead of focusing on the characteristics of a single watershed.

Parameter equifinality

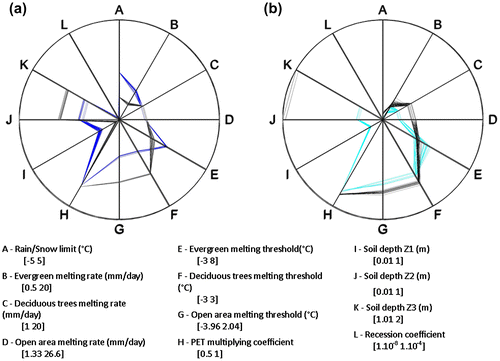
Figure 3 shows the range covered by the 250 sets of parameters used in setting up the 20 models in HYDROTEL. The figure was computed by putting together for each model a radar plot of the calibration parameter values. For every set of parameters, a line was drawn to link every individual parameter. The computation of the 250 lines made it possible to picture the range covered by the selected sets of parameters within a predefined physical interval that limits the automatic calibration algorithm. These limits were based on the information provided by previous sensitivity analyses, operational experience and previous calibration exercises.

Figure 3. Radar plots of the 12 parameters used in the automatic calibration of HYDROTEL for each study watershed. Parameter A is part of the interpolation coefficients, parameters B through G relate to the snow model, and parameters H through L relate to the soil group of parameters. The dark blue plots refer to the Kling-Gupta efficiency objective function (KGE OF) while the light blue plots refer to the Nash-log OF.

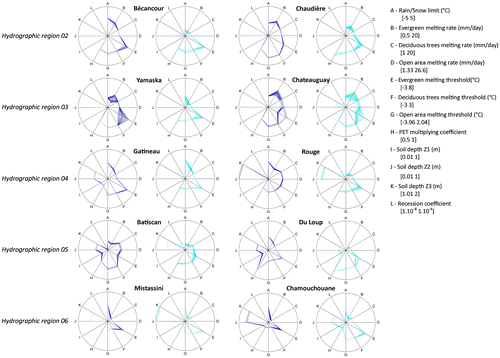
For most watershed models, the parameter equifinality is limited. Indeed, parameter equifinality for the Batiscan watershed, for the KGE OF, covers a maximum of 9.2% of the physical range for the deciduous melting threshold parameter (C in Figure 3), but about 5% for the rain/snow limit (A in Figure 3), for example. The maximum parameter equifinality is obtained for the evergreen melting threshold on the Yamaska watershed for the KGE OF with an equifinality covering 45.6% of the physical range. Overall, the ‘most equifinal parameters’ are the evergreen melting rate (B in Figure 3) and threshold (E in Figure 3).

Streamflows

Tangible evidence of the equifinality of the 20 models is displayed by the narrow ranges of OF values resulting from the 250 calibrations and validations. This was expected despite the careful consideration given to the number of calibration parameters used to avoid over parameterization and to limit the possibility of equifinality. Figure 4 shows the KGE and Nash-log values obtained in calibration and validation for the Chamouchouane watershed. KGE as well as Nash-log calibration values belong to equally narrow ranges: [0.9464, 0.9472] and [0.9064, 0.9072]. For the validation period, ranges are larger, but still quite narrow with 100% and 68% of KGE and Nash-log values fitting in the equally narrow ranges [0.8225, 0.8305] and [0.6340, 0.6420], respectively. Model performances are not as good in validation as in calibration. But as Table 5 shows, differences in performances exceed a 15% difference only 3 times for the 20 models. Moreover, the validation period performances either increase or decrease in comparison with calibration values, and that vouches for the split-sample strategy chosen. Indeed, Table 5 introduces the median loss of performances computed from the individual losses of each of the 250 calibrations/validations, which are different from what could be computed from Table 6.

Figure 4. Distribution of the objective function (OF) values for the Chamouchouane watershed: (a) Kling-Gupta efficiency (KGE) calibration period; (b) KGE validation period; (c) Nash-log calibration period; (d) Nash-log validation period.

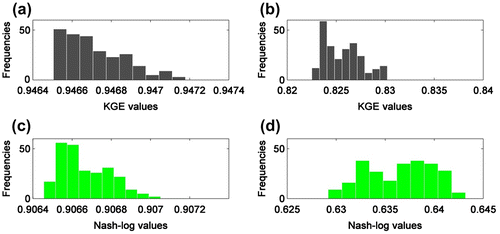
Table 5. Median of the KGE and Nash-log loss of performance (positive values) between the calibration and validation periods.

Watershed	KGE (%)	Nash-log (%)
Batiscan	15	14
Bécancour	8	−8
Chamouchouane	13	20
Chateauguay	11	−14
Chaudière	5	−6
Du Loup	16	1
Gatineau	15	0
Mistassini	8	18
Rouge	7	9
Yamaska	−1	−6

KGE: Kling-Gupta efficiency objective function.

Table 6. Summary of the KGE and Nash-log values for the 10 watersheds over the calibration and validation periods.

Watershed	Calibration						Validation
	KGE			Nash-log			KGE			Nash-log
	1st decile	Median	9th decile	1st decile	Median	9th decile	1st decile	Median	9th decile	1st decile	Median	9th decile
Batiscan	0.946	0.946	0.947	0.894	0.896	0.897	0.799	0.805	0.810	0.670	0.674	0.694
Bécancour	0.872	0.874	0.875	0.795	0.799	0.801	0.797	0.807	0.814	0.701	0.706	0.717
Chamouchouane	0.947	0.947	0.947	0.907	0.907	0.907	0.823	0.826	0.829	0.632	0.637	0.641
Chateauguay	0.859	0.860	0.860	0.767	0.768	0.768	0.763	0.767	0.775	0.692	0.695	0.699
Chaudière	0.916	0.916	0.916	0.805	0.810	0.815	0.869	0.871	0.875	0.695	0.709	0.721
Du Loup	0.944	0.945	0.945	0.842	0.842	0.842	0.792	0.796	0.802	0.700	0.703	0.704
Gatineau	0.907	0.907	0.907	0.827	0.828	0.828	0.766	0.768	0.771	0.684	0.686	0.691
Mistassini	0.955	0.955	0.956	0.904	0.905	0.905	0.873	0.875	0.876	0.646	0.652	0.660
Rouge	0.947	0.947	0.947	0.887	0.887	0.887	0.876	0.878	0.880	0.700	0.702	0.704
Yamaska	0.828	0.832	0.835	0.761	0.762	0.764	0.833	0.839	0.845	0.609	0.626	0.637

KGE: Kling-Gupta efficiency objective function.

Table 6 shows that results of Figure 4 are also valid for the alternate watersheds included in this paper. Indeed, for the calibration period, both KGE and Nash-log values can be constrained in a 0.01 interval, while for the validation period they are within a 0.15 interval. What is notable is that ranges seem larger for the Nash-log than for the KGE OFs. Also, the performances in calibration using the Nash-log OF are lower; whereas the mean of the KGE values is 0.916, the mean of the Nash-log values is 0.840. For validation, this gap widens with a mean KGE of 0.823 and a mean Nash-log of 0.679. This important difference may be attributed to the relative inability of Nash-log to represent high flows. Indeed, high flows are less correctly reproduced by Nash-log when low flows are assessed using the KGE OF. This explains the observed difference in performances.

The simulated streamflow envelopes shown in Figure 5 clearly illustrate parameter uncertainty with respect to the Rouge watershed. The hydrographs were computed according to the following steps: (1) for every 250 simulated flow series, mean values were generated for each day of the year, over the calibration period (9 hydrological years) and validation period (8 hydrological years); (2) then, for each model and simulation period, daily minimum and maximum values were taken from the entire set of mean series and plotted in order to obtain streamflow envelopes. As depicted in Figure 5 which introduces the individual streamflow uncertainty envelopes for the alternate watersheds, the impact of parameter uncertainty is:

•	Small (most of the time under 0.1 mm/day) for both simulation periods and OFs; and
•	Concentrated around the spring peak flow for the Nash-log OF (reaching a maximum of 1 mm/day).

Figure 5. Streamflow uncertainty envelopes for the Rouge watershed: (a) calibration (9-year mean) and (b) validation periods (8-year mean). The black and green envelopes stand for simulated flows under the Kling-Gupta efficiency (KGE) and Nash-log objective functions (OFs), respectively, while the blue line depicts the observed values.

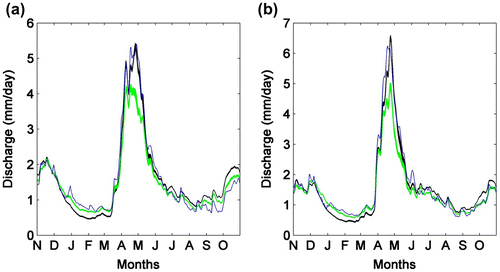
The OF uncertainty is shown by the global envelope that encompasses individual bands associated with the KGE and Nash-log series of modelled streamflows. Figure 5 and alternate figures show that OF uncertainty is more important than parameter uncertainty most of the year (except during the recession of the spring peak flow where the envelopes overlap). Moreover, the spread of the global envelope for the 10 watersheds reveals that OF uncertainty is generally more pronounced in the fall and the spring peak flows.

Hydrological indices

Figure 6 introduces, for the Chamouchouane watershed, the boxplots of the seasonal hydrological indices for each OF. The two boxplots per year represent the parameter uncertainty (250 sets of parameter) for the KGE and Nash-log OFs for each hydrological index. The union of the two boxplots represents the OF uncertainty. Results do not show the 30-d Qmin distributions as they are quite similar to the 7-d Qmin distributions, their median being just slightly greater and their interquartile range being similar.

Figure 6. Boxplots of the seasonal hydrological indices for the Chamouchaoune watershed for the calibration (1) and validation (2) periods: (as1) and (as2) display the distribution of the maximum summer peakflows; (aw1) and (aw2) the distribution of maximum winter peakflows; (bs1) and (bs2) the distribution of summer 7-day minimum flows; and (bw1) and (bw2) the distribution of winter 7-day minimum flows. The black and green boxplots illustrate the distribution of simulated flows under the Kling-Gupta efficiency (KGE) and Nash-log objective functions (OFs), while the blue dots depict the observed values. Outliers are represented by red crosses

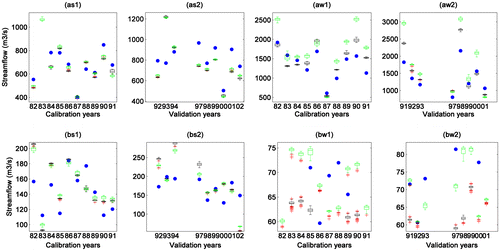
Figure 6 shows that the impact of parameter uncertainty is rather small during both simulation periods (calibration and validation). Indeed, for both OFs and both simulation periods, differences between the 1st and 3rd quartiles remain under 5% of the hydrological index values. Parameter uncertainty is more important for winter Nash-log hydrological indices than for KGE values, whereas they are comparable for summer indices. The impact of OF uncertainty is for all hydrological indices, for almost every year, and for both simulation periods this impact is more important than that of the parameter uncertainty. This is especially the case for winter 7-d Qmin and 30-d Qmin where the uncertainty is at least 5 times larger than the parameter uncertainty. This also applies to winter Qmax, where it is at least twice as important. The main findings characterizing almost all watersheds are the following:

•	Parameter uncertainty is: o Quite stable across years and simulation periods; o Smaller in summer than in winter, especially for Qmax; and o Similar for both OFs, both seasons and all hydrological indices (with a few exceptions related to the performance of the calibration).
•	OF uncertainty is: o Rather stable across years for every individual seasonal hydrological index; o More important than parameter uncertainty across the years, simulation periods and seasons; and o Larger in winter than in summer and more important for 7-d Qmin and 30-d Qmin.

Snow water equivalent

Figure 7 shows the SWE uncertainty envelopes for the Yamaska watershed for the calibration and validation periods as well as the two OFs. The envelopes were computed using the same method as that used for the streamflows, except that since HYDROTEL is a semi-distributed model, mean areal values over the RHHUs were first computed to produce a single data series for each calibrated parameter set and each simulation period.

Figure 7. Snow water equivalent (SWE) uncertainty envelopes for the Yamaska watershed: (a) calibration (9-year mean) and (b) validation periods (8-year mean). The black and green envelopes illustrate the distribution of soul water content variation under the Kling-Gupta efficiency (KGE) and Nash-log objective functions (OFs). The line indicates the period of overlapping between the uncertainty envelopes.

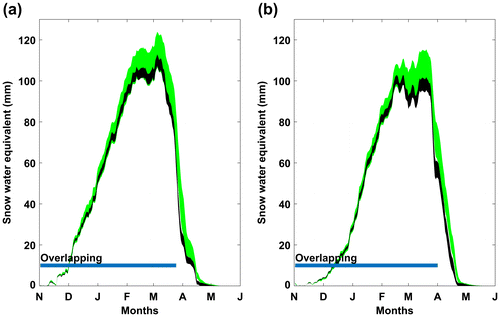
Figure 7 shows that parameter uncertainty relative to SWE is less important at the beginning and the end of the snow season, while reaching a maximum at the peak where the envelopes are the widest. OF uncertainty for SWE, contrary to that for streamflows, is less important than parameter uncertainty as the individual envelopes overlap almost the entire snow season. Parameter uncertainty is more important for the Nash-log OF than for the KGE OF. However, these observations cannot be generalized when examining in detail the results for the other watersheds. Nonetheless, the overall results can be separated into six groups:

(1)	For Yamaska and Chateauguay, the parameter uncertainty is larger than the OF uncertainty for the whole year, with individual envelopes being wider at the beginning of February and at the end of March. SWE is higher for the Nash-log OF than for the KGE OF.
(2)	For Chamouchouane and Mistassini, the parameter uncertainty is larger than the OF uncertainty for the whole year, with individual envelopes overlapping the entire year.
(3)	For Gatineau, the parameter uncertainty is larger than the OF uncertainty from November to the end of February. OF uncertainty then becomes larger than parameter uncertainty, with individual envelopes not overlapping anymore. Individual envelopes are quite narrow throughout the year and KGE simulated SWE is slightly more important than the Nash-log simulated values.
(4)	For Batiscan, results are similar to those of group (3), differing only in that individual envelopes become slightly wider, indicating a more important parameter uncertainty.
(5)	For Du Loup and Rouge, results indicate a larger OF uncertainty for the whole year, with narrow individual envelopes not overlapping. KGE simulated SWE values are more important than Nash-log values, with a maximum difference of 50 mm at peak values.
(6)	For Bécancour and Chaudière, results are similar to those of group (5), differing only in that individual envelopes become wider, indicating that parameter uncertainty is larger.

Actual evapotranspiration

Figure 8 depicts the seasonal AET for the Bécancour watershed obtained for both simulation periods and OFs. They were computed as the sum of AET over each hydrological year and season after applying the same methodology as that for the areal SWE in obtaining a single data series. Parameter uncertainty can be assessed through the amplitude of each boxplot, while OF uncertainty is assessed through the combination of the KGE boxplots (black) and Nash-log boxplots (green).

Figure 8. Seasonal actual evapotranspiration (AET) for the Bécancour watershed: (a) summer calibration; (b) summer validation; (c) winter calibration; and (d) winter validation. The black and green boxplots stand for simulated AET distributions under the Kling-Gupta efficiency (KGE) and Nash-log objective functions (OFs), respectively. Outliers are represented by red crosses. The superscripts w and d on the x-axis stand for the wettest and driest years of each simulation period, respectively.

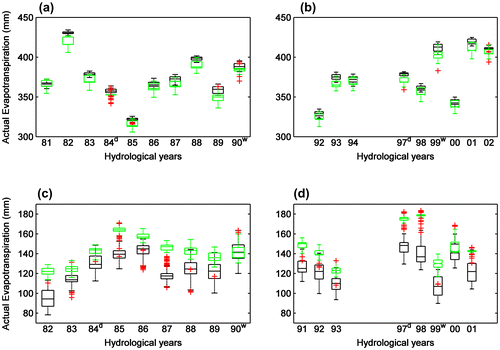
Figure 8 shows that parameter uncertainty for the summer season covers around 5% of the AET values for both simulation periods and OFs, but for winter it goes as high as 50%. For summer, OF uncertainty is less significant than parameter uncertainty for many years, as illustrated by the overlapping of the individual boxplots (1981, 1983, 1985, 1986, 1987, 1988, 1992, 1994, 1998, 2000 and 2002). Nevertheless, OF uncertainty is more important than parameter uncertainty for all years but winter 1990. Also, it is noteworthy that parameter uncertainty is less variable across years during summer than winter; indeed, the boxplots have the same width. Last, Nash-log parameter uncertainty is comparable to or larger than summer KGE parameter uncertainty, whereas it is the opposite for winter. However, these observations cannot be generalized when examining in detail the results of the other watersheds (alternate watersheds). Nonetheless, the overall results can be separated into six groups:

(1)	For Batiscan, Châteauguay, Du Loup and Yamaska, both types of uncertainty are constant across simulation periods, years and seasons. OF uncertainty remains around 5%, does not go beyond 10% of the simulated AET values and is more important than parameter uncertainty, while parameter uncertainty is similar for both OFs.
(2)	For Rouge, results are similar to those of group (1), differing only with respect to OF uncertainty being larger, around 10%, for both seasons of the simulation periods and all years.
(3)	For Gatineau and Mistassini, results are similar to those of group (2) but have a larger parameter uncertainty for Nash-log simulated values than for KGE values. This behavior is more pronounced in summer than in winter, and more so for Mistassini than for Gatineau.
(4)	For Chaudière, results are similar to those of group (2) but have an OF uncertainty that flirts with 20%.
(5)	For Chamouchouane, results are similar to those of group (1) because of the constant OF and parameter uncertainties. The difference is that OF uncertainty is nonexistent as individual boxplots overlap for all seasons, years and simulation periods. Parameter uncertainty related to the Nash-log OF is more important than that of KGE simulated values
(6)	For Bécancour, results were described in the previous paragraph and are different from the other groups as they display variability across years and seasons that other watersheds do not show.

The only result, apart from the relative consistency across the years highlighted in group (6), that stands across all watersheds except Bécancour in summer and Yamaska, is that simulated AET values are higher for all years and all seasons under the Nash-log OF. This is not a surprising result as it pertains to the nature of the OF with respect to the water balance. That is, if a smaller percentage of precipitation gets discharged through rivers (Nash-log vs. KGE), another way to balance the equation for HYDROTEL is to increase water output through evapotranspiration.

Shallow groundwater variations

Figure 9 shows the envelopes of areal GWC variations for the calibration and validation periods as well as the two OFs for the Du Loup watershed. The envelopes were computed using the same method as that used for the areal SWE.

Figure 9. Shallow groundwater content uncertainty envelopes for the Du Loup watershed: (a) calibration (9-year mean) and (b) validation periods (8-year mean). The black and green envelopes illustrate the distribution of simulated flows under the Kling-Gupta efficiency (KGE) and Nash-log objective functions (OFs), respectively.

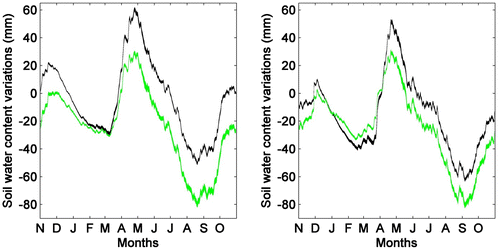
Figure 9 shows that parameter uncertainty is small and constant for both OFs throughout the whole year with a maximum uncertainty under 2 mm. On the contrary, OF uncertainty is substantial for the whole year (20 to 40 mm for the calibration period; 10 to 20 mm for the validation period), but between January and March. For this latter period, the shallow ground water reserves are at their lowest point and individual envelopes overlap during the calibration period or are close to overlapping during the validation period. However, these observations do not hold when examining in detail the results for the alternate watersheds. Nonetheless, the overall results can be separated into six groups:

(1)	For Rouge and Mistassini, the GWC variation patterns are similar to those of Du Loup. Maximum reserves are reached in early May after the snow has melted; they continuously decrease until early September where they reach their minimum, then increase until the end of the fall season in early December. Finally, they decrease again to a near minimum value around early March at the onset of melt season. OF and parameter uncertainties were described in the previous paragraph.
(2)	For Batiscan, results show similar GWC variation patterns to those of group (1). The difference lies in the parameter uncertainty that covers most of the OF uncertainty, but still remains under 10 mm. Indeed, for the calibration period, OF uncertainty is less important than parameter uncertainty from November until the end of September. For the validation period, the overlap is reduced to the period from December until the end of May. Still, even in the remaining months, OF uncertainty is less important than that of group (1), incidentally not getting larger than 20 mm.
(3)	For Chamouchouane and Gatineau, results show similar GWC variation patterns to those of groups (1) and (2), but behave almost like the opposite of group (1) with respect to OF and parameter uncertainties. OF uncertainty is non-existent for the whole year, except for a few days around peak value. Parameter uncertainty is small (less than 2 mm) and individual envelopes overlap.
(4)	For Bécancour, results show similar GWC variation patterns to those of group (1), apart from the decrease during the snow season that is less pronounced. Parameter uncertainty is more important for both OFs than that of group (1); it represents a maximum of 10 mm for both OFs in the calibration period, but around 5 mm and close to 10 mm, respectively, for Nash-log and KGE simulated GWC. OF uncertainty as a result is still more significant than parameter uncertainty despite a lag between the OFs that makes the individual envelopes overlap around peak flow values.
(5)	For Chaudière, results show similar GWC variation patterns to those of Bécancour (group (4)) but it is clearly different from any other watershed with respect to the OF and parameter uncertainties. The Nash-log parameter uncertainty covers almost all KGE values and has 40- and 20-mm wide intervals, respectively, for the calibration and validation periods. The KGE parameter uncertainty is less than 2 mm for the whole year, which results in a non-existent OF uncertainty for the calibration period while still being significant between August and December for the validation period.
(6)	For Chateauguay and Yamaska, the GWC variation patterns differ from those of groups (1) to (5). The GWC is at a minimum around the end of August. The reserves are then replenished from September until the end of November, before decreasing only slightly, as opposed to groups (1) and (2), during the snow season and attaining their maximum values after the snow has melted. Parameter uncertainty is small, under 2 and 5 mm for KGE and Nash-log simulated GWC, respectively, and relatively constant across the year. OF uncertainty is more important (maximum of 20 and 30 mm for calibration and validation, respectively) for the whole year, but just after peak value (May and June) for the calibration period and around peak value (April) for the validation period.

It is noteworthy that the two variation patterns relative to GWC, highlighted in the above groups, reflect the geographical location of the watersheds. That is, Bécancour, Châteauguay, Chaudière and Yamaska are located on the south shore of the St. Lawrence River, while Batiscan, Chamouchouane, Du Loup, Gatineau, Mistassini and Rouge are located on the north shore.

Discussion

Automatic calibration with DDS

In the Material and methods section, it is mentioned that DDS is better suited than SCE-UA (Duan et al. 1992, 1993, 1994) for distributed watershed models requiring extensive computational time and, thus, leading to a low number of model evaluations before converging to a good solution (Tolson and Shoemaker 2007; Arsenault et al. 2014; Yen et al. 2016). This is mostly due to DDS dynamically adjusting the neighborhood of the best solution by changing the dimension of the search (Tolson and Shoemaker 2007). In other terms, DDS mimics manual calibrations of watershed models as follows: (1) early in the calibration exercise, a number of model parameters are modified to overcome relatively poor solutions; and (2) later, to avoid losing the current gain in objective function values, parameters are modified one at a time. To avoid introducing a bias in the search algorithm, this paper used a random initial solution, but used the same random solution for every watershed in order to keep the experiments consistent.

The stochastic nature of DDS means that multiple optimization trials initialized with different initial solutions can terminate at different final solutions (Tolson and Shoemaker 2008). To be consistent with the framework described in the introduction, i.e. that a majority of the HYDROTEL application studies involved manual calibration, it was decided to work with only one optimization trial and a budget of 5000 model runs to answer the research question with respect to equifinality given this framework. Besides, the radar plots of parameter equifinality shown in Figure 3 do not seem to behave in a pattern related to the geographical location, the climate, or geological characteristics of each watershed. Indeed, the study watersheds are part of three different geological provinces (Thériault and Beauséjour 2012): (1) the Greenville Province made of allochthonous material north of the St. Lawrence River; (2) the St. Lawrence platform around the river; and (3) the Appalachian province made of Humber material south of the river. They also belong to three different climate classes defined by Litynski (1988), but mostly to class 14 that stands for moderate temperature, subhumid precipitation and a long growing season. As a consequence, parameter regionalization is not obvious. This was pointed out as well by Ricard et al. (2013), who showed that a global calibration strategy over southern Québec was preferable although in some cases the performances of watershed calibration using HYDROTEL was reduced when compared to local calibrations.

OF uncertainty

Overall, results for all the studied hydrological processes suggest that OF uncertainty is more important than parameter uncertainty. In other words, OF uncertainty is seen when the largest of the individual envelopes or boxplots relative to each objective function (KGE and Nash-log) is smaller than the union of either envelopes or boxplots. Readers should note that results obtained for the NSE_Q and NSE√Q OFs are in complete agreement with the previous statement. Figure 5 and alternate figures do not clearly show the impact of OF uncertainty because individual envelopes often overlap. However, when considering the seasonal hydrological indices (Figure 6 and alternate figures), the SWE (Figure 7 and alternate figures), the AET (Figure 8 and alternate figures), and the GWC (Figure 9 and alternate figures), OF uncertainty is overall clearly highlighted.

Some studies highlight the importance of model structure uncertainty over parameter equifinality (Poulin et al. 2011; Futter et al. 2015; Mockler et al. 2016; Shoaib et al. 2016). Poulin et al. (2011) used HYDROTEL and HSAMI to assess the effects of model structure and parameter equifinality on the uncertainty related to hydrological modelling. Their study revealed that the impact of hydrological model structure was more significant than the effect of parameter uncertainty (assessed through 68 sets of parameters). Yet the uncertainty attributed to model structure with respect to streamflows and SWE was of the same order of magnitude as the OF uncertainty assessed in this paper. This would mandate the combination of the two studies to clearly assess whether the impacts of model structure and OF uncertainty are equivalent or complementary in assessing the consequences of considering the effects of equifinality on modelled hydrological processes.

Figure 6 and alternate figures showed the boxplots of the seasonal hydrological indices for both OFs (see Results section). They also indicated observed values as blue dots; less than 50% of the latter are not included within the interval of the simulated values for any of the hydrological indices (Qmax, 7-d Qmin and 30-d Qmin). This could be seen as a calibration performance issue, but results suggest otherwise. Indeed, all observed values are included within the interval of the simulated values for the summer 7d-Qmin for the Châteauguay watershed while all but one observed values are included for the Yamaska watershed (refer to Table 6). This would suggest rather that KGE and Nash-log OFs are not able to force the model to represent the hydrological indices properly. This may be related to the nature of both OFs that are computed over daily data vs. hydrological indices computed over a period of time (7 and 30 days for 7-d Qmin as well as 30-d Qmin, respectively). However, for Qmax, this is simply related to the misrepresentation of maximum flows. This result is rather important as hydrological indices are often used in impact assessment studies. This would mandate the use of specific OFs related to low or high flows, or even the use of multi-objective functions.

Parameter uncertainty

Despite the fact that the OF uncertainty is overall more important than the consequences of parameter equifinality, parameter uncertainty relative to SWE (see Results section) is generally more important than OF uncertainty. Indeed it is more important for the whole year for Châteauguay, Chamouchouane, Mistassini and Yamaska, and for a few months (November until the end of February) for Gatineau and Batiscan. Seasonal results also suggest that parameter uncertainty can be important or more significant even than OF uncertainty for specific seasons or years (Figure 6, Figure 8 and alternate figures). To get a better understanding of the reasons why parameter uncertainty would prevail only for a few years, driest and wettest years were defined as the hydrological years with the least total amount of precipitation for the simulation periods (indicated on the x-axis of seasonal hydrological indices and AET figures as d and w). The effects of driest and wettest years were assessed in terms of prevalence of any of the two types of uncertainties and magnitudes of uncertainties on both types of years, but also on the following year. Nothing particular stood out that could be construed as a general result that could have given insights about the evolution of the prevalence of the two types of uncertainties in the following years. To get this type of insight, it would probably be necessary to perform calibrations under different sets of contrasting conditions (dry vs. wet years). This refers to parameter identifiability as researched by Wilby (2005) on snowless watersheds, or to the application of testing schemes such as those performed by Seiller et al. (2012) and inspired by KlemeŠ (1986).

Parameter equifinality

Ben Nasr (2014) as well as Bouda et al. (2014) pointed out, in sensitivity analyses carried out for two snow-dominated watersheds in southern Québec (Beaurivage and Montmorency modelled using HYDROTEL), that the depth of the lower boundary of the three soil layers (z1, z2, z3), the potential evapotranspiration multiplying factor (PETF), and the recession coefficient (RC) were consistently amongst the most sensitive parameters (refer to Table 4). In both studies, sensitivity was assessed from an initial optimal solution and parameter values were modified (± 25%), but variations of ± 6.25% already gave substantial flow modifications. These results are within the same order of magnitude as the equifinality measured through the proposed methodology, and explain why some parameters in Figure 3 are more equifinal than others. Typically, parameters that were identified by Ben Nasr (2014) and Bouda et al. (2014) as the most sensitive parameters are less equifinal than others. This result is not surprising as it pertains to the following statement: The more sensitive a parameter, the less uncertain it can be around a global optimum for the OF to remain optimum.

The choice to work with 5000 model runs ensured that the OF values remained within a 0.01 interval (refer to Table 6) for 250 sets of parameters that captured parameter equifinality. Working with 500 sets of parameters did not provide a larger parameter equifinality, nor did working with 100 sets of parameters provide the complete parameter equifinality. This is important as Poulin et al. (2011) reported that parameter uncertainty increases with increasing numbers of calibration parameters and/or calibrations. This allows the current authors to go beyond their research in making sure that the present conclusions cannot be disputed with respect to the impact that parameter equifinality has on global or individual uncertainty envelopes.

To make sure that working with one optimization trial did not impair the possibility of capturing the equifinality of the parameters, the smallest watershed model in terms of modelled area (to minimize computational time) with the smallest parameter equifinality was calibrated for another 5000-simulation-optimization trial started at a different initial random solution. As shown in Figure 10, this demonstrates that parameter equifinality can be increased if the calibration methodology is modified. Nonetheless, the covered part of the physical range does not come close to the maximum equifinality obtained for the Yamaska watershed in Figure 3. Thus, it can be assumed that the results introduced in this paper would not be drastically modified by a change in the calibration methodology. Plus it would contradict the choice made not to conduct a formal uncertainty analysis, as this methodology of using two or more optimization trials would get closer to the DDS-AU methodology introduced by Tolson and Shoemaker (2008).

Figure 10. Radar plots of the 12 parameters used in the automatic calibration of HYDROTEL for each study watershed. Parameter A is part of the interpolation coefficients, parameters B through G relate to the snow model, and parameters H through L relate to the soil group of parameters. Figure (a) refers to the Kling-Gupta efficiency (KGE) objective function (OF), and (b) to the Nash-log OF. The dark and light blue data refer to the first optimization trial of Figure 4; black data indicate the second optimization trial.

To summarize, it could be said that this paper shows the consequences of the existence of many good sets of parameters for modelled hydrological processes around a global optimum rather than properly evaluating their formal statistical uncertainty. If that were the aim, the methodology would have entailed working with one optimization trial per set of parameters, which would have resulted in a total of 125,000 simulations (250 sets of parameters * 500 simulations) since DDS typically needs 500 simulations to find a good global solution (compared to 10,000 for SCE-UA). Note that the computing time for a 10-year calibration period (with a prior 1-year spin-up) of one optimization trial of 5000 simulations already took an average of 45 h (on a 64-bit computer with a quad-core 2.53 GHz processor) for each watershed and every OF, resulting in a total calibration time of 900 h or 37.5 days (45 h * 10 watersheds * 2 OFs) for the results presented in this paper (excluding the two OFs that were left out of this paper).

Conclusion

In the last decade, HYDROTEL has almost always been applied within the optimal parameter set paradigm at the risk of avoiding important issues such as model acceptability and uncertainty (Beven 2006a). This paper builds on the work carried out on hydrological uncertainty by assesing the impact of equifinality and OF-related uncertainty on five modelled hydrological variables and indices: (1) daily flows; (2) seasonal hydrological indices (7-d Qmin, 30-d Qmin, and Qmax); (3) snow water equivalent (SWE); (4) shallow ground water content (GWC) variations; and (5) actual evapotranspiration (AET). This assessment was carried out for 10 watersheds spread out over five hydrographic regions of the St. Lawrence River, and spread out across southern Québec (Canada).

Overall, as indicated in Table 7, the results for all of the studied hydrological processes but the SWE suggest that OF uncertainty is more important than the uncertainty arising from parameter equifinality. This would mean that within the context of a study with a limited budget, it would be advisable to prioritize using different objective functions rather than using many sets of optimal parameters. This result is rather important as it reinforces the choice made in the last decade with HYDROTEL. Nonetheless, parameter uncertainty with respect to SWE is more important than OF uncertainty for eight of the 10 studied watersheds, for 4 to 7 months of the year (snow season less than 7 months long). Plus, despite satisfactory performances for both simulation periods, parameter uncertainty with respect to streamflows is rather small during the whole year, except around spring peak flow, while OF uncertainty is generally more pronounced in the fall and during the spring peak flows. Overall, this shows that one type of uncertainty or the other is rather significant during half of the year. Seasonal results with respect to hydrological indices and AET also suggest that parameter uncertainty can be important, or more significant, even, than OF uncertainty for specific seasons or years. These results are of the utmost importance for impact assessment studies where the variables of interest are not solely the daily flow data used for calibration, but rather hydrological indices or internal variables. This would mean that parameter uncertainty does need to be taken into account or at least needs to be further researched to better understand the mechanisms behind the phenomena. This study demonstrates, using a substantial set of watersheds, that aside from the technico-philosophical debate started in 2006, equifinality is not too technical to take into account and has a tangible, significant effect on the uncertainties associated with modeled hydrological processes. As such, future work should systematically include equifinality by using at least two sets of equifinal parameters without forgetting to assess OF uncertainty.

Table 7. Dominant type of uncertainty for each study watershed for the five modelled hydrological variables.

It is noteworthy that the methodology applied in this paper for the HYDROTEL model can be replicated for other hydrological models. Uncertainty associated with OFs and parameter equifinality still needs to be better understood and studied. To improve the understanding of HYDROTEL, and other physically based hydrological models, future work should focus on identifying or using OFs tailored for hydrological indices relevant to impact assessment studies. Finally, for a specific assessment, there is a need to consider as well the question of the uncertainty associated with model structure.

Acknowledgements

The authors would like to thank Marco Braun of Ouranos (Consortium on Regional Climatology and Adaptation to Climate Change, Montreal, QC, Canada), for his scientific support as well as giving us access to the meteorological data; the Quebec Hydrological Expertise Centre (CEHQ) for allowing us to use parts of their modelling platform; and especially Simon Lachance Cloutier for his technical support, and Sébastien Tremblay of INRS (Centre Eau Terre Environnement) for his computer support throughout the project. Financial support for this project was provided by the Natural Sciences and Engineering Research Council (NSERC) of Canada through the Discovery Grant Program (A.N. Rousseau, principal investigator).