A nonstationary peaks-over-threshold approach for modelling daily precipitation with covariate-dependent thresholds

Abstract

The estimation of extreme precipitation events is a topic of growing interest and concern, particularly in highly urbanized areas. The Fifth Assessment Report by the Intergovernmental Panel on Climate Change (IPCC) reported that land-surface air temperatures have increased and that more extreme precipitation events are expected in a warmer climate. Hydrometeorological data often display nonstationary characteristics in a changing climate, prompting numerous studies worldwide. This research proposes a peaks-over-threshold (POT) approach using both stationary and covariate-dependent nonstationary thresholds (bivariate and multivariate models). The generalized Pareto (GP) distribution is fit to threshold exceedance data, which accounts for potential nonstationarity in the variability of the extreme events. The analysis herein focuses on coastal British Columbia (BC), which includes the Greater Vancouver Regional District (Metro Vancouver), due to the potential impacts of climate change in the region. Results from quantile estimates and an uncertainty analysis indicate that in the winter and summer months, there is stronger evidence of stationarity in 50-year quantiles. A trend analysis is also performed on the magnitude and frequency of POT events for winter and summer for two time periods (1976–2014 and 1986–2014). Results of this analysis indicate that globally significant trends are found in the threshold exceedance and frequency of peak events data.

L’estimation des événements de précipitations extrêmes est un sujet d'intérêt et de préoccupation croissant, en particulier dans les zones fortement urbanisées. Le cinquième rapport d’évaluation du Groupe d’experts intergouvernemental sur l’évolution du climat (GIEC) a signalé que les températures de l’air à la surface du sol ont augmenté et que des précipitations plus extrêmes sont attendues dans un climat plus chaud. Les données hydrométéorologiques présentent souvent des caractéristiques non stationnaires dans un climat changeant, ce qui a donné lieu à de nombreuses études dans le monde entier. Cette recherche propose une approche de point plus de seuil en utilisant à la fois des seuils non stationnaires et dépendants des covariables (modèles bivariés et multivariés). La distribution de Pareto généralisée est adaptée aux données de dépassement de seuil, ce qui explique la non-stationnarité potentielle de la variabilité des événements extrêmes. L’analyse présentée ici porte sur la côte de la Colombie-Britannique, qui comprend le district régional du métro Vancouver, en raison des impacts potentiels du changement climatique dans la région. Les résultats des estimations quantiles et une analyse de l’incertitude indiquent que pendant les mois d’hiver et d’été, il y a des preuves plus fortes de la stationnarité dans les quantiles de 50 ans. Une analyse des tendances est également effectuée sur l’ampleur et la fréquence des événements POT pour l’hiver et l’été pour deux périodes (1976-2014 et 1986-2014). Les résultats de cette analyse indiquent que des tendances globalement significatives sont trouvées dans le dépassement du seuil et la fréquence des données sur les événements de pointe.

Introduction

Intensifications of the magnitude and/or frequency of severe precipitation events could result in more extensive and frequent flooding and can have far-reaching socioeconomic consequences in highly populated or urbanized areas. For example, the widespread 2013 Alberta, Canada, floods affected approximately 100,000 residents, resulted in four deaths, and caused US$5.7 million in damages (EM-DAT 2016). The Fifth Assessment Report by the Intergovernmental Panel on Climate Change (IPCC) states that global land-surface air temperatures have increased and that increases in extreme precipitation are consistent with a warmer climate (Hartmann et al. 2013). Hartmann et al. (2013) also note that there is convincing evidence of increases in the frequency and intensity of heavy precipitation in North America. Therefore, the potential for nonstationarity in the magnitude and frequency of extreme precipitation events is of paramount concern. Additionally, with the assertion by Milly et al. (2008) that ‘stationarity is dead’, the time-independence of the statistics of historical rainfall records is brought into question.

Hydrometeorological quantile estimates for low-frequency, high-magnitude events are essential for civil infrastructure design. For instance, several Canadian provinces have imposed guidelines requiring that stormwater infrastructure adequately contain/convey runoff from a 100-year rainfall event (Stephens et al. 2002; Ontario Ministry of the Environment [OME] 2008). Standard statistical techniques assume data to be independently and identically distributed (IID), meaning the data arise from the same statistical probability distribution (Katz et al. 2002). This assumption is not valid in the presence of nonstationarity, thus establishing a need for covariate-dependent approaches in a changing climate. Estimating hydrometeorological extremes in a changing climate has henceforth become a topic which has gained a great deal of interest (Kharin and Zwiers 2005; Nadarajah 2005; El Adlouni et al. 2007; Hundecha et al. 2008; Sugahara et al. 2009; Rajagopalan 2010; Villarini et al. 2010; Beguería et al. 2011; Burn et al. 2011; Ouarda and El-Adlouni 2011; Villarini et al. 2011; Gilroy and McCuen 2012; Roth et al. 2012; Tramblay et al. 2013; Li and Tan 2015).

The extremes within hydrological data can be characterized in a variety of manners. Two commonly used techniques include the block maxima series and the partial duration series, or peaks over threshold (POT). The block maxima series is comprised of the largest peak value of a data set in a predetermined block length, typically selected to be 1 year and resulting in the annual maximum series (Katz et al. 2002). This research adopts the POT technique, in which all values that fall above a suitably high threshold are retained for analysis (Coles 2001). In addition to the peak annual data, this method facilitates the inclusion of supplementary extreme events in wet years. The timing of exceedances of a sufficiently high threshold are frequently modelled using a homogeneous Poisson process, while excesses over the threshold are commonly modelled using the generalized Pareto (GP) distribution, typically referred to as the Poisson–GP model (Khaliq et al. 2006). The GP distribution parameters may, however, be characterized by temporal covariates (Renard et al. 2006; Sugahara et al. 2009; Kyselý et al. 2010; Beguería et al. 2011; Roth et al. 2012; Tramblay et al. 2013; Sungwook et al. 2016) including the use of a nonhomogeneous Poisson process with the inclusion of a covariate-dependent intensity parameter (Katz 2010; Beguería et al. 2011). A number of studies have focused on modelling nonstationarity in the selected threshold (Kyselý et al. 2010; Northrop and Jonathan 2011; Roth et al. 2012; Jonathan, Ewans, et al. 2013; Jonathan, Randell, et al. 2013, 2014; Roth et al. 2014), but to the authors’ knowledge, none has developed a goodness-of-fit technique for selecting the most appropriate stationary or nonstationary threshold/GP model combination. Furthermore, this study addresses the confounding issue of time dependence and large-scale ocean–atmosphere phenomena in nonstationary threshold selection.

The purpose of this study is to assess nonstationarity in both threshold models and GP distribution parameters to determine those models that provide superior goodness of fit and less uncertainty for the purpose of quantile estimation. Through this POT analysis a combination of bivariate and multivariate (linear and quadratic) covariate-dependent threshold models are evaluated. This research focuses on coastal British Columbia (BC), Canada. Extreme precipitation is associated with numerous hazards in the area, including flooding and landslides (Walker et al. 2008). With approximately 75% of BC’s population living in coastal BC, primarily in Metro Vancouver (Walker et al. 2008), research of this nature is required to determine the magnitude and potential changes in extreme precipitation events that may be expected in one of Canada’s most populated regions.

The Rocky Mountains act as a barrier to arctic air masses, giving rise to mild seasonal temperatures in coastal BC (Hare and Thomas 1979). Although the area is one of the highest seismic activity zones in Canada (Chang et al. 2012), extreme weather events are the foremost hazard, affecting British Columbians more than any other climate hazard (Walker et al. 2008; Moore et al. 2010). The climate in southern BC is influenced by the El Niño Southern Oscillation (ENSO) and the Pacific Decadal Oscillation (PDO), both of which are large-scale ocean–atmosphere phenomena (Walker et al. 2008). Several indices are used to describe ENSO; the Niño 3.4 index is used herein. The Niño 3.4 index is a measure of the area average sea surface temperature (SST) from 5°S–5°N and 170°E–120°W (Rayner et al. 2003). The PDO Index is the leading principal component of the North Pacific monthly sea surface variability (poleward of 20°N; Mantua et al. 1997).

Methodology

A POT approach is developed for the analysis of hydrometeorological data using stationary and nonstationary thresholds in which the resulting threshold exceedance data are modelled using the GP distribution. Trend detection is carried out on stationary threshold exceedance data using the Mann–Kendall nonparametric trend test (Mann 1945; Kendall 1975) on total daily precipitation and rainfall frequency.

Climate oscillation selection

Due to the potential influence of both ENSO and PDO on coastal BC’s climate, the correlation between both of these climate indices and the precipitation data is assessed (Gershunov and Barnett 1998; Walker et al. 2008). The Niño 3.4 Index is obtained from the National Oceanic & Atmospheric Administration – Earth System Research Library (NOAA-ESRL) Physical Sciences Division (https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Data/nino34.long.anom.data), while the PDO Index is retrieved from NOAA National Climate Data Center (http://www.ncdc.noaa.gov/teleconnections/pdo/). An analysis of the correlation between total monthly precipitation at each observation station and the Niño 3.4 and PDO indices is carried out through a cross-correlation analysis.

Generalized Pareto distribution model

The most prominent benefit of the POT approach over the block maxima approach is that more data are retained for analysis, as opposed to using only one peak value in a given block length. The Balkema–de Haan–Pickands theorem states that for a series of IID data, excesses over a sufficiently large threshold can be approximated using the GP distribution (Balkema and de Hann 1974; Pickands 1975). Also, in the POT framework it can be demonstrated that the occurrence of exceedances over a high threshold (u) follows a Poisson distribution with rate parameter .

For a sequence of IID random variables , where x_i > u, the cumulative distribution function, , of x_i - u for a suitably large is given by (Coles 2001):(1)

where σ and κ are the scale and shape parameters, respectively. In the event that κ = 0, the distribution reduces to the exponential distribution, which is not employed in this analysis. The quantile function, Q_p of the GP distribution is required to calculate the T-year event, which is an event exceeded, on average, once every T = 1/(1 − p), where 0 < p < 1. The quantile function is commonly expressed in terms of the scale and shape parameters, rate parameter and T-year event (Coles 2001):(2)

In the event that data are nonstationary and therefore not IID, the GP distribution can be expressed in terms of covariates. If distributional parameters are, for example, a function of time, the cumulative distribution function of the GP distribution may be expressed as (Coles 2001):(3)

where are the time-dependent data; and are the time-varying scale and shape parameters, respectively, and are expressed most generally by (O’Brien and Burn 2014):

(4)

(5)

when m = 1, Equation (4) reduces to a linear model, whereas if m = 2, Equation (4) assumes a quadratic form. Evidence of a constant shape parameter has been found in various hydrometeorological studies and this assumption is used hereafter (Vinnikov and Robock 2002; Kharin and Zwiers 2005; Kyselý et al. 2010; Kay and Jones 2012).

If nonstationarity is present in the mean of the original data, the use of a stationary threshold will result in a nonhomogeneous Poisson process for the excesses. This inhomogeneity can be modelled using a nonstationary rate parameter (Katz 2010; Beguería et al. 2011); however, the use of a nonstationary threshold will result in a homogeneous Poisson process. The latter approach is used herein to model potential changes in the central tendency of the data.

Threshold selection

The distribution of exceedances over a threshold asymptotically approaches the GP distribution, given that a suitably high threshold is chosen. Therefore, threshold selection must be done with care to avoid undue bias or, in the case of too high a threshold, high variance (Coles 2001). To ascertain whether change-points exist in the data, Pettitt’s test (Pettitt 1979) is applied prior to both stationary and nonstationary threshold selection. The following sections discuss the stationary and nonstationary threshold selection criteria that are applied for this research.

Stationary threshold

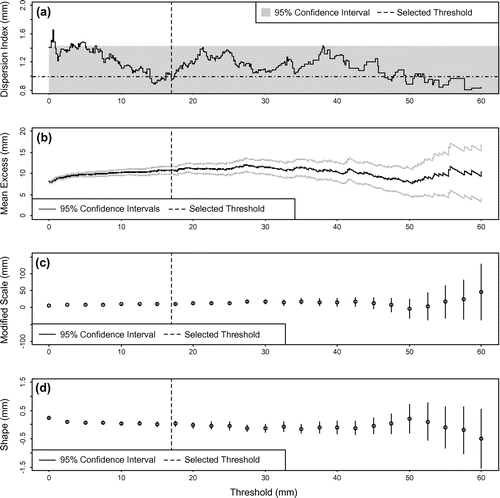
Stationary thresholds are selected through the use of several exploratory plots (Lang et al. 1999; Mailhot et al. 2013; Osman et al. 2013; Roth et al. 2016; Sungwook et al. 2016). Assessing the validity of the homogeneous Poisson process assumption is carried out through the dispersion index plot (Cunnane 1979), where an optimally selected threshold has a dispersion index equal to 1 (Cunnane 1979; Lang et al. 1999). The mean residual life plot depicts the mean excess above a given threshold versus a range of threshold values. The GP distribution provides a suitable fit to excesses over the selected threshold when linearity is apparent in the mean residual life plot. Complimentary threshold choice (TC) plots involve fitting the GP distribution to a range of threshold exceedances and assessing the stability of the resulting distributional parameters. These include the scale and shape parameters for the GP distribution (Coles 2001). An overview of the threshold selection process is provided in Figure 1 for the Mission West Abbey summer season data. Figure 1(a) demonstrates that an appropriate threshold range falls somewhere between 14 and 17 mm. A final threshold of 17 mm was selected as it provides slightly more linearity in Figure 1(b), which is the mean residual life plot. The modified scale and shape parameters are also suitably stable after this point, and are depicted in Figure 1(c) and (d), respectively.

Figure 1. Stationary threshold selection plots for the Mission West Abbey station summer season data: (a) dispersion index plot; (b) mean residual life plot; (c) modified scale parameter plot; (d) shape parameter plot. Indicates a dispersion index of 1.

Nonstationary threshold

Quantile regression is used to determine nonstationary thresholds, which relies on the fact that sample quantiles can be determined by the solution of a linear optimization problem. Given a set of observations (x_i), the τ^th regression quantile is the solution of

(6)

where:

(7)

(Koenker and Basset 1978; Koenker 2005). In the event that the covariate in question varies linearly with time (t), for example, the τ^th conditional quantile function becomes:

(8)

which can be estimated by:(9)

where x_t is a set of time-dependent observations, and β₀ and β₁ are the intercept and the slope components of the regression quantiles, respectively. For a more detailed explanation of quantile regression, please refer to Koenker (2005).

This research follows the methodology of Roth et al. (2014), which provides a basis for time-dependent threshold selection. That is, for a selected time-dependent threshold, the TC plot of the scale parameter for the selected threshold (τ₀) should be approximately constant and the mean residual life plot should be approximately linear for all . In addition to the mean residual life plot and TC plots, dispersion index plots were examined for all to ensure a homogeneous Poisson process for threshold exceedances.

Four bivariate quantile regression models are used for nonstationary threshold modelling along with two multivariate models, all of which incorporate a climate oscillation index and/or time as covariates.

Trend detection

There exist comparable trend detection tests in terms of their power of trend detection (Yue et al. 2002) yet the Mann–Kendall test is widely applied and is therefore used for this research (Mann 1945; Kendall 1975). The presence of positive/negative serial correlation in hydrometric data can increase/decrease the likelihood of finding a significant trend (von Storch 1995). Although the data used for this analysis were declustered to ensure independence of events, any potential residual serial correlation was accounted for using the nonparametric block bootstrap (BBS) technique (Kundzewicz and Robson 2000). This approach is carried out by resampling data in blocks, the length of which is selected based on the number of contiguous lags of significant autocorrelation. After resampling is carried out a large number of times (2000 is implemented for this research), the empirical distribution of the results can be used to assess the significance of trends in the data set. The benefit in using the BBS technique is that the autocorrelation structure of the data is preserved, whereas most techniques require the adoption of a lag-one autoregressive model [AR(1)]. For more information regarding the BBS technique, please refer to Khaliq et al. (2009) or Önöz and Bayazit (2012).

To determine whether significant (local) trends found using the Mann–Kendall test have occurred by chance, the field (global) significance is determined. Field significance is determined using a group block bootstrapping approach (GBBS) which assesses the significance of increasing and decreasing trends separately (Yue et al. 2003; Khaliq et al. 2009). The goal of this technique is to determine the number of significant trends that occur by chance for a selected number of stations while maintaining the serial structure of the original data. Vector resampling of years is carried out in blocks that preserve the serial structure of the original data. Each station having data for the block bootstrapped year vector is added into a resampled data set, and this continues until the desired number of station years are met (i.e. the resampled data set contains the same number of station-years of data as the original data set). This process is repeated a large number of times (1000 herein), where trend detection is carried out for each resampled data set. The empirical distribution of trends and subsequent p-value are then determined, which are then employed to determine field significance.

Parameter estimation

The method of maximum likelihood (ML) is used for parameter estimation due to the ease of incorporation of covariates into distributional parameters. In the case of a stationary model, the log-likelihood function, , is expressed as (Coles 2001):

(10)

where θ is a vector of parameters, is the probability density function, and x_i is the time-independent series of data. In the event that parameter estimation is to be carried out in a nonstationary (time-dependent) context, the log-likelihood function is denoted by (O’Brien and Burn 2014):

(11)

where θ_t is a vector of nonstationary parameters, is the density function, x_t are the time-dependent at-site data; and represents the nonstationary distribution parameters. Due to the complex nature of the log-likelihood function, parameter estimates are commonly determined numerically through the use of non-linear optimization techniques; the Nelder–Mead simplex algorithm is used for this analysis (Nelder and Mead 1965).

Model selection

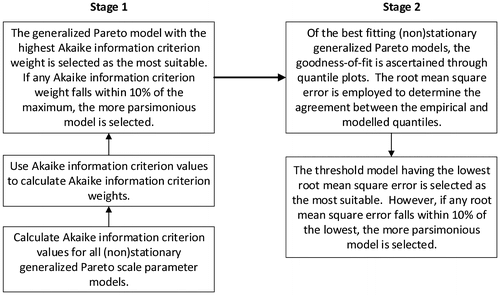
Figure 2 outlines the two-stage approach that is applied in choosing the most suitable model for each data set. The first stage involves calculating Akaike information criterion (AIC) weights that are used as goodness-of-fit criteria for the (non)stationary GP model selection. After the most suitable GP model is selected for each threshold, the best fitting threshold models are selected by means of the root mean square error (RMSE).

Figure 2. Schematic of model selection process.

Akaike weights are initially employed as a goodness-of-fit measure to facilitate the selection of the stationary or nonstationary scale parameter models for each threshold. The AIC is given by (Akaike 1974):

(12)

where K is the number of parameters. Using raw AIC values, the difference between the minimum AIC value and those of the other models is determined (Burnham and Anderson 2002):

(13)

where is the difference in AIC with respect to the minimum AIC; AIC_j is the raw AIC for each model; and minAIC is the minimum AIC value. Akaike weights are then calculated by (Burnham and Anderson 2002):

(14)

where is the AIC weight for model j and The GP distribution model with the largest AIC weight is selected as the most suitable. If any AIC weight falls within 10% of the maximum, the more parsimonious model is selected. Estimates of the GP distribution model parameters are determined using the ‘ismev’ package in R (Heffernan and Stephenson 2009; R Core Team 2016). The ‘gp.fit’ function in this package allows for the estimation of stationary and nonstationary GP distribution parameters through ML estimation, with the option of adding a trend component into selected parameters.

Having selected the best-fitting GP model for each threshold (stationary or nonstationary), the goodness of fit of the threshold models is ascertained through a quantile plot (Q–Q) comparison. In the event of a nonstationary scale parameter and/or nonstationary threshold, a residual quantile plot is produced by transforming data to a standard exponential distribution (Coles 2001), where (for example) time-dependent parameters are included:

(15)

where is the transformed exponential time-dependent data, and u_t is the nonstationary threshold at time t. The selection of the best-fitting threshold was determined using the RMSE, through which the agreement between the empirical and modelled quantiles is assessed. The threshold model having the lowest RMSE is selected, although if any threshold model falls within 10% difference of the lowest RMSE, the model with the smaller number of parameters is selected to preserve model parsimony.

Uncertainty

A balanced resampling approach is implemented for the calculation of quantile confidence intervals (CI). This technique involves first creating a large number of copies (999 is used herein) of the original sample data and concatenating the copies. This concatenated vector of data is then randomly permutated and broken back into the original number of copies. The resulting 999 bootstrapped resamples can then be used to estimate the uncertainty present in the quantile estimates (Burn 2003).

In the event that nonstationarity is present in the scale parameter of the original data set of interest, data are transformed to remove the covariate-dependence before resampling. Given that the GP distribution is applied for this research and using time as an example, nonstationary data were transformed to IID data using the following (Coles 2001):

where is the transformed residual series at time t, x_t is the original data series at time t, and u_t is the time-dependent threshold. Data are transformed before bootstrapping and final samples are calculated using the inverse of Equation (14).

Application

Case study area

Total daily precipitation data, retrieved from the National Climate Data Archive of Environment and Climate Change Canada, are used for this research. Data from 30 gauges throughout coastal BC are used for the implementation of a POT analysis. Before threshold selection is carried out, data are separated into winter season events, spanning from mid-October to mid-April, and summer season events, encompassing the remainder of the year. Winter storms in BC are dominated by midlatitude cyclonic activity, resulting in substantial precipitation amounts. The summer climate is characterized by a subtropical high-pressure system that results in less frequent and intense storms (Walker et al. 2008). Therefore, seasonal partitioning of the data is necessary to reflect the different storm-generating mechanisms.

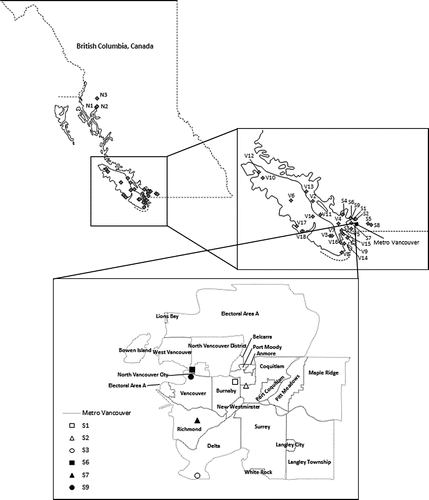
Figure 3 shows the locations of 30 observation stations used in the analysis, six of which are located in Metro Vancouver. Table 1 provides a spatial summary of the station characteristics in three geographical areas, which include the North Coast, the South Coast and Vancouver Island. The elevations and locations of the meteorological stations have a discernible impact on the mean annual precipitation recorded at these locations. Substantial variability in mean annual precipitation is evident throughout coastal BC. Windward areas and those at higher elevations receive greater annual precipitation amounts. Also, the rain shadow of Vancouver Island produces drier conditions in the south coast interior (Moore et al. 2010).

Figure 3. Location of the 30 meteorological stations used for the analysis.

Table 1. Summary of stations used for analysis.

Station name	Station ID	Start year	End year	Latitude (°N)	Longitude (°W)	Elevation (m)	Mean annual precipitation (mm)	Percentage of missing data (%)
North Coast
(N1) Kitimat 2	1064321	1966	2014	49.34	121.76	16.8	2629	3.5
(N2) Kitimat Townsite	1064320	1954	2014	54.05	128.63	98.0	2120	4.2
(N3) Terrace PCC	1068131	1968	2014	54.50	128.62	67.0	1099	3.4
South Coast
(S1) Burnaby Simon Fraser U	1101158	1965	2014	49.28	122.92	365.8	1732	8.7
(S2) Coquitlam Como Lake Ave.	1101889	1972	2014	49.27	122.87	160.0	1626	13.4
(S3) Delta Tsawwassen Beach	1102425	1971	2014	49.01	123.09	2.4	902	1.9
(S4) Gibsons Gower Point	1043152	1961	2014	49.39	123.54	34.0	1313	2.4
(S5) Mission West Abbey	1105192	1962	2014	49.15	122.27	197.0	1823	2.3
(S6) N Vancouver Wharves	1105669	1962	2014	49.31	123.12	7.0	1579	8.7
(S7) Richmond Nature Park	1106PF7	1977	2014	49.17	123.09	3.0	1171	5.0
(S8) Sumas Canal	1107785	1957	2014	49.11	122.11	9.0	1544	11.3
(S9) Vancouver Harbour CS	1108446	1925	2014	49.30	123.12	2.5	1377	9.8
Vancouver Island
(V1) Alberni Robertson Creek	1030230	1961	2014	49.34	124.98	73.8	2068	2.7
(V2) Courtenay Grantham	1021988	1960	2014	49.76	125.00	81.0	1285	9.6
(V3) Cowichan Lake Forestry	1012040	1949	2014	48.82	124.13	176.8	2126	1.6
(V4) Gabriola Island	1023042	1967	2014	49.15	123.73	46.0	850	8.1
(V5) Galiano North	10130MN	1975	2014	48.99	123.57	6.0	859	6.8
(V6) Gold River Townsite	1033232	1975	2014	49.78	126.06	119.0	2524	8.0
(V7) Lake Cowichan	1012055	1960	2014	48.83	124.05	171.0	1747	9.4
(V8) Metchosin	1015105	1968	2014	48.37	123.56	140.0	967	4.3
(V9) North Pender Island	1015638	1972	2014	48.76	123.29	98.0	666	21.5
(V10) Port Alice	1036240	1924	2014	50.39	127.46	21.0	3117	1.4
(V11) Qualicum R Fish Research	1026565	1962	2014	49.39	124.62	7.6	1268	2.0
(V12) Quatsino	1036570	1900	2014	50.53	127.65	3.4	2534	4.4
(V13) Quinsam River Hatchery	1026639	1975	2014	50.02	125.30	45.7	1555	3.0
(V14) Saanichton CDA	1016940	1914	2014	48.62	123.42	61.0	858	0.7
(V15) Saltspring ST Mary’s L	1016995	1976	2014	48.89	123.55	45.7	956	1.2
(V16) Shawnigan Lake	1017230	1911	2014	48.65	123.63	159.0	1216	1.0
(V17) Tofino A	1038205	1959	2014	49.08	125.77	24.5	3236	0.8
(V18) Ucluelet Kennedy Camp	1038332	1964	2014	48.95	125.53	40.0	3309	2.3

The precipitation data used for this analysis were initially screened for obvious transcription errors and uncharacteristically low or high values. Observation stations for this analysis were retained for analysis if they have no more than four consecutive years of missing observations. All stations with daily data west of the mainland Coast Mountains meeting these criteria were included in the analysis. Table 1 provides a summary of the percentage of missing data at each of the 30 retained meteorological stations. All the stations, aside from North Pender Island, have less than 20% missing observations from the period of record; 27 of the stations have less than 10% missing data. It is acknowledged that bias may be present in the precipitation measurements due to variations in wind speed and differences in instrumentation. Furthermore, the current analysis employs a 2-day separation time between maxima as a means of retaining peak precipitation from individual events (Coles 1993; Caires et al. 2006; Kyselý and Beranová 2009; Roth et al. 2012). Also, all data were found to be free of step-changes prior to parameter estimation.

Results

Threshold selection and models

Correlations between climate indices and monthly precipitation amounts were assessed for positive and negative lags of cross-correlation function (CCF) plots at the 5% significance level for the Niño 3.4 and PDO indices. It was determined that the PDO index is more strongly correlated with the monthly precipitation amounts in both the summer (73% of cases for PDO/27% for Niño 3.4) and winter seasons (76% of cases for PDO/24% for Niño 3.4). For this reason, the PDO index and/or time are used as covariates for the univariate and bivariate thresholds and GP models used for this analysis. Table 2 outlines the nonstationary threshold models employed.

Table 2. Quantile regression threshold models.

+

GP distribution – model selection

The GP distribution is fit to threshold exceedance data established through the use of stationary and nonstationary thresholds; the shape parameter was kept constant in all instances. The stationary and nonstationary GP distribution models used for this analysis are outlined in Table 3. Using the log-likelihood estimates provided by the ‘gp.fit’ function, AIC weights are calculated for the stationary and nonstationary threshold exceedance data. Results from the Mission West Abbey observation station are provided in Table 4 for the summer season data as an example of the model selection process, and are typical of all results. The GP scale parameter model with the highest weight is selected as the most appropriate model for all thresholds except for u_cov2 and u_cov6, where u_cov2 is the linear, time-dependent threshold and u_cov6 is the quadratic time- and PDO-dependent threshold. In these two instances, there was a tie for the highest weight; therefore, the more parsimonious model was selected for both threshold models.

Table 3. Peaks over threshold data for the generalized Pareto distribution quantile functions.

Stationary generalized Pareto Dist. Quantile Function
Nonstationary generalized Pareto Dist. Quantile Function

u/u_cov denotes a stationary threshold (u) or one of the six nonstationary thresholds (u_cov) models in Table 2.

Table 4. Akaike information criterion weights for the Mission West Abbey observation station – summer season.

Stationary/Nonstationary generalized Pareto Dist	Stationary threshold()	Nonstationary threshold models ()
	0.005	0.009	0.039	0.040	0.032	0.025	0.004
	0.012	0.011	0.033	0.046	0.041	0.020	0.006
	0.200	0.297	0.291	0.250	0.259	0.352	0.281
	0.246	0.221	291	0.201	0.232	0.201	0.281
	0.030	0.053	0.091	0.187	0.165	0.071	0.031
	0.374	0.344	0.184	0.167	0.162	0.235	0.269
	0.133	0.064	0.072	0.109	0.110	0.097	0.128

Bold and italicized cells represent the distribution with the best fit (highest Akaike information criterion weight).

The best fitting threshold model was then determined using the models that provided the highest AIC weights. This is carried out through the comparison of quantile or residual quantile plots (for nonstationary models), where the agreement between the model and empirical quantiles is measured using the RMSE. An example is provided in Figure 4, showing the results for the summer season quantile plots at the Mission West Abbey observation station. Figure 4(c) was chosen as the most suitable model as it is the most parsimonious within 10% difference of the minimum RMSE of all the threshold models. Tables 5 and 6 outline the final selection of models, the associated parameter estimates of the GP distribution models, and the applicable stationary or nonstationary threshold parameters.

Figure 4. Comparison of residual quantile plots of above threshold data from the summer season at observation station Mission West Abbey: (a) stationary threshold and quadratic PDO-dependent scale parameter; (b) linear time-dependent threshold and linear PDO-dependent scale parameter; (c) linear PDO-dependent threshold and linear PDO-dependent scale parameter; (d) linear time- and PDO-dependent threshold and linear PDO-dependent scale parameter; (e) quadratic time-dependent threshold and linear PDO-dependent scale parameter; (f) quadratic PDO-dependent threshold and linear PDO-dependent scale parameter; (g) quadratic time- and PDO-dependent threshold and linear PDO-dependent scale parameter.

Note: the root mean square error for the selected model is bolded and italicized.

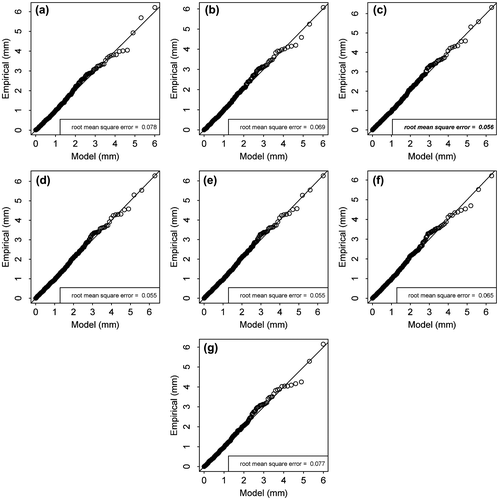
Table 5. Final threshold selection and model parameters for the winter season data.

	Threshold model parameter(s)					Generalized Pareto distribution model parameters
						Scale parameter(s)					Shape parameter ()
Nth Coast
(N1) Kitimat 2	34.76	−0.054	–	–	–	20.85	0.4947	−0.0133	–	–	−0.034
(N2) Kitimat Townsite	29.19	−0.115	0.001	−0.790	0.580	16.50	–	–	–	–	0.023
(N3) Terrace PCC	10.00	–	–	–	–	12.90	−0.0582	–	–	–	0.041
South Coast
(S1) Burnaby Simon Fraser U	24.19	−0.052	–	−1.547	–	14.78	–	–	–	–	0.017
(S2) Coquitlam Como Lake Ave.*	21.00	–	–	–	–	14.72	–	–	–	–	0.078
(S3) Delta Tsawwassen Beach*	9.90	–	–	–	–	8.29	–	–	–	–	−0.008
(S4) Gibsons Gower Point*	13.60	–	–	–	–	10.34	–	–	–	–	−0.085
(S5) Mission West Abbey*	23.39	–	–	–	–	12.84	–	–	–	–	0.081
(S6) N Vancouver Wharves*	22.00	–	–	–	–	13.53	–	–	–	–	0.018
(S7) Richmond Nature Park	14.01	−0.010	–	–	–	9.90	–	–	–	–	0.004
(S8) Sumas Canal	23.60	–	–	–	–	14.00	0.0614	–	–	–	−0.016
(S9) Vancouver Harbour CS	23.38	0.094	−0.001	–	–	9.80	0.1573	−0.0014	–	–	0.063
Vancouver Island
(V1) Alberni Robertson Creek*	26.70	–	–	–	–	21.50	–	–	–	–	−0.090
(V2) Courtenay Grantham	22.61	−0.041	–	–	–	14.95	–	–	–	–	−0.043
(V3) Cowichan Lake Forestry*	33.20	–	–	–	–	20.85	–	–	–	–	−0.026
(V4) Gabriola Island	13.23	−0.010	–	–	–	9.66	–	–	–	–	−0.013
(V5) Galiano North	12.66	–	–	0.417	–	10.97	–	–	–	–	−0.059
(V6) Gold River Townsite	35.60	–	–	–	–	28.85	−0.2162	–	–	–	−0.040
(V7) Lake Cowichan	30.18	–	–	0.175	–	21.05	0.1540	–	–	–	−0.052
(V8) Metchosin	15.73	0.010	–	−1.503	–	7.63	0.5492	−0.0104	−1.5826	0.0625	0.075
(V9) North Pender Island	11.85	–	–	−0.090	–	10.55	–	–	–	–	−0.007
(V10) Port Alice	46.29	0.092	–	2.148	–	17.93	0.0747	–	1.3582	–	0.158
(V11) Qualicum R Fish Research*	21.10	–	–	–	–	14.16	–	–	–	–	0.069
(V12) Quatsino	30.72	–	–	1.096	–	16.90	–	–	–	–	−0.002
(V13) Quinsam River Hatchery	18.02	–	–	−0.615	–	16.29	–	–	–	–	−0.146
(V14) Saanichton CDA	15.87	0.023	–	–	–	8.40	0.0394	–	–	–	0.022
(V15) Saltspring ST Mary’s L*	13.00	–	–	–	–	10.57	–	–	–	–	−0.030
(V16) Shawnigan Lake*	22.10	–	–	–	–	13.65	–	–	–	–	−0.019
(V17) Tofino A*	42.20	–	–	–	–	22.94	–	–	–	–	0.058
(V18) Ucluelet Kennedy Camp*	40.96	–	–	–	–	24.74	–	–	–	–	0.024

* Denotes those sites having a stationary threshold and stationary generalized Pareto distribution model.

Table 6. Final threshold selection and model parameters for the summer season data.

	Threshold model parameter (s)					Generalized Pareto distribution model parameters
						Scale parameter (s)					Shape parameter
									.
North Coast
(N1) Kitimat 2*	18.00	–	–	–	–	16.81	–	–	–	–	0.051
(N2) Kitimat Townsite	18.27	0.037	–	–	–	13.32	–	–	–	–	0.112
(N3) Terrace PCC*	10.40	–	–	–	–	7.40	–	–	–	–	0.158
South Coast
(S1) Burnaby Simon Fraser U	12.97	0.024	–	0.713		14.18	−0.0697	–	–	–	−0.043
(S2) Coquitlam Como Lake Ave.	9.69	–	–	0.589	0.573	14.69	–	–	−0.5935	−0.9711	−0.144
(S3) Delta Tsawwassen Beach*	5.51	–	–	–	–	7.08	–	–	–	–	−0.091
(S4) Gibsons Gower Point	9.85	−0.026	–	–	–	9.19	–	–	–	–	−0.100
(S5) Mission West Abbey	14.46	–	–	0.116	–	12.65	–	–	1.1586	–	−0.047
(S6) N Vancouver Wharves	21.88	0.006	–	−0.182	–	12.69	−0.0903	–	–	–	−0.032
(S7) Richmond Nature Park*	6.80	–	–	–	–	9.09	–	–	–	–	−0.089
(S8) Sumas Canal	16.69	0.018	–	–	–	10.09	0.0728	–	–	–	0.024
(S9) Vancouver Harbour CS*	15.80	–	–	–	–	9.90	–	–	–	–	0.032
Vancouver Island
(V1) Alberni Robertson Creek*	13.10	–	–	–	–	12.45	–	–	–	–	0.053
(V2) Courtenay Grantham	10.82	–	–	1.266		7.10	–	–	–	–	0.175
(V3) Cowichan Lake Forestry	12.94	0.008	–	–	–	11.86	–	–	–	–	0.048
(V4) Gabriola Island	5.80	–	–	–	–	7.05	–	–	0.268	−0.428	−0.034
(V5) Galiano North*	6.93	–	–	–	–	5.50	–	–	–	–	0.108
(V6) Gold River Townsite*	19.00	–	–	–	–	13.43	–	–	–	–	0.158
(V7) Lake Cowichan*	11.30	–	–	–	–	10.11	–	–	–	–	0.183
(V8) Metchosin	6.28	0.026	–	–	–	5.55	–	–	–	–	0.155
(V9) North Pender Island	4.84	0.027	–	–	–	5.18	–	–	–	–	0.037
(V10) Port Alice	27.38	−0.006	–	0.397	–	21.94	–	–	–	–	0.009
(V11) Qualicum R Fish Research	9.43	–	–	0.844	–	7.45	–	–	–	–	0.035
(V12) Quatsino	20.53	−0.032	–	0.508	–	11.66	–	–	0.425	0.714	0.087
(V13) Quinsam River Hatchery	10.59	–	–	–	–	7.48	–	–	−0.639	–	0.125
(V14) Saanichton CDA	7.92	0.019	–	–	–	5.45	–	–	–	–	0.117
(V15) Saltspring ST Mary’s L	5.98	–	–	0.519	–	5.31	–	–	–	–	0.073
(V16) Shawnigan Lake	7.27	0.010	–	–	–	7.37	−0.017	–	–	–	0.081
(V17) Tofino A*	25.78	–	–	–	–	17.17	–	–	–	–	0.054
(V18) Ucluelet Kennedy Camp	29.02	−0.423	0.008	–	–	17.99	–	–	–	–	0.084

* Denotes those sites having a stationary threshold and stationary generalized Pareto distribution model.

Trend detection summary

A summary of the trend analysis of the magnitude and frequency of the POT data is presented in Figures 5 through 8. Two analysis periods are examined (39 and 29 years) for all 30 stations and for the winter and summer seasons at 5% and 10% significance levels.

Figure 5. Winter season stationary threshold exceedance trend locations. Bold and italicized legend fonts indicate trends that are globally significant.

Note: only locations showing trends are shown. Depicted trends may be for either a 29- or 39-year analysis period at 5% and 10% significance levels.

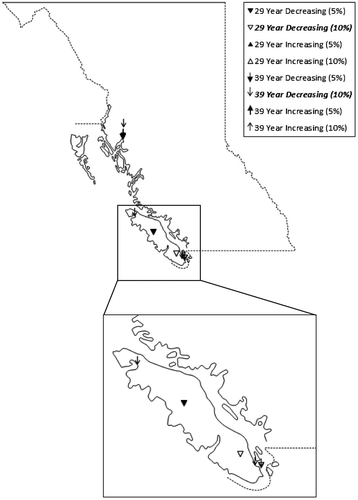
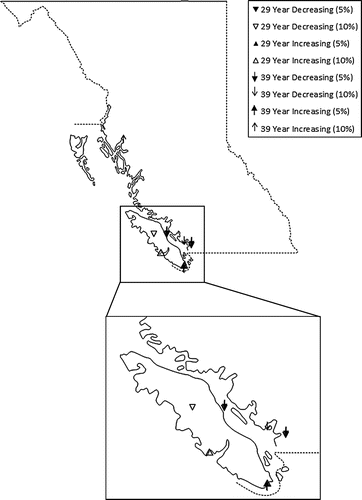
Figure 5 indicates that the winter season threshold exceedance data are dominated by decreasing trends. Trends are observed at 5% and 10% significance levels for threshold exceedances for both analysis periods at several sites in the North Coast and Vancouver Island regions. Although a number of statistically significant decreasing trends were identified, only those for the 1976–2014 (39-year) period at the 10% significance level were determined to be field significant. A globally significant increasing trend is also identified in Figure 6 for the 1986–2014 (29-year) analysis period at 5% and 10% significance levels at the Metchosin (V8) station only.

Figure 6. Winter season frequency of stationary threshold exceedance trend locations. Bold and italicized legend fonts indicate trends that are globally significant.

Note: only locations showing trends are shown. Depicted trends may be for either a 29- or 39-year analysis period at 5% and 10% significance levels.

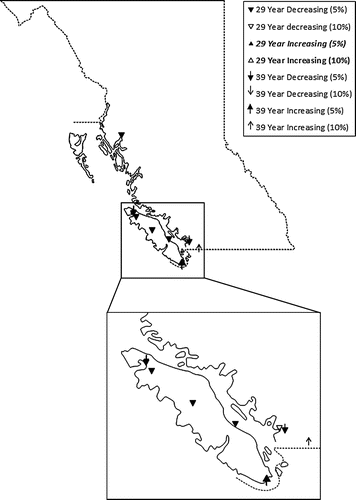
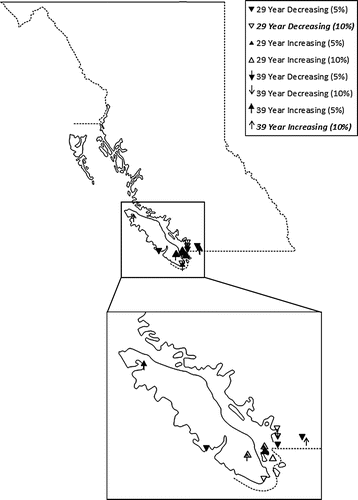
Results of the Mann–Kendall trend test for the summer season above threshold and frequency data (Figures 7 and 8, respectively) indicate that there are a number of both increasing and decreasing trends, which are located primarily in the South Coast and Vancouver Island region. It should be noted, however, that globally significant trends were only found in the peak data (Figure 7), which include 39-year increasing trends at the 10% significance level and 29-year decreasing trends at the 10% significance level. These results highlight the importance of trend identification in different analysis periods.

Figure 7. Summer season stationary threshold exceedance trend locations. Bold and italicized legend fonts indicate trends that are globally significant.

Note: only locations showing trends are shown. Depicted trends may be for either a 29- or 39-year analysis period at 5% and 10% significance levels.

Figure 8. Summer season frequency of stationary threshold exceedance trend locations.

Note: only locations showing trends are shown. Depicted trends may be for either a 29- or 39-year analysis period at 5% and 10% significance levels.

Quantile estimation summary

Quantile estimates are calculated for the 50-year events for each of the winter and summer season data using Equation (2), and are illustrated in Figures 9 and 10, respectively. If a stationary model is determined to be the best fit, a comparison with nonstationary quantiles is not warranted and is therefore not presented. For all the remaining data sets, a comparison between the best-fitting stationary and nonstationary model quantiles is provided. Due to the inclusion of PDO as a covariate, the quantile estimates are not consistently smooth, particularly in the case of a PDO-dependent GP scale parameter. Trends identified through the Mann–Kendall trend test are included in the top right corner of Figures 9 and 10 as a means of comparison.

For the winter season data, 12 of the 30 sites are identified as stationary through the model selection technique. All of the sites in the North Coast region are identified as nonstationary (decreasing), whereas 56% (5 of 9) and 39% (7 of 18) of sites in the South Coast and Vancouver Island regions are, respectively. Of the remaining four stations on the South Coast, two (S1 and S7) display very mild nonstationarity, while the remaining two (S8 and S9) reveal increasing 50-year quantiles. Within the Vancouver Island region, seven of the stations have stationary quantiles (V1, V3, V11, V15, V16, V17 and V18), while seven of the remaining stations show nominal changes in quantiles with respect to time (V2, V4, V5, V8, V9, V12 and V13). The four remaining sites exhibit discernable nonstationarity, three of which are increasing (V7, V10 and V14) and one of which is decreasing (V6). A decreasing trend was also identified at station V6 at the 5% significance level for the 29-year period (1986–2014). An inconsistent decreasing trend is identified at station V14, but this could be due to the marked difference in the period of record of the station data and the 29- or 39-year time frames. The magnitude of uncertainty in the quantile estimates is similar for both stationary and nonstationary models, aside from site V10 which has smaller stationary CIs. Given that the stationary threshold and GP model provides substantially less uncertainty for this particular site, confidence in these nonstationary estimates is low.

The summer season data show slightly less stationarity, with 10 of the 30 sites having time-independent quantiles. In the North Coast region, two of the three sites are stationary, with the remaining nonstationary site (N2) showing little discernable change over the period of record. Three of the nine sites in the South Coast region are stationary (S3, S7 and S9) and three have minimal nonstationarity or fluctuate around a constant mean value (S2, S4 and S5). Of the remaining three stations, two show decreasing and one increasing 50-year quantiles, although nonstationary estimates for station S6 have slightly more uncertainty than their stationary counterparts. Finally, Vancouver Island contains five stationary sites, but of those remaining, only two (V16 – decreasing and V18 – increasing) show apparent changes in 50-year peak return period precipitation estimates. In agreement with the winter season findings, the uncertainty levels in the stationary and nonstationary 50-year quantile estimates are relatively comparable, aside from those of site V18. There is noticeably more uncertainty in the nonstationary quantiles for this station; therefore, there is minimal confidence in these estimates.

Regional pattern overview

Figure 9 demonstrates that the North Coast, winter-season 50-year quantile estimates are generally decreasing, although one site (N2) shows very little change over the period of record. Furthermore, the trend analysis identified a decreasing trend at N1 for the 1986–2014 period at the 5% significant level, and a decreasing trend for the 1976–2014 period was detected at site N3 at the 10% significance level. One trend was also identified in the North Coast region frequency data in the winter season, a variable for which the trend results are field significant (Figure 6). Although the detected trends in the magnitude of the POT data were not determined to be field significant, these findings suggest overall decreasing peak precipitation in the winter months. An analysis of Figure 10 reveals that there is minimal indication of nonstationarity in the summer peak quantile estimates, as well as no trends being identified at those sites. The GP and threshold model parameters in the winter season for the North Coast displayed both PDO- and time-dependence, although the models selected for the summer months are dominated by stationarity (Tables 5 and 6). Furthermore, divergent nonstationary behaviour is observed in the winter quantile estimates at stations N1 and N2, although these two stations are very closely located. Differences in the nonstationary quantile estimates at these two stations may be due to other factors such as changes in instrumentation and location over time.

Figure 9a. (N1–S9). 50-year nonstationary and/or stationary quantiles and their associated 95% confidence intervals – winter season.

Note: the notation in the top left of each plot is the associated station from Table 1; the symbol in the top right corner indicates the trend results for exceedance data for the 29- or 39-year period of record; D indicates a decreasing trend; I indicates an increasing trend; and 5 or 10 indicates the significance level (%). The threshold exceedance trend results are provided as a means of interpretation of model fit and comparison.

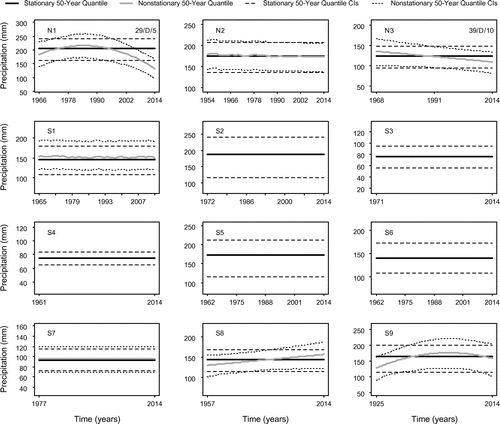
Figure 9b. (V1–V12). 50-year nonstationary and/or stationary quantiles and their associated 95% confidence intervals – winter season.

Note: the notation in the top left of each plot is the associated station from Table 1; the symbol in the top right corner indicates the trend results for exceedance data for the 29- or 39-year period of record; D indicates a decreasing trend; I indicates an increasing trend; and 5 or 10 indicates the significance level (%). The threshold exceedance trend results are provided as a means of interpretation of model fit and comparison.

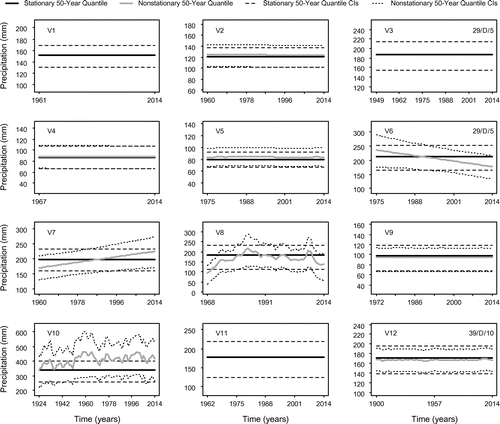
Figure 9c. (V13–V18). 50-year nonstationary and/or stationary quantiles and their associated 95% confidence intervals – winter season.

Note: the notation in the top left of each plot is the associated station from Table 1; the symbol in the top right corner indicates the trend results for exceedance data for the 29- or 39-year period of record; D indicates a decreasing trend; I indicates an increasing trend; and 5 or 10 indicates the significance level (%). The threshold exceedance trend results are provided as a means of interpretation of model fit and comparison.

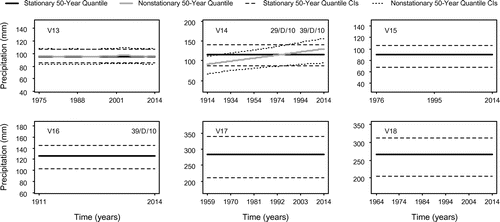
Figure 10a. (N1–S9). 50-year nonstationary and/or stationary quantiles and their associated 95% confidence intervals – summer season.

Note: the notation in the top left of each plot is the associated station from Table 1; the symbol in the top right corner indicates the trend results for exceedance data for the 29- or 39-year period of record; D indicates a decreasing trend; I indicates an increasing trend; and 5 or 10 indicates the significance level (%). The threshold exceedance trend results are provided as a means of interpretation of model fit and comparison.

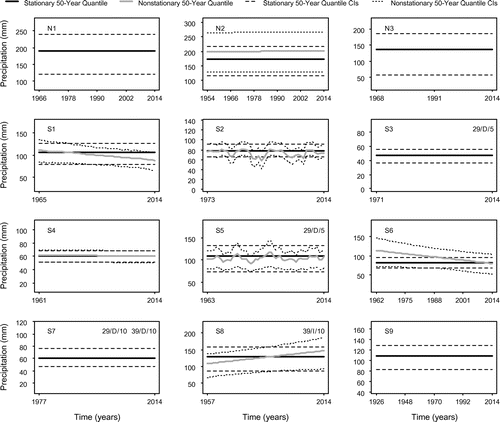
Figure 10b. (V1–V12). 50-year nonstationary and/or stationary quantiles and their associated 95% confidence intervals – summer season.

Note: the notation in the top left of each plot is the associated station from Table 1; the symbol in thetop right corner indicates the trend results for exceedance data for the 29- or 39-year period of record; D indicates a decreasing trend; I indicates an increasing trend; and 5 or 10 indicates the significance level (%). The threshold exceedance trend results are provided as a means of interpretation of model fit and comparison.

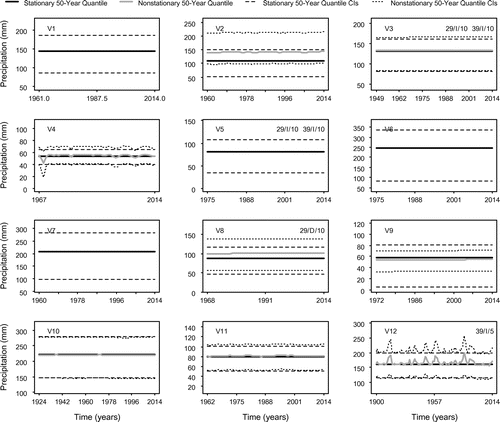
Figure 10c. (V13–V18). 50-year nonstationary and/or stationary quantiles and their associated 95% confidence intervals – summer season.

Note: the notation in the top left of each plot is the associated station from Table 1; the symbol in the top right corner indicates the trend results for exceedance data for the 29- or 39-year period of record; D indicates a decreasing trend; I indicates an increasing trend; and 5 or 10 indicates the significance level (%). The threshold exceedance trend results are provided as a means of interpretation of model fit and comparison.

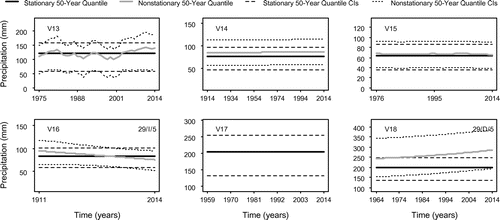
Figures 5 and 6 illustrate that Vancouver Island is dominated by decreasing trends in above-threshold occurrences and the frequency of those occurrences in the winter season. Globally significant decreasing trends were identified for the above-threshold occurrences for the 39-year period decreasing trends at the 10% significance level. Additionally, one field-significant increasing trend was identified (Figure 6) for the winter 1986–2014 period at 5% and 10% significance levels. A combination of increasing and decreasing trends were found in the summer months in the magnitude and frequency of POT events; however, only increasing above-threshold trends for the 39-year period (10% significance level) and decreasing trends for the 29-year period (10% significance level) were found to be field significant. The winter quantile estimates have somewhat contradictory results, given that a number of sites are discernably increasing. Also, the summer 50-year quantile estimates were predominantly stationary, yet a number of significant trends were identified through the trend analysis. Finally, an analysis of the threshold models from Tables 5 and 6 selected for Vancouver Island suggests that the central tendency of the winter and summer season data is influenced by both time and PDO. An analysis of the GP scale parameter estimates reveals that the winter variability is more likely stationary.

The South Coast region is characterized by relatively stationary quantiles for both seasons, although, several fluctuate about a constant mean. However, two sites have noticeably increasing 50-year quantile estimates in the winter, and summer quantiles indicate that several sites have discernably increasing and decreasing quantiles as well. Two significant decreasing trends were identified in the winter season, while summer season trends for both the frequency and magnitude of POT events were generally decreasing. Additionally, the South Coast region shows a mixture of time- and PDO-dependence in the summer in all model parameters, while the winter season appears to be rather stationary.

Discussion

This section includes a comparison of this analysis with other similar studies. Such comparison is a challenging task due to differences in methodologies, but is nonetheless a valuable undertaking.

In an analysis of daily precipitation data throughout Canada, Stone et al. (2000) found decreasing trends in heavy precipitation frequency in winter months in coastal BC, which is consistent with the findings of this work. Increases in the frequency of peak summer events were also identified by Stone et al. (2000); however, their research did not find globally significant trends in summer frequency data. Zhang et al. (2000) found statistically significant increases in gridded daily precipitation in summer months in the southwestern portion of BC for the 1900–1998 and 1950–1998 periods. The findings of the quantile analysis for the South Coast region herein are in agreement with these findings. Zhang et al. (2000) also identified significant increasing trends in an area similar to that of the North Coast region for the 1900–1998 period, which is generally consistent with the quantile analysis of this area. In a Canada-wide analysis, Vincent and Mekis (2006) examined numerous precipitation and temperature indices from 1950 to 2003. They found an increase in the number of days with snow and rain in coastal BC, although these finding were not statistically significant. However, significant increasing trends in very wet days (95th percentile) were primarily identified on Vancouver Island and in the North Coast region, which is inconsistent with the results of this research, given that the detected trends in frequency of over-threshold events were generally decreasing (significant or otherwise). Burn et al. (2011) used hourly precipitation to carry out a POT analysis of events of varying duration in BC. The results of this analysis for the summer season found statistically and globally significant trends in the frequency of above-threshold events for 24-h-duration storms (40-year period). However, no globally significant trends were found in the summer frequency data herein. Also, the winter season frequency data of Burn et al. (2011) are dominated by increasing trends, although none was field significant. These trend results are somewhat consistent with those of the winter trend analysis carried out herein, whereby a globally significant increasing trend was found for the winter frequency data. The winter peak magnitude data herein are dominated by decreasing trends. However, some evidence of increasing winter quantiles was found in the Vancouver Island and South Coast regions.

Mote (2003) found predominantly increasing trends in daily precipitation for the winter season from 1950 to 2000 in southern coastal BC, which is consistent with the quantile estimates from the South Coast region. Mote (2003) also found a mixture of increasing and decreasing trends on Vancouver Island, which is also consistent with the results herein. In an analysis of Canadian daily total rainfall, Vincent and Mekis (2009) found increasing trends in summer and decreases in winter precipitation in southwestern BC. These results are somewhat similar to those found for the North Coast region in the winter and the South Coast region in the summer. Although the work of Mote (2003) and Vincent and Mekis (2009) used daily precipitation indices, they did not assess peak precipitation trends; therefore, a direct comparison between these two studies is not possible.

General circulation model (GCM) projections for coastal BC indicate the potential for wetter winter seasons and drier conditions in the summer months (British Columbia Ministry of Environment [BCME] 2007; Walker et al. 2008). The results established through the trend analysis are somewhat consistent with the above-noted projections for the winter season given that globally and statistically significant increasing trends in frequency were found for the 29-year analysis period at both significance levels. Also in agreement, a number of trends in the summer season were found to be decreasing. It should also be noted that the results of the quantile analysis provided better agreement with likely climate change projections.

Whitfield et al. (2010) describe the PDO as a powerful post hoc explanatory concept, limiting the forecasting potential with this index. Therefore, care should be taken in extrapolating the quantile estimates past the period of record, particularly in instances with strong quadratic behaviour. One of the anonymous reviewers suggested that concave quadratic behaviour may possibly be due to a period of predominant La Niña between approximately 1990 and 2012, which led to a long period of cold PDO SSTs.

Conclusions

This paper incorporates existing nonstationary extreme-value approaches to develop a methodology for the selection of stationary/nonstationary thresholds. Nonstationary threshold selection is carried out through quantile regression, which allows for the inclusion of bivariate and multivariate models. A two-stage selection process is proposed, in which AIC weights are initially employed to determine the best-fitting (non)stationary GP distribution model for each threshold. Threshold/GP distribution models are then compared through the use of Q–Q plots. This methodology is developed as a complementary approach to trend detection which allows the user to visually identify potential trends in peak quantile estimates.

There is more evidence of stationarity in the North Coast winter and summer over-threshold data, which is confirmed by the quantiles and trend analyses. Similar results are revealed for the South Coast region, although there is some evidence of increasing quantiles in the winter. Vancouver Island shows the most potential for nonstationary increasing peak 50-year quantiles in both seasons, although there is some evidence of decreases in the winter. Through the trend analysis, it was revealed that a number of significant trends were found in the magnitude and frequency of POT data for both seasons.

In general, the results from the quantile and trend analyses are in agreement with previously published work. Furthermore, dissimilarities in the trend and quantiles analyses reinforce the usefulness of investigating trends through various means and highlight the importance of comparisons within various periods of record. Based on this historical data trend analysis, there is less risk of serious precipitation-related winter events; however, the frequency of these events is increasing in recent years. Furthermore, the quantile analysis suggests that there is moderate risk of increases/decreases in winter or summer hydrometeorological hazards in coastal BC.

Acknowledgements

The authors greatly appreciate the useful comments by the Associate Editor and two anonymous reviewers. The authors gratefully acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). Data used for this research were obtained from Environment and Climate Change Canada’s Historical Climate Database.