Modelling of Physical Processes and Assessment of Climate Change Impacts in Great Bear Lake

Abstract

Polar lakes are highly sensitive to changes in the climate. As a contribution to the International Polar Year (IPY), the impact of climate warming on the thermal characteristics of Great Bear Lake is studied. During the summer of 2008, time series observations of meteorological, hydrological and physical limnological parameters in the lake were obtained to characterize the thermal regime. These observations and the forecasted forcing from a regional version of the Canadian operational Global Environmental Multiscale (GEM) model are used to simulate the ice-free hydrodynamics in Great Bear Lake using the high-resolution, three-dimensional hydrodynamic Princeton Ocean Model (POM). The model results of surface and sub-surface temperatures are first compared with satellite and in-lake measurements. The model simulates weak stratification and predicts mean cyclonic circulation reasonably well. The impact of climate warming caused by greenhouse gases is studied using Canadian Regional Climate Model (CRCM) scenarios for the base climate (1970–2000) and future warmer climate (2041–70). This scenario predicts an increase in surface temperature of over 2°C in the northeast corner, whereas in the rest of the lake the increases vary from 0.5° to 1°C. The results show that brief thermal stratification is possible in the deeper waters. The increase in water temperature caused by climate warming in the lake appears largely because of the positive increase in net longwave radiation and sensible heat flux, which result from changes in the temperature gradient between the air and the lake and slightly reduced wind speeds in the climate warming projections.

RÉSUMÉ [Traduit par la rédaction] Les lacs des régions polaires sont extrêmement sensibles aux changements dans le climat. Notre contribution dans le cadre de l'Année polaire internationale (IPY) consiste à étudier les répercussions du réchauffement climatique sur les caractéristiques thermiques du Grand lac de l'Ours. Pendant l’été 2008, nous avons effectué des observations de séries chronologiques par rapport aux paramètres météorologiques, hydrologiques et limnologiques physiques dans le lac afin de caractériser le régime thermique. Ces observations conjuguées au forçage radiatif prévu établi à partir de la version régionale du modèle global environnemental multiéchelle canadien (GEM), utilisé pour produire les prévisions météorologiques opérationnelles, nous permettent de simuler l'hydrodynamique sans glace dans le Grand lac de l'Ours au moyen d'un modèle hydrodynamique tridimensionnel à haute définition, le modèle océanique de Princeton (POM). Nous comparons d'abord les températures subsurfaces et de surface obtenues au moyen du modèle, aux mesures satellitaires et du lac. Le modèle présente la simulation d'une stratification faible et il prédit raisonnablement bien la circulation cyclonique moyenne. Nous étudions les répercussions du réchauffement climatique causé par les gaz à effet de serre en nous servant des scénarios du MRCC pour le climat de référence (1970–2000) et le climat plus doux à l'avenir (2041–2070). Ce scénario prévoit une hausse de la température de surface, supérieure à 2°C dans la partie nord-est. En revanche, l'augmentation de la température dans le reste du lac varie de 0,5° à 1°C. Les résultats démontrent qu'une brève stratification thermique est possible en eau profonde. L'augmentation de la température de l'eau attribuable au réchauffement climatique dans le lac semble essentiellement due à l'augmentation du rayonnement de grandes longueurs d'onde et du flux de chaleur sensible nets, qui s'explique par les changements survenus dans le gradient de température entre l'air et le lac et par la légère diminution de la vélocité des vents dans les prévisions relatives au réchauffement climatique.

Keywords:

• hydrodynamic model
• climate warming
• GEM
• Great Bear Lake
• CRCM

1 Introduction

Some of the largest increases in air temperature anywhere in the world have been observed in the Mackenzie River Basin (Stewart et al., 1998). Lakes within this polar region are projected to be highly sensitive to climate variability and change. Research involving both observations and modelling aid our understanding of the impacts of climate change on these lakes.

Lakes of various sizes, shapes and depths occupy extensive areas in the Mackenzie River Basin with an estimated lake coverage of approximately 11% (Rouse et al., 2005, 2008) with about 32,370 lakes occupying the central part of the basin. Small, shallow lakes, though numerous, consitute only a small percentage of the total lake area (Rouse et al., 2008). Within this basin, Great Bear Lake with a surface area of 31,153 km² crosses the Arctic Circle and is considered a polar lake. Great Slave Lake has a surface area of 28,450 km² and is located to the south of Great Bear Lake.

Early research on Great Bear Lake was conducted by Johnson (1994), and Rawson (1950) conducted much earlier research on the more accessible Great Slave Lake. These investigations were largely based on limited ship observations and observations over a grid of stations and provided data to describe water temperature distributions during the ice-free period. As part of the Mackenzie Global Energy and Water Cycle Experiment (GEWEX) Study (MAGS; 1998–2004), expanded investigations were conducted on both lakes. The magnitude and interannual variability of the hydrometeorology, thermal response and heat content of Great Slave Lake were assessed (e.g., Schertzer et al., 2003; Rouse et al., 2008), and a three-dimensional (3-D) hydrodynamic model was used to simulate the thermal structure (Leon et al., 2005). During MAGS, Rouse et al. (2008) compared thermal and energy balances between Great Slave Lake and Great Bear Lake with limited observations available on Great Bear Lake at that time. They observed that Great Bear Lake is very responsive to climatic variability, being influenced by the relation between the length of the ice-free season and absorbed solar radiation. However, the impact of climatic warming on the thermal characteristics of Great Bear Lake has not been quantified.

The Mackenzie River Basin has experienced some of the greatest warming in Canada during the last 50 years, for example, at Deline (M1; Fig. 1), the mean annual temperature has risen by over 1.5°C since 1950 (Woo et al., 2007). Further, the warming was concentrated in the winter with summer temperatures not exhibiting any apparent trends. The freeze-up and break-up of lake ice and ice-cover duration have been shown to be sensitive indicators of climate variability and change (Howell et al., 2009). Reports have indicated that Great Bear Lake has been covered with ice from late November to July; however, lake-ice conditions vary significantly from year to year (Walker et al., 1999; Blanken et al., 2003). Currently, the lake has an ice-free period of approximately 3–4 months. The longest ice-free period occurred during an intense El Niño in 1998 (Walker et al., 1999).

Fig. 1 Bathymetry (metres) of Great Bear Lake in the model domain and temperature moorings (solid red circles), APEX profiling buoys (solid green circles) and meteorological stations (solid blue squares).

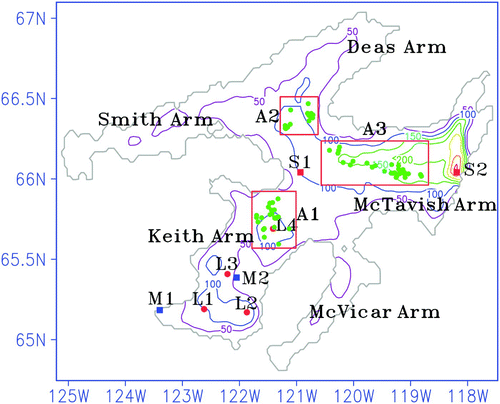
Meyer et al. (1994) conducted a preliminary analysis of the impact of climate change on hypothetical and real lakes at different latitudes, including Great Bear Lake. They suggested that the lake is currently in a cold monomictic stage experiencing complete vertical mixing once in three years. Using a one-dimensional (1-D) model, their preliminary climate change simulations with the Geophysical Fluid Dynamics Lab (GFDL) steady-state climate scenario suggested that under atmospheric doubling of CO₂, the consequent increase in air temperature would result in a reduction in the duration of ice cover from 82% of the year to only 65%. As a result of increased air temperature, which was assumed to be as much as 9°C, strong convective mixing in the lake could potentially occur in the spring and autumn. This suggests that the lake could change its mictic state from cold monomictic to become dimictic (overturn twice yearly in the spring and the fall) with physical processes similar to temperate lakes such as the Laurentian Great Lakes. Such a change would have profound implications for the lake physical limnological characteristics (e.g., ice extent, ice-free period and water temperature) as well as on aquatic ecosystem components (e.g., fisheries) on which northern communities depend.

However, the model predictions of Meyer et al. (1994) have major limitations because their meteorological forcing data were not applicable to this region, and the model results are ambiguous because they were not verified with measurements in the lake. Furthermore, large lakes such as Great Bear Lake exhibit significant horizontal and vertical variability in thermal structure and circulation; hence, the 1-D assumption is invalid. On the other hand, because of their sizes northern lakes will have significant impacts on the local weather and climate. Long et al. (2007) coupled the Canadian Regional Climate Model (CRCM) with lake models for the northern Great Lakes and conducted experiments to assess the impact of lakes on the regional climate. However, the impact of climate projections on the lakes was not assessed.

As part of the International Polar Year (IPY), intensive field observations were conducted to measure the surface meteorology, water currents and thermal structure on Great Bear Lake, including both ice-free and year-round measurements during 2008–09. This research represents the most intensive observational program conducted on Great Bear Lake to date. The primary purposes of this paper are to provide an overview of the hydrometeorological conditions; to describe the characteristics of the lake temperature field based on fixed and temperature autonomous moorings and satellite observations; and to develop and verify a 3-D hydrodynamic model for assessing the spatial and temporal variability in temperature and circulation of the lake. The combination of data and model simulations are used to assess the sensitivity of the lake to climate variability and to project potential changes in lake temperature based on a series of climate projections from the CRCM.

2 Observations and meteorological forcing

The meteorological measurements were conducted at several locations (Fig. 1) during the summer of 2008, which included air temperature, relative humidity, wind speed and direction, atmospheric pressure and precipitation. Solar and longwave radiation fluxes were also measured at Deline (M1) and on Lionel Island (M2). A total of three summer temperature moorings were deployed in Keith Arm. Additional “year-round” fixed temperature moorings were placed at the mouth of Keith Arm, the mouth of Smith-Dease Arm and in McTavish Arm. Autonomous Profiling EXplorer (APEX) temperature profilers were installed in proximity to these locations and were allowed to drift with the currents. The Global Positioning System (GPS) position and temperature profile data were transmitted via the Argos satellite. We chose a parking depth of 100 m for the APEX profilers to coincide with comparable depths at other fixed moorings. The profilers were programmed to ascend to the surface every three days for the entire year. This particular frequency maximized the operational longevity of the profilers. The multiple lake moorings provide relevant spatial representation to force and verify thermal and hydrodynamic models under current climatic conditions. The verified lake model will then be used to assess the thermal conditions in climate change scenarios.

The complexity of the terrain surrounding the lakes causes significant variability in atmospheric conditions. For example, the airflow is strongly affected by the different types of land cover surrounding the lake and the thermal structure of the atmosphere. These in turn can have a considerable impact on the lake hydrometeorological conditions. The two land-based stations in Keith Arm might not adequately represent the lake-wide meteorological forcing for 3-D hydrodynamic models. To help compensate for this, we also obtained 3-hourly output from the regional version of the Global Environmental Multiscale (GEM) model, which is used for operational forecasts in the region. The GEM model central domain has a uniform resolution of 15 km covering the entire North American continent and adjacent oceans. The regional forecast system is run at the Canadian Meteorological Centre (CMC) twice daily for 48 h forecasts. Although the forecast system does not include lakes explicitly, surface temperatures derived from satellite data are assimilated at 24 h cycles (Mailhot et al., 2006). The model forcing datasets are generated from 24 h forecasts of GEM at the surface (10 m). In order to assess the model forcing, the observed hydrometeorological variables at two stations were used.

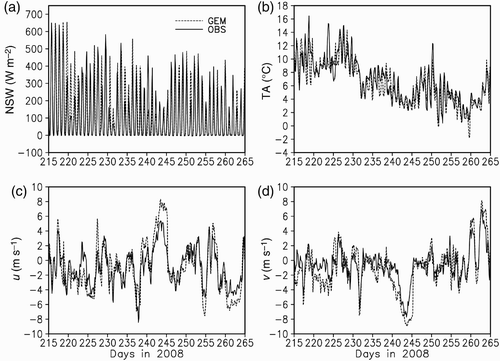
Figure 2 shows the comparison of 3-hourly time variations of the net radiation, air temperature and wind speeds from both GEM and from observations at M1 and M2. Here both the model forcing and observations are averaged at the two locations. In general, GEM forecasts follow the observed values fairly closely. However, on some occasions, GEM slightly overestimates solar radiation and wind speeds during a storm. For each variable at each station, the correlations between observations and the model are greater than 0.9. The averaged percentage differences in wind speeds between the GEM results and observations are 11% and 10.5% for the u and v components, respectively. However, as observed in Lake Ontario (Huang et al., 2010), the net heat flux from GEM and observations are quite close despite the treatment of the lakes as static.

Fig. 2 A comparison of time series of 3-hourly atmospheric variables averaged at stations M1 and M2 and GEM forecasted variables for August to September 2008.

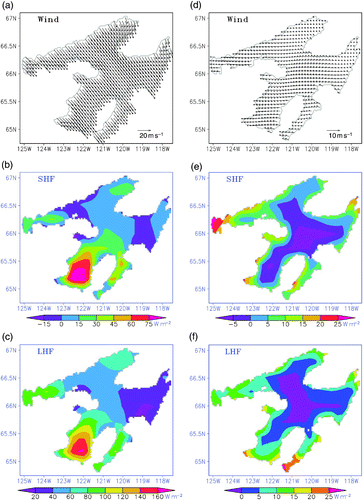
To depict the spatial variability of meteorological forcing, GEM-derived daily averaged wind fields and heat fluxes during a strong wind episode and a typical day in summer are shown in Figs 3a–3f. During the large northwesterly storm event on 31 August they were mostly uniform over the lake (Fig. 3a). However, significant spatial variation can be noticed in the heat fluxes. Figures 3b and 3c show that, in general, sensible and latent heat fluxes are positive during this period. Significantly higher values in Keith Arm are caused by larger air-lake temperature differences and higher wind speeds in this region. In contrast, during a typical summer day (3 September 2008) the winds were moderate and blowing from the west (Fig. 3d). Significant variability in both magnitude and direction can be noticed. During this period both sensible and latent heat fluxes are of comparable magnitude and distinctively different between coastal regions and deeper waters. The sensible heat flux is negative above the deep cold waters. These examples suggest that to simulate the physical processes realistically, it is essential to account for the spatial variability in meteorological forcing. Since the forecasted fields from the GEM are able to provide adequate forcing, it has been used to simulate the ice-free hydrodynamics in Great Bear Lake using a high-resolution, 3-D hydrodynamic model.

Fig. 3 The spatial distribution of 10 m wind vector, latent heat flux (LHF), sensible heat flux (SHF), at the surface produced by GEM on 31 August (left panels) and 3 September (right panels) 2008.

3 Numerical model

The lake hydrodynamic model is based on the latest version of the Princeton Ocean Model (POM) which was originally developed in the 1980s (Blumberg and Mellor, 1987). In a recent study Long et al. (2007) coupled a coarse resolution POM to the CRCM for Great Bear Lake and Great Slave Lake. Because of the success of the model in predicting surface temperature we chose to implement the same model for studying the thermal structure and dynamics of Great Bear Lake. The POM for Great Bear Lake has 31 vertical sigma levels and a uniform horizontal grid size of 2 km. The centres of the sigma levels are located at −0.0005, −0.0020, −0.005, −0.009, −0.015, −0.026, −0.036, −0.046, −0.057, −0.067, −0.078, −0.089, −0.10, −0.12, −0.122, −0.132, −0.142, −0.152, −0.162, −0.172, −0.182, −0.192, −0.2, −0.3, −0.4, −0.5, −0.6, −0.7, −0.8, −0.99, respectively. The version of POM used here is the same as the one used for Lake Ontario (Huang et al., 2010).

The conservation equations of heat, mass and momentum are solved by POM on an Arakawa C-grid using the finite differencing method. It uses a terrain-following vertical coordinate system (i.e., the sigma coordinate) scaled on the water column depth. The vertical mixing coefficients are determined by a level 2.5 turbulence closure parameterization (Mellor and Yamada, 1982). In this scheme, the vertical diffusivities for momentum (K_M ) and heat (K_H ) are defined according to K_M = lqS_M and K_H  = lqS_H , respectively; where l, the turbulent length scale and q ²/2, the turbulent kinetic energy (TKE), are solved by prognostic equations. The coefficients, S_M and S_H , are functions of the Richardson number. In addition, the sub-model for breaking wave TKE is injected into the surface (Mellor and Blumberg, 2004), but the recent wave-induced mixing (Mellor, 2008) is not introduced into this version. A mode splitting technique is used in POM, such that a shorter time step is used to solve the barotropic mode associated with the free surface, and a longer time step is used to solve the baroclinic mode relating to the 3-D temperature, turbulence and currents. The model uses the Smagorinsky (1963) eddy parameterization for horizontal diffusion, with the multiplier (horizontal turbulence Prandtl number) set to 0.1 (Mellor and Blumberg, 1985). The optical category of water is set to Jerlov's type I (Jerlov, 1976) for the shortwave radiation penetration because it produced better results than other categories (Huang et al., 2010). More information on the model is available in the POM Users’ Guide (Mellor, 2004).

At the lake surface, POM is forced by wind stress and surface net heat flux (SNHF). The SNHF is given by (Q):

where S is the absorbed solar radiation; NL is the net longwave radiation; LH is the latent heat flux and SH is the sensible heat flux. The east–west and north–south components of the wind stress are given by:

where |V| is the wind speed; u and v are the wind speed components in the east–west and north–south directions; ρ _a is air density; C_d = 1.3 × 10⁻³ is the drag coefficient (Huang et al., 2010). The surface latent heat flux and sensible heat fluxes are calculated using a common bulk formulation (Fischer et al., 1979) during model integration. The surface net longwave radiation is also calculated during model integration. Surface heat flux components are defined as positive when they tend to heat the lake. The salinity is set to a constant value of 0.2 (practical salinity scale used) to reflect the freshwater condition of the lake (Sheng and Rao, 2006). Atmospheric variables, including surface net shortwave radiation, 10 m wind components, air temperature and relative humidity and cloud cover, were used to force POM. A bilinear interpolation method was used to map the GEM forcing fields onto the POM grids. All the model runs start on 1 August and end on 30 September 2008. Considering that the vertical temperature gradients and spatial variability are very small in early summer, we initialized the model with a uniform value of 3.3°C based on observations.

4 Model validation

A total of nine numerical experiments (Table 1) were carried out based on different surface forcings and bottom topographies of the lake. The results from the observed forcing (OF) are first compared with the experiment driven by the GEM forecast. In the OF run, the average values of surface meteorological parameters at M1 and M2 are used as forcing for the model. For the atmospheric model forcing (CTRL), the lake model is driven by the spatially interpolated wind stress and heat fluxes from the GEM forecast. The model errors in simulating the surface temperatures are quantified using the root mean square error (RMSE) between the simulated and satellite-based Advanced Very High Resolution Radiometer (AVHRR) data. The RMSE is defined by:

Table 1. Summary of model sensitivity experiments.

Experiments	Heat Flux	Wind Stress	Bottom Bathymetry
CTRL	GEM Forcing	GEM winds	Real
OF	Observations	Average of M1&M2	Real
SEN1	SNHF × 1.2	GEM winds	Real
SEN2	SNHF × 1.4	GEM winds	Real
SEN3	SNHF = 0	GEM forcing	Real
SEN4	SNHF = 0	GEM forcing	Uniform
SEN5	GEM forcing	GEM forcing	Uniform
WSP	GEM Forcing	Wind Speed × 1.1	Real
WSN	GEM Forcing	Wind Speed × 0.9	Real

where and are modelled and observed water temperatures, respectively, for the sample case i (out of M sample cases). The RMSE values of the lake-wide average of surface temperatures are somewhat higher (0.84°C) in the OF experiment compared with GEM forcing (0.6°C). This is different from the Lake Ontario results (Huang et al., 2010), which showed that observed forcing was superior to GEM forecasts. The main reason for this discrepancy is the spatial limitation of the observations, which were obtained from two land-based stations, whereas the GEM output has a resolution of 15 km over the lake.

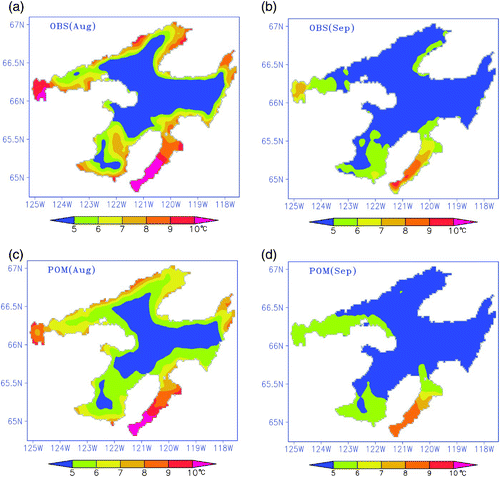
For these reasons, the GEM forcing experiment (CTRL) is considered for further verification of the hydrodynamic model. Monthly mean lake surface temperature (LST) from the CTRL run of the model is first validated against satellite-derived AVHRR data. Later, we compare the vertical thermal structure produced by the model with thermistor chain data. The use of two different datasets for the POM validation helps to evaluate both spatial and temporal variability of modelled temperatures. The August mean surface temperature shows strong variability with higher temperatures along the coast and temperatures between 4° and 5°C in the major offshore areas of the lake (Fig. 4a). Temperatures in the shallow regions (McVicar Arm and Smith Arm) are generally warmer (8°–10°C) compared to deeper offshore waters. In Keith Arm, temperatures are also higher in the shallow areas. During September (Fig. 4b), the observed surface temperatures varied between 8°C in the shallow waters and 4°C in the rest of the lake. Monthly surface temperature patterns obtained from the model are shown in Figs 4c and 4d for August and September, respectively. In general, the pattern of the modelled August temperatures was similar to the observations. However, model temperatures are somewhat cooler in Keith Arm and slightly warmer in the deeper waters. The mean September temperatures largely correspond with the observations. The possible cause of the discrepancy between model solutions and observations is that the satellite observations of skin temperature can be higher than the surface layer temperature as simulated by the model (Bussières and Schertzer, 2003).

Fig. 4 Near-surface temperature averaged over August and September 2008 from AVHRR data and the CTRL run, respectively.

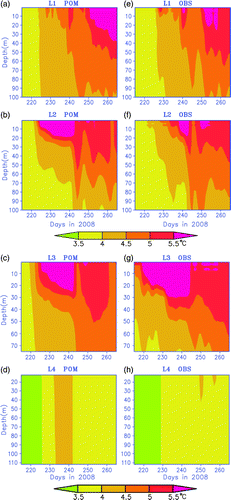
To examine the model skill in simulating the vertical thermal structure of temperature, the time-depth distributions of the simulated temperatures are compared with the observations made at four thermistor stations. Here, L1, L2 and L3 are located within Keith Arm and L4 is near the mouth of Keith Arm close to the main lake (McTavish Arm). The observations (Figs 5e–5h), during the brief summer, show that Keith Arm is isothermal (<4°C) until day 227 after which weak stratification forms. However, station L3 warmed up much earlier because of its shallow depth. In the main lake (L4), the water column appears to be isothermal and less than 4°C throughout the period except for a brief warming period on days 248 and 254. Therefore, as in temperate lakes (e.g., Rodgers, 1987; Rao et al., 2004) a thermal bar develops in Great Bear Lake dividing the stratified shallow areas of the lake from the unstratified deeper regions. Although the strength of the stratification (thermocline) is not strong, it is deeper in shallow areas (L3) compared to those in the deep water region (L1 and L2). The time-depth changes in water temperature from the model are presented in Figs 5a–5d. The dominant features of the evolving thermal structure of the water column are reasonably well captured by POM. In the coastal area the model is able to reproduce the wind-induced changes in the structure. Many studies on large temperate lakes (e.g., Huang et al., 2010) show that POM produces diffused thermoclines. However, since the stratification is weak in Great Bear Lake, the thermal structure produced by the model appears to be more representative.

Fig. 5 Time-depth distributions of the modelled and observed temperatures at moorings L1, L2, L3 and L4, respectively.

In the deeper waters of the main lake, observations from APEX profilers (A1, A2 and A3) show isothermal temperatures in the top 100 m of the lake (Figs 6a–6f). The APEX profilers returned temperature profiles at a resolution of 1 m every three days. The profilers moved from their initial positions because of surface and sub-surface currents. Figure 1 shows the locations of the profilers over the two-month period during the summer of 2008. Because model-generated temperatures are Eulerian in nature, we spatially averaged the model results within the grid boxes containing the APEX profilers for comparison with observations. The spatial averaging did not introduce significant errors because of the relatively uniform temperatures within the grid squares. The model errors in simulating the vertical thermal structure are quantified using the RMSE between the simulated and observed temperatures at stations L1, L2 and L3 (Fig. 7a) and APEX profilers (Fig. 7b). The RMSE ranges from 0.6°C at the surface to 0.1°C in the sub-surface. In general, the model produced smaller RMSE values below the wind-mixed layer. The ranges of model errors are similar to that of earlier POM simulations of the Great Lakes (Beletsky et al., 2006). Huang et al. (2010) noted that in the Great Lakes region, the slightly higher error of the simulation with GEM forcing is expected because GEM treats the lake as static, therefore, does not account for temperature variations in the mixed layer in the lake. However, these results show that this is not a major concern in the present simulation.

Fig. 6 Time-depth distributions of the grid-averaged modelled and observed temperatures at A1, A2 and A3, respectively.

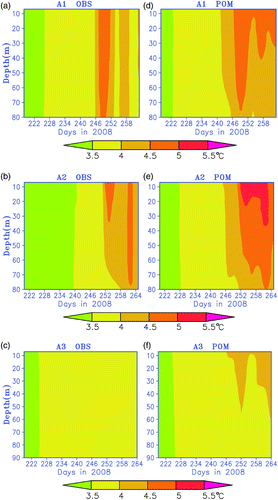
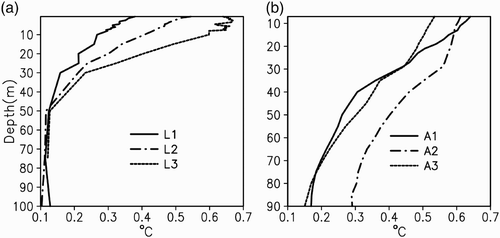
Fig. 7 The vertical distributions of RMSE between modelled and observed temperatures at the three temperature moorings (L1, L2 and L3) and the grids around the APEX profilers (A1, A2 and A3).

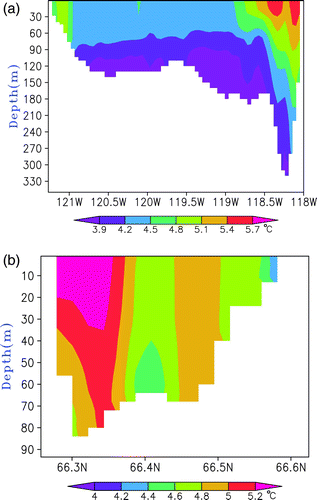
The model's ability to simulate short-term wind influence is further analyzed during a northwesterly wind episode on day 244 (Fig. 2a). On this day, surface heat losses caused by cold winds from the northwest increased the vertical mixing and resulted in a brief interruption of the warming cycle at stations L1 and L3. Although stratification is not prominent in the lake, cooler temperatures at the surface indicate upwelling along the western shoreline and possible downwelling along the eastern shoreline. This is clearly evident in Fig. 8a, where the water temperatures were plotted along a cross-section at 66.3°N. Further, the warmer waters penetrated to deeper parts of the lake along the eastern shoreline making the lake temporarily stratified. In the north–south transect (Fig. 8b), temperatures were cooler in the shallow regions of the northern shoreline and both downwelling and penetration of warmer waters close to the bottom is observed in the south. The model-simulated lake-wide temperature distributions during this period agreed well with satellite and mooring observations and were consistent with what one would expect with wind-forced dynamics. The spatial differences in temperature are significant and are probably influenced by the circulation in the lake. Furthermore these temperature differences will influence the air-water exchanges in the climate models.

Fig. 8 Cross-section of the modelled water temperature from the CTRL run on 31 August 2008 (a) along 66.3°N and (b) along 122°W.

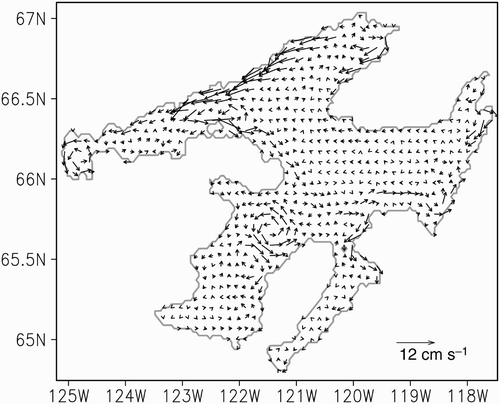
The summer mean circulation predicted by the model shows cyclonic circulation in the lake (Fig. 9). These characteristics are qualitatively similar to the lake-wide circulation in the Laurentian Great Lakes, which is attributed to both wind stress curl and baroclinic forcing in the closed basins (Beletsky et al., 1999).

Fig. 9 The seasonal mean (averaged over August to September 2008) of depth-averaged currents.

5 Sensitivity of model results to meteorological forcing

The sensitivity of the model in predicting temperature and circulation in Great Bear Lake with different surface forcing fields has not been previously tested. Further, to understand the potential effects of climate warming on lake temperatures, sensitivity experiments with incremental increases in meteorological forcing are very useful in providing a range of projections. In this study, we examine the sensitivity of the POM model simulations by increasing and decreasing net heat fluxes by 20% and 40% and winds by ±10% (Table 1). However, only two sensitivity runs are presented in this section because our main focus is understanding the effect of climate warming on the lake. As discussed in the previous section, the GEM forecast was used to drive the CTRL run; therefore, the same forcing was used to drive the sensitivity runs. All the model runs in the sensitivity tests also start on 1 August and end on 30 September. Because the vertical temperature gradients and spatial variability are very small in early summer, the initial temperatures were simply initialized at 3.3°C everywhere just as they were in the CTRL run.

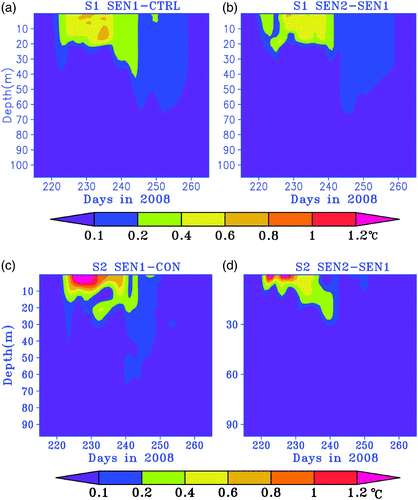
Figure 10 shows that at station S1, the temperatures in the upper water column increased by a maximum of 0.7°C with a 20% increase in the net heat flux from the control run. The seasonal thermocline was established at much shallower depths (approximately10 m) for a slightly longer period than for the base conditions. However, in the offshore zone, the temperatures increased more significantly at the surface and were higher than 5°C from day 226 to day 239. A further increase in net heat fluxes to 40% greater than the control run increased the temperatures in the epilimnion but did not show significant increases below the thermocline. In general, these sensitivity experiments revealed that the temperatures in the upper water column increased by 5%–7% with a 20% increase in the net heat flux with noticeable changes in the epilimnion at S1, whereas at S2 it increased by 7% only close to the surface. The model is also run with increasing (WSP) and decreasing (WSN) wind speeds by 10% (figures not shown). By comparison, increasing (decreasing) the wind speed by 10% results in decreasing (increasing) the surface temperature by 0.1°C. However, temperatures increased at sub-surface depths by 0.3°C because of a deeper mixed layer with a 10% increase in winds, whereas a 10% decrease in winds did not show much variation. These results are more or less consistent with the sensitivity studies carried out for Lake Ontario (Huang et al., 2010).

Fig. 10 Time series of the vertical distribution of temperature differences between sensitivity experiments and the CTRL runs.

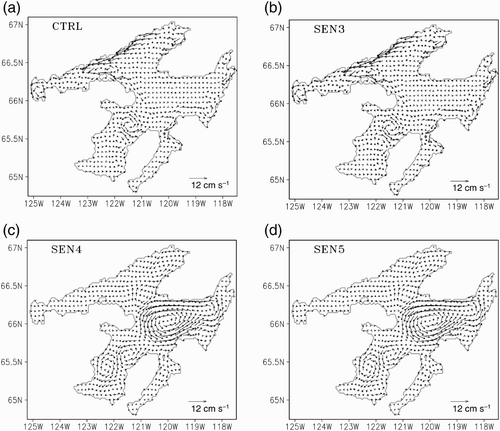
To assess the circulation we carried out sensitivity runs (Table 1) with uniform bathymetry at mean lake depth, with and without heat fluxes. Only the main characteristics are discussed here. During the simulation period, winds are primarily from the northwest with occasional strong northerly winds (see Figs 2c and 2d). Although horizontal temperature gradients are small in the main part of the lake, small gradients exist between near-shore and offshore areas. Because of the effect of lake surface temperatures on atmospheric stability and the presence of horizontal temperature gradients in the lake, even a spatially uniform wind field exerts wind stress with positive vorticity during summer. Although this may play a role in the cyclonic circulation in the lake, its effect cannot be assessed in this study. The water column shows stratification in the coastal areas and is isothermal in the major part of the lake. However, the mean circulation is not significantly different between model runs with and without the heat fluxes. Further, modelled surface currents are similar to those at depth. This suggests that the currents are primarily barotropic during summer, and the horizontal density gradients are not important in generating the mean circulation. This is in contrast to the Laurentian Great Lakes, which are influenced by both barotropic and baroclinic forcings during summer (e.g., Simons, 1980). The topography of the lake plays a major role in the wind-driven circulation (Fig. 11: SEN3). In the flat-bottom case (SEN4 and SEN5), the main cyclonic gyre is shifted to mid-lake (Figs 11c and 11d). The strong coastal currents along the north shore are absent for the model runs with and without heat fluxes. Further cyclonic and anticyclonic gyres in Keith Arm are slightly stronger than the real bathymetry simulations. Therefore, it appears that the circulation in the lake is mainly driven by winds and the gyres are the barotropic response of the changing depth.

Fig. 11 The seasonal mean of depth-averaged currents averaged over August to September 2008 for various sensitivity runs described in Table 1.

6 Impact of climate change on the thermal structure of Great Bear Lake

The projected changes in the climate (IPCC, 2007) will have a range of impacts on the thermal characteristics of lakes in different regions of the world. Over the years, a variety of 1-D models have been used to explore the potential impact of climate change on lakes. These include studies by Hondzo and Stefan (1993), De Stasio et al. (1996) and Stefan et al. (1996) in North America and Perroud et al. (2009) and Peeters et al. (2002) in Europe. In thermally stratified lakes, these predict substantial increases in the epilimnetic temperatures, earlier onset of stratification and increases in the duration and strength of stratification and consequent changes in the length of the ice-free period. The projected changes in hypolimnetic temperatures are less consistent with decreases as well as increases in temperature being recorded in some stratified lakes.

McCormick (1990) applied a 1-D mixing model to study the potential future temperature structure of Lake Michigan using the conditions at that time and the Global Climate Model (GCM) scenarios for doubled CO₂ concentrations. The model results suggested sharper temperature gradients at the thermocline and increased duration of summer stratification. A similar approach was used by Boyce et al. (1993) for Lake Ontario to examine the thermal response under present conditions and a hypothetical climate change scenario based on output from the Canadian Climate Centre Model (CCCII GCM). Their model results suggested an increase in surface water temperatures and prolonged stratification in Lake Ontario. In the context of the northern Great Lakes, although the potential impacts of climate warming on the lake circulation and temperature are not assessed, Long et al. (2007) developed a coupled model to study the interactions of lakes and the atmosphere. In their coupled model, the lake effect on the regional climate is studied for the MAGS period, but the thermal structure of the lake as a result of climate warming is not assessed.

Potential future changes in climate over Great Bear Lake were obtained from the latest set of global climate model simulations produced for the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4) (IPCC, 2007). Results from several GCMs are available for this region. However, GCM results have to be downscaled to the region either by statistical or dynamical downscaling methods. The CRCM is driven by the output from the second generation Canadian Global Climate Model. The CRCM is applied at a resolution of 45 km horizontal grid size over North America, and the surface is treated as land with surface temperatures from the Canadian Meteorological Centre's analyses. The climate projections are based on the twentieth century scenario (20C3M) for the period 1971–2000 and the Special Report on Emissions Scenarios (SRES) A2 scenario for the period 2001–2100 (EC, 2010) for these simulations. Although Scenario A2 leads to a relatively large increase in the global surface mean temperature by the end of the century, this closely resembles the studies using doubled CO₂ concentrations (IPCC, 2007). Therefore, in this study, we use 6-hour outputs from CRCM simulations of two emission scenarios, respectively. The climate scenario runs (SR) are forced by a future warmer climate (2041–70) and the base climate runs used 1971–2000 outputs from scenarios produced by the CRCM. Atmospheric variables including surface net shortwave radiation, 10 m wind components, air temperature and relative humidity and cloud cover were used to force the POM. As might be expected, the most pronounced change was that projected for air temperature and the largest differences were those associated with the more extreme A2 scenario.

In the base run (BR) the water temperatures were initialized at 3.3°C on 1 August and simulations were continued until 30 September, similar to the CTRL run. However, for the future climate projection run (SR), initial water temperatures were not available. Meyer et al. (1994), based on simulations from the GFDL, show that with a projected increase in air temperature of 9°C, the period of ice cover on the lake will be reduced to 65% from the current conditions. This is an increase of 60 days for open-water conditions in the lake. Since an ice model is not available in the current POM, we used a simple response temperature model to obtain the initial lake temperatures for the hydrodynamic model.

The rate of change of temperature (dT/dt) can be written in terms of the net rate of surface heat exchange as dT/dt = Q/(Dρ _w Cp), where Q is defined in Eq. (1), D is the depth of the upper mixed layer, taken as 45 m (Rouse et al., 2008), ρ _w is the density of fresh water and Cp is the specific heat of water at constant pressure. Because this model does not include a lake-ice component, we assumed that complete ice cover on the lake occurs after the water temperature reaches 0°C. The model achieved satisfactory calibration with 2007 data for the lake-wide average surface temperature (RMSE = 0.4°C) during the open-water period. Therefore, this is suitable for generating initial conditions for future climate scenarios. Using the model, we obtained an initial water temperature of 3.3°C on 29 June. The water temperature reached a maximum of 6.2°C on 8 August and became ice covered (0°C) on 4 November in this scenario. Therefore, for future climate scenarios (SR), the POM model was run between 29 June and 30 September 2008.

Figure 12a shows the difference in surface temperatures between the future climate scenario run and the base run. The largest increases in surface temperature (>2°C) were observed in the northeast corner of Great Bear Lake and near the southern shoreline (1°–1.5°C) in Keith Arm. In the major part of the lake, surface temperatures in the future climate scenario increased by only 0.5°–1°C. The increase in water temperature is confined to the upper 5–10 m of the water column (not shown). Stratification appeared briefly in the deep water with a surface temperature over 4.5°C between 9 and 24 August. The difference in net surface heat flux produced by the CRCM future climate scenario shows that heat fluxes in the northeast corner are larger (10–14 W m⁻²) than in other regions of the lake (Fig. 12b). This spatial distribution of heat fluxes compares well with the surface temperature distribution in the future climate.

Fig. 12 The spatial distributions of the difference in (a) lake surface temperature and (b) surface net heat flux between SR and BR experiments.

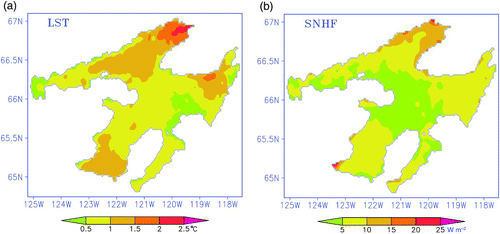
The changes in climatic variables influence the flux of heat between the atmosphere and the lake in different ways (Figs 13a to 13d). The change in net longwave radiation and sensible heat flux accompanying the future climate scenario is much larger than the changes in the net shortwave radiation and latent heat flux. The predicted spatial distribution of both the net longwave radiation (NLW) and sensible heat flux (SHF) coincide well with the spatial distribution of surface temperatures in the lake. The increase in air temperature gives rise to increases in the sensible heat flux and the downward longwave radiation. The net result creates an increase in water temperature.

Fig. 13 The spatial distributions of the differences in the components of the heat fluxes between SR and BR experiments averaged over the entire simulation period.

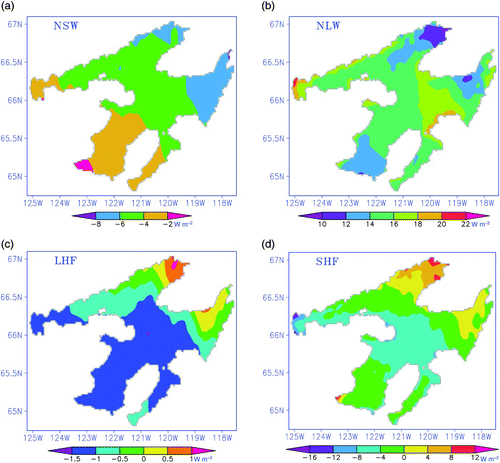
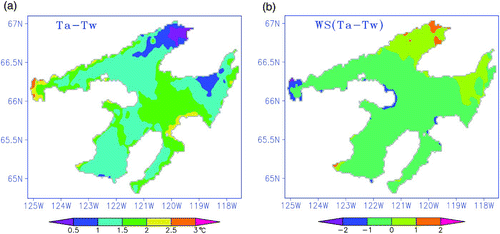
The calculation of the gradient of air and lake temperatures (DT = Ta − Tw) in the warming scenario (Fig. 14a) indicates that the temperature gradient is consistent with the spatial distribution of net longwave radiation. Similarly, the sensible heat flux difference agrees well with the differences in the product of wind speed and DT (Fig. 14b). Therefore, the increase in water temperature caused by climate warming in Great Bear Lake is primarily a result of a positive increase in the net longwave radiation and sensible heat flux, which resulted from the product of wind speed and the temperature gradient between air and lake.

Fig. 14 The spatial distributions of the differences between the SR and BR experiments averaged over the entire simulation period for (a) air-water temperature and (b) the product of wind speed and the temperature gradient.

7 Summary and conclusions

Meteorological and limnological data were collected during an intensive field program in Great Bear Lake during the 2008–09 period. These data represent the most intensive and spatially distributed measurements conducted on this lake to date. The data formed the basis for verification of a 3-D model that simulates temperature and currents in Great Bear Lake under present conditions and the extension of the model to assess the potential impacts of a change in climatic conditions on lake temperature.

Meteorological observations at Deline (M1) and Lionel Island (M2) within Keith Arm were not spatially representative of the whole-lake case for the purposes of 3-D modelling. Consequently, output from the regional version of the GEM was used. Hourly time variations in principal variables such as net radiation, air temperature and wind speeds from GEM compared well with land-based observations at M1 and M2, with correlations exceeding 0.9. Atmospheric model forcing is based on spatially interpolated wind stress and heat fluxes from the GEM forecast.

Lake temperatures were derived from fixed moorings and autonomous temperature profilers. Surface temperature was derived from AVHRR satellite observations. The multiple lake moorings provided relevant spatial representation to force and verify thermal and hydrodynamic models under current climate conditions. With respect to lake-wide averaged surface temperature, the RMSE values from GEM forcing were lower (0.6°C) compared with results using observed forcing (0.84°C). Consequently, for sensitivity experiments, the forcing from the GEM model was used as the control experiment.

The in-lake data were used to validate a high-resolution 3-D hydrodynamic model (POM). The atmospheric forcing for POM is derived from a regional configuration of the Canadian atmospheric forecasting model GEM. The GEM model forecast forcing shows considerable skill in reproducing the observed time variations in surface temperature and the vertical stratification conditions on synoptic and seasonal time scales. The model simulates significant spatial variability in surface temperatures with warm shallow coastal areas (8°–10°C) compared to cooler offshore waters (approximately 4°C) during summer. The model also predicted thermal stratification in the coastal areas and isothermal conditions in the deeper parts of the lake. Furthermore, the model results confirm that Great Bear Lake coastal dynamics are similar to temperate lakes with upwelling and downwelling cycles during favourable wind conditions. The model also predicts mean cyclonic circulation reasonably well. These results show that some parts of the lake undergo stratification and de-stratification; however, the deeper cooler waters have temperatures close to 4°C and do not vary significantly during the year.

Model sensitivity experiments reveal that increasing the surface net heat flux causes an increase in water temperature that is confined to the surface and near-surface layers in the coastal regions. In the deeper waters the increase in surface temperature is comparatively weaker, but exceeds 5°C resulting in brief stratification. By comparison, increasing (decreasing) the wind speed by 10% results in decreasing (increasing) the surface temperature. Sub-surface warming is possible with higher winds.

Potential changes in the thermal structure of Great Bear Lake as a result of future changes in the climate of the region were assessed by using the output from the latest set of GCM simulations. Two scenarios from the CRCM for the base climate (1970–2000) and the future warmer climate (2041–70) were used for this purpose. The surface temperatures increased by over 2°C in the northeast corner, whereas in the rest of the lake the increases were around 0.5°–1°C. In general, slight warming is observed in the upper 5–10 m of the water column. The results show that brief thermal stratification is possible in the deeper waters. The increase in water temperature caused by climate warming in the lake appears mainly because of the positive increase in net longwave radiation and sensible heat flux, which resulted from changes in the air-to-lake temperature gradient and slightly reduced wind speeds in the climate projections.

The present study focused on the brief open water conditions in the lake. The response of deep cold monomictic Great Bear Lake to projected changes in climate warming needs to be analyzed in the long term. An ice component is needed to simulate the lake state in winter. In summary, we believe that the model shows promise in simulating the lake dynamics reasonably well. Therefore, this model is suitable for assessing the impacts of climate warming in deep polar lakes. Long et al. (2007) showed that coupling similar lake models will improve the regional climate predictions. This is encouraging for further development of the coupled atmosphere–lake modelling system for the Mackenzie River Basin.

Acknowledgements

The authors wish to thank Normand Bussières for providing the satellite data for Great Bear Lake. Tony Zhang helped in processing the data for the lake model. Research Support Branch of the National Water Research Institute (NWRI) provided technical support for the field deployments. Funding for field measurements was obtained from Environment Canada's contribution to the IPY program. Anning Huang is supported by a Natural Sciences and Engineering Research Council (NSERC) Visiting Fellow program to Canadian government laboratories.