A Time-Averaged Covariance Method in the EnKF for Argo Data Assimilation

Abstract

In the ensemble Kalman filter (EnKF), ensemble size is one of the key factors that significantly affects the performance of a data assimilation system. A relatively small ensemble size often must be chosen because of the limitations of computational resources, which often biases the estimation of the background error covariance matrix. This is an issue of particular concern in Argo data assimilation, where the most complex state-of-the-art models are often used. In this study, we propose a time-averaged covariance method to estimate the background error covariance matrix. This method assumes that the statistical properties of the background errors do not change significantly at neighbouring analysis steps during a short time window, allowing the ensembles generated at previous steps to be used in present steps. As such, a joint ensemble matrix combining ensembles of previous and present steps can be constructed to form a larger ensemble for estimating the background error covariance. This method can enlarge the ensemble size without increasing the number of model integrations, and this method is equivalent to estimating the background error covariance matrix using the mean ensemble covariance averaged over several assimilation steps. We apply this method to the assimilation of Argo and altimetry datasets with an oceanic general circulation model.

Experiments show that the use of this time-averaged covariance can improve the performance of the EnKF by reducing the root mean square error (RMSE) and improving the estimation of error covariance structure as well as the relationship between ensemble spread and RMSE.

RÉSUMÉ [Traduit par la rédaction] Dans le filtre de Kalman d'ensemble (EnKF), la taille de l'ensemble est l'un des facteurs clés qui ont une influence importante sur la performance d'un système d'assimilation de données. Il faut souvent choisir une taille d'ensemble assez petite à cause des limites des ressources informatiques, ce qui biaise souvent l'estimation de la matrice de covariance de l'erreur de fond. Cette question revêt une importance particulière pour l'assimilation des données Argo, qui fait souvent appel à des modèles de pointe très complexes. Dans cette étude, nous proposons une méthode de covariance moyennée dans le temps pour estimer la matrice de covariance de l'erreur de fond. Cette méthode suppose que les propriétés statistiques des erreurs de fond ne changent pas de façon importante d'une étape d'analyse à la suivante durant un court laps de temps, ce qui permet d'utiliser dans les étapes courantes les ensembles générés aux étapes précédentes. Ainsi, on peut construire une matrice d'ensembles conjoints combinant les ensembles des étapes précédentes et courantes pour former un plus grand ensemble dans le but d'estimer la covariance de l'erreur de fond. Cette méthode peut accroître la taille de l'ensemble sans augmenter le nombre d'intégrations du modèle; elle équivaut à estimer la matrice de covariance de l'erreur de fond en utilisant la covariance moyenne de l'ensemble calculée sur plusieurs étapes d'assimilation. Nous appliquons cette méthode à l'assimilation des ensembles de données Argo et d'altimétrie avec un modèle de circulation océanique générale.

Des essais montrent que l'emploi de cette covariance moyennée dans le temps peut améliorer la performance de l'EnKF en réduisant l’écart-type et en améliorant l'estimation de la structure de la covariance de l'erreur de même que la relation entre l'étalement et l'écart-type l'ensemble.

Keywords:

• Argo
• EnKF
• covariance matrix
• data assimilation

1 Introduction

Since the ensemble Kalman filter (EnKF) was proposed by Evensen (1994), it has been widely applied in oceanography, meteorology and other fields (Bonavita, Torrisi, & Marcucci, 2010; Deng, Tang, & Wang, 2010; Oke, Brassington, Griffin, & Schiller, 2008; Oke, Schiller, Griffin, & Brassington, 2005; Ott et al., 2004; Reichle, Mclauglin, & Entekhabi, 2002). An important issue in the application of the EnKF is the achievement of a realistic range of ensemble members from which the background error covariance is diagnosed (Turner, Walker, & Oke, 2008). A larger ensemble can generally result in a smaller error level and improve agreement between ensemble spread and ensemble mean error (Mitchell & Houtekamer, 2002). However, the high computational cost often makes a large ensemble impractical in a realistic data assimilation system and forces modellers to choose a relatively small ensemble size. Unfortunately, a small ensemble often causes problems, such as underestimating the amplitude of background error covariance and generating very noisy correlation functions (Mitchell & Houtekamer, 2002). A number of techniques have been proposed to reduce the negative effects of the small ensemble; for example, the covariance localization and covariance inflation methods (Anderson & Anderson, 1999; Hunt, Kostelich, & Szunyogh, 2007; Mitchell & Houtekamer, 2000). Houtekamer and Mitchell (1998) found that the smaller the ensemble, the more severe the localization required to address noisy covariance. Over-localization may generate severe imbalance between state variables and excite unrealistic gravity waves (Mitchell & Houtekamer, 2002), causing strong initial shock when assimilation analyses are used to initialize forecasts and, in turn, this results in a sharp decrease in forecast skill. Thus, a challenge in the EnKF assimilation is to find an appropriate compromise between sufficient ensemble members and computational cost.

One approach to allowing sufficient ensemble members without sacrificing computational efficiency is the Ensemble Optimal Interpolation (EnOI), which was proposed and applied in some data assimilation systems (e.g., Evensen, 2003; Oke, Allen, Miller, Egbert, & Kosro, 2002). This approach assumes that the temporal variability of model states is representative of the forecast error; thus, the analysis is computed in the space spanned by a stationary ensemble of sampled model states (e.g., during a long model integration). The drawback of this method is that the spatial structure of the covariance matrix is assumed to be constant over the assimilation cycles, thus, it cannot reflect the temporal evolution of forecast error.

In this study, we propose a method to increase ensemble size without extra model integrations and use it to assimilate Argo profiles and satellite sea level anomaly (SLA) data into a realistic oceanic general circulation model. The rest of this paper is organized as follows. Section 2 briefly describes the data, model and assimilation system; Section 3 addresses the evaluation methods; Section 4 explores the impacts of this method on the performance of the EnKF; and a summary and concluding remarks are presented in Section 5.

2 The ocean data assimilation system

a Data

The data used for assimilation are the best-copy temperature and salinity profiles (hereafter BCTS) and the delayed low-resolution (1° × 1°, Mercator grid) gridded SLA of the Pacific Ocean derived from satellite altimetric data for the period 2005–07 (Dibarboure, Lauret, Mertz, Rosmorduc, & Maheu, 2009). The BCTS data assembles profiles from Argo floats, expendable bathythermographs (XBT), conductivity-temperature-depth (CTD) sensors and the Tropical Atmosphere and Ocean-TRIangle Trans-Ocean buoy Network (TAO/TRITON) to provide the most complete datasets without duplication. These profiles are downloaded from NOAA (2009a). Only the profiles that are flagged “good” are chosen for assimilation.

The SLA data are a homogeneous, inter-calibrated and highly accurate long time series of SLAs from altimetric data downloaded from Aviso (2009). Because the resolution of the SLA data is much higher than the model resolution in most of the model domain, a thinning scheme is used to reduce the resolution of the SLA data assimilated. The datasets used for validation include the Ocean Surface Current Analyses—Real time (NOAA, 2009b); NODC_WOA98 (Levitus) data (NOAA, 2009c) and the observed Niño3.4 Sea Surface Temperature Anomaly (SSTA) index (NOAA, 2009d). The surface current is derived from satellite altimeter and vector wind data, and its details are described by Bonjean and Lagerloef (2002) and Helber, Weisberg, Bonjean, Johnson, and Lagerloef (2007). The delayed mode Argo profiles (NOAA, 2009c) and SLAs (Aviso, 2009) for the period 2002–04 are also used in this study for estimating the root mean square error (RMSE) of the control run, which will be used to estimate the amplitude of the additive model error.

b The Ocean General Circulation Model (OGCM)

The OGCM is the ocean component (with free-surface) of version 2.3 of the Nucleus for European Modelling of the Ocean (NEMO; Madec, 2008). It is constructed based on the ORCA2 configuration. Both global and regional versions of the model are used. The former is for climatology runs and the latter is for control and assimilation runs. The regional model is a subset of the ORCA2 configuration covering the Pacific Ocean between 60°N and 60°S and between 116°E and 66°W, for a total of 90×95 horizontal grid points. The horizontal resolution in the zonal direction is 2°, while the resolution in the meridional direction is 0.5° within 5° of the equator, smoothly increasing to 2.0° at 30°N and 30°S and then decreasing to 1.0° at 60°N and 60°S. There are 31 unevenly spaced levels along the vertical with 24 levels concentrated in the upper 2000 m. The interval of the levels varies from 10 m near the “surface” (within the first 105 m) to 500 m below the 3000 m level. The maximum depth is set to 5000 m, and a realistic topography based on the Earth Topography at 5 arc-minutes (ETOPO5) global atlas is used (Ferry, Rémy, Brasseur, & Maes, 2007). The National Centers for Environmental Predication (NCEP) reanalysis wind stress (Behringer, Ji, & Leetmaa, 1998; NOAA, 2009e) and monthly climatological heat and freshwater fluxes (Esbensen & Kushnir, 1981) are used to force the model. During the integration, the heat flux Q_s is adjusted by

where Q ₀ is the climatological heat flux, T is the model SST, T ₀ is the Levitus climatological SST (Levitus & Boyer, 1998), and λ is the relaxation rate, set to −40 W m⁻² K⁻¹. For a 50 m mixed-layer depth, this value corresponds to a relaxation time scale of 2 months (Madec, 2008).

To reduce the model bias in temperature and salinity, two nudging schemes were used. First, the global version of the OGCM, started from rest, is nudged (with a relaxation time scale of 20 days) towards the Levitus climatological temperature and salinity using the conventional nudging method and the climatological winds for 10 years. Second, the spectral nudging method, proposed by Thompson, Wright, Lu, and Demirov (2006), is used to nudge the global model towards the same climatology at the prescribed frequency of 0.1 cycles per year for 50 years. The seasonal cycle of monthly mean currents derived from the above spectral nudging run of the last 30 years and the seasonal cycles of Levitus climatological temperature and salinity are used to generate the east, west, south and north boundary conditions for the regional OGCM, as proposed by Madec (2008). Furthermore, the regional OGCM, with the same spectral nudging scheme and the initial conditions from the last step of the spectral nudging run of the global model, is forced by the observed (NCEP reanalysis) winds for the period 1980–2004 (control run). The model states are stored every 5 days during the 1985–2004 period (the first 5-year runs are discarded to extract the stable model states) to construct a pool used to generate additive random noises for assimilation runs. Starting from 31 December 2004, two types of runs are conducted from January 2005 to December 2007: 1) the control run without data assimilation, as a reference for the validation of the assimilation system, and 2) the assimilation runs.

To evaluate the effects of spectral nudging on model climatology, we also conducted a control run for the period 1980–2004 using the regional OGCM without the nudging scheme. The initial condition is from the last step of a 200-year climatology run of the global model without nudging starting from rest. The boundary conditions are provided by the mean seasonal cycle of the last 30 years of the 200-year climatology run. The 25-year outputs from the two control runs were used to represent their respective climatologies.

c The Data Assimilation System

The data assimilation system is based on the EnKF (Evensen, 1994, 2003). The forecast ensemble member is updated by

where M is the non-linear model, is the analysis of the i ^th ensemble member at assimilation cycle k-1 and q _{k , i} is the model error. Then, the subsequently analyzed state for the i ^th member at the k ^th assimilation cycle is

where y _{k , i} is a perturbed observation that will be defined by Eq. (12) below; H is a linear operator that converts the model state to the observation type and location; and K _k is the Kalman gain, which is estimated by (Deng et al., 2010; Evensen, 2003);

where is the background error covariance matrix and R _k is the observation error covariance matrix. In this study, the state X is composed of five component variables, including temperature (T), salinity (S), zonal current (U), meridional current (V) and SLA. The ensemble size for the standard experiment (N) is 31, and the assimilation interval is 5 days.

The localization method proposed by Houtekamer and Mitchell (2001) is used to speed up the analysis processes and eliminate the spurious correlation between distant locations in the background covariance matrix due to the limited ensemble size (e.g., Deng et al., 2010; Gaspari & Cohn, 1999; Houtekamer & Mitchell, 2001; Hunt et al., 2007; Oke et al., 2005, 2008). This localization method assimilates all observations that may affect the analysis of a given model grid point simultaneously and obtains the analysis independently for each model grid point (Ott et al., 2004; Szunyogh et al., 2008). In this study, we perform local analysis grid by grid for the top 24 model levels. To obtain the analysis at a model grid point, we define a local domain around the model grid point, and all observations within this domain are assimilated. The domain is 3000 km in longitude, 1500 km in latitude and three model levels in the vertical. The grid point is at the centre of this domain. The incremental analysis update (IAU) proposed by Bloom, Takas, da Silva, and Ledvina (1996) is also used to avoid model dynamical instability, which incorporates the analysis increment directly into prognostic equations of the model as an additional forcing term (Balmaseda, Anderson, & Vidard, 2007; Castruccio, Verron, Gourdeau, Brankart, & Brasseur, 2008). As in Keppenne, Rienecher, Kurkowski, and Adamec (2005), the analysis increment is added to the model state gradually over the 5-day integration. In this study, there are a total of 120 integration steps in the 5-day window. Thus, each integration step accounts for only 1/120 of the increment. To reduce the burden of computation, the assimilation domain is set to the region 116°E–66°W and 30°S–55°N. In the following, we briefly describe the estimation methods used to obtain the model error (q _{k , i} ), the background error covariance matrix () and the observation error covariance matrix (R _k ), respectively.

1 Model Errors

Usually, the model error is composed of systematic errors resulting from imperfections in the physics or dynamics of the model and random errors caused by stochastic noise. In this study, we consider only the latter in assimilation experiments because the former could be expected to be greatly reduced by the spectral nudging scheme.

An important issue in the EnKF is to characterize realistic correlation structures in designing the random model error (q _{k , i} ) in space (horizontal and vertical) and among model variables. Evensen (2003) proposed a simple method to construct a spatially coherent random error (perturbation) that has been widely used in the EnKF. A challenge in applying this method is the determination of the de-correlation scales characterizing the coherences between different variables and different model levels. In this study, we propose an approach to generating a random model error ensemble that can characterize the coherent structure. Theoretically, the random model error covariance at the k ^th assimilation cycle can be decomposed as

where W is the correlation structure and Λ is the variance of the error, representing the error amplitude, and Z is an augmented ensemble, composed of T, S, U, V and SLA. Each element of Z is the departure of the corresponding model variable from its temporal mean (model seasonal cycle), normalized by its standard deviation, obtained from the control run. During the control run period, 1985–2004, we store output every 5 days to form a pool, as mentioned in Section 2b. Thus, the perturbation fields are constructed by randomly taking a Z from the pool, multiplied by the amplitude Λ ^1/2.

The perturbation amplitude has a significant effect on the performance of the EnKF. A large perturbation amplitude may overestimate random model error, whereas a small amplitude could quickly damp the perturbation, leading to very small ensemble spreads. A straightforward strategy is to assume that the perturbation amplitude is proportional to the RMSE of the model simulation. For temperature, salinity and SLA, the RMSE could be estimated from the control run against their observed counterparts. However, there are insufficient observations to estimate RMSEs for U and V, and thus, their perturbation amplitudes were approximated using their climatological variances from the control run instead of the RMSE values. For simplicity, we only consider the vertical variations of the perturbation amplitudes. We calculate the RMSE for each model level using all paired observation-model data for the period 2002–04 at that level and average the standard deviations over the horizontal model domain to obtain their vertical profiles. After a few sensitive experiments with different combinations of the perturbation amplitudes, we set the amplitude Λ ^1/2 to 10% of the RMSE for temperature and salinity at each vertical level and 0.013 m for SLA (10% of SLA RMSE). We set 10% of the standard deviations of U and V as their perturbation amplitudes. It should be noted that these settings are somewhat artificial but were tuned by the sensitive experiments towards the best assimilation performance for the 31-member standard EnKF experiment (hereafter referred to as Exp1), which will act as a reference experiment for comparisons.

2 Background Error Covariance Matrix

In this study, the background error covariance matrix at an assimilation step (k) is estimated using an enlarged ensemble, formed by ensemble members at neighbouring steps k, k − 1 and k − 2. This method increases the ensemble size without increasing the number of model integrations. Thus, it is computationally efficient except that slightly more disk space is required to store previous ensemble members. In principle, this method is somewhat similar to the EnOI but treats the assumption of the background error covariance structures differently. It assumes only that the error covariance structures are similar within a short time window of three neighbouring assimilation steps. The background error covariance estimated from the enlarged ensemble is equivalent to the mean covariance averaged over the neighbouring assimilation steps. Thus, the time-averaged covariance will not significantly modify the main structure of the covariance matrix but can effectively filter the noisy components of the error covariance matrix. It should be noted that this time-averaged covariance is used only to estimate the background error covariance matrix and that all other procedures are kept in the framework of the standard EnKF.

Thus, the model background error covariance matrix at the k ^th assimilation cycle is calculated from the ensemble members by

where

and

N = 31 is the number of ensemble members at each assimilation cycle. indicates the covariance matrix of the enlarged ensemble consisting of J sets of deviation ensemble members. In this study, J at the values of 1, 2 and 3 corresponds to experiment 1 (Exp1), experiment 2 (Exp2) and experiment 3 (Exp3), respectively. Thus, the corresponding covariance is calculated using the 31 ensemble members of the current assimilation cycle (k), 62 and 93 ensemble members, obtained from the current assimilation (k) and the previous one (k − 1) and previous two (k − 1 and k − 2) assimilation cycles. Exp1 is the standard EnKF method, and the background error covariance matrix in Exp2 (or Exp3) is just the mean covariance matrix averaged over 2 (or 3) neighbouring assimilation steps. The differences in the three experiments originate only from the differences in the calculation of the background error covariance matrices, as indicated by the value of J in Eq. (5).

The covariance localization function used to reduce spurious correlations between distant locations due to the limited ensemble size is assumed to be Gaussian and defined as below (e.g., Deng et al., 2010; Gaspari & Cohn, 1999; Houtekamer & Mitchell, 2001; Oke et al., 2005):

where dx, dy and dz are the distances between the analysis grid and its surrounding grids in the zonal, meridional and vertical directions, respectively. The localization length scales are set to Lx = 3000 km × cos (θ), Ly = 1500 km × cos (θ) and Lz = 100 m in the three directions, according to sensitivity experiments, where θ is the latitude at the analysis grid.

An inflator, γ, similar to that used by Anderson (2001), Zheng (2009) and Li, Kalnay, Miyoshi, and Danforth (2009), is used to adjust the ensemble covariance matrix, i.e.,

The open circle between ρ and denotes a Schur product (an element by element matrix multiplication), and ρ is defined in Eq. (6). Unlike the method used by Hamill, Whitaker, and Snyder (2001) and Anderson (2007), the above inflation is directly applied to the background covariance matrix itself, rather than to the ensemble members. In determining the covariance inflator γ at each assimilation step in Eq. (7), we adopt the relationship between innovation, background error and observation error proposed by Mitchell and Houtekamer (2000) when they estimated the amplitude of additive model error:

where is the trace of the observation-minus-forecast covariance, is the trace of the covariance matrix of the forecast ensemble in observation space, and is the trace of the observation error covariance matrix.

In practice, the inflators for temperature, salinity and SLA are calculated independently, and then their minimum value is used to inflate the entire covariance matrix. When the minimum value is less than zero or greater than 1, γ is set to zero and 1.0, respectively. Thus, the value of γ varies between 0 and 1 during the assimilation according to Eq. (8). Such a treatment may not inflate enough for some variables but avoids over-inflation, which might cause an over-fitting problem during the data assimilation. In addition, the value of γ also reflects the consistency between the forecast mean error square and the sum of the background error variance and observation error variance. The closer γ approaches zero, the better the consistency.

3 Observation Error Covariance Matrix

As mentioned in Section 2a, the Argo profiles and other in situ observations are assimilated in this study. Argo floats have a 10-day re-sampling period; thus, the available Argo profiles are sparse on any specific day. To solve the temporal sparsity of Argo data, we treat all Argo data within a time window of 8 days as the observations for the assimilation, with 5 days before the analysis time and 2 days after the analysis time. Oke et al. (2008) and Balmaseda et al. (2007) used this strategy when they assimilated Argo data. The 8-day window is longer than the assimilation interval of 5 days. The longer window was chosen to include more observations at a single assimilation step as used by Huang, Xue, and Behringer (2008), Oke et al. (2008) and Smith and Haines (2009).

Observation errors include measurement error, representation error and the error associated with the time difference between the analysis and observation (called age error), which can be assumed to be Gaussian with a mean of zero and a variance of , , and , respectively. Thus, we have

Based on previous work (e.g., Cummings, 2005; Desroziers, Berre, Chapnik, & Poli, 2005; Janic & Cohn, 2006) and some assumptions which may contain some arbitrary components, we set these values as shown below:

	ε instr = 0.1°C for temperature
	ε instr = 0.1 (practical salinity scale used) for salinity

where S _mod is the model standard deviation derived from the simulated temperature (salinity) anomalies from the control run for the period 1985–2004, |t^a−t^o| is the difference between analysis time and observation time in units of days, and κ is an adjustable coefficient set to 0.2. We use S _mod in Eqs (10) and (11) because we lack sufficient observations to calculate the climatology variance.

The function of the horizontal grid and vertical level is S _mod. However, it is difficult to tune the amplitudes of the representation error and age error using a three-dimensional S _mod. For simplicity, we assume that S _mod changes only with depth and use the averaged value over all horizontal grids at a vertical level.

In this study, the observation perturbation is drawn from the Gaussian distribution with the mean equal to zero and the variance equal to the observation error variance . For SLA, the observation error standard deviation is set to 7 cm. If we denote the observation vector by at the k ^th data assimilation cycle, the i ^th member of perturbed observation, y_{k , i} , can be expressed by

where is the observation perturbation. The perturbed observations will be used in all assimilation experiments conducted in this study.

3 Metrics used for evaluation

a Amplitude of the Model Bias

The biases of the regional models could be computed at each model grid by comparing the mean states averaged over the 25-year control runs with the Levitus climatology. To estimate the overall impact of the spectral nudging scheme on model climatology, we define the amplitude of model bias (AMB) as

where is the model climatology defined in Section 2b, is the Levitus climatology, and G is the number of model ocean grids at a model level. We use the amplitude of the bias, not the bias itself, because the impact of the sign of the bias (positive or negative) on the spatial average should be removed.

b Root Mean Square Error (RMSE)

The RMSE for the 5-day forecast ensemble mean is defined by

where Y is the variable of evaluation; the superscript “o” denotes the observations, and “m” denotes the model; L is the number of total observations within a region (or grid cell) of evaluation and T is the total number of assimilation steps. At each step, the observations within a 5-day window centred on the forecast day are used to calculate the RMSE. These observations are independent data relative to the forecast because they are not assimilated into the model until the current assimilation cycle finishes. To measure the improvement in Exp3 relative to Exp1, a relative RMSE is defined by

where RMSE_Exp3 denotes the RMSE of Exp3 andRMSE_Exp1 denotes the RMSE of Exp1. The negative (positive) ℜ1 values indicate that Exp3 reduces the forecast RMSE more (less) than in Exp1.

As mentioned in Section 2c, the background error covariance matrix is the only factor that controls the differences among these assimilation experiments. A detailed comparison of the covariance matrices among the three experiments can help us detect the possible reasons for the advantage of the time-averaged covariance method.

c Ensemble Spread and the Correlation Function

All of the data assimilation experiments in this study use the same inflation and localization scheme, therefore, we will focus on the analysis of the ensemble covariance matrix prior to inflation and localization. Instead of examining the covariance matrix directly, we will analyze the ensemble spread and correlation function separately. The former reflects the amplitude of the variance and the latter reflects the spatial structure of the covariance matrix. The advantage of the correlation function over the covariance function is that the correlation function is a dimensionless variable which is convenient for comparisons between the correlation structures among different model variables.

The background error covariance matrix in Eq. (5) at each assimilation cycle can be decomposed into its variance (spread) and its spatial structure (correlation function), namely,

where D is the ensemble variance matrix, which is a diagonal matrix, and C is the correlation matrix. Each element in D ^1/2, referred to hereafter as the ensemble spread, can be calculated by

where is the i ^th diagonal element of the background error covariance matrix. The correlation function between two different grids, denoted by i1 and i2, is estimated by

where is the element of representing the covariance between i1 and i2.

d Agreement Between the Ensemble Spread and the RMSE

The agreement between the ensemble spread and the RMSE for the forecast ensemble mean is a good measure of ensemble quality (Bengtsson, Magnusson, & Källén, 2008; Cheng, Tang, Jackson, Chen, & Deng, 2010; Jolliffe & Stephenson, 2003). The closer the forecast ensemble spread is to the RMSE of the forecast ensemble mean, the better the ensemble represents the uncertainty of the model state. For convenience of comparison, the degree of the agreement is measured using a relative spread, the ratio of the ensemble spread to the RMSE of forecast ensemble mean, defined by

where mSpread and mRMSE are the spatially averaged forecast ensemble spread and the forecast ensemble mean RMSE over a region (or grid cell). As will be shown in the following section, the main problem with Exp1 is the underestimation of the background error variance due to the small ensemble size. Thus, a large relative spread of ℜ2 can better reflect the range of forecast error.

4 Results

a Evaluation of the Spectral Nudging Version of the Ocean Model

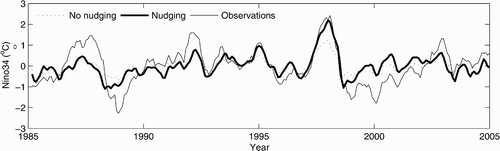
The purpose of the application of the spectral nudging in this study is to reduce the model bias. It is necessary to examine the effects of the spectral nudging scheme on the model climatology prior to performing assimilation experiments. Two runs, one with the spectral nudging scheme and the other without this scheme, are performed for the period 1980 to 2004, as mentioned in Section 2b. The run without the spectral nudging scheme has large biases; for example, there is a large warm bias in the subtropical southern Pacific Ocean and a cold bias in the subtropical northern Pacific Ocean at 180 m (Deng, Tang, & Freeland, 2011). However, the mean bias averaged over the entire Pacific Ocean is very small in both runs because of the cancellation between positive and negative biases in different regions. To avoid this cancellation between positive and negative biases at different grids, we calculated the AMB of temperature (salinity) against the Levitus climatological temperature (salinity) to represent the overall amplitude of the model biases over the Pacific Ocean. The model mean temperature (salinity) is based on the output of the two 25-year runs for the Pacific Ocean. The vertical distribution of the AMB is presented in Fig. 1, clearly showing the significant improvement in the spectral nudging scheme in the temperature and salinity model climatology at all depths below approximately 200–250 m. However, the spectral nudging scheme increases the AMB for temperature in the top 200 m. This is most likely because of the difference in time scales between the heat flux adjustment and the spectral nudging. The former only relaxes the model sea surface temperature (SST) to the climatological SST, which corresponds to a relaxation time scale of 2 months for a 50 m mixed-layer depth (Madec, 2008), whereas the latter relaxes the model temperature and salinity with 10-year and longer time scales at all levels to the corresponding climatological values. The impact of the former is confined to model levels near the surface because only SST is relaxed. Increments from these two schemes may overestimate (or underestimate) the difference between model temperature and the climatological temperature when their signs are the same (or different). It should be noted that the negative impact of the spectral nudging scheme on the model temperature climatology near the surface is not important for the simulation of signals with a period shorter than 10 years, such as that associated with El Niño-Southern Oscillation (ENSO) variability. Figure 2 is the simulation of the Niño3.4 SSTA index (mean sea surface temperature anomalies averaged over the region 120°W–170°W and 5°S–5°N) from the two runs. Compared to observations, spectral nudging does not destroy the interannual and shorter time-scale variations and even generates more realistic amplitudes of the Niño3.4 SSTA index than the original version of the model during some periods. The spectral nudging scheme is very efficient in reducing model biases in the subsurface temperature and salinity at all model levels, and this advantage will relieve the burden on data assimilation in working with the model biases.

Fig. 1 Amplitude of model biases (AMB) of temperature (a) and salinity (b) as a function of depth from the control run without nudging (dashed line) and the control run with spectral nudging (thick solid line). Here, the AMB is calculated against the Levitus climatological temperature and salinity.

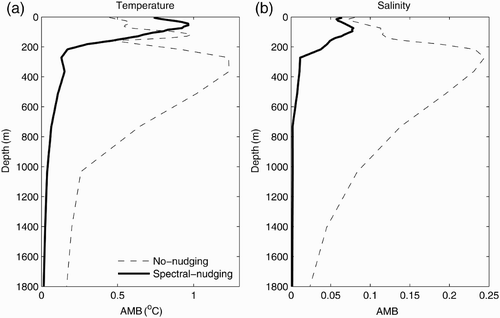
Fig. 2 Monthly Niño3.4 SST anomaly from the control run without spectral nudging (dotted line), the control run with spectral nudging (thick solid line) and from observations (thin solid line) for the period January 1985 to December 2004.

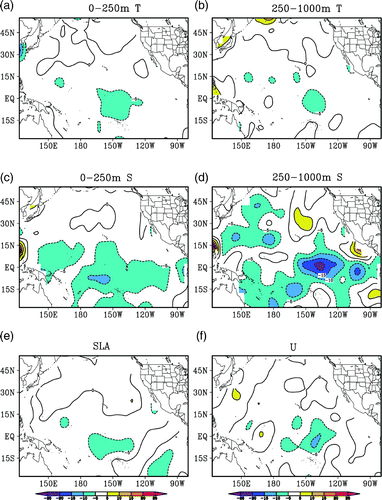
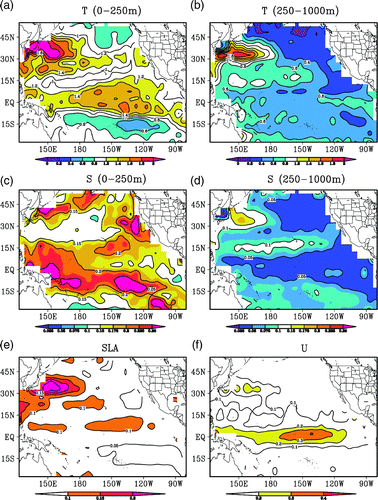
The positive effects of assimilating in situ observations (e.g., Argo profiles) and SLAs into realistic ocean models have been verified by many studies (Cummings et al., 2009; Huang et al., 2008; Smith & Haines, 2009; Xie & Zhu, 2010). In this study, we will focus on the effects of the time-averaged covariance method. We performed model validation for the 2005–07 period by calculating the RMSE for temperature and salinity between the control (CTL) run and the observed BCTS profiles within a 5-day window centred on the forecast day. For the same period, we further calculated the RMSE for SLA and the zonal surface current (U) between the CTL and the observations. The RMSE is calculated for each 5° (longitude) × 5° (latitude) bin from 30°S–55°N and 120°E–80°W. The larger size of the bins relative to the model resolution (2°) ensures that there are sufficient observations to obtain robust estimates of the RMSE. The temperature RMSEs averaged over the top 250 m (hereafter layer1) and 250–1000 m (hereafter layer2) are shown in Fig. 3a and Fig. 3b, respectively. Figure 3a shows two large RMSE areas located in the Kuroshio area and the central and eastern equatorial Pacific Ocean and two relatively small RMSE areas located in the northeast Pacific Ocean and the southeast tropical Pacific region. Figure 3b shows that large RMSE values in layer2 occur in the Kuroshio area, while small values occur in the northeast Pacific Ocean. Figure 3c shows that the large RMSE values of salinity in layer1 occur in a belt between the equator and 15°S and areas near the coast of the North Pacific Ocean. In the deep layer, the large salinity RMSEs occur in the Kuroshio region and the RMSEs are very small in the tropical equatorial region and the northeast Pacific region (Fig. 3d). The maximum RMSE values of SLA occur in the Kuroshio region (Fig. 3e), and the maximum RMSE values of zonal surface current occur in the central-to-eastern equatorial region (Fig. 3f). Apparently, there are always large errors in the Kuroshio region and the central-to-eastern equatorial Pacific region, indicating the difficulty of simulating the ocean state in these regions because of the coarse resolution of the model, which lacks the resolution required to reproduce strong eddy activity and is unable to simulate the small-scale variations in these regions. Figure 3 will act as a reference for evaluating the assimilation performances later in the paper.

Fig. 3 Mean RMSEs of temperature (a, b), salinity (c, d), SLA (e) and surface zonal current (f) from the control run for the 2005–07 period; the observations are the BCTS profile data. The contour interval is 0.2°C for temperature, 0.05 for salinity, 0.05 m for SLA and 0.1 m s⁻¹ for the zonal surface current.

b Evaluation of the Data Assimilation System

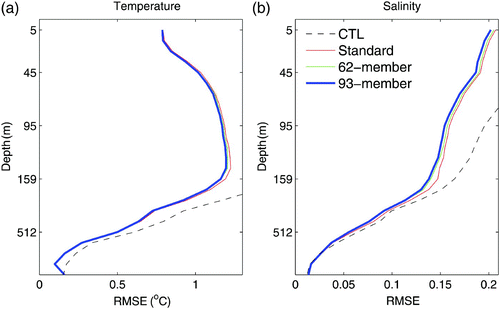
Considering the sparse distribution of in situ observations, we used a 5-day window, centred on the analysis time, to calculate a 5-day forecast RMSE; that is, all observations falling within this window were used to calculate the RMSE. These observations were not assimilated into the model until the current assimilation step was finished. Therefore, they are independent data relative to the forecast. The overall impacts of the assimilation on the reduction of the RMSE can be demonstrated by the vertical RMSE profiles of temperature and salinity, averaged over the entire assimilation region for the three years, as shown in Fig. 4. Compared to the CTL, all experiments significantly reduce the RMSE of temperature and salinity at all model levels. This is more visible in Fig. 5, which shows the spatial distribution of mean RMSEs for Exp1 obtained using the same procedure as that used for Fig. 3. As shown in Fig. 5, Exp1 significantly reduces the RMSE of temperature and salinity almost everywhere in layer1 compared with CTL (Fig. 3). In layer2, Exp1 also significantly reduces the RMSE of temperature and salinity over almost all regions. For SLA (Fig. 5e) and the zonal surface current (Fig. 5f), Exp1 cannot reduce RMSEs in the Kuroshio area but generates smaller RMSEs in most areas, especially in the tropical equatorial region. These results indicate that this data assimilation system is capable of improving the simulation of the ocean state and is a suitable test bed for the investigation of some new techniques.

Fig. 4 Mean RMSEs of temperature (a) and salinity (b) averaged over the entire assimilation domain as a function of depth, from the control experiment (CTL, dotted black line), the standard EnKF assimilation (Exp1, thin red line), the 62-member time-averaged covariance experiment (Exp2, blue dashed line) and the 93-member time-averaged covariance experiment (Exp3, thick solid line); the observations are the BCTS profiles.

Fig. 5 Mean RMSEs of temperature (a, b), salinity (c, d), SLA (e) and surface zonal current (f) from Exp1 for the 2005–07 period; the observations are the BCTS profile data. The contour interval is 0.2°C for temperature, 0.05 for salinity, 0.05 m for SLA and 0.1 m s⁻¹ for the zonal surface current.

c Effect of the Time-Averaged Covariance Method on the RMSE

Two experiments are also performed that are the same as Exp1 except for the difference in the construction of the background error covariance as mentioned in Section 2c. The RMSE vertical profiles are also plotted in Fig. 4. Compared with Exp1, Exp2 (62-member) and Exp3 (93-member) reduce more temperature RMSE at some model levels between 50 m and 250 m and salinity RMSE at levels above 500 m, indicating the positive contribution of the time-averaged covariance method on the reduction of forecast error. However, the improvements in Exp2 and Exp3 relative to Exp1 are not very evident at some levels in Fig. 4, especially for temperature. The specific reason is unknown, but there are two possibilities. First, external wind forcing, which is not perturbed in constructing the ensemble, plays a more important role than the internal model process in the top of the ocean, making the forecast in the top ocean layer less sensitive to ensemble size. Second, the spatial and temporal averaging over the entire domain and over the entire period reduces the contrast among these experiments because, as will be shown below, the time-averaged covariance method does not necessarily improve the assimilation everywhere. In addition, the adaptive background error covariance inflation, which “corrects” the covariance matrix, also reduces the difference between Exp1 and Exp2 and Exp3. We will discuss this issue further in the following section.

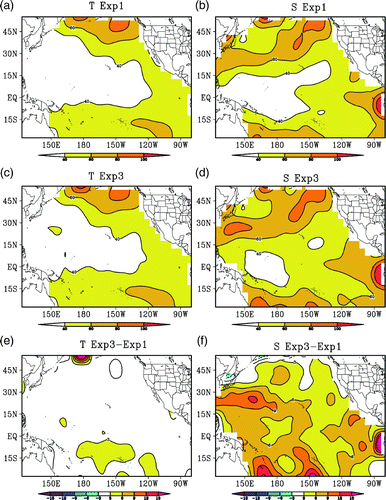
The distribution of the ratio ℜ1 defined in Eq. (15) is shown in Fig. 6. It indicates that the reduction in the RMSE resulting from the time-averaged covariance is not spatially uniform. For convenience, we will compare the mean RMSEs averaged over the top 250 m (layer1) and over depths between 250 and 1000 m (layer2) in Exp3 with those in Exp1. Compared with Exp1, Exp3 reduces more RMSE in most areas south of 30°N in layer1 (Fig. 6a) and layer2 (Fig. 6b). Similarly, Exp3 reduces more salinity RMSE than in Exp1 in most areas in the two layers. The most evident reductions in RMSE occur in the equatorial region centred at 140°W, where Exp3 reduces more than 5% of the RMSEs of temperature, SLA, U and salinity in layer1. For salinity, the reductions reach 20–25% in layer2. However, one also finds that Exp3 generates larger RMSEs than Exp1 in some areas, for example, the region north of 30°N and some regions near the coast. Interestingly, the areas where the time-averaged covariance cannot reduce the RMSE usually have relatively low RMSEs in the CTL and Exp1. We will consider a possible reason for this phenomenon below.

Fig. 6 Ratio, ℜ1 (%), of the mean RMSE differences between Exp3 and Exp1 to the RMSE of Exp1. The contour interval is 10%.

d Effects of the Time-Averaged Covariance on the Ensemble Spread

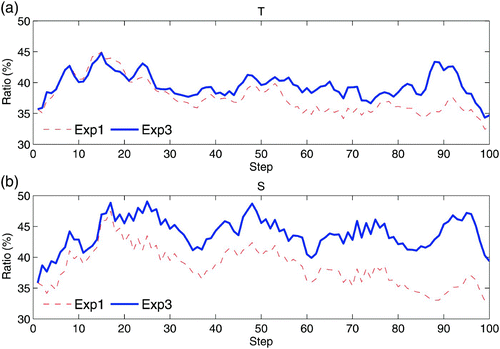
The ensemble spread significantly affects the performance of ensemble-based data assimilation systems. Many studies have discussed the adjustment of ensemble spread in developing a reliable assimilation system; for example, various inflation methods were proposed (Anderson & Anderson, 1999; Mitchell & Houtekamer, 2000). In this study, the adaptive scheme (Eq. (9)) is used to adjust the ensemble spread at each assimilation cycle for the three experiments. The mean value of the inflator γ, averaged over the 3-year assimilation period, is 0.203, 0.085 and 0.029 for Exp1, Exp2 and Exp3, respectively. The large γ of Exp1 suggests that the standard EnKF with 31 members greatly underestimates the forecast error variance. The smaller inflator values for Exp2 and Exp3 are evidence of the merits of this time-averaged covariance method (i.e., the amplitudes of the error covariance estimated using the super-ensemble approach is more realistic and does not require strong inflation). It should be noted that the inflation associated with these different inflators for the three experiments prevents the adjusted ensemble covariance in each of the experiments from continuing to underestimate the background error, reducing the impacts of difference in ensemble spreads (before inflation) of the original ensemble in Exp1 and the time-averaged covariance in Exp2 and Exp3. Although, the construction of the background error covariance matrix is different in the three experiments, comparisons show that the differences in absolute spread among the three experiments are not evident. Figure 7 shows the relative spreads of ℜ2 in layer1 for Exp3 and Exp1. As can be seen, the spatial patterns ofℜ2 are similar for Exp1 (Figs 7a and 7b) and Exp3 (Figs 7c and 7d). The small differences in ℜ2 for temperature indicate the limited impact of the time-averaged covariance method on ℜ2 for temperature (Fig. 7e). Figure 7f shows positive values for the differences in salinity ℜ2 in most regions, indicating the stronger positive impact of the time-averaged covariance method on salinity assimilation. It is not surprising that the areas with large relative spreads in Figs 7a and 7c correspond mostly to small RMSEs in Figs 5a and 5b and vice versa.

Fig. 7 Ratio, ℜ2 (%), of the ensemble spread to forecast RMSE, averaged over the top 250 m from Exp1 for T and S (a, b), and from Exp3 for T and S (c, d) as well as the differences in ℜ2 between Exp3 and Exp1 for T and S (e, f).

As shown in Fig. 6, the largest improvement in Exp3 relative to Exp 1 occurs in the tropical Pacific region. Figure 8 shows the averaged ℜ2 over the region 140°E–90°W, 10°S–10°N for layer1, as a function of the assimilation step, for the first 100 steps. It is evident that the ℜ2 for Exp3 is almost always greater than that for Exp1 for both temperature and salinity, indicating that the time-averaged covariance helps improve the agreement between the ensemble spread and the forecast error. The benefits of the time-averaged covariance are very clear for salinity assimilation.

Fig. 8 Time series of the mean ℜ2 (%), averaged over the region 140°E–90°W, 10°S–10°N in the top 250 m, from Exp1 (red dashed line) and Exp3 (blue solid line), for (a) temperature and (b) salinity, for the first 100 assimilation steps.

e Comparisons of the Ensemble Correlation Structure

Because the correlation structure of the background error covariance matrix affects the transformation of the observation information between locations and between variables, it is also a key factor that affects the performance of the EnKF assimilation system. A properly constructed correlation structure for the error covariance matrix can improve the data assimilation and vice versa. The dimensional size of the correlation matrix C of is very large for the five-variable model state over the entire model domain. Thus, we present only the correlation function at selected model grids.

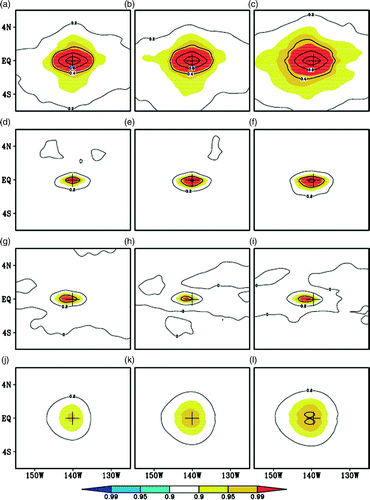
Because the three experiments are run separately, comparing the correlation structure at a specific step cannot detect the essential difference. Therefore, we averaged the correlation functions over the data assimilation period to obtain the mean correlation function. Figure 9 is the averaged correlation function of temperature at a model grid point (140°W, 0°N,150 m, denoted as A), against temperature, salinity and zonal current at the same depth and SLA for the three experiments. Namely, the values are the mean correlation coefficients averaged over the assimilation cycles for the period 2005–07. This model grid point is chosen because the most evident improvement of the time-averaged covariance method occurs around this model grid point. The depth of 150 m is chosen because it is approximately the depth of the thermocline. As seen in Fig. 9, the correlation decreases with distance from the centre of the maximum. For temperature, this centre is exactly at the selected point A. The correlation length is shorter in the meridional direction than in the zonal direction, especially for temperature. A striking feature in Fig. 9 is that the increase in ensemble size does not change the main spatial pattern of the correlation structure but a larger ensemble size can generate significant correlation structure. The correlation structure appears to become broader in the meridional direction. This is particularly apparent for the correlation between T-T, T-S and T-SLA (Fig. 9a compared with 9c, 9d compared with 9f, and 9j compared with 9l). Apparently, the 62-member ensemble increases the area of significant correlation more than the 31-member ensemble, and the 93-member ensemble further increases the area. The increase in the significant correlation area in Exp2 and Exp3 indicates that the information from the temperature observation at point A can be transferred to neighbouring model grid points and that the coherence between A and surrounding grid points (or variables) is stronger and more stable. However, the impact on the T-U correlation is not evident.

Fig. 9 Mean correlation functions of the temperature at the grid (140°W, 0°N, 150 m), against T (a–c), S (d–f), U (g–i) and SLA (j–l), obtained from Exp1 (left), Exp2 (middle) and Exp3 (right), averaged over the 2005–07 period. The contour interval is 0.2, and the correlations that pass the 0.90, 0.95 and 0.99 confidence level using a Student's t-test are shaded. The “+” marks the position of the grid.

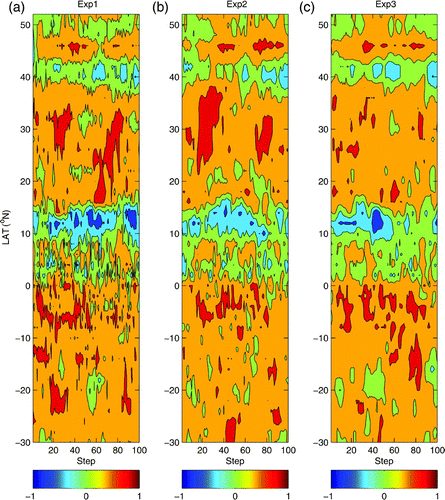
The basic properties of water masses in the ocean are salinity and temperature. The study of the temperature-salinity (T-S) relationship in data assimilation is of great interest. Here, we will further investigate the effects of the time-averaged covariance on the T-S relationship. Shown in Fig. 10 is the latitude-time section of the T-S relation at 150 m, along longitude 140°W, for the first 100 steps. Comparing Exp1, Exp2 and Exp3 reveals that the main characteristics of the T-S relationship were unchanged; for example, a strong positive T-S correlation between 15° and 40°N and a strong negative T-S correlation along 12°N and 42°N were observed. However, it is evident that the T-S correlation is much noisier and is dominated by shorter temporal and spatial scales in Exp1 compared with a relatively smoother and more stable T-S correlation in Exp2 and Exp3. In the tropical region, the contrast between Exp3 and Exp1 is more obvious. The better T-S correlation structure in Exp3 is possibly the main reason for its improved assimilation performance relative to Exp1 because temperature data are dense in the equatorial Pacific Ocean. The improvement in the correlation structure in Exp3 is mainly a result of the larger ensemble size, which reduces the impact of sampling error on the estimation of error covariance.

Fig. 10 Latitude-time section of the T-S correlation along 140°W for the first 100 steps. The contours are −0.8, −0.4, 0, 0.4 and 0.8.

5 Summary and discussion

In this study, we assimilate in situ temperature and salinity profiles and sea level height data into an OGCM for the Pacific Ocean using the EnKF. The spectral nudging scheme is used to reduce the model bias online. The results show that the spectral nudging method can significantly reduce model bias, especially in the subsurface, without sacrificing the interannaual and short time-scale variations.

A time-averaged covariance method is proposed to construct a proxy background error covariance matrix in the EnKF. This method averages background error covariance matrices estimated by the ensembles of neighbouring assimilation steps. It is equivalent to estimating the background error covariance matrix with a super ensemble that includes all deviation ensemble members of several neighbouring assimilation cycles. Thus, the ensemble size is enlarged without increasing model integrations. It is in some ways similar to the EnOI but more reasonable in addressing the variations in the background error covariance with the assimilation cycles. EnOI assumes that the background error covariance is unchanged during the assimilation period, whereas this time-averaged covariance method only assumes that the background error covariance structures are not changed within a short time window of several assimilation steps. Thus, the time-averaged covariance method will not significantly modify the main structure of the covariance matrix but will effectively filter out the noisy components in the background error covariance matrix.

Three assimilation experiments with different time-averaged covariances were conducted to examine the impacts of this method. Comparing the results of the three experiments reveals that the time-averaged covariance method can improve the performance of the assimilation system for many regions in terms of the reduction in RMSE. Compared to observations, the improvements are evident in the tropical region. Although this method cannot greatly increase the absolute ensemble spread, the comparison of the relative ensemble spreads shows that the time-averaged covariance can increase the relative ensemble spread and, thus, improve the agreement between the ensemble spread and the forecast error. These improvements are mainly a result of the improved correlation structure of the background error covariance matrix. The correlation functions of the time-averaged covariance are much smoother and more robust than that of the standard EnKF, while the main structure of the correlation functions remains unchanged. This method may be useful for practical assimilation systems when computational resources are limited.

Because the coarse-resolution model lacks the resolution required to reproduce strong eddy activity, it is unable to simulate small-scale variations in the Kuroshio region, which are closely associated with variations in the SLAs and currents. In addition, we consider only the representation error of observations in the vertical direction and ignore the horizontal variation for simplicity. This may degrade the performance of the assimilation system, especially in some regions where the observations have relatively large representation errors, such as the Kuroshio region. In this time-averaged covariance scheme, the ensemble members from previous time steps are used for the current time step. Thus, the time-averaged covariance method provides only a sub-optimal estimation for the forecast error covariance matrix.

Acknowledgements

This work was supported by the BC-China Innovation and Commercialization Strategic Development Program (ICSD-2007-Tang-Y), the open grant of the State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, China and the International Corporation Program of China (2008DFA22230).