Reconstruction of Three-Dimensional Pacific Temperature with Argo and Satellite Observations

Abstract

Combining Argo temperature and salinity profiles with satellite-derived sea surface temperature (SST), weekly three-dimensional temperature fields of the Pacific Ocean were reconstructed for the period January 2000 to December 2010. The data reconstruction methodology we used has three salient features: the first is a combined application of the Optimal Interpolation (OI) and the Multivariate Data Interpolating Empirical Orthogonal Function (MDINEOF) methods, the second is an emphasis on the multivariate nature of the vertical thermohaline structure, and the third is the inclusion of a continuous satellite-derived SST dataset to compensate for the discontinuities and the lack of surface observations in Argo data. Comparisons with other observations and data products indicate that our gridded temperature product is able to capture the main features of temperature distribution as well as its variability from intraseasonal to interannual time scales, thus providing a useful new dataset for ocean and climate studies.

RÉSUMÉ [Traduit par la rédaction] En combinant les profils de température et de salinité Argo avec les températures de la surface de la mer dérivées des données satellitaires, nous avons reconstruit les champs tridimensionnels hebdomadaires de température de l'océan Pacifique pour la période de janvier 2000 à décembre 2010. La méthodologie de reconstruction des données que nous avons utilisée présente trois points saillants : le premier est une application combinée des méthodes de l'interpolation optimale et de la fonction orthogonale empirique d'interpolation de données multivariées (MDINEOF), le deuxième est une mise en évidence de la nature multivariée de la structure thermohaline verticale et le troisième est l'inclusion d'un ensemble continu de données de température de la surface de la mer dérivées des données satellitaires pour compenser les discontinuités et le manque d'observations de surface dans les données Argo. Les comparaisons avec d'autres observations et produits de données montrent que notre produit de températures à des points de grille est capable de discerner les caractéristiques principales de la distribution des températures de même que sa variabilité de l’échelle intrasaisonnière à l’échelle interannuelle, ce qui fournit un nouvel ensemble de données utile pour les études océaniques et climatiques.

Keywords:

• Argo
• multivariate DINEOF
• satellite observation
• data reconstruction

1 Introduction

Oceanic temperature is one of the most useful oceanographic variables, directly linked to the ocean dynamics through the distribution of mass. The three-dimensional distribution of temperature and its temporal evolution can greatly affect global ocean circulation, climate processes and biogeochemistry (Archer et al., 2004; Mosedale, Stephenson, Collins, & Mills, 2006). However, measurements of oceanic temperature, especially subsurface temperature, were sparse and spatiotemporally irregular before the start of the Argo program, which hardly satisfies the needs of scientific studies. How to fill the data gaps and reconstruct three-dimensional oceanic temperature fields has always been a challenge.

The World Ocean Atlas (WOA), first produced in 1994 (with later editions in 1998, 2001, 2005 and 2009; NOAA, 2011), is a three-dimensional gridded product in common use, but it has limitations because it only provides climatological fields. Carton, Chepurin, Cao, and Giese (2000), Carton, Chepurin, and Cao (2000) produced an oceanic reanalysis dataset by sequential estimation with empirically modelled error covariance, but the accuracy of the product depends on the model error and the assimilation method. Ishii, Kimoto, Sakamoto, and Iwasaki (2006) reconstructed gridded monthly temperature fields from 1945 to 2006, but the dataset is limited to the upper 700 m.

An effective approach to dealing with the sparseness of in situ data is to combine them with remotely sensed satellite observations, because the latter usually have much better temporal and spatial coverage. For example, Fujii and Kamachi (2003) reconstructed temperature and salinity profiles from in situ temperature profiles, sea surface temperature (SST) and satellite altimetry in the region east of Japan, using a variational method with vertically coupled temperature–salinity Empirical Orthogonal Function (EOF) modes. Guinehut, Le Traon, Larnicol, and Philipps (2004) reconstructed the large-scale, monthly mean, 200 m depth temperature fields by combining satellite data with Argo temperature profiles. Reynolds, Rayner, Smith, Stokes, and Wang (2002) produced an SST product using both in situ and satellite-derived data. Alvera-Azcárate, Barth, Beckers, and Weisberg (2007) proposed a technique called Multivariate Data Interpolating Empirical Orthogonal Function (MDINEOF) to reconstruct SST fields from satellite-based wind and chlorophyll observations, suggesting that the combination of SST with other variables significantly improves the results obtained by the reconstruction of SST alone.

The situation of sparse observations has been greatly improved with the initiation of the global Argo observing network (Argo Science Team, 1998); the network can provide high-quality temperature and salinity profiles simultaneously for the upper 2000 m of the global ocean. Gridded Argo temperature and salinity products have been reconstructed by several organizations (Argo, 2011), but these products often have relatively low temporal resolution, and the quality of the products still needs improvement, especially for the early years before the completion of the Argo network at the end of 2007 (Wang, Liu, & Xu, 2006).

The goal of this study is to reconstruct weekly three-dimensional temperature fields in the Pacific Ocean (120°E to 70°W, 90°S to 70°N). The spatial grid is 3° by 3°, and the period is January 2000 to December 2010. This was accomplished in two steps: first the Optimal Interpolation (OI) method was used to generate initial fields by interpolating Argo scattered profiles to a fixed grid, with “missing values” assigned to locations where Argo observations are sparse; then the MDINEOF method was used to fill in the missing values and produce the final gridded temperature fields. Our approach differs from that of previous Argo products in three aspects: first is the combination of Argo profiles with satellite-derived SST observations; second is an emphasis on the multivariate nature of the vertical thermohaline structure; and third is the application of the OI-MDINEOF combined methodology for data reconstruction.

2 Data

a Argo Data

All the Argo temperature and salinity profiles in the Pacific Ocean for our 11-year study period from 2000 to 2010 are included in the analysis. These profiles reach depths up to 2000 m and have an average sampling cycle of about 10 days (Roemmich & Owens, 2000). Although data quality control was performed by various Argo data centres, we carried out an extra quality control to check for salinity drift, profiling position and erroneous spikes (Wang, Zhang, Wang, An, & Jin, 2010). The Argo temperature and salinity data are linearly interpolated to 36 standard levels (5, 10, 20, 30, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300, 325, 350, 375, 400, 425, 450, 475, 500, 550, 600, 700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1750 and 2000 m). The number of observations decreases with depth, with 365,392 at 10 m, 367,701 at 500 m, 295,288 at 1000 m, 201,615 at 1500 m, and 188,038 at 1750 m. The number of observations also increases gradually with time from 2000 to 2005, resulting in gradually decreasing errors in our reconstructed dataset; after 2006 the error holds steady (around 0.8°C for a depth-averaged value).

b Satellite SST Data

Although a growing subset of Argo floats began measuring temperature between 4 m depth and a few centimetres from the sea surface, there are still few data records from the surface to 4 m depth, and there are also temporal discontinuities for the Argo floats. Continuous satellite-derived SST is thus used for the same period as the Argo data to compensate for these deficiencies. Before July 2002 SST data were derived from the Advanced Very High Resolution Radiometer (AVHRR) sensor, whereas after July 2002 SST data were derived from both AVHRR and the Advanced Microwave Scanning and Radiometer-EOS (AMSR-E) sensors; the latter is not affected by cloud cover. Both datasets were obtained from the NOAA National Environmental Satellite, Data, and Information Service (NESDIS, 2011). These SST analyses include a bias correction of the satellite data with respect to in situ data from ships and buoys using an empirical orthogonal teleconnection (EOT) algorithm. A description of the complete analysis procedure and data quality assessment can be found in Reynolds et al. (2007).

c Data for Product Evaluation

To carry out an independent evaluation of our reconstructed temperature product, we use the World Ocean Atlas 2009 (WOA09), World Ocean Database 2009 (WOD09), Ishii dataset (Ishii et al., 2006) and the Tropical Atmosphere Ocean (TAO) moored array data for comparison. The WOA09 is a set of objectively analyzed (1° grid) climatological fields of in situ temperature and salinity at standard depth levels for annual, seasonal and monthly compositing periods for the world's oceans (Levitus, 2009). The WOD09 is a scientifically quality-controlled database of selected historical in situ surface and subsurface oceanographic measurements. The WOD09 data are stored in 11 datasets (OSD, CTD, MBT, XBT, SUR, APB, MRB, PFL, DRB, UOR, and GLD), each one representing a group of similar oceanographic probes. The Ishii dataset consists of 1° × 1° gridded temperature fields given as monthly means down to 700 m from 1945 to 2006. It is produced by an objective analysis that explicitly considers background and observational errors through variational methods (e.g., Derber & Rosati, 1989; Ishii, Kimoto, & Kachi, 2003). The TAO (2011) data are from moored ocean buoys, which provide upper ocean measurements of the equatorial Pacific Ocean (PMEL, 2011).

3 Methods

a Optimal Interpolation

The OI method has been described in many references, where it is variously referred to as the Gauss-Markov theorem, optimal or statistical interpolation, or objective analysis (Bretherton, Davis, & Fandry, 1976; Emery & Thomson, 2004; Gandin, 1963). It gives an unbiased linear estimate at grids from a weighted linear combination of observations at irregular locations (Bretherton et al., 1976; Wilkin, Bowen, & Emery, 2002). In this study, OI is used to generate initial gridded data from Argo profiles that are scattered in time and space. The choice of spatial correlation length scales depends on the sampling density and the desired use of the gridded field (Hadfield, Wells, Josey, & Hirschi, 2007). In this study, the spatial scale is set to 500 km based on the correlation scales calculated by Hadfield et al. (2007). For a more detailed description of the OI method, please refer to Hadfield et al. (2007) and Chang, Rosati, Zhang, and Harrison (2009), among others.

In the traditional OI method, the reconstructed data at locations with very sparse observations nearby will approach the value of the background (first-guess) field. In this study, however, such locations are flagged as missing values. The number of locations with missing values accounts for 31.80% in all. The percentages are 29.31%, 34.57% and 41.41% for 10 m, 1000 m and 1750 m, respectively. The missing values are then filled using the MDINEOF method.

b MDINEOF

The DINEOF method is a more objective data filling method because it considers the relationship between variabilities internally without subjective parameter estimation (Alvera-Azcárate, Barth, Rixen, & Beckers, 2005; Beckers & Rixen, 2003). MDINEOF is a multivariate version of DINEOF developed by Alvera-Azcárate et al. (2007). Although their application was used for SST and chlorophyll observations at the surface, we focus on salinity and temperature in the vertical. At each spatial grid point, temperature and salinity time series are transformed into a state matrix X:

where M is the number of vertical levels, and N is the number of temporal grids at each level (i.e., the number of vertical profiles); T_i,j , S_i,j denote the temperature and salinity values, respectively, at the ith vertical level and time j. For convenience, let M′ = 2M, X_i,j  = T_{i .j} , X_{i + M,j}  = S_i,j , (1 ≤ i ≤ M, 1 ≤ j ≤ N), then X is a matrix with M′ rows and N columns. For our study, there are 37 standard levels both in temperature and salinity (M = 37 containing the surface layer) and 574 weeks for each grid after optimal interpolation, so M′ = 74 and N = 574. Note that satellite SST data rather than Argo data are used at the surface to compensate for the discontinuity of Argo observations in some temporal grids. For each spatial grid, the state matrix X often contains some values flagged as missing values, which can be effectively filled using a MDINEOF calculation. In the MDINEOF method, about 1% of data at grids were randomly extracted as cross-validation data to determine the optimal mode and calculate cross-validation errors. For a more detailed introduction to the MDINEOF method, please refer to the description in some earlier works (e.g., Alvera-Azcárate et al., 2005, 2007; Beckers & Rixen, 2003; Wang, Zhang, Liu, Wang, & Jin, 2008).

4 Results

a Mean Temperature Fields and Seasonal Variability

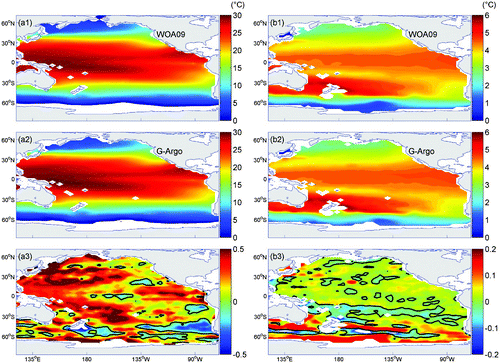
Figure 1 shows the horizontal distribution of annual mean temperature at 10 m and 1000 m depth in the Pacific Ocean. In close agreement with WOA09, our gridded Argo product (G-Argo hereafter) depicts the large-scale features in the temperature fields well. At the surface, the warmest waters are found in the western Pacific Ocean warm pool and along the Intertropical Convergence Zone (ITCZ), and the coldest waters are in the polar regions. At 1000 m, the temperature distribution is different from that at the surface, with the warmest waters in the western Pacific Ocean occurring around 40°S. The spatial correlation coefficients between G-Argo and WOA09 reach 0.9994 at the surface and 0.9946 at 1000 m. The differences between the two products are generally small but not negligible, as evident in the lower panels of Fig. 1. Compared to WOA09, the G-Argo temperature is warmer overall, with the largest differences occurring in the subtropical gyres, the eastern equatorial Pacific Ocean and the Southern Ocean. These differences are probably a result of the different periods for time averaging and the sampling bias of the observations, and may also be caused by the different analysis methods (Chang et al., 2009).

Fig. 1 Annual mean temperature climatology at 10 m (left panels) and 1000 m (right panels). Panels (a1) and (b1): WOA09 data; panels (a2) and (b2): reconstructed G-Argo data; panels (a3) and (b3): the difference between G-Argo and WOA09 data.

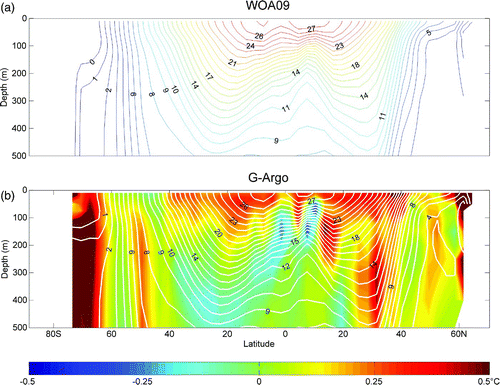
Next we compare the zonal-mean meridional vertical temperature distributions of G-Argo and WOA09 (Fig. 2). The upper 500 m of the tropics and the subtropics is characterized by relatively high temperatures, with troughs and ridges corresponding to the various zonal currents. The overall meridional-vertical distribution patterns of G-Argo are in good agreement with those of WOA09. However, the differences between the two are evident in Fig. 2b. Compared to WOA09, G-Argo is warmer at the surface but slightly cooler in the subsurface layers of the tropical and subtropical regions, and the largest difference occurs in the Southern Ocean. Some of these may be associated with the long-term temperature trend (Ishii et al., 2006; Levitus, Antonov, & Boyer, 2005; Xu & Zhu, 2010).

Fig. 2 Zonal mean annual temperature climatology of WOA09 (upper panel) and G-Argo (lower panel) in the upper 500 m. Temperature contours are 1.0°C. The difference between G-Argo and WOA09 data is shown in the lower panel as coloured shading.

In order to examine the seasonal variation of temperature in the Pacific, Fig. 3 compares the leading EOF mode of the G-Argo temperature at 10 m with that of the Ishii dataset for the period 2000–06. This mode accounts for 91.37% and 91.87% of the total variance in G-Argo and Ishii datasets, respectively, representing a strong annual cycle. The large-scale features of the seasonal variations in the two datasets are very similar. The corresponding spatial correlation coefficient of the two leading EOF modes is 0.987 significant at the 95% confidence level. The root-mean-square of their differences is 0.295°C. In boreal (austral) summer, the temperature anomaly is the highest at mid-latitudes in the northern (southern) hemisphere, especially on the western side of the North Pacific Ocean. In the west, cold air blows off the continents during the boreal winter and cools the ocean. The cooling dominates the heat budget (Stewart, 2005). In the tropics the amplitude of the temperature anomaly is mostly less than 2°C. The principal components (PCs) of the first mode EOFs (Fig. 3c) of the two products are essentially a sinusoid with a 1-year period and are in very good agreement, with a correlation coefficient as high as 0.999. Figure 4 compares the second EOF mode between G-Argo and the Ishii dataset. This mode accounts for 2.85% and 2.95% of the total variance in the G-Argo and Ishii datasets, respectively. The spatial patterns in the two datasets are again very similar. The corresponding spatial correlation coefficient of the two second EOF modes is 0.865. The root-mean-square of their differences is 0.162°C. In boreal September and February (December and May), the anomaly is negative (positive) in the tropics while positive (negative) poleward of 40°. The PCs of the two products have a semi-annual cycle and are again in very good agreement with each other, with a correlation of 0.938.

Fig. 3 The leading EOF patterns of surface temperature in the Pacific Ocean from (a) the Ishii dataset and (b) the G-Argo product, and (c) their corresponding principal components, based on the 2000–06 period. This mode is apparently dominated by an annual cycle, accounting for 91.37% (G-Argo) and 91.98% (Ishii dataset) of the total variance.

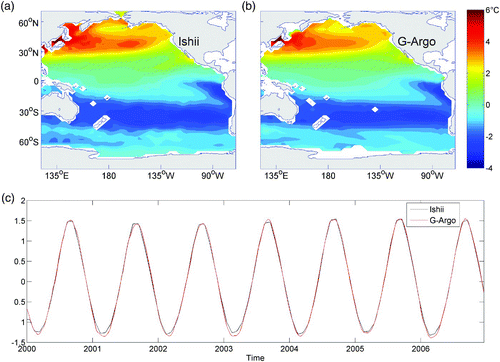
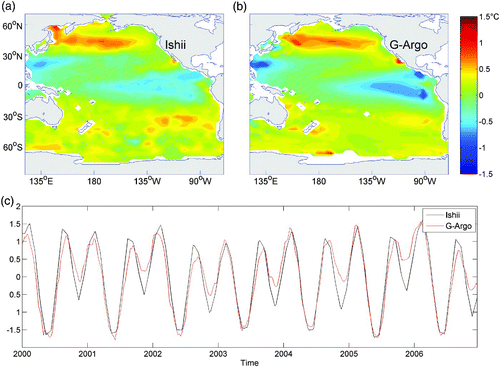
Fig. 4 As in Fig. 3 but for the second EOF mode. This mode is apparently dominated by a semi-annual cycle, accounting for 2.89% (G-Argo) and 2.96% (Ishii dataset) of the total variance. The correlation of the corresponding PCs is 0.968.

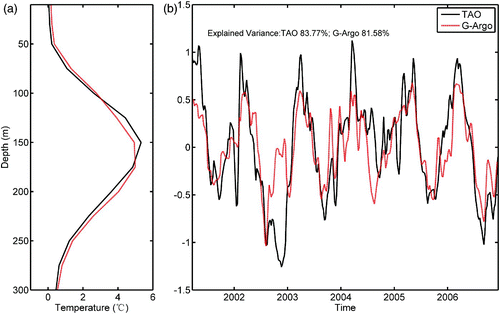
To evaluate the variability below the surface, Fig. 5 compares the time series of G-Argo temperatures from the surface to 750 m with that of the TAO mooring at 147°E, 5°N, for the period January 2000 to December 2010. The G-Argo temperature data at this location were obtained by bilinear interpolation. Both datasets show a strong seasonal variability, especially in the upper 200 m. In general, G-Argo agrees with the TAO observations, though there are some differences in the thermocline (Fig. 5c), which might be caused, in part, by their larger standard deviation. A vertical EOF analysis is performed at this location for each of the two datasets from March 2001 to December 2006 when the TAO observations are continuous in time, and the first mode of variability is shown in Fig. 6. It is clear that this mode is dominated by seasonal variability in both products. It accounts for 81.58% and 83.77% of the total variance for G-Argo and TAO, respectively, with the correlation between the two PCs being 0.77. The differences may be caused, in part, by both the observation error and the smoothing of Argo data.

Fig. 5 Time series of temperature profiles at 147°E, 5°N for the period January 2000 to December 2010. Upper panel: TAO observations; Middle panel: reconstructed G-Argo data; Bottom panel: G-Argo minus TAO. Units are metres.

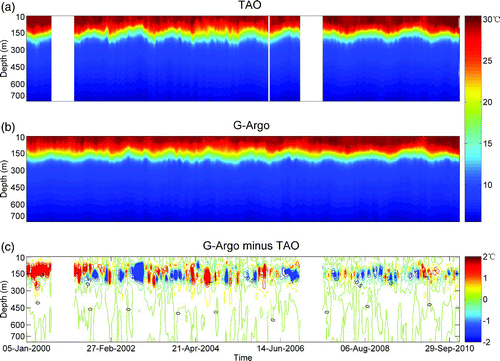
Fig. 6 The first vertical EOF modes (left panel) and their corresponding principal components (right panel) for the time series of TAO and G-Argo data at 147°E, 5°N.

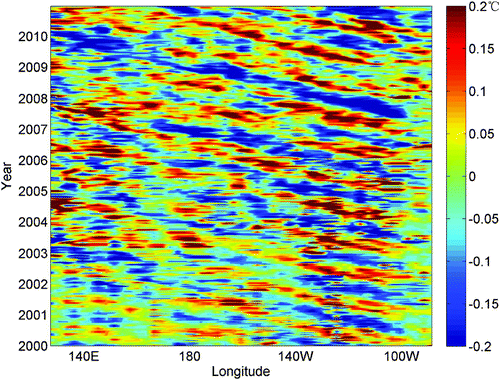
It is interesting to note that the temperatures below the thermocline also show a robust seasonal variation. Figure 7 shows the time series of the temperature anomaly at 1000 m from 130°E to 90°W along 10.5°N. The alternating negative and positive wind anomaly bands suggest that the seasonal variability of the temperature below the thermocline is evident, which is consistent with the results of Hosoda, Minato, and Shikama (2006). We conclude that the seasonal signal in the deeper ocean can also be captured well by the G-Argo dataset.

Fig. 7 The G-Argo anomaly time series at 1000 m along 10.5°N for the period 2000–10.

b Low-frequency and Intraseasonal Variations

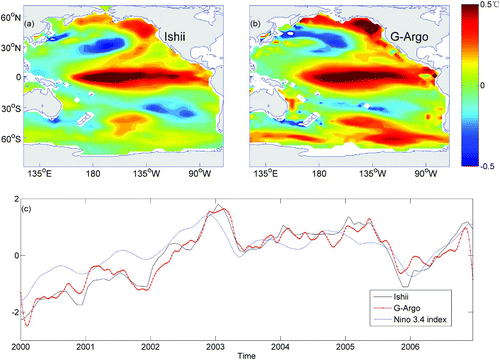
Now we subtract the annual cycle from both the G-Argo and Ishii datasets by removing the monthly mean climatology. Because the Ishii data are monthly, the signals with periods shorter than 30 days were filtered for the G-Argo data. An EOF analysis is then performed on the remaining fields, and the leading modes of the G-Argo and Ishii data at the surface are shown in Fig. 8. The patterns of the low-frequency variability of the two datasets are generally similar. The corresponding spatial correlation coefficient is 0.824, and the root-mean-square of the differences between two modes is 0.117°C. It can be seen that the strongest signals are located in the central and eastern equatorial Pacific Ocean, while patterns with the opposite sign are found in the mid-latitudes of both hemispheres. Temporal variability coincides quite well with the occurrence of El Niño-Southern Oscillation (ENSO) events. The correlation of the corresponding PCs is as high as 0.944, and their correlations with the NINO3.4 index are 0.802 (G-Argo) and 0.880 (Ishii) (Fig. 8c). Note that only data from 2000 to 2006 are used here because the final year of the Ishii dataset is 2006.

Fig. 8 The leading EOF patterns of surface temperature after removing the annual cycle from (a) the G-Argo product and (b) the Ishii dataset and (c) their corresponding principal components, based on the 2000–06 period. The NINO3.4 index (dashed curve) is also plotted in (c) for comparison.

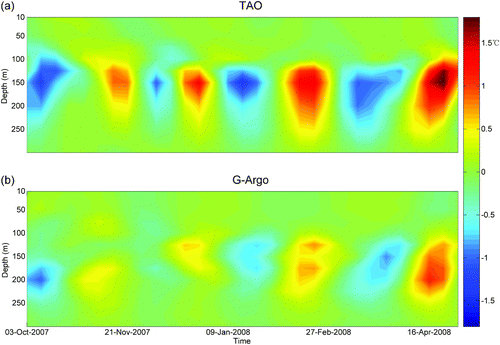
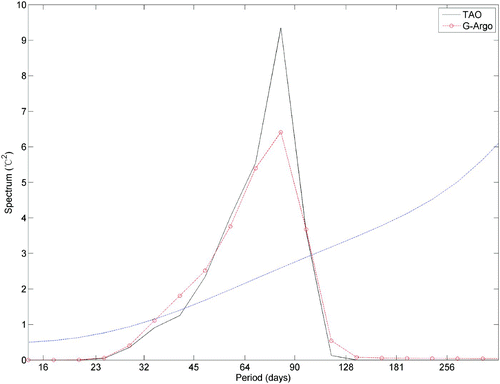
Because G-Argo is a weekly dataset, it has a higher temporal resolution than Ishii's monthly reanalysis. Therefore, it is possible to examine the intraseasonal variability in our product and compare it with the in situ observations from TAO. In order to extract the intraseasonal signals, a 20–90 day Lanczos band-pass filter is applied to both the TAO and G-Argo data. Figure 9 shows a subset of filtered data for the period 3 October 2007 to 13 May 2008 at a TAO mooring station (147°E, 5°N). Both datasets show that the intraseasonal temperature anomalies can penetrate from the surface to 300 m depth, though the strongest signals are in the upper 100–200 m. To quantify the intraseasonal variability further, we carried out a spectral analysis on the intraseasonal time series at 50 m depth (Fig. 10). Both G-Argo and TAO datasets show a prominent power density peak around 82 days. The weaker signal in G-Argo is again caused by data smoothing. It is worth noting that although the number of observations before 2003 are much fewer, a comparison between G-Argo and TAO datasets for the 2001–03 period confirms that G-Argo data can resolve the intraseasonal variability well even for that period (not shown).

Fig. 9 The intraseasonal variability of temperature at 147°E, 5°N for the period 3 October 2007 to 13 May 2008 from (a) TAO and (b) G-Argo.

Fig. 10 The power spectra of the intraseasonal time series of TAO and G-Argo temperature at 50 m depth at 147°E, 5°N. The dashed blue line denotes the 95% confidence level.

5 Summary and discussion

We combined Argo temperature and salinity data with satellite-derived SSTs to reconstruct the three-dimensional temperature field in the Pacific Ocean for the period January 2000 to December 2010. The methodology we used has three salient features: the first is a combined application of OI and MDINEOF methods; the second is an emphasis on the multivariate nature of the vertical thermohaline structure; and the third is the inclusion of a continuous satellite-derived SST dataset to compensate for the discontinuities and the lack of surface observations in Argo data. Comparisons with other observations and data products indicate that our gridded product captures the main patterns of temperature distribution as well as its variability on intraseasonal to interannual time scales, thus providing a useful new dataset for ocean and climate studies.

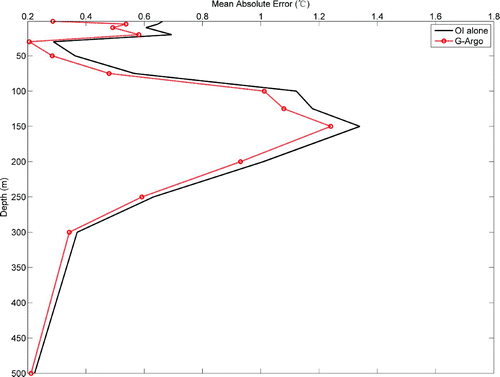
Because OI by itself is a useful method for reconstructing gridded products, a natural question is whether a combination of OI and the MDINEOF method is better than OI alone. The mean absolute errors between the estimated values from both products and the TAO observations are shown in Fig. 11 as a function of depth. It is clear that the OI-MDINEOF combination is more accurate than OI alone.

Fig. 11 Mean absolute error in comparison with TAO observations at different depths. The solid black line denotes the optimal interpolation error alone, and the red line with circles denotes the G-Argo product error.

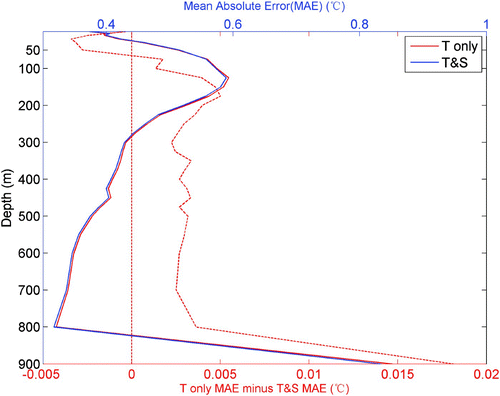
In order to examine whether the combination of temperature and salinity is better than temperature alone in our reconstruction, we use WOD09 data as independent data to verify it. Figure 12 shows the mean absolute errors between the constructed dataset from the two methods and the WOD09 data. It shows that the mean absolute errors are almost same for the two methods. The error difference between the two methods shows that the combined method is better than using temperature alone in water deeper than 75 m (Fig. 12). However, the salinity input also causes some errors in water shallower than 75 m, which may partly be attributed to the strong association of the surface salinity with freshwater flux.

Fig. 12 Mean absolute errors with depth of the reconstructed products derived from temperature alone (solid red line) and temperature and salinity together (solid blue line). The differences between them are shown by the dashed red line. A difference larger than zero indicates that the reconstructed product derived from temperature and salinity together is better than that from temperature alone.

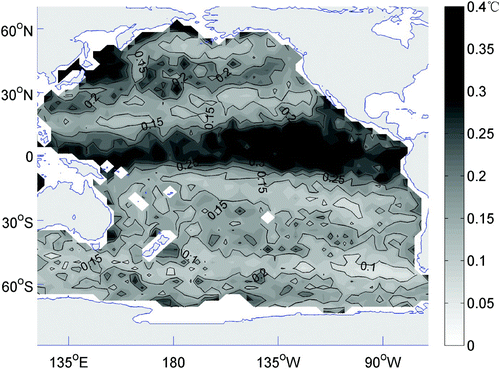
Another important issue in our methodology that needs further discussion is the distribution of the root-mean-square errors for cross-validation data (Fig. 13). It shows a rather strong difference between tropical and extratropical regions, with relatively large errors (>0.25°C) in the tropical Pacific Ocean but smaller errors (<0.25°C) elsewhere. This indicates that our method for temperature data reconstruction is somewhat less effective in the tropics. Because fewer optimal modes are selected by the MDINEOF method in the tropics than in the subtropics (not shown), the distribution of errors for cross-validation data may be associated with the spatial distribution of the optimal mode number based on the cross-validation method.

Fig. 13 Distribution of the average root-mean-square errors in all layers for the cross-validation of the MDINEOF construction in the Pacific Ocean.

Acknowledgements

The Argo data used in this paper were collected and made freely available by the International Argo Program and the national programs that contribute to it (http://www.argo.ucsd.edu, http://argo.jcommops.org/, http://www.argo.org.cn/). Argo is part of the Global Ocean Observing System. This study was completed at the State Key Laboratory of Satellite Ocean Environment Dynamics and was supported by the National Natural Science Foundation of China (41206002, 41125019, 41276088), the National Basic Research Program (2007CB816005) and the scientific research fund of the Second Institute of Oceanography (JG1102). Thanks to Prof. Xu Jianping for his help with our product access (www.argo.org.cn). The suggestions of two anonymous reviewers have greatly improved our original manuscript and are appreciated.