Improving Statistical Downscaling of General Circulation Models

Abstract

We present a new method for the statistical downscaling of coarse-resolution General Circulation Model (GCM) fields to predict local climate change. Most atmospheric variables have strong seasonal cycles. We show that the prediction of the non-seasonal variability of maximum and minimum daily surface temperature is improved if the seasonal cycle is removed prior to the statistical analysis. The new method consists of three major steps. First, the average seasonal cycles of both predictands and predictors are removed. Second, a principal component-based multiple linear regression model between the deseasonalized predictands and predictors is developed and validated. Finally, the regression is used to make projections of future changes in maximum and minimum daily surface temperature at Shearwater, Nova Scotia. This projection is made using the local grid-scale variables of the Canadian General Circulation Model Version 3 (CGCM3) climate model as predictors. Our statistical downscaling method indicates significant skill in predicting the observed distribution of temperature using GCM predictors. Projections suggest minimum and maximum temperatures at Shearwater will be up to about five degrees warmer by 2100 under the current “business-as-usual” scenario.

RÉSUMÉ [Traduit par la rédaction] Nous présentons une nouvelle méthode pour la réduction d'échelle statistique des champs des modèles de circulation générale (MCG) à faible résolution pour prévoir les changements du climat local. La plupart des variables atmosphériques ont des cycles saisonniers bien marqués. Nous démontrons que la prédiction de la variabilité non saisonnière de la température de surface quotidienne minimum et maximum est meilleure si on retranche le cycle saisonnier avant de procéder à l'analyse statistique. Voici les trois grandes étapes de cette nouvelle méthode. D'abord, nous retirons les cycles saisonniers moyens des prédictants et des prédicteurs. Ensuite, nous concevons et validons un modèle de régression linéaire multiple sur composantes principales entre les prédictants et les prédicteurs désaisonnalisés. Enfin, nous nous servons de la régression afin d'établir des projections pour les changements à venir dans la température de surface quotidienne minimum et maximum à Shearwater en Nouvelle-Écosse. Cette projection est établie au moyen des variables locales à l'échelle du maillage de la troisième version du modèle canadien de circulation générale (MCCG3). Notre méthode de réduction d'échelle statistique se révèle très efficace pour prédire la répartition observée de la température au moyen des prédicteurs du MCG. D'après les projections, les températures minimum et maximum à Shearwater connaîtront une augmentation d'environ cinq degrés d'ici 2100 dans le scénario actuel de type « statu quo ».

Keywords:

• statistical downscaling
• multiple linear regression
• principal components
• seasonal cycle
• local climate change

1 Introduction

General Circulation Models (GCMs) have been used extensively to predict future climate change. The determination of the impact of climate change on a particular species, ecosystem, or natural resource requires climate change scenarios on a regional or even site-specific spatial scale. Most climate models use very coarse spatial resolution (see Fig. 1) and are usually unable to resolve the effects of local topography or other subgrid-scale processes, which may have a strong influence on the climate of a specific location. In order to obtain climate change scenarios with sufficient spatial resolution, model variables must, therefore, be downscaled from the large-scale, coarse-resolution GCM fields using either dynamical or statistical methods (Houghton et al., 2001; Maraun et al., 2010; Wilby et al., 2002). Dynamical downscaling involves the use of a high-resolution regional circulation model embedded in a large-scale GCM to represent the atmospheric physics and circulation over a limited area of interest more realistically. Statistical Downscaling (SD) involves the development of a regression model between observations of a local climate variable (predictand) and the grid-scale atmospheric variables (predictors) at a specific site. The GCM-derived predictors can then be used in a trained regression model to make projections.

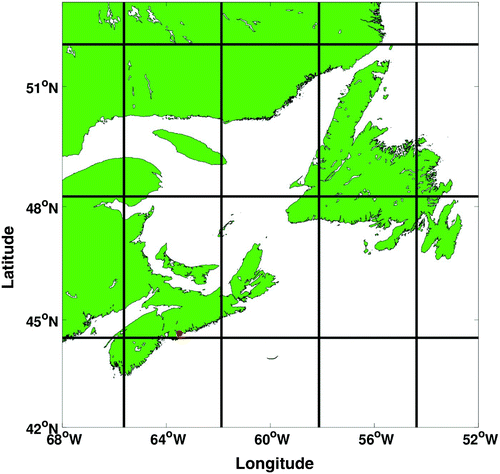
Fig. 1 Grid boxes from a general circulation model (CGCM3) with horizontal resolution of about 300 km by 400 km are plotted over Atlantic Canada. Observations used in this study were taken at Shearwater Airport, Nova Scotia, Canada (44.63°N, 63.5°W). Shearwater Airport (red dot) is about 4 km east of the downtown core of Halifax, Nova Scotia, Canada.

Various regression procedures have been used in SD (Maraun et al., 2010). These include linear regression (Cheng et al., 2008), canonical correlation analysis (von Storch et al., 1993), and artificial neural networks (Schoof & Pryor, 2001). An investigation using various SD methods to predict temperatures in central Europe indicated that Multiple Linear Regression (MLR) using one circulation- and one temperature-related variable produced the best predictions (Huth, 2002). Other studies have shown that SD is capable of capturing past low frequency climate variability (Dibike et al., 2008; Gachon & Dibike, 2007). The predictions of SD are, however, sensitive to the choice of reanalysis dataset used to train the regression. The NCEP and ERA-40 reanalysis products are developed by the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) (Kistler & Kalnay, 2001) and the European Centre for Medium-range Weather Forecasts (ECMWF) (Uppala et al., 2005), respectively. It has been shown that the use of ERA-40 and NCEP variables to downscale surface temperature can produce statistically different predictions (Koukidis & Berg, 2009). Differences in the biases associated with these reanalysis products can affect the development of the downscaling scenarios.

The SD method presented in this paper attempts to develop the best possible linear regression for the prediction of local climate change, based on the 6-hourly fields produced by the Canadian General Circulation Model Version 3 (CGCM3; Jeong et al., 2012). The present method belongs to the SD type of perfect prognosis methods that develop statistical relationships between the observed large-scale predictors and observed local-scale predictands (Maraun et al., 2010). The large-scale observations are often replaced by surrogate observed data such as those obtained from reanalysis products. In comparison with other perfect prognosis SD methods, the present SD method has two important additional steps carried out prior to the construction of the MLR model. The first additional step is to remove the seasonal cycles from both predictands and predictors. Most atmospheric variables have significant variance in their seasonal cycles. Without prior removal of the seasonal cycle, the MLR model will attempt to reproduce the seasonal cycle at the expense of capturing the non-seasonal (e.g., day-to-day and synoptic) variability. Reliable prediction of the non-seasonal variability is of critical importance in predicting future extremes in daily maximum and minimum temperatures. The second additional step is to conduct an objective predictor selection process. This includes comparing the distribution of each GCM predictor with its “observed” counterpart. The introduction of GCM predictors with unrealistic distributions into an observationally trained regression will undermine the projections generated from the regression. As there is no way to guarantee a priori the accuracy of a GCM predictor distribution at a particular location, this predictor selection procedure must be carried out independently for each site.

Temperature-dependent predictors such as surface temperature, humidity, and geopotential height are required in order for the SD method to capture the effect of global warming (Jeong et al., 2012; Maraun et al., 2010; Wilby et al., 2002). There is a difficulty, however, concerning the use of grid-scale GCM surface temperature as a predictor in the regression model. The SD of surface temperature would be very simple if the GCM had a realistic distribution of surface temperature. The GCM surface temperature could then be rescaled using a linear regression trained by observations and projections obtained by shifting the mean using the model trend. Unfortunately, the mean and variability of surface variables in GCMs are often unrealistic and cannot generally be used in linear downscaling (Dibike et al., 2008).

The structure of the paper is as follows. Section 2 describes the predictands and predictors. Section 3 outlines the predictor selection process and the development of the regression. Section 4 discusses the performance of the MLR model. Section 5 presents the projections of the predictands. The main results are discussed in Section 6 and summarized in Section 7.

2 Predictands, predictors, and seasonal cycles

a Predictands T_min and T_max

The MLR model is trained with a 40-year record (1961–2000) of homogenized daily maximum and minimum surface temperatures (Vincent et al., 2002) at Shearwater, Nova Scotia (Fig. 1). Here, homogenized refers to observations that have been corrected for instrument and location changes. The 29 February data from all leap years during the 40-year period have been removed, so that all years have 365 days of data. The total number of T _min (or T _max) data for the 1961–2000 period is therefore 14,600.

The observed time series of T _min and T _max, shown in Fig. 2, have significant temporal variability. The largest source of the variance in T _min and T _max is the seasonal cycle. In addition to temporal variability at lower (interannual) frequencies, there are higher frequency fluctuations in T _min and T _max about the seasonal cycle, which represent the day-to-day weather variability.

Fig. 2 The black line in (a) represents observed T _min (degrees Celsius) from Shearwater Airport, Nova Scotia, for a 5-year period, 1961–65. The red line in (a) represents the fitted seasonal cycle (fitted over the historical period 1961–2000). Time series in (b) represents the daily anomaly constructed by subtracting the red line from the black line in (a). Time series in (c) and (d) are analogous to (a) and (b) except they are for T _max.

The following linear regression of sines and cosines and their associated regression coefficients (α_n and β_n ) is used to remove the seasonal cycle from the observed time series in Fig. 2 over the 40-year period 1961–2000:

where, S(t) represents the seasonal cycle fit to the original data, μ is a constant mean value; ω = 2π/365 d ^{− 1}, and t is time in units of days since 1 January 1961, which repeats from 1 to 365 days giving a value of the seasonal cycle each day of the year. Linear trends in the daily data were removed prior to the determination of regression coefficients. The values of the regression coefficients are listed in Table 1. The choice of the three harmonics used in Eq. (1) was motivated by the fact that the use of less than three harmonics did not adequately represent the seasonal cycle in the observed T _min and T _max whereas a larger number of harmonics allows the non-seasonal (such as month-to-month) variability to be included in S(t) (overfitting).

Table 1. Regression coefficients for the seasonal cycles of observed T _min and T _max at Shearwater, Nova Scotia, in units of degrees Celsius.

Variable	T min	T max
μ	3.07	10.82
α 1	−9.47	−10.12
β 1	−5.79	−5.65
α 2	−0.49	−0.09
β 2	0.06	0.18
α 3	−0.21	−0.02
β 3	−0.72	−0.23

b NCEP and CGCM3 predictors

This study uses two predictor datasets. Both were downloaded from the Canadian Climate Change Scenarios Network website (www.cccsn.ec.gc.ca). The first predictor dataset is a 6-hourly reanalysis product developed by NCEP (Kistler & Kalnay, 2001). The NCEP fields are loosely referred to as observations in this study and used to train the downscaling regression model. The NCEP fields are produced by a general circulation model with a horizontal resolution of 2.5° × 2.5° but with observations assimilated into the model. The second predictor dataset is a 6-hourly climate model dataset generated from a purely prognostic coupled ocean–atmosphere–sea-ice model run using CGCM3. This CGCM3 run had a spatial resolution of 3.75° × 3.75° in the horizontal, and 31 vertical levels. It uses the same ocean component as CGCM2 (Flato & Boer, 2001). However, CGCM3 uses an updated atmospheric component known as the third generation Atmospheric General Circulation Model (AGCM3; McFarlane et al., 2006), which incorporates major improvements in the treatment of land processes, water vapour transport, and cumulus parameterization.

This study considered the use of twenty-five NCEP reanalysis variables as predictors for the 1961–2000 period (Table 2). Some of these variables, including geopotential height, specific humidity, and surface mean temperature, are directly related to temperature and, therefore, expected to respond to changes in radiative forcings from greenhouse gases. Most of the other predictors in Table 2 are dynamical variables. Unfortunately, the CGCM3 model generates wind distributions which are inconsistent with those generated by NCEP. The CGCM3 model does, however, generate realistic distributions of geostrophic wind (Gachon et al., 2008). Because our intent is to develop a regression that can be used to make projections using the CGCM3 grid-scale variables as predictors, all wind variable predictors listed in Table 2 refer to geostrophic winds.

Table 2. Original names (set of 25) of NCEP and CGCM3 predictors. The subsets for each season chosen through the predictor selection process are also shown by the checkmark. Winds in the table are geostrophic winds.

Number	Original	Winter	Summer
1	Mean sea level pressure	✓	✓
2	1000 hPa wind speed	✓	✓
3	1000 hPa zonal wind	✓	✓
4	1000 hPa meridional wind	✓
5	1000 hPa vorticity		✓
6	1000 hPa wind direction
7	1000 hPa divergence
8	500 hPa wind speed	✓	✓
9	500 hPa zonal wind	✓	✓
10	500 hPa meridional wind	✓	✓
11	500 hPa vorticity	✓	✓
12	500 hPa wind direction
13	500 hPa divergence
14	500 hPa geopotential height	✓
15	850 hPa wind speed	✓	✓
16	850 hPa zonal wind	✓	✓
17	850 hPa meridional wind	✓	✓
18	850 hPa vorticity	✓	✓
19	850 hPa wind direction
20	850 hPa divergence
21	850 hPa geopotential height	✓	✓
22	500 hPa specific humidity		✓
23	850 hPa specific humidity	✓	✓
24	1000 hPa specific humidity	✓
25	Surface mean temperature	✓

The NCEP predictors were first interpolated to the lower resolution (3.75° × 3.75°) CGCM3 Gaussian grid. This ensures that the two different predictor datasets refer to the same geographic space. The 6-hourly interpolated NCEP predictors were then used to generate daily mean values, so that each NCEP predictor had the same temporal resolution as the daily T _min and T _max. The NCEP predictors were converted to Z-scores by taking the difference with respect to the time means  then normalizing by the standard deviation (σ) over the 30-year period 1961 to 1990:

Finally, the NCEP predictors were detrended and deseasonalized using Eq. (1), to obtain daily anomalies similar to the predictands T _min and T _max. More details on the construction of the NCEP predictors can be found in Gachon et al. (2008).

The CGCM3 predictor dataset was chosen from the twenty-five 6-hourly grid-scale variables listed in Table 2. The CGCM3 dataset is a 140-year model run extending from 1961 to 2100. During the 1961–90 model historical period, CGCM3 was integrated with forcings from observed greenhouse gases. During the 1991–2100 model future period, the model was integrated using the “business-as-usual” A2 scenario (Nakicenovic et al., 2000). The 6-hourly CGCM3 predictors were converted to daily means, and then Z-scores, using a procedure identical to that described above for the NCEP predictors. For each CGCM3 predictor, the mean and standard deviation used in Eq. (2) were calculated from the 1961–90 standardization period. The independent conversion of the NCEP and CGCM3 predictors to Z-scores removes biases in the mean and variance from the two historical datasets. It should be noted that, because of the limited duration (40 years) of the surface observations, the present SD method is not able to resolve the climate variability on time scales longer than 40 years.

For the 1961–2000 historical period, the CGCM3 Z-scores (now considered predictors) were detrended and deseasonalized in the same manner as the NCEP predictors. For the 2001–2100 future period, the removal of the trend and seasonal cycle deserves some discussion. The intent of this work is to use the CGCM3 predictors in a regression model to make projections. It is important, therefore, that the CGCM3 predictors be detrended and deseasonalized during the periods in which the regression model is applied. Accordingly, the 2001–2100 future period is subdivided into four intervals: 2001–10, 2011–40, 2041–70, and 2071–2100. Within each of these four future intervals, the CGCM3 predictors were detrended and then deseasonalized using Eq. (1). After doing so, each CGCM3 predictor, in each future period, will have a zero mean value μ. (An alternative approach to removing the mean and trend will be discussed in Section 6a.) The mean of each CGCM3 predictor during the 1961–90 standardization period is almost identical to the mean during the defined historical period (1961–2000). In the future periods, however, each CGCM3 predictor will, in general, have a different mean from the 1961–90 mean. This produces Z-scores with a non-zero mean value. The predictors are being used to predict the climate of each of the future periods. It is therefore essential that the non-zero mean values be retained. Accordingly, within each of the four future intervals, the non-zero mean value of each CGCM3 predictor (Z-score) is retained by adding back the mean determined by Eq. (1) after the seasonal cycle is removed.

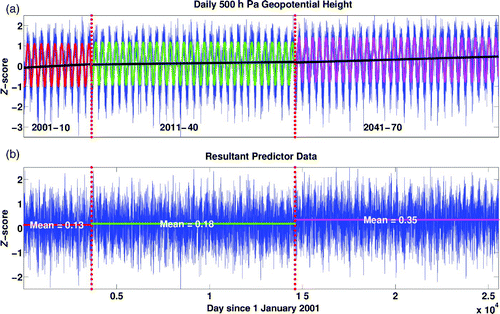
The above procedure is illustrated in Fig. 3. The top panel shows the time series of the Z-score corresponding to the daily mean CGCM3 500 hPa geopotential height above Shearwater in three of the four future intervals (the 2071–2100 interval has been removed for clarity). Within each interval, we show the linear trend in black, and the seasonal cycles of the future periods 2001–10 (red), 2011–40 (green), and 2041–70 (magenta). The lower panel shows the time series of the Z-scores with the linear trend and seasonal cycle within each interval removed. This procedure retains the average deviation in the predictor within each time interval from the 1961–90 standardization period. The changes in the mean value of a predictor during a particular time interval reflect a climate change signal from the model which would be expected to affect the evolution of the predictands T _min and T _max.

Fig. 3 (a) Time series of the geopotential height (blue) at 500 hPa produced by the CGCM3 at the model grid box containing Shearwater, Nova Scotia, during the period 2001–70. The vertical red dotted lines divide the future period into three separate future periods: 2001–10, 2011–40 and 2041–70. The black line in (a) represents the linear trend (with the mean) in each future period. The seasonal cycle fitted to each future period (red, green, magenta) detrended data (geopotential height (blue) minus trend (black)) is also shown in (a). Time series in (b) are daily anomalies constructed by taking the geopotential height minus the trend in each period and finally subtracting the seasonal cycle in each future period. Panel (b) also shows the seasonal cycle mean which was added for each period as the final step.

3 Predictor selection and regression model

The SD method used here consists of three major steps. The first step is to select the appropriate NCEP and CGCM3 predictors. The second step is to develop an MLR model using historical observations and validate its performance using independent observations. Once a skilful historical regression has been determined, the CGCM3 predictors can be used in the regression to determine whether they are able to capture the statistical properties of the historical predictand distribution. Finally, the CGCM3 predictors are used in the trained MLR model to make predictions of the future evolution of the predictand distribution.

a Predictor Selection Process

The NCEP and CGCM3 predictors used in the regression model are chosen from a subset of the 25 potential predictors listed in Table 2. As discussed in Section 2, daily anomalies of each potential predictor are generated by the conversion of each predictor to a Z-score and the removal of the linear trend and seasonal cycle. Some of the 25 predictors are eliminated as follows.

First, under the β-plane approximation, the geostrophic divergence is linearly related to the geostrophic meridional wind (Holton, 2004):

Here , and f_o refers to a mid-latitude Coriolis parameter. The geostrophic divergence and geostrophic meridional wind are, therefore, identical from a statistical point of view. The introduction of both into a regression model would lead to inflation of the regression coefficients. In general, significant covariance among the predictors can lead to a problem known as “overfitting.” In this case, for example, the geostrophic divergence and meridional geostrophic wind speed have a correlation of one. If both of these predictors are included in the regression, the regression will become overfit because the regression coefficients will be large and compensating for both predictors (known as “inflation” of the regression coefficients). Because the least squares estimate of the regression coefficients requires taking the inverse of a matrix (predictor matrix multiplied by its transpose), identical predictors make the matrix to be inverted ill conditioned, and the regression coefficients larger than they would be otherwise. The regression will attempt to predict the predictand variance by having a large regression coefficient associated with the first predictor and an opposing large regression coefficient associated with the other predictor to compensate. To avoid this situation, we removed the geostrophic divergence from consideration as a predictor at all three levels (500 hPa, 850 hPa, and the surface) in favour of meridional wind speed.

In general, the relationship between surface temperature and the local meteorological variables can be expected to depend on season. The predictor selection process was therefore conducted independently for the winter (DJF), spring (MAM), summer (JJA), and fall (SON).

As mentioned earlier, one of the most important criteria used in the predictor selection process is that the predictor have a realistic distribution. Here, for example, the CGCM3 predictors should be similar to those of NCEP. Climate variables that do not have the same distributions as the reanalysis (or observed) variables can undermine the accuracy of projections obtained from regression models (Wilby & Dawson, 2004). However, it is necessary that some balance be made between retaining enough predictors to ensure a good regression model and retaining only those predictors whose distributions are properly represented by the GCM. The predictor selection process cannot be based solely on regression accuracy but must also take into account the suitability of the GCM predictors in the trained regression to obtain projections.

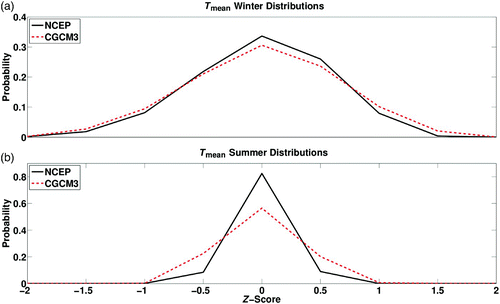
The following objective selection process was conducted for the 22 remaining NCEP/GCM predictors in each season (the original 25 minus 3 divergence predictors, see Table 2). First, the distribution of each predictor (NCEP or CGCM3) was calculated by separating the time series data of each predictor into bins, with the width of each bin being 0.5 of a Z-score. The number of data points in each bin, normalized by the total number of time series data, yields the sample probability in each bin. This defines the predictor distribution. For the winter, spring, and fall, we eliminate predictors having an absolute probability difference between the NCEP and CGCM3 distributions, in any bin, larger larger than 0.04. In summer, a maximum allowable difference of 0.04 yields only four predictors, which are too few for a skilful regression. The summer criterion was therefore relaxed to 0.08. Figure 4 shows the distributions of the 1961–2000 NCEP and CGCM3 surface daily mean temperature in winter and summer at the grid cell containing Shearwater. In summer, the CGCM3 model is unable to simulate the surface daily mean NCEP temperature accurately and does not pass the 0.08 criterion. In winter, however, the surface mean CGCM3 temperature distribution is similar to NCEP and passes the 0.04 criterion. As a result, the surface mean temperature is used as a predictor in winter but not summer. The 17 final predictors to be used for the winter regression, and 15 predictors for the summer regression, are listed in Table 2.

Fig. 4 Distributions of T _mean in (a) winter and (b) summer generated from NCEP (black) and CGCM3 (red) datasets between 1961 and 2000 at Shearwater, Nova Scotia. Both the NCEP and CGCM3 predictors are Z-scores. The distribution is created by binning the data in bins 0.5 of a Z-score wide. The probability is calculated by taking the number of measurements occurring in each bin and dividing by the total number of measurements.

b Multiple Linear Regression Development

The NCEP predictor subsets in each season, listed in Table 2, were transformed into principal components prior to their introduction into the regression model. This generates a new set of predictors which are independent of each other (i.e., no correlation). It also enables a ranking of the principal components in terms of the fraction of the variance in the original predictor dataset that each principal component is able to explain. Table 3 shows the ranking of the 17 principal components calculated from the 17 members of the NCEP winter predictor subset. During winter, the first four principal components explain more than 80% of the variance in the original 17 NCEP predictors. Although this is of interest, it is of secondary importance for our purposes. The main reason for the introduction of the principal components is to have independent predictors and avoid inflation of the regression coefficients. The principal components with the largest explained variance of the original predictor set are not necessarily the most useful for predicting T _min or T _max. Table 4 shows the ranking of the principal components determined from the summer predictor subset.

Table 3. The numbers in the percent (%) column refer to the fraction of total variance explained in the original dataset by each of the seventeen principal components (PCs) for winter. Here R refers to the correlation coefficient of each PC with T _min and T _max, and γ refers to the regression coefficient, in units of degrees Celsius, of those PCs used in the winter regression.

PC	%	T min		T max
		R	γ	R	γ
1	29.43	−0.30	−0.76	−0.41	−0.93
2	24.03	0.03	—	−0.22	−0.56
3	19.94	0.52	1.64	0.51	1.43
4	9.08	0.34	1.63	0.32	1.33
5	5.89	0.17	1.07	0.16	0.82
6	3.53	−0.27	−2.00	−0.30	−2.08
7	2.70	−0.28	−2.44	−0.26	−1.99
8	2.05	−0.09	—	−0.03	—
9	1.11	0.11	1.42	0.09	—
10	0.90	−0.29	−4.42	−0.15	−2.04
11	0.51	−0.06	—	−0.06	—
12	0.32	0.09	—	0.08	—
13	0.20	0.02	—	0.03	—
14	0.14	−0.01	—	−0.01	—
15	0.13	−0.02	—	−0.05	—
16	0.02	−0.02	—	−0.05	—
17	0.02	−0.05	—	−0.07	—

Table 4. The numbers in the percent (%) column refer to the fraction of total variance explained in the original dataset by each of the fifteen Principal Components (PCs) for summer. Here R refers to the correlation coefficient of each PC with T _min and T _max, and γ refers to the regression coefficient, in units of degrees Celsius, of those PCs used in the summer regression.

PC	%	T min		T max
		R	γ	R	γ
1	30.97	−0.26	−0.34	−0.16	−0.32
2	20.93	−0.39	−0.64	0.14	0.38
3	17.10	0.06	—	0.28	0.83
4	7.96	0.00	—	0.14	0.72
5	6.96	−0.08	—	−0.16	−0.80
6	5.17	0.35	1.16	0.45	2.32
7	3.42	−0.03	—	0.05	—
8	2.72	−0.14	−0.69	−0.11	−0.84
9	1.56	−0.15	−0.93	0.01	—
10	0.99	0.09	—	0.24	2.98
11	0.87	−0.02	—	−0.09	—
12	0.71	0.03	—	0.06	—
13	0.46	0.11	0.99	0.08	—
14	0.14	0.01	—	−0.05	—
15	0.05	0.34	11.83	0.34	18.67

Once the NCEP principal components were determined, their correlation coefficients (R) with T _min and T _max (the predictands) could be calculated. These coefficients are shown in Tables 3 and 4, respectively, for winter and summer. It can be shown that the inclusion of principal components whose absolute value R is less than 0.1 does not significantly improve the root mean square error in the prediction of T _min and T _max during the 1961–90 historical period. Principal components having a correlation (R) less than this minimum correlation value, known as the correlation cutoff, were therefore excluded from the regression model. Tables 3 and 4 list the regression coefficients for the winter and summer seasons for the principal components included in the regression model.

4 Validation of regression and regression results

a Prediction of T_min and T_max using NCEP Predictors

The principal components which explain the largest variance in the predictands should have a physical relationship with the predictands. During winter, the principal component with the largest correlation with both T _min and T _max explains roughly 27% of the total variance in T _min (R = 0.52), and 26% of the total variance in T _max (R = 0.51), and is labelled PC-3 in Table 3. This principal component is mainly composed of the NCEP meridional wind at the 1000, 850, and 500 hPa pressure levels, consistent with the expectation that the day-to-day surface temperature variability at Shearwater during winter be dominated by meridional temperature advection.

In summer, principal component PC-2 (Table 4) accounts for the largest variance in T _min, with a correlation coefficient of −0.39, corresponding to approximately 15% of the total variance in T _min. This principal component is dominated by the NCEP specific humidity at 500 hPa. The leading principal component for T _max during summer is PC-6, which explains approximately 20% of the total variance in T _max (R = 0.45). PC-6 in summer is dominated by 850 hPa specific humidity. The strongest predictors for T _min and T _max in summer are principal components constructed primarily from the lower and mid-tropospheric specific humidity. PC-2 in summer, which is constructed of negatively weighted 500 hPa specific humidity, has a negative correlation with T _min. This indicates that as the 500 hPa specific humidity increases, PC-2 decreases and T _min increases. Similarly, the correlation coefficient between PC-6 and T _max in summer is positive, and PC-6 is constructed of positively weighted 850 hPa specific humidity. This indicates that, as the 850 hPa specific humidity increases, T _max also increases. The relationship between surface temperature and higher level specific humidity requires more consideration. A large feature governing weather and temperature in Nova Scotia in summer is the subtropical ridge. This is a warm core feature that is vertically stacked. From a weather perspective, as the ridge sets up to the south of Nova Scotia, specific humidity tends to increase at all levels (because of moisture advection) assuming that the relative humidity remains constant.

The predictive skill of the MLR model can be assessed using cross validation. The regression model is first trained using observed values of T _min and T _max between 1961 and 1990 as the predictands and the NCEP principal component values as predictors. The trained MLR model is then used to predict T _min and T _max between 1991 and 2000, and the results are compared with observations. For each season, the predictive skill of the regression model during the 10-year validation period can be quantified using the correlation between predicted and observed T _min and T _max. Table 5 shows the percentage of the variance in observed T _min and T _max explained by the regression model, for both the training (1961–90) and validation (1991–2000) periods. For each season, the percentages of explained variance for the training and validation periods are almost identical. This demonstrates the ability of the MLR model to predict observed T _min and T _max using predictor data that is independent of the training period. Table 5 also shows that the MLR model is significantly more skilful during winter than summer.

Table 5. The percentage of total variance explained by the regression for T _min and T _max during the training period (1961–90) and the validation period (1991–2000) for winter and summer.

Season	Training T min	Validation T min	Training T max	Validation T max
Winter	74	76	77	77
Summer	52	53	55	56

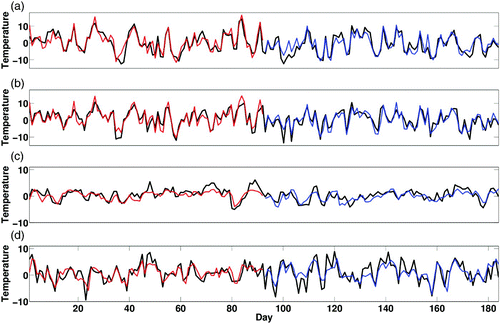
Figure 5 shows two years (1990–91) of predicted and observed daily anomalies in T _min and T _max. The first year (1990) is within the training period; the second year (1991) is within the validation period. The predictability of the MLR model, using the NCEP principal components, does not significantly change during the transition from the training to validation periods. The daily anomalies in T _min and T _max, predicted by the regression model, can be used to generate values of T _min and T _max by addition of the seasonal cycle.

Fig. 5 (a) Time series of observed daily anomalies of T _min (degrees Celsius) in winter (black) for two years (1990–91). The NCEP prediction of the daily T _min anomaly in winter for the last year of the training period (1990) is shown in red. The blue line represents the winter T _min NCEP prediction of the daily anomaly for the first year of the validation period (1991). (b) As in (a) except for T _max in winter. Time series in (c) and (d) are the same as in (a) and (b), except for summer.

The validity of linear regression models is based on assuming that the regression errors exhibit normality, homoscedasticity, and independence. We found that the regression errors do, indeed, obey a normal distribution, that the errors do not generate patterns when plotted against each predictor, and that the errors do not exhibit trends or patterns in time. The comparisons shown in Fig. 5 confirm that the NCEP principal components of the regression model do not overfit and do not violate the main assumptions of linear regression. Note, the normality and homoscedasticity assumptions could be relaxed by using a generalized vector linear model (Maraun et al., 2010).

b Prediction of T_min and T_max using CGCM3 Predictors

For each season, the CGCM3 predictors were defined in the same way as the NCEP predictors. The CGCM3 principal components were also defined in terms of the CGCM3 predictors, using the same expressions used to define the NCEP principal components (Table 2). In other words, the CGCM3 principal components were calculated by projecting the CGCM3 variables onto the NCEP-derived eigenvectors, based on the assumption that the NCEP eigenvectors represent the true directions of variance. If the distributions of the CGCM3 predictors are similar to the NCEP predictors, the distributions of the CGCM3 and NCEP principal components should also be similar to each other. The CGCM3 principal components, when used in the NCEP-derived regresssion model, should therefore be able to make reasonable estimates of the predictand distributions (T _min and T _max) during the historical period.

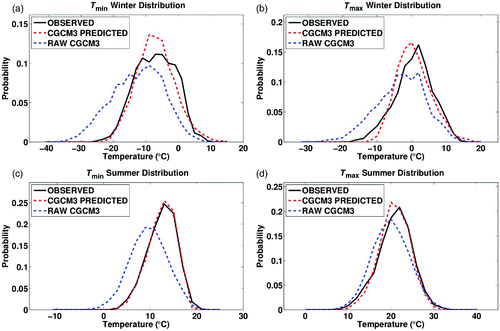
The CGCM3 model fields used in this study were generated by free-running model simulations (i.e., without data assimilation). It is therefore not meaningful to compare the T _min and T _max values generated by the regression model directly, using the CGCM3 principal components, with measurements of T _min and T _max on individual days. In Fig. 6, we compare the distributions of observed T _min and T _max with the T _min and T _max distributions generated by adding the observed seasonal cycle to the T _min and T _max anomalies produced by the regression model with the CGCM3 principal components. We also show the T _min and T _max distributions generated from the raw grid cell CGCM3 temperatures. The summer and winter distributions are both calculated from the 40-year 1961–2000 historical period. The regression model, with the CGCM3 principal components, predicts the distribution of surface temperature much more accurately than the raw CGCM3 climate model data. The most significant improvement occurs for T _min in winter. However, improvement is noted in all seasons for both predictand variables.

Fig. 6 Distributions of the observed (black), CGCM3 predicted (red dashed) and raw CGCM3 (blue dashed) total T _min and T _max in winter and summer for the period 1961–2000. To create the distribution the data were separated into bins that were two degrees Celsius wide over the range of the data. The sample probability on the vertical axis refers to the number of measurements occurring within a particular bin divided by the total number of measurements.

5 Projections

When implemented in a regression model, the CGCM3 predictors are able to simulate the distribution of T _min and T _max during the historical period (1961–2000) reasonably well. The CGCM3 predictors should, therefore, be able to predict the distribution of daily surface T _min and T _max in the future period (2001–2100), provided the historical statistical relationships between the predictands and predictors continue to be valid during the future period and that the changes in the predictor variables are well characterized by the CGCM3 climate model (Wilby & Wigley, 2000).

The twenty-five CGCM3 predictors were detrended and deseasonalized and their mean values retained, within the three 30-year future periods 2011–40, 2041–70, and 2071–2100, as discussed previously. These predictors were then divided into seasons, with the predictors that passed the historical predictor selection tests (see Table 2) used to define the future CGCM3 principal components. This was again done by projecting the CGCM3 predictors onto the NCEP derived eigenvectors. The CGCM3 principal components were then used in the historically trained regression model to predict the future daily anomalies in T _min or T _max. This approach assumes that the response of surface temperature to slowly varying changes in the mean value of a principal component, on long time scales, is similar to the daily time-scale response that has been determined through the fitting of the regression during the historical period.

The daily anomalies in future T _min and T _max, calculated by the regression model using the CGCM3 principal components, were then converted to T _min or T _max values by adding the seasonal cycle from the 1961–2000 historical period. Figure 7 shows the CGCM3 predicted distributions of winter and summer T _min and T _max during the three future periods. The future distributions shift toward progressively warmer temperatures. The largest shift occurs for T _min during winter.

Fig. 7 Distribution of CGCM3 predicted total T _max and T _min in winter and summer in the historical period (1961–90) and three future periods (2011–40, 2041–70, 2071–2100). The distributions are created by binning the data in two degree Celsius bins. The sample probability is found by dividing the number of measurements in a particular bin by the total number of measurements.

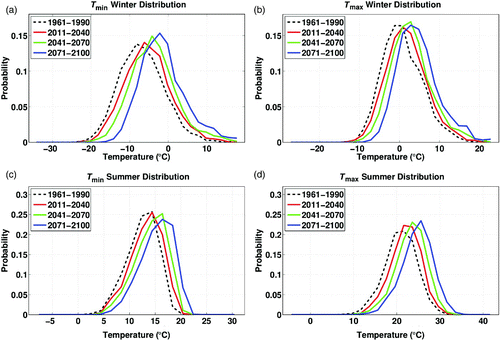
Table 6 lists the mean and standard deviation for T _min during winter and summer for each of the three future 30-year intervals. For reference, we also show the mean and standard deviation for T _min during the 1961–2000 historical period. The mean winter T _min increases by 5.58°C from the historical to final future period, and the mean summer T _min increases by 2.75°C. These changes give rise to a significant effective reduction in the amplitude of the seasonal cycle in T _min relative to the historical period. Because the seasonal cycle from the historical period was added to the future daily anomalies of T _min predicted by the regression model, this reduction in the T _min seasonal cycle originated from the regression. During the future periods, the CGCM3 principal components have non-zero means, arising from the trends in the climate variables. Because we use regressions which are seasonally dependent, the non-zero means in the principal components give rise to seasonally dependent non-zero means in the T _min daily anomalies.

Table 6. The mean and standard deviation for the predicted future distributions of CGCM3-predicted total T _min in the winter and summer seasons for the three future periods (2011–40, 2041–70, 2071–2100). The change in mean (δ_μ ) from the historical to each future tri-decade is also shown. The historical observed distribution mean and standard deviation are also shown. The units in this table are degrees Celsius.

Period	Season	μ	δμ	σ	Historical μ	Historical σ
2011–40	Winter	−5.33	1.67	5.92
2041–70	Winter	−3.78	3.22	6.00	−7.00	6.10
2071–2100	Winter	−1.42	5.58	5.94
2011–40	Summer	13.31	0.77	3.03
2041–70	Summer	14.12	1.58	3.06	12.54	3.08
2071–2100	Summer	15.29	2.75	3.10

The predictions of winter and summer T _max during the three future periods are listed in Table 7. There is a modest decrease in the T _max seasonal cycle, resulting from a 3.97°C increase in T _max during winter and a 3.75°C increase in T _max during summer.

Table 7. The mean and standard deviation for the predicted future distributions of CGCM3-predicted total T _max in the winter and summer seasons for the three future periods (2011–40, 2041–2070, 2071–2100). The change in mean (δ_μ ) from the historical to each future tri-decade is also shown. The historical observed distribution mean and standard deviation are also shown. The units in this table are degrees Celsius.

Period	Season	μ	δμ	σ	Historical μ	Historical σ
2011–40	Winter	1.77	1.13	5.06
2041–70	Winter	2.92	2.28	5.15	0.64	5.48
2071–2100	Winter	4.61	3.97	5.17
2011–40	Summer	22.08	1.11	3.50
2041–70	Summer	23.25	2.28	3.48	20.97	3.99
2071–2100	Summer	24.72	3.75	3.56

6 Discussion

a Alternative Approaches for Future Prediction

In the above discussion, the linear trend and seasonal cycles of the CGCM3 grid variables were removed within each future period. These grid variables did retain, however, non-zero mean values with respect to the historical period. This method permits the construction of stationary principal components during the time periods in which the trained regression is to be applied but still allows the climate forcings to influence the predicted daily T _min and T _max. However, there are other ways in which stationary principal component time series could be constructed and still incorporate the trends from the climate model. For example, the CGCM3 climate variables could be detrended and deseasonalized and have their means removed over the entire future period (2001–2100) prior to introduction into the regression model. In this case, the regression would only predict changes in the shape of the distribution. The trends in daily T _min and T _max could then be taken directly from the raw CGCM3 trends in the surface grid box at Shearwater, using the 1961–2000 period as a baseline. This alternative calculation for future daily T _min predicts, by the 2080s, an additional 1.2°C warming in winter and an additional 1.8°C warming in summer, relative to the method used in Section 5.

The main advantage of this alternative method is that the CGCM3 model includes non-linear dynamics. It should therefore, in principle, be superior to a linear regression model in predicting changes in the mean values of surface variables under climate change. On the other hand, because of the known deficiency of coarse-resolution climate models in the representation of surface variables, the regression model should more realistically capture the relationship between changes in surface temperature with changes in other climate variables, provided these changes are within the range of the variability observed during the historical period.

b Predictive Power of Surface Mean Temperature

During summer, the daily mean surface temperature was excluded as a predictor by the objective predictor selection procedure discussed in Section 3. This was done because the CGCM3 model did not accurately reproduce the observed distribution of surface temperature. To demonstrate that daily mean surface temperature is not needed in projections of T _max, we conducted a sensitivity study in which we used the same downscaling method as described above but with the daily mean surface temperature also included as a predictor in summer. During the 2071–2100 period, this results in an additional 0.1°C warming relative to the results listed in Table 7. The same sensitivity study was also conducted at many other locations in eastern Canada. We again found that the mean surface temperature from the CGCM3 model was not essential to the projections. This demonstrates that other temperature-related variables, such as geopotential height, which are more accurately represented by the CGCM3 climate model, are more useful in predicting climate change using our regression model. Caution should be exercised, however, when eliminating CGCM3 temperature-related variables as predictors. If the GCM does simulate their distribution properly, these variables should also be included in the predictor set. As a best practice, each GCM variable should be compared with observations at each location.

c The Advantage of Removing the Seasonal Cycle before Training the Regression

We conducted an additional experiment to demonstrate the advantages of removing the seasonal cycles prior to training the regression. We used the same SD method and set of NCEP predictors (see Table 2) described above, except that the seasonal cycles of the predictand and predictor data were not removed prior to the training of the regression. This SD method predicts T _min and T _max, rather than the anomalies, during the 1961–2000 historical period. However, the anomalies in T _min and T _max can be calculated by removal of the seasonal cycle using Eq. (1). The relative skill of each method was then quantified using the following calculation of γ ² (Thompson et al., 2003):

In this equation, var refers to the variance, while O and P refer to the observed and predicted daily anomalies of T _min or T _max. In general, smaller values of γ ² reflect higher skill. The γ ² values associated with predicting the daily anomalies of T _min and T _max during winter and summer, for each method, are listed in Table 8. For T _min, the removal of the seasonal cycle decreases γ ² from 0.26 to 0.25 in winter and from 0.71 to 0.51 in summer. For T _max, the removal of the seasonal cycle decreases γ ² from 0.23 to 0.22 in winter and from 0.52 to 0.45 in summer. Although the improvements associated with removal of the seasonal cycle are marginal in winter, they are quite significant during summer. However, these improvements are smaller than they would otherwise be because we still separate regressions for each winter and summer.

Table 8. Values of γ ² for predicting the daily anomalies of T _min and T _max in winter and summer during the historical period (1961–2000) using the SD method with and without removal of the seasonal cycles from predictors and predictands prior to training the regression model. Values of γ ² in predicting T _max with SDSM are also shown.

Cases	T min		T max
	Winter	Summer	Winter	Summer
Seasonal cycles removed	0.25	0.51	0.22	0.45
Seasonal cycles included	0.26	0.71	0.23	0.52
Annual regression	0.30	1.01	0.31	0.82
SDSM	–—	–—	0.78	1.04

d Annual Regression

The overall importance of removing seasonality can be determined from an annual regression in which, in addition to retaining the seasonal cycle in both predictors and predictands, a single regression is carried out for the entire year. In the predictor selection process, we adopted a maximum allowable difference in the probability distribution of 0.04 (see Section 3a). This resulted in an eighteen member predictor dataset. This dataset was then transformed into principal components using the methods described earlier. Using the same criteria as used previously, we used five principal components in the final regressions for both T _min and T _max. Both regressions had an explained variance larger than 90%. However, much of this explained variance is simply replicating the seasonal cycle. If Eq. (1) is used to remove the seasonal cycle from the predicted T _min and T _max, we can obtain predictions for the daily anomalies. These can then be compared with the observed daily anomalies during the historical period. The third row of Table 8 shows the γ ² values generated using the annual regression. In all cases, these values are larger than the the preferred original method, in which we both removed the seasonal cycle and carried out separate regressions for winter and summer. This third method is also less accurate than the method just described, in which the seasonal cycles were not removed, but separate regressions were still carried out for winter and summer. The improvements associated with applying separate regressions for different seasons, and with the seasonal cycle removal, are particularly large in summer.

e Statistical Downscaling Model (SDSM)

We also used a well-known downscaling software package known as SDSM version 4.2.9 (Wilby et al., 2002) to downscale T _max and help quantify the benefits of removing the seasonal cycle. This package developed a linear regression, using the NCEP predictor and predictand datasets from 1961 to 1990 as the training period. There is no option to remove the seasonal cycles in the predictors and predictand. In its predictor selection process, SDSM uses partial correlation but does not determine whether the corresponding GCM predictors properly represent the distributions of the observed predictors and does not convert the predictors to principal components. The predictors chosen by the SDSM software were meridional and zonal geostrophic wind at the surface, 850 hPa meridional geostrophic wind speed and geopotential height, and 500 hPa meridonal geostrophic wind speed, vorticity, and geopotential height. Using these NCEP predictors, the predictions of T _max by the SDSM regression model can be compared with observations during the 1991–2000 validation period. Although the regression predicts T _max, the anomalies can be obtained by using Eq. (1) to remove the seasonal cycle. The accuracy of the SDSM regression was quantified by calculating γ ² for T _max during the validation period. As shown in the fourth row of Table 8, the winter and summer values of γ ² were larger than with any of the other three methods discussed in this paper and significantly larger than the default method (compare rows 1 and 4). The main differences between the annual and SDSM regression is that the annual regression uses a different predictor selection process and uses principal components in the regression. These two differences also appear to improve the regression significantly. It should be mentioned that SDSM is a useful tool for downscaling climate variables using monthly regression which would certainly help with the seasonal cycle issue.

7 Summary

General Circulation Models (GCMs), which incorporate the known equations of motion, equations of state, conservation laws, and our best understanding of how subgrid-scale processes should be parameterized, are useful tools for predicting the climate response to particular forcings. However, because of their coarse resolution, GCMs often perform poorly on the local scale, especially for surface variables (Giorgi & Mearns, 1991). In SD, the mechanistic predictive power of GCMs on larger scales is combined with a regression model that is trained with observed relationships between a local surface variable and the grid-scale variables of a reanalysis dataset. This combination should, in principle, be able to make more robust predictions of climate change at particular locations, especially in regions with high surface heterogeneity. Care must be taken with SD, however, to ensure that the GCM grid-scale variables behave in a way that is consistent with the reanalysis variables and that the historical regressions not be extrapolated outside their observed range of validity.

In this study, NCEP reanalysis variables were used to train a regression model to predict daily T _min and T _max at Shearwater, located in a region with strong sea surface temperature gradients and complex coastlines. The seasonal cycles of both predictors (NCEP variables) and predictands (T _min and T _max) were removed prior to their introduction into a seasonally based principal component regression model. We demonstrated that the removal of the seasonal cycle forces the regression coefficients to simulate the synoptic variability and increases the accuracy of the regression model. We have also shown that the accuracy of the regression model can be increased by using different regressions in different seasons (here winter and summer). This can be expected to be the case when the meteorological mechanisms which generate daily temperature anomalies have a seasonal variation. In addition, our regression model used principal components defined in terms of the NCEP grid-scale variables rather than the climate model variables themselves. Using this model, the regression model was able to simulate the observed distribution of T _min and T _max at Shearwater much more accurately than the raw grid-scale CGCM3 surface temperature. Finally, we used the CGCM3 principal components in the regression model to predict the expected changes in T _min and T _max at Shearwater during three future periods: 2011–40, 2041–70, and 2071–2100. These projections indicate that the daily minimum and maximum temperatures at Shearwater will be up to five degrees warmer by 2100 under the A2 “business-as-usual” scenario and that there is a significant reduction in the seasonal variation of the daily T _min.

Acknowledgements

The authors would like to acknowledge the Data Access Integration (DAI) team for providing the data and technical support. The DAI data download gateway is made possible through collaboration between the Global Environmental and Climate Change Centre (GEC3), the Adaptation and Impacts Research Division (AIRD) of Environment Canada, and the Drought Research Initiative (DRI). The Ouranos Consortium (in Quebec) provided IT support to the DAI team. JS is funded by The Lloyd's Register Educational Trust, which is an independent charity working to achieve advances in transportation, science, engineering, and technology education, training and research worldwide for the benefit of all. RJG is grateful for continuing support from GEOMAR. This work was also supported by Environment Canada. The authors thank Stephen Vallee for maintaining and executing the software models and for assisting with the preparation of the manuscript.