New HEAVY Models for Fat-Tailed Realized Covariances and Returns

ABSTRACT

We develop a new score-driven model for the joint dynamics of fat-tailed realized covariance matrix observations and daily returns. The score dynamics for the unobserved true covariance matrix are robust to outliers and incidental large observations in both types of data by assuming a matrix-F distribution for the realized covariance measures and a multivariate Student's t distribution for the daily returns. The filter for the unknown covariance matrix has a computationally efficient matrix formulation, which proves beneficial for estimation and simulation purposes. We formulate parameter restrictions for stationarity and positive definiteness. Our simulation study shows that the new model is able to deal with high-dimensional settings (50 or more) and captures unobserved volatility dynamics even if the model is misspecified. We provide an empirical application to daily equity returns and realized covariance matrices up to 30 dimensions. The model statistically and economically outperforms competing multivariate volatility models out-of-sample. Supplementary materials for this article are available online.

KEY WORDS:

• Generalized autoregressive score (GAS) dynamics
• Heavy tails
• Matrix-F distribution
• Multivariate volatility

1. INTRODUCTION

A substantial body of literature focuses on modeling volatilities and correlations of financial asset returns; see Bauwens, Laurent, and Rombouts (2006) and Asai, McAleer, and Yu (2006) for surveys. More recently, the increasing availability of intraday data has led to the introduction of new types of volatility models that include so-called “realized measures” of variances and covariances. These new models lead to more accurate measurements and forecasts of the conditional variance of daily financial returns. Examples of such models in the univariate case are the multiplicative error model (MEM) (Engle and Gallo 2006), the HEAVY (high-frequency-based volatility) model (Shephard and Sheppard 2010), and the Realized GARCH model (Hansen, Huang, and Shek 2012). These models consist of dynamic specifications for both returns and realized (variance) measures. In the multivariate context, Noureldin, Shephard, and Sheppard (2012) extended the univariate version of the HEAVY model and Jin and Maheu (2013) developed dynamic component models of returns and realized covariance matrices based on time-varying Wishart distributions. A related model is the Wishart autoregressive (WAR) model for the covariance matrix of Gourieroux, Jasiak, and Sufana (2009), although the authors apply it to realized covariance matrices, discarding the daily return observations. Likewise, the multivariate volatility models of Chiriac and Voev (2011) and Bauer and Vorkink (2011) also focus on (multivariate) realized measures only, as does the conditional autoregressive Wishart (CAW) model of Golosnoy, Gribisch, and Liesenfeld (2012).

The asset prices used to estimate the above models are typically subject to the presence of fat-tails and jumps. These may not only affect the daily return observations, but also the realized measures. In particular, depending on the chosen estimator, the realized measure estimates either integrated variance, or both integrated variance and variation due to jumps. The latter may obviously substantially inflate realized measures occasionally whenever jumps occur; see, for example, Lee and Mykland (2008) on the estimation of spot variances in the presence of jumps. Huang and Tauchen (2005) showed the importance of jumps and argued that they account for up to 7% of S&P 500 index variation.

None of the methods described earlier shows how to deal with fat tails in the realized covariance measures and returns simultaneously. In fact, most of the earlier methods center around the use of a Wishart distribution for the realized covariance matrix. The Wishart distribution is rather ill-suited to handle outliers and incidental large observations. In this article, we therefore develop a new model for the covariance matrix dynamics based on joint measurements of possibly fat-tailed intraday-based realized covariance matrices and daily returns. Our set-up is particularly suitable for cases where no explicit robustification methods are applied while estimating realized measures. The new model is observation driven, thus allowing for easy likelihood evaluation, estimation, and inference. We describe the dynamics of the unobserved true daily return covariance matrix by adopting the generalized autoregressive score framework (GAS) of Creal, Koopman, and Lucas (2011, 2013); see also Harvey (2013). The GAS framework uses the score of the conditional density function to drive the dynamics of the time-varying parameters, which in our case is the unknown covariance matrix. Score-driven dynamics possess information theoretical optimality properties even if the model is mis-specified; see Blasques, Koopman, and Lucas (2015). The framework has been successfully applied in the recent literature to a variety of different areas. For example, Creal, Koopman, and Lucas (2011) used the GAS framework to model volatilities and correlations in stock returns; Lucas, Schwaab, and Zhang (2014) developed new dynamic copula models under skewness and fat tails and applied this to systemic risk measurement; Harvey and Luati (2014) described a new framework for dynamic local level models and state filtering based on scores; Creal et al. (2014) introduced observation-driven mixed measurement dynamic factor models to describe default and loss-given-default dynamics; Andres (2014) studied score-driven models for positive random variables; and Oh and Patton (2016) studied high-dimensional factor copula models based on GAS dynamics for systemic risk measurement.

The key ingredient in our dynamic modeling framework for realized covariance matrices is the matrix-F distribution. For an introduction to the matrix-F distribution, see, for example, Konno (1991). Though the matrix-F distribution has been around for some time, we have not found any applications to economic or financial data. This is the more surprising given the typical fat-tailed nature of such data. Incidental large observations may easily corrupt the estimated dynamic pattern of the underlying covariance matrix if distributions with relatively thin tails are used; see Creal, Koopman, and Lucas (2011), Janus, Koopman, and Lucas (2014), Harvey (2013), and Lucas, Schwaab, and Zhang (2014). The matrix-F distribution provides a coherent approach to address such sensitivities.

The use of the matrix-F distribution together with the GAS dynamics of Creal, Koopman, and Lucas (2013) automatically yields a robust recursive method for filtering the covariance matrix dynamics. The form of this recursion is new, and a direct generalization of both Wishart (thin-tailed) dynamics, and multivariate Student's t (vector rather than matrix) dynamics. By a suitable choice of scaling, our recursion retains a convenient matrix format, rendering our approach numerically highly efficient, also in higher dimensional settings. The matrix format of our recursion contrasts sharply with the approaches of Lucas, Schwaab, and Zhang (2014) or Hansen, Janus, and Koopman (2016), which become infeasible in higher dimensions due to the use of vectorization and subsequent scaling operations.

We establish intuitive parameter restrictions for the stationarity and ergodicity properties of our new model. In particular, we show that our stochastic recurrence relation can be seen as a special case of the semipolynomial Markov chains studied by Boussama (2006). The stationary of the model then hinges on the simple and intuitive condition that the autoregressive roots in the GAS recursion lie outside the unit circle. In addition, we show that the positive definiteness of the filtered covariance matrices can easily be ensured.

Most closely related to our current study is Jin and Maheu (2016). They developed a model based on an infinite mixture of inverse-Wishart distributions to improve the fit compared to the standard Wishart distribution to empirical realized covariance matrices. Our approach differs from theirs in two important ways. First, the covariance matrix dynamics in our approach are score driven and therefore reflect the fat-tailedness of the data better. In particular, the filtered covariance matrix estimates are less susceptible to outliers and incidental influential observations, either in daily returns, or in realized measures, or both. Second, unlike Jin and Maheu (2016), our approach is fully observation driven and estimated via classical maximum likelihood. Computationally, therefore, the estimation of our model is much less intensive than the Bayesian estimation procedure of the model of Jin and Maheu.

We illustrate the performance of the new model both in a controlled simulation environment and in an empirical application. The simulation results indicate that the model can filter unobserved volatility patterns even if the model is not correctly specified. Moreover, we show that our framework can easily handle cross-sectional dimensions up to 50. Further, we show that when the (co)variance dynamics are generated by a stochastic volatility (SV) type process, our model outperforms existing multivariate models such as the CAW model of Golosnoy, Gribisch, and Liesenfeld (2012) and the normal-Wishart model of Hansen, Janus, and Koopman (2016).

In our empirical application, we use the new model to describe daily returns and daily realized measures of 30 equities from the S&P 500 index over the period January 2001 to July 2014. We show that the volatilities and correlations estimated by our model produce fewer spikes despite incidental large tail observations. The differences follow directly from the fat-tailed nature of the observation densities we assume and the GAS transition dynamics used to drive the time variation in the daily covariance matrices. We compare density forecasts of the covariance matrix based on our matrix-F distribution and the familiar Wishart distribution used in competing model specifications. The results reveal that the matrix-F provides a much better fit to the data. In addition, the matrix-F distribution also outperforms density forecasts produced by the inverse-Wishart distribution. Density forecasts of returns associated with the new model show that the GAS model strongly beats the BEKK-t and the normal- and inverse-Wishart models. Finally, we assess the economic significance by considering mean-variance efficient portfolios. The results indicate that our proposed model produces significantly lower ex post conditional portfolio standard deviations than competing models.

The rest of this article is set up as follows. In Section 2, we introduce the new GAS model for multivariate returns and realized covariance matrices under fat-tails. In Section 3, we study the performance of the model in a simulation setting. In Section 4, we apply the model to a high-dimensional panel of 30 daily equity returns and daily realized measures from the S&P 500 index. We conclude in Section 5. The appendix gathers the proofs.

2. MODELING FRAMEWORK

2.1. The HEAVY GAS tF Model

Let $y_t\in {\mathbb{R}}^k$ denote the vector of (demeaned) asset returns over day t, t = 1, …, T, and let $R{C}_t\in {\mathbb{R}}^{k\times k}$ denote the corresponding realized covariance matrix, where RC_t is computed using high-frequency data, for example, a standard realized covariance matrix estimator based on 5 min returns. We assume that y_t is fat-tailed and follows a standardized Student's t distribution with ν₀ degrees of freedom and positive definite time varying covariance matrix $V_t\in {\mathbb{R}}^{k\times k}$. The conditional observation density for y_t is (1) $$\begin{array}{ccc}\hfill p_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)& =& \frac{\Gamma (({\nu }_0+k)/2)}{\Gamma ({\nu }_0/2){\left[({\nu }_0-2)\pi \right]}^{k/2}{\left|V_t\right|}^{1/2}}\hfill \\ & & \times {\left(1+\frac{y_t{V}_t^{-1}{y}_t}{{\nu }_0-2}\right)}^{-({\nu }_0+k)/2},\hfill \end{array}$$(1) where ${\mathcal{F}}_t$ denotes the information set containing all returns and realized covariances up to and including time t. We assume that ν₀ > 2, such that the covariance matrix exists.

Whereas a Student's t distribution for y_t is fairly standard in the literature, the distribution of the realized covariance matrix RC_t has received much less attention. Typically, one assumes a Wishart distribution for RC_t ; see, for example, Noureldin, Shephard, and Sheppard (2012); Gourieroux, Jasiak, and Sufana (2009); and Golosnoy, Gribisch, and Liesenfeld (2012). As the empirical data used in Section 4 show, however, the Wishart distribution is strongly rejected by the data. In particular, for the diagonal elements of RC_t we strongly reject the scaled χ² (i.e., univariate Wishart) distribution, whereas we cannot reject a scaled F-distribution. As realized measures are (weighted) sums of high-frequency returns that potentially contain outliers, this may require the more flexible F-distribution. Using this empirically relevant finding, we assume in this article that the realized covariance matrix follows a conditional matrix-F distribution with ν₁ and ν₂ degrees of freedom. The corresponding conditional observation density is (2) $$\begin{array}{ccc}& & p_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2)\hfill \\ & & {\displaystyle =K({\nu }_1,{\nu }_2)\times \frac{{\left|\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}\right|}^{{\nu }_1/2}{\left|R{C}_t\right|}^{({\nu }_1-k-1)/2}}{{\left|{\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}R{C}_t\right|}^{({\nu }_1+{\nu }_2)/2}},}\hfill \end{array}$$(2) with positive definite expectation ${\mathbb{E}}_t\left[R{C}_t\right|{\mathcal{F}}_{t-1}]=V_t$, degrees of freedom parameters ν₁, ν₂ > k − 1, and (3) $$\begin{array}{ccc}\hfill K({\nu }_1,{\nu }_2)& =& \frac{{\Gamma }_k(({\nu }_1+{\nu }_2)/2)}{{\Gamma }_k({\nu }_1/2){\Gamma }_k({\nu }_2/2)},\hfill \\ \hfill {\Gamma }_k\left(x\right)& =& {\pi }^{k(k-1)/4}·\prod _{i=1}^k\Gamma (x+(1-i)/2),\hfill \end{array}$$(3) where Γ _k (x) denotes the multivariate Gamma function; see Konno (1991), Tan (1969), and Gupta and Nagar (2000). The matrix-F distribution is the multivariate analog of the univariate F distribution, which in turn is a ratio of two independent χ² distributions. Similarly, the matrix-F distribution is obtained by considering a Wishart times an inverse-Wishart distributed random matrix. When ν₂ → ∞, the matrix-F distribution degenerates to the Wishart distribution (the multivariate analog of a χ² distribution) with ν₁ degrees of freedom. We thus nest the Wishart as a special case. The model of Jin and Maheu (2016) uses an infinite mixture of inverse-Wishart distributions to create fatter tails for RC_t . The inverse-Wishart, however, does not nest the regular Wishart distribution.

Figure 1 illustrates the difference between the Wishart distribution and the matrix-F distribution for various values of k, ν₁, and ν₂. We make use of the statistical result that if a k × k matrix RC_t is F(ν₁, ν₂) distributed, then a single entry on the diagonal of RC_t , denoted by RC _{ii, t} , is F(ν₁, ν₂ − (k + 2)) distributed; see Gupta and Nagar (2000). The panels (A)–(C) plot the pdf of RC _{ii, t} for k = 15, while panels (D)–(F) show the corresponding pdfs for k = 30. All pdfs have a mean that equals one. The solid line is the pdf of the F distribution with a specific combination of k, ν₁, and ν₂. In particular, the parameter combinations in panels (A) and (D) correspond to empirically estimated values.

Figure 1. The rescaled matrix-F and the Wishart distribution. This figure shows pdfs associated with a matrix-F distribution with ν₁ and ν₂ degrees of freedom and a Wishart distribution with ν₁ degrees of freedom for a k × k matrix RC_t . We plot the pdf of one of the main-diagonal entries RC _{ii, t} (i = 1, …k), for k = 15 (upper panels) and k = 30 (lower panels) for various degrees of freedom. The solid line corresponds with the F distribution, while the dashed line represents the Wishart (χ²) distribution.

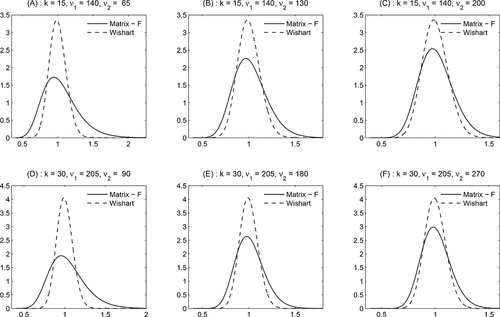
The figure shows that the matrix-F distribution results in a much wider dispersion for the same mean than the Wishart distribution. This holds particularly for panels (A) and (D), but is also visible in panels (B) and (E). Hence, a matrix-F distribution for a 15 (resp. 30) dimensional covariance matrix is distinct from a Wishart distribution even for degrees of freedom parameters as high as ν₁ = 140 (resp. 205) and ν₂ = 65 (resp. 90). This result comes back in the empirical application, where we show that the matrix-F distribution clearly outperforms the Wishart distribution with respect to density forecasting of the realized covariance matrix.

The conditional observation densities for y_t and RC_t both depend on the common time-varying covariance matrix V_t . To describe the dynamics of the unobserved matrix V_t , we use the generalized autoregressive score (GAS) framework of Creal, Koopman, and Lucas (2011, 2013); see also Harvey (2013), Creal et al. (2014), Lucas, Schwaab, and Zhang (2014), and Hansen, Janus, and Koopman (2016). The approach is observation driven in the classification of Cox (1981). An important advantage of this framework over parameter-driven approaches is that the likelihood function is available in closed form, and therefore estimation and inference by means of maximum likelihood methods are straightforward.

The GAS recursion for V_t is given by (4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) where $S_t\in {\mathbb{R}}^{k\times k}$ is the scaled score as derived below, α and β are scalars, and $\Omega \in {\mathbb{R}}^{k\times k}$ is a matrix of intercepts. A straightforward extension is to let α and β be diagonal matrices, or to follow the set-up of Golosnoy, Gribisch, and Liesenfeld (2012) and consider V _{t + 1} = CC′ + A S_t  A′ + B V_t  B′ for triangular parameter matrices A, B, and C.

The recursion in (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ) is reminiscent of the dynamic conditional correlation (DCC) recursion of Engle (2002). The main difference is that we use the scaled score S_t rather than the outer product y_ty′ _t of past returns. Unlike Creal, Koopman, and Lucas (2011), Lucas, Schwaab, and Zhang (2014), and Hansen, Janus, and Koopman (2016), our score is a matrix-valued rather than a vector-valued variable. This substantially increases the numerical efficiency of our procedure in high dimensions. Whereas we only need to keep track of matrices of size k × k, these other approaches need to track $\frac{1}{2}k(k+1)\times \frac{1}{2}k(k+1)$ sized matrices due to vectorization and scaling manipulations. Note that further lags of V_t and S_t can be added on the right-hand side of (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ), as well as “asymmetry” effects as in Cappiello, Engle, and Sheppard (2006). In particular, inspired by Corsi (2009) and Jin and Maheu (2016), a richer specification for V _{t + 1} would be the “GAS-HAR” recursion to accommodate the long-memory-type persistence in V _{t + 1}: (5) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+{\beta }_1{V}_{{\ell }_1,t}+{\beta }_2{V}_{{\ell }_2,t}+{\beta }_3{V}_{{\ell }_3,t},\end{array}$$(5) with V _{ℓ, t} = ℓ^{− 1}∑^ℓ _{i = 1} V _{t − i} . With ℓ₁ = 1, ℓ₂ = 5, and ℓ₃ = 22, we obtain the standard HAR setting; see Corsi (2009). Note that there is a slight difference between (5(5) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+{\beta }_1{V}_{{\ell }_1,t}+{\beta }_2{V}_{{\ell }_2,t}+{\beta }_3{V}_{{\ell }_3,t},\end{array}$$(5) ) and the models of Jin and Maheu (2013) and Corsi (2009) as we put the “HAR-dynamics” on V_t rather than on RC_t . We label the model in (5(5) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+{\beta }_1{V}_{{\ell }_1,t}+{\beta }_2{V}_{{\ell }_2,t}+{\beta }_3{V}_{{\ell }_3,t},\end{array}$$(5) ) as the HEAVY GAS HAR model.

We assume that conditional on V_t and ${\mathcal{F}}_{t-1}$, returns y_t and realized covariances RC_t are independent. Extensions to include conditional dependence between a vector-valued random variable y_t and a matrix-valued random variable RC_t currently appear nontrivial, and we leave such extensions for future research. Assuming independence, the total log-likelihood at time t, denoted by ${\mathcal{L}}_t$, equals the sum of the log-likelihood contributions corresponding to the Student's t and matrix-F densities. Likewise, the score ∇ _t of the conditional observation density of (y_t , RC_t ) with respect to V_t is equal to the sum of the scores of (1(1) $$\begin{array}{ccc}\hfill p_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)& =& \frac{\Gamma (({\nu }_0+k)/2)}{\Gamma ({\nu }_0/2){\left[({\nu }_0-2)\pi \right]}^{k/2}{\left|V_t\right|}^{1/2}}\hfill \\ & & \times {\left(1+\frac{y_t{V}_t^{-1}{y}_t}{{\nu }_0-2}\right)}^{-({\nu }_0+k)/2},\hfill \end{array}$$(1) ) and (2(2) $$\begin{array}{ccc}& & p_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2)\hfill \\ & & {\displaystyle =K({\nu }_1,{\nu }_2)\times \frac{{\left|\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}\right|}^{{\nu }_1/2}{\left|R{C}_t\right|}^{({\nu }_1-k-1)/2}}{{\left|{\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}R{C}_t\right|}^{({\nu }_1+{\nu }_2)/2}},}\hfill \end{array}$$(2) ), that is, (6) $${\mathcal{L}}_t=log{p}_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)+log{p}_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2),\left[4pt\right]$$(6) (7) $${\nabla }_t=\partial {\mathcal{L}}_t/\partial V_t={\nabla }_{y,t}+{\nabla }_{RC,t},\left[3pt\right]{\nabla }_{y,t}=\partial log{p}_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)/\partial V_t,\left[3pt\right]{\nabla }_{RC,t}=\partial log{p}_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2)/\partial V_t.$$(7) This leads to the following result.

Proposition 1.

For the Student's t density (1(1) $$\begin{array}{ccc}\hfill p_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)& =& \frac{\Gamma (({\nu }_0+k)/2)}{\Gamma ({\nu }_0/2){\left[({\nu }_0-2)\pi \right]}^{k/2}{\left|V_t\right|}^{1/2}}\hfill \\ & & \times {\left(1+\frac{y_t{V}_t^{-1}{y}_t}{{\nu }_0-2}\right)}^{-({\nu }_0+k)/2},\hfill \end{array}$$(1) ) and the matrix-F distribution (2(2) $$\begin{array}{ccc}& & p_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2)\hfill \\ & & {\displaystyle =K({\nu }_1,{\nu }_2)\times \frac{{\left|\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}\right|}^{{\nu }_1/2}{\left|R{C}_t\right|}^{({\nu }_1-k-1)/2}}{{\left|{\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}R{C}_t\right|}^{({\nu }_1+{\nu }_2)/2}},}\hfill \end{array}$$(2) ), the corresponding k × k score matrices ∇ _{y, t} and ∇ _{RC, t} are (8) $${\nabla }_{y,t}=\frac{1}{2}{V}_t^{-1}\left[w_t{y}_t{y}_t^{\text{'}}-V_t\right]V_t^{-1}\left[4pt\right]$$(8) (9) $${\nabla }_{RC,t}=\frac{{\nu }_1}{2}{V}_t^{-1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}\right.\left[4pt\right]\left.\times R{C}_t{\left({\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}R{C}_t\right)}^{-1}-V_t\right]V_t^{-1},$$(9) where w_t = (ν₀ + k)/(ν₀ − 2 + y′ _t V ^{− 1} _t y_t ), and where derivatives have been taken with respect to a general nonsymmetric matrix V_t rather than a positive definite symmetric matrix V_t .

Proofs of all propositions are provided in the supplementary appendix.

Creal, Koopman, and Lucas (2013) proposed to scale the score ∇ _t to account for the curvature in the log conditional observation density with respect to V_t . They did so using powers of the inverse conditional Fisher information matrix. In the context of our current model with vector-valued and matrix-valued random variables, this would lead to a cumbersome and numerically inefficient procedure. We therefore propose a much more straightforward and numerically efficient way to scale the score expressions in Equations (8(8) $${\nabla }_{y,t}=\frac{1}{2}{V}_t^{-1}\left[w_t{y}_t{y}_t^{\text{'}}-V_t\right]V_t^{-1}\left[4pt\right]$$(8) ) and (9(9) $${\nabla }_{RC,t}=\frac{{\nu }_1}{2}{V}_t^{-1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}\right.\left[4pt\right]\left.\times R{C}_t{\left({\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}R{C}_t\right)}^{-1}-V_t\right]V_t^{-1},$$(9) ) while still accounting for curvature of the raw score ∇ _t as a function of V_t . In particular, we scale $vec\left({\nabla }_t\right)$ by a scalar multiple of (V_t ⊗V_t ) and obtain (10) $$vec\left(S_t\right)\equiv \frac{2}{{\nu }_1+1}(V_t\otimes V_t)vec\left({\nabla }_t\right)=\frac{2}{{\nu }_1+1}vec\left(V_t{\nabla }_t{V}_t\right)\Rightarrow \left[4pt\right]$$(10) (11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) where w_t is defined in Proposition 1, $vec(·)$ stacks the columns of a matrix into a vector, and ⊗ denotes the Kronecker product. Alternative forms of scaling may also be considered, but the computational advantages of (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) are substantial and typically outweigh the numerical complications incurred with more complex forms of scaling. This proves absolutely critical (as demonstrated in Sections 3 and 4) when comparing the newly developed approach with the competing setup of Hansen, Janus, and Koopman (2016). We label the model given by Equations (1(1) $$\begin{array}{ccc}\hfill p_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)& =& \frac{\Gamma (({\nu }_0+k)/2)}{\Gamma ({\nu }_0/2){\left[({\nu }_0-2)\pi \right]}^{k/2}{\left|V_t\right|}^{1/2}}\hfill \\ & & \times {\left(1+\frac{y_t{V}_t^{-1}{y}_t}{{\nu }_0-2}\right)}^{-({\nu }_0+k)/2},\hfill \end{array}$$(1) ), (2(2) $$\begin{array}{ccc}& & p_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2)\hfill \\ & & {\displaystyle =K({\nu }_1,{\nu }_2)\times \frac{{\left|\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}\right|}^{{\nu }_1/2}{\left|R{C}_t\right|}^{({\nu }_1-k-1)/2}}{{\left|{\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{V}_t^{-1}R{C}_t\right|}^{({\nu }_1+{\nu }_2)/2}},}\hfill \end{array}$$(2) ), (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ), and (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) the HEAVY GAS tF model. Let us now discuss the basic intuition underlying the score Equation (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ). The first term in (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) relates to the multivariate Student's t distribution and has two important features. First, this score considers the deviations of the weighted outer product w_ty_ty′ _t from the local covariance matrix V_t . When ν₀ → ∞, that is, when the Student's t distribution collapses to the normal distribution, the weights collapse to w_t ≡ 1 for all t and the dynamics of V_t resemble the covariance dynamics of a multivariate GARCH model, that is, y_ty′ _t − V_t . In that case also the scaling matrix (V_t ⊗V_t ) is directly proportional to the inverse conditional Fisher information matrix. Second, as discussed in Creal, Koopman, and Lucas (2011), the impact of “large values” y_ty′ _t on V_t is tempered by w_t if the density for y is heavy-tailed, that is, if 1/ν₀ > 0. Put differently, w_t decreases when y′ _t V_t ^{− 1} y_t explodes. This gives the covariance matrix dynamics as driven by the multivariate Student's t distribution an attractive and embedded robustness feature. The interpretation is that if y_t is drawn from a heavy-tailed distribution, large values of y_ty′ _t could arise as a result of the heavy-tailed nature of the distribution rather than as a result of a substantial change in the underlying covariance matrix. The score-based approach automatically accounts for this.

The second term in (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) is new and results from the matrix-F distribution. The expression has a highly similar form and interpretation as the Student's t score discussed before. The main difference is that RC_t is a matrix-valued rather than a vector-valued random variable. Due to the fat-tailedness of the matrix-F distribution, “large” values of RC_t as measured by V ^{− 1} _t RC_t do not automatically lead to substantial changes in the covariance matrix V_t . Instead, the matrix “weight” (I _k + ν₁ V ^{− 1} _t RC_t /(ν₂ − k − 1))^{− 1} takes the same role as w_t in (8(8) $${\nabla }_{y,t}=\frac{1}{2}{V}_t^{-1}\left[w_t{y}_t{y}_t^{\text{'}}-V_t\right]V_t^{-1}\left[4pt\right]$$(8) ) and downweights the impact of a large V ^{− 1} _t RC_t 's on future values of V_t . When ν₂ → ∞, the matrix-F distribution collapses to the Wishart distribution with ν₁ degrees of freedom and the second term of the scaled score S_t in (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) collapses to ν₁ (ν₁ + 1)^{− 1} (RC_t − V_t ), which is directly in line with the expressions in Hansen, Janus, and Koopman (2016). The parameter ν₂ thus takes the same robustification role for the realized covariance measures RC_t as the parameter ν₀ takes for the returns y_t .

Looking at the two terms in (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) simultaneously, the value of ν₁ clearly trades off the relative contributions of the Student's t score and the matrix-F score when updating V_t . If ν₁ is large, the information in RC_t is deemed relatively precise compared to a weaker signal contained in the outer product of daily returns y_ty′ _t . In that case, the score is dominated by the second term in the scaled score. The converse holds if ν₁ is low. In the limit ν₁ → ∞, RC_t measures V_t exactly, and the weight of the score part due to y_t drops out entirely from the model formulation. Each of the three degrees of freedom, ν₀, ν₁, and ν₂ has indeed its own clear role in the model formulation, as well as its precise economic intuition.

We complete the model presentation by providing parameter restrictions to ensure positive definiteness of the covariance matrices V_t . We also prove a result on the suitability of the derivative concept used in Proposition 1.

Proposition 2.

Consider the sequence of covariance matrices {V_t } generated by Equation (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ). Assume that the realized measures RC_t are positive semidefinite for each time t. Given the scaled score steps as in Equation (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ) and given an initial positive definite matrix V ₁ and positive semidefinite matrix Ω, then V_t is positive definite for each t ⩾ 1 if β > α > 0.

The parameter restrictions β > α > 0 can easily be imposed during the estimation stage.

To formulate our final result in this section, we define the operator $devec(·)$ as the inverse of $vec(·)$, that is, $devec(vec(V\left)\right)=V$. Similarly, we define the operators $vech(·)$ and $devech(·)$, with $vech\left(V\right)$ stacking the lower triangular elements of a symmetric matrix V into a vector, and $devech(vech(V\left)\right)=V$. Finally, we define the selection matrix $\mathcal{S}$ with 1's and 0's such that $vec\left(V\right)=\mathcal{S}vech\left(V\right)$ for a symmetric matrix V. We now obtain the following result.

Proposition 3.

For symmetric k × k matrices V and ∇, (12) $$\begin{array}{ccc}& & devec\left({\left(V^{-1}\otimes V^{-1}\right)}^{-1}vec\left(\nabla \right)\right)\hfill \\ & & =devech\left({\left({\mathcal{S}}^{\text{'}}(V^{-1}\otimes V^{-1})\mathcal{S}\right)}^{-1}{\mathcal{S}}^{\text{'}}vec\left(\nabla \right)\right).\hfill \end{array}$$(12)

The result in Proposition 3 is important given that in Proposition 1 we ignored the fact that V_t is symmetric when taking derivatives. We subsequently scaled the resulting vectorized derivative $vec\left({\nabla }_t\right)$ by a scalar multiple of the inverse of (V ^{− 1} _t ⊗V_t ^{− 1}) to obtain our score step S_t in (11(11) $$S_t=\frac{w_t{y}_t{y}_t^{\text{'}}-V_t}{{\nu }_1+1}+\frac{{\nu }_1}{{\nu }_1+1}\left[\frac{{\nu }_1+{\nu }_2}{{\nu }_2-k-1}R{C}_t\right.\left[4pt\right]\times \left.{\left({\mathrm{I}}_k+\frac{{\nu }_1{V}_t^{-1}R{C}_t}{{\nu }_2-k-1}\right)}^{-1}-V_t\right],$$(11) ). Analogously, we scale the score with respect to $vech\left(V_t\right)$, that is, $\partial {\mathcal{L}}_t/\partial vech\left(V_t\right)={\mathcal{S}}^{\text{'}}vec\left({\nabla }_t\right)$, by the inverse of ${\mathcal{S}}^{\text{'}}(V_t^{-1}\otimes V_t^{-1})\mathcal{S}$. Proposition 3 now states that these two approaches yield precisely the same score steps S_t as both ∇ _t and V_t are symmetric. It thus appears immaterial whether or not we account for the fact that V_t is symmetric when taking derivatives, as long as we use the appropriate form of scaling. Clearly, this does not necessarily hold for other forms of scaling, and therefore provides a further advantage to our current definition of S_t .

2.2. Stationarity and Ergodicity

A useful feature of our HEAVY GAS tF model is that under the assumption of correct specification the scores ∇ _{y, t} and ∇ _{RC, t} are martingale differences by design and therefore have conditional expectation 0. This follows directly from the fact that they are scores of a correctly specified density. To obtain stationarity of V_t , however, we need to study the probabilistic properties of the new model as generated by the nonlinear recursion (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ). We obtain the following result.

Proposition 4.

If 0 < α < β < 1, the process generated by the HEAVY GAS tF model is stationary, geometrically ergodic, and β-mixing.

A key step in the proof of Proposition 4 is to rewrite the scaled score as (13) $$\begin{array}{ccc}& & V_t^{-1/2}{S}_t{\left(V_t^{\text{'}}\right)}^{-1/2}\hfill \\ & & =\frac{({\nu }_0+k)}{({\nu }_1+1)({\nu }_0-2)}{\epsilon }_{y,t}{\epsilon }_{y,t}^{\text{'}}{\left(1+\frac{1}{{\nu }_0-2}{\epsilon }_{y,t}^{\text{'}}{\epsilon }_{y,t}\right)}^{-1}\hfill \\ & & +\frac{{\nu }_1({\nu }_1+{\nu }_2)}{({\nu }_1+1)({\nu }_2-k-1)}{\epsilon }_{RK,t}\hfill \\ & & \times {\left({\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{\epsilon }_{RK,t}\right)}^{-1}-{\mathrm{I}}_k,\hfill \end{array}$$(13) where ϵ _{y, t} has Student's t distribution with mean zero, covariance matrix I _k , and degrees of freedom ν₀, and ϵ _{RK, t} has a matrix-F distribution with expectation I _k , and degrees of freedom parameters ν₁ and ν₂. The right-hand side of (13(13) $$\begin{array}{ccc}& & V_t^{-1/2}{S}_t{\left(V_t^{\text{'}}\right)}^{-1/2}\hfill \\ & & =\frac{({\nu }_0+k)}{({\nu }_1+1)({\nu }_0-2)}{\epsilon }_{y,t}{\epsilon }_{y,t}^{\text{'}}{\left(1+\frac{1}{{\nu }_0-2}{\epsilon }_{y,t}^{\text{'}}{\epsilon }_{y,t}\right)}^{-1}\hfill \\ & & +\frac{{\nu }_1({\nu }_1+{\nu }_2)}{({\nu }_1+1)({\nu }_2-k-1)}{\epsilon }_{RK,t}\hfill \\ & & \times {\left({\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{\epsilon }_{RK,t}\right)}^{-1}-{\mathrm{I}}_k,\hfill \end{array}$$(13) ) does not depend on V_t . Moreover, the terms on the right-hand side are transformations of (matrix) Beta distributed random variables and have finite expectations and variances if 2 < ν₀ < ∞, k − 1 < ν₁ < ∞, and k − 1 < ν₂ < ∞; see Tan (1969).

A further inspection of the proof of Proposition 4 and Theorem 2 in Boussama (2006) shows that we can easily generalize the result to models with dynamics of the type (14) $$\begin{array}{c}\hfill V_{t+1}=\Omega +A{S}_t{A}^{\text{'}}+B{V}_t{B}^{\text{'}},\end{array}$$(14) for k × k matrices A and B. Such models allow for possible rich volatility spillover effects, that is, through loadings but also though scaled score. In the same vein, the proofs show that the GAS HAR tF model of Equation (5(5) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+{\beta }_1{V}_{{\ell }_1,t}+{\beta }_2{V}_{{\ell }_2,t}+{\beta }_3{V}_{{\ell }_3,t},\end{array}$$(5) ) is stationary and ergodic if β _j > 0 for j = 1, 2, 3, ℓ^{− 1} ₁β₁ + ℓ^{− 1} ₂β₂ + ℓ^{− 1} ₃β₃ > α > 0, and β₁ + β₂ + β₃ < 1.

It is also clear from (13(13) $$\begin{array}{ccc}& & V_t^{-1/2}{S}_t{\left(V_t^{\text{'}}\right)}^{-1/2}\hfill \\ & & =\frac{({\nu }_0+k)}{({\nu }_1+1)({\nu }_0-2)}{\epsilon }_{y,t}{\epsilon }_{y,t}^{\text{'}}{\left(1+\frac{1}{{\nu }_0-2}{\epsilon }_{y,t}^{\text{'}}{\epsilon }_{y,t}\right)}^{-1}\hfill \\ & & +\frac{{\nu }_1({\nu }_1+{\nu }_2)}{({\nu }_1+1)({\nu }_2-k-1)}{\epsilon }_{RK,t}\hfill \\ & & \times {\left({\mathrm{I}}_k+\frac{{\nu }_1}{{\nu }_2-k-1}{\epsilon }_{RK,t}\right)}^{-1}-{\mathrm{I}}_k,\hfill \end{array}$$(13) ) that we can establish the existence of moments for V_t using the feature that the (matrix) Beta random variables are “bounded” in the appropriate matrix sense. For 0 < β < 1, we then directly obtain the unconditional first moment of V_t as $\mathbb{E}\left[V_t\right]={(1-\beta )}^{-1}\Omega$. A number of these features are discussed for the univariate case in Harvey (2013). Proposition 4 generalizes these results to the fully multivariate matrix context.

2.3. Estimation

We collect matrix-valued Ω and scalar-valued α, β, ν₀, ν₁, ν₂ into a static parameter vector θ for the GAS specification of (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ) and estimate θ by maximum likelihood. Note that β should be replaced by (β₁, β₂, β₃) when estimating the GAS HAR specification of (5(5) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+{\beta }_1{V}_{{\ell }_1,t}+{\beta }_2{V}_{{\ell }_2,t}+{\beta }_3{V}_{{\ell }_3,t},\end{array}$$(5) ). We maximize the log-likelihood ${\mathcal{L}}_T\left(\theta \right)={\sum }_{t=1}^T{\mathcal{L}}_t$, where ${\mathcal{L}}_t$ is defined in Equation (6(6) $${\mathcal{L}}_t=log{p}_y\left(y_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_0)+log{p}_{RC}\left(R{C}_t\right|V_t,{\mathcal{F}}_{t-1};{\nu }_1,{\nu }_2),\left[4pt\right]$$(6) ). The starting value V ₁ can be either estimated or set equal to RC ₁. We further reduce the number of parameters following Hansen, Janus, and Koopman (2016) by using a covariance targeting approach to estimate Ω. As $\Omega =(1-\beta )\mathbb{E}\left[V_t\right]$ for 0 < β < 1, we replace Ω during estimation by (1 − β) times the sample mean of RC_t . For the GAS HAR tF model, we multiply the sample mean of RC_t by (1 − β₁ − β₂ − β₃). This should be a consistent estimator for the expectation under a standard ergodicity assumption. Hence, we are left only with five scalar-valued parameters for the basic GAS tF specification: α, β, ν₀, ν₁, and ν₂. The GAS HAR tF requires two extra parameters (β = {β₁, β₂, β₃}). The resulting maximum likelihood estimation procedure is fast and numerically efficient. In our empirical section, we use it to estimate the parameters of dynamic systems up to 30 dimensions. Proceeding to even higher dimensional systems is feasible as well as we show in the simulation exercise in Section 3 for the case k = 50. For empirical data, however, such high dimensions are probably better addressed by studying covariance models with factor structures.

3. SIMULATION EXPERIMENT

3.1. Monte Carlo Analysis Based on the Correctly Specified Model

We now perform a Monte CarloTable 1.study to investigate the statistical properties of the maximum likelihood estimator for θ. We simulate time series of T daily returns and daily realized covariances of dimension k. We use T = 500, 1000, and k = 5, 15, 30, 50. We generate data using the HEAVY GAS tF model as the true data-generating process (DGP) and set α = 0.8, β = 0.97, ν₀ = 12, ν₁ ∈ {140, 205, 300}, and ν₂ ∈ {65, 90, 150}. In addition, Ω = (1 − β)V ₀ with V ₀ a matrix with V_jj = 4 (j = 1, …, k) and V_ij = 4ρ (i ≠ j) with ρ = 0.7. The parameters resemble values found in the empirical application of Section 4. For each simulated series, we estimate θ by maximum likelihood.

Table 1 presents the results. All parameters are estimated near their true values. Standard deviations shrink as either the sample size T or the cross-sectional dimension k grows. Interestingly, there appears to be a small downward bias in b for larger dimensions k ⩾ 15. Nevertheless, the table demonstrates that our model is able to deal with dimensions as large as k = 30, 50.

Table 1. Parameter estimations of HEAVY GAS DGP. This table shows Monte Carlo averages and standard deviations (in parentheses) of parameter estimates from simulated HEAVY GAS processes. The table reports the mean and the standard deviation in parentheses based on 1000 replications

		k = 5			k = 15
Coef.	True	T = 500	T = 1000	True	T = 500	T = 1000
α	0.80	0.797 (0.036)	0.798 (0.025)	0.80	0.801 (0.022)	0.800 (0.016)
β	0.97	0.966 (0.005)	0.968 (0.004)	0.97	0.966 (0.002)	0.968 (0.001)
ν0	12.00	12.419 (2.233)	12.179 (1.460)	12.00	12.097 (1.195)	12.054 (0.803)
ν1	22.00	22.063 (0.794)	22.037 (0.559)	140.00	140.57 (4.025)	140.28 (2.829)
ν2	35.00	35.127 (2.049)	35.054 (1.435)	65.00	65.030 (0.813)	64.998 (0.588)
		k = 30			k = 50
α	0.80	0.799 (0.010)	0.799 (0.007)	0.80	0.799 (0.005)	0.799 (0.004)
β	0.97	0.966 (0.001)	0.968 (0.001)	0.97	0.967 (0.001)	0.969 (0.000)
ν0	12.00	12.083 (0.857)	12.046 (0.610)	12.00	12.096 (0.757)	12.059 (0.545)
ν1	205.00	205.72 (2.605)	205.29 (1.825)	300.00	300.82 (2.152)	300.35 (1.464)
ν2	90.00	90.025 (0.473)	90.020 (0.346)	150.00	150.01 (0.497)	150.00 (0.343)

3.2. Monte Carlo Analysis Based on Mis-Specified Models

One of the main aims of the new HEAVY GAS tF model is to obtain estimates of the unobserved V_t and to do so robustly in the presence of heavy-tailed distributions for the observations y_t and RC_t . Given $\widehat{\theta }$, such estimates follow directly from the recursion (4(4) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+\beta V_t,\end{array}$$(4) ) of the GAS model. To see how well the model does in tracking unknown dynamics of the covariance matrix V_t , we perform the following experiment. First, we consider a deterministic process for the daily volatilities and correlation of a bivariate return vector y_t . Over the tth day, we simulate n intraday returns y _{i, t} , i = 1, …, n. The returns are iid with covariance matrix V_t /n: $$\begin{array}{ccc}\hfill y_{i,t}& \stackrel{\text{iid}}{\sim }& N(0,V_t/n),\hfill \\ \hfill {\sigma }_t& =& 4+sin\left(2\pi t\right),{\rho }_t=0.5sin\left(2\pi t\right),\hfill \end{array}$$where σ² _t and ρ _t σ² _t are the variance and covariance at day t = 1, …, T. Using the intraday returns, we construct the daily return y_t and the realized covariance matrix RC_t , computed as ∑ ⁿ _{i = 1} y _{i, t} y ^′ _{i, t} . We set T = 1000 and n = 50.

In a second experiment, we let the (co)variances vary in a stochastic rather than a deterministic way. This DGP combines the fat-tailedness of returns and realized covariance matrices with stochastic volatility dynamics for the covariance matrix V_t . It does so in the following way: (15) $$\begin{array}{ccc}\hfill y_t|{\mathcal{F}}_{t-1}& \sim & t({\nu }_0,V_t),R{C}_t|{\mathcal{F}}_{t-1}\sim F({\nu }_1,{\nu }_2,V_t),\hfill \\ \hfill V_t& =& \bar{V}+\gamma V_{t-1}+{\eta }_t,{\eta }_t\sim F({\nu }_{\eta ,1},{\nu }_{\eta ,2},V_{0,\eta }),\hfill \\ \hfill V_0& =& 4\left(\begin{array}{cc}\hfill 1& \hfill 0.7\\ \hfill 0.7& \hfill 1\end{array}\right),\hfill \end{array}$$(15) with η _t a 2 × 2 matrix drawn from a matrix-F distribution with mean V _{0, η} = κ(1 − γ)V ₀, and ν_{η, 1} and ν_{η, 2} degrees of freedom. We set ν₀ = 5, ν₁ = 20, ν₂ = 18, γ = 0.98, T = 1000, ν_{η, 1} = 8, ν_{η, 2} = 7, κ = 5, and $\bar{V}=(1/2)(1-\gamma )V_0$. All these values are chosen such that we obtain reasonable volatility and correlation patterns.

We compare our model with two alternatives. First, we demonstrate the difference between the fat-tailed matrix-F distribution and the Wishart distribution in the context of the GAS framework by considering the model of Hansen, Janus, and Koopman (2016), which we label HJK. Second, we consider the CAW model of Golosnoy, Gribisch, and Liesenfeld (2012). This model assumes a conditional Wishart distribution for RC_t and specifies its dynamics as (16) $$\begin{array}{c}\hfill V_t=\Omega +\alpha R{C}_t+\beta V_{t-1},\end{array}$$(16) which is in fact similar toFigure 2.the observation equation of the Multivariate HEAVY model of Noureldin, Shephard, and Sheppard (2012). As in the HEAVY GAS tF model, α and β are scalars and we estimate the matrix Ω by means of covariance targeting. After simulating 1500 paths from the DGP of (15(15) $$\begin{array}{ccc}\hfill y_t|{\mathcal{F}}_{t-1}& \sim & t({\nu }_0,V_t),R{C}_t|{\mathcal{F}}_{t-1}\sim F({\nu }_1,{\nu }_2,V_t),\hfill \\ \hfill V_t& =& \bar{V}+\gamma V_{t-1}+{\eta }_t,{\eta }_t\sim F({\nu }_{\eta ,1},{\nu }_{\eta ,2},V_{0,\eta }),\hfill \\ \hfill V_0& =& 4\left(\begin{array}{cc}\hfill 1& \hfill 0.7\\ \hfill 0.7& \hfill 1\end{array}\right),\hfill \end{array}$$(15) ), we report the mean and the standard deviation of the root mean squared error (RMSE) corresponding to each path, which is defined as (17) $$\begin{array}{ccc}\hfill \text{RMSE}& =& {\left[\frac{1}{T}\sum _{t=1}^T{\parallel V_t-{\widehat{V}}_t\parallel }^2\right]}^{1/2}\hfill \\ & =& {\left[\frac{1}{T}\sum _{i,j,t}{(V_{ij,t}-{\widehat{V}}_{ij,t})}^2\right]}^{1/2},\hfill \end{array}$$(17) with ${\widehat{V}}_t$ the estimated covariance matrix from a particular model, and ‖ · ‖ denoting the (matrix) Frobenius norm.

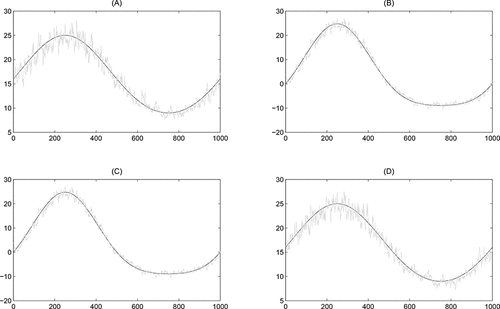
Figure 2 presents results for one particular realization of the deterministic DGP. The black lines represent the true values of the volatility, correlation, or covariance. The figure shows that the new model easily recovers the patterns for the volatility, correlation, and covariance.

Figure 2. Model fit for a deterministic DGP. This figure shows a realization of the simulated (co)variance process of (15(15) $$\begin{array}{ccc}\hfill y_t|{\mathcal{F}}_{t-1}& \sim & t({\nu }_0,V_t),R{C}_t|{\mathcal{F}}_{t-1}\sim F({\nu }_1,{\nu }_2,V_t),\hfill \\ \hfill V_t& =& \bar{V}+\gamma V_{t-1}+{\eta }_t,{\eta }_t\sim F({\nu }_{\eta ,1},{\nu }_{\eta ,2},V_{0,\eta }),\hfill \\ \hfill V_0& =& 4\left(\begin{array}{cc}\hfill 1& \hfill 0.7\\ \hfill 0.7& \hfill 1\end{array}\right),\hfill \end{array}$$(15) ) (black line) with T = 1000 and the fit from the HEAVY GAS tF model (gray line). Panels A and D represent the volatilities, while panels B and C present the correlation and covariance, respectively.

Turning to the stochastic (co)variance case, Table 2 reports the means of the RMSE as defined in (17(17) $$\begin{array}{ccc}\hfill \text{RMSE}& =& {\left[\frac{1}{T}\sum _{t=1}^T{\parallel V_t-{\widehat{V}}_t\parallel }^2\right]}^{1/2}\hfill \\ & =& {\left[\frac{1}{T}\sum _{i,j,t}{(V_{ij,t}-{\widehat{V}}_{ij,t})}^2\right]}^{1/2},\hfill \end{array}$$(17) ) over all 1500 simulation paths of the three models with respect to the true DGP. The standard deviations of the means are reported in parentheses. Note that all models are misspecified in this case. The HEAVY GAS tF model produces the lowest average RMSE. Compared to the HJK model, it does so by using the matrix-F distribution rather than the Wishart distribution when estimating the parameters. This also affects the score dynamics of the transition equation for V_t . Compared to the CAW model, both the HJK and the HEAVY GAS tF model do better. Apparently, using the information in the daily returns both for estimating the static model parameters and for filtering the covariance matrix is helpful for estimating the true covariance matrix dynamics. Overall, the results highlight the advantage of modeling the realized covariance matrix by a fat-tailed matrix-F distribution in combination with the GAS framework for the matrix dynamics. The impact of large incidental jumps is downweighted by the HEAVY GAS tF model, producing a lower RMSE than the Wishart-based models, which lack a similar property.

Table 2. Statistical fit on stochastic DGP. This table shows Monte Carlo averages and standard deviations (in parentheses) of the RMSE defined in (17(17) $$\begin{array}{ccc}\hfill \text{RMSE}& =& {\left[\frac{1}{T}\sum _{t=1}^T{\parallel V_t-{\widehat{V}}_t\parallel }^2\right]}^{1/2}\hfill \\ & =& {\left[\frac{1}{T}\sum _{i,j,t}{(V_{ij,t}-{\widehat{V}}_{ij,t})}^2\right]}^{1/2},\hfill \end{array}$$(17) ) over all simulation paths of three misspecified models with respect to the true bivariate covariance matrix, which is simulated from the SV process of (15(15) $$\begin{array}{ccc}\hfill y_t|{\mathcal{F}}_{t-1}& \sim & t({\nu }_0,V_t),R{C}_t|{\mathcal{F}}_{t-1}\sim F({\nu }_1,{\nu }_2,V_t),\hfill \\ \hfill V_t& =& \bar{V}+\gamma V_{t-1}+{\eta }_t,{\eta }_t\sim F({\nu }_{\eta ,1},{\nu }_{\eta ,2},V_{0,\eta }),\hfill \\ \hfill V_0& =& 4\left(\begin{array}{cc}\hfill 1& \hfill 0.7\\ \hfill 0.7& \hfill 1\end{array}\right),\hfill \end{array}$$(15) ). We compare the HEAVY GAS tF model with the HJK model and the CAW model. The table reports the mean and the standard deviation of the mean in parentheses based on 1500 simulation paths

	HGAS tF	HJK	CAW
mean	11.42	12.66	13.49
st. dev.	(0.14)	(0.17)	(0.18)

4. EMPIRICAL APPLICATION: U.S. EQUITY RETURNS

4.1. Data

We apply the HEAVY GAS tF model to daily realized (co)variances and daily (open-to-close) returns of 30 randomly chosen U.S. equities from the S&P 500 index over the period January 2, 2001, until July 31, 2014, a total of 3415 trading days. Table 3 Figure 3.lists the ticker symbols. For each stock, we observe consolidated trades (transaction prices) extracted from the Trade and Quote (TAQ) database with a time-stamp precision of 1 sec. We first clean the high-frequency data following the guidelines of Brownlees and Gallo (2006) and Barndorff-Nielsen et al. (2009). Second, we follow Noureldin, Shephard, and Sheppard (2012) and construct realized covariance matrices using 5 min returns with subsampling.

Table 3. Kolmogorov–Smirnov test on the distribution of realized variances. This table shows p-values associated with the Kolmogorov–Smirnov test on realized variances of 30 equities. The columns represent the Ticker symbol as well as p-values corresponding with the null hypothesis that RC_t is χ² or F distributed

Ticker	H0: χ^2	H0: F	Ticker	χ^2	F	Ticker	χ^2	F
AA	0.00	0.05	MCD	0.00	0.01	BHI	0.00	0.82
AXP	0.00	0.00	PFE	0.00	0.86	BAC	0.00	0.00
BA	0.00	0.20	PG	0.00	0.22	C	0.00	0.00
CAT	0.00	0.44	WMT	0.00	0.25	DD	0.00	0.11
GE	0.00	0.05	XOM	0.00	0.84	DOV	0.00	0.93
HD	0.00	0.23	AIG	0.00	0.01	DUK	0.00	0.17
HON	0.00	0.19	AEP	0.00	0.48	F	0.00	0.06
IBM	0.00	0.06	ABT	0.00	0.86	JNJ	0.00	0.11
JPM	0.00	0.05	AEE	0.00	0.05	KEY	0.00	0.46
KO	0.00	0.15	BAX	0.00	0.87	LLY	0.00	0.97

To empirically motivate the use of the matrix-F distribution, Table 3 lists p-values for Kolmogorov–Smirnov (KS) tests. The tests take the sequence of realized variances for each stock and test whether their distribution equals a rescaled χ², that is, the univariate version of the Wishart distribution. We also compute the tests for the null of a rescaled F distribution. Table 3 indicates that in all cases the χ² or Wishart distribution is strongly rejected by the realized variance data. By contrast, the null hypothesis that the realized variances come from an F distribution is rejected at the 5% significance level for only 5 out of the 30 stocks. Part of this is of course because the unconditional distribution of RC _{ii, t} is fatter tailed than a χ² due to the time variation in V _{ii, t} . However, our subsequent empirical results show that the F distribution also significantly improves upon the χ² distribution in a conditional distribution sense.

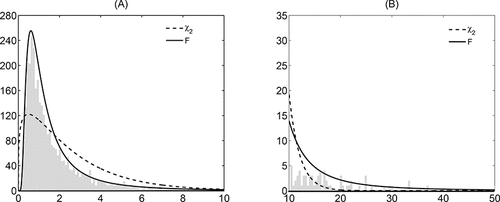
More insight in the rejection of the Wishart or χ² distribution is given in Figure 3. The left-hand panel shows the histogram of the RC _{ii, t} series of Boeing (BA), as well as the best-fitting χ² and F distributions. The left-hand panel is truncated at RC _{ii, t} = 10. The right panel shows the same three items, but for tail observations of RC _{ii, t} > 10. Combining the information in the two panels, the overall histogram is peaked at the left and suggests a fat right tail as values larger than 10 occur quite often. In addition, it is clear that the χ² distribution neither captures the peak at small values of RC _{ii, t} , nor the fat tail for large values of RC _{ii, t} . The F distribution on the other hand captures both of these features quite well. This example therefore strongly suggests that the matrix-F distribution may lead to an empirically more congruent model than the familiar Wishart distribution when modeling the entire matrix RC_t .

Figure 3. The fit of the probability distribution of the realized variance of BA. This figure shows a histogram of the realized variances (RV) of Boeing over the period 2001–2014. Panel A shows the histogram for $\text{RV}<10$, while panel B shows the remaining part of the histogram for values of RV larger than 10. The solid and dashed curves present the best-fitting F and χ² distribution, respectively.

4.2. In-Sample Performance

Using the full sample of 3415 trading days, we estimate the static parameters of the HEAVY GAS tF model. We compare the outcomes to several related volatility models. First, we estimate the parametric IW-A model of Jin and Maheu (2016), which is given by the following specification: (18) $$p\left(R{C}_t\right|{\mathcal{F}}_{t-1};{\nu }_{IW})=I{W}_k\left(R{C}_t\right|{\nu }_{IW},({\nu }_{IW}-k-1)V_t).V_t=\Omega +\sum _{j=1}^M{\beta }_j{\Gamma }_{t-1,{\ell }_j}\left[4pt\right]$$(18) (19) $${\Gamma }_{t-1,{\ell }_j}={\ell }_j^{-1}\sum _{i=1}^{{\ell }_j}R{C}_{t-i},$$(19) with Ω a k × k matrix and β _j (j = 1, …, M) a scalar. Based on the results of Jin and Maheu (2016), we set M equal to 3 with ℓ₁ = 1, ℓ₂ = 12, and ℓ₃ = 60. Second, we consider the HEAVY GAS HAR tF model of (5(5) $$\begin{array}{c}\hfill V_{t+1}=\Omega +\alpha S_t+{\beta }_1{V}_{{\ell }_1,t}+{\beta }_2{V}_{{\ell }_2,t}+{\beta }_3{V}_{{\ell }_3,t},\end{array}$$(5) ) with similar values for ℓ₁, ℓ₂, and ℓ₃ as in the IW-A model. Third, we estimate the same two contemporary benchmarks as in the simulation section: the Wishart-based CAW model of Golosnoy, Gribisch, and Liesenfeld (2012), see Equation (16(16) $$\begin{array}{c}\hfill V_t=\Omega +\alpha R{C}_t+\beta V_{t-1},\end{array}$$(16) ), and the HJK model of Hansen, Janus, and Koopman (2016). The HJK model uses GAS dynamics for the vech-torized form of the Cholesky decomposition of V_t and assumes a conditional normal distribution for the daily returns y_t and a Wishart distribution for the daily realized measures RC_t . The form of scaling adopted by Hansen, Janus, and Koopman (2016) forces them to keep track of scaling matrices of order $\frac{1}{2}k(k+1)\times \frac{1}{2}k(k+1)$, which makes the model hard to operationalize in higher dimensions. For k = 15, for example, this amounts to matrices of size 120 × 120, while for k = 30, the sizes even become 480 × 480. Because of the computational burden, we implement the HJK model only up to dimension k = 15.

Table 4 presents the parameter estimates and standard errors. Standard errors are based on the inverse negative Hessian of the likelihood evaluated at the optimum. We show the results for two selections of k = 5 stocks, a selection of k = 15 stocks, and the full set of k = 30 equities. In addition, we present the log-likelihood values ${\mathcal{L}}^{*}$, and the Bayesian information criterion (BIC) values (in 1000's) corresponding to the RC_t observations. This is done to make the models comparable, as the CAW model and the IW-A model do not have a model equation for the daily return observations.

Table 4. Parameter estimates, likelihoods, and information criteria. This table reports maximum likelihood parameter estimates of the HEAVY GAS (HAR) tF model, the IW-A model of Jin and Maheu (2016), the HJK model of Hansen, Janus, and Koopman (2016), and the CAW model of Golosnoy, Gribisch, and Liesenfeld (2012), applied to daily equity returns and/or daily realized covariances. Panels A.1 and A.2 list results for two randomly chosen sets containing five different assets. Panel B considers 15 assets and panel C shows the results for the full set of 30 assets. Standard errors are provided in parentheses. We report the total likelihood ${\mathcal{L}}^{*}$ and the BIC (in thousands) of the IW-A and the CAW model and the likelihood associated with the realized covariance matrix (i.e., the matrix-F and the Wishart distributions) for the GAS models. Data are observed over the period January 2, 2001 until July 31, 2014 (T = 3415 trading days)

	α	β(β1)	β2	β3	ν0	ν1(ν IW )	ν2	${\mathcal{L}}^{*}$	BIC
Panel A.1: BA/HD/JPM/PFE/PG
GAS tF	0.859	0.989			10.09	69.86	35.26	−11,906	23.85
	(0.017)	(0.000)			(0.615)	(1.429)	(0.414)
GAS-H tF	0.963	0.869	0.083	0.042	10.37	70.87	35.90	−11,387	22.82
	(0.018)	(0.006)	(0.007)	(0.003)	(0.652)	(1.339)	(0.398)
HJK	0.054	0.965				17.83		−21,529	43.10
	(0.001)	(0.001)				(0.099)
CAW	0.336	0.647				19.74		−18,030	36.08
	(0.005)	(0.005)				(0.111)
IW-A		0.379	0.400	0.194		22.89		−13,104	26.24
		(0.005)	(0.007)	(0.006)		(0.105)
Panel A.2: CAT/HON/IBM/MCD/WMT
GAS tF	0.826	0.990			10.33	72.54	34.53	−4828	9.70
	(0.020)	(0.000)			(0.643)	(1.999)	(0.438)
GAS-H tF	0.931	0.878	0.075	0.041	10.58	72.85	35.17	−4387	8.81
	(0.019)	(0.006)	(0.007)	(0.003)	(0.673)	(1.579)	(0.417)
HJK	0.044	0.975				18.97		−12,324	24.69
	(0.001)	(0.001)				(0.106)
CAW	0.313	0.670				20.26		−10,046	20.12
	(0.005)	(0.005)				(0.115)
IW-A		0.338	0.442	0.190		23.05		−5552	11.14
		(0.005)	(0.007)	(0.006)		(0.107)
Panel B: AA/AXP/BA/CAT/GE/HD/HON/IBM/JPM/KO/MCD/PFE/PG/WMT/XOM
GAS tF	0.666	0.993			12.69	140.3	64.26	149,088	−298.1
	(0.005)	(0.000)			(0.506)	(0.802)	(0.218)
GAS-H tF	0.784	0.883	0.070	0.043	12.97	141.9	65.06	152,279	−304.4
	(0.006)	(0.002)	(0.003)	(0.001)	(0.519)	(0.790)	(0.221)
HJK	0.026	0.979				37.47		88,987	−177.9
	(0.000)	(0.000)				(0.070)
CAW	0.235	0.753				39.32		104,666	−209.3
	(0.001)	(0.001)				(0.074)
IW-A		0.246	0.467	0.257		44.40		139,138	−278.2
		(0.002)	(0.003)	(0.003)		(0.062)
Panel C: All equities (k = 30)
GAS tF	0.520	0.997			12.65	203.8	91.71	937,986	−1876
	(0.002)	(0.000)			(0.407)	(0.430)	(0.161)
GAS-H tF	0.648	0.891	0.065	0.042	13.03	204.8	92.78	948,944	−1898
	(0.002)	(0.001)	(0.002)	(0.001)	(0.383)	(0.417)	(0.131)
CAW	0.173	0.821				57.04		725,787	−1452
	(0.001)	(0.001)				(0.050)
IW-A		0.180	0.468	0.332		66.07		883,287	−1767
		(0.001)	(0.002)	(0.001)		(0.038)

The results in Table 4 suggest that allowing for fat tails in the distribution of the realized covariances improves the fit. The differences between the log-likelihood of the matrix-F-based model and the Wishart-based models are substantial and increase rapidly when the dimension becomes larger. Also the differences in BIC values are large and favor the HEAVY GAS(HAR) tF model for all values of k considered. The log-likelihoods and BIC values also indicate that the Inverse-Wishart distribution improves upon the Wishart distribution, confirming the findings of Jin and Maheu (2016). Still, the matrix-F clearly gives the best fit for realized covariance matrices. In addition, allowing for a richer structure for V_t improves the fit, although the improvement is less substantial than the improvement due to theFigure 4.matrix-F distribution. The log-likelihood of the HAR specification of the GAS tF model increases compared to the regular GAS tF specification by about 500 (panel A.1), 3000 (panel B), and 11,000 (panel C) points at the cost of estimating only two extra parameters. The increases compared to the inverse-Wishart distribution are around 1300, 10,000, and 55,000 points, whereas the increases compared to the models with a Wishart distribution are considerably larger.

Looking at the individual parameter estimates, we first note that the estimates of β are comparably high for the HEAVY GAS tF and the HJK models, and also similar to the persistence parameter β + α for the CAW model and β₁ + β₂ + β₃ for the IW-A and GAS-H(AR) tF model. This holds for all dimensions k = 5, 15, 30 considered. The α parameters cannot be compared directly between the different models. For example, the HJK model takes the $vech$ of the Choleski decomposition of V_t as its time-varying parameter, whereas the HEAVY GAS tF and CAW models take V_t itself as the time-varying parameter. It is interesting to see that the parameter estimates in panels A.1 and A.2 are highly similar, despite the fact that they use nonoverlapping sets of stocks. The degree of persistence as well as the strength of the dependence of V_t on past values of y_t and RC_t thus seems a shared feature between stocks.

The three degrees of freedom parameters reveal that both the realized measures (ν₂) and the returns (ν₀) are fat-tailed. Recall that the matrix-F distribution converges to the Wishart distribution if ν₂ → ∞. The degrees of freedom ν₂ may seem high at first sight, but as was shown in Figure 1, the empirically estimated values of ν₁ and ν₂ still produce a noticeable differences between the Wishart and the matrix-F distribution. The values of ν₀ and ν₂ also moderate the impact of outliers and incidental large observations y_t and RC_t on future values of V _{t + 1} via the score dynamics. This is clearly seen by the estimated values of ν₁ between the HEAVY GAS tF model and the HJK model. The large values of ν₁ for the HEAVY GAS tF model signal that the model puts almost all attention on the realized kernels RC_t when determining the dynamics of V_t . The information in y_ty′ _t is hardly used, particularly in high dimensions (k = 30). By contrast, the HJK model still puts about 5% (k = 5) to 3% (k = 15) of the weight on the score of the distribution for y_t . We can attribute the difference to the fact that the robust filtering approach of the HEAVY GAS tF filter based on the matrix-F distribution provides a much better estimate of the time-varying covariance matrix V_t . Failing to account for the fat-tailedness of RC_t results in a more blurred signal from the realized measures and a relatively smaller weight on RC_t compared to a model with robust dynamics.

Figure 4 plots a small selection of the fitted volatilities and correlations. We show the results for PG and PFE, according to the HEAVY GAS tF model and the HJK model. The upper-left and lower-right graphs show the estimated volatilities, while the upper-right and lower-left graphs present the estimated covariances and (implied) correlations, respectively.

Figure 4. Estimated volatilities and correlations. This figure depicts estimated volatilities of PFE and PG at the main diagonal and their pairwise correlations and covariances at the off-diagonal, estimated by the HEAVY GAS tF and HJK model. The black line corresponds with the HEAVY GAS tF model, while the gray line denotes the fit from the HJK model. The estimation is based on the full sample, which runs from January 2, 2001, until July 31, 2014 (3415 observations).

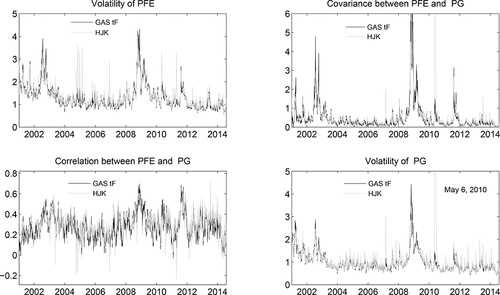
The figure shows that the robust transition scheme based on the matrix-F GAS dynamics is successful in mitigating the impact of incidental large RC_t observations on the estimates of V_t . The HJK model, being based on thin-tailed densities, is much more sensitive to such observations. Important episodes where we see large differences are at the start of 2005 for Pfizer (PFE), or around the May 2010 flash crash for Procter & Gamble (PG). Note that in case of real stress periods (such as the financial crisis) the HEAVY GAS tF model produces larger volatilities than the HJK model. Interestingly, apart from the main striking differences for Pfizer and Procter & Gamble, we also see a range of other days where the HJK model produces a short-lived spike in the estimated V_t , whereas the fat-tailed HEAVY GAS tF model is much more stable around those times.

The patterns for the correlations and covariances reveal similar features. The correlation between PFE and PG clearly displays sudden incidental drops, for example, around 2005, during the flash crash of May 2010, but also at the start of 2003 and the end of 2006. Incidental spikes in the covariances are visible for the HJK model in 2006, 2010, and 2013. Again, the robust HEAVY GAS tF model results in much more stable correlation and covariance patterns that are filtered from the data.

4.3. Out-of-Sample Performance

We assess the short-term forecasting performance of the models by considering one-step ahead forecasts. Similar to the in-sample analysis of the previous subsection, we compare the HEAVY GAS (HAR) tF model with the HJK model, the CAW model, and the IW-A model. We perform both a statistical and an economic evaluation. The former is based on one-step ahead density forecasts of the realized covariance matrix and the returns. Recall that the HJK, CAW, and IW-A models assume an (inverse-) Wishart distribution for the realized covariance matrix, while the Heavy GAS (HAR) tF model assumes a matrix-F distribution. In addition, we estimate V_t by a simple EWMA scheme $$V_{t+1}=\beta V_t+(1-\beta )R{C}_t,$$with β = 0.96, and plug the resulting estimates into the matrix-F density as estimated by the HEAVY GAS tF model.

We use a moving-window approach in the forecasting exercise with an in-sample period of 1500 observations. This corresponds roughly to 6 calendar years. The out-of-sample period contains P = 1914 observations including the Great Financial Crisis, which therefore constitutes an important test for the robustness of the model. We reestimate our model repeatedly after each 25 observations, which roughly corresponds to monthly updating of the parameters. Also note that it is conceptually straightforward to go to multi-step ahead predictions with the GAS tF specification, as the score has a conditional expectation equal to zero. So given V _{T + 1}, as the one-step ahead forecast, V _{T + h} = Ω + βV _{T + h − 1} for h > 1. Our results remain qualitatively the same for longer forecast horizons.

We use the log scoring rule (see Mitchell and Hall 2005; Amisano and Giacomini 2007) to differentiate between the density forecasts of the models. Define the difference in log score between the two density forecasts M ₁ and M ₂ corresponding to the variable of interest X_t (either the return y_t or the realized covariance matrix RC_t ) as (20) $$\begin{array}{c}\hfill d_{ls,t}=S_{ls,t}(X_t,M_1)-S_{ls,t}(X_t,M_2),\end{array}$$(20) for t = R, R + 1, …T − 1 with R the length of the estimation window and S _{ls, t} (X_t , M_j ) (j = 1, 2) the log score of the density forecast corresponding to model M_j at time t, (21) $$\begin{array}{c}\hfill S_{ls,t}(X_t,M_j)=log{p}_t\left(X_t\right|V_t,{\mathcal{F}}_{t-1},M_j),\end{array}$$(21) where p_t ( · ) is the probability distribution function of the matrix-F or (inverse-) Wishart distribution in case of the realized covariance matrix and the Normal or Student's-t distribution in case of the returns, respectively. The null hypothesis of equal predictive ability is given by $H_0:\mathbb{E}\left[d_{ls}\right]=0$ for all P out-of-sample forecasts. This null can be tested by means of a Diebold and Mariano (1995) (DM) statistic given by (22) $$\begin{array}{c}\hfill {\text{DM}}_{ls}=\frac{\bar{d}}{\sqrt{{\widehat{\sigma }}^2/N}},\end{array}$$(22) with $\bar{d}$ the out-of-sample average of the log score differences and ${\widehat{\sigma }}^2$ a HAC-consistent variance estimator of the true variance σ² of d _{ls, t} . Under the assumptions of the framework of Giacomini and White (2006) ${\text{DM}}_{ls}$ asymptotically follows a standard normal distribution. A significantly positive value means that model M ₁ has a superior forecast performance over model M ₂.

In addition to a statistical out-of-sample comparison of the different models, we also provide an economic comparison. Following Chiriac and Voev (2011), we consider global minimum variance portfolios (GMVP), motivated by the mean-variance optimization setting of Markowitz (1952). The model that provides the most accurate forecasts of the covariance matrix should give a lower portfolio variance than the portfolio variance of the competing models. Let us assume that the investor aims to minimize the one-step ahead portfolio volatility over period t + 1 subject to a fully invested portfolio, given his best estimate of the covariance matrix at time t. The resulting GMVP weights w _{t + 1|t} are given by the solution of the quadratic problem (23) $$\begin{array}{c}\hfill min{w}_{t+1|t}^{\text{'}}{V}_{t+1|t}{w}_{t+1|t}\mathrm{s}.\mathrm{t}.w_{t+1|t}^{\text{'}}\iota =1,\end{array}$$(23) with ι a k × 1 vector of ones. Similar as Chiriac and Voev (2011), we assess the predictive ability of the different models by comparing the ex post realizations of the conditional standard deviation, which are given by ${\sigma }_{p,t}=\sqrt{w_{t+1|t}^{\text{'}}R{C}_{t+1}{w}_{t+1|t}}$. We again test whether the differences in portfolio standard deviation between the different models are significant using the DM test statistic as defined in (22(22) $$\begin{array}{c}\hfill {\text{DM}}_{ls}=\frac{\bar{d}}{\sqrt{{\widehat{\sigma }}^2/N}},\end{array}$$(22) ).

Table 5 shows the average values of the log score and the ex post portfolio standard deviations over the out-of-sample period for two sets of 5 assets, a set of 15 assets, and the complete set of 30 assets. In addition, we provide corresponding t-statistics for the difference in the log predictive density scores of the realized covariance matrix and returns between the HEAVY HAR GAS tF model and the competing models. Likewise, ${\text{DM}}_{{\sigma }_p}$ represents the t-statistic based on the portfolio standard deviations of the HEAVY HAR GAS tF model and the HEAVY GAS tF, HJK, CAW, IW-A, EWMA, or BEKK-t model. Note that some of the models considered lack a distributional assumption for either the returns (CAW, IW-A), for the realized measures (BEKK-t), or for both (EWMA). To allow a density forecast comparison for these models, we have to choose the missing distribution. For the IW-A model, we follow Jin and Maheu (2016) and a Student's t distribution for the returns with ν _IW − k + 1 degrees of freedom, with ν _IW the degrees estimated for the inverse Wishart. For the CAW and EWMA model, we use a Student's t distribution with ν₀ degrees of freedom for the returns estimated for the HEAVY GAS tF. Finally, for the BEKK-t and EWMA we assume a matrix-F distribution for the realized covariance matrices with ν₁ and ν₂ equal to their estimated values in the HEAVY GAS tF model, such that the underlying distributions equal those of the HEAVY GAS tF model.

Table 5. Out-of-sample log-scores and ex post conditional standard deviations. This table shows the mean of log scores, defined in (21(21) $$\begin{array}{c}\hfill S_{ls,t}(X_t,M_j)=log{p}_t\left(X_t\right|V_t,{\mathcal{F}}_{t-1},M_j),\end{array}$$(21) ) and ex post portfolio standard deviation, based on one-step ahead predictions of the covariance matrix, according to the HEAVY (HAR) GAS tF, HJK, CAW, IW-A, and the EWMA model for two pairs of five assets (panel A), one pair of 15 assets (panel B) and for all equities (panel C, k = 30). The highest (lowest) value of the predictive log-score (portfolio standard deviation) across the models are marked bold. In addition, we report HAC-based test-statistics on the difference in predictive ability (${\text{DM}}_{\text{DF}}$) and portfolio standard deviation $\left({\text{DM}}_{{\sigma }_p}\right)$ between the HEAVY GAS HAR tF model and the other considered models. The superscripts *^**, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. The out-of-sample period goes from 2007 until July 2014 and contains 1914 observations

	GAS HAR tF	GAS tF	HJK	CAW	IW-A	EWMA	BEKK-t
Panel A: BA/HD/JPM/PFE/PG
S^ls (RCt )	–2.11	–2.23	–6.22	–4.44	–2.72	–4.47	–9.08
${\text{DM}}_{\text{DF}}$		(3.13)^***	(6.72)^***	(3.61)^***	(4.50)^***	(11.90)^***	(21.18)^***
S^ls (yt )	–7.30	–7.31	–7.49	–7.31	–7.32	–7.37	–7.40
${\text{DM}}_{\text{DF}}$		(2.59)^***	(8.77)^***	(1.37)	(2.86)^***	(6.96)^***	(5.70)^***
σ p	0.790	0.791	0.810	0.794	0.794	0.797	0.824
${\text{DM}}_{{\sigma }_p}$		(–6.00)^***	(–5.81)^***	(–3.73)^***	(–3.08)^***	(–4.82)^***	(–16.41)^***
Panel B: k = 15
S^ls (RCt )	58.28	57.52	34.62	42.03	53.86	49.08	5.96
${\text{DM}}_{\text{DF}}$		(3.68)^***	(11.51)^***	(8.28)^***	(4.45)^***	(11.85)^***	(20.92)^***
S^ls (yt )	–19.95	–19.98	–20.54	–19.99	–20.09	–20.07	–20.30
${\text{DM}}_{\text{DF}}$		(5.33)^***	(14.50)^***	(3.42)^***	(7.35)^***	(7.17)^***	(9.45)^***
σ p	0.629	0.630	0.648	0.632	0.632	0.637	0.695
${\text{DM}}_{{\sigma }_p}$		(–6.00)^***	(–5.81)^***	(–3.73)^***	(–3.08)^***	(–4.82)^***	(–16.41)^***
Panel C: All equities (k = 30)
S^ls (RCt )	316.48	313.39		238.97	294.60	292.20	109.08
${\text{DM}}_{\text{DF}}$		(5.08)^***		(16.73)^***	(7.45)^***	(12.93)^***	(26.59)^***
S^ls (yt )	–40.74	–40.82		–40.74	–40.94	–40.78	–41.87
${\text{DM}}_{\text{DF}}$		(8.17)^***		(0.08)	(4.75)^***	(1.20)	(16.75)^***
σ p	0.571	0.572		0.574	0.574	0.579	0.654
${\text{DM}}_{{\sigma }_p}$		(–3.83)^***		(–3.58)^***	(–3.34)^***	(–8.72)^***	(–18.45)^***

The results reinforce our earlier analysis, but now in an out-of-sample setting. The test statistics show that the HEAVY GAS tF model significantly outperforms the HJK, CAW, IW-A, EWMA, and the BEKK-t models with respect to one-step ahead density forecasts of the realized covariance matrix. This result has two implications. First, considering a matrix-F distribution for the realized covariance matrix is more accurate in terms of density fit than an (inverse-)Wishart distribution. This is in line with our in-sample results. The differences in the mean predictive log score are large and statistically significant with respect to the Wishart distribution. We see again that the matrix-F distribution also significantly outperforms the inverse-Wishart distribution, although the differences are not as large as with respect to the Wishart distribution. Second, the GAS HAR dynamics based on the matrix-F distribution provide improved density forecasts densities. This is, for example, seen when comparing the EWMA, BEKK-t, GAS tF, and GAS HAR tF approaches. The HJK model appears the most problematic in terms of out-of-sample density forecasts. Note that this model not only uses the Wishart rather than the matrix-F distribution for RC_t , but also parameterizes the Choleski matrix of V_t rather than V_t itself. Both features result in a worse density forecast.

The HEAVY GAS HAR tF model performs clearly the best for density forecasts of the realized covariance matrices. Table 5 also shows that for density forecasts of the returns the HEAVY GAS HAR tF shares its position with the CAW model. Differences between these models are minor and typically not statistically significant, except for k = 15 where the GAS HAR tF model produces better predictive return densities than the CAW model. Furthermore, also the GAS tF, IW-A, and the BEKK-t models are beaten by the GAS HAR dynamics, irrespective of the dimension of the returns.

Finally, the table shows that the HEAVY GAS HAR tF model also uniformly outperforms its competitors in the economic evaluation. For all dimensions, the ${\text{DM}}_{{\sigma }_p}$ statistics are negative and statistically significant at the 1% (5% in case of GAS tF in panel C) level, indicating that the HEAVY HAR GAS tF model produces the lowest ex post portfolio standard deviation compared to the competing models. We conclude that the new model with HAR dynamics also does well in an out-of-sample context, both statistically and economically.

5. CONCLUSIONS

We introduced a new dynamic multivariate HEAVY model that combines return observations and (ex post) observed realized covariance matrices to estimate the unobserved common underlying covariance matrix dynamics. The proposed model explicitly acknowledges that both realized covariance matrices and returns are typically fat-tailed. The proposed setup is particularly suitable for cases where no explicit robustification methods are applied while estimating realized measures. Using the GAS dynamics of Creal, Koopman, and Lucas (2011, 2013) based on a matrix-F distribution for the realized covariance matrices and a Student's t distribution for the returns, we derived an observation-driven model for the unobserved covariances with robust propagation dynamics. We proved that stationarity and ergodicity of the model. Positive definiteness of the filtered covariance matrices is ensured under simple and intuitive parameter restrictions.

An important feature of our model is that it retains the matrix format for the transition dynamics of the covariance matrices, unlike score-driven models proposed earlier. This makes the model computationally highly efficient. We showed that the model adequately captures both deterministic and stochastic volatility (SV) dynamics, even though the GAS model itself is misspecified in such settings. Using U.S. equity data over 2001–2014, the model also improves both the in-sample and out-of-sample fit of the covariance matrices for high-dimensional datasets of up to 30 dimensions. These improvements are both statistically and economically significant and persist over the episodes including the recent financial crisis. We conclude that the model provides a valuable tool when modeling combinations of fat-tailed matrix-valued and vector-valued random variables. Moreover, the matrix-F distribution used here can also prove useful beyond the scope of the current article, such as in for instance a Bayesian context.

SUPPLEMENTARY MATERIALS

The supplementary material contains the proofs of the theoretical results in the article.

ACKNOWLEDGMENTS

The authors appreciate the comments of participants at the 8th Annual SoFiE Conference (Aarhus, June 2015), the 9th meeting of the NESG (Tilburg, June 2014), and seminar participants at the Econometrics Brown Bag Seminar Series at Vrije Universiteit Amsterdam.

Lucas and Opschoor thank the Dutch National Science Foundation (NWO, grant VICI453-09-005) for financial support. The views expressed herein are those of the authors, and not necessarily those of UBS, and UBS Asset Management, which does not accept any responsibility for the contents, and opinions expressed in this article.