Bank Business Models at Zero Interest Rates

Abstract

We propose a novel observation-driven finite mixture model for the study of banking data. The model accommodates time-varying component means and covariance matrices, normal and Student’s t distributed mixtures, and economic determinants of time-varying parameters. Monte Carlo experiments suggest that units of interest can be classified reliably into distinct components in a variety of settings. In an empirical study of 208 European banks between 2008Q1–2015Q4, we identify six business model components and discuss how their properties evolve over time. Changes in the yield curve predict changes in average business model characteristics.

KEY WORDS:

• Bank business models
• Clustering
• Finite mixture model
• Low interest rates
• Score-driven model.

1. INTRODUCTION

Banks are highly heterogeneous, differing widely in terms of size, complexity, organization, activities, funding choices, and geographical reach. Understanding this diversity is of key importance, for example, for the study of risks acting upon and originating from the financial sector, for impact assessments of unconventional monetary policies and financial regulations, as well as for the benchmarking of banks to appropriate peer groups for supervisory purposes.¹ While there is broad agreement that financial institutions suffer in an environment of extremely low interest rates, see, for example, Nouy (2016), it is less clear which types of banks (business models) are affected the most. A study of banks’ business models at low interest rates provides insight into the overall diversity of business models, the strategies adopted by individual institutions, and which types of banks are impacted the most by time variation in the yield curve.² We study these questions in a novel modeling framework.

This article proposes an observation-driven finite mixture model for the analysis of high-dimensional banking data. The framework accommodates time-varying mean and covariance parameters and allows us to robustly cluster banks into approximately homogeneous groups. We first present a simple baseline mixture model for normally distributed data with time-varying component means, and subsequently consider extensions to time-varying covariance matrices, Student’s t distributed mixture densities, and economic predictors of time-varying parameters. We apply our modeling framework to a multivariate panel of N = 208 European banks between 2008Q1–2015Q4, that is, over T = 32 quarters, considering D = 13 bank-level indicator variables for J groups of similar banks. We thus track banking sector data through the 2008–2009 global financial crisis, the 2010–2012 euro area sovereign debt crisis, as well as the relatively calmer but persistent low-interest rate environment of the post-crises period between 2013–2015. We identify J = 6 business model components and discuss how these adjust to changes in the yield curve.

In our finite mixture model, all time-varying parameters are driven by the score of the local (time t) objective function using the so-called generalized autoregressive score (GAS) approach developed by Creal, Koopman, and Lucas (2013); see also Harvey (2013). In this setting, the time-varying parameters are perfectly predictable one-step ahead. This feature makes the model observation-driven in the terminology of Cox (1981). The likelihood is known in the closed form through a standard prediction error decomposition, facilitating parameter estimation via likelihood-based expectation-maximization (EM) procedures. Our approach extends the standard score-driven approach of Creal, Koopman, and Lucas (2013) by using the scores of the EM-based criterion function rather than that of the usual predictive likelihood function.

Extensive Monte Carlo experiments suggest that our model is able to reliably classify units of interest into distinct mixture components, as well as to simultaneously infer the relevant component-specific time-varying parameters. In our simulations, the cluster classification is perfect for sufficiently large distances between the time-varying cluster means and sufficiently informative signals relative to the variance of the noise terms.³ This holds under correct model specification as well as under specific forms of model mis-specification. As the simulated data become less informative or the time-varying cluster means are closer together, the share of correct classifications decreases, but generally remains high. Estimation fit and the share of correct classifications decrease further if we incorrectly assume a thin-tailed mixture specification when the data are generated by a fat-tailed mixture distribution. As a result, robust models based on fat-tailed mixtures are appropriate for the fat-tailed bank accounting ratios in our empirical sample.

We apply our model to classify European banks into distinct business model components. We distinguish (A) large universal banks, including globally systemically important banks (G-SIBs), (B) international diversified lenders, (C) fee-based banks, (D) domestic diversified lenders, (E) domestic retail lenders, and F) small international banks. The similarities and differences between these components are discussed in detail in the main text. Based on our component mean estimates and business model classification, we find that the global financial crisis between 2008–2009 affected banks with different business models differently. This is in line with findings by Altunbas, Manganelli, and Marques-Ibanez (2011) and Chiorazzo et al. (2016), who study U.S.-based institutions.

In addition, we study how banks’ business models adapt to changes in yield curve factors, specifically level and slope of the yield curve. The yield curve factors are extracted from AAA-rated euro area sovereign bonds based on a Svensson (1995) model. We find that, as long-term interest rates decrease, banks on average (across all business models) grow larger, hold more assets in trading portfolios to offset declines in loan demand, hold more sizeable derivative books, and, in some cases, increase leverage and decrease funding through customer deposits. Each of these effects—increased size, leverage, complexity, and a less stable funding base—are intuitive, but also potentially problematic from a financial stability perspective. This corroborates the unease expressed by Yellen (2014) and Draghi (2016).

From a methodological point of view, our article also contributes to the literature on clustering of time series data. This literature can be divided into four strands. Static clustering of time series refers to a setting with fixed cluster classification, that is, each time series is allocated to one cluster over the entire sample period. Dynamic clustering, by contrast, allows for changes in the cluster assignments over time. Each approach can be further split into whether the cluster-specific parameters are constant (static) or time-varying (dynamic).

Wang et al. (2013) is an example of static clustering with static parameters. They clustered time series into different groups of autoregressive processes, where the autoregressive parameters are constant within each cluster and cluster assignments are fixed over time.

Fruehwirth-Schnatter and Kaufmann (2008) used static clustering with elements of both static and dynamic parameters. First, they clustered time series into different groups of regression models with static parameters. Later, they generalized this to static clustering into groups of different hidden Markov models (HMMs), each switching between two regression models. The HMM can be regarded as a specific form of dynamic parameters for the underlying regression model. Their method was used by Hamilton and Owyang (2012) to differentiate between business cycle dynamics among groups of U.S. states. Also, Smyth (1996) clustered time series into groups characterized by different hidden Markov models.

Creal, Gramacy, and Tsay (2014b) is an example of dynamic clustering with static parameters. They developed a model for credit ratings based on market data. Their main objective was to classify firms into different rating categories over time. They therefore allowed for transitions across clusters (dynamic clustering), while the parameters in their underlying mixture model are kept constant.

Finally, Catania (2016) is an example of dynamic clustering with dynamic parameters. He proposed a score-driven dynamic mixture model, which relies on score-driven updates of almost all parameters, allowing for time-varying parameters and changing cluster assignments and time-varying cluster assignment probabilities. Due to the high flexibility of the model, a large number of observations is required over time. The application in Catania (2016) to conditional asset return distributions typically has a sufficiently large number of observations.

Our approach falls in the category of static clustering methods with dynamic parameters. We use static clustering as banks do not tend to switch their business model frequently over short periods of time; see, for example, Ayadi and de Groen (2015). Also, in contrast to the application used by for instance Catania (2016), our banking data are observed over only a moderate number of time points T, while the number of units N and the number of firm characteristics D are high. Given static clustering, the properties of bank business models are unlikely to be constant throughout the periods of market turbulence and shifts in bank regulations experienced in our sample. We therefore require the cluster components to be characterized by dynamic parameters using the score-driven framework of Creal, Koopman, and Lucas (2013).

Our article also contributes to the literature on identifying bank business models. Roengpitya, Tarashev, and Tsatsaronis (2014), Ayadi, Arbak, and de Groen (2011), and Ayadi and de Groen (2015) also used cluster analysis to identify bank business models. Conditional on the identified clusters, the authors discussed bank profitability trends over time, study banking sector risks and their mitigation, and consider changes in banks’ business models in response to new regulation. Our statistical approach is different in that our components are not identified based on single (static) cross-sections of year-end data. Instead, we consider a panel framework, which allows us to pool information over time, leading to a more accurate assessment.

We proceed as follows. Section 2 presents a static and baseline dynamic finite mixture model. We then propose extensions to incorporate time-varying covariance matrices, as well as Student’s t distributed mixture distributions, and introduce model diagnostics. Section 3 discusses the outcomes of a variety of Monte Carlo simulation experiments. Section 4 applies the model to classify European financial institutions. Section 5 studies to which extent banks’ business models adapt to an environment of exceptionally low interest rates. Section 6 concludes. A Web appendix provides further technical and empirical results.

2. STATISTICAL MODEL

2.1 Mixture Model

We consider multivariate panel data consisting of vectors ${\mathbf{y}}_{i,t}\in {\mathbb{R}}^{D\times 1}$ of firm characteristics for firms i = 1, …, N and times t = 1, …, T, where D denotes the number of observed characteristics. We model ${\mathbf{y}}_{i,t}$ by a J-component mixture model of the form (1) $$\begin{array}{c}\hfill {\mathbf{y}}_{i,t}=z_{i,1}·({\mu }_{1,t}+{\Omega }_{1,t}^{1/2}{e}_{i,t,1})+\cdots +z_{i,J}·({\mu }_{J,t}+{\Omega }_{J,t}^{1/2}{e}_{i,t,J}),\end{array}$$(1) where μ_{j, t} and Ω_{j, t} are the mean and covariance matrix of mixture component j = 1, …, J at time t, respectively, e_{i, t, j} is a zero-mean, D-dimensional vector of disturbances with identity covariance matrix, and z_{i, j} are unobserved indicators for the mixture component of firm i. In particular, if firm i is in mixture component j then z_{i, j} = 1, while z_{i, k} = 0 for $k\ne j$. The posterior expectations of z_{i, j} given the data can be used to classify firms into specific mixture components later on. We define ${\mathbf{z}}_i={(z_{i,1},\dots ,z_{i,J})}^{\text{'}}$ and assume ${\mathbf{z}}_i$ has a multinomial distribution with $Pr[z_{i,j}=1]={\pi }_j\in [0,1]$ and π₁ + ⋅⋅⋅ + π_J = 1. Finally, we assume that ${\mathbf{z}}_i$ and e_{i, t, j} are mutually, cross-sectionally, and serially uncorrelated. The model could be further enhanced with an error components structure for e_{i, t, j} if for instance cross-sectional correlation is an issue. We leave such extensions for future research.

We specify the precise dynamic functional form of μ_{j, t} and Ω_{j, t} later in this section using the score-driven dynamics of Creal, Koopman, and Lucas (2013). For the moment, it suffices to note that μ_{j, t} and Ω_{j, t} will both be functions of past data only, and therefore predetermined. Finite mixture models with static cluster-specific parameters have been widely used in the literature. For textbook treatments, see, for example, McLachlan and Peel (2000) and Fruehwirth-Schnatter (2006).

To write down the likelihood of the mixture model in (1(1) $$\begin{array}{c}\hfill {\mathbf{y}}_{i,t}=z_{i,1}·({\mu }_{1,t}+{\Omega }_{1,t}^{1/2}{e}_{i,t,1})+\cdots +z_{i,J}·({\mu }_{J,t}+{\Omega }_{J,t}^{1/2}{e}_{i,t,J}),\end{array}$$(1) ), we stack the observations up to time t, ${\mathbf{y}}_{i,1},\dots ,{\mathbf{y}}_{i,t}$, into the matrix $\mathbf{Y}{}_{i,t}={\left({\mathbf{y}}_{i,1}\dots {\mathbf{y}}_{i,t}\right)}^{\text{'}}\in {\mathbb{R}}^{t\times D}$. We also stack the parameters characterizing each mixture component j, such as the μ_{j, t}’s and Ω_{j, t}’s for all times t, and any remaining parameters characterizing the distribution of e_{i, t, j} (such as the degrees of freedom of a Student’s t), into a parameter vector ${\theta }_j\left(\Theta \right)$, where $\Theta$ gathers all static parameters of the model. Note that also the multinomial probabilities π_j are functions of $\Theta$, that is, ${\pi }_j={\pi }_j\left(\Theta \right)$. However, if no confusion is caused we use the short-hand notation π_j and ${\theta }_j$ for ${\pi }_j\left(\Theta \right)$ and ${\theta }_j\left(\Theta \right)$, respectively. The likelihood function is given by a standard prediction error decomposition as (2) $$\begin{array}{c}\hfill logL\left(\Theta \right)=\sum _{i=1}^{N}log\left[\sum _{j=1}^J{\pi }_j·f_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right],\end{array}$$(2) where $$f_j(\mathbf{Y}{}_{i,T};{\theta }_j)=\prod _{t=1}^T{f}_j\left({\mathbf{y}}_{i,t}\mid \mathbf{Y}{}_{i,t-1};{\theta }_{j,t}\right),$$and $f_j({\mathbf{y}}_{i,t}\mid \mathbf{Y}{}_{i,t-1};{\theta }_{j,t})$ is the conditional distribution of ${\mathbf{y}}_{i,t}={\mu }_{j,t}+{\Omega }_{j,t}^{1/2}{e}_{i,t,j}$ given the past data and given the (predetermined) parameters for time t as gathered in ${\theta }_{j,t}$.

Before proceeding, we note that the mixture model in (1(1) $$\begin{array}{c}\hfill {\mathbf{y}}_{i,t}=z_{i,1}·({\mu }_{1,t}+{\Omega }_{1,t}^{1/2}{e}_{i,t,1})+\cdots +z_{i,J}·({\mu }_{J,t}+{\Omega }_{J,t}^{1/2}{e}_{i,t,J}),\end{array}$$(1) ) describes the firm characteristics using time-invariant cluster indicators ${\mathbf{z}}_i$ rather than time-varying indicators z_{i, t}. Our choice follows from the specific application in Section 4. Banks are unlikely to switch their business model over limited time spans such as ours. For instance, a large universal bank is unlikely to become a small retail lender from one year to the next, as strategy choices, distribution channels, brand building, and clientele formation are all slowly varying economic processes. This is why we opt for static cluster indicators. In a different empirical context, a different modeling choice might be called for. For example, Creal, Gramacy, and Tsay (2014b) considered corporate credit ratings, which are much more likely to change over shorter periods of time, such that some of their specifications use time-varying cluster assignments. To explicitly check whether the assumption of fixed cluster assignments is supported by our data, we use the diagnostics developed in Section 2.5. Our findings indicate that the vast majority of banks indeed only belongs to one cluster for all time points.

Given our choice for static rather than dynamic cluster allocation, it becomes important to allow for time-variation in the cluster means μ_{j, t} (and possibly in the variances Ω_{j, t}). Even though banks are less likely to switch their business model, the average characteristics of business models may change over shorter time spans, particularly if such time spans include stressful periods as is the case in our sample. This allows us to answer questions relating to how the properties of business models changed, and in particular whether some business models (and if so, which) increased their risk characteristics during the low interest rate period we study in Section 4. Such results are also important for policy makers, such as the single supervisory mechanism in Europe to decide on the riskiness of banks and on adequate capital and liquidity levels for peer groups of banks.

2.2 EM Estimation

As is common in the literature on mixture models, we do not estimate $\Theta$ directly by numerically maximizing the log-likelihood function in (2(2) $$\begin{array}{c}\hfill logL\left(\Theta \right)=\sum _{i=1}^{N}log\left[\sum _{j=1}^J{\pi }_j·f_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right],\end{array}$$(2) ). Instead we use the expectation maximization (EM) algorithm to estimate the parameters; see Dempster, Laird, and Rubin (1977) and McLachlan and Peel (2000).⁴ To write down the EM algorithm and formulate the score-driven parameter dynamics for μ_{j, t} and Ω_{j, t} later on, we define the complete data for firm i as the pair $(\mathbf{Y}{}_{i,T},{\mathbf{z}}_i)$. If ${\mathbf{z}}_i$ is known, the corresponding complete data likelihood function is given by (3) $$\begin{array}{c}\hfill log{L}_c\left(\Theta \right)=\sum _{i=1}^N\sum _{j=1}^J{z}_{i,j}\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right].\end{array}$$(3) Because ${\mathbf{z}}_i$ is unobserved, however, (3(3) $$\begin{array}{c}\hfill log{L}_c\left(\Theta \right)=\sum _{i=1}^N\sum _{j=1}^J{z}_{i,j}\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right].\end{array}$$(3) ) cannot be maximized directly. Following Dempster, Laird, and Rubin (1977), we instead maximize its conditional expectation over ${\mathbf{z}}_i$ given the observed data $\mathbf{Y}{}_T=(\mathbf{Y}{}_{1,T},\dots ,\mathbf{Y}{}_{N,T})$ and some initial or previously determined parameter value ${\Theta }^{(k-1)}$, that is, we maximize with respect to $\Theta$ the function (4) $$\begin{array}{ccc}& & Q(\Theta ;{\Theta }^{(k-1)})\hfill \\ & & =\mathbb{E}\left[log{L}_c\left(\Theta \right)\left|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right.\right]\hfill \\ & & =\mathbb{E}\left[\sum _{i=1}^N\sum _{j=1}^J{z}_{i,j}\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right]|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right]\hfill \\ & & =\sum _{i=1}^N\sum _{j=1}^J\mathbb{P}\left[z_{i,j}=1\left|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right.\right]\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right].\hfill \end{array}$$(4) The conditionally expected likelihood (4(4) $$\begin{array}{ccc}& & Q(\Theta ;{\Theta }^{(k-1)})\hfill \\ & & =\mathbb{E}\left[log{L}_c\left(\Theta \right)\left|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right.\right]\hfill \\ & & =\mathbb{E}\left[\sum _{i=1}^N\sum _{j=1}^J{z}_{i,j}\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right]|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right]\hfill \\ & & =\sum _{i=1}^N\sum _{j=1}^J\mathbb{P}\left[z_{i,j}=1\left|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right.\right]\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right].\hfill \end{array}$$(4) ) can be optimized iteratively by alternately updating the conditional expectation of the component indicators ${\mathbf{z}}_i$ (E-Step) and subsequently maximizing the remaining part of the function with respect to $\Theta$ (M-Step).

In the E-Step, the conditional component indicator probabilities are updated using (5) $$\begin{array}{ccc}\hfill {\tau }_{i,j}^{\left(k\right)}& :=& \mathbb{P}\left[z_{i,j}=1\mid \mathbf{Y}{}_T,{\Theta }^{(k-1)}\right]\hfill \\ & =& \frac{{\pi }_j^{(k-1)}{f}_j\left(\mathbf{Y}{}_{i,T};{\theta }_j^{(k-1)}\right)}{f\left(\mathbf{Y}{}_{i,T};{\Theta }^{(k-1)}\right)}=\frac{{\pi }_j^{(k-1)}{f}_j\left(\mathbf{Y}{}_{i,T};{\theta }_j^{(k-1)}\right)}{{\sum }_{h=1}^J{\pi }_h^{(k-1)}{f}_h\left(\mathbf{Y}{}_{i,T};{\theta }_h^{(k-1)}\right)}.\hfill \end{array}$$(5) We again point out that the τ^(k)_{i, j}s do not depend on time, as banks in our application in Section 4 are statically assigned to clusters. An alternative would be to use dynamic cluster assignments as in Catania (2016), in which case the densities $f_j(\mathbf{Y}{}_{i,T};{\theta }_j^{(k-1)})$ above would have to be replaced by their time t counterparts $f_j({\mathbf{y}}_{i,t}\mid \mathbf{Y}{}_{i,t-1};{\theta }_{j,t}^{(k-1)})$ and would result in time-specific posterior probabilities τ^(k)_{i, j, t}; see also the diagnostic statistics introduced in Section 2.5.

Once the τ^(k)_{i, j}s are updated, we move to the M-Step. Maximizing $Q(\Theta ;{\Theta }^{(k-1)})$ with respect to π_j under the constraint π₁ + ⋅⋅⋅ + π_J = 1, we obtain (6) $$\begin{array}{c}\hfill {\pi }_j^{\left(k\right)}=\frac{1}{N}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)},j=1,\dots ,J.\end{array}$$(6) The optimization of $Q(\Theta ;{\Theta }^{(k-1)})$ with respect to the remaining parameters in $\Theta$ can sometimes be done analytically, for instance in the case of the normal finite mixture model with static location μ_{j, t} ≡ μ_j and scale Ω_{j, t} ≡ Ω_j. Otherwise, numerical maximization methods need to be used. The E-step and M-step are iterated until the difference $L\left({\Theta }^{(k+1)}\right)-L\left({\Theta }^{\left(k\right)}\right)$ has converged. The EM algorithm increases the likelihood on each step, and convergence typically occurs within 15 iterations in our application. After convergence, when $\Theta$ has been estimated, we can use the final τ^(k)_{i, j} to assign banks to clusters. We do so by assigning bank i to cluster j which has the highest τ^(k)_{i, j} across j. Note that due to the EM perspective of the score steps, filtering ${\widehat{\mu }}_{j,t}$ for a panel of firms is not a straightforward recursion from time t = 1, …, T as in the standard setting for score-driven models. In particular, for given τ^(k)_{i, j}, we can compute μ_{j, t}, and the other way around. Given that both quantities need to be estimated, however, the filtering problem for μ_{j, t} requires the simultaneous solution of τ_{i, j}. We solve this problem via the additional alternation of E-steps and M-steps in the EM algorithm.

2.3 Normal Mixture With Time-Varying Means

As explained in Section 2.1, it is important to allow for time-varying cluster means. We first do so for the case of a normal mixture with time varying means and constant covariance matrices. We set $f_j({\mathbf{y}}_{i,t}\mid \mathbf{Y}{}_{i,t-1};{\theta }_{j,t})=\varphi ({\mathbf{y}}_{i,t};{\mu }_{j,t},{\Omega }_j)$, where φ( · ; μ, Ω) denotes a multivariate normal density function with mean μ and variance Ω. In this section, we introduce a version of the score-driven approach of Creal, Koopman, and Lucas (2013) to the parameter dynamics of μ_{j, t}; compare also Harvey (2013) and Creal et al. (2014a). Rather than using the score of the log-density as in Creal, Koopman, and Lucas (2013), however, we use the score of the EM criterion in (4(4) $$\begin{array}{ccc}& & Q(\Theta ;{\Theta }^{(k-1)})\hfill \\ & & =\mathbb{E}\left[log{L}_c\left(\Theta \right)\left|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right.\right]\hfill \\ & & =\mathbb{E}\left[\sum _{i=1}^N\sum _{j=1}^J{z}_{i,j}\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right]|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right]\hfill \\ & & =\sum _{i=1}^N\sum _{j=1}^J\mathbb{P}\left[z_{i,j}=1\left|\mathbf{Y}{}_T;{\Theta }^{(k-1)}\right.\right]\left[log{\pi }_j+log{f}_j(\mathbf{Y}{}_{i,T};{\theta }_j)\right].\hfill \end{array}$$(4) ) to drive the parameter dynamics. Our simulation section shows that the score-driven dynamics can fit various patterns for the cluster means, both in correctly specified and mis-specified settings.

For simplicity and parsimony, we consider the integrated score-driven dynamics as discussed by Lucas and Zhang (2016), (7) $$\begin{array}{c}\hfill {\mu }_{j,t+1}={\mu }_{j,t}+A_1{s}_{{\mu }_{j,t}},\end{array}$$(7) where $A_1=A_1\left(\Theta \right)$ is a diagonal matrix that depends on the unknown parameter vector $\Theta$, and where $s_{{\mu }_{j,t}}$ is the scaled first derivative of the time t EM objective function ${\sum }_{i=1}^N{\sum }_{j=1}^J{\tau }_{i,j}^{\left(k\right)}log\varphi ({\mathbf{y}}_{i,t};{\mu }_{j,t},{\Omega }_j)$ with respect to μ_{j, t}, where we dropped the part ∑^N_{i = 1}∑_{j = 1}^Jτ^(k)_{i, j}log π_j as it does not depend on μ_{j, t}. The score is given by (8) $$\begin{array}{ccc}\hfill {\nabla }_{{\mu }_{j,t}}& =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}log\varphi ({\mathbf{y}}_{i,t};{\mu }_{j^{\text{'}},t},{\Omega }_{j^{\text{'}}})\right)\hfill \\ & =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}\left[-\frac{1}{2}log\left|2\pi {\Omega }_{j^{\text{'}}}\right|\right.\right.\hfill \\ & & -\left.\left.\frac{1}{2}{({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})}^{\text{'}}{\Omega }_{j^{\text{'}}}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})\right]\phantom{\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}}\right)\hfill \\ & =& {\Omega }_j^{-1}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left({\mathbf{y}}_{i,t}-{\mu }_{j,t}\right).\hfill \end{array}$$(8)

The score in (8(8) $$\begin{array}{ccc}\hfill {\nabla }_{{\mu }_{j,t}}& =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}log\varphi ({\mathbf{y}}_{i,t};{\mu }_{j^{\text{'}},t},{\Omega }_{j^{\text{'}}})\right)\hfill \\ & =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}\left[-\frac{1}{2}log\left|2\pi {\Omega }_{j^{\text{'}}}\right|\right.\right.\hfill \\ & & -\left.\left.\frac{1}{2}{({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})}^{\text{'}}{\Omega }_{j^{\text{'}}}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})\right]\phantom{\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}}\right)\hfill \\ & =& {\Omega }_j^{-1}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left({\mathbf{y}}_{i,t}-{\mu }_{j,t}\right).\hfill \end{array}$$(8) ) is based on the EM local objective function. One might ask how this score relates to the standard score as proposed originally in Creal, Koopman, and Lucas (2013). In Web Appendix A, we show that if the density of the mixing variable z_i does not depend on f_t, then the standard predictive density score and the EM score evaluated at the MLE optimum are identical. The result was also used to account for missing values by Lucas, Opschoor, and Schaumburg (2016). The current finite mixture model is a special case of this more generic result.

To scale our score for μ_{j, t}, we compute the inverse of the expected negative Hessian under mixture component j. In particular, we take the derivative of (8(8) $$\begin{array}{ccc}\hfill {\nabla }_{{\mu }_{j,t}}& =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}log\varphi ({\mathbf{y}}_{i,t};{\mu }_{j^{\text{'}},t},{\Omega }_{j^{\text{'}}})\right)\hfill \\ & =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}\left[-\frac{1}{2}log\left|2\pi {\Omega }_{j^{\text{'}}}\right|\right.\right.\hfill \\ & & -\left.\left.\frac{1}{2}{({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})}^{\text{'}}{\Omega }_{j^{\text{'}}}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})\right]\phantom{\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}}\right)\hfill \\ & =& {\Omega }_j^{-1}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left({\mathbf{y}}_{i,t}-{\mu }_{j,t}\right).\hfill \end{array}$$(8) ) with respect to the transpose of μ_{j, t}, switch sign, and compute the inverse, thus obtain a scaling matrix Ω_j/∑^N_{i = 1}τ^(k)_{i, j}. This yields a corresponding scaled score update of the form (9) $$\begin{array}{ccc}\hfill {\mu }_{j,t+1}& =& {\mu }_{j,t}+A_1·\frac{{\sum }_{i=1}^N{\tau }_{i,j}({\mathbf{y}}_{i,t}-{\mu }_{j,t})}{{\sum }_{i=1}^N{\tau }_{i,j}}.\hfill \end{array}$$(9) This updating mechanism is highly intuitive: the component means are updated by the prediction errors for that component, accounting for the posterior probabilities that the observation was drawn from that same component. For example, if the posterior probability τ^(k)_{i, j} that ${\mathbf{y}}_{i,t}$ comes from component j is negligible, the update of μ_{j, t} does not depend on the observation of firm i.

We note that we do not scale the score by the inverse Fisher information matrix as suggested in for instance Creal, Koopman, and Lucas (2013). So far, there is no optimality theory for the choice of the scale for the score, and different proposals can be found in the literature. Computing the information matrix for the mixture model is hard, particularly if we take into account that also τ^(k)_{i, j} is a function of ${\mathbf{y}}_{i,t}$. We can show, however, that our proposed way of scaling the score collapses to the inverse information matrix if the mixture components are sufficiently far apart.

All static parameters can now be estimated using the EM-algorithm. Starting from an initial ${\Theta }^{(k-1)}$ and an initial mean μ^{(k − 1)}_{j, 1}, we compute μ^{(k − 1)}_{j, 2}, …, μ_jT^{(k − 1)} using the recursion (9(9) $$\begin{array}{ccc}\hfill {\mu }_{j,t+1}& =& {\mu }_{j,t}+A_1·\frac{{\sum }_{i=1}^N{\tau }_{i,j}({\mathbf{y}}_{i,t}-{\mu }_{j,t})}{{\sum }_{i=1}^N{\tau }_{i,j}}.\hfill \end{array}$$(9) ). We compute the posterior probabilities as (10) $$\begin{array}{c}\hfill {\tau }_{i,j}^{\left(k\right)}=\frac{{\pi }_j^{(k-1)}{\prod }_{t=1}^T\varphi \left({\mathbf{y}}_{i,t};{\mu }_{j,t}^{(k-1)},{\Omega }_j^{(k-1)}\right)}{{\sum }_{h=1}^J{\pi }_h^{(k-1)}{\prod }_{t=1}^T\varphi \left({\mathbf{y}}_{i,t};{\mu }_{ht}^{(k-1)}{\Omega }_h^{(k-1)}\right)}.\end{array}$$(10) Next, the M-Step maximizes (11) $$\begin{array}{ccc}& & \sum _{i=1}^N\sum _{t=1}^T\sum _{j=1}^D{\tau }_{i,j}^{\left(k\right)}\hfill \\ & & \times \left[-\frac{1}{2}log\left(\right|2\pi {\Omega }_j\left|\right)-\frac{1}{2}{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\Omega }_j^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right],\hfill \end{array}$$(11) with respect to A₁ and Ω_j. The initial values μ_{j, 1} can also be estimated if J and D are not too large. Otherwise, the number of parameters becomes infeasible. Alternatively, one can initialize the time-varying means μ_{j, 1} by the τ_{i, j}-weighted average of the first cross-section(s). Given the values of J and D in our empirical study, we opt for this latter approach. We set μ_{j, 1} equal to the weighted unconditional sample average in the simulation study, and to the weighted average of the first cross-section in the empirical application. Given μ_{j, 1} and A₁, the optimization with respect to Ω_j can be done analytically. The optimization with respect to A₁ has to be carried out numerically.

The E-step and M-step are iterated until convergence. To start up the EM algorithm, we initialize the weights τ_{i, j} randomly. To robustify the optimization algorithm, we use a large number of random starting values and pick the highest value for the final converged criterion function.

2.4 Extensions

2.4.1 Time-Varying Component Covariance Matrices

This section derives the scaled score updates for time-varying component covariance matrices Ω_{j, t}. If we also want to endow the time-varying covariance matrices with integrated score dynamics, we have (12) $$\begin{array}{ccc}\hfill {\Omega }_{j,t+1}& =& {\Omega }_{j,t}+A_2{s}_{{\Omega }_{j,t}},\hfill \end{array}$$(12) where $s_{{\Omega }_{j,t}}$ is again defined as the scaled first partial derivative of the expected likelihood function with respect to Ω_{j, t}. Following equation (8(8) $$\begin{array}{ccc}\hfill {\nabla }_{{\mu }_{j,t}}& =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}log\varphi ({\mathbf{y}}_{i,t};{\mu }_{j^{\text{'}},t},{\Omega }_{j^{\text{'}}})\right)\hfill \\ & =& \frac{\partial }{\partial {\mu }_{j,t}}\left(\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}\left[-\frac{1}{2}log\left|2\pi {\Omega }_{j^{\text{'}}}\right|\right.\right.\hfill \\ & & -\left.\left.\frac{1}{2}{({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})}^{\text{'}}{\Omega }_{j^{\text{'}}}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j^{\text{'}},t})\right]\phantom{\sum _{i=1}^N\sum _{j^{\text{'}}=1}^J{\tau }_{i,j^{\text{'}}}^{\left(k\right)}}\right)\hfill \\ & =& {\Omega }_j^{-1}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left({\mathbf{y}}_{i,t}-{\mu }_{j,t}\right).\hfill \end{array}$$(8) ), the unscaled score with respect to Ω_{j, t} is (13) $$\begin{array}{ccc}\hfill {\nabla }_{{\Omega }_{j,t}}& =& \frac{1}{2}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}{\Omega }_{j,t}^{-1}\left[({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}-{\Omega }_{j,t}\right]{\Omega }_{j,t}^{-1}.\hfill \end{array}$$(13) Taking the total differential of this expression, and subsequently taking expectations ${\mathrm{E}}_j[·]$ conditional on mixture component j, we obtain (14) $$\begin{array}{ccc}& & \frac{1}{2}{\mathrm{E}}_j\left[\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left(\mathrm{d}{\Omega }_{j,t}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\Omega }_{j,t}^{-1}\right.\right.\hfill \\ & & +\left.\left.{\Omega }_{j,t}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}\mathrm{d}{\Omega }_{j,t}^{-1}-\mathrm{d}{\Omega }_{j,t}^{-1}\phantom{\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}}\right)\right]\hfill \\ & & =\frac{1}{2}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\mathrm{d}{\Omega }_{j,t}^{-1}=-\left(\sum _{i=1}^N\frac{1}{2}{\tau }_{i,j}^{\left(k\right)}\right){\Omega }_{j,t}^{-1}\mathrm{d}{\Omega }_{j,t}{\Omega }_{j,t}^{-1}.\hfill \end{array}$$(14) Vectorizing (14(14) $$\begin{array}{ccc}& & \frac{1}{2}{\mathrm{E}}_j\left[\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left(\mathrm{d}{\Omega }_{j,t}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\Omega }_{j,t}^{-1}\right.\right.\hfill \\ & & +\left.\left.{\Omega }_{j,t}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}\mathrm{d}{\Omega }_{j,t}^{-1}-\mathrm{d}{\Omega }_{j,t}^{-1}\phantom{\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}}\right)\right]\hfill \\ & & =\frac{1}{2}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\mathrm{d}{\Omega }_{j,t}^{-1}=-\left(\sum _{i=1}^N\frac{1}{2}{\tau }_{i,j}^{\left(k\right)}\right){\Omega }_{j,t}^{-1}\mathrm{d}{\Omega }_{j,t}{\Omega }_{j,t}^{-1}.\hfill \end{array}$$(14) ), we obtain $-\left(\frac{1}{2}{\sum }_{i=1}^N{\tau }_{i,j}^{\left(k\right)}\right){({\Omega }_{j,t}\otimes {\Omega }_{j,t})}^{-1}\mathrm{vec}\left(\mathrm{d}{\Omega }_{j,t}\right)$, where $\mathrm{vec}(·)$ concatenates the columns of a matrix into a column vector, and where the negative inverse of the matrix in front of $\mathrm{vec}\left(\mathrm{d}{\Omega }_{j,t}\right)$ is our scaling matrix to correct for the curvature of the score. Multiplying the vectorized version of (13(13) $$\begin{array}{ccc}\hfill {\nabla }_{{\Omega }_{j,t}}& =& \frac{1}{2}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}{\Omega }_{j,t}^{-1}\left[({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}-{\Omega }_{j,t}\right]{\Omega }_{j,t}^{-1}.\hfill \end{array}$$(13) ) by this scaling matrix, we obtain the scaled score (15) $$\begin{array}{ccc}\hfill \mathrm{vec}\left(s_{{\Omega }_{j,t}}\right)& =& {\left(\frac{1}{2}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\right)}^{-1}({\Omega }_{j,t}\otimes {\Omega }_{j,t})·\mathrm{vec}\left({\nabla }_{{\Omega }_{j,t}}\right)\hfill \\ \hfill & =& {\left(\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\right)}^{-1}·\mathrm{vec}\left(2{\Omega }_{j,t}{\nabla }_{{\Omega }_{j,t}}{\Omega }_{j,t}\right)\iff \hfill \\ \hfill s_{{\Omega }_{j,t}}& =& \frac{{\sum }_{i=1}^N{\tau }_{i,j}^{\left(k\right)}\left[({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}-{\Omega }_{j,t}\right]}{{\sum }_{i=1}^N{\tau }_{i,j}^{\left(k\right)}}.\hfill \end{array}$$(15) The estimation of the model can be carried out using the EM algorithm as before, replacing Ω_j by Ω_{j, t} in equations (10(10) $$\begin{array}{c}\hfill {\tau }_{i,j}^{\left(k\right)}=\frac{{\pi }_j^{(k-1)}{\prod }_{t=1}^T\varphi \left({\mathbf{y}}_{i,t};{\mu }_{j,t}^{(k-1)},{\Omega }_j^{(k-1)}\right)}{{\sum }_{h=1}^J{\pi }_h^{(k-1)}{\prod }_{t=1}^T\varphi \left({\mathbf{y}}_{i,t};{\mu }_{ht}^{(k-1)}{\Omega }_h^{(k-1)}\right)}.\end{array}$$(10) ) and (11(11) $$\begin{array}{ccc}& & \sum _{i=1}^N\sum _{t=1}^T\sum _{j=1}^D{\tau }_{i,j}^{\left(k\right)}\hfill \\ & & \times \left[-\frac{1}{2}log\left(\right|2\pi {\Omega }_j\left|\right)-\frac{1}{2}{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\Omega }_j^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right],\hfill \end{array}$$(11) ).

2.4.2 Student’s t Distributed Mixture

This section robustifies the dynamic finite mixture model by considering panel data that are generated by mixtures of multivariate Student’s t distributions. Assuming a multivariate normal mixture is not always appropriate. For example, extreme tail observations can easily occur in the analysis of accounting ratios when the denominator is close to zero, implying pronounced changes from negative to positive values.

To use the EM-algorithm for mixtures of Student’s t distributions, we use the densities (16) $$\begin{array}{c}\hfill f_j({\mathbf{y}}_{i,t};{\theta }_{j,t})=\frac{\Gamma (({\nu }_j+D)/2)}{\Gamma ({\nu }_j/2){\left|\pi {\nu }_j{\Omega }_{j,t}\right|}^{1/2}}\\ & & \times {\left(1+{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\left({\nu }_j{\Omega }_{j,t}\right)}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right)}^{-(\nu +D)/2}.\hfill \end{array}$$(16) Both the E-steps and the M-steps of the algorithm are unaffected save for the fact that we use Student’s t rather than Gaussian densities. The main difference follows for the dynamic models, where the score steps now take a different form. Using (16(16) $$\begin{array}{c}\hfill f_j({\mathbf{y}}_{i,t};{\theta }_{j,t})=\frac{\Gamma (({\nu }_j+D)/2)}{\Gamma ({\nu }_j/2){\left|\pi {\nu }_j{\Omega }_{j,t}\right|}^{1/2}}\\ & & \times {\left(1+{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\left({\nu }_j{\Omega }_{j,t}\right)}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right)}^{-(\nu +D)/2}.\hfill \end{array}$$(16) ), the scores for the location parameter μ_{j, t} and scale matrix Ω_{j, t} are (17) $$\begin{array}{c}\hfill {\nabla }_{{\mu }_{j,t}}={\Omega }_{j,t}^{-1}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}{w}_{i,j,t}·\left({\mathbf{y}}_{i,t}-{\mu }_{j,t}\right),\end{array}$$(17) (18) $$\begin{array}{c}\hfill {\nabla }_{{\Omega }_{j,t}}=\frac{1}{2}\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}{\Omega }_{j,t}^{-1}\left[w_{i,j,t}·({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right.\\ \hfill \times \left.{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}-{\Omega }_{j,t}\right]{\Omega }_{j,t}^{-1},\end{array}$$(18) (19) $$\begin{array}{c}\hfill w_{i,j,t}=(1+{\nu }_j^{-1}D)\\ \hfill /\left(1+{\nu }_j^{-1}{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\Omega }_{j,t}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right).\end{array}$$(19) The main difference between the scores of the Student’s t and the Gaussian case is the presence of the weights w_{i, j, t}. These weights provide the model with a robustness feature: observations ${\mathbf{y}}_{i,t}$ that are outlying given the fat-tailed nature of the Student’s t density receive a reduced impact on the location and volatility dynamics by means of a lower value for w_{i, j, t}; compare Creal, Koopman, and Lucas (2011, 2013) and Harvey (2013). We use the same scale matrices for the score as in Sections 2.3 and 2.4.1. For the location parameter, which is our main parameter of interest, the scaling matrix for the Student’s t case is proportional to that for the normal, such that any differences are included in the estimation of the smoothing parameter A₁. We obtain the scaled scores (20) $$\begin{array}{c}\hfill s_{{\mu }_{j,t}}=\left(\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}{w}_{i,j,t}·\left({\mathbf{y}}_{i,t}-{\mu }_{j,t}\right)\right)/\left(\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\right),\end{array}$$(20) (21) $$\begin{array}{c}\hfill s_{{\Omega }_{j,t}}=\left(\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}(w_{i,j,t}·({\mathbf{y}}_{i,t}-{\mu }_{j,t}){({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}-{\Omega }_{j,t})\right)\\ \hfill /\left(\sum _{i=1}^N{\tau }_{i,j}^{\left(k\right)}\right).\end{array}$$(21) The intuition is the same as for the Gaussian case, except for the fact that the scaled score steps for μ_{j, t} and Ω_{j, t} are redescending to zero and bounded, respectively, if ${\mathbf{y}}_{i,t}$ is extremely far from μ_{j, t}. Also note that for ν_j → ∞ we see in (19(19) $$\begin{array}{c}\hfill w_{i,j,t}=(1+{\nu }_j^{-1}D)\\ \hfill /\left(1+{\nu }_j^{-1}{({\mathbf{y}}_{i,t}-{\mu }_{j,t})}^{\text{'}}{\Omega }_{j,t}^{-1}({\mathbf{y}}_{i,t}-{\mu }_{j,t})\right).\end{array}$$(19) ) that w_{i, j, t} → 1, such that we recover the expressions for the Gaussian mixture model.

2.4.3 Explanatory Covariates

The score-driven dynamics for component-specific time-varying parameters can be extended further to include contemporaneous or lagged economic variables as additional conditioning variables. For example, a particularly low interest rate environment may push financial institutions, overall or in part, to take more risk or change their asset composition; see, for example, Hannoun (2015), Abbassi et al. (2016), and Heider, Saidi, and Schepens (2017). Using additional yield curve-related conditioning variables allows us to incorporate and test for such effects. Let X_t be a vector of observed covariates, and $B_j=B_j\left(\Theta \right)$ a matrix of unknown coefficients that need to be estimated. In the case of a Student’s t distributed mixture, the score-driven updating scheme then changes slightly to (22) $$\begin{array}{ccc}\hfill {\mu }_{j,t+1}& =& {\mu }_{j,t}+A_1·\frac{{\sum }_{i=1}^N{\tau }_{i,j}^{\left(k\right)}{w}_{i,j,t}({\mathbf{y}}_{i,t}-{\mu }_{j,t})}{{\sum }_{i=1}^N{\tau }_{i,j}^{\left(k\right)}}+B_j·X_t.\hfill \end{array}$$(22) Again, in the case of a Gaussian mixture, w_{i, j, t} = 1. The covariates can also be made firm and cluster component specific, that is, X_{i, j, t}.

2.5 Diagnostics: Stability of Cluster Allocation Over Time

The assumption that component membership is time-invariant implies that pooling information over t = 1, …, T is optimal. This is of substantial help to robustly classify each unit i. Although our sample covers only 32 quarters (8 years), it is clear that switches in component membership become more likely as the sample period grows. In such a case, we have to trade off estimation efficiency against estimation bias.

To check whether component probabilities τ_{i, j} are time-varying, we consider the point-in-time diagnostic statistic (23) $$\begin{array}{ccc}\hfill {\widehat{\tau }}_{ij|t}& =& \frac{{\widehat{\pi }}_j{f}_j\left({\mathbf{y}}_{i,t}\left|\mathbf{Y}{}_{i,t-1};{\theta }_{j,t}\left(\widehat{\Theta }\right)\right.\right)}{{\sum }_{h=1}^J{\widehat{\pi }}_h{f}_h\left({\mathbf{y}}_{i,t}\left|\mathbf{Y}{}_{i,t-1};{\theta }_{h,t}\left(\widehat{\Theta }\right)\right.\right)},\hfill \end{array}$$(23) which can be viewed as the time t posterior probability that firm i belongs to cluster component j, computed using the estimates under the null of time-invariant cluster assignments. A filtered counterpart using information from time 1 to t can be constructed by replacing $f_j({\mathbf{y}}_{i,t}\mid \mathbf{Y}{}_{i,t-1};{\theta }_{j,t}\left(\widehat{\Theta }\right))$ by ${\prod }_{s=1}^t{f}_j({\mathbf{y}}_{i,s}\mid \mathbf{Y}{}_{i,s-1};{\theta }_{j,s}\left(\widehat{\Theta }\right))$. If ${\widehat{\tau }}_{i,j|t}$ is close to 1 or 0 for all t for a specific (i, j), firm i is unlikely to have switched clusters. Otherwise, switches may be a concern. We discuss time series plots of τ_{i, j|t} for diagnostic purposes in our application in Section 4.

3. SIMULATION STUDY

3.1 Simulation Design

This section investigates the ability^{Figure 1} of our score-driven dynamic mixture model to simultaneously (i) correctly classify a dataset into distinct components, and (ii) recover the dynamic cluster means over time. In addition, we investigate the performance of several model selection criteria from the literature in detecting the correct model when the number of clusters is unknown. In all cases, we pay particular attention to the sensitivity of the EM algorithm to the (dis)similarity of the clusters, the number of units per cluster, and the impact of model misspecification.

We simulate from a mixture of dynamic bivariate densities. These densities are composed of sinusoid mean functions and iid disturbance terms that are drawn from a bivariate Gaussian distribution or a bivariate Student’s t distribution with five or three degrees of freedom. The covariance matrices are chosen to be time-invariant identity matrices.

The sample sizes are chosen to resemble typical sample sizes in studies of banking data. We thus keep the number of time points small to moderate, considering T ∈ {10, 30}, and set the number of cross-sectional units equal to N = 100 or to N = 400. The number of clusters used to generate the data is fixed at J = 2 throughout. In our first set of simulation results in Section 3.2, we assume J = 2 is known. In a second set of simulations, we do not assume to know the number of clusters, but determine it using different model selection criteria. To save space in the main text, the description of these criteria has been moved to Web Appendix B, together with the outcomes of these simulations.

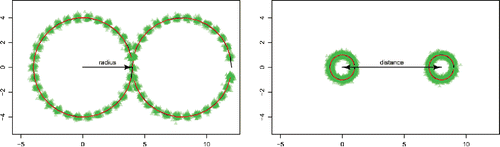
In our baseline setting, visualized in Figure 1, we generate data from two clusters located around means that move in two nonoverlapping circles over time. Across our different simulation designs, the data have different signal-to-noise ratios in the sense that the radius of the circles is large or small relative to the variance of the error terms. In addition, we also consider two more challenging settings where the two circles overlap completely: the circles have the same center, but differ in the orientation of the time-varying mean component (clockwise vs. counterclockwise). Again, we consider circles with a large and small radius, respectively, while keeping the variance of the error terms fixed and thus changing the signal-to-noise ratio in the simulation set-up.

Figure 1. True mean processes (black) together with median filtered means over 100 simulation runs (red) and the filtered means (green triangles). Both panels correspond to simulation setups under correct specification with circle centers that are 8 units apart (distance = 8). The left panel corresponds to the simulation setup with radius 4, while the right panel depicts the mean circles with radius 1.

Finally, we investigate the impact of two types of model misspecification. First, we incorrectly assume a Gaussian mixture in the estimation process when the data are generated by a mixture of Student’s t densities with five degrees of freedom (ν = 5). Alternatively, we simulate from a t(3)-mixture, but fix the degrees of freedom parameter to five in the estimation. In both cases, we check the effect of misspecifying the tail behavior of the mixture distribution. In total, we consider 96 different simulation settings.

3.2 Simulation Results for Classification and Tracking

Using the score-driven model set-up and EM estimation methodology from Section 2, we classify the data points and estimate the component parameters from the simulated data. The static parameters to be estimated include the distinct entries of the covariance matrices, and the diagonal elements of the smoothing matrix A₁, which, for simplicity, we assume to be equal across dimensions and components, that is, A₁ = a₁I_D.

Figure 1 illustrates our simulation setup with two examples. The data-generating processes are plotted as solid black lines. In each panel, the true process is compared to the pointwise median of the estimated paths over simulation runs (solid red line), as well as the filtered mean estimates for each simulation run (green triangles). The actual observations are dispersed much more widely around the black circles, as for each point on the circle they are drawn from the bivariate standard normal distribution, thus ranging from approximately μ_{j, t} − 2.5 to μ_{j, t} + 2.5 with 99% probability. Our methodology allocates each data point to its correct component and in addition tracks the dynamic mean processes accurately.

Table 1 presents mean squared error (MSE) statistics as our main measure of estimation fit. MSE statistics for time-varying component means are computed as the squared deviation of the estimated means from their true counterparts, averaged over time and simulation runs. The top panel of Table 1 contains MSE statistics for eight simulation settings. Each of these settings considers N_j = 100/2 = 50 units per component. The bottom panel of Table 1 presents the same information for N_j = 400/2 = 200 units per component. In each case, we also report the proportion of correctly classified data points, averaged across simulation runs.

Table 1. Simulation outcomes

			T=10			T=30
N	rad.	dist.	MSE	% C1	% C2	MSE	% C1	% C2
			correct specification
100	4	8	0.34	100	100	0.36	100	100
100	4	0	0.34	100	100	0.36	100	100
100	1	8	0.04	100	100	0.04	100	100
100	1	0	0.04	99.18	99.28	0.04	100	99.99
			misspecification 1
100	4	8	0.34	100	100	0.37	100	100
100	4	0	0.35	100	100	0.37	100	100
100	1	8	0.05	100	99.98	0.05	100	100
100	1	0	0.12	89.31	84.67	0.08	96.62	93.8
			misspecification 2
100	4	8	0.42	100	100	0.46	100	100
100	4	0	0.42	100	100	0.46	100	100
100	1	8	0.05	100	100	0.05	100	100
100	1	0	0.07	94.14	93.78	0.05	99.7	99.62
			correct specification
400	4	8	0.32	100	100	0.34	100	100
400	4	0	0.32	100	100	0.34	100	100
400	1	8	0.02	100	100	0.03	100	100
400	1	0	0.04	98.38	98.31	0.03	99.98	99.99
			misspecification 1
400	4	8	0.32	100	100	0.35	100	100
400	4	0	0.32	100	100	0.35	100	100
400	1	8	0.03	100	100	0.03	100	100
400	1	0	0.06	94.16	91.68	0.03	99.71	99.61
			misspecification 2
400	4	8	0.41	100	100	0.44	100	100
400	4	0	0.41	100	100	0.44	100	100
400	1	8	0.03	100	100	0.04	100	100
400	1	0	0.05	95.03	95.18	0.06	97.74	97.78

NOTES: Mean squared error (MSE) and average percentage of correct classification for each cluster (% C1 and % C2) across simulation runs. Considered sample sizes are N = 100, 400 and T = 10, 30. Radius (rad.) refers to the radius of the true mean circles and is a measure of the signal-to-noise ratio. Distance (dist.) is the distance between circle centers and measures the distinctness of clusters. Correct specification refers to the case of simulating from a normal mixture and estimating assuming a mixture of normal distributions. In the case of misspecification 1, data are simulated from a t-mixture with 5 degrees of freedom, but the model is estimated assuming normal mixtures. In the case of misspecification 2, a t(3)-mixture is used to simulate the data while in the estimation, a fixed value ν = 5 is assumed.

Not surprisingly, the performance of our estimation methodology depends on the simulation settings. For a high signal-to-noise ratio (i.e., a large circle radius) and a large distance between the unconditional means, the cluster classification is close to perfect, both under correct specification and model misspecification. Interestingly, the distance between circles is irrelevant for estimation fit and classification ability in the case of large radii (signal-to-noise ratios).

As the distance between means and the circle radii decrease, the shares of correct classifications decrease as well. Both estimation fit and share of correct classification decrease further if we assume a Gaussian mixture although the data are generated from a mixture of fat-tailed Student’s t distributions. This indicates a sensitivity to outliers when assuming a Gaussian mixture in the case of fat-tailed data. Incorrectly assuming five degrees of freedom when the data are generated by a t(3)-mixture, on the other hand, leads to little bias. Consequently, a misspecified t-mixture model allows us to obtain more robust estimation and classification results than a Gaussian mixture model when the data are fat-tailed. This is because also the t(5) based score-dynamics for μ_{j, t} already discount the impact of outlying observations, although not as strictly as the score-based dynamics of a Student’s t(3) distribution.

In our empirical study of banking data, the number of clusters, that is, bank business models, is unknown a priori. A number of model selection criteria and so-called cluster validation indices have been proposed in the literature, and comparative studies have not found a dominant criterion that performs best in all settings; see, for example, Milligan and Cooper (1985) and de Amorim and Hennig (2015). We therefore run an additional simulation study to see which model selection criteria are suitable to choose the optimal number of components in our multivariate panel setting. We refer to Web Appendix B for the results. The Davies–Bouldin index (DBI; see Davies and Bouldin (1979)), the Calinski–Harabasz index (CHI; see Calinski and Harabasz 1974), and the average Silhouette index (SI; see de Amorim and Hennig 2015) perform well.

4. BANK BUSINESS MODELS

4.1 Data

The sample under study consists of N = 208 European banks, for which we consider quarterly bank-level accounting data from SNL Financial between 2008Q1–2015Q4. This implies T = 32. We assume that differences in banks’ business models can be characterized along six dimensions: size, complexity, activities, geographical reach, funding strategies, and ownership structure. We select a parsimonious set of D = 13 indicators from these six categories. We consider banks’ total assets, leverage with respect to CET1 capital (size), net loans to assets ratio, risk mix, assets held for trading, derivatives held for trading (complexity), share of net interest income, share of net fees and commissions income, share of trading income, ratio of retail loans to total loans (activities), ratio of domestic loans to total loans (geography), loans to deposits ratio (funding), and an ownership index (ownership).

We refer to Web Appendix C for a detailed discussion of our data, including data transformations and SNL Financial field keys. Web Appendix C also discusses our treatment of missing observations and banks’ country location.

4.2 Model Selection

This section motivates the model specification employed in our empirical analysis. We first discuss our choice of the number of clusters. We then determine the parametric distribution, pooling restrictions, and choice of covariance matrix dynamics.

Table 2 presents likelihood-based and distance-based information criteria, as well as different cluster validation indices for different values of J = 2, …, 10. The log-likelihood fit increases monotonically with the number of clusters. Likelihood-based information criteria turn out to be sensitive to the specification of the penalty term. They either select the maximum number (AICc, BIC) or minimum number (AICk, BaiNg2) of components; see Web Appendix B for definitions of the different criteria. Distance-based cluster validation indices such as the CHI, DBI, and SI suggest J = 6. Each of these takes a local maxium/minimum at this value. In practice, experts consider between five and up to more than ten different bank business models; see, for example, Ayadi, Arbak, and de Groen (2011) and Bankscope (2014, p. 299). With these considerations in mind, to be conservative and in line with Table 2 and the simulation results as reported in Web Appendix B, we choose J = 6 components for our subsequent empirical analysis.

Table 2. Information criteria

J	loglik	AICc	BIC	AICk	BaiNg2	CHI	DBI	SI
2	1134.4	−1828.8	−393.8	2525.4	−0.218	12.71	3.61	11.0
3	9159.9	−17652.0	−15520.5	2973.5	−0.074	9.00	4.03	1.3
4	13700.4	−26497.4	−23677.2	3243.5	−0.038	8.08	3.79	1.4
5	17055.1	−32963.1	−29462.2	3615.3	0.059	7.42	3.84	1.1
6	19812.8	−38226.5	−34053.3	3990.6	0.157	7.90	3.18	1.9
7	21522.2	−41384.0	−36547.6	4085.8	0.040	7.25	3.27	1.1
8	25142.2	−48353.6	−42863.3	4576.8	0.227	7.57	2.86	1.1
9	27341.3	−52471.3	−46337.1	5035.6	0.386	7.43	2.85	1.8
10	29883.8	−57265.3	−50497.7	5281.3	0.369	6.31	3.23	0.5

NOTES: Likelihood- and distance-based information criteria as well as cluster-validation indices for different values of J = 2, …, 10. The panel refers to a model specification with time-varying component means μ_{j, t}, time-invariant Ω_j, and ν estimated as a free parameter. Each statistic is the maximum (respectively minimum) obtained from 5,000 random starting values for the model parameters. We refer to Web Appendix B for exact formulas and literature references for all reported selection criteria. The average Silhouette index (SI) is multiplied by 100. The top three suggested values are printed in bold.

Table 3 motivates our additional empirical choices. We estimate a range of models with varying degrees of flexibility: normal versus Student’s t, static versus dynamic covariance matrices, and a scalar versus a diagonal A₁. We observe two large likelihood improvements. First, allowing for fat-tailed rather than Gaussian mixtures increases the likelihood by more than 3400 points for the static covariance case, and more than 7800 points for dynamic covariance matrices. Second, allowing covariance matrices to be dynamic increases the likelihood more than 4100 points for Gaussian mixtures, and more than 9500 points for the Student’s t case. Allowing A₁ to be diagonal only results in a minor likelihood increase, and the diagonal elements are all quite similar. We therefore adopt a Student’s t model with scalar A₁, estimated degrees of freedom ν, and dynamic covariance matrices Ω_{j, t} as our main empirical specification. The autoregressive matrices are given by A₁ = a₁ · I_D, and A₂ = a₂ · I_D. Unknown parameters to be estimated in the M-step are therefore Θ = (a₁, a₂, ν)′. Using this parameter specification, we combine model parsimony with the ability to study a high-dimensional array of data.

Table 3. Model specification

Density	ν	Value	A1	Ωj; Ωj, t	loglik	Δloglik
N	—	∞	scalar	static	17,131.4
t	fixed	≡ 5	scalar	static	20,485.3	3,353.9
t	fixed	≡ 5	vector	static	20,499.6	14.3
t	est	6.6	scalar	static	20,617.1	117.5
t	est	6.6	vector	static	20,631.2	14.1
N	—	∞	scalar	dynamic	21,305.9	674.7
t	fixed	≡ 10	scalar	dynamic	28,606.0	7,300.1
t	est	5.7	scalar	dynamic	29,190.3	584.3

NOTES: Log-likelihoods and differences in log-likelihoods for different model specifications. The estimates are conditional on the same (optimal) allocation of banks to J = 6 components; cluster validation indices are not presented for this reason.

Web Appendix D presents the estimated diagnostic^{Figure 2}statistics as defined in Section 2.5. Specifically, we report all time t posterior probabilities that unit i belongs to cluster component j for all 208 banks in our sample. In addition, we present histograms of the maximum average point-in-time and filtered component probabilities. The plots indicate that there is one most suitable business model for almost all banks in our data.

Web Appendix E compares our cluster allocation outcomes with a 2016 supervisory ECB/SSM bank survey (“thematic review”) that asked a subset of banks in our sample which other banks they consider to follow a similar business model. We find that our classification outcomes for these banks approximately, but not perfectly, correspond to bank managements’ own views.

Web Appendix F studies to which extent the clustering outcomes change by leaving out variables d = 1, …, D one-at-a-time and then reestimating the model. All variables turn out to be important in the sense that they have a substantial influence on the clustering outcome. In addition, the clustering outcomes are not dominated by a single variable, such as for instance total assets.

4.3 Discussion of Bank Business Models

This section studies the different business models implied by the J = 6 different component densities. Specifically, we assign labels to the identified components to guide intuition and for ease of reference. These labels are chosen in line with Figure 2, Figure G1 in Web Appendix G, and the identities of the firms in each component. In addition, our labeling is approximately in line with the examples listed in SSM (2016, p. 10).

Figure 2. Time-varying component medians. Filtered component medians for 12 indicator variables; see Table C.1. The component medians coincide with the component means unless the variable is transformed; see the last column of Table C.1 in Web Appendix C. The ownership variable is omitted since it is time-invariant. The component mean estimates are based on a Student's t mixture model with J = 6 components and time-varying component means μ_{j, t} and covariance matrices Ω_{j, t}. We distinguish large universal banks, including G-SIBs (black line), international diversified lenders (red line), fee-focused lenders (blue line), domestic diversified lenders (green dashed line), domestic retail lenders (purple dashed line), and small international banks (light-green dashed line).

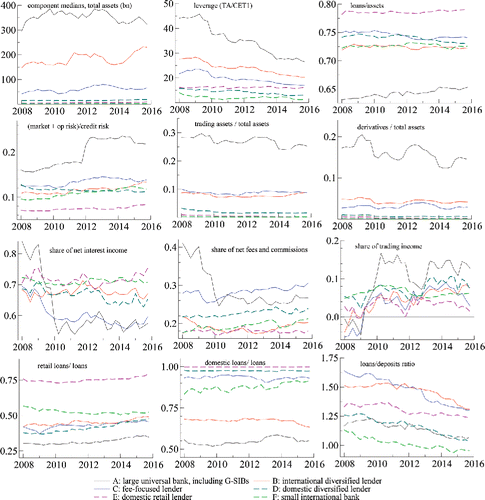
Figure 2 plots the component median estimates for each indicator variable and business model component (except ownership, which is time-invariant). Web Appendix G presents additional figures, such as boxplots of the time series averages of each variable for each business model group. In addition, Web Appendix G presents the filtered component-specific time-varying standard deviations $\sqrt{{\Omega }_{j,t}(d,d)}$ for variables d = 1, …, D − 1. The standard deviations tend to decrease over time starting from the high dispersion observed during the financial crisis (2008–2009). The standard deviation estimates also differ across business models.

We distinguish

(A)	Large universal banks, including G-SIBs (14.9% of firms; comprising, for example, Barclays plc, Credit Agricole SA, Deutsche Bank AG.)
(B)	International diversified lenders (11.1% of firms; for example, ABN Amro NV, BBVA SA, Confederation Nationale du Credit Mutuel SA.)
(C)	Fee-focused bank (15.9% of firms; for example, Monte Dei Paschi di Sienna, Banco Populare, Bankinter SA.)
(D)	Domestic diversified lenders (26.9 % of firms; for example, Aareal Bank AG, Abanca Corporacion Bancaria SA, Alpha Bank SA.)
(E)	Domestic retail lenders (17.8% of firms; for example, Alandsbanken Abp, Berner Kantonalbank, Newcastle Building Society.)
(F)	Small international banks (13.5% of firms; for example, Alpha Bank Skopje, AS Citadele Banka, AS SEB Pank.)

Large universal banks, including G-SIBs (black line) stand out as the largest institutions, with up to € 2 trn in total assets per firm for globally significantly important banks. Approximately 60% of operating revenue tends to come from interest-bearing assets such as loans and securities holdings. This leaves net fees and commissions as well as trading income as significant other sources. Large universal banks are the most leveraged at any time between 2008Q1–2015Q4, even though leverage, that is, total assets to CET1 capital, decrease by more than a third from pre-crisis levels, from approximately 45 to below 30; see Figure 2. Large universal banks hold significant trading and derivative books, both in absolute terms and relative to total assets. Naturally, such large banks engage in significant cross-border activities, including lending (between 40% and 50% of loans are cross-border loans).

International diversified lenders (red line) are second in terms of firm size, with total assets ranging between approximately € 100–500 bn per firm. As the label suggests, such banks lend significantly across borders and to both retail and corporate clients. The share of nondomestic loans to total loans is approximately 30%, and the share of retail loans ranges between approximately 20%–60%. International diversified lenders also serve their corporate customers by trading securities and derivatives on their behalf, resulting in significant trading and derivatives books. In addition, such banks tend to be non-deposit funded, as indicated by a high loans-to-deposits ratio between 100 and 200%.

Fee-focused banks (blue line) achieve most of their income from net fees and commissions (approximately 30%). This group contains banks that focus on fee-based commercial banking activities, such as transaction banking services, trade finance, credit lines, advisory services, and guarantees. In addition, however, this component appears to contain “weak” banks which do not generate much income in their traditional lines of business. The component mean for net interest income is low, raising the share of net fees and commissions. Fee-focused banks tend to exhibit a relatively high loans-to-assets ratio of approximately 70%, and also tend to focus on domestic loans (approximately 80%). Median total assets are typically below 100 bn per firm.

Domestic diversified lenders (green dashed line) are relatively numerous, comprising approximately 27% of firms, and are of moderate size. Total assets are typically below € 50 bn per firm. Domestic diversified lenders tend to be well capitalized, as implied by relatively low leverage ratios (of typically less than 20). Trading and derivatives books are small. Lending is split approximately evenly between corporate and retail clients. Nondomestic loans are typically below 20%.

Finally, domestic retail lenders and small international banks are the smallest firms, with typically less than € 25 bn in total assets. Domestic retail lenders and small international banks have much in common. Both types of banks display low leverage, suggesting they are well capitalized. The relatively largest part of their risk is credit risk (risk mix). Neither group holds significant amounts of securities or derivatives in trading portfolios. Approximately two-thirds of their income comes from interest-bearing assets, making it the dominant source of income.

Domestic retail lenders differ from small international^{Table 4, Table 5} banks in two ways: asset composition and geographical focus. Domestic retail lenders focus almost exclusively on loans (as indicated by a high loans-to-assets ratio) and domestic retail clients. By contrast, small international banks own substantial nonloan assets, and also serve nondomestic and nonretail (corporate) clients. The loans-to-deposits ratio is low for small international banks, at approximately one.

Figure 2 can also be used to discuss bank heterogeneity during the great financial crisis between 2008–2010 and the euro area sovereign debt crisis between 2010–2012, as well as overall banking sector trends during our sample. We refer the interested reader to Web Appendix H.

5. BANK BUSINESS MODELS AND THE YIELD CURVE

This section studies the extent to which banks adapt their business models to changes in the yield curve. We first review European interest rate developments before discussing parameter estimates.

5.1 Low Interest Rates

Figure 3 plots fitted zero-coupon yield curves for maturities between one and twenty years at different times during our sample (left panel). European government bond yields experienced a pronounced downward shift during our sample, ultimately reaching ultra-low and in part negative values. The yield curve factors underlying the yield curve estimates are based on a Svensson (1995) four-factor model and are extracted daily from market prices of AAA-rated sovereign bonds issued by euro area governments. The yield curve factor estimates can be obtained from the ECB’s website.

Figure 3. Yield curve and factor plots. All yield curve and factor plots refer to AAA-rated euro area government bonds, and are based on a Svensson (1995) four-factor model. Yield factor estimates are taken from the ECB. The left panel plots fitted Svensson yield curves on four dates—mid-2008Q1, mid-2010Q1, mid-2015Q1, and mid-2015Q4, for maturities between one and 20 years, and based on all yield curve factors. The right panel plots the level factor estimate, along with the model-implied short rate (given by the sum of the level and slope factor).

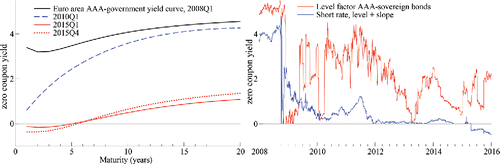
Figure 3 also plots the level factor, along with the implied short rate (right panel). The slope factor fluctuates around a value of approximately −2 in our sample and is not reported. Long-term yields increase up to approximately 4% between 2009–2011 following an initial sharp drop during the global financial crisis. Between 2013–2015, nominal yields decline to historically low levels. In 2015, European 10-year rates are often below 1%. Short-term rates become negative in 2015 following a cut of the ECB’s deposit facility rate to negative values. Low nominal interest rates do not necessarily only reflect unconventional monetary policies, including the ECB’s Public Sector Purchase Programme (PSPP; or “Quantitative Easing”). Decreasing inflation rates, inflation risk premia, demographic factors, and an imbalance between global saving and investment likely also play a role; see, for example, Draghi (2016).

5.2 Fixed Effects Panel Regression Results

Table 4 presents fixed effects panel regression estimates of bank-level accounting variables Δ₄y_{i, t}(d), d = 1, …, 12, on a constant and contemporaneous as well as one-year lagged changes in two yield curve factors, level and slope. We consider four-quarter differences since most banks report at an annual frequency. Table 4 pools bank data across business model components. Table 5 reports the regression coefficients for the one-year changes in the yield curve level, pooled as well as disaggregated across business model clusters. Web Appendix I reports all estimates for each variable and business model group.

Table 4. Factor sensitivity estimates

	Δ4$ln$(TAt)	Δ4$ln$(Levt)	Δ4(TL/TA)t	Δ4$ln$(RMt)	Δ4(AHFT/TA)t	Δ4(DHFT/TA)t
Δ4 levelt	−0.0508^*^*^*	−0.0260^*^*	1.824^*^*^*	0.00586	−0.00688^*^*	−0.0111^*^*^*
	(0.0118)	(0.0116)	(0.292)	(0.0125)	(0.00327)	(0.00354)
Δ4 slopet	−0.0514^*^*^*	−0.0267^*^*	1.470^*^*^*	−0.00336	−0.00489	−0.0105^*^*^*
	(0.0123)	(0.0112)	(0.303)	(0.0141)	(0.00304)	(0.00339)
Δ4 levelt − 4	−0.0169^*^*^*	0.00685	0.213^*^*	−0.00465	0.000441	0.00237
	(0.00422)	(0.00490)	(0.0984)	(0.00527)	(0.00133)	(0.00159)
Δ4 slopet − 4	−0.0346^*^*^*	−0.00777	0.118	−0.00742	−0.000742	−0.000591
	(0.00540)	(0.00567)	(0.143)	(0.00645)	(0.00153)	(0.00179)
constant	0.0104^*	−0.0425^*^*^*	0.236	0.0201^*^*^*	−0.00238^*	−0.00107
	(0.00578)	(0.00344)	(0.138)	(0.00541)	(0.00127)	(0.00140)
Observations	3,064	2,640	2,902	2,179	2,285	2,286
Number of groups	208	206	208	203	208	208
Bank FE	YES	YES	YES	YES	YES	YES
Within R^2	0.0508	0.00758	0.0251	0.00218	0.0207	0.0656
	Δ4(NII/OR)t	Δ4(NFC/OI)t	Δ4(TI/OI)t	Δ4(RL/TL)t	Δ4(DL/TL)t	Δ4(L/D)t
Δ4 levelt	1.931	0.371	−0.0509	0.00562^*^*^*	1.225^*^*^*	−0.230
	(2.040)	(0.664)	(1.871)	(0.00194)	(0.291)	(0.498)
Δ4 slopet	2.712	1.606^*^*	1.041	0.00615^*^*^*	1.182^*^*^*	−1.047
	(1.868)	(0.740)	(1.610)	(0.00174)	(0.395)	(0.700)
Δ4 levelt − 4	−1.160^*^*	−1.293^*^*^*	0.686	−0.00210^*^*^*	−0.200	0.277
	(0.536)	(0.414)	(0.433)	(0.000714)	(0.196)	(0.279)
Δ4 slopet − 4	−2.191^*^*^*	−1.335^*^*	1.243^*^*	0.000269	−0.111	0.0282
	(0.631)	(0.572)	(0.509)	(0.00102)	(0.189)	(0.349)
constant	0.118	−0.0291	−0.0375	0.00728^*^*^*	0.362	−1.973^*^*^*
	(0.839)	(0.313)	(0.711)	(0.00117)	(0.212)	(0.362)
Observations	2,836	2,827	2,737	1,895	1,498	2,417
Number of groups	208	208	208	181	172	207
Bank FE	YES	YES	YES	YES	YES	YES
Within R^2	0.00287	0.00391	0.00745	0.00578	0.00633	0.00426

NOTES: Fixed effects panel regression estimates for annual changes in bank-level accounting data Δ₄y_it(d), d = 1, …, 12, on a constant and contemporaneous and one-year lagged annual changes in yield curve factors level and slope. Specifically, ${\Delta }_4{y}_{it}\left(d\right)=b_1{\Delta }_4{\text{level}}_t+b_2{\Delta }_4{\text{slope}}_t+b_3{\Delta }_4{\text{level}}_{t-4}+b_4{\Delta }_4{\text{slope}}_{t-4}+\text{constant}+\text{fixed}{\text{effects}}_i+{ϵ}_{it}$. Dependent variables are as listed in Table C.1 of the Web Appendix. Standard errors are Driscoll–Kraay standard errors with three lags; stars denote significance at a 10%, 5%, and 1% level.

Table 5. Sensitivities to changes in the term structure level (Δ₄l_t)

Dependent variable	All	A	B	C	D	E	F
Δ4 $ln$(TA)t	−0.0508^*^*^*	−0.126^*^*^*	−0.0612^*^*^*	−0.0501^*^*^*	−0.0286^*^*^*	−0.0375	−0.0301
	(0.0118)	(0.0216)	(0.00568)	(0.0150)	(0.00809)	(0.0432)	(0.0253)
Δ4 $ln$(Lev)t	−0.0260^*^*	−0.0678^*	−0.0358	0.0107	0.00223	−0.0745^*^*^*	−0.0474
	(0.0116)	(0.0354)	(0.0235)	(0.0177)	(0.0204)	(0.0255)	(0.0341)
Δ4 (TL/TA)t	1.824^*^*^*	3.391^*^*^*	2.236^*^*^*	2.495^*^*^*	1.204^*^*^*	1.446^*^*	0.0682
	(0.292)	(0.666)	(0.394)	(0.234)	(0.258)	(0.611)	(0.619)
Δ4 $ln$(RM)t	0.00586	−0.0807	−0.101^*^*^*	0.0567	0.0257^*	0.0206	0.0850^*
	(0.0125)	(0.0702)	(0.0254)	(0.0364)	(0.0143)	(0.0304)	(0.0462)
Δ4 (AHFT/TA)t	−0.00688^*^*	−0.0290^*^*	−0.00814^*^*^*	−0.00926^*^*^*	0.00168	0.000203	0.00138^*^*^*
	(0.00327)	(0.0115)	(0.00203)	(0.00310)	(0.00168)	(0.000869)	(0.000416)
Δ4 (DHFT/TA)t	−0.0111^*^*^*	−0.0474^*^*^*	−0.0165^*^*^*	−0.0107^*^*^*	−0.00197	0.00135^*^*	0.000454
	(0.00354)	(0.0135)	(0.00412)	(0.00164)	(0.00138)	(0.000554)	(0.000306)
Δ4 (NII/OR)t	1.931	−6.797	4.614	5.992^*^*	2.985	0.184	−2.010
	(2.040)	(4.742)	(5.120)	(2.195)	(1.753)	(4.745)	(3.212)
Δ4 (NFC/OI)t	0.371	1.447	1.703	0.234	−0.986	0.184	2.591
	(0.664)	(0.954)	(1.767)	(0.728)	(0.987)	(1.631)	(2.216)
Δ4 (TI/OI)t	−0.0509	12.40^*^*^*	0.623	−1.792	−1.755	−4.171	1.448
	(1.871)	(4.188)	(2.611)	(2.585)	(1.725)	(3.010)	(1.518)
Δ4 (RL/TL)t	0.00562^*^*^*	0.00129	0.00252	0.0108^*^*^*	0.00141	0.0113^*^*^*	−0.00195
	(0.00194)	(0.00316)	(0.00480)	(0.00351)	(0.00373)	(0.00398)	(0.00828)
Δ4 (DL/TL)t	1.225^*^*^*	1.158^*	3.736^*^*^*	1.418^*^*^*	0.384	0.0161	2.581^*
	(0.291)	(0.563)	(1.009)	(0.374)	(0.447)	(0.205)	(1.466)
Δ4 (L/D)t	−0.230	−1.754	−3.275^*	2.924	−1.534	0.347	0.620
	(0.498)	(1.837)	(1.705)	(2.080)	(1.510)	(1.642)	(1.462)

NOTES: Yield level factor sensitivities for bank-level accounting data, controlling for changes in the slope factor and lagged changes in the yield curve. Factor sensitivity parameters are reported as pooled across all business models (Column 2: All) as well as disaggregated across business model components A–F (Columns 3–8). Estimates are obtained by fixed effects panel regression. Standard errors are Driscoll–Kraay standard errors with three lags.

We discuss five findings. First, as long-term interest rates decrease, banks on average grow larger in terms of total assets, by approximately 5% in response to a 100 bps drop in the level factor. The coefficient estimates for short-term rates and lagged changes in yields are negative as well. This finding is in line with banks’ incentive to extend the balance sheet to offset squeezed net interest margins for new loans and investments. In addition, and trivially, some bank assets are worth more at lower rates.

Second, bank leverage is predicted to increase as yields decline. This correlation needs to be interpreted with caution. Leverage declined most strongly between 2010 and 2012, when euro area yields were increasing owing to the sovereign debt crisis. In addition, leverage is influenced by changes in financial regulation which we do not control for.

Third, the composition of bank assets is sensitive to changes in the yield curve factors. The loans-to-assets ratio decreases by approximately 2% on average across business models in response to a 100 bps drop in long-term rates. By contrast, the sizes of banks’ trading and derivative books increase to some extent. This change in balance sheet composition is driven mostly by the larger banks (components A to C; Table 5), and could reflect a decreased demand for new loans from the private sector in an environment of strongly declining rates; see Abbassi et al. (2016). In this environment, large banks may invest in tradable securities such as government bonds instead of expanding their respective loan books; see Acharya and Steffen (2015).

Fourth, we observe little variation in the shares of income sources in response to falling yields. In particular, the share of net interest income is not significantly (at 5%) associated with contemporaneous changes in yields. Two opposing effects could be at work. On the one hand, banks funding cost also decrease, and may even do so at a faster rate than long-duration loan rates. In addition, banks’ long-term loans and bond holdings are worth more at lower rates, leading to mark-to-market gains. On the other hand, low long-term interest rates squeeze net interest margins for newly acquired loans and bonds. The former effects could approximately balance the latter in our sample.

Finally, some banks appear to decrease their deposits-to-loans ratio in response to falling short-term rates. We refer to Web Appendix I, Table I.4, for the respective coefficient estimates. As the slope factor declines by 100 bps, banks in components A, B, and D decrease their deposits-to-loans ratio by approximately 2–5%.

Changes in term structure factors can also be added to the econometric specification as discussed in Section 2.4.3. Given the limited number of T = 32 time series observations, however, we need to pool the coefficients B_j across mixture components B_j ≡ B to reduce the number of parameters. Web Appendix J discusses the parameter estimates. The increased log-likelihood values suggest a slightly better fit than the baseline specification. Coefficients in B are, however, rarely statistically significant according to their t-values.

We conclude that bank business model characteristics appear to adjust to changes in the yield curve. Given their direction for falling rates—increased size, increased leverage, increased complexity through larger trading and derivatives books, and possibly less stable funding sources—the effects are potentially problematic and need to be assessed from a financial stability perspective.

6. CONCLUSION

We proposed a novel score-driven finite mixture model for the study of banking data, accommodating time-varying component means and covariance matrices, normal and Student’s t distributed mixtures, and term structure factors as economic determinants of time-varying parameters. In an empirical study of European banks, we classified more than 200 financial institutions into six distinct business model components. Our results suggest that the global financial crisis and the euro area sovereign debt crisis had a substantial yet different impact on banks with different business models. In addition, banks’ business models adapt over time to changes in long-term interest rates.

SUPPLEMENTARY MATERIALS

The Web appendix provides further technical and empirical results.

ACKNOWLEDGMENTS

Lucas and Schaumburg thank the European Union Seventh Framework Programme (FP7-SSH/2007–2013, grant agreement 320270-SYRTO) for financial support. Schaumburg also thanks the Dutch Science Foundation (NWO, grant VENI451-15-022) for financial support. Parts of this article were written while Schwaab was on secondment to the ECB’s Single Supervisory Mechanism (SSM). We are particularly grateful to Klaus Düllmann, Heinrich Kick, and Federico Pierobon from the SSM. We also thank the three Referees and the Editor whose many insightful suggestions have helped us to reshape and improve the article.

The views expressed in this article are those of the authors, and they do not necessarily reflect the views or policies of the European Central Bank.

Notes

1 For example, the assessment of the viability and the sustainability of a bank’s business model plays a pronounced role in the European Central Bank’s new Supervisory Review and Examination Process (SREP) for Significant Institutions within its Single Supervisory Mechanism; see SSM (2016). Similar procedures exist in other jurisdictions.

2 An improved understanding of the financial stability consequences of low-for-long interest rates is a top policy priority. For example, Fed Chair Yellen (2014) pointed to “... the potential for low interest rates to heighten the incentives of financial market participants to reach for yield and take on risk, and... the limits of macroprudential measures to address these and other financial stability concerns.” Similarly, ECB President Draghi (2016) explained that “One particular challenge has arisen across a large part of the world. That is the extremely low level of nominal interest rates.... Very low levels are not innocuous. They put pressure on the business model[s] of financial institutions... by squeezing net interest income. And this comes at a time when profitability is already weak, when the sector has to adjust to post-crisis deleveraging in the economy, and when rapid changes are taking place in regulation.”

3 We use the terms “component,” “mixture component,” and “cluster” interchangeably.

4 As pointed out by a referee, newer and faster versions of the EM algorithm are available, such as the ECM algorithm of Meng and Rubin (1993) and the ECME algorithm of Liu and Rubin (1994). All of these converge to the same optimum. Computation time for the EM was not a major issue in our setting, with the algorithm typically converging in 15 iterations. We therefore leave such extensions for future work.