Poorly Measured Confounders are More Useful on the Left than on the Right

ABSTRACT

Researchers frequently test identifying assumptions in regression-based research designs (which include instrumental variables or difference-in-differences models) by adding additional control variables on the right-hand side of the regression. If such additions do not affect the coefficient of interest (much), a study is presumed to be reliable. We caution that such invariance may result from the fact that the observed variables used in such robustness checks are often poor measures of the potential underlying confounders. In this case, a more powerful test of the identifying assumption is to put the variable on the left-hand side of the candidate regression. We provide derivations for the estimators and test statistics involved, as well as power calculations, which can help applied researchers interpret their findings. We illustrate these results in the context of estimating the returns to schooling.

KEY WORDS:

• Balancing
• Hausman test
• Robustness checks
• Specification testing
• Variable addition.

MATHEMATICS SUBJECT CLASSFICATION:

• C31
• C52

1. INTRODUCTION

The identification of causal effects depends on explicit or implicit assumptions, which typically form the core of a debate about the quality and credibility of a particular research design. In regression-based strategies, this is the claim that variation in the regressor of interest is as good as random after conditioning on a sufficient set of control variables. In instrumental variables models, it involves the assumption that the instrument is as good as randomly assigned. In panel or differences-in-differences designs, it is the parallel trends assumption. The credibility of a design can be enhanced when researchers can show explicitly that these assumptions are supported by the data. This is often done through some form of balancing tests or robustness checks.

The research designs mentioned above are all variants of regression strategies. If the researcher has access to a variable for a potentially remaining confounder, tests of the identifying assumption take two canonical forms. The variable can be added as a control on the right-hand side (RHS) of the regression. The identifying assumption is confirmed if the estimated effect of interest is insensitive to this variable addition—we call this the coefficient comparison test. Alternatively, the variable can be placed on the left-hand side (LHS) of the regression instead of the outcome variable. A zero coefficient on the causal variable of interest then confirms the identifying assumption. This is the balancing test, which is typically carried out using baseline characteristics or pretreatment outcomes in a randomized trial or in a regression discontinuity design.

Researchers often rely on one or the other of these tests. The main point of our article is to show that the balancing test, using the proxy for the candidate confounder on the LHS of the regression, is generally more powerful. This is particularly the case when the available variable is a noisy measure of the true underlying confounder. The attenuation due to measurement error often implies that adding the candidate variable on the RHS as a regressor does little to eliminate any omitted variables bias. The same measurement error does comparatively less damage when putting this variable on the LHS. Regression strategies work well in finding small but relevant amounts of variation in noisy dependent variables. We collect basic results for the relevant parameters in the presence of measurement error in Section 3.

These two testing strategies are intimately related through the omitted variables bias formula. The omitted variables bias formula shows that the coefficient comparison test involves two regression parameters, the coefficient from the balancing test and the coefficient from the added regressor in the outcome equation. Both of these parameters have to be nonzero for the coefficient comparison test to fail and actual confounding to take place. The balancing test focuses on a single parameter. The two tests, therefore, investigate the same hypothesis under the maintained assumption that the added regressor matters in the outcome equation. The ultimate source of the power loss in the coefficient comparison test comes from estimating a nuisance parameter. This is a standard reason for power differences in the econometrics literature but turns out to be relatively unimportant in the numerical examples we present. The nuisance parameter in the coefficient comparison test is more difficult to estimate when there is more measurement error in the added regressor. In the examples we study in Section 5, measurement error is the source of quantitatively meaningful power differences between the two tests.

A second point we are making is that the two strategies, coefficient comparison and balancing, both lead to explicit statistical tests. The balancing test is a simple t-test used routinely by researchers. When adding a covariate on the RHS, comparing the coefficient of interest across the two regressions can be done using a generalized Hausman test. In practice, we have not seen this test carried out in applied papers, where researchers typically just eye-ball the results (an exception is Gelbach 2016). We provide the relevant test statistics and discuss how they behave under measurement error in Section 4. We demonstrate the superior power of the balancing test under different scenarios in Section 5.

The principles underlying our analysis are well known but the consequences do not seem to be fully appreciated in applied work. McCallum (1972) and Griliches (1977) are classic references for the issues arising when regression controls are measured with error. Battistin and Chesher (2014) discuss identification in the presence of a mismeasured covariate in nonlinear models based on assumptions about the degree of measurement error in the covariate. We follow McCallum (1972) and Griliches (1977) in framing our discussion around the omitted variables bias arising in linear regressions, the general framework used most widely in empirical studies. The insights we exploit build on Pischke and Schwandt (2012) but we go beyond the analysis in all of these papers in our explicit discussion of testing, which forms the core of our inquiry.

Our focus is on specification testing for a particular research design. The statistical model we discuss below—a baseline regression and an augmented regression with additional covariates—bears a close relationship to models in a large literature, which attempts to use control strategies for point or interval identification. One recent strand of this literature is interested in the selection of control variables in a causal regression and inference for the parameter of interest after such an initial variable selection step (Belloni, Chernozhukov, and Hansen, 2014a,b; Chernozhukov et al. 2017; Chernozhukov et al. 2018). A second strand uses the relationship between a treatment variable of interest and observed covariates to model the corresponding relationship with additional unobserved confounders in order to estimate the true causal effect (Altonji, Elder, and Taber 2005; Altonji et al. 2016; Oster forthcoming). Although this literature is focused on identification of the causal parameter, the tools can be used for specification checking as well, so in practice the conceptual difference to our approach may not be quite as sharp. Nevertheless, the parameters of interest are different, and our focus is on statistical inference about the credibility of a given baseline design rather than identification of the causal parameter.

Also, related is an older literature by Hausman (1978), Hausman and Taylor (1980), and Holly (1982) (see also the summary in MacKinnon 1992, sec. II.9), which considers the relative power of the Hausman test compared to alternatives, in particular an F-test for the added covariates in the outcome equation when potentially multiple covariates are added. This comparison effectively maintains that there is a lack of balance, and instead tests whether the added regressors matter for explaining the outcome. While this is a different exercise from ours, this literature highlights the potential power of the Hausman test when it succinctly transforms a test with multiple restrictions (like the F-test for the added covariates) into a test with a single restriction (the coefficient comparison test). We discuss how to extend our framework to multiple added controls in Section 5.3. Our basic findings largely carry over to this setting but we also reach the conclusion that the Hausman test has a role to play when the goal is to summarize a large number of restrictions.

Griliches (1977) used estimates of the returns to schooling as example for the methodological points he makes. Such estimates have formed a staple of labor economics ever since. We use Griliches’ data from the National Longitudinal Survey of Young Men (NLS) to briefly illustrate our power results in Section 6. It is well suited for our purposes because the data contain various test score measures, which can be used as controls in a regression strategy (as in Griliches 1977), as well as a myriad of other useful variables on individual and family background. The empirical results illustrate and support our theoretical claims.

2. A SIMPLE FRAMEWORK

Consider the following simple framework starting with a population regression equation: (1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) where y_i is an outcome like log wages, s_i is the causal variable of interest, like years of schooling, and e^s_i is the regression residual. The researcher proposes this short regression model to be causal, that is, β^s is the parameter of interest. This might be the case because the data come from a randomized experiment, so the simple bivariate regression is all we need. More likely, the researcher has a particular research design applied to observational data. For example, in the case of a regression strategy controlling for confounders, y_i and s_i would be residuals from regressions of the original outcome and treatment variables on the chosen controls. In the case of panel data or differences-in-differences designs, the controls are sets of fixed effects. In the case of instrumental variables, s_i would be the predicted value from a first stage regression. In practice, (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ) encompasses a wide variety of empirical approaches, and should be thought of as a short-hand for these. We have this broader interpretation in mind but for presentational clarity we use the simple bivariate regression throughout the discussion in our article. All subsequent regression equations and results also inherit the structure of the actual underlying research design but we illustrate results in terms of the simple bivariate formulation in (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ). We also suppress constants to avoid clutter.

Now consider the possibility that the population regression parameter β^s from (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ) may not actually capture a causal effect. There may be a candidate confounder x_i, so that the long regression (2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) generates a coefficient β^l that might differ from β^s. To make things concrete, in the returns to schooling context, x_i would be a measure of the remaining part of an individual’s earnings capacity which is also related to schooling, like ability, or family background.

Researchers who find themselves in a situation where they start with a proposed causal model (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ) and a measure for a candidate confounder x_i typically do one of two things: They either regress x_i on s_i and check whether s_i is significant, or they include x_i on the RHS of the original regression as in (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ), and check whether the estimate of β changes materially when x_i is added to the regression of interest. The first strategy constitutes a test for “balance,” a standard check for successful randomization in an experiment. The second strategy is a “coefficient comparison test.” An appreciable difference between β^l and β^s suggests that the original estimate β^s does not have a causal interpretation. Researchers typically interpret passing either of these tests as strengthening the case for a causal interpretation of the parameter β^s. In case the tests reject, the researcher concludes that neither parameter is likely to be causal, and the research design is a flawed one.

It is tempting to conclude that strategy (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) is preferable because the comparison of β^l and β^s does not just carry information about the validity of regression (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ) but also provides a better estimate β^l. It is important to caution against this interpretation. If x_i is an imperfect control or there are multiple omitted variables in (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ), then (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) does not necessarily reduce the omitted variables bias (Frost 1979 or more recently De Luca, Magnus, and Peracchi forthcoming and Kassenboehmer and Schurer 2018). The literatures along the lines of Altonji, Elder, and Taber (2005) and Belloni, Chernozhukov, and Hansen (2014b) all start from the premise that there is a set of regressors x_i so that regression (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) is preferable, at least in principle. Only in the special case, where x_i is the only missing confounder and we measure it without error will the parameter β^l from the controlled regression be the causal effect of interest. In practice, there is usually little reason to believe that these two conditions are met, and hence a difference between β^l and β^s only indicates a poor research design.

The relationship between the two testing strategies is easy to see. Write the regression of x_i on s_i, which we will call the balancing regression, as (3) $$x_i=\delta s_i+u_i.$$(3) The change in the coefficient on s_i after adding x_i to the regression (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ) is given by the omitted variables bias formula (4) $${\beta }^s-{\beta }^l=\gamma \delta .$$(4) This change consists of two components, the coefficient γ on x_i in the outcome Equation (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) and the coefficient δ from the balancing regression.

Here, we consider the relationship between these two approaches: the balancing test, consisting of an investigation of the null hypothesis (5) $$H_0:\delta =0,$$(5) compared to the inspection of the coefficient movement β^s − β^l. The latter strategy of comparing β^s and β^l is often done informally, but it can be formalized as a statistical test of the null hypothesis (6) $$H_0:{\beta }^s-{\beta }^l=0,$$(6) which we will call the coefficient comparison test. From (4(4) $${\beta }^s-{\beta }^l=\gamma \delta .$$(4) ), it is clear that (6(6) $$H_0:{\beta }^s-{\beta }^l=0,$$(6) ) amounts to (7) $$H_0:{\beta }^s-{\beta }^l=0\iff \gamma =0\text{or}\delta =0.$$(7) This highlights that the two approaches formally test the same hypothesis under the maintained assumption γ ≠ 0. We may often have a strong sense that γ ≠ 0; that is, we are dealing with a variable x_i which we believe affects the outcome, but we are unsure whether it is related to the regressor of interest s_i. In this case, both tests would seem equally suitable. Nevertheless, in other cases γ may be zero, or we may be unsure. In this case, the coefficient comparison test seems to dominate because it directly addresses the question we are after, namely, whether the coefficient of interest β is affected by the inclusion of x_i in the regression.

Be this as it may, our main point is a practical one, that the coefficient comparison test suffers particularly when a true confounder (γ ≠ 0) is measured with error. In general, confounders like x_i may not be easy to measure. If the available measure for x_i contains classical measurement error, the estimator of γ in (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) will be attenuated, and the comparison β^s − β^l will be too small (in absolute value) as a result. The estimator of δ from the balancing regression is still consistent in the presence of classical measurement error; this regression simply loses precision because the mismeasured variable is on the LHS. The measurement error drives a wedge between the asymptotic values of the two test statistics and the balancing test becomes relatively more powerful than the coefficient comparison test. In order to make these statements precise, we start by reviewing results for the relevant population parameters in the case of classical measurement error in the following section, before moving on to inference, power calculations, and simulations.

3. POPULATION PARAMETERS IN THE PRESENCE OF MEASUREMENT ERROR

The candidate variable x_i is not observed. Instead, the researcher works with the mismeasured variable (8) $$x_i^m=x_i+m_i.$$(8) We start by assuming the measurement error m_i is classical, that is, E(m_i) = 0, $\text{cov}(x_i,m_i)=0$, $\text{cov}(s_i,m_i)=0$. In Section 5, we also investigate the impact of mean-reverting measurement error. As a result of the measurement error, the researcher compares the regressions (9) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^s{s}_i+e_i^s\hfill \\ \hfill y_i& =& {\beta }^m{s}_i+{\gamma }^m{x}_i^m+e_i^m.\hfill \end{array}$$(9)

Notice that the short regression does not involve the mismeasured x_i, so that β^s = β^l + γδ as before. However, the population regression coefficients β^m and γ^m are now different from β^l and γ from Equation (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) (10) $$\begin{array}{ccc}\hfill {\beta }^m& =& {\beta }^l+\gamma \delta \theta \hfill \\ \hfill {\gamma }^m& =& \gamma (1-\theta ).\hfill \end{array}$$(10) The amount of measurement error is captured by the parameter θ $$\theta =\frac{{\sigma }_m^2}{{\sigma }_u^2+{\sigma }_m^2},$$where σ²_• denotes the variance of the random variable in the subscript (McCallum 1972; Garber and Klepper 1980). 1 − θ is the multivariate attenuation factor, which takes the role of the familiar attenuation factor λ = σ²_x/(σ_x² + σ²_m) in a bivariate regression. Recall that u_i is the residual from the balancing regression (3(3) $$x_i=\delta s_i+u_i.$$(3) ). Notice that θ involves only the variation in x^m_i which is orthogonal to s_i. This is the part of the variation in x^m_i relevant to the estimate of γ^m in regression (9(9) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^s{s}_i+e_i^s\hfill \\ \hfill y_i& =& {\beta }^m{s}_i+{\gamma }^m{x}_i^m+e_i^m.\hfill \end{array}$$(9) ), which also has s_i as a regressor. Approaches along the lines of Battistin and Chesher (2014), Altonji, Elder, and Taber (2005), and Oster (forthcoming), which effectively treat Equation (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ) as structural, require assumptions on θ or a function of it for point identification.

The population coefficient β^m differs from β^l but less so than β^s. In fact, with classical measurement error β^m lies between β^s and β^l, as can be seen from (10(10) $$\begin{array}{ccc}\hfill {\beta }^m& =& {\beta }^l+\gamma \delta \theta \hfill \\ \hfill {\gamma }^m& =& \gamma (1-\theta ).\hfill \end{array}$$(10) ). The parameter γ^m is attenuated compared to γ; the attenuation is bigger than in the case of a bivariate regression of y_i on x^m_i without the regressor s_i if x^m_i and s_i are correlated because σ²_u < σ_x².

These results highlight a number of issues. The gap β^s − β^m is too small compared to the desired β^s − β^l, directly affecting the coefficient comparison test. This is a consequence of the fact that γ^m is biased toward zero. Ceteris paribus, this is making the assessment of the hypothesis γ = 0 more difficult, which in turn affects the inference for β^s = β^l.

Finally, with the mismeasured x^m_i, the balancing regression becomes (11) $$\begin{array}{ccc}\hfill x_i^m& =& {\delta }^m{s}_i+u_i^m\hfill \\ & =& \delta s_i+u_i+m_i.\hfill \end{array}$$(11) This regression involves measurement error in the dependent variable, which has no effect on the population parameter δ^m = δ. Because the variance of the residual in (11(11) $$\begin{array}{ccc}\hfill x_i^m& =& {\delta }^m{s}_i+u_i^m\hfill \\ & =& \delta s_i+u_i+m_i.\hfill \end{array}$$(11) ) is larger than in (3(3) $$x_i=\delta s_i+u_i.$$(3) ), the estimator ${\widehat{\delta }}^m$ is less efficient than $\widehat{\delta }$ in the case with no measurement error.

4. INFERENCE

In this section, we consider how conventional standard errors and test statistics for the quantities of interest are affected in the homoscedastic case (see online Appendix A for details on the setup, derivations, and an extension to robust standard errors). The primitive disturbances are s_i, u_i, e_i, and m_i, which we assume to be uncorrelated with each other. Other variables are determined by (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ), (3(3) $$x_i=\delta s_i+u_i.$$(3) ), and (8(8) $$x_i^m=x_i+m_i.$$(8) ). We use these results to analyze the power of the two alternative tests in the next section. Starting with theoretical results for the baseline homoscedastic case, we extend these results in simulations. Our basic conclusions are the same in all these different scenarios.

Start with the estimator ${\widehat{\delta }}^m$ and its associated t-statistic. ${\widehat{\delta }}^m$ is still a consistent estimator for δ but its standard error is inflated compared to the case with no measurement error. Denoting the estimated standard error of a given estimator by $\widehat{\mathrm{se}}(•)$, a test based on the t-statistic $t_{{\delta }^m}={\widehat{\delta }}^m/\widehat{\mathrm{se}}\left({\widehat{\delta }}^m\right)$ remains consistent because m_i is correctly accounted for in the residual of the balancing regression (11(11) $$\begin{array}{ccc}\hfill x_i^m& =& {\delta }^m{s}_i+u_i^m\hfill \\ & =& \delta s_i+u_i+m_i.\hfill \end{array}$$(11) ). However, the t-statistic is asymptotically smaller in absolute value than in the error-free case. As n → ∞, the scaled t-statistic is $$\mathrm{plim}\left(\frac{1}{\sqrt{n}}{t}_{{\delta }^m}\right)=\sqrt{1-\theta }\frac{\delta }{\left(\frac{{\sigma }_u}{{\sigma }_s}\right)}.$$This means the null hypothesis (5(5) $$H_0:\delta =0,$$(5) ) is rejected less often. The test is less powerful than in the error-free case (θ = 0); the power loss is captured by the term $\sqrt{1-\theta }$.

We next turn to ${\widehat{\gamma }}^m$, the estimator for the coefficient on the mismeasured x^m_i in (9(9) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^s{s}_i+e_i^s\hfill \\ \hfill y_i& =& {\beta }^m{s}_i+{\gamma }^m{x}_i^m+e_i^m.\hfill \end{array}$$(9) ). The parameter γ is of interest since it determines the coefficient movement β^s − β^l = γδ in conjunction with the result from the balancing regression. For ease of exposition, we impose conditional homoscedasticity of e^m_i given s_i and x^m_i here and leave the more general case to the online Appendix A.3.2. Denote the asymptotic standard error by se(•), that is, $\mathrm{se}(•)\equiv \frac{1}{\sqrt{n}}\text{plim}\left\{\sqrt{n}\widehat{\mathrm{se}}(•)\right\}$. The asymptotic standard error for ${\widehat{\gamma }}^m$ is $$se\left({\widehat{\gamma }}^m\right)=\frac{\sqrt{1-\theta }}{\sqrt{n}}\sqrt{\theta {\gamma }^2+\frac{{\sigma }_e^2}{{\sigma }_u^2}}.$$Measurement error enters the standard error in two ways: the first is an attenuation factor compared to the standard error for a correctly measured x_i, while the second is an additive effect that depends on the value of γ. The parameters in the two terms are not directly related, so $\mathrm{se}\left({\widehat{\gamma }}^m\right)\gtrless \mathrm{se}\left(\widehat{\gamma }\right)$. Measurement error does not necessarily inflate the standard error here.

The two terms have a simple, intuitive interpretation. Measurement error attenuates the parameter γ^m toward zero, the attenuation factor is 1 − θ. The standard error is attenuated in the same direction; this is reflected in the $\sqrt{1-\theta }$ factor, which multiplies the remainder of the standard error calculation. The second influence from measurement error comes from the term θγ², which results from the fact that the residual variance $\text{var}\left(e_i^m\right)$ is larger when there is measurement error. The increase in the variance is related to the true γ, which enters the residual.

The t-statistic for testing whether γ^m = 0 has a limit $$\mathrm{plim}\left(\frac{1}{\sqrt{n}}{t}_{{\gamma }^m}\right)=\sqrt{1-\theta }\frac{\gamma }{\sqrt{\theta {\gamma }^2+\frac{{\sigma }_e^2}{{\sigma }_u^2}}}.$$In addition to the two sources of measurement error in the standard error, the t-statistic involves the attenuation factor 1 − θ for the coefficient γ^m. As in the case for the balancing regression, the t-statistic for ${\widehat{\gamma }}^m$ is smaller than t_γ for the error-free case. But in contrast to the balancing test statistic $t_{{\delta }^m}$, measurement error reduces $t_{{\gamma }^m}$ relatively more, due to the fact that measurement error in a regressor both attenuates the relevant coefficient toward zero (captured by $\sqrt{1-\theta }$) and introduces additional variance into the residual (the θγ²-term) in the denominator. As a result, classical measurement error makes the assessment of whether γ = 0 more difficult compared to the assessment of whether δ = 0. As we will see, this contributes to the greater power of the balancing test statistic.

Finally, consider the quantity β^s − β^m, which enters the coefficient comparison test. Before proceeding, we note that the covariance term in the expression for the asymptotic variance of ${\widehat{\beta }}^s-{\widehat{\beta }}^m$(12) $$\text{var}\left({\widehat{\beta }}^s-{\widehat{\beta }}^m\right)=\text{var}\left({\widehat{\beta }}^s\right)+\text{var}\left({\widehat{\beta }}^m\right)-2\text{cov}\left({\widehat{\beta }}^s,{\widehat{\beta }}^m\right)$$(12) reduces the sampling variance of ${\widehat{\beta }}^s-{\widehat{\beta }}^m$. This covariance term is positive and generally sizable compared to $\text{var}\left({\widehat{\beta }}^s\right)$ and $\text{var}\left({\widehat{\beta }}^m\right)$ since the regression residuals e^s_i and e^m_i are highly correlated. Because $2\text{cov}({\widehat{\beta }}^s,{\widehat{\beta }}^m)$ gets subtracted, looking at the standard errors of ${\widehat{\beta }}^s$ and ${\widehat{\beta }}^m$ alone can potentially mislead the researcher into concluding that the two coefficients are not significantly different from each other when in fact they are.

The coefficient comparison test itself can be formulated as a t-test as well, since we are interested in the movement in a single parameter, that is, $$t_{({\beta }^s-{\beta }^m)}=\frac{{\widehat{\beta }}^s-{\widehat{\beta }}^m}{\widehat{\mathrm{se}}({\widehat{\beta }}^s-{\widehat{\beta }}^m)},$$where $\widehat{\mathrm{se}}({\widehat{\beta }}^s-{\widehat{\beta }}^m)$ is a consistent standard error estimator. Using (4(4) $${\beta }^s-{\beta }^l=\gamma \delta .$$(4) ) and (10(10) $$\begin{array}{ccc}\hfill {\beta }^m& =& {\beta }^l+\gamma \delta \theta \hfill \\ \hfill {\gamma }^m& =& \gamma (1-\theta ).\hfill \end{array}$$(10) ), we obtain (13) $$\mathrm{plim}\left(\frac{1}{\sqrt{n}}{t}_{\left({\beta }^s-{\beta }^m\right)}\right)=\sqrt{1-\theta }\frac{\delta \gamma }{\sqrt{{\gamma }^2\frac{{\sigma }_u^2}{{\sigma }_s^2}+\theta {\delta }^2{\gamma }^2+{\delta }^2\frac{{\sigma }_e^2}{{\sigma }_u^2}}}.$$(13) Under the alternative hypothesis (δ ≠ 0) and the maintained assumption γ ≠ 0, the three test statistics are asymptotically related in the following way: (14) $$\mathrm{plim}{\left(\frac{1}{\frac{1}{\sqrt{n}}{t}_{\left({\beta }^s-{\beta }^m\right)}}\right)}^2=\mathrm{plim}{\left(\frac{1}{\frac{1}{\sqrt{n}}{t}_{{\delta }^m}}\right)}^2+\mathrm{plim}{\left(\frac{1}{\frac{1}{\sqrt{n}}{t}_{{\gamma }^m}}\right)}^2.$$(14)

This result highlights a number of things. First of all, under the maintained hypothesis γ ≠ 0, the balancing test alone is more powerful. This is not surprising at all, since the balancing test only involves estimating the parameter δ, while the coefficient comparison test involves estimating both δ and γ. Imposing γ ≠ 0 in the coefficient comparison test is akin to $t_{{\gamma }^m}\to \infty$, and this would restore the equivalence of the balancing and coefficient comparison tests. Note that the power advantage from imposing γ ≠ 0 exists regardless of the presence of measurement error.

The second insight is that measurement error affects the coefficient comparison test in two ways. The test statistic is subject to both the attenuation factor $\sqrt{1-\theta }$ and the term θδ²γ² in the variance, which is inherited from the t-statistic for ${\widehat{\gamma }}^m$. Importantly, however, all these terms interact in the coefficient comparison test. In our numerical exercises below, it turns out that the way in which measurement error attenuates γ^m compared to γ is a major source of the power disadvantage of the coefficient comparison test. Our simulations demonstrate that the differences in power between the coefficient comparison and balancing tests can be substantial when there is considerable measurement error in x^m_i.

5. POWER COMPARISONS

5.1 Asymptotic and Monte Carlo Results with Classical Measurement Error

The ability of a test to reject when the null hypothesis is false is described by the power function of the test. The power functions here are functions of d, the values the parameter δ might take on under the alternative hypothesis, while we keep γ ≠ 0 fixed. Using our results from the previous section, it is easy to demonstrate that under the alternative hypothesis δ ≠ 0 (15) $${\mathrm{Power}}_{t_{{\delta }^m}}\left(d\right)>\mathrm{Power}{}_{t_{\left({\beta }^s-{\beta }^m\right)}}(d;\gamma ).$$(15) We give a full derivation in the online Appendix A.

In practice, this result may or may not be important. In addition, when the standard error is estimated, the powers of the two tests may differ from the theoretical results above. Therefore, we carry out a number of Monte Carlo simulations to assess the performance of the two tests.

Table 1 displays the parameter^{Figure 1}values we use as well as the implied values of the population R² of regression (9(9) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^s{s}_i+e_i^s\hfill \\ \hfill y_i& =& {\beta }^m{s}_i+{\gamma }^m{x}_i^m+e_i^m.\hfill \end{array}$$(9) ). The values were chosen so that for intermediate amounts of measurement error in x^m_i the R²s are reflective of regressions fairly typical of those in applied microeconomics, for example, a wage regression. Note that the amounts of measurement error we consider are comparatively large. In our empirical application, we use variables like mother’s education and the presence of a library card in the household as measures of family background. We suspect that these variables pick up at most a minor part of the true variation of family background, even in the presence of other covariates, so that values of θ = 0.7 or θ = 0.85 for the measurement error are not unreasonable.

Table 1. Parameters for power calculations and implied R²s

σ^2s = 1		β = 1
σ^2u = 3		γ = 3
σ^2e = 30		n = 100
	R^2
d	θ = 0	θ = 0.7	θ = 0.85
0	0.48	0.16	0.09
0.5	0.53	0.23	0.16
1.0	0.59	0.33	0.27
1.5	0.66	0.44	0.39
2.0	0.72	0.54	0.50

NOTE: The implied population R²s do not depend on n, but the subsequent power calculations do.

In Figure 1, we start by plotting the theoretical power functions for both tests for three different magnitudes of the measurement error. We calculate these power functions using the t-distribution with n − 2 degrees of freedom, consistent with how Stata 14 performs the balancing test (this distribution choice makes little difference with our sample size of 100). The thin lines show the power functions with no measurement error. The power functions can be seen to increase quickly with d, and both tests reject with virtual certainty once d exceeds values of 1. The balancing test is slightly more powerful but this difference is small, and only visible in the figure for a small range of d.

Figure 1. Theoretical rejection rates. d is the value the coefficient in the balancing equation takes on under the alternative hypothesis.

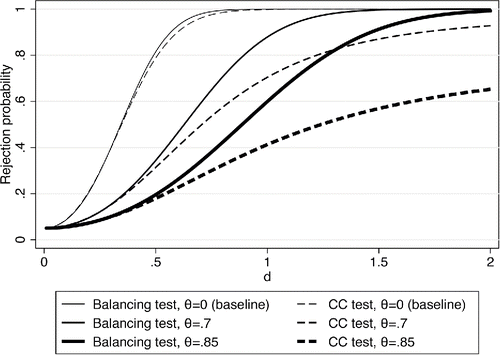
The medium thick lines correspond to θ = 0.7, that is, 70% of the variance of x^m_i is measurement error after partialling out s_i. Measurement error of that magnitude visibly affects the power of both tests. The balancing test still rejects with certainty for d > 1.5, while the coefficient comparison test does not reject with certainty for the parameter values considered in the figure. This discrepancy becomes even more pronounced when we set θ = 0.85 (thick lines). The power of the coefficient comparison test does not rise above 0.65 in this case, while the balancing test still rejects with probability 1 when d is around 2.

The results in Figure 1 highlight that there are parameter combinations where the balancing test has substantially more power than the coefficient comparison test. In other regions of the parameter space, the two tests have more similar power, for example, when d < 0.5. While we highlight the consequences of measurement error throughout the article, we should note that formally any particular value of θ can be mimicked by an appropriate combination of values for γ and σ²_u. This is an immediate consequence of the fact that the classical measurement error model is underidentified by one parameter. In that sense “measurement error” is simply a label for a certain set of parameter values. It is always difficult to choose empirically relevant values for simulations, and we take comfort from the fact that the results emerging from this section are also reflected in the empirical example in Section 6.

Before going on to simulations of more complicated cases, we contrast the theoretical power functions in Figure 1, based on asymptotic approximations, to simulated rejection rates of the same tests in Monte Carlo samples. Figure 2 shows the power functions for the two tests without measurement error (θ = 0) and with a large amount of measurement error (θ = 0.85), as well as their simulated counterparts. We computed 25,000 replications in these simulations, and each repeated sample contains 100 observations. Without measurement error, the theoretical power functions are closely aligned with the empirical rejection rates (thinner lines). Adding measurement error, this is also true for the balancing test (the solid thicker lines are on top of each other and not distinguishable) but not for the coefficient comparison test (broken thicker lines).

Figure 2. Theoretical and simulated rejection rates. Comparison of asymptotic rejection rates (from Figure 1) with rejection rates based on Monte Carlo simulations. Baseline refers to the theoretical rejection rates without measurement error. d is the value the coefficient in the balancing equation takes on under the alternative hypothesis.

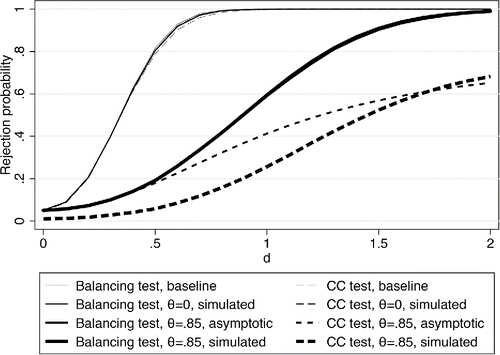
Figure 2 reveals that the empirical rejection rates of the coefficient comparison test in the presence of measurement error deviate substantially from the power function calculation based on the asymptotic approximation. This discrepancy is almost completely explained by the fact that we use the asymptotic values of standard errors in the calculations but estimated standard errors in the simulations. The joint distribution between the coefficient and standard error estimators is difficult to characterize, especially in the case of the coefficient comparison test, so we abstract away from the sampling variation in estimating the standard errors in the theoretical derivations of the power functions. Figure 2 shows that the test is severely distorted under the null in the simulations; it barely rejects more than 1% of the time for a nominal size of 5%. While this problem leads to too few rejections under the null, it is important to note that the same issue arises for positive values of d until about d = 1.5. For larger values of d, the relationship reverses. In other words, for moderate values of d, the coefficient comparison test statistic is biased downwards under the alternative, and the test has too little power. This highlights another advantage of the balancing test—a standard t-test where no such problem arises. We note that this is a small sample problem, which goes away when we increase the sample size (in unreported simulations). We suspect that this problem is related to the way in which the coefficient comparison test effectively combines the simple $t_{{\delta }^m}$ and $t_{{\gamma }^m}$ test statistics in a nonlinear fashion, as can be seen in Equation (14(14) $$\mathrm{plim}{\left(\frac{1}{\frac{1}{\sqrt{n}}{t}_{\left({\beta }^s-{\beta }^m\right)}}\right)}^2=\mathrm{plim}{\left(\frac{1}{\frac{1}{\sqrt{n}}{t}_{{\delta }^m}}\right)}^2+\mathrm{plim}{\left(\frac{1}{\frac{1}{\sqrt{n}}{t}_{{\gamma }^m}}\right)}^2.$$(14) ), and the fact that $t_{{\gamma }^m}$ sometimes is close to 0 in small samples despite the fact that we fix γ substantially above 0.

5.2 Monte Carlo Results with Mean-Reverting Measurement Error

The homoscedastic case with classical measurement error is highly stylized and does not correspond well to the situations typically encountered in empirical practice. We explore the case of mean-reverting measurement error (Bound et al. 1994) using simulations in this subsection. Some additional results can be found in the online Appendix D. We generate measurement error as $$m_i=\kappa x_i+{\mu }_i,$$where κ is a parameter and $\text{cov}(x_i,{\mu }_i)=0$, so that κx_i captures the error related to x_i and μ_i the unrelated part. When − 1 < κ < 0, the error is mean reverting, that is, the κx_i-part of the error reduces the variance in x^m_i compared to x_i.

The case of mean-reverting measurement error captures a variety of ideas, including the one that we may observe only part of a particular confounder made up of multiple components. Imagine we would like to include in our regression a variable x_i = w_1i + w_2i, where w_1i and w_2i are two orthogonal variables. We observe x^m_i = w_1i. For example, x_i may be family background, w_1i is mother’s education and other parts of family background correlated with it, and w_2i are all relevant parts of family background which are uncorrelated with mother’s education. As long as selection bias due to w_1i and w_2i is the same, this amounts to the mean-reverting measurement error formulation above. Note that $\lambda =\text{var}\left(x_i\right)/\text{var}\left(x_i^m\right)>1$ in this case, so the mismeasured x^m_i has a lower variance than the true x_i. This scenario is also isomorphic to the model studied by Oster (forthcoming). See online Appendix B for details.

The mismeasured x^m_i can now be written as $$x_i^m=\left(1+\kappa \right)\delta s_i+\left(1+\kappa \right)u_i+{\mu }_i,$$so mean reversion directly affects the coefficient in the balancing regression, which will be smaller than δ for a negative κ. As a result, the balancing test will reject less often. At the same time, a negative κ offsets and possibly reverses the attenuation bias on γ. This brings the power functions of the balancing and coefficient comparison tests closer together.

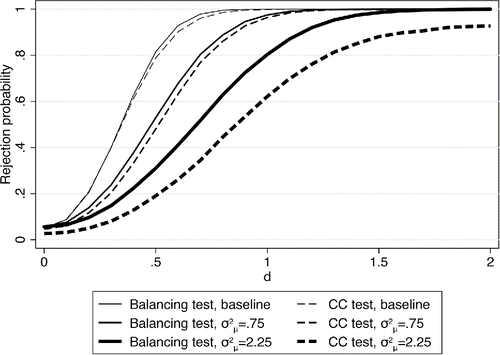
For the^{Figure 3}simulations we set κ = −0.5, so the error is mean reverting. We also fix σ²_μ in the simulations. However, it is important to note that the nature of the measurement error will change as we change the value of d under the alternative hypotheses. x_i depends on δ and the correlated part of the measurement error depends in turn on x_i. We show results for two cases with σ²_μ = 0.75 and σ²_μ = 2.25. Under the null, these two parameter values correspond to λ = 2 and λ = 1, respectively. The case λ = 2 corresponds to the Oster (forthcoming) model just described with $\text{var}\left(w_{1i}\right)=\text{var}\left(w_{2i}\right)$. These models exhibit relatively large amounts of mean reversion. Figure 3 demonstrates that the balancing test again dominates for these parameter values. The gap is small for the σ²_μ = 0.75 case but grows with σ²_μ, the classical portion of the measurement error. This finding is not surprising as the mean-reversion part in the measurement error biases the estimate of γ in the opposite direction from the classical part and can in principle flip the sign of the bias around. As a result, the coefficient comparison test could have greater power.

Figure 3. Simulated rejection rates with mean-reverting measurement error. Comparison of baseline rejection rates (from Figure 1) with simulated rejection rates based on mean-reverting measurement error and robust standard errors. d is the value the coefficient in the balancing equation takes on under the alternative hypothesis.

5.3 Multiple Controls

So far we have concentrated on the case of a single added regressor x_i. Often in empirical practice, we may want to add a set of additional covariates at once. It is straightforward to extend our framework to that setting. Some interesting new issues arise in this analysis.

Suppose there are k added regressors, that is, x_i is a k × 1 vector, and (16) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^l{s}_i+{\mathbf{x}}_i^{\text{'}}\gamma +e_i\hfill \\ \hfill {\mathbf{x}}_i& =& \delta s_i+{\mathbf{u}}_i\hfill \\ \hfill {\beta }^s-{\beta }^l& =& {\gamma }^{\text{'}}\delta ,\hfill \end{array}$$(16) where $\gamma$, $\delta$, and u_i are k × 1 vector analogs of their scalar counterparts in Section 2. The coefficient comparison test compares the βs from Equations (1(1) $$y_i={\beta }^s{s}_i+e_i^s,$$(1) ) and (16(16) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^l{s}_i+{\mathbf{x}}_i^{\text{'}}\gamma +e_i\hfill \\ \hfill {\mathbf{x}}_i& =& \delta s_i+{\mathbf{u}}_i\hfill \\ \hfill {\beta }^s-{\beta }^l& =& {\gamma }^{\text{'}}\delta ,\hfill \end{array}$$(16) ) just as before. Lee and Lemieux (2010) suggest a balancing test for multiple covariates in the context of evaluating regression discontinuity designs. Let x_(j) denote the n × 1 vector of all the observations on the jth x-variable. Stack all the x-variables on the LHS of the regression to obtain $$\left[\begin{array}{c}{\mathbf{x}}_{\left(1\right)}\\ {\mathbf{x}}_{\left(2\right)}\\ ...\\ {\mathbf{x}}_{\left(k\right)}\end{array}\right]=\left[\begin{array}{cccc}\hfill \mathbf{s}& \hfill \mathbf{0}& \hfill \mathbf{0}& \mathbf{0}\\ \hfill \mathbf{0}& \hfill \mathbf{s}& \hfill \mathbf{0}& \mathbf{0}\\ \hfill \mathbf{0}& \hfill \mathbf{0}& \hfill ...& \mathbf{0}\\ \hfill \mathbf{0}& \hfill \mathbf{0}& \hfill \mathbf{0}& \mathbf{s}\end{array}\right]\left[\begin{array}{c}{\delta }_1\\ {\delta }_2\\ ...\\ {\delta }_k\end{array}\right]+\left[\begin{array}{c}{\mathbf{u}}_{\left(1\right)}\\ {\mathbf{u}}_{\left(2\right)}\\ ...\\ {\mathbf{u}}_{\left(k\right)}\end{array}\right],$$where s = [s₁, s₂, …, s_n]′ and u_(j) is the vector of residuals corresponding to covariate x_(j). The balancing test is an F-test for the joint significance of the $\delta$ coefficients, the null is $\delta ={\displaystyle \mathbf{0}}$.

We will call this stacking of equations the LHS balancing test. While it is the natural multivariate extension, an alternative would be to regress s on the covariates $\mathbf{x}$$$s_i={\pi }^{\text{'}}{\mathbf{x}}_i+v_i,$$(including any other covariates implicit in the regressions in Equation (16(16) $$\begin{array}{ccc}\hfill y_i& =& {\beta }^l{s}_i+{\mathbf{x}}_i^{\text{'}}\gamma +e_i\hfill \\ \hfill {\mathbf{x}}_i& =& \delta s_i+{\mathbf{u}}_i\hfill \\ \hfill {\beta }^s-{\beta }^l& =& {\gamma }^{\text{'}}\delta ,\hfill \end{array}$$(16) )) and test whether the coefficient vector $\pi$ is significantly different from zero. This is a standard F-test. We refer to this test as the RHS balancing test. Notice that even though the balancing variables are now on the right, this is conceptually still a balancing test. Applied researchers sometimes use this RHS test; for example, Bruhn and McKenzie (2009) reported it being used in some experimental studies in development economics.

While putting the balancing^{Figure 4}variables on the RHS might at first glance seem unusual, it turns out that the LHS and RHS tests are closely related. This should not be surprising as both tests exploit the joint covariance matrix of the x_(j) and s. This can be seen most clearly in the case of a single covariate x_i (i.e., k = 1), where the LHS and the RHS tests using a conventional covariance matrix for homoscedastic residuals are numerically identical.

The intuition for this is the following: In the single covariate case, the F-test amounts to the overall F-test for the significance of the regression. This, in turn, is a function of the R² of the regression. Since only two variables x_i and s_i are involved, this is the square of the correlation coefficient between the two. But the correlation coefficient is not directional, so the forward and reverse regression have to deliver the same F-statistic (in the case when covariates are present in the regression, replace the R² and correlation coefficient with their partial equivalents in this argument).

With multiple covariates (k > 1), the LHS and RHS tests are no longer equivalent. However, the scaled F-statistics of the two tests have the same probability limit in the special case, where the LHS regression has a spherical error structure $\mathrm{var}\left({\mathbf{u}}_i\right)={\sigma }^2{I}_k$ and the RHS regression is homoscedastic, as we show in the online Appendix C. (See Ludwig, Mullainathan, and Spiess 2017 for a similar result.)

How do the balancing tests with multiple covariates perform in practice? Figures 4 and 5 show simulations using a similar design as described in Table 1 for all k balancing equations. We set k = 4 and generate normally distributed, spherical errors and impose homoscedasticity and independence when performing the joint test of the δ_j's or the π_j's. Our experiments with other moderate values of k for the most part did not reveal different insights. With multiple covariates, there are different ways of specifying the alternative hypotheses now. The null hypothesis may fail for one, various, or all of the k covariates. We show rejection rates under two polar versions of the alternative hypothesis. Figure 4 shows simulations for the case where all covariates are unbalanced, that is, δ₁ = δ₂ = ⋅⋅⋅ = δ_k = d. Figure 5 analyzes the case where only the first covariate is unbalanced, while the others remain balanced, that is, δ₁ = d, δ₂ = ⋅⋅⋅ = δ_k = 0.

Figure 4. Simulated rejection rates with multiple controls: All covariates unbalanced. Simulated rejection rates for simultaneous tests for adding four additional covariates at once. All covariates are unbalanced under the alternative hypothesis; d is the value the coefficient in the balancing equation takes on under the alternative hypothesis for all covariates simultaneously.

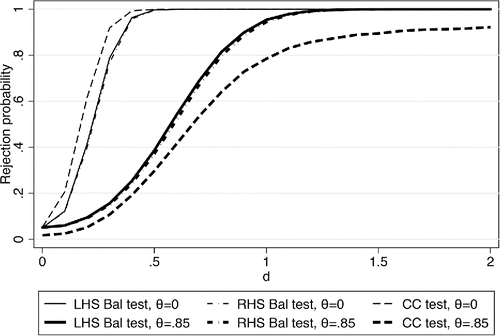
Figure 5. Simulated rejection rates with multiple controls: One covariate unbalanced. Simulated rejection rates for simultaneous tests for adding four additional covariates at once. Only one of the four covariates is unbalanced under the alternative hypothesis; d is the value the coefficient in the balancing equation takes on under the alternative hypothesis for this covariate.

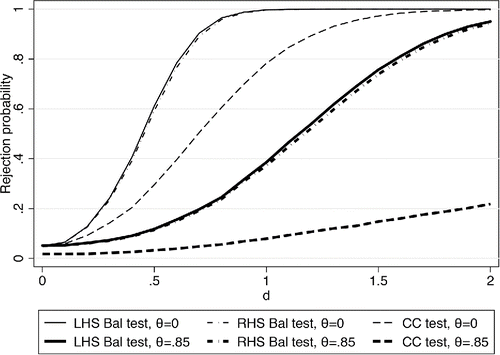
These figures highlight a number of results. The LHS and RHS balancing tests are indeed very similar as their power functions virtually lie on top of each other in both figures. When all covariates are unbalanced as in Figure 4 and when measurement error is absent, the Hausman test turns out to be an efficient test in combining the k separate hypotheses into one single test-statistic, which is generated from the estimates of only two parameters, the long and short βs. The balancing tests, on the other hand, have to rely on the estimation of k parameters. In this case, the rejection rates for the coefficient comparison test (thin broken lines), therefore, lie above the ones for both the balancing tests (thin solid and dash-dot lines). In the presence of measurement error, however, the balancing tests are again more powerful than the coefficient comparison test as can be seen from the juxtaposition of the thicker lines.

This power advantage of the balancing tests is greater when only one covariate is unbalanced as can be seen in Figure 5. Both tests are less powerful in this case, but the power loss for the coefficient comparison test is now much more pronounced. This is particularly noticeable in the case with measurement error in the covariates (thick lines) but the balancing tests outperform the coefficient comparison test even without measurement error in this case. Empirically relevant cases may often lie in between these extremes. Researchers may be faced with a set of potential controls to investigate, some of which may be unbalanced with the treatment while others are not. Figures 4 and 5 demonstrate that the balancing test will frequently be the most powerful tool in such a situation, but the coefficient comparison test also has a role to play in the multivariate case.

The simulations reveal some further insights. With measurement error, the small sample issue of the coefficient comparison test, which we highlighted in Figure 2, arises again. On top of this, we found in unreported simulations that both the LHS and RHS balancing tests with robust standard errors (clustered standard errors across equations for the LHS test and heteroscedasticity-robust standard errors for the RHS test) have a size distortion under the null hypothesis and reject too often. This is due the standard small sample distortion of these covariance matrices discussed in the literature (MacKinnon and White 1985; Chesher and Jewitt 1987; Angrist and Pischke 2009, chap. 8). We find that this bias tends to get worse when more covariates are added. Applied researcher may be most interested in the testing strategies discussed here when k is large (so that a series of single variable balancing tests is unattractive), and will want to rely on a robust covariance matrix. An upward size distortion may be less of an issue for a conservative researcher in a balancing test (where it means the researcher will falsely decide not to go ahead with a research design where the covariates are actually balanced) than in a test for the presence of nonzero treatment effects (where the same bias leads to false discoveries). Nevertheless, we suspect that most applied researchers would prefer a test with a correct size under the null and a steep power function. As a result, research on improvements for the bias problem in multivariate tests is therefore particularly important (we discuss some current approaches in our working paper, Pei, Pischke, and Schwandt 2017).

The upshot is that it is in principle straightforward to extend the balancing test to multiple covariates. An interesting finding is that a RHS test offers a computationally simple alternative that closely mimics the performance of the more standard LHS balancing test. Yet, at this point implementation issues related to the small sample bias of robust covariance estimators also hamper our ability to confidently carry out balancing tests for multiple covariates. Moreover, sometimes we are interested in the robustness of the original results when the number of added regressors is very large. An example would be a differences-in-differences analysis in a state-year panel, where the researcher is interested in checking whether the results are robust to the inclusion of state specific trends. The balancing test does not seem to be the right framework to deal with this situation. The coefficient comparison test has a role to play in this scenario.

6. EMPIRICAL ANALYSIS

We illustrate the theoretical results in the context of estimating the returns to schooling using data from the NLS. This is a panel study of about 5000 male respondents interviewed from 1966 to 1981. The dataset has featured in many prominent analyses of the returns to education, including Griliches (1977) and Card (1995). We use the NLS extract posted by David Card and augment it with the variable on body height measured in the 1973 survey. We estimate regressions similar to Equation (2(2) $$y_i={\beta }^l{s}_i+\gamma x_i+e_i,$$(2) ). The variable y_i is the log hourly wage in 1976 and s_i is the number of years of schooling reported by the respondent in 1976. Our samples are restricted to observations without missing values in any of the variables used.

Table 2 presents OLS regressions for the return to schooling controlling for the respondent’s score on the Knowledge of the World of Work test (KWW), a variable used by Griliches (1977) as a proxy for ability. Additional covariates are experience, race, and past and present residence. The estimated return to schooling is 0.061.

Table 2. Regressions for returns to schooling and specification checks controlling for the KWW score

	Log hourly earnings					Mother’s years of education	Library card at age 14	Body height in inches
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Years of education	0.0609	0.0596	0.0608	0.0603	0.0591	0.2500	0.0133	0.0731
	(0.0059)	(0.0060)	(0.0059)	(0.0059)	(0.0060)	(0.0422)	(0.0059)	(0.0416)
KWW score	0.0070	0.0068	0.0069	0.0069	0.0067	0.0410	0.0076	0.0145
	(0.0015)	(0.0016)	(0.0016)	(0.0015)	(0.0016)	(0.0107)	(0.0016)	(0.0117)
Mother’s years of		0.0053			0.0048
education		(0.0037)			(0.0037)
Library card at age 14			0.0097		0.0045
			(0.0215)		(0.0216)
Body height in inches				0.0078	0.0075
				(0.0034)	(0.0034)
p-values
Coefficient comparison test		0.161	0.651	0.156	0.084
LHS balancing test: Individual						0.000	0.025	0.079
LHS balancing test: Joint							0.000
RHS balancing test: Joint							0.000

NOTE: The number of observations is 1773 in all regressions. Heteroscedasticity robust standard errors in parentheses. The joint LHS balancing test is conducted via the suest Stata command. All regressions control for experience, experience-squared, indicators for black, for southern residence and residence in an SMSA in 1976, indicators for region in 1966 and living in an SMSA in 1966.

In columns (2)–(4), we include variables that might proxy for the respondent’s family background, mother’s education (column 2), whether the household had a library card when the respondent was 14 (column 3), and body height measured in inches (column 4). Mother’s education captures an important component of a respondent’s family background. The library card measure has been used by researchers to proxy for parental attitudes (e.g., Farber and Gibbons 1996). Body height is determined by parents’ genes and by nutrition and disease environment during childhood. It is unlikely a particularly powerful control variable but it is predetermined and correlated with family background, self-esteem, and ability (e.g., Persico, Postlewaite, and Silverman 2004 and Case and Paxson 2008).

Conditional on the KWW score, these three variables are only weakly correlated with earnings and only the coefficient for body height is marginally significant. The estimated return to education moves very little when these additional controls are included; the differences to column (1) are in the order of 0.001. In column (5), we enter all three variables simultaneously. The coefficients on the controls are slightly attenuated, and the return to education falls slightly further to 0.059. Below the estimates in columns (2)–(5), we display the p-values comparing each of the estimated returns to education to the one from column (1). None of the tests reject at the 5% level. These results from the coefficient comparison test seem to confirm the impression that the coefficient movements are not statistically significant.

It might be tempting to conclude from this evidence that the return to schooling estimated in column (1) should be given a causal interpretation but this conclusion is premature. A first caution actually comes from the coefficient comparison test in column (5), which is significant at the 10% level. The coefficient movement of 0.002 is not large, and the individual standard errors in columns (1) and (5) of 0.006 do not suggest that this movement might be significant. Equation (12(12) $$\text{var}\left({\widehat{\beta }}^s-{\widehat{\beta }}^m\right)=\text{var}\left({\widehat{\beta }}^s\right)+\text{var}\left({\widehat{\beta }}^m\right)-2\text{cov}\left({\widehat{\beta }}^s,{\widehat{\beta }}^m\right)$$(12) ) warns that relying on the individual standard errors can be rather misleading. Nevertheless, most researchers would probably not find the evidence in columns (1)–(5) worrisome enough to abandon their research project.

More potent warnings emerge from the balancing regressions in columns (6)–(8), where we regress maternal education, the library card, and body height on education while controlling for the KWW score. The education coefficient is positive and strongly significant for mother’s education and the library card, and more marginally so for body height. Moreover, both the LHS and RHS joint balancing tests reject the hypothesis that all three controls are balanced with a p-value of virtually zero. The magnitudes of the coefficients, particularly, mother’s education, are substantively important. These estimates reflect selection bias: individuals with more education have significantly better educated mothers, were more likely to grow up in a household with a library card, and experienced more body growth when young. Our interpretation of these results is that education levels are related to family background in these regressions but the available background measures are fairly useless as controls when put on the RHS. These measurement problems matter less for the estimates in columns (6)–(8), and these specifications are therefore informative about the role of selection. Comparing the p-values at the bottom of the table to the corresponding ones for the coefficient comparison test in columns (2)–(4) demonstrates the superior power of the balancing test and illustrates the message of our article in a forceful fashion.

7. CONCLUSION

Using predetermined characteristics as dependent variables offers a useful specification check for a variety of identification strategies popular in empirical economics. We argue that this is the case even for variables which might be poorly measured and are of little value as control variables. Such variables are available in many datasets. We encourage researchers to be more inventive in finding such measures and perform balancing tests with them more frequently. We show that this is generally a more powerful strategy than adding the same variables on the RHS of the regression as controls and looking for movement in the coefficient of interest.

We have illustrated our theoretical results with an application to the returns to education. We find the balancing test indeed to be useful for gauging selection bias due to confounders, even when they are potentially measured poorly. It is important to point out that the balancing test does not address any other issues that may also haunt a successful empirical investigation of causal effects. One possible issue is measurement error in the variable of interest. This is exacerbated as more potent controls are added to a regression. Griliches (1977) showed that a modest amount of measurement error in schooling may explain patterns of returns in controlled and uncontrolled regressions. Another issue, also discussed by Griliches, is that controls like test scores might themselves be influenced by schooling, which would make them bad controls.

ACKNOWLEDGMENTS

We thank Suejin Lee for excellent research assistance and the editor Rajeev Dehejia, two referees, an associate editor, Alberto Abadie, Josh Angrist, Panle Jia Barwick, Matias Cattaneo, Bernd Fitzenberger, Brigham Frandsen, Daniel Hungerman, Rachael Meager, Doug Miller, Francesca Molinari, Franco Peracchi, Pedro Souza, and participants at various seminars and conferences for helpful comments. This research has been supported by a grant from the Economic and Social Research Council [ES/M010341/1] to the Centre for Economic Performance at the LSE.