Fast and Flexible Bayesian Inference in Time-varying Parameter Regression Models

Abstract

In this article, we write the time-varying parameter (TVP) regression model involving K explanatory variables and T observations as a constant coefficient regression model with KT explanatory variables. In contrast with much of the existing literature which assumes coefficients to evolve according to a random walk, a hierarchical mixture model on the TVPs is introduced. The resulting model closely mimics a random coefficients specification which groups the TVPs into several regimes. These flexible mixtures allow for TVPs that feature a small, moderate or large number of structural breaks. We develop computationally efficient Bayesian econometric methods based on the singular value decomposition of the KT regressors. In artificial data, we find our methods to be accurate and much faster than standard approaches in terms of computation time. In an empirical exercise involving inflation forecasting using a large number of predictors, we find our models to forecast better than alternative approaches and document different patterns of parameter change than are found with approaches which assume random walk evolution of parameters.

Keywords:

• Clustering
• Hierarchical priors
• Singular value decomposition
• Time-varying parameter regression

1 Introduction

Time-varying parameter (TVP) regressions and vector autoregressions (VARs) have shown their usefulness in a range of applications in macroeconomics (e.g., Cogley and Sargent 2005; Primiceri 2005; D’Agostino, Gambetti, and Giannone 2013). Particularly when the number of explanatory variables is large, Bayesian methods are typically used since prior information can be essential in overcoming over-parameterization concerns. These priors are often hierarchical and ensure parsimony by automatically shrinking coefficients. Examples include Belmonte, Koop, and Korobilis (2014), Kalli and Griffin (2014), Bitto and Frühwirth-Schnatter (2019), and Huber, Koop, and Onorante (2021). Approaches such as these have two characteristics that we highlight so as to motivate the contributions of our article. First, they use Markov Chain Monte Carlo (MCMC) methods which can be computationally demanding. They are unable to scale up to the truly large data sets that macroeconomists now work with. Second, the regression coefficients in these TVP models are assumed to follow random walk or autoregressive (AR) processes. In this article, we develop a new approach which is computationally efficient and scaleable. Furthermore, it allows for more flexible patterns of time variation in the regression coefficients.

We achieve the computational gains by writing the TVP regression as a static regression with a particular, high dimensional, set of regressors. Using the singular value decomposition (SVD) of this set of regressors along with conditionally conjugate priors yields a computationally fast algorithm which scales well in high dimensions. One key feature of this approach is that no approximations are involved. This contrasts with other computationally fast approaches to TVP regression which achieve computational gains by using approximate methods such as variational Bayes (Koop and Korobilis 2018), message passing (Korobilis 2021) or expectation maximization (Rockova and McAlinn 2021).

Our computational approach avoids large-scale matrix operations altogether and exploits the fact that most of the matrices involved are (block) diagonal. In large-dimensional contexts, this allows fast MCMC-based inference and thus enables the researcher to compute highly nonlinear functions of the time-varying regression coefficients while taking parameter uncertainty into account. Compared to estimation approaches based on forward-filtering backward-sampling (FFBS, see Carter and Kohn 1994; Frühwirth-Schnatter 1994) algorithms, the computational burden is light. In particular, we show that it rises (almost) linearly in the number of covariates. For quarterly macroeconomic datasets that feature a few hundred observations, this allows us to estimate and forecast, exploiting all available information without using dimension reduction techniques such as principal components.

Computational tractability is one concern in high- dimensional TVP regressions. The curse of dimensionality associated with estimating large-dimensional TVP regressions is another. To solve over-parameterization issues and achieve a high degree of flexibility in the type of coefficient change, we use a sparse finite mixture representation (see Malsiner-Walli, Frühwirth-Schnatter, and Grün 2016) for the time-varying coefficients. This introduces shrinkage on the amount of time variation by pooling different time periods into a (potentially) small number of clusters. We also use shrinkage priors which allow for the detection of how many clusters are necessary. Shrinkage toward the cluster means is then introduced by specifying appropriate conjugate priors on the regression coefficients. At a general level, this model is closely related to random coefficient models commonly used in microeconometrics (see, e.g., Allenby, Arora, and Ginter 1998; Lenk and DeSarbo 2000). We propose three different choices for this prior. The first of these is based on Zellner’s g-prior (Zellner 1986). The second is based on the Minnesota prior (Doan, Litterman, and Sims 1984; Litterman 1986) and the final one is a ridge-type prior (see, e.g., Griffin and Brown 2013). As opposed to a standard TVP regression which assumes that the states evolve smoothly over time, our model allows for abrupt changes (which might only happen occasionally) in the coefficients. This resembles the behavior of regime switching models (see, e.g., Hamilton 1989; Frühwirth-Schnatter 2001). Compared to those, our approach has two additional advantages: it remains agnostic on the precise law of motion of the coefficients, and it endogenously finds the number of regimes.¹

We investigate the performance of our methods using two applications. Based on synthetic data, we first illustrate computational gains if K and T become large. We then proceed to show that our approach effectively recovers key properties of the data generating process. In a real data application, we model U.S. inflation dynamics. Our framework provides new insights on how the relationship between unemployment and inflation evolves over time. Moreover, in an extensive forecasting exercise we show that our proposed set of models performs well relative to a wide range of competing models. Specifically, we find that our model yields precise point and density forecasts for one-step-ahead and four-step-ahead predictions. Improvements in forecast accuracy are especially pronounced during recessionary episodes.

The remainder of the article is structured as follows. Section 2 introduces the static representation of the TVP regression model while Section 3 shows how the SVD can be used to speed up computation. Section 4 provides an extensive discussion of our prior setup. The model is then applied to synthetic data in Section 5 and real data in Section 6. Finally, the last section summarizes and concludes the article and the online appendix provides additional details on computation and further empirical findings.

2 A Static Representation of the TVP Model

Let ${\left\{y_t\right\}}_{t=1}^T$ denote a scalar response variable² that is described by a TVP regression given by(1) $$y_t={\mathit{x}}_t^{\prime }{\mathit{\beta }}_t+\sigma {\eta }_t,\hspace{1em}{\eta }_t\sim \mathcal{N}(0,1),$$(1) where ${\mathit{x}}_t$ is a K-dimensional vector of regressors, ${\mathit{\beta }}_t$ is a set of K time-varying regression coefficients and ${\sigma }^2$ is the error variance. For now, we assume homoscedastic errors, but will relax this assumption later in the article.

The TVP regression can be written as a static regression model as follows:(2) $$\underset{\mathit{y}}{\underbrace{\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_T\end{array}\right)}}=\underset{\mathit{Z}}{\underbrace{\left(\begin{array}{cccc}{\mathit{x}}_1^{\prime }& {\mathbf{0}}_{K\times 1}^{\prime }& \dots & {\mathbf{0}}_{K\times 1}^{\prime }\\ \mathit{\varphi }{\prime }_2& \mathit{x}{\prime }_2& \dots & {\mathbf{0}}_{K\times 1}^{\prime }\\ ⋮& ⋮& \ddots & ⋮\\ \mathit{\varphi }{\prime }_T& \mathit{\varphi }{\prime }_T& \dots & {\mathit{x}}_T^{\prime }\end{array}\right)}}\underset{\mathit{\beta }}{\underbrace{\left(\begin{array}{c}{\mathit{\beta }}_1\\ {\mathit{\beta }}_2\\ ⋮\\ {\mathit{\beta }}_T\end{array}\right)}}+\sigma \underset{\mathit{\eta }}{\underbrace{\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ ⋮\\ {\eta }_T\end{array}\right)}}.$$(2)

Equation (2)(2) $$\underset{\mathit{y}}{\underbrace{\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_T\end{array}\right)}}=\underset{\mathit{Z}}{\underbrace{\left(\begin{array}{cccc}{\mathit{x}}_1^{\prime }& {\mathbf{0}}_{K\times 1}^{\prime }& \dots & {\mathbf{0}}_{K\times 1}^{\prime }\\ \mathit{\varphi }{\prime }_2& \mathit{x}{\prime }_2& \dots & {\mathbf{0}}_{K\times 1}^{\prime }\\ ⋮& ⋮& \ddots & ⋮\\ \mathit{\varphi }{\prime }_T& \mathit{\varphi }{\prime }_T& \dots & {\mathit{x}}_T^{\prime }\end{array}\right)}}\underset{\mathit{\beta }}{\underbrace{\left(\begin{array}{c}{\mathit{\beta }}_1\\ {\mathit{\beta }}_2\\ ⋮\\ {\mathit{\beta }}_T\end{array}\right)}}+\sigma \underset{\mathit{\eta }}{\underbrace{\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ ⋮\\ {\eta }_T\end{array}\right)}}.$$(2) implies that the dynamic regression model in Equation (1)(1) $$y_t={\mathit{x}}_t^{\prime }{\mathit{\beta }}_t+\sigma {\eta }_t,\hspace{1em}{\eta }_t\sim \mathcal{N}(0,1),$$(1) can be cast in the form of a standard linear regression model with KT predictors stored in a $T\times KT$-dimensional design matrix Z. Notice that the rank of Z is equal to T and inverting $\mathit{Z}\prime \mathit{Z}$ is not possible. We stress that, at this stage, we are agnostic on the evolution of ${\mathit{\beta }}_t$ over time. A common assumption in the literature is that the latent states evolve according to a random walk. Such behavior can be achieved by setting ${\mathit{\varphi }}_t={\mathit{x}}_t$ for all t, implying a lower triangular matrix Z. If ${\mathit{\varphi }}_t={\mathbf{0}}_{K\times 1}$ for all t, then we obtain a block-diagonal matrix Z which, in combination with a Gaussian prior on $\mathit{\beta }$ would imply a white-noise state equation.

The researcher may want to investigate whether any explanatory variable has a time-varying, constant or a zero coefficient. In such a case, it proves convenient to work with a different parameterization of the model which decomposes $\mathit{\beta }$ into a time-invariant ($\mathit{\gamma }$) and a time-varying part ($\tilde{\mathit{\beta }}$)(3) $$\mathit{y}=\mathit{X\gamma }+\mathit{Z}\tilde{\mathit{\beta }}+\sigma \mathit{\eta },$$(3) with $\mathit{X}=({\mathit{x}}_1,\dots ,{\mathit{x}}_T)\prime$ denoting a T × K matrix of stacked covariates and ${\mathit{\beta }}_t=\mathit{\gamma }+{\tilde{\mathit{\beta }}}_t$, with ${\tilde{\mathit{\beta }}}_t$ being the relevant elements of $\tilde{\mathit{\beta }}$.³

Thus, we have written the TVP regression as a static regression, but with a huge number of explanatory variables. That is, $\tilde{\mathit{\beta }}$ is a KT-dimensional vector with K and T both being potentially large numbers.

This representation is related to a noncentered parameterization (Frühwirth-Schnatter and Wagner 2010) of a state-space model. The main intuition behind Equation (3)(3) $$\mathit{y}=\mathit{X\gamma }+\mathit{Z}\tilde{\mathit{\beta }}+\sigma \mathit{\eta },$$(3) is that parameters tend to fluctuate around a time-invariant regression component $\mathit{\gamma }$, with deviations being driven by ${\tilde{\mathit{\beta }}}_t$. This parameterization, in combination with the static representation of the state space model, allows us to push the model toward a time-invariant specification during certain points in time, if necessary. This behavior closely resembles characteristics of mixture innovation models (e.g., Giordani and Kohn 2008), and allows the model to decide the points in time when it is necessary to allow for parameter change.

In the theoretical discussion which follows, we will focus on the time-varying part of the regression model$$\widehat{\mathit{y}}=\mathit{y}-\mathit{X\gamma }=\mathit{Z}\tilde{\mathit{\beta }}+\sigma \mathit{\eta },$$since sampling from the conditional posterior of $\mathit{\gamma }$ (under a Gaussian shrinkage prior and conditional on $\mathit{Z}\tilde{\mathit{\beta }}$) is straightforward. In principle, any shrinkage prior can be introduced on $\mathit{\gamma }$. In our empirical work, we use a hierarchical Normal-Gamma prior of the form:$${\gamma }_j|{\tau }_j\sim \mathcal{N}(0,{\tau }_j),\hspace{1em}{\tau }_j|\psi \sim \mathcal{G}(\vartheta ,\vartheta \psi /2),\hspace{1em}\psi \sim \mathcal{G}(a_0,a_1),$$ where γ_j is the jth element of $\mathit{\gamma }$ for $j=1,\dots ,K$. We set $\vartheta =0.1$ and $a_0=a_1=0.01$ and use MCMC methods to learn about the posterior for these parameters. The relevant posterior conditionals are given in Griffin and Brown (2010) and Section A of the online appendix.

3 Fast Bayesian Inference Using SVDs

3.1 The Homoscedastic Case

In static regressions with huge numbers of explanatory variables, there are several methods for ensuring parsimony that involve compressing the data. Traditionally principal components or factor methods have been used (see Stock and Watson 2011). Random compression methods have also been used with TVP models (see Koop, Korobilis, and Pettenuzzo 2019).

The SVD of our matrix of explanatory variables, Z, is$$\underset{T\times KT}{\underbrace{\mathit{Z}}}=\underset{T\times T }{\underbrace{\mathit{U}}}\underset{T\times T}{\underbrace{\mathbf{\Lambda }}}\underset{ T\times KT}{\underbrace{\mathit{V}\prime }}$$whereby U and V are orthogonal matrices and $\mathbf{\Lambda }$ denotes a diagonal matrix with the singular values, denoted by $\mathit{\lambda }$, of Z as diagonal elements.

The usefulness and theoretical soundness of the SVD to compress regressions is demonstrated in Trippe et al. (2019). They use it as an approximate method in the sense that, in a case with K regressors, they only use the part of the SVD corresponding to the largest M singular values, where M < K. In such a case, their methods become approximate.

In our case, we can exploit the fact that .. ($T\ll KT$) and use the SVD of Z as in Trippe et al. (2019). But we do not truncate the SVD using only the M largest singular values, instead we use all T of them. But since the rank of Z is $T(\ll KT)$, our approach translates into an exact low-rank structure implying no loss of information through the SVD.

Thus, using the SVD we can exactly recover the big matrix Z. The reason for using the SVD instead of Z is that we can exploit several convenient properties of the SVD that speed up computation. To be specific, if we use a Gaussian prior, this leads to a computationally particularly convenient expression of the posterior distribution of $\tilde{\mathit{\beta }}$ which avoids complicated matrix manipulations such as inversion and the Cholesky decomposition of high-dimensional matrices. Hence, computation is fast.

We assume a conjugate prior of the form$$\tilde{\mathit{\beta }}|{\sigma }^2\sim \mathcal{N}({\mathit{b}}_0,{\sigma }^2{\mathit{D}}_0),$$with ${\mathit{D}}_0={\mathit{I}}_T\otimes \mathbf{\Psi }$ being a KT-dimensional diagonal prior variance-covariance matrix, where ${\mathit{I}}_T$ denotes a T-dimensional identity matrix and $\mathbf{\Psi }$ a K-dimensional diagonal matrix that contains covariate-specific shrinkage parameters on its main diagonal. Our prior will be hierarchical so that $\mathbf{\Psi }$ will depend on other prior hyperparameters $\mathit{\theta }$ to be defined later.

Using textbook results for the Gaussian linear regression model with a conjugate prior (conditional on the time-invariant coefficients $\mathit{\gamma }$), the posterior is(4) $$\tilde{\mathit{\beta }}|\text{Data},\mathit{\gamma },{\sigma }^2,\mathit{\theta }\sim \mathcal{N}({\mathit{\mu }}_{\tilde{\beta }},{\sigma }^2{\mathit{V}}_{\tilde{\beta }}).$$(4)

In conventional regression contexts, the computational bottleneck is typically the KT × KT matrix ${\mathit{V}}_{\tilde{\beta }}$. However, with our SVD regression, Trippe et al. (2019), show this to take the form:(5) $$\begin{array}{c}{\mathit{V}}_{\tilde{\beta }}={\left({\mathit{D}}_0^{-1}+\mathit{V} \text{diag} (\mathit{\lambda }\odot \mathit{\lambda })\mathit{V}\prime \right)}^{-1}\\ ={\mathit{D}}_0-{\mathit{D}}_0\mathit{V} {\left(\text{diag} {(\mathit{\lambda }\odot \mathit{\lambda })}^{-1}+\mathit{V}\prime {\mathit{D}}_0\mathit{V}\right)}^{-1}\mathit{V}\prime {\mathit{D}}_0,\end{array}$$(5) (6) $${\mathit{\mu }}_{\tilde{\beta }}={\mathit{V}}_{\tilde{\beta }}(\mathit{Z}\prime \widehat{\mathit{y}}+{\mathit{D}}_0^{-1}{\mathit{b}}_0),$$(6) with $\odot$ denoting the dot product. Crucially, the matrix $\mathbf{\Xi }={(\text{diag} {(\mathit{\lambda }\odot \mathit{\lambda })}^{-1}+\mathit{V}\prime {\mathit{D}}_0\mathit{V})}^{-1}$ is a diagonal matrix if Z is block-diagonal and thus trivial to compute. For a lower triangular matrix Z and a general prior covariance matrix, this result does not hold. However, if we set ${\mathit{D}}_0=\theta \times {\mathit{I}}_{KT}$ (i.e., assume a ridge-type prior) the matrix $\mathbf{\Xi }$ again reduces to a diagonal matrix.⁴ The main computational hurdle boils down to computing $\mathit{V}\mathbf{\Xi }\mathit{V}\prime$, but, for a block-diagonal Z it is a sparse matrix and efficient algorithms can be used. In case we use a lower triangular Z coupled with a ridge-prior, computation can be sped up enormously by noting that ${\mathit{\mu }}_{\tilde{\mathit{\beta }}}=\left[\mathit{V}\text{diag}\left(\frac{\mathit{\lambda }}{{\theta }^{-1}{\mathit{\iota }}_T+{\mathit{\lambda }}^2}\right)\right]\mathit{U}\prime \widehat{\mathit{y}}+{\mathit{D}}_0^{-1}{\mathit{b}}_0$. The resulting computation time, conditional on a fixed T, rises approximately linearly in K because most of the matrices involved are (block) diagonal and sparse. The key feature of our algorithm is that we entirely avoid inverting a full matrix. The only inversion involved is the one of $\mathbf{\Xi }$ which can be carried out in O(T) steps.

To efficiently simulate $\tilde{\mathit{\beta }}\sim \mathcal{N}({\mathit{\mu }}_{\tilde{\beta }},{\sigma }^2{\mathit{V}}_{\tilde{\beta }})$ using Equation (5)(5) $$\begin{array}{c}{\mathit{V}}_{\tilde{\beta }}={\left({\mathit{D}}_0^{-1}+\mathit{V} \text{diag} (\mathit{\lambda }\odot \mathit{\lambda })\mathit{V}\prime \right)}^{-1}\\ ={\mathit{D}}_0-{\mathit{D}}_0\mathit{V} {\left(\text{diag} {(\mathit{\lambda }\odot \mathit{\lambda })}^{-1}+\mathit{V}\prime {\mathit{D}}_0\mathit{V}\right)}^{-1}\mathit{V}\prime {\mathit{D}}_0,\end{array}$$(5) , we exploit Algorithm 3 proposed in Cong, Chen, and Zhou (2017). In the first step, this algorithm samples $\mathit{a}\sim \mathcal{N}({\mathbf{0}}_{TK},{\mathit{D}}_0)$ and $\mathit{b}\sim \mathcal{N}({\mathbf{0}}_T,\text{diag} {(\mathit{\lambda }\odot \mathit{\lambda })}^{-1})$. In the second step, a valid draw of $\tilde{\mathit{\beta }}$ is obtained by computing $\tilde{\mathit{\beta }}={\mathit{\mu }}_{\tilde{\beta }}+\sigma (\mathit{a}-{\mathit{D}}_0\mathit{V}\mathbf{\Xi }(\mathit{V}\prime {\mathit{D}}_0\mathit{a}+\mathit{b})$. Step 2 is trivial since $\mathbf{\Xi }$ is diagonal for a block-diagonal Z and also for a lower triangular Z with a ridge-prior. Hence, sampling of $\tilde{\mathit{\beta }}$ is fast and scalable to large dimensions.

In this subsection, we have described computationally efficient methods for doing Bayesian estimation in the homoscedastic Gaussian linear regression model when the number of explanatory variables is large. They can be used in any Big Data regression model, but here we are using them in the context of our TVP regression model written in static form as in Equation (3)(3) $$\mathit{y}=\mathit{X\gamma }+\mathit{Z}\tilde{\mathit{\beta }}+\sigma \mathit{\eta },$$(3) . These methods involve transforming the matrix of explanatory variables using the SVD. If the matrices of prior hyperparameters, ${\mathit{b}}_0$ and ${\mathit{D}}_0$, were known and if homoscedasticity were a reasonable assumption, then textbook, conjugate prior, results for Bayesian inference in the Gaussian linear regression model are all that is required. Analytical results are available for this case and there would be no need for MCMC methods. This is the case covered by Trippe et al. (2019). However, in macroeconomic data sets, homoscedasticity is often not a reasonable assumption. And it is unlikely that the researcher would be able to make sensible choices for ${\mathit{b}}_0$ and ${\mathit{D}}_0$ in this high-dimensional context. Accordingly, we will develop methods for adding stochastic volatility and propose a hierarchical prior for the regression coefficients.

3.2 Adding Stochastic Volatility

Stochastic volatility typically is an important feature of successful macroeconomic forecasting models (e.g., Clark 2011). We incorporate this by replacing ${\sigma }^2$ in Equation (3)(3) $$\mathit{y}=\mathit{X\gamma }+\mathit{Z}\tilde{\mathit{\beta }}+\sigma \mathit{\eta },$$(3) with $\mathbf{\Sigma }=\text{diag}({\sigma }_1^2,\dots ,{\sigma }_T^2)\otimes {\mathit{I}}_K$. This implies that the prior on $\tilde{\mathit{\beta }}$ is$$\tilde{\mathit{\beta }}|\mathbf{\Sigma }\sim \mathcal{N}({\mathit{b}}_0,\mathbf{\Sigma }{\mathit{D}}_0).$$

Note that the prior in a specific period is given by$${\tilde{\mathit{\beta }}}_t|{\sigma }_t^2\sim \mathcal{N}({\mathit{b}}_{0t},{\sigma }_t^2\mathbf{\Psi }),$$with ${\mathit{b}}_{0t}$ being the relevant block associated with the tth period. Thus, it can be seen that the degree of shrinkage changes with ${\sigma }_t^2$, implying less shrinkage in more volatile times. From a computational perspective, assuming that ${\sigma }_t^2$ scales the prior variances enables us to factor $\mathbf{\Sigma }$ out of the posterior covariance matrix and thus obtain computational gains because ${\mathit{D}}_0$ does not need to be updated for every iteration of the MCMC algorithm. From an econometric perspective, the feature that shrinkage decreases if error volatilities are large implies that, in situations characterized by substantial uncertainty, our approach naturally allows for large shifts in the TVPs and thus permits swift adjustments to changing economic conditions. Our forecasting results suggest that this behavior improves predictive accuracy in turbulent times such as the global financial crisis.

We assume that $h_t=\hspace{0.17em}\text{log}\hspace{0.17em}({\sigma }_t^2)$ follows an AR(1) process$$\begin{array}{c}{h}_t={\mu }_h+{\rho }_h(h_{t-1}-{\mu }_h)+{\sigma }_h{v}_t,\hspace{1em}{v}_t\sim \mathcal{N}(0,1),\\ h_0\sim \mathcal{N}\left(\mu ,\frac{{\sigma }_h^2}{1-{\rho }_h^2}\right).\end{array}$$

In our empirical work, we follow Kastner and Frühwirth-Schnatter (2014) and specify a Gaussian prior on the unconditional mean ${\mu }_h\sim \mathcal{N}(0,10)$, a Beta prior on the (transformed) persistence parameter $\frac{{\rho }_h+1}{2}\sim \mathcal{B}(25,5)$ and a nonconjugate Gamma prior on the process innovation variance ${\sigma }_h^2\sim \mathcal{G}(1/2,1/2)$. Bayesian estimation of the volatilities proceeds using MCMC methods based on the algorithm of Kastner and Frühwirth-Schnatter (2014). A small alteration to this algorithm needs to be made due to the dependency of the prior of $\widetilde{{\mathit{\beta }}_t}$ on ${\sigma }_t^2$ (see the online appendix for details).

3.3 Posterior Computation

Conditional on the specific choice of the prior on the regression coefficients (discussed in the next section) we carry out posterior inference using a relatively straightforward MCMC algorithm. Most steps of this algorithm are standard and we provide exact forms of the conditional posterior distributions, the precise algorithm and additional information on MCMC mixing in the online appendix. Here, it suffices to note that we repeat our MCMC algorithm 30,000 times and discard the first 10,000 draws as burn-in.

4 A Hierarchical Prior for the Regression Coefficients

4.1 General Considerations

With hierarchical priors, where ${\mathit{b}}_0$ and/or ${\mathit{D}}_0$ depend on unknown parameters, MCMC methods based on the full conditional posterior distributions are typically used. In our case, we would need to recompute the enormous matrix ${\mathit{V}}_{\tilde{\beta }}$ and its Cholesky factor at every MCMC draw. This contrasts with the nonhierarchical case with fixed ${\mathit{b}}_0$ and ${\mathit{D}}_0$ where ${\mathit{V}}_{\tilde{\beta }}$ is calculated once. Due to this consideration, we wish to avoid using MCMC methods based on the full posterior conditionals.

Many priors, including the three introduced here, have ${\mathit{D}}_0$ depending on a small number of prior hyperparameters. These can be simulated using a Metropolis–Hastings (MH) algorithm. With such an algorithm, updating of ${\mathit{V}}_{\tilde{\beta }}$ only takes place for accepted draws (in our forecasting exercise roughly 30% of draws are accepted). Since priors which feature closed form full conditional posteriors for the hyperparameters imply that ${\mathit{V}}_{\tilde{\beta }}$ needs to be recomputed for each iteration in our posterior simulator, this reduces computation time appreciably.

4.2 The Prior Covariance Matrix

In this article, we consider three different hierarchical priors for $\tilde{\mathit{\beta }}$. Since our empirical application centers on forecasting inflation, the predictors ${\mathit{x}}_t$ will be structured as follows ${\mathit{x}}_t=(y_{t-1},\dots ,y_{t-p_y},\mathit{d}{\prime }_{t-1},\dots ,\mathit{d}{\prime }_{t-p_d},1)\prime ,$ with ${\mathit{d}}_t$ denoting a set of N exogenous regressors and p_y and p_d being the maximum number of lags for the response and the exogenous variables, respectively. In what follows, we will assume that $p=p_y=p_d$. In principle, using different lags is easily possible.

The first prior is inspired by the Minnesota prior (see Litterman 1986). It captures the idea that own lags are typically more important than other lags and, thus, require separate shrinkage. It also captures the idea that more distant lags are likely to be less important than more recent ones. Our variant of the Minnesota prior translates these ideas to control the amount of time-variation, implying that coefficients on own lags might feature more time-variation while parameters associated with other lags feature less time-variation. The same notion carries over to coefficients related to more distant lags which should feature less time-variation a priori.

This prior involves two hyperparameters to be estimated: $\mathit{\theta }=({\zeta }_1,{\zeta }_2)\prime$. These prior hyperparameters are used to parameterize $\mathbf{\Psi }$ to match the Minnesota prior variances$${\left[\mathbf{\Psi }\right]}_{ii}=\{\begin{array}{c}\frac{{\zeta }_1^2}{l^2}\hspace{1em}\text{on}\mathrm{ }\text{the}\mathrm{ }\text{coefficients}\mathrm{ }\text{associated}\mathrm{ }\text{with}\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{y}_{t-l} (l=1,\dots ,p)\hfill \\ \mathrm{ }\frac{{\zeta }_2^2}{l^2}\frac{{\widehat{\sigma }}_y^2}{{\widehat{\sigma }}_j^2}\mathrm{ }\text{on}\mathrm{ }\text{the}\mathrm{ }\text{coefficients}\mathrm{ }\text{related}\mathrm{ }\text{to}\mathrm{ }{d}_{jt-l}\hfill \\ \mathrm{ }{\zeta }_2^2\mathrm{ }\text{on}\mathrm{ }\text{the}\mathrm{ }\text{intercept}\mathrm{ }\text{term}.\hfill \end{array}$$

Here, we let ${[\mathbf{\Psi }]}_{ii}$ denote the (i, i)th element of $\mathbf{\Psi }$, d_jt refers to the jth element of ${\mathit{d}}_t,{\widehat{\sigma }}_y^2,{\widehat{\sigma }}_j^2$ denotes the OLS variance obtained by estimating an AR(p) model in y_t and d_jt, respectively. The hyperpriors on ζ₁ and ζ₂ follow a Uniform distribution:$${\zeta }_j\sim \mathcal{U}({\mathfrak{s}}_{0,j},{\mathfrak{s}}_{1,j})\hspace{1em}\text{for}\hspace{1em}j=1,2.$$

The second prior we use is a variant of the g-prior involving a single prior hyperparameter: $\theta =\xi$. This specification amounts to setting $\mathbf{\Psi }=\xi \times \mathbf{\Omega },$ where $\mathbf{\Omega }$ is a diagonal matrix with the $(i,i)$th element being defined as ${[\mathbf{\Omega }]}_{ii}={\widehat{\sigma }}_y^2/{\widehat{\sigma }}_j^2$. For reasons outlined in Doan, Litterman, and Sims (1984), we depart from using the diagonal elements of ${(\mathit{X}\prime \mathit{X})}^{-1}$ to scale our prior and rely on the OLS variances of an AR(p) model as in the case of the Minnesota-type prior. The third prior is a ridge-type prior which simply sets $\mathbf{\Psi }=\xi \times {\mathit{I}}_K$. This specification is used in the case of a lower triangular Z for reasons outlined in Section 3. While being simple, this prior has been shown to work well in a wide range of applications (Griffin and Brown 2013).

Similar to the Minnesota prior we again use a Uniform prior on ξ in both cases$$\xi \sim \mathcal{U}({\mathfrak{s}}_0,{\mathfrak{s}}_1).$$

Since we aim to infer $\xi ,{\zeta }_1$ and ζ₂ from the data we set ${\mathfrak{s}}_0={\mathfrak{s}}_{0,1}={\mathfrak{s}}_{0,2}={10}^{-10}$ close to zero and $\{{\mathfrak{s}}_1,{\mathfrak{s}}_{1,1},{\mathfrak{s}}_{1,2}\}$ is specified as follows:(7) $${\mathfrak{s}}_1={\mathfrak{s}}_{1,j}=\kappa \frac{T}{K^2}\hspace{1em}\text{for}\hspace{1em}j=1,2.$$(7)

Here, κ is a constant being less or equal than unity to avoid excessive overfitting in light of large K and T. Since large values of κ translate into excessive time variation in ${\tilde{\mathit{\beta }}}_t$, we need to select κ carefully. The hyperparameters of this prior are inspired by the risk inflation criterion put forward in Foster et al. (1994) which would correspond to setting $\xi =1/K^2$. Since this prior was developed for a standard linear regression model, it would introduce too little shrinkage in our framework (or, if we set $\xi =1/{(TK)}^2$ too much shrinkage, ruling out any time-variation). Our approach lets the data speak but essentially implies that the bound of the prior is increasing in T and decreasing in the number of covariates. Intuitively speaking, our prior implies that if the length of the time series increases, the prior probability of observing substantial structural breaks also increases slightly.

In the empirical application, we infer κ over a grid of values and select the κ that yields the best forecasting performance in terms of log predictive scores. Further discussion of and empirical evidence relating to κ (and G) is given in Section C of the online appendix.

The methods developed in this article will hold for any choice of prior covariance matrix, ${\mathit{D}}_0$, although assuming it to be diagonal greatly speeds up computation. In this subsection, we have proposed three forms for it which we shall (with some abuse of terminology) refer to as the Minnesota, g-prior and ridge-prior forms, respectively, in the following material.

4.3 The Prior Mean

As for the prior mean, ${\mathit{b}}_0$, it can take a range of possible forms. The simplest option is to set it to zero. After all, from Equation (3)(3) $$\mathit{y}=\mathit{X\gamma }+\mathit{Z}\tilde{\mathit{\beta }}+\sigma \mathit{\eta },$$(3) , it can be seen that ${\tilde{\mathit{\beta }}}_t$ measures the deviation from the constant coefficient case which, on average, is zero. This is what we do with the Minnesota prior and if we set Z to be lower triangular.⁵ However, it is possible that we can gain estimation accuracy through pooling information across coefficients by adding extra layers to the prior hierarchy. In this article, we do so using a sparse finite location mixture of Gaussians and adapt the methods of Malsiner-Walli, Frühwirth-Schnatter, and Grün (2016) to the TVP regression context. Sparse finite mixtures, relative to Dirichlet process mixtures, have the advantage of being finite dimensional while allowing the number of clusters to be random a priori. The number of groups can then be inferred during MCMC sampling by counting the number of nonempty regimes.⁶

In the discussion below, we refer to these two treatments of the prior mean as nonclustered and clustered, respectively. With the g-prior, we consider both clustered and nonclustered approaches.

We emphasize that both of these specifications for the prior mean are very flexible and let the data decide on the form that the change in parameters takes. This contrasts with standard TVP regression models, where it is common to assume that the states evolve according to random walks. This implies that the prior mean of ${\mathit{\beta }}_t$ is ${\mathit{\beta }}_{t-1}$.

With the clustered approach, we assume that each ${\tilde{\mathit{\beta }}}_t$ has a prior of the following form:$$f_{\mathcal{N}}({\tilde{\mathit{\beta }}}_t|{\mathit{\mu }}_1,\dots ,{\mathit{\mu }}_G,\mathit{w},{\sigma }_t^2,\mathbf{\Psi })=\sum _{g=1}^G{w}_g{f}_{\mathcal{N}}({\tilde{\mathit{\beta }}}_t|{\mathit{\mu }}_g,{\sigma }_t^2\mathbf{\Psi }),$$where $f_{\mathcal{N}}$ denotes the density of a Gaussian distribution and w are component weights with ${\sum }_{g=1}^G{w}_g=1$ and $w_g\ge 0$ for all g. ${\mathit{\mu }}_g (g=1,\dots ,G)$ denotes G component-specific means with G being a potentially large integer that is much smaller than T (i.e., $G\ll T)$.

An equivalent representation, based on auxiliary variables δ_t, is(8) $$\widetilde{{\mathit{\beta }}_t}|{\delta }_t=g\sim \mathcal{N}({\mathit{\mu }}_g,{\sigma }_t^2\mathbf{\Psi }),$$(8) with $\text{Pr}({\delta }_t=g)=w_g$ being the probability that $\widetilde{{\mathit{\beta }}_t}$ is assigned to group g. Equation (8)(8) $$\widetilde{{\mathit{\beta }}_t}|{\delta }_t=g\sim \mathcal{N}({\mathit{\mu }}_g,{\sigma }_t^2\mathbf{\Psi }),$$(8) can be interpreted as a state evolution equation which resembles a hierarchical factor model since each $\widetilde{{\mathit{\beta }}_t}$ clusters around the different component means ${\mathit{\mu }}_g$. As opposed to assuming a random walk state evolution, which yields smoothly varying TVPs, this model provides more flexibility by pulling $\widetilde{{\mathit{\beta }}_t}$ towards $G\le T$ prior means. Under the prior in Equation (8)(8) $$\widetilde{{\mathit{\beta }}_t}|{\delta }_t=g\sim \mathcal{N}({\mathit{\mu }}_g,{\sigma }_t^2\mathbf{\Psi }),$$(8) , our model can be interpreted as a random coefficients model (for a Bayesian treatment, see, for example, Frühwirth-Schnatter, Tüchler, and Otter 2004).

Before proceeding to the exact prior setup, it is worth noting that the mixture model is not identified with respect to relabeling the latent indicators. In the forecasting application, we consider functions of the states which are not affected by label switching. Thus, we apply the random permutation sampler of Frühwirth-Schnatter (2001) to randomly relabel the states in order to make sure that our algorithm visits the different modes of the posterior. In what follows, we define ${\mathit{m}}_t={\mathit{\mu }}_g$ if ${\delta }_t=g$. Using this notation, the prior mean is given by ${\mathit{b}}_0=({\mathit{m}}_1^{\prime },\dots ,\mathit{m}{\prime }_T)\prime$.

For the weights $\mathit{w}=(w_1,\dots ,w_G)\prime$, we use a symmetric Dirichlet prior$$\mathit{w}|\pi \sim \text{Dir}(\pi ,\dots ,\pi ).$$

Here, π denotes the intensity parameter that determines how the model behaves in treating superfluous components. If $\pi \le K/2$, irrelevant components are emptied out while if $\pi >K/2$, the model tends to duplicate component densities to handle overfitting issues. This implies that careful selection of π is crucial since it influences the number of breaks in ${\tilde{\mathit{\beta }}}_t$. The literature suggests different strategies based on using traditional model selection criteria or reversible jump MCMC algorithms to infer G from the data. Our approach closely follows Malsiner-Walli, Frühwirth-Schnatter, and Grün (2016) and used a shrinkage prior on π. The prior we adopt follows a Gamma distribution:$$\pi \sim \mathcal{G}(a,aG),$$with a = 10 being a hyperparameter that determines the tightness of the prior (Malsiner-Walli, Frühwirth-Schnatter, and Grün 2016). The prior on w and π can be rewritten as follows:$$\mathit{w}\sim \text{Dir}(a/G,\dots ,a/G),\hspace{1em}a\sim \mathcal{G}(10,10).$$

Frühwirth-Schnatter, Malsiner-Walli, and Grün (2020) and Greve et al. (2020) analyzed this prior choice and show that it performs well.⁷

To assess which elements in ${\mathit{\mu }}_g$ determine the group membership, we use yet another shrinkage prior on the component means$${\mathit{\mu }}_g|\mathbf{\Pi },\tilde{\mathit{\beta }}\sim \mathcal{N}({\mathit{\mu }}_0,\mathbf{\Pi }),$$whereby $\mathbf{\Pi }=\mathbf{\Upsilon }\mathit{R}\mathbf{\Upsilon }$ with $\mathbf{\Upsilon }=\text{diag}(\sqrt{{\upsilon }_1},\dots ,\sqrt{{\upsilon }_K})$ and $\mathit{R}=\text{diag}(R_1^2,\dots ,R_K^2)$. We let R_j denote the range of ${\tilde{\mathit{\beta }}}_j=({\tilde{\beta }}_{j1},\dots ,{\tilde{\beta }}_{jT})\prime$. The prior on ${\upsilon }_j (j=1,\dots ,K)$ follows a Gamma distribution:$${\upsilon }_j\sim \mathcal{G}(c_0,c_1),$$ translating into the Normal-Gamma prior of Griffin and Brown (2010). In the empirical application, we set $c_0=c_1=0.6$, with $c_0<1$ being crucial for pushing the idiosyncratic group means ${\mathit{\mu }}_g$ strongly toward the common mean ${\mathit{\mu }}_0$ (Malsiner-Walli, Frühwirth-Schnatter, and Grün 2016). For ${\mathit{\mu }}_0$, we use an improper Gaussian prior with mean set equal zero and infinite variance.

This location mixture model is extremely flexible in the types of parameter change that are possible. It allows us to capture situations where the breaks in parameters are large or small and frequent or infrequent. It can effectively mimic the behavior of break point/Markov switching models, standard time-varying parameter (TVP) models, mixture innovation models and many more. The common variance factor implicitly affects the tightness of the prior and ensures (conditional) conjugacy.

Compared to a standard TVP model which assumes a random walk state evolution, our prior on ${\mathit{\beta }}_t$ is invariant with respect to time, up to a scaling factor σ_t. If σ_t is constant, $({\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_T)$ has the same prior distribution as $({\mathit{\beta }}_{\rho (1)},\dots ,{\mathit{\beta }}_{\rho (T)})$ for any permutation ρ. In our general case, temporal dependence is not an assumption, but arises through appropriately choosing ${\mathit{x}}_t$ and by allowing for prior dependence on σ_t. In the extreme case where ${\mathit{x}}_t$ does not include lagged values of y_t (we include several lags of y_t in our empirical work) and σ_t is constant, the dynamic nature of the model is lost since the model is invariant to reordering the time series with respect to t and no dependency is imposed.

5 Illustration Using Artificial Data

In this section we illustrate our modeling approach that uses the g-prior and clustering by means of synthetic data simulated from a simple data-generating process (DGP).

We begin by illustrating the computational advantages arising from using the SVD, relative to a standard Bayesian approach to TVP regression which involves random walk evolution of the coefficients and the use of FFBS as well as a model estimated using the precision sampler all without a loop (AWOL, see Chan and Jeliazkov 2009; McCausland, Miller, and Pelletier 2011; Kastner and Frühwirth-Schnatter 2014). Figure 1(a) shows a comparison of the time necessary to generate a draw from $p(\tilde{\mathit{\beta }}|\text{Data},\mathit{\gamma },{\sigma }^2)$ using our algorithm based on the SVD, the FFBS algorithm and the AWOL sampler as a function of $K\in \{1,2,\dots ,150\}$ and for T = 200.⁸

Fig. 1 Runtime comparison: SVD, FFBS and AWOL.

NOTE: The figure shows the actual and theoretical time necessary to obtain a draw of $\tilde{\mathit{\beta }}$ using our proposed SVD algorithm for Z being block-diagonal and lower triangular, an AWOL sampler (implemented in R through the shrinkTVP package of Knaus et al. 2021) and the FFBS algorithm. The dashed red lines refer to the SVD approach with a lower triangular Z and a ridge-prior, the orange dashed line refers to the SVD algorithm with block-diagonal Z, the dashed green lines refer to the AWOL sampler, while the dashed blue lines indicate the FFBS. The dots refer to theoretical run times. Here, we fit a nonlinear trend on the empirical estimation times.

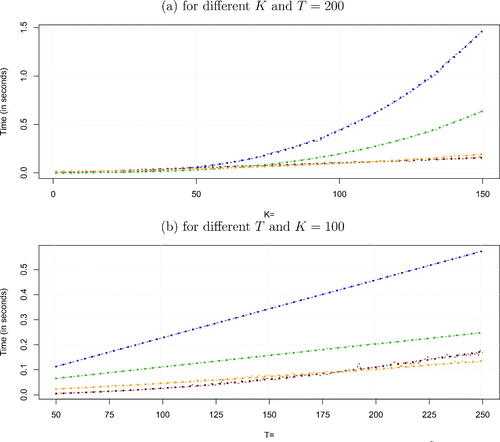
To illustrate how computation times change with T, Figure 1(b) shows computation times as a function of $T\in \{50,\dots ,250\}$ for K = 100. The dashed lines refer to the actual time (based on a cluster with 400 IntelE5-2650v3 2.3 GHz cores) necessary to simulate from the full conditional of the latent states while the dots indicate theoretical run times through a (non)linear trend.

In Panel (a), we fit a (non)linear trend on the empirical estimation times of the different approaches. This implies that while the computational burden is cubic in the number of covariates K for the FFBS approach, our technique based on using the SVD suggests that runtimes increase (almost) linearly in K. Notice that the figure clearly shows that traditional algorithms based on FFBS quickly become infeasible in high dimensions. Up to $K\approx 50$, our algorithm (for both choices of Z) is slightly slower while the computational advantage increases remarkably with K, being more than four times as fast for K = 100 and over nine times as fast for K = 150. When we compare the SVD to the AWOL algorithm, we also observe sizeable improvements in estimation times. For K = 150, our proposed approach is almost four times faster. This performance is even more impressive given that our SVD approach is implemented in R, a high-level interpreted language, while both FFBS and AWOL are efficiently implemented in Rcpp (Eddelbuettel et al. 2011).

Panel (b) of the figure shows that, for fixed K, computation times increase linearly for most approaches if T is varied. The main exception is the case of a lower triangular Z, with computation times growing nonlinearly in T. This is because this approach relies on several nonsparse matrix-vector products. Since T is typically moderate in macroeconomic data this does not constitute a main bottleneck of the algorithm for general matrices Z. It is, moreover, noteworthy that the slope of the line referring to FFBS is steeper than the ones associated with the SVD (for block-diagonal Z) and AWOL approaches. This reflects the fact that one needs to perform a filtering (that scales linearly in T) and smoothing step (that is also linear in T). This brief discussion shows that the SVD algorithm scales well and renders estimation of huge dimensional models feasible.

We now assume that y_t is generated by the following DGP:$$y_t={\tilde{\beta }}_t+{\epsilon }_t,\hspace{1em}{\epsilon }_t\sim \mathcal{N}(0,{0.1}^2),$$for $t=1,\dots ,160$, γ = 0, and ${\tilde{\beta }}_t\sim \mathcal{N}(m_t,{0.1}^2)$. ${\tilde{\beta }}_t$ depends on m_t which evolves according to the following law of motion:$$\begin{array}{c}{m}_t=3\times I(t\le 60)+1\times I(60<t\le 85)-3\\ \times I(85<t\le 120)-1\times I(t>120),\end{array}$$ with $I(•)$ being the indicator function that equals 1 if its argument is true.

Analyzing this stylized DGP allows us to illustrate how our approach can be used to infer the number of latent clusters that determine the dynamics of ${\tilde{\beta }}_t$. In what follows, we simulate a single path of y_t and use this for estimating our model. We estimate the model using the g-prior with clustering and set G = 12. In this application, we show quantities that depend on the labeling of the latent indicators. This calls for appropriate identifying restrictions and we introduce the restriction that ${\mu }_1<\dots <{\mu }_G$. This is not necessary if interest centers purely on predictive distributions and, thus, we do not impose this restriction in the forecasting section of this article.

Before discussing how well our model recovers the true state vector ${\tilde{\beta }}_t$, we show how our modeling approach can be used to infer the number of groups G. Following Malsiner-Walli, Frühwirth-Schnatter, and Grün (2016), the number of groups is estimated during MCMC sampling as follows:$$G_0^{(j)}=G-\sum _{g=1}^{G}I\left(T_g^{(j)}=0\right)$$with $T_g^{(j)}$ denoting the number of observations in cluster g for the $j^{\text{th}}$ MCMC draw. This yields a posterior distribution for G₀. Its posterior mode can be used as a point estimate of G.

In Table 1, we report the posterior probability of a given number of regimes by simply computing the fraction of draws with $G_0=g$ for $g=1,\dots ,12$. The table suggests that the probability that $G_0=4$ is around 66%. This indicates that our algorithm successfully selects the correct number of groups, since the mode of the posterior distribution equals four. It is also worth noting that the posterior mean of π is very small at 0.09, suggesting that our mixture model handles irrelevant components by emptying them instead of replicating them (which would be the case if π becomes large). Notice, however, that .$G_0=5$ also receives some posterior support. We have a probability of about 26 percent associated with a too large number of regimes. In the present model, this slight overfitting behavior might be caused by additional noise driven by the shocks to the states $$, with our mixture model trying to fit the noise.

Table 1 Posterior probabilities for a given number of groups $G(=12)$.

$G_0=$	1	2	3	4	5	6	7	8	9	10	11	12
	0.00	0.00	0.00	0.66	0.26	0.07	0.01	0.00	0.00	0.00	0.00	0.00

Next, we assess whether our model is able to recover ${\tilde{\beta }}_t$ and m_t. Figure 2 shows the pointwise 16th and 84th percentiles of the posterior distribution (in solid black) of ${\tilde{\beta }}_t$ (see Panel (a)) and m_t (see Panel (b)) over time. The gray shaded areas represent the 16th and 84th percentiles of the posterior of ${\tilde{\beta }}_t$ obtained from estimating a standard TVP regression model with random walk state equations and stochastic volatility. Apart from the assumption of random walk evolution of the states, all other specification choices are made so as to be as close as possible to our SVD approach. In particular, this model features the hierarchical Normal-Gamma prior (see Griffin and Brown 2010) on both the time-invariant part of the model and the signed square root of the state innovation variances (Bitto and Frühwirth-Schnatter 2019). It is estimated using a standard FFBS algorithm. We refer to this model as TVP-RW-FFBS.

Fig. 2 Posterior distribution of ${\tilde{\beta }}_t$ and m_t.

NOTE: Panel (a) shows 16th/84th posterior percentiles of ${\tilde{\beta }}_t$ for our proposed model (solid black lines) and a standard TVP regression with random walk state equation (gray shaded area). The red line denotes the actual outcome. Panel (b) shows the 16th/84th percentiles of the posterior distribution of m_t (in solid black) and the true value of m_t (in solid red).

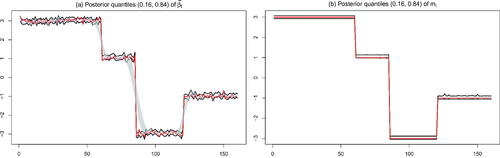
In Figure 2, the red lines denote the true value of ${\tilde{\beta }}_t$ and m_t, respectively. Panel (a) clearly shows that our model successfully detects major breaks in the underlying states, with the true value of ${\tilde{\beta }}_t$ almost always being located within the credible intervals. Our modeling approach not only captures low frequency movements but also successfully replicates higher frequency changes. By contrast, the posterior distribution of the TVP-RW-FFBS specification is not capable of capturing abrupt breaks in the latent states. Instead of capturing large and infrequent changes, the TVP-RW-FFBS approach yields a smooth evolution of ${\tilde{\beta }}_t$ over time, suggesting that our proposed approach performs comparatively better in learning about sudden breaks in the regression coefficients.

Considering Panel (b) of Figure 2 reveals a similar picture. Our approach yields credible sets that include the actual outcome of m_t for all t. This discussion shows that our model also handles cases with infrequent breaks in the regression coefficients rather well. As compared to standard TVP regressions that imply a smooth evolution of the states, using a mixture model to determine the state evolution enables us to capture large and abrupt breaks.

The previous discussion has shown that our model works well if the DGP is characterized by relatively few breaks. In the next step, we test the model under a less favorable DGP: we assume that the law of motion of ${\tilde{\beta }}_t$ is a random walk with a state innovation variance of one and ${\tilde{\beta }}_0=3$. The results are shown in Figure 3 and Table 2. Panel (a) shows that even when the DGP is characterized by many small breaks, our model is flexible enough to capture this behavior as well. This is because we essentially pool coefficients but also allow for idiosyncratic (i.e., time-specific) deviations from the common mean. If we consider Panel (b) we observe that the mean process m_t captures the bulk of the variation in ${\tilde{\beta }}_t$. Table 2 suggests that even if we set G = 30, the sparse finite mixture allocates substantial posterior mass to lower values of G (with values of G between 15 and 21), but still is able to retrieve over 80% of the posterior mass. Hence, even if the true DGP is a random walk and G is much smaller than T, our approach accurately recovers the full history of the latent states.

Fig. 3 Posterior distribution of ${\tilde{\beta }}_t$ and m_t.

NOTE: Panel (a) shows 16th/84th posterior percentiles of ${\tilde{\beta }}_t$ for our proposed model (solid black lines) and a standard TVP regression with random walk state equation (gray shaded area). Panel (b) shows the 16th/84th percentiles of the posterior distribution of m_t (in solid black). The red lines denote the actual outcome of ${\tilde{\beta }}_t$.

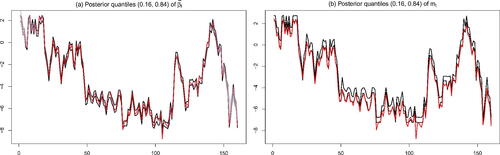
Table 2 Posterior probabilities for a given number of groups …

$G_0=$	12	13	14	15	16	17	18	19	20	21	22	23
	0.01	0.02	0.04	0.07	0.13	0.18	0.16	0.15	0.12	0.07	0.03	0.02

6 An Application to the US Inflation

6.1 Data and Selected In-Sample Features

Modeling and forecasting inflation is of great value for economic agents and policymakers. In the most central banks, inflation is the main policy objective and the workhorse forecasting model is based on some version of the Phillips curve. The practical forecasting of inflation is difficult (see Stock and Watson 2007) and the persistence of low inflation in the presence of a closing output gap in recent years has led to a renewed debate about the usefulness of the curve as a policy instrument in the United States (see, e.g., Ball and Mazumder 2011; Coibion and Gorodnichenko 2015).

There are three main issues when forecasting inflation. A first problem is that the theoretical literature relating to the Phillips curve and the determination of inflation includes a large battery of very different specifications, emphasizing domestic vs. international variables, forward vs. backward looking expectations or including factors such as labor market developments. The overall number of potential predictors can be quite large (see Stock and Watson 2008). Second, within each econometric specification there is considerable uncertainty about which indicator should be used as a proxy for the economic cycle (see Moretti, Onorante, and Zakipour Saber 2019). Third, there are structural breaks that make different variables and specifications more or less important at different times (see Koop and Korobilis 2012). The Great Recession, for example, is universally considered as a structural break that requires appropriate econometric techniques.

The mainstream literature has dealt with the curse of dimensionality which arises in TVP regressions with many predictors in several ways. Until recently, the two main approaches included principal components or strong Bayesian shrinkage. A comparison of the two approaches can be found in De Mol, Giannone, and Reichlin (2008). Following Raftery, Kárný, and Ettler (2010), a second stream of research uses model combination to deal with the curse of dimensionality and the fact that models can change over time (e.g., Koop and Korobilis 2012). Finally, a recent (but expanding) stream of literature forecasts inflation using machine learning techniques (Medeiros et al. 2021). These methods, although useful, suffer from the “black box problem;” while their accuracy compares well with other techniques, they are not able to show how the result is obtained and thus do not offer a simple interpretation.⁹

For the reasons above, inflation forecasting is an ideal empirical application in which we can investigate the performance of our methods. An important criterion is the capacity of our approach to generalize standard TVP models, which are less flexible because they are based on random walk or autoregressive specifications to determine the evolution of the states. A second challenge is the correct detection of well-known structural breaks. In addition, we assess the forecasting performance of our methods relative to alternative approaches.

Following Stock and Watson (1999), we define the target variable as follows:$$y_{t+h}=\hspace{0.17em}\text{ln}\hspace{0.17em}\left(\frac{P_{t+h}}{P_t}\right)-\hspace{0.17em}\text{ln}\hspace{0.17em}\left(\frac{P_t}{P_{t-1}}\right),$$with $P_{t+h}$ denoting the price level (CPIAUCSL) in period t + h. Using this definition, we estimate a generalized Phillips curve involving 49 covariates plus the lagged value of y_t that cover different segments of the economy. Further information on the specific variables included and the way they are transformed is provided in Section B of the online appendix. The design matrix ${\mathit{x}}_t$ includes $p=p_y=p_d=2$ lags and an intercept and thus features K = 101 covariates.

Before we use our model to perform forecasting, we provide some information on computation times, illustrate some in-sample features of our model and briefly discuss selected posterior estimates of key parameters.

Table 3 shows empirical runtimes (in minutes) for estimating the different models for this large dataset. As highlighted in the beginning of Section 5, our approaches start improving upon FFBS-based algorithms in terms of computation time if K exceeds 50, with the improvements increasing nonlinearily in K. Hence, it is unsurprising that, for our present application with K = 101, our algorithm (without clustering) is almost five times faster than using FFBS and twice as fast as the efficient AWOL sampler. If clustering is added, our approach is still more than three times faster than FFBS. The additional computational complexity from using the clustering prior strongly depends on G. If G is close to T (which typically does not occur in practice and we thus do not consider this case), then the computation time increases and the advantage of using the SVD is diminished. This arises since estimating the location parameters of the mixtures becomes the bottleneck in our MCMC algorithm. Finally, using a random walk state evolution equation (i.e., a lower triangular Z) with a ridge-prior yields the strongest gains in terms of computational efficiency, being almost six times faster than FFBS and over twice as fast than the AWOL sampler.

Table 3 Runtime comparison of empirical exercise (K = 101; $T=212;G=30$) with 30,000 draws from the posterior distribution.

	SVD			FFBS	shrinkTVP	TIV
	WN (g-prior clustering)	WN (g-prior)	RW (ridge-prior)	RW	RW
Time (in minutes)	103	76	64	377	150	16

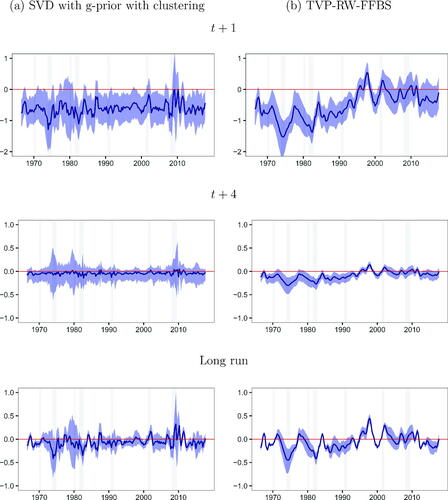
To further illustrate the properties of the estimated parameters in our SVD approach using the g-prior with clustering we now turn to a small-scale model. In this case, the number of coefficients is relatively small and features such as multipliers with an economic interpretation can be easily plotted. This model is inspired by the New Keynesian Phillips curve (NKPC). The dependent variable is inflation and the right hand side variables include two lags of unemployment and inflation. We set G = 30, thus allowing for a relatively large number of clusters.

Figure 4 plots multipliers (i.e., the cumulative effect on inflation of a change in unemployment at various horizons). A comparison of SVD to TVP-RW-FFBS shows many similarities. For instance, both models are saying an increase in unemployment has a negative effect on inflation in the very short term for much of the time. This is what the NKPC would lead us to expect. However, for SVD this negative effect remains for most of the time after the financial crisis, whereas for TVP-RW-FFBS, it vanishes and the NKPC relationship breaks down. Another difference between the two approaches can be seen in many recessions where the estimated effect changes much more abruptly using our approach than with TVP-RW-FFBS. This illustrates the great flexibility of our approach in terms of the types of parameter change allowed for. And this flexibility does not cost us much in terms of estimation precision in the sense that the credible intervals for the two approaches have similar width.

Fig. 4 Posterior means of multipliers.

NOTE: Blue shaded areas are 68% credible intervals and gray shaded areas denote NBER recessions.

Figure 5 displays the posterior of G₀, the number of clusters selected by the algorithm. The posterior is spread over a range of values, although almost all of the posterior probability is associated with a number of clusters between ten and 20. $G_0=1$ implies that ${\tilde{\mathit{\beta }}}_t$ is centered around a nonzero value that is time-invariant and there is little posterior evidence in this figure indicating support for this. This is the lower bound on the number of clusters. The upper bound on the number of clusters is 30, but the posterior probability lies in a region far below 30 indicating that the algorithm is successfully finding parsimonious representations for the time variation in parameters. It is worth stressing that these statements hold for the small NKPC model. For the large model with K = 101, we find the number of clusters to be even smaller. In this case the posterior mode is eight clusters. This inverse relationship between K and G₀ is to be expected. That is, as model size increases, more of the variation over time can be captured by the richer information set in ${\mathit{x}}_t$, leaving less of a role for time variation in coefficients. Our clustering algorithm automatically adjusts to this effect.

Fig. 5 Posterior distribution of number of nonempty clusters (G₀).

NOTE: G₀ refers to the nonempty groups with G = 30. The red line denotes the median of G₀.

6.2 Forecasting Evidence

The forecasting design adopted is recursive. We consider an initial estimation period from 1965Q1 to 1999Q4. The remaining observations (2000Q1 to 2018Q4) are used as a hold-out period to evaluate our forecasting methods. After obtaining $h\in \{1,4\}$-step-ahead predictive distributions for a given period in the hold-out, we include this period in the estimation sample and repeat this procedure until we reach the end of the sample. In order to compute longer horizon forecasts, we adopt the direct forecasting approach (see, e.g., Stock and Watson 2002). To assess forecasting accuracy, we use root mean square forecast errors (RMSEs) for point forecasts and log predictive likelihoods (LPLs, these are averaged over the hold-out period) for density forecasts. We evaluate the statistical significance of the forecasts relative to random walk (RW) forecasts using the Diebold and Mariano (1995) test.

We compare four variants of our SVD approach (i.e., the Minnesota prior, the g-prior with and without clustering and the SVD model with a random walk-type state evolution, labeled TVP-RW-SVD) to alternatives which vary in their treatment of parameter change and in the number of explanatory variables. With regards to parameter change, we consider the time-invariant (TIV) model (which sets ${\tilde{\mathit{\beta }}}_t=\mathbf{0}$ for all t) and the TVP-RW-FFBS approach which has random walk parameter change. Moreover, as an alternative treatment of the TVPs we consider the model of Chan, Eisenstat, and Strachan (2020) which introduces a factor structure in the latent states (labeled TVP-fac-FFBS).

With regard to the number of explanatory variables, we consider models with two lags of all 50 of them (labeled FULL in the tables), none of them as well as some specifications which contain a subset of them. To be specific, we present results for all these models using the NKPC specification discussed in the preceding sub-section (labeled NKPC in the tables). We also have versions of the model where the intercept is the only explanatory variable, thus leading to an unobserved components model (labeled UCM in the tables).¹⁰

In addition, we include some simple benchmarks that have been used elsewhere in the literature. These include a constant coefficient AR(2) model, a TVP-AR(2) and an AR(2) augmented with the two lags of the first three principal components of ${\mathit{d}}_t$ (this is labeled PCA3). This model is closely related to the diffusion index model of Stock and Watson (2002). Additionally, we also compress the data to three dimensions using targeted random compressions (labeled TARP, see Mukhopadhyay and Dunson 2020). For each of these two dimension reduction techniques, we also present forecasts for a TVP-RW-FFBS model. All models considered include stochastic volatility.

Table 4 contains our main set of forecasting results. Note first that, with some exceptions, the FULL models do best, indicating that there is information in our K = 50 variables useful for inflation forecasting. If we focus on results for the FULL models, then it can be seen that, for h = 1 all of the approaches forecast approximately as well as each other. But for h = 4, there are substantial improvements provided by our SVD approaches relative to the competitors. At this forecast horizon, it is interesting to note that the very parsimonious UCM version of the TVP-RW-FFBS provides point forecasts that are almost as good as those provided by the FULL SVD approaches. However, the density forecasts provided by the UCM are appreciably worse than those provided by the SVD approaches. The FULL SVD approaches are also beating approaches based on dimension reduction (PCA, TARP), even if we allow for time-variation in the coefficients for these models.

Table 4 Forecasting performance of SVD approaches relative to benchmarks.

Specification			Forecast horizon
TVP/TIV	Type	κ	1-step	4-steps
AR(p)
TIV	Benchmark		0.90	0.77${}^{***}$
			(0.08)	(0.23${}^{***}$)
TVP-RW-FFBS	Benchmark		0.90	0.75${}^{***}$
			(0.08)	(0.26${}^{***}$)
FULL
TIV	Benchmark		0.82${}^{*}$	0.61${}^{**}$
			(0.15)	(0.37)
TVP-fac-FFBS	Benchmark		0.83${}^{**}$	0.63
			(0.17${}^{**}$)	(0.25)
TVP-RW-FFBS	Benchmark		0.78${}^{*}$	0.92
			(0.16)	(0.01)
TVP-RW-SVD	ridge-prior	0.001	0.81${}^{**}$	0.62${}^{**}$
			(0.14)	(0.43${}^{***}$)
TVP-WN-SVD	g-prior	0.1	0.80${}^{***}$	0.59${}^{**}$
			(0.15${}^{**}$)	(0.42${}^{*}$)
TVP-WN-SVD	g-prior (clustering)	0.05	0.80${}^{***}$	0.57${}^{***}$
			(0.17${}^{**}$)	(0.48${}^{***}$)
TVP-WN-SVD	Minnesota	0.1	0.82${}^{**}$	0.61${}^{**}$
			(0.16${}^{*}$)	(0.37${}^{*}$)
NKPC
TIV	Benchmark		0.91	0.82${}^{***}$
			(0.06)	(0.12)
TVP-RW-FFBS	Benchmark		0.92	0.86
			(0.07)	(-0.28${}^{*}$)
TVP-WN-SVD	g	0.001	0.89	0.79${}^{***}$
			(0.07)	(0.13)
TVP-WN-SVD	g-prior (clustering)	0.001	0.90	0.80${}^{***}$
			(0.07)	(0.12)
TVP-WN-SVD	Minnesota	0.001	0.91	0.81${}^{***}$
			(0.05)	(0.13)
PCA3
TIV	Benchmark		0.92	0.83${}^{***}$
			(0.06)	(0.18${}^{***}$)
TVP-RW-FFBS	Benchmark		0.88	0.86
			(0.09)	(0.05)
TARP
TIV	Benchmark		0.99	0.85${}^{***}$
			(0.01)	(0.15${}^{***}$)
TVP-RW-FFBS	Benchmark		0.92${}^{***}$	0.82
			(0.14${}^{***}$)	(0.17)
UCM
TVP-RW-FFBS	Benchmark		0.86${}^{***}$	0.59${}^{**}$
			(0.16)	(0.16)
TVP-WN-SVD	g-prior (clustering)	1	0.88${}^{*}$	0.71
			(0.08)	(0.14)

NOTE: The table shows RMSEs with LPL’s in parentheses below. Asterisks indicate statistical significance for each model relative to a random walk at the 1 (${}^{***}$), 5 (${}^{**}$) and 10 (${}^{*}$) percent significance levels.

Comparing the results of our SVD-based models with a block-diagonal Z to the ones which constrain the state evolution (i.e., TVP-RW-FFBS, TVP-fac-FFBS and TVP-RW-SVD) sheds light on how much the increased flexibility improves forecasting accuracy. In terms of one-step-ahead forecasts, we find that our flexible approaches yield very similar forecasts to the ones of TVP regressions with random walk state equations. This is consistent with the statement that for short-term forecasting, our model yields forecasts which are competitive to established methods in the literature. When we consider multi-step-ahead forecasts we find pronounced improvements in terms of point and density forecasts for the FULL and NKPC models. Notice the better performance of TVP-fac-FFBS and TVP-RW-SVD relative to TVP-RW-FFBS. In the latter case, this is driven by the ridge-type prior which strongly shrinks the TVPs toward zero whereas in the former case, the better performance can be attributed to the parsimonious factor structure on the TVPs.

With two different forecast horizons and two different forecast metrics, we have four possible ways of evaluating any approach. For three of these, the FULL SVD approach using the g-prior with clustering performs best. The only exception to this is for RMSEs for h = 1, although even here FULL SVD with g-prior is the second best performing approach. The improvements relative to our other SVD approaches which do not involve clustering are small, but are consistently present. This indicates the benefits of the clustering prior.

In general, the TIV approaches do well (for h = 4 even better than TVP-RW-FFBS) in terms of point forecasts, but the density forecasts produced by our SVD approaches are slightly better. This suggests there is only a small amount of time-variation in this data set, but that our SVD approach (particularly when we add the hierarchical clustering prior) is effectively capturing structural breaks in a manner that the random walk evolution of the TVP-RW-FFBS and TVP-RW-SVD cannot.

Figure 6 provides evidence of forecast performance over time for selected models used in this forecasting exercise. The lines in this figure are cumulated log predictive Bayes factors relative to a random walk.

Fig. 6 Evolution of log predictive Bayes factor relative to RW.

NOTE: The log predictive Bayes factors are cumulated over the hold-out. For the TVP-SVD models the solid line refers to the g-prior with clustering, the dashed line to the Minnesota prior and the dot-dashed line to the g-prior without clustering (each with block-diagonal Z), while the dotted line refers to the ridge-prior (with lower triangular Z). The dashed black lines refer to the maximum Bayes factor at the end of the hold-out sample. The gray shaded areas indicate the NBER recessions in the US.

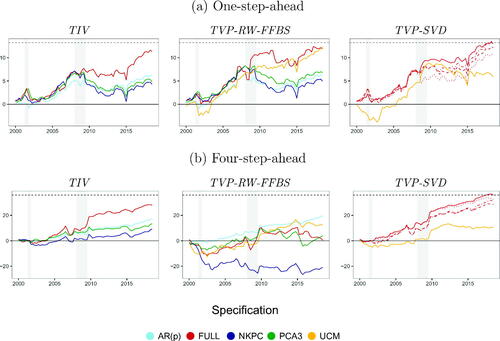
One pattern worth noting is that the benefits of using the FULL model increase after the beginning of the financial crisis. This is true not only for our SVD models, but also for the TIV model. However, notice that during the crisis, the slope of the line associated with the FULL SVD approach becomes steeper, indicating that the model strongly outperforms the RW for that specific time period. This potentially arises from the fact that during recessions, we typically face abrupt structural breaks in the regression parameters and our approach is capable of detecting them.

To examine how our model performs in turbulent times we focus on forecast accuracy in the Great Recession. It is worthwhile to keep in mind that inflation was fairly stable through 2008Q3. 2008Q4 and 2009Q1 were the periods associated with a substantial fall in inflation. Subsequently, inflation became more stable again. Accordingly, it is particularly interesting to look at 2008Q4 and 2009Q1 as periods of possible parameter change. We find that the FULL SVD approach performs comparable to a no-change benchmark model. The simple RW model can be expected to handle a one-off structural break well in the sense that it will forecast poorly for the one period where the break occurs and then immediately adjust to the new lower level of the series. Our FULL SVD approach handles the 2008Q4 and 2009Q1 period about as well as the RW. Subseqeuently, its forecasts improve relative to a RW. This improvement occurs in the middle of the Great Recession for h = 1 and a bit later for h = 4. In contrast, the TVP-RW-FFBS and TVP-RW-SVD models with the large dataset experience a big drop in forecasting performance at the beginning of the Great Recession and tend not to outperform the random walk after 2010. However, both do well in late 2009. We conjecture that this pattern of performance reflects two things. First, similarly to our SVD-based models which do not constrain the state evolution, both allow for structural breaks, but are slow to adjust to them. Second, they overfit the data and, thus, provide wide predictive distributions. In the latter half of 2009, after the structural break had occured, when there was still uncertainty about the new pattern in inflation, having this wider predictive distribution benefitted forecast performance.

This discussion provides evidence that our model works well under stressful conditions. The main mechanism driving the strong forecast performance is that the prior variance is allowed to adapt over time and if uncertainty increases (i.e., ${\sigma }_t^2$ becomes large), the prior variances increase as well and thus make larger jumps in the parameters more probable.

It can also be seen that our SVD approaches with block diagonal Z tend to perform similarly to one another and never forecast very poorly. This contrasts with the TVP-RW-FFBS and TVP-RW-SVD models which sometimes forecast well, but sometimes yield imprecise forecasts (see, e.g., results for h = 4 using the NKPC data set).

Overall, we find our SVD approaches, and in particular the version that uses the clustering prior, to exhibit the best forecast performance among a set of popular benchmarks. And it is worth stressing that they are computationally efficient and, thus, scaleable. The reason this application uses K = 101 explanatory variables as opposed to a much larger number is due to our wish to include the slower TVP-RW-FFBS approach so as to offer a comparison with the most popular TVP regression model. If we were to have omitted this comparison, we could have chosen K to be much larger.

Finally, a brief word on prior sensitivity is in order. The two key (hyper)parameters of our model are κ and G. In Section C of the Online Appendix we carried out an extensive prior robustness analysis. In this analysis we find that the precise choice of κ plays a limited role for predictive performance unless it is set too large. This statement holds for large models but, to a somewhat lesser extent, also for smaller models. In the smaller models, we find that predictive performance is slightly more sensitive to the choice of κ and the researcher thus has to select this hyperparameter with some care. When it comes to the choice of G, we find that as long as it is not set too small, forecasting accuracy does not change substantially. This finding indicates that our shrinkage prior on π successfully empties out irrelevant clusters if G is large. In an extreme case, that is, if G is set too small a priori, we lose important information on how states evolve over time and this is deleterious for predictive accuracy.

7 Conclusions

In many empirical applications in macroeconomics, there is strong evidence of parameter change. But there is often uncertainty about the form the parameter change takes. Conventional approaches to TVP regression models have typically made specific assumptions on how the states evolve over time (e.g., random walk or structural break). In the specification used in this article, no restriction is placed on the form that the parameter change can take. However, our very flexible specification poses challenges in terms of computation and surmounting over-parameterization concerns. We have addressed the computational challenge through using the SVD of the high-dimensional set of regressors. We show how this leads to large simplifications since key matrices become diagonal or have banded forms. The over-parameterization worries are overcome through the use of hierarchical priors and, in particular, through the use of a sparse finite mixture representation for the time-varying coefficients.

In artificial data, we demonstrate the speed and scaleability of our methods relative to standard approaches. In an inflation forecasting exercise, we show how our methods can uncover different forms of time-variation in parameters than other approaches. Furthermore, they forecast well. Since our approach is capable of quickly adjusting to changing economic conditions and outliers, it might also be well suited when applied to macroeconomic forecasting in extreme periods such as the Covid-19 pandemic.

Acknowledgments

We thank the participants of the 6th NBP Workshop on Forecasting (Warsaw, 2019), the 11th European Seminar on Bayesian Econometrics (Madrid, 2021) and internal seminars at the University of Salzburg, the FAU Erlangen-Nuremberg and the ECB, four anonymous referees as well as Anna Stelzer, Michael Pfarrhofer and Paul Hofmarcher for helpful comments and suggestions.

Supplemental Materials

The supplementary material consists of three sections. In Section A, we provide additional technical details such as all full conditional posterior distributions and the resulting MCMC sampler. Section B provides a brief overview on the dataset used in the empirical work while Section C includes additional empirical results such as convergence diagnostics and robustness checks.

Additional information

Funding

The first two authors gratefully acknowledge financial support by the Austrian Science Fund (FWF): ZK 35 and by funds of the Oesterreichische Nationalbank (Austrian Central Bank, Anniversary Fund, project number 18127).

Notes

1 Other approaches which remain agnostic on the transition distribution of the coefficients are, for example, Kalli and Griffin (2018) and Kapetanios, Marcellino, and Venditti (2019).

2 This setup can be easily extended to VAR models. In particular, recent articles (see, e.g., Carriero, Clark, and Marcellino 2019; Koop, Korobilis, and Pettenuzzo 2019; Tsionas, Izzeldin, and Trapani 2019; Cadonna, Frühwirth-Schnatter, and Knaus 2020; Huber, Koop, and Onorante 2021; Kastner and Huber 2020; Carriero et al. 2021) work with a structural VAR specification which allows for the equations to be estimated separately. Accordingly, the size of the system does not penalize the estimation time. This extension is part of our current research agenda.

3 In the case of lower triangular Z, the ${\tilde{\mathit{\beta }}}_t$ ’s can be interpreted as the shocks to the latent states with the actual value of the TVPs in time t given by ${\sum }_{s=1}^t{\tilde{\mathit{\beta }}}_s$.

4 Notice that if the condition number (i.e., the ratio of the largest and the smallest element in $\mathit{\lambda }$ ) is very large, numerical issues can arise. This is the case if ${\mathit{x}}_t\approx \mathbf{0}$. In our simulations and real data exercises, we never encountered computational issues. If these arise, then a simple solution would be to use a truncated SVD and discard eigenvalues smaller than a threshold very close to zero.

5 Using the Minnesota prior in combination with the clustering specification introduced in this sub-section is less sensible. That is, its form, involving different treatments of coefficients on lagged dependent variables and exogenous variables and smaller prior variances for longer lag length already, in a sense, clusters the coefficients into groups. A similar argument holds for a lower triangular matrix Z since that would translate into a random walk with a (potentially) time-varying drift term.

6 For a detailed discussion on the relationship between sparse finite mixtures and Dirichlet process mixtures, see Frühwirth-Schnatter and Malsiner-Walli (2019).

7 The R package fipp, which is available on CRAN, allows for investigating how influential the prior on a is and whether alternative specifications substantially change the posterior of the number of nonempty groups.

8 The AWOL sampler is implemented in R through the shrinkTVP package (Knaus et al. 2021).

9 A survey of these techniques is given in Hassani and Silva (2015).

10 For the SVD versions of the UCM models, we only present results for the g-prior with clustering as the other priors imply white-noise behavior for inflation which is not sensible.