Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study

Abstract

This study illuminates claims that teachers' mathematical knowledge plays an important role in their teaching of this subject matter. In particular, we focus on teachers' mathematical knowledge for teaching (MKT), which includes both the mathematical knowledge that is common to individuals working in diverse professions and the mathematical knowledge that is specialized to teaching. We use a series of five case studies and associated quantitative data to detail how MKT is associated with the mathematical quality of instruction. Although there is a significant, strong, and positive association between levels of MKT and the mathematical quality of instruction, we also find that there are a number of important factors that mediate this relationship, either supporting or hindering teachers' use of knowledge in practice.

This study illuminates claims that teachers' mathematical knowledge plays an important role in their teaching of this subject matter. Such claims stem originally from the “educational production function literature,” or research that examines the contribution of student, teacher, and school resources to student learning. As far back as the Equality of Educational Opportunity study (Coleman, 1966) scholars identified a unique contribution of teacher knowledge to student achievement (in mathematics, see also Hanushek, 1972; Hill, Rowan, & Ball, 2005; Mullens, Murnane, & Willett, 1996; Rowan, Chiang, & Miller, 1997). At the same time, scholars studying teacher knowledge have also identified an impact on instruction (e.g., Borko, Eisenhart, Brown, Underhill, Jones, & Agard, 1992; Fennema & Franke, 1992; Leinhardt & Smith, 1985; Putnam, Heaton, Prawat, & Remillard, 1992; Sowder, Phillip, Armstrong, & Shappelle, 1998). Taken in combination, there is evidence for the proposition that stronger teacher knowledge yields benefits for classroom instruction and student achievement.

Yet despite these observations, and despite a wealth of current policy initiatives built on these observations, there is a lack of detailed understanding regarding how teacher knowledge affects classroom instruction and student achievement. Teacher knowledge presumably works through instruction to cause student learning, yet this relationship is not completely understood. Large-scale educational production function studies never peer inside classrooms to compare the practice of higher-knowledge and lower-knowledge teachers. Studies in the teacher knowledge and mathematics education literatures have raised strong plausible propositions regarding how knowledge matters for teaching; but with sample sizes of one teacher per study in many cases, and few objective measures of teachers' mathematical knowledge, generalizations have to date been limited.

The lack of specifics regarding how knowledge affects instruction leaves critical gaps in our theoretical knowledge, and significant holes in recommendations for both policy and teacher education. How does knowledge get expressed in instruction? Do teachers with stronger knowledge offer a qualitatively different form of instruction by focusing students' attention on mathematical meaning, as many hypothesize? Or, do these teachers simply avoid the mathematical errors made by less knowledgeable teachers? In what tasks of teaching does teacher knowledge make itself most apparent? How is this relationship mediated by teacher beliefs, practices, and curriculum materials? The strength and nature of the relationship between teacher knowledge and instruction has important implications for both policy and the focus of resources in teacher education.

In this article, we illuminate the dynamics of knowledge use in teaching by examining the relationship between five teachers' mathematical knowledge for teaching (MKT) and the mathematical quality of their instruction (MQI). By “mathematical knowledge for teaching,” we mean not only the mathematical knowledge common to individuals working in diverse professions, but also the subject matter knowledge that supports that teaching, for example, why and how specific mathematical procedures work, how best to define a mathematical term for a particular grade level, and the types of errors students are likely to make with particular content. By “mathematical quality of instruction” we mean a composite of several dimensions that characterize the rigor and richness of the mathematics of the lesson, including the presence or absence of mathematical errors, mathematical explanation and justification, mathematical representation, and related observables.

Using a sample of ten teachers, each of whom completed a pencil-and-paper assessment of MKT and allowed us to videotape nine lessons, we ask:

• What is the overall strength of the relationship between teachers' MKT and the mathematical quality of their instruction?

• What does MKT afford instruction? How does a lack of MKT constrain instruction?

In addition, we ask two more exploratory questions:

• What factors mediate the expression of MKT in instruction?

• In which tasks of teaching is MKT—whether strong or weak—most apparent?

Notably, our measures of teachers' MKT have been linked to gains in student achievement (Hill et al., 2005) in a study of school improvement. A one standard deviation increase in teacher performance on the measures translates to a 1/10^th standard deviation increase in student scores over a year of instruction. Although the best research design would have examined the instruction of high- and low-knowledge teachers in this student achievement dataset, that was not possible; instead we sought a smaller sample of new teachers for more intensive data collection efforts. However, given that performance on the MKT measures has been linked to student achievement, we can tentatively assume that any covariation between the mathematical quality of instruction and MKT helps explain this link.

In what follows, we describe the literature that launched this line of inquiry, the methods of inquiry themselves, and our results.

BACKGROUND: AN ELABORATION ON SUBJECT MATTER KNOWLEDGE FOR TEACHING

Teacher educators and other scholars have been investigating the nature and effects of teachers' mathematical knowledge for over three decades. In the early years of this work and continuing on through the “educational production function” literature, scholars typically used proxy variables, such as the number of mathematics and mathematics methods courses taken (Begle, 1979; Goldhaber & Brewer, 2001; Monk, 1994) to stand in for direct measures of teacher knowledge in models predicting student achievement. Finding few stable effects, however, and inspired by Shulman's 1986 formulation of knowledge for teaching, many scholars began more descriptive studies of teachers' mathematical knowledge. Through interviews, teacher tests, and direct observation, these scholars began to both uncover problems with teachers' basic mathematical knowledge (e.g., Ball, 1990; Even, 1993; Ma, 1999; Post, Harel, Behr, & Lesh, 1991; Simon, 1993; Tirosh, Fischbein, Graeber, & Wilson, 1999) and also to explore its characteristics.

Many studies in this tradition were qualitative and used preservice teachers as subjects. And critically, many focused on illuminating the construct of teacher mathematical knowledge rather than on quantitatively examining the strength of the relationship between teacher knowledge and the quality of instruction. In fact, many influential studies, including Ball (1990), Ma (1999), Post et al. (1991), and Simon (1993) used logical claims rather than direct observation to make the case that this knowledge is critical to instruction. Other studies (Cohen, 1990; Heaton, 1992; Putnam et al., 1992) offered intensive analyses of deficiencies in teachers' mathematics instruction, but did not pair these with results from a measure of teachers' knowledge such as an interview or written assessment. Several key studies (Borko et al., 1992; Fennema, Franke, Carpenter, & Carey, 1993; Leinhardt & Smith, 1985; Lloyd & Wilson, 1998; Sowder et al., 1998; Swafford, Jones, & Thornton, 1997; Thompson & Thompson, 1994) did collect simultaneous measures of teacher knowledge and classroom instruction. Studies in the latter two categories provide a basis for our logic and video coding scheme, and thus we review their findings in depth in what follows.

These studies can be generally classified into one of two groups: “deficit” and “affordance” approaches. In the former, the authors draw linkages between a teacher's lack of mathematical understanding and patterns in her mathematics instruction; in the latter, the authors highlight the affordances strong mathematical (and related) understandings create for classroom culture and instruction. We review each group separately.

Deficit studies published during the period 1990–1995 (Cohen, 1990; Heaton, 1992; Putnam et al., 1992; Stein, Baxter, & Leinhardt, 1990) set the stage for policymakers' concerns about the mathematical quality of classroom work. In every study in this genre, the authors observe significant mathematical errors or imprecisions during classroom instruction, from inappropriate metaphors for mathematical procedures (Heaton, 1992) to incomplete definitions (Stein et al., 1990), to plain mathematical mistakes (Putnam et al., 1992). Several analyses also went beyond errors to identify other patterns arising in the instruction of less knowledgeable teachers. Although Cohen (1990) does not present an independent assessment of “Mrs. Oublier's” mathematical knowledge, he directly attributes many characteristics of her instruction to her lack of such knowledge. In a lesson on estimation, Mrs. Oublier accepted wildly inaccurate guesses rather than pressing for more reasonable answers or estimation strategies. She also missed opportunities to develop student understanding, failing to push students for explanations and the types of discussion that would lead to productive mathematical insight. Heaton (1992) also does not provide an independent gauge of “Sandra Stein's” mathematical knowledge, but like Cohen, she identifies significant problems in Sandra's mathematics instruction, including inappropriate metaphors for teaching inverse functions and a pronounced lack of mathematical sense-making. Stein et al. (1990) document one teacher's limited knowledge of functions and observe that he offered students a definition for this topic that was missing several key elements. He also used a poor analogy for functions with students and presented material in a way that did not provide a foundation for future development of the topic. Along the same lines, Valerie Taft, the fifth-grade teacher considered in Putnam (1992), did not always engage students in tasks that moved the mathematics along. For a lesson on the concept of average, this teacher spent a considerable amount of time having students conduct a survey about their favorite ice-cream flavor, only to then realize that the results of this survey did not actually lend themselves to discussing the concept of average. Many of the observations made in these deficit studies provide a basis for our coding scheme, for the most obvious implication of low mathematical knowledge is the presence of mathematical errors and poor mathematical choices in the classroom.

The more recent “affordance” studies focus on the practice of teachers engaged in using new curriculum materials (Lloyd & Wilson, 1998), new forms of teaching (Lampert, 2001), and intensive professional development (Fennema & Franke, 1992; Fennema et al., 1993; Sowder et al., 1998; Swafford et al., 1997). They examine what higher-or high-knowledge teachers can do with students and mathematics that others cannot. For instance, the Cognitively Guided Instruction (CGI) program improves teachers' knowledge of how students think about and learn number and operations concepts. One CGI graduate used her knowledge to interpret and to respond to her students' thinking, to focus student attention on how to solve problems, and to broaden the types of problems available to her students. She also encouraged classroom discussion and multiple solution strategies (Fennema & Franke, 1992; Fennema et al., 1993). Notably, her instruction was stronger in the area of addition and subtraction, the focus of the professional development, than in fractions. A two-year professional development program at San Diego State University (Sowder et al., 1998) prepared teachers with knowledge of rational number. Participating teachers taught more of the content covered in that program, had instructional goals that included conceptual understanding as well as skills development, probed for student understanding, and asked for explanations. Swafford et al. (1997) report similar results: a geometry professional development program increased teachers' geometry content knowledge and their use of open-ended questioning and student discussion. Lloyd and Wilson (1998) is the sole curriculum study in this set, finding that one teacher's “comprehensive and well-organized conceptions” of functions (p. 270) contributed to rich classroom enactment of a reform-oriented high school curriculum unit from Core-Plus. This teacher emphasized the conceptual nature of functions, carefully worked with definitions of functions, linked representations, and probed for student explanation and meaning. On the whole, the affordance studies show, as Fennema and Franke (1992) write, teachers with more knowledge differ in the “richness of the mathematics available for the learner” (pp. 149–50).

Two studies provide important addenda to these observations about the connections between mathematical knowledge and teaching. Borko et al. (1992) found that a preservice teacher who was well-prepared and knowledgeable in upper-level mathematics nevertheless had significant difficulties explaining division of fractions in response to a student question. And Thompson and Thompson (1994) show that although a teacher had strong conceptual knowledge on a pencil-and-paper test and in a professional development setting, he had trouble talking conceptually about rates during a tutoring session. These two cases, along with the affordance literature already mentioned, suggest that there is knowledge used in classrooms beyond formal subject matter knowledge, a contention also supported by Shulman's (1986) notion of “pedagogical content knowledge.” And more generally, the affordance studies included attempts to identify what mathematics knowledge matters in the work of teaching—in many ways, making Shulman's theory specific to teaching mathematics.

Both the affordance and deficit studies have been tremendously generative for the field. Yet this field, as a whole, suffers several shortcomings. To start, many of these studies are necessarily fine-grained, covering only one mathematical topic in the context of one lesson. Furthermore, most analyze this relationship within one teacher. The studies' measures of teacher knowledge have not been linked to student achievement. Most focus on either affordances or deficits, failing to mention the other. And as these authors would be quick to point out, these were exploratory studies, meant to uncover relationships between knowledge and instruction, but not to formally describe or test these relationships. While each study, for instance, contributes several suggestions for how teacher knowledge influences instruction, there has yet to be a more comprehensive framework describing this relationship. In fact, in the ten years since these studies were published, there has been very little follow-up work formally testing the links outlined here. Yet policymakers, and in particular many teacher educators, have built much on the assumption that the results from these studies generalize.

In this article, we describe an attempt to test more formally the relationship between teacher subject matter knowledge and instruction, estimating its magnitude quantitatively and describing the factors that impinge on it qualitatively. We do so with a new instrument and through a new lens, examining the mathematical quality of instruction and the mathematical knowledge for teaching held by the teacher. We take many of the suggestions from the literature above—errors, representations, mathematical explanations—and formalize them as elements of the quality of mathematics in instruction. We add a dimension not explicitly discussed in this literature, but that our prior exploratory work has led us to understand as critical to the mathematical quality of instruction. And we are able, through the use of in-depth case studies, to examine how teachers' knowledge is called on in the course of instruction. Identifying these sites of knowledge use can help guide further studies in this arena.

The work described in this article is also different from existing research in many ways. Rather than studying each teacher as a separate entity, we compare across teachers with different levels of mathematical knowledge for teaching (MKT) to understand how MKT is expressed in instruction. We also measure and analyze teachers' MKT using a rigorously developed and validated instrument, one that has been linked to student achievement gains (Hill, Rowan, & Ball, 2005). We developed a formal framework for viewing the mathematical quality of instruction (MQI), and use it to quantify the relationship between MKT and MQI. We also use more exploratory techniques, such as grounded theory, to uncover the additional ways in which MKT appears in instruction, and how MKT intersects with other teacher characteristics to produce instruction.

Besides the literature cited earlier, the work described here builds on other theoretical and empirical work (Ball & Bass, 2003; Ball, Hill, & Bass, 2005; Ball, Thames, & Phelps, in press; Hill, Rowan, & Ball, 2005; Hill, Schilling, & Ball, 2004). In this work, we delineate four unique forms of “mathematical knowledge for teaching,” or the mathematical knowledge that teachers need to carry out their work as teachers. MKT includes both the domains traditionally conceived as pedagogical content knowledge (knowledge of content and students [KCS], knowledge of content and teaching [KCT]), as well as two types of subject matter knowledge itself: common content knowledge [CCK], or content knowledge that is used in the work of teaching in ways in common with how it is used in many other professions or occupations that also use mathematics; and specialized content knowledge [SCK], or content knowledge that is tailored in particular for the specialized uses that come up in the work of teaching, and is thus not commonly used in those ways by most other professions or occupations (Ball et al., 2008). Although we do not use these categories extensively in what follows, they form the basis for our instrument design, described in the next section.

METHOD

General Analytic Strategy

Our strategy for determining the role mathematical knowledge plays in the mathematical quality of teaching involved both quantitative and qualitative analyses. To answer our first two research questions about the overall strength and nature of the MKT–MQI relationship, we began by scoring teachers' lessons on a rubric designed to represent facets of the mathematical quality of instruction, and correlating these scores with teachers' score on a pencil-and-paper assessment of mathematical knowledge for teaching. To confirm the strength of this relationship, and to challenge ourselves to uncover competing explanations for it, we next turned to more in-depth qualitative analysis via the construction of comparative case studies.

We chose the case study method in part because it can illuminate causal links that are impossible to discern from large-scale correlational research (Yin, 1994). We used these case studies in two ways. The first is closer to positivist traditions in social science research: by selecting cases to test our hypotheses. Details on the specifics of case selection are provided later, but we elaborate on the hypotheses here.

Specifically, we expected that teachers with stronger MKT would offer students fewer of the “deficits” and more of the “affordances” seen in the literature and, perhaps, additional benefits as well. Teachers with weak MKT would have teaching characterized by few affordances and many deficits. Table 1 formalizes these expectations by naming key aspects of MQI. Using findings from the deficit literature described earlier, we identified three key themes (shown in Table 1): errors, responding to students inappropriately, and the (lack of) connection of classroom work to mathematics. Using findings from the affordances literature, we identified two further themes: richness of the mathematics (Fennema & Franke, 1992) and responding to students appropriately. The last category, mathematical language, is rooted in our own analysis of the videotapes during the exploratory phase of the study (Learning Mathematics for Teaching, 2006; Sleep, 2007), which convinced us that teachers' use of mathematical language is both highly variable and also a key feature of the mathematical quality of classroom instruction.

TABLE 1 Elements of Mathematical Quality of Instruction

• Mathematics errors—the presence of computational, linguistic, representational, or other mathematical errors in instruction;

∘ Contains subcategory specifically for errors with mathematical language

• Responding to students inappropriately—the degree to which teacher either misinterprets or, in the case of student misunderstanding, fails to respond to student utterance;

• Connecting classroom practice to mathematics—the degree to which classroom practice is connected to important and worthwhile mathematical ideas and procedures as opposed to either non-mathematical focus, such as classroom management, or activities that do not require mathematical thinking, such as students following directions to cut, color, and paste, but with no obvious connections between these activities and mathematical meaning(s);

• Richness of the mathematics—the use of multiple representations, linking among representations, mathematical explanation and justification, and explicitness around mathematical practices such as proof and reasoning;

• Responding to students appropriately—the degree to which teacher can correctly interpret students' mathematical utterances and address student misunderstandings;

• Mathematical language—the density of accurate mathematical language in instruction, the use of language to clearly convey mathematical ideas, as well as any explicit discussion of the use of mathematical language.

This is not a definitive list of the ways one might observe or measure the mathematical quality of classroom work. Clearly, there are other perspectives we might have adopted, including exploring students' opportunities to interact with mathematics (e.g., students' explanations, justifications, mathematical analyses and argument), gauging student discourse (e.g., O'Connor, 1999), and measuring the cognitive demand of tasks (e.g., Stein & Lane, 1996). The organization of themes here, however, reflects initial hypotheses about the ways teachers' mathematical knowledge shapes classroom instruction.

We also used the cases in a second way, one that allowed us to answer our research questions about the role of other factors in influencing the mathematical quality of instruction and the tasks of teaching in which mathematical knowledge becomes apparent. Here, we relied on the grounded theory methods developed by Glaser and Strauss (1967). Although we did not engage in rigorous micro-analysis of data, as described in Strauss and Corbin (1998), we viewed each case holistically, trying to understand the mathematical quality of each teacher's instruction as a function not only of her MKT, but also other influences. A more in-depth analysis of a key lesson or a sequence of lessons then helped illuminate these influences, and also provided a platform to closely examine teacher–student interactions for evidence of mathematical knowledge in use. This exploratory analysis also foreshadows the next iteration of rubric development; the ideas presented in Table 1 are neither complete nor comprehensive, and specific themes, such as teachers' online management of the mathematical elements of tasks, both appear repeatedly throughout our analysis and deserve greater attention in future frameworks.

Sample and Data Collection

The data collected for the videotape study were part of a larger measures-development project with multiple goals. This project investigates the mathematical knowledge needed for teaching, and how such knowledge develops as a result of experience and professional learning. One result of our work has been a set of multiple-choice measures of teachers' MKT. The sampling and data collection described in this article grows from our efforts to validate these measures by examining the relationship between teachers' MKT and MQI scores.

We recruited ten teachers to participate in this study based on their commitment to attend professional development workshops. As such, this is a convenience sample—but one that we hoped would draw teachers with a wide range of mathematical knowledge for teaching. Our teachers taught various grades from second to sixth, although the sixth-grade teacher was moved to eighth grade in the second year of taping. Seven teachers taught in districts serving families from a wide range of social, economic, and cultural backgrounds, including many non-native English speakers. For example, one elementary school enrolled students speaking over 50 different languages. Three other teachers taught in the same school in a small, primarily Caucasian yet mixed socioeconomic district. Because these ten teachers had registered early for the professional development, they might be considered unusually motivated to improve their mathematics teaching; however, their scores on our MKT measure reflect a wide range (22nd to 99th percentile in a larger sample) at the beginning of the study.

We collected four types of data from each teacher: the paper-and-pencil MKT assessment, videotapes of classroom practice, post-observation debriefings, and interviews. First, all teachers completed our MKT measures at the beginning of the study. The paper-and-pencil assessment was one of the forms designed by our project in 2002. The survey contained 34 problems in number and operations (12), geometry (14), and algebra (8). This assessment was also designed to capture two elements of MKT: teachers' common and specialized content knowledge. The first two sample items in Appendix A illustrate distinctions between these categories. In the first, respondents are asked to determine the value of x in 10 ^X = 1. This is mathematics knowledge teachers use; students learn about exponential notation in the late elementary grades, and teachers must have adequate knowledge to provide instruction on this topic. However, many adults, and certainly all mathematicians would know enough to answer this item correctly; it is “common” content knowledge, not specialized for the work of teaching. Consider, however, another type of item. Here teachers inspect three different approaches to solving a multi-digit multiplication problem—35 × 25—and assess whether those approaches would work with any two whole numbers. To respond to this situation, teachers must draw on mathematical knowledge, including making sense of the steps shown in each example, then gauging whether the steps might make sense and work for all whole numbers. Appraising nonstandard solution methods is not a common task for adults who do not teach. Yet this task is entirely mathematical, not pedagogical; in order to make sound instructional decisions, teachers must be able to size up and evaluate the mathematics of these alternatives—often swiftly, on the spot. Other “specialized” items ask teachers to show or represent numbers or operations using pictures or manipulatives, and to provide explanations for common mathematical rules (e.g., why any number can be divided by 4 if the number formed by the last two digits is divisible by 4).

In addition to completing the MKT instrument at the start of the study, teachers were videotaped three times in the spring of 2003 prior to the week-long mathematics-intensive professional development, three times in the fall of 2003, and three times again the following spring of 2004. The professional development, California's Mathematics Professional Development Institutes (MPDIs, see Hill & Ball, 2004), offered five additional days of follow-up sessions in the fall of 2003. The videotaping was done by LessonLab using high-quality professional equipment, including a separate microphone for the teacher, boom microphone for the students, and a custom-designed stand that allowed for fluid movement of the camera around the classroom. Following every lesson, teachers were interviewed about the lesson using prompts like “What were the goals of the lesson?” “Do you think students learned what you had intended?” and “Did you struggle with anything, mathematically, during the lesson?” These interviews were also videotaped and all videotapes transcribed. Finally, we collected curriculum materials for most of the videotaped lessons.

We also conducted general and clinical interviews with these teachers, averaging between 1–2 hours, at each wave of videotape collection. In the general interviews, we asked teachers about the nature of their recent professional development experiences, their views of teaching mathematics, and their general knowledge of key mathematical topics (e.g., mathematical explanation). The clinical task-based interviews (cf., Koichu & Harel, 2007) engaged each of the teachers in solving 18 MKT items on numbers and operations, geometry, and pattern, functions, and algebra. While solving these tasks, the teachers were asked to recall how they had solved the problem on a prior survey. At the end of each task, and when deemed necessary, the interviewer would further probe teachers' thinking by asking for more explanations or clarifications. These tasks represented both common and specialized content knowledge, as well as a third domain, knowledge of student and content. These items did not perform well in large-scale pilots, yet we found that in open-ended interviews, they did provide insight into teachers' dexterity with student thinking. The third item in Appendix A illustrates this category. In it, a student is making a mistake fairly typical of those who do not understand that in order to compare fractions, the fractions must be in reference to the same unit or whole. In clinical interviews, teachers had opportunities to reveal their thinking about these types of items.

Scoring MQI and MKT

To help us select cases for in-depth analysis, we began by determining teachers' performance on both MQI and MKT. Concurrent with the receipt of the videotape data, we designed a method for producing teacher-level scores for the facets of MQI listed in Table 1. After experimenting with different coding schemes and levels of analysis, we settled on two ways to accomplish this goal: by breaking each lesson into 5-minute segments; then coding each segment at each of 33 codes designed to represent the aspects of mathematical quality outlined in Table 1 (three codes for instructional format and content, 12 codes for teacher's mathematical knowledge, eight codes for teacher's use of mathematics with students, and ten equity codes); and by assigning each tape a lesson score of low (1), medium (2), or high (3). This lesson score represents the coders' overall evaluation of the teacher's mathematical knowledge as manifested in the particular lesson. The overall lesson score for each teacher represents the average of all nine lesson scores.

The detailed MQI coding rubric and protocol is described in a technical report available at www.sitemaker.umich.edu/lmt. We reached an average whole-group inter-rater reliability of 85% prior to forming pairs in which we first independently coded each videotape, then reconciled our codes with another. Coders were randomly assigned to pairs, and videotapes were randomly assigned to those pairs. We used multiple codes from this rubric to construct each scale described in Table 1, including mathematical errors, richness of mathematics, and so forth. To construct these scales, we first determined code groupings theoretically by sorting them into collections of related codes. For example, we grouped four codes centered around the teacher's use of language in the classroom: conventional notation (which we considered written language), technical language, general language, and explicit talk about meaning and use of mathematical language. We then used scaling analyses to ensure that items placed together in a scale belonged together. Scales were then revised based on these results. We chose to use scales, rather than specific codes, to represent teachers' MQI in order to compress data for presentation, and because we were measuring an underlying or latent trait; because of measurement error on any specific code, it makes sense to use multiple, rather than single, items to represent such a trait. A detailed report is available in a technical paper (Learning Mathematics for Teaching, 2006) and summarized in Table 2. Appendix B lists the codes that comprise each scale.

TABLE 2 Scale Descriptives: Mean, Standard Deviation, Number of Items, and Reliability (Cronbach's Alpha)

Scale	Scale Mean	Standard Deviation	# of Items	Reliability (Teacher Level)
Connects classroom activities to mathematics	0.36	0.39	3	0.91
Responds to students appropriately	0.51	0.30	2	0.76
Responds to students inappropriately	0.14	0.09	2	0.54
Mathematical language	1.46	0.53	4	0.70
Errors (total)	0.86	0.56	8	0.85
Language errors	0.56	0.35	3	0.75
Richness of the mathematics	1.39	0.45	7	0.87

The results from these scaling analyses led to several counterintuitive outcomes, including the breaking apart of several codes and their placement under different constructs. For example, the codes “interprets student productions” and “uses student errors” were each decomposed to fit into two different scales. Scaling results indicated that positive instances of these codes created one scale, and negative instances (misinterpretations, misuse of student ideas and errors) of these codes comprised a different scale. These scaling results suggest that interpreting student statements properly and using student errors appropriately are not necessarily opposed or mutually exclusive behaviors from their negative counterparts.

Scaling results also suggested that some codes fit into multiple scales. For example, the code “explicit talk about the meaning and use of mathematical language” fit both the richness of mathematics scale and the language scale. Although this results in “double-counting” the explicit talk code in two scales, it theoretically and empirically fits both places, and we elected to retain it as such.

Once all videos were coded, we calculated teacher scores for both the video codes and MKT assessment. These ten teachers' pencil-and-paper responses were scored with a much larger dataset (n = 636) that included teachers who had signed up for professional development but not attended, teachers who attended MPDIs, and others. This sample was thus non-random and not representative of the general population of teachers; however, it does place the case study teachers in a wider context. Percentile rankings for these ten teachers are drawn from this larger dataset. The item response theory (IRT) reliability of the overall measure used in the correlations described later is 0.94.

Teacher scores on specific MQI dimensions and the overall lesson score were obtained by averaging codes that comprised a construct, then aggregating to the lesson then teacher level. We aggregated across waves of data (May, October, May) on evidence that no growth occurred in MQI during this time frame. An ANOVA using wave as the independent variable also indicated there was no more similarity among lessons within a wave than across waves on either the overall lesson score or the MQI scales.

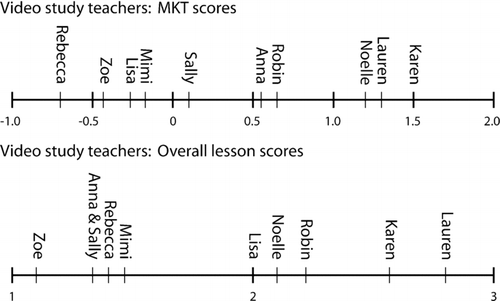
Table 3 compares the MKT of teachers on the pencil-and-paper measure with the mathematical quality of their instruction, as measured by our rubric. There is a strong correspondence; Spearman correlations range from 0.30 to 0.83, with some correlations significant even in this small set of teachers. Table 4 details teachers' scores on the MKT and MQI measures.

TABLE 3 Correlations of Video Scales to MKT Scores

Scale	Correlation to Measure Scores (Spearman's rho)
Connecting classroom activities to mathematics	−0.49
Responding to students appropriately	0.65 (∗)
Responding to students inappropriately	−0.41
Mathematical language	0.30
Errors Total	−0.83 (∗∗)
Error—language subscale	−0.80 (∗∗)
Richness of the mathematics	0.53

TABLE 4 Teachers' MKT Scores and Videotape Scale Scores

	NKT Score	Percentile Rank	Overall Lesson Score	Connections to Math	Respond to Students Approp.	Respond to Student Inapprop.	Mathematical Language	Error—Total	Error-Language subscale	Richness of Math
Karen	1.50	93	2.56	0.98	0.41	0.06	0.50	0.05	0.07	0.15
Lauren	1.30	94	2.78	0.98	0.46	0.00	0.45	0.01	0.01	0.24
Noelle	1.21	89	2.11	0.95	0.26	0.05	0.27	0.06	0.11	0.04
Robin	0.64	78	2.22	0.97	0.45	0.03	0.62	0.06	0.11	0.14
Anna	0.56	68	1.33	0.61	0.08	0.08	0.22	0.09	0.17	0.02
Sally	0.09	59	1.33	0.73	0.16	0.13	0.29	0.17	0.35	0.05
Mimi	−0.19	52	1.44	0.77	0.17	0.15	0.23	0.24	0.43	0.06
Lisa	−0.23	35	2.00	0.97	0.33	0.07	0.45	0.10	0.19	0.09
Zoe	−0.43	35	1.11	0.91	0.12	0.11	0.30	0.18	0.29	0.05
Rebecca	−0.71	22	1.40	0.93	0.10	0.04	0.32	0.12	0.21	0.02

Case Selection

At the start of work on this article, we had completed the coding and analysis presented in Table 3 and Table 4, and wanted to return to more qualitative analyses to deepen our understanding of the mechanisms at work. Presenting a detailed exploration of the relationship between MKT and the quality of the mathematics in instruction for all ten teachers was beyond the scope of this article. Given the strong results presented just above, we elected to present five cases that could answer our core questions and illustrate how mathematical knowledge influenced the quality and richness of mathematics in instruction. Choosing which cases to present was key. We followed Yin's (1994) advice about case selection: “Each case [was] carefully selected so that it either (a) predicts similar results (a literal replication) or (b) produces contrasting results but for predictable reasons (a theoretical replication)” (p. 46).

Because we had coded the videotapes (the dependent variables) prior to revealing teachers' scores on our pencil-and-paper test (the independent variable), we could not follow the procedures recommended by Yin (1994) and King, Keohane, and Verba (1994) to select cases on different values of the independent variable and then inspect for differences in the dependent variable. Instead, noting the strong correlations presented earlier, we set two criteria for our selection process. First, we wanted a range of teacher knowledge as measured on our pencil-and-paper assessment. This allowed us to examine links between the strength of mathematical knowledge and the quality of the mathematics in instruction. Second, to search for alternative explanations for the mathematical quality of instruction, we wanted to examine both teachers whose pencil-and-paper and video rubric scores converged and those for whom these scores diverged. We hypothesized that the group with divergent scores would be the most likely to have other factors impinging on the mathematical quality of their instruction.

Figure 1 shows that six teachers had similar ranks on both measures. We selected two of these convergent cases: a high-MKT/high-MQI (Lauren) and a low-MKT/low-MQI (Zoe). We use these teachers to illustrate the role MKT plays in supporting or hindering the mathematical rigor of instruction. To evaluate alternative hypotheses for the MQI, we also selected two teachers whose pencil-and-paper and video-based ranks diverged: one for whom the mathematical quality of her instruction was significantly worse than one would anticipate from her MKT score (Anna), and one whose mathematical quality of instruction was significantly better (Rebecca). As Table 4 indicates, although Anna ranked 5th in MKT, she ranked poorly in overall lesson score and on many of the videotape scale scores (last on connection to mathematics, responding to student appropriately, and mathematical language). In contrast, Rebecca, who ranked last in MKT, performed relatively better than other teachers on some of her videotape scale scores (ranking 6th on connections to mathematics and mathematical language). Finally, because of our interest in how strong mathematical knowledge supports (or does not support) teaching, we selected a fifth high-rank case (Noelle), whose scores are both convergent and divergent, and whose teaching offers a contrast to Lauren's.

FIGURE 1 Video teachers' ranking on MKT and overall lesson scores.

Analyzing Qualitative Data

After case selection, we assembled, viewed, and read all available evidence for each of our five teachers. We interpreted each teacher in light of her overall lesson scores as well as her performance on the MQI characteristics listed in Table 1 and specific items on our pencil and paper assessment. In particular, we evaluated the possibility that factors other than MKT shaped the mathematical quality of instruction, examining transcripts of interviews and generating patterns across the recorded lessons. We also conducted a rough form of what Yin (1994) terms “pattern-matching,” noting where both MKT and aspects of teachers' mathematical quality of instruction appeared to support the hypothesis that MKT matters and instances in which this hypothesis was not supported. Our ability to look separately at each dimension of MQI listed in Table 1 assisted in this process.

This analysis forms the backbone of the cases described in what follows. After introducing each teacher, we describe the ways in which elements of her instruction match her MKT score; where supporting evidence from interview transcripts or clinical interviews is available, we cite that evidence. For each teacher, we also select the most salient themes in her instruction as a means to illustrate differences between low- and high-knowledge teachers. We also use each case to suggest answers to our more exploratory questions about where MKT is most visible in classroom instruction, and what other factors might explain the quality of the mathematics in instruction.

RESULTS

We present case results in the order of the four structuring questions. They are:

• What is the overall strength of the relationship between teachers' MKT and the mathematical quality of their instruction?

• What does MKT afford instruction? How does a lack of MKT constrain instruction?

• What factors mediate the expression of MKT in instruction?

• In which tasks of teaching is MKT, whether strong or weak, most apparent?

First, we present the convergent cases of Lauren and Zoe. Lauren's high MKT and high MQI help us evaluate the accuracy and completeness of “affordance” claims about the relationship of teacher knowledge to classroom practice, and to assess whether high-knowledge teachers have any “deficit” characteristics. Zoe's low MKT and low MQI allow us to evaluate the accuracy and completeness of the “deficit” model. Comparing across these cases and putting them in the larger context of our sample of ten illustrates the role teacher knowledge plays in instruction. Next we consider Noelle, Anna, and Rebecca, whose cases both illustrate the relationship between MKT and the mathematical quality of instruction and suggest other factors that shape it. Table 4 shows all case study teachers' scale scores for the key measures.

This is a complex article; some foreshadowing of the structure will help the reader organize what is to come. The cases of Lauren and Zoe share a similar structure. After providing some background, we present lesson segments for each teacher to illustrate central characteristics of their teaching. At the end of these excerpts, we note other central features of their teaching and consider the generalizability of our findings to other lessons and teachers in our sample. Anna and Rebecca also share a similar structure. After providing some background, we consider briefly, as we do with Lauren and Zoe, how their MKT and MQI scores converge or match. We then provide evidence for how their MKT and MQI scores do not match—in other words, how the MQI scores diverge from expectations set up by their MKT score. Noelle, a teacher whose scores are both convergent and divergent, has a mix of these two structures.

Lauren

Lauren is our first convergent case, one that illustrates a strong association between MKT and the mathematical quality of instruction. Lauren scored in the 94th percentile in the larger sample, and first in overall lesson score (i.e., label of high, medium, low for each lesson, averaged to the teacher level) for the video study teachers. Her instruction illustrates the expectations drawn from the “affordance” literature described earlier: it is mathematically rich, linguistically clean, and responsive to students' ideas and misunderstandings. Lauren also displays few of the problems identified in the “deficit” literature: all activities are carefully linked back to an important mathematical point and few errors occur. We can also use Lauren to identify additional sites where mathematical knowledge appears useful to instruction, including her attention to equity and providing all students access to the mathematics. After presenting some background information, we use a lesson on probability to demonstrate these characteristics.

Background

Lauren teaches fourth grade in a culturally and linguistically diverse school. At the time of our study, she had been teaching for 15 years, earning a multiple subjects teaching credential at college graduation and working on her master's degree at a local university during the course of the study.

Lauren's classroom is neat and well organized. A few posters sprinkle the walls, each serving an instructional rather than aesthetic purpose. Students' desks form three paired rows, facilitating the group work and collaboration that occur through many of her lessons. The aisles between the rows allow space for Lauren to kneel and join groups of students working on mathematical tasks, also a frequent occurrence. When designing lessons, Lauren draws from a variety of sources, including Marilyn Burns' Math Solutions and materials from Dale Seymour, both of which are commonly used in professional development workshops, as well as the district curriculum, Harcourt Brace. In the lesson we focus on in what follows, Lauren has combined a lesson from Investigations in Number, Data, and Space, a National Science Foundation-supported curriculum, with a lesson from Math Solutions' About Teaching Mathematics: A K–8 Resource, a set of mainly supplementary mathematics activities written by Marilyn Burns.

Lauren's lessons follow a slightly different script than the typical U.S. lesson (e.g., those described in Hiebert & Stigler, 2000). Although there are still well-defined segments that might be named “teacher introduction” and “student work time,” these segments do not consist of only a teacher talking or students completing a worksheet. Instead, Lauren's lessons have a back-and-forth rhythm; Lauren introduces an idea or sets up a problem, then students work, often together, on a mathematical task. After only a few minutes, Lauren reunites the group to discuss results from the initial student work, cover more mathematical territory, and set up the next student task. Students work some more, and the cycle repeats. This back and forth is atypical in our sample of ten teachers.

Lauren describes her mathematical knowledge as weak in some areas, especially algebra, and reports that at times she finds complex mathematical problems or tasks frustrating. She cites her insecurity about mathematics as a motivating force in her attendance at content-specific professional development workshops. Her survey responses indicate that in the year before this study, she attended over 75 hours of mathematics-related professional development activities and also devoted 60 hours to math courses at a local university. This work seems to have paid off. Lauren performed well on our pencil-and-paper MKT measures, earning the highest score on the geometry measures and the second highest average score across all three mathematical domains. The clinical interview suggests why. Lauren persistently digs into the mathematics of the more difficult items, even ones she ultimately answers incorrectly. Her interviews also confirm the centrality of her professional learning in building her knowledge; when Lauren delivered a correct answer, she often commented that she had learned the topic in her mathematics professional development. In fact, one of the few incorrect answers she gave was common to all teachers in her school (that zero is neither odd nor even) and resulted from the math coach in her building passing this “knowledge” along to teachers.

Lauren's instruction is notable for the strong presence of rich mathematics, careful attention to language, and her responsiveness to students. In this next section, we illustrate these characteristics through a discussion of a lesson on the probability of events with two outcomes.

Lauren's Teaching: Probability and the “Likelihood Line:” Rich Mathematics and Language

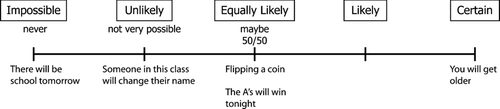
Lauren begins the lesson by drawing students' attention to a “likelihood line” constructed the week before and placed high over head on a classroom wall, for all to see (Figure 2).

FIGURE 2 Likelihood line.

Beneath the line are written events with dichotomous outcomes, like “The A's will win tonight,” “We'll have school on Saturday,” and “You will get older,” all neatly arranged during the previous week's lesson according to students' estimation of their likelihood. Before reviewing the placement of these events with students, Lauren reminds the class of the definition of probability: “Probability helps us to figure out how likely it is that an event will happen.” This definition is read word for word from the Investigations materials.

Our first observation about teacher knowledge and mathematics instruction taken from the opening minute of this lesson will be, perhaps, surprising to many. Teachers are everywhere urged to make judicious (Stein, Remillard, & Smith, 2007) or, in some cases, scant (Ben-Perez, 1990) use of curriculum materials; teachers are largely seen as active co-constructors of curricula. Yet in this lesson, Lauren closely follows the curriculum, and in fact, directly quotes the book's definition of probability. In doing so, Lauren has conveyed a definition that is both mathematically accurate and intelligible for ten-year-olds. The decision to use her curriculum materials rather than formulating this definition herself, de novo, allows her to ensure that in the moment of instruction, this definition will be carefully balanced and articulate.

Lauren then has her students review the placement of various events on this likelihood line. There is a pattern in her discourse: she solicits student answers and then asks for explanation, taking care to review enough of the substance of what has gone before so that all students could follow the reasoning. She begins the discussion by asking students to name an event that would be equally likely:

Lauren:   [What is an event that would be] Equally likely? Equally likely. Jessie.

Jessie:   The A's will win tonight.

Lauren:   The A's will win tonight. Did the A's win? Do you guys know?

Students:   They did win.

Lauren:   They won. They won Friday night. You know what … we had a big discussion about where to put this on the likelihood line. Who can remember what the discussion was about? We had to discuss this one awhile before agreeing on where it would go. Evan?

Evan:   We were trying to figure out whether to put it on likely or equally likely.

Lauren:   And why? Why was that?

Evan:   … since A's is the stronger team, it might … they might like win since it's stronger than the other team that they were playing that night.

Lauren:   Okay. So we had a big discussion about that do you remember? Because some of you were like [name of teacher], that it would be fifty-fifty, they were either gonna win or gonna lose. It goes right there in the middle. And then there was some discussion about who's a better team and … and how that might affect where we would place this on our likelihood line.

There are several noteworthy aspects to this brief snippet of conversation. Lauren invites students to review prior discussions, asking for a summary of the conclusions the class has already drawn about likelihood. But besides the conclusions, she asks for the insides of the argument: that the likelihood of the baseball team winning might depend on the strength of the opposing team, or it might be proportionate to the number of possible outcomes. Instead of assuming that all students remember the discussion, Lauren asks them to reconstruct the argument. She invites enough elaboration that different conclusions could be reasonably drawn by students, that the likelihood of the A's winning is fifty–fifty, or that their prior performance relative to other teams might make a win more or less likely. This foreshadows a developmental shift students will hopefully accomplish during this unit, moving from more simple views of probability (e.g., working with only independent events and assuming all events are equally likely) to more complex views of probability, including estimating the conditional probability from prior information.

Also telling is the set of events Lauren and her class have placed on the likelihood line. As Lauren moves on in her review, she asks students to name an impossible event (students will have school on Saturday), an unlikely event (a student in the class changing their name this year), a likely event (having science lab), and a certain event (students will get older) before asking students to place two new events (it will snow in their coastal California city on Friday; a student will be absent tomorrow) on the line. Some of these events are suggested in the Investigations materials, but many are added by Lauren or her students. All these events are carefully chosen, from a mathematical perspective, to have only two outcomes (yes or no) and also to be specific with regard to the parameters of the future event (e.g., it will snow on Friday). And notably, these contexts are designed to be relevant and interesting to children from a variety of backgrounds and with a variety of interests.

Students are encouraged to consider their classmates' mathematical arguments and to agree or disagree with them. This is a deeply mathematical practice, and it is ever-present in her instruction. In the next several minutes of instruction, Lauren has students work in pairs to determine the likelihood that one or more students will be absent from class the next day; she then invites disagreement and seeks out multiple conclusions during the ensuing class discussion:

Lauren:   Okay, who wants to come up, tell me where you think you should put it. Tell me [if] your group agreed with you or … thought differently. Sameer?

Sameer:   We decided in-between equally likely and likely because it's spring and a lot of like … there's allergies … people could get allergies could be sick and be absent. So we put it in-between equally likely and likely.

Lauren:    Okay, compared to earlier in the year, you think … kids being out sick could maybe be on the increase right now cause of allergies. Did you all kind of agree with that or …

Sameer:    We agreed.

Lauren:    All right. Sameer, would you take that pointer and pass it to somebody who may have a slightly … different response? Go ahead and pass it to whomever you'd like.

(Student 2):    I think that it could be fifty-fifty because … well mostly now we aren't getting anybody that's absent and sometimes we do get absents. But now we're not mostly getting absent students so it could be fifty-fifty cause we never know like today we don't have anybody absent and tomorrow, we might have someone absent.

Lauren:   Okay.

In this classroom, students have constant opportunities to think mathematically, to report on their thinking, and to politely agree or disagree with one another according to classroom customs enforced by Lauren. Providing explanations for thinking, as well as mathematical ideas and procedures more generally, is the accepted norm. We see echoes of this in Lauren's own mathematical work in the clinical interview. She frequently gave explanations for her own thinking, elaborations of mathematical ideas, and conceptual discussions of procedures, just as we see in her teaching. This underscores our claim that Lauren is a case that illustrates the convergence between high MKT and high MQI.

After wrapping up a review of the likelihood line, Lauren moves the class into the next activity for the day: “mathematizing” the informal understanding of probability students have just developed (Van den Heuvel-Panhuizen, 2000; Cobb, Gravemeijer, Yackel, McClain, & Whitenack, 1997). Lauren tapes a second likelihood line to the chalkboard and again reads from her notes, this time from the Math Solutions materials:

Lauren:    Sometimes, people use numbers instead of words to describe a probability of an event. In fact, that's what mathematicians use. They use numbers instead of words. Okay, the number we give to an impossible event. Something's that impossible, that can't happen. I'm hearing people whisper, what is it?

Students:    [Zero.] [Zero percent!]

As Lauren writes 0, a student gets Lauren's attention, telling her he “thinks [he] knows the rest.” Lauren asks him to continue:

Lauren:    Okay, why don't you tell me… what you're thinking the number would be for certain.

Student:    A hundred.

Lauren:    A hundred. A hundred what?

Student:    Percent.

At this point, Lauren faces a choice. Students began by nominating zero as the number that would represent an impossible event. The corresponding notation for recording a certain event would be to assign it a probability of 1, rather than 100 percent. However, this representation is perhaps unfamiliar to students in the class; hearing “a 100 percent chance” is more prevalent than hearing “a probability of 1” in everyday life. As we imagine many teachers do, Lauren must now work to reconcile these two recording methods with one another, and continue to link them to the likelihood line:

Lauren:   A hundred percent. So I heard … did you whisper zero percent when I put zero up here? [Student answers yes.] Okay. I'll go ahead and write … I'll write a hundred percent here (beneath certain) … tell me what you're thinking by a hundred percent. What do you mean by a hundred percent?

Student:   For sure. Definite.

Lauren:   Okay, so what does a hundred percent mean to you?

Student:   It WILL happen.

Lauren:   It's definitely gonna happen. Good. And mathematicians, when they're using numbers, they refer to the number one for an event that is certain. [Directly below certain and parallel to the zero she wrote under impossible, Lauren writes a one] That it's going to happen. Okay, hundred percent chance, it's definitely going to happen.

Lauren then reinforces the connection between the two methods for recording probability as she continues to mathematize the likelihood line:

Lauren:   Anybody have an idea of what we would put for equally likely. When we were brainstorming our vocabulary, on Friday … one of you came up with fifty-fifty for describing equally likely. Can someone tell me what number we would put up to represent that? Anick?

Anick:   Half.

Lauren:   Half. Tell me what you're thinking with half?

Anick:   Like fifty is half cause a hundred percent and a hundred percent is full. So fifty would be half of a hundred so I'm thinking like fifty-fifty means like each half is equal, so I would put half.

Lauren:   Okay. Very good. So we'll put half here. And I'll go ahead a write fifty percent here [underneath the ½]. Do fifty percent and one half mean the same? [She points to the 50% and ½]

Students:   Yes.

Lauren is consistent in her use and linking of multiple representations while mathematicizing the likelihood line; she starts by linking 100% and 1, moves to one half, 50% and .5, and places these all beneath the terms originally used to describe the likelihood of events. This seems to us significant; linking representations is widely regarded as one important method for teaching mathematics to students (NCTM, 2000). In our dataset, however, it is rarely done; Lauren and another high-MKT teacher link in 20% and 35% of clips, respectively. The other eight teachers range from 0 to 6% on this specific code.

Moreover, in this episode, Lauren is explicit about mathematical practices, noting that mathematicians use numbers rather than words to express probability. By making explicit note of this transition from informal to formal mathematical ways of describing likelihood, Lauren signals not only the connections between these two ways of thinking, but also the unique nature of mathematical thought. And again, we see Lauren repeatedly pressing students for mathematical explanations. When a student offers the correct answer (“half”), Lauren does not accept that answer outright, as many teachers would; instead, she presses for a mathematical explanation (“Half. Tell me what you're thinking with half?”).

This narrative description of Lauren's implementation of the probability lesson also suggests her care and precision with mathematical language. As shown by her thoughtful definition of probability, she is careful in her use of what we call “technical” mathematical language, or the terms in the elementary curriculum that derive from the discipline of mathematics, and that must be used with mathematical accuracy. In fact, Lauren correctly uses technical language in 65% ¹ of her lesson clips and inappropriately uses such language in only 1% of her clips; she is second only to the teacher who uses the heavily scripted Saxon curriculum (who uses technical language correctly in 80% of clips) in this regard. However, Lauren also goes beyond using technical language accurately; teaching also requires that such definitions be interpretable by students. For instance, offering fourth-graders a college-level definition for probability is of little use. In this lesson, in which Lauren's goal is to “expose [students] to the vocabulary,” she chooses curriculum materials that define the “technical” vocabulary for probability in an accessible way.

Lauren also translates fluently between the “general” language used in everyday life and the more specialized language of elementary mathematics. Students often speak about mathematical ideas using non-mathematical terms; for teachers, the work of bridging between everyday and mathematical language is omnipresent and, we argue, a critical mathematical skill in teaching (see O'Connor, 1999; Pimm, 1987 for discussions of language; Sleep, 2007 for a discussion of teacher knowledge and language). In this case, Lauren has used the likelihood line to array and organize a set of terms often used by students to describe different levels of likelihood. Although most terms are from the Investigations materials themselves, Lauren has chosen to replace “maybe” (which Investigations placed at the 50% mark, but which is colloquially meant to indicate any event that is neither certain or impossible) with the more precise yet still understandable “equally likely.” Lauren appears to be thinking carefully through the words she chooses for the line. Her marks on the “general language” code are similarly high to those for technical language.

This episode also illustrates one answer to our fourth question, about other tasks where teachers' mathematical knowledge appears. Watching this and other lessons, we can see how Lauren uses mathematical knowledge to enact a commitment to equitable outcomes among students. This is evident both through her efforts to make mathematical thinking and reasoning explicit and in her choices of culturally appropriate, child-accessible, and sensitive contexts. For instance, her careful review of the argument about the statement “The A's will win tonight” serves to make all students aware of the ideas on the table and, thus, ensures that all are equally able to participate. Similarly, she picked events for the likelihood line that would be equally accessible for all children to consider, regardless of socioeconomic or ethnic background. Many of the events are school-related (“We'll have school on Saturday;” “We'll have science lab on Friday”) and are experiences common to everyone in the class. Similarly, Lauren accords respect and value to her students' experiences—for example, although she accepts as “unlikely” the idea that a child will change their name this year, she acknowledges without judgment that some children in the class have changed their names, a not uncommon practice for immigrant children.

This attention to equity is a constant theme throughout Lauren's lessons. In one remarkable example, Lauren anticipates that a word problem that uses a muffin pan as a representation for arrays will be incomprehensible for students who have no idea what a muffin pan is. She produces a muffin pan to show the class and, after learning that several students are not familiar it, gives a brief explanation. This was a conscious move on Lauren's part:

I'm not sure I would bring a muffin pan with me, you know? But, I've just had some things come up working at this school that I—I knew, I was not surprised that there was a child in this class that didn't know what a muffin pan was … you know, there's just a lot of cultural things that we can assume kids know that they, that they don't. And that comes up a lot.

Real-world contexts for mathematics are thought to give relevance and meaning to mathematics, so that mathematics is less abstract and more connected to the worlds of children. But for students who are not familiar with middle-class American objects and activities, the use of contexts might actually obscure the mathematics. Lauren is sharply aware of the ways she must intervene to ensure the mathematics of the “real life” examples reaches students.

Finishing the Likelihood Line: Responding to Students Appropriately, Rich Mathematics

We continue with the lesson to illustrate two more mathematical features of Lauren's instruction: her ability to hear and interpret students' mathematical statements, and her encouragement of multiple solution methods. After making links between equally likely, 50% and ½, Lauren next asks what the numeric equivalent would be for the label “unlikely.” The first student called on says twenty percent; Lauren presses him for an explanation, but after a long pause he defers, saying he can't explain why. The next student answers twenty-five percent:

Student:   It's twenty five percent because if … I thought if I can count from the inside … from inside each will equal up to twenty and then the lines represent every five so … five, ten, fifteen, twenty and then twenty-five goes on the line.

Lauren:   Okay, so you're seeing five lines?

Student:   Broken up into four spaces.

Lauren:   So you're saying twenty-five percent would go here (indicating unlikely).

Although the official likelihood line has only five hash marks (see Figure 2), Lauren hears in this student's response a method for assigning values “inside” each pair of hash marks, presumably drawing in his mind additional marks to divide each quarter of the line into fifths. Rather than ignoring this answer, Lauren assumes this student has a legitimate method and asks clarifying questions. Here and more generally (in fact, in 62% of her clips), Lauren listens carefully to students and can interpret vague and sometimes contradictory statements. This seems an important skill, and one that we argue is intimately connected to teachers' mathematical knowledge. Students arrive at school not knowing the mathematical “register” (Pimm, 1987), often rendering their utterances incomplete, imprecise, and at the extreme, incomprehensible. Yet Lauren “heard” mathematical ideas even in very garbled statements. Her clinical interviews suggest why: when presented with problems featuring an unusual method or reasoning (e.g., non-standard methods for computation) Lauren digs into the mathematics, trying to decipher what the student has done, testing the method with different numbers, and sometimes referring to more general mathematical principles in justifying her solution.

Immediately following this initial solution, another student offers another way to arrive at this answer. Lauren draws him out to make his reasoning visible to the class:

Josh:   I know another way too. You just subtract twenty-five off of all of them. So likely it's gonna be, I'm not gonna say the answer though.

Lauren:   No go ahead. Tell me what you mean by subtracting twenty-five percent. Can you clarify that for us?

Josh:   So, one hundred minus twenty-five is seventy-five. Seventy-five minus twenty-five is fifty. And fifty minus twenty-five is twenty-five. And twenty-five minus twenty-five is zero.

Lauren:   All right. How many of you agree with what he's saying. [Class indicates yes.] Okay.

Students in Lauren's class appear comfortable with the multiple methods for arriving at the answer. But more importantly for our hypotheses, Lauren herself seems knowledgeable about multiple solution methods and can follow students' thinking as they discuss them.

Lauren is also skilled at recognizing and using student errors in the course of instruction. This can be seen a bit in her patience in waiting for the initial student to justify his answer of 20% for “unlikely.” More generally, Lauren hears and uses student errors in over a quarter of the clips; she is tied with three other high-knowledge teachers in this regard. This closely matches Lauren's performance in the clinical interview, where she got nearly every question tapping knowledge of content and students correct, quickly and confidently identifying the student misunderstanding.

Generalizability of These Themes

Some of the themes examined here can also be found in earlier research on the relationship between teacher knowledge and instruction in this lesson. Several authors have explored how teacher knowledge supports mathematical explanations, representations, and more generally, “conceptual” teaching of mathematics (e.g., Lloyd & Wilson, 1998). Our work confirms that these “affordances” are present in Lauren's lessons above. One question is the degree to which the features of instruction illuminated in this episode generalize to Lauren's other lessons, and to other high-knowledge teachers more broadly.

Table 4 confirms that the aforementioned descriptions generalize well to Lauren's other lessons, as shown by her scale scores for the richness of the mathematics (0.24), the density and precision of mathematical language use (0.45), and responding to students appropriately (0.46). Scores on specific codes that make up these scales help give these figures meaning. Lauren is explicit about the use of mathematical language in 30% of her clips, and has high general and technical language “density” scores (65% and 65%, respectively). Lauren uses multiple representations in 26% of clips and links between such representations in 20% of clips; she or her students provide a mathematical explanation in 37% of clips; she is explicit about mathematical reasoning and practices in 23% and 21% of her clips, respectively. Although these percentages might seem low, they must be interpreted in light of the fact that nearly half of Lauren's clips are devoted to either small-group or individual student work time. When students are working publicly with their teacher, that work is saturated with rigorous mathematics.

Other high-MKT teachers share some of Lauren's strengths. Although only one of the other ten video study teachers shares her high explicitness scores and no other teacher attends to equity in the same way Lauren does, among the four other top-scoring teachers, three fare well on the richness of the mathematics scale (the exception, Noelle, is discussed later). Three of the four high-scoring teachers have strong density/accuracy of language scale scores, and all often respond appropriately to mathematically ambiguous student statements and errors.

We have used Lauren to illustrate what MKT can afford instruction. We could also have easily used her case to shed light on the “deficits” model of the relationship between MKT and instruction, in that her strong MKT appears to protect her from many of the troubles facing lower-MKT teachers. She makes few mathematical errors in the course of instruction (0.01); she facilitates students' connections of classroom activity to mathematical ideas or procedures, rather than engaging the class in activities masquerading as mathematics or spending time in management activities (0.98); and she never misinterprets a student idea or fails to respond productively to a student mistake (0.00). The four other high-MKT teachers are also nearly always doing mathematics and make few mathematical errors in their instruction.

We argue that this demonstrates a substantial link between strong MKT and high mathematical quality of instruction. In terms of both affordances and deficits, high-MKT teachers provide better instruction for their students. The symmetry of this relationship is striking; not only do high-knowledge teachers avoid mathematical errors and missteps, they appear able to deploy their mathematical knowledge to support more rigorous explanations and reasoning, better analysis and use of student mathematical ideas, and simply more mathematics overall.

Lauren also provides insight into additional classroom tasks in which mathematical knowledge is apparent and necessary. Lauren's use of equitable practices and care with the contextualization of real-life problems no doubt improves the quality of mathematics instruction for all students, but especially for those who do not come from dominant-culture households. Another such task of teaching is the choosing and sequencing of mathematical tasks. This is clearly a place where Lauren's skillful choices are a function of high MKT. Lauren often patches together tasks on a particular topic drawn from a number of curriculum materials. She does this in a way that is logical, building mathematical ideas that are sequential. For example, Lauren chose an introduction to probability that was conceptual and highly intuitive from Investigations, and in the same lesson included a sampling task from About Teaching Mathematics as a first foray into concrete statistical work. This was followed by another Math Solutions activity in which students built their own spinners and made predictions about the probability of different outcomes. This example shows what we call directionality, one of the two facets of telos, which we discuss more in the case of Noelle: a purposeful sequencing and linking of tasks in ways that support students' progression from early conceptual work on a topic to increasingly specific and mathematically complex goals. These tasks appear to be chosen based on their mathematical point, and she works toward this mathematical point across the lesson. She links ideas from earlier lessons even when the tasks are taken from separate curricula. This is clearly an example of a task of teaching that is highly dependent on mathematical knowledge for teaching.

Zoe

Zoe is our second convergent case, selected to illustrate the association between low MKT and the quality of mathematics instruction. Zoe has the second-lowest MKT score in our video study sample and performs at about the 35th percentile in our larger sample. Her instruction illustrates the expectations derived from the “deficit” literature described earlier: it is filled with errors and imprecise language. Likewise, the “affordances” offered Lauren by her strong MKT are in no way present for Zoe. In fact, Zoe provides a “negative case” of rich mathematics—the superficial teaching of mathematical topics that offer many opportunities for conceptual connections and meaning-making. Following some background about Zoe, we illustrate how and why this occurs by focusing on one lesson around the properties of addition and practice of addition and subtraction.

Background

Zoe teaches upper elementary in a predominantly white suburban school. In the first year of our study, which took place during Zoe's ninth year of teaching, Zoe taught in a classroom that contained a mix of both fourth- and fifth-grade students. In the second year, she taught a straight fourth-grade class.

Zoe establishes a friendly rapport with her students, relating to her class with a casual authority. Students sit in groups of five to seven, taking notes in their binders as Zoe writes on the board or corrects their papers. They are expected to listen to the teacher and each other, and to be “on task” at all times. At the same time, Zoe recognizes her students' tween-ness, making occasional sarcastic remarks, commenting about shoes and clothing, and chuckling alongside students at funny moments in the classroom. Zoe's large, organized classroom is filled but not overstuffed. While student work and colorful teacher-made posters dot the walls, teddy bears and other artifacts of early-grade education are not present.

This orderliness extends to Zoe's mathematics lessons, which follow the archetypal American structure closely (Hiebert & Stigler, 2000; Stodolsky, 1988). She begins lessons by explaining their objectives and relationship to other topics students have recently studied. This presentation often goes on at length, with a minimum of student talk interrupting its flow. Zoe then guides students through several practice problems, often on the whiteboard or overhead. Next, students complete assigned worksheet or textbook exercises, usually individually, but sometimes in groups. Zoe circulates as they work, answering questions and checking answers. Finally, there is a brief wrap-up.

Zoe's lessons follow the textbook loosely, combining excerpts from Houghton-Mifflin with teacher-made materials. In her first interview, she noted that Houghton-Mifflin did not meet her students' needs, particularly when it came to what she called “math prompts,” or problems designed to require complex mathematical thinking: “I write all my own math prompts because they just don't do well in the books. They're too easy and then the kids miss them because they're not challenging enough.” Zoe is also mistrustful of her textbook, noting that she and teachers in her school had noticed mathematical errors in a draft edition used several years prior.

Zoe's original teaching credential was for multiple subjects with an English concentration. In an interview, she referenced this generalist background as a reason for deficiencies in her mathematics teaching. While she reported feeling comfortable teaching some subjects, she said that mathematics was not one of them. Her frankness about her lack of expertise was coupled with a specific diagnosis of areas of weakness (algebra and order of operations) and also a willingness to sign up for professional development to remediate those areas of concern.

Zoe's performance on our MKT measure—second from the bottom among the case study teachers—confirmed this self-analysis. Her clinical interview illuminates why. She moved quickly through the items, noting that she went with her “gut feeling” rather than thinking through the mathematics carefully. When confronted with an unfamiliar mathematical method or representation, she did not persist long in trying to unpack it, often preferring to answer “I'm not sure.” In reflecting on the clinical interview, she noted that, “I think the hardest ones for me are … figuring out what the kids did wrong or what the kids' method was … or the ones where the rules, the rules that I'm not familiar with, whether or not they worked.” She seemed unwilling or unable to follow student thinking, and in fact got all knowledge of content and student questions incorrect in the first wave interview, a rarity given that this set of items is, on average, much easier than items assessing content knowledge (Hill, Ball, & Schilling, in press).

An observer focusing mainly on pedagogical skills might rate Zoe's lessons well. They follow a predictable structure, including a statement of lesson goals and relations to other mathematical topics. There is mathematics taking place in nearly all segments of all lessons. Students appear comfortable asking questions during quiet work sessions, and Zoe responds quickly to remediate student confusions both during the introduction and independent work time. However, a closer look at the mathematics within these lessons suggests that only certain kinds of mathematics are being done and often with significant error and/or mathematical ambiguity. This leads us to the three themes explored in Zoe's case: her lack of precision and care around mathematical language; her frequent mathematical mistakes; and her constant proceduralization of important mathematical ideas and problems and concomitant lack of rich mathematics. To illustrate, we describe one lesson that begins with a review of the properties of addition followed by practice in multi-digit addition and subtraction.

Zoe's Teaching: Properties of Addition: Problems with Language and Mathematical Errors.

As the class comes to order, Zoe begins, as usual, with a description of the lesson objectives. She tells students that she will review “three properties of addition” and that “I'm going to go ahead and go through the terms again, and addition, and subtraction and just give you, we're going to start with properties and go over through them again. Because there's things I want you to think about this week when we're doing it.” She also tells students they will practice multi-digit addition and subtraction problems, adding that “I'm going to ask you some questions about the numbers because we've been discussing number sense and how the numbers work together and how they are. It's not just three hundred and twenty-four, there's actually a lot of different things, other things going on with that three hundred and twenty-four.” Even in this brief introduction, we can already see one of the centrally defining characteristics of Zoe's mathematics lessons. Although her utterances do communicate a basic sense for the content of the lesson, they are linguistically and mathematically garbled. Subtraction appears in an introduction to the properties of addition; unclear referents (e.g., “things” and “when you're doing it”) abound; her attempt to communicate about place value and the benefits of understanding place value in multi-digit operations (“… there's actually a lot of different things, other things going on with that three hundred and twenty-four”) might hint to more able students that the lesson is about to focus on place value, but leave weaker students mystified. In addition to hindering the conveyance of mathematical content, this confusion has implications for equity; where Lauren is careful to level the playing field by conveying mathematical terms concisely and accurately, Zoe's language leaves open possibilities for misunderstanding, particularly among students who arrive at school less prepared to decipher what she is thinking.

After this introduction, Zoe begins reviewing the zero property of addition by reciting a definition from the teacher's guide held in the crook of her arm: “When you add zero to a number, the sum is that number.” After reading this definition, she provides an example: 6 + 0 = 6. She then asks the class whether they recall how to identify the zero property of addition:

Zoe:   And we talked about that we could identify zero property of addition because it had an addition sign and it has a what in it? Can somebody raise their hand and tell me? Joella?

Joella:   A minus sign sort of?

Zoe:   No. … [if] we're looking for the zero property of addition what are we looking for besides an addition sign in the—

Student:   A zero?

Zoe:   A zero. So we want to make sure we have a zero in there, okay? So we know the zero property of addition is going to have an addition sign and a zero.

This exchange illustrates the second and third critical aspects of Zoe's instruction: the introduction of mathematical missteps and errors into instruction, and her tendency to proceduralize mathematical ideas. As Zoe's curriculum materials correctly noted, zero is the additive identity because when you add it to any number, the resulting sum is the original number. However, in “translating” this definition for her students—a task teachers are often called on to do—Zoe used the presence of an addition sign and a zero to distinguish instances of this property. Her translation focused on superficial notational features, rather than on the central mathematical ideas of the property. Confounding matters further, Zoe wrote the following on the board for students to copy: “When you add zero to a number.” Zoe omitted a key part of the definition—that the sum is the original number.

The same pattern of reading and writing the definition and then providing a numeric example continues as Zoe moves on to the associative property of addition. But before supplying the definition, she first tries to connect the associative property to the order of operations, another mathematical idea the class had previously discussed, by remarking that associativity is akin to “the parentheses, exponents, the order of operations that we need to do things in, okay? That has to do with your parentheses and we're going to talk about the associative property right now, that has parentheses in it.” Although making connections to other mathematical ideas is an important strategy in teaching, again the connections emphasized here—that the associative property is like order of operations because they both involve parentheses—are procedural and superficial.

Zoe then reads the definition for the associative property from the textbook and writes it on the board for students to copy, this time writing the same definition that she reads: “When you change the way addends are grouped, the sum stays the same.” She also provides an example on the board: (387 + 950) + 5 = 387 + (950 + 50). A student quickly points out her error, and Zoe changes the 50 to a 5. Although her definition and corrected example are both technically accurate, the way in which she modified her numerical example precludes her illustrating an important idea connected to the associative property: changing the grouping of numbers often facilitates more efficient computation. In this case, if she had changed the 5 to a 50 on the left-hand side of the original equation, she could have demonstrated one of the benefits of being able to choose the way addends are grouped. Regrouping (387 + 950) + 50 to 387 + (950 + 50) would result in the computationally friendlier 387 + 1000, whereas in computing 387 + 950 + 5, there are no obvious advantages to the order in which the addition is performed. Highlighting this application of the associative property was certainly not necessary for reviewing its definition; however, Zoe missed the opportunity to discuss a practical use of the property (see Kahan, Cooper, & Bethea, 2003 for a discussion of “teachable moments”).

Finally, Zoe reviews the commutative property of addition:

When we look at commutative, I like it cause, to me I always think that it's the opposite of and you'll see that. I think you'll remember this when we were talking about it. It says, [she reads from textbook] when you change the order of the addends, the sum stays the same. [Stops reading and looks up]. You're just changing the order. You're not grouping it differently; you're changing the order in which you first see it.

Although using the phrase “the opposite of” introduces ambiguity during Zoe's translation of the textbook definition, Zoe's description of the commutative property is largely accurate. However, she copies the wrong definition from the textbook onto the board: “When you change the way addends are grouped, the sum will stay the same.” This is the same definition she had written for the associative property just moments earlier. Her example (5 + 7 = 7 + 5) is an instance of the commutative property, but therefore does not match the definition she had copied. She then explains what she has written on the board:

Okay, a little example of it up here. If I have five plus seven and those are my two numbers I'm dealing with, do you see those two numbers on the other side of the equal sign? [Students indicate yes]. Are they in the same order? They're not. That's what they mean by commutative. It's, they're there, all the same numbers they're just, they're in the exact opposite order. They go [reads from board] “when you change the way addends are grouped the sum will stay the same.” Now, I say five plus seven equals seven plus five. Could I have three numbers in a different order? Yes.

Later, as students are working and Zoe is circulating, one student points out that the definitions for the associative and commutative properties are the same. Zoe responds:

Yeah, 'cause they do mean the same thing. 'Cause, you're just really; it's really just changing, it's the same thing it's just, you're going to see parentheses in one and the other one you'll see it in a different order, just, but you won't see the parentheses. So, that's going to be part of the thing you look for. For associative you're going to have parentheses in there and addition. For the commutative, you're going to look more for just a different arrangement of the numbers, but they're not saying specifically isolate anything first, and then with your zero property you're going to be able to put in the zero and that addition sign. That's how you're going to be able to identify, especially when we had that quiz.

In this case, Zoe's lack of mathematical knowledge appears to have impeded her ability to deliver accurate information to students. It is not hard to mis-copy a definition from a textbook. However, a teacher with more solid knowledge of the properties of addition might have noticed the error during the comparison of the example (5 + 7 = 7 + 5) and definition. Even a teacher whose mathematics was relatively weak might have corrected the error once the student pointed out the similarities between the definitions for the associative and commutative properties; instead, Zoe chose to continue the argument (“Yeah, cause they do mean the same thing”) while instructing the student that these were separable only by surface features—the parentheses and the different arrangement of numbers. Though she says this privately to the student, she then repeats this observation to the entire class.

This is a significant error. Unlike her failure to provide an initially correct example for the associative property [(387 + 950) + 5 = 387 + (950 + 50)], it is not computational in nature, nor is it corrected in the course of instruction. Rather, students walk away from this lesson with an incorrect definition for commutativity, a correct but garbled example, and a coda that indicates students should look for superficial markers to identify the property. This error is not corrected in the next lesson we recorded, nor in the next.

Within the first 16 minutes of this lesson, Zoe has already demonstrated three of the major factors that contribute to the low mathematical quality of her instruction. Admittedly, these are particularly egregious examples of mathematical errors, poor language use, and the proceduralization of mathematical ideas, but these same issues continue to plague the remainder of the lesson, as well as all of Zoe's lessons in the study. This next episode from the same lesson provides another example of how Zoe proceduralizes mathematical concepts, in this case, an alternative algorithm for subtraction. Although her introduction to the lesson implied that this part would focus on “number sense and how the numbers work together,” we will see, as with the properties of addition described earlier, Zoe's effort to teach mathematical concepts lacks meaning and connections.

Partial Differences Method: The Proceduralization of an Alternative Algorithm

After reviewing the properties of addition, Zoe turns students toward a review of two methods for solving multi-digit addition and subtraction problems. We focus in particular on her efforts to teach subtraction using an alternative algorithm, sometimes referred to as the “partial differences method.” In this method, each column is subtracted individually, and the results, including the sign, are recorded. These partial differences are then combined to arrive at the final answer. For example, to calculate 563 – 195, three subtractions are completed (500 − 100 = 400; 60 − 90 = −30; and 3 − 5 = −2) and then reconciled, as follows:

In the past two decades, there has been growing use of such “non-standard algorithms” in the United States, fueled by the belief that they benefit students by making the place value underpinnings of the algorithm more apparent, by being less prone to errors, by providing students a flexible set of methods for solving problems, or by incorporating algorithms used in other cultures and countries. Some curriculum materials ask teachers to let students “discover” algorithms themselves; in many more, teachers are instructed to teach these algorithms with explanations, and with explicit comparisons between different algorithms—activities thought to develop students' conceptual understandings.

In fact, our initial teacher survey contained three items involving alternative methods for multi-digit subtraction. Teachers were asked to inspect different student methods—including two items showing the partial differences method described earlier—and determine whether the methods could be used in any similar case of subtraction. Zoe correctly answered only one of these three items. She subsequently, however, attended a summertime professional development session (the MPDI) in which she reported learning about this method. It is this experience that provided the impetus for her use of this method in the classroom. Here, following a review of the standard procedure for multi-digit subtraction, she reviews the partial differences method with students, using the problem 372–39:

Zoe:   We have to look first here [indicating the tens column] and that tells me seven and three. What else is it telling me? Mika?

Mika:   There's seven tens and three tens.

Zoe:   Okay, and together seven tens and three tens is going to give me?

Student:   Four tens.

Zoe:   What am I going to do? Am I going to add these? Or?

Student:   Subtract.

Zoe:   Yeah, so what do I need to do?

Student:   Seventy minus thirty. [Writes 70 – 30 = 40]

Zoe:   Okay, so I'm going to say seventy subtract thirty, and what's my answer going to be? Positive or negative?

Student:   Negative.

Zoe:   Amelia?

Amelia:   Positive.

Zoe:   Positive. So, I'm going to say I have forty, okay. So, then I look at my ones place and I'm going to say two-Toby?

Toby:   Minus nine equals negative seven.

Zoe:   [Writes 2 – 9 = –7] Good. And that is because, and I've talked to you guys about this. If I have two dollars and I spend nine, I spent seven more than I needed to. Right? So I'm in the hole seven dollars, okay? I'm going to take this for my total. I dealt with my tens place. I dealt with my ones place. My only person, little guy over here [pointing to the hundreds place] and I haven't dealt with is my hundreds. And I have how many hundreds?

Students:   Three.

Zoe:   Okay, I'm going to put three hundred out here. What am I going to do first to this three hundred? What does that tell me, Aurelia?

Aurelia:   You're going to add forty.

Zoe:   I'm going to add forty to that. And so I'm going to get three forty. Now what do I have to do to it? Josh?

Josh:   You have to minus the seven?

Zoe:   Subtract the seven? Yes, I subtract the seven, and we end up with what? This is a part I can do in my head.

Student:   Three hundred and thirty three.

Zoe:   Yeah.

At the end of this exchange, Zoe has recorded the following work on the board:

This presentation likely does have elements of what professional developers hoped teachers would communicate to students. Zoe ensures students use correct language (subtracting rather than “minusing”), including noting that the 7 and 3 really signify 70 and 30. Yet beyond this, Zoe has enacted the partial differences method quite differently than advocates of alternative algorithms might hope. In large part, she offers students a procedural description of steps, rather than insight into the method and why it works. The connection she makes to other mathematical content is superficial: Both here and in her post-lesson interview, she links this algorithm to the teaching of operations with negative number more generally [“And so now when I deal with negative integers, they're not going to have a problem with it. They're already dealing with them and it's no big deal.”]. But this reference fails to illustrate the central mechanism enabling this elegant method: it uses place value to decompose the numbers, recording how many more or less than zero there are in each of the hundreds, tens, and ones places. The adding of positive and negative numbers in the last step allows the user to work with round numbers to reconcile the partial differences, arriving at an answer. Yet none of this—explanation, justification, or even a sense for why this method works in this particular case—occurs in this segment. There is no comparison made to the standard method. She accepts Josh's assertion that in the final step one must subtract a seven, rather than adding a negative seven, which is a more accurate and generalizable characterization of the procedure. Furthermore, there is no discussion of why the partial differences are reconciled using addition, when the operation in the original problem is subtraction.

It is reasonable to think that, because this was a review lesson, Zoe might have intentionally decided not to attend to explanations for this method. Yet during our third wave of data collection, Zoe once again taught this procedure, this time privately to three students who had joined the class mid-year. Again, her instruction consisted largely of a description of steps toward executing such problems, rather than any substantial or even partial explanation for why this method works.

Further, this portion of the lesson had a host of more minor problems. Here and elsewhere in our video records, Zoe consistently teaches this algorithm by focusing first on the tens, next on the ones, and finally on the hundreds. Although she never explicitly tells students they must go in this order, the rigidity of her presentation provides further evidence for the proceduralization of this algorithm and her lack of appreciation for its underlying structure; in fact, one can go in any order and, provided place value is accounted for, arrive at the correct answer. Her language (e.g., “little person,” “little guy”) is often colloquial and imprecise. When a student answers the four tens will be negative, she quickly moves on to find a student who answers that they should be positive; no remediation for the student's confusion is supplied. In writing the problem vertically, she uses the bar (conventionally thought to represent an equals sign) incorrectly, writing essentially 300 + 40 = 340 – 7 = 333. Although Zoe explicitly noted in the first part of this lesson that an equals sign balances two equal amounts, she violates that precept here.

Zoe reports she learned this algorithm in the course of professional development. However, she appears to view this method as a convenient way to introduce or reinforce negative numbers, rather than as a means toward helping students understand our number system. In her interview, she evidences little appreciation for the algorithm, and more generally, for mathematical explanation and justification:

Interviewer:   Do you have a view about what makes a good mathematical explanation?

Zoe:   Um … I think a good mathematical explanation kind of gives me the origins, gives me what it's related to, and shows me other ways to solve it. So I want … and why, why does this work?

Zoe mixed what could be considered a correct definition for explanation—Why does something work?—with other aspects of the mathematics (e.g., alternative solution methods). And more generally, her interviews reveal the difficulty she has clearly articulating and explaining mathematical ideas. Although the questions she answered correctly varied in their complexity (for example, she incorrectly identified the number halfway between 1.1 and 1.11, but in the same interview, correctly analyzed one of the more difficult questions about an alternative method for dividing fractions), her explanations for her correct answers were often scattered and incomplete, similar in quality to the explanations offered to her students.

There are other noteworthy aspects of Zoe's instruction. Her response to students and, in particular, students having problems with the mathematics, is uneven. At times, she accurately hears and diagnoses students' misunderstandings. In other instances, she responds inappropriately, given the mathematical and pedagogical issues at hand. In fact, Zoe's main strategy for responding to student confusions or questions is to simply demonstrate the mathematical idea or procedure once again. In walking around the room to examine student work, for instance, Zoe often responds to a student question by picking up the pencil and completing the problem for the student.

The parts of Zoe's lessons—teacher presentation, student practice, wrap-up—often seem disconnected from one another in terms of mathematical content. For example, in one lesson, Zoe introduces mathematical terminology having to do with whole number addition and subtraction (addends, difference, estimate, regrouping) and then devotes the rest of the lesson to division problems with remainders. In other cases, Zoe fails to capitalize on possible connections between topics. For instance, in the lesson detailed above, she shifts from introducing properties of addition to computational practice with standard and alternative algorithms for both addition and subtraction. When a student asked how the two parts of the lesson related, Zoe replied, “… those [definitions on the board] aren't giving examples of what those [problems on the worksheet] are. Those [on the worksheet] are just problems to solve. This [on the board] is just your vocabulary. … Your examples, these are your properties up there. Down here you're not doing the properties, you're just solving the algorithm.” In her response, she misses the mathematical connection between the topics, failing to notice that the properties she just reviewed are implicitly utilized in the computational algorithms.

Generalizability of These Themes

The three themes examined here can also be found in the “deficit” research described earlier. Our research, however, offers an opportunity to estimate the prevalence of these characteristics and their generalizability to other teachers in our sample. Unfortunately, many of the characteristics illustrated above in Zoe's instruction were common to other teachers who scored poorly on the MKT assessment.

Zoe's scale score for errors was 0.18; this scale was composed of codes for errors in technical (29% of clips) and general (52% of clips) language; errors in explanation (16% of clips); errors in recording the mathematics of the lesson on the board or other public areas (6% of clips); and outright mathematical errors (14% of clips). In many cases, a single clip contained multiple errors. Two other teachers included in the larger video study, but not this case exploration, also had error scale scores between 0.20–0.25 and similar code-level percentages. These errors ranged from smaller mathematical slips of the tongue (e.g., calling “equations” “expressions” or vice versa) to major problems, such as the aforementioned commutativity error. Not coincidentally, these teachers scored similarly to Zoe on the MKT assessment. Overall, the correlation between our error code and teacher MKT score (using Spearman's rho) is −0.83.

Conversely, Zoe's scale score on the “richness of the mathematics” measure was 0.05. The codes that comprise this measure demonstrate why: in no clip did Zoe use multiple models to demonstrate mathematical ideas; in only 11% of clips did Zoe or a student correctly explain a mathematical idea or procedure; there was no mathematical justification or proof; while she is explicit about the use of mathematical terms in 18% of her clips, she is explicit about mathematical reasoning and practices in only 4% and 2% of her clips, respectively. Overall, her instruction was largely procedural. This was, in fact, true for the majority of teachers in this study; seven out of ten were in single digits on the “richness of the mathematics” scale score, including the three teachers described later. Not coincidentally, the teachers with the higher proportions of mathematically rich lesson segments had higher MKT scores, as well.

This sheds new light on how mathematical knowledge for teaching might relate to the mathematical quality of classroom mathematics instruction. Currently, many studies focus on the omissions created by the lack of strong basic mathematical knowledge. Teachers without mathematical knowledge cannot provide explanations, justifications, or make careful use of representations. But just as troubling, and perhaps even more so, is our observation that a lack of MKT leaves teachers unable to navigate common and necessary elements of even very basic instruction. When students do not understand an idea, teachers cannot just restate the textbook definition until they do; they must create a translation between the textbook and student ideas. For this, MKT is critical. When presenting a new idea, teachers must forge linkages to prior lessons or student knowledge; again, MKT is critical. When a student becomes confused, a teacher must follow that confused thinking until a diagnosis and remediation plan can be made. MKT plays a role here, too. When illustrating a procedure or idea, a teacher must select numbers or examples that best represent the underlying concepts, and that will not confuse students; again, MKT plays a role. In all these teaching tasks, teachers' MKT is paramount.

Finally, like Cohen's Mrs. Oublier, Zoe raises the issue of missed opportunities in mathematics instruction. In the aforementioned lesson, Zoe missed an opportunity to emphasize the mathematical utility of the associative property, missed opportunities to connect the properties of addition to students' worksheet problems, and missed opportunities to make use of student errors. Many of the teachers described later have similar moments in their instruction. It is easy to criticize teachers for not making the most of such opportunities; representations can always be bettered, student ideas explored further, instructional tasks improved to maximize learning. Yet teachers, who operate in real time, make hard choices regarding the allocation of classroom resources and attention. What to us may look like a missed opportunity might be, on a teacher's part, a conscious decision, one made to solve classroom management problems or stick within the confines of a 45-minute lesson. We strove to balance these two perspectives in our coding and analysis of videotape, typically giving teachers the benefit of the doubt and only reluctantly criticizing instructional choices. However, in some cases, including those described here, we argue that those instructional choices harmed the mathematics of the lesson as much as an outright error or contorted definition would. Making these decisions is difficult, and we know some will disagree; more deliberative discussions about such instances seem warranted.

Noelle

Noelle is unique in that she represents both a convergent and divergent case. We use her case first to demonstrate how strong MKT correlates with the mathematical quality of instruction along several key dimensions: in carefully using mathematical language; in providing opportunities for students to engage in rich mathematics; and in supporting students' thinking about mathematics. However, Table 4 shows that our overall perceptions of Noelle's lessons did not match her MQI scores on several dimensions including mathematical language and richness of the mathematics. This led us to a new analysis, one in which we identified a central flaw in Noelle's lessons: the lack of content-focused telos, or an end and a purpose. Although Noelle's lessons offer students the opportunity to engage with mathematical justification and explanations, cognitively rich tasks, and the careful use of language in the moment, these moments rarely build toward a greater purpose, synthesis, or closure. Following some background on Noelle's lessons, we offer an illustration of both the convergent and divergent aspects of Noelle's instruction, and consider how this case informs our theory more generally.

Background

Noelle's third-grade classroom is spacious. The walls are covered with several posters and bulletin boards with student work aesthetically displayed; colorful student artwork hangs from the ceiling. The classroom is neat and well-organized with several resources: two computer stations, a television, a library, and a globe. Students' desks are arranged into groups of four or five, and students themselves are diverse, with a range of native languages. Noelle appears comfortable in the classroom; she is confident, poised, and very much in control.

Noelle's lessons share the same format. Instead of asking students to solve “thirty or forty routine problems” of the same type, Noelle prefers to engage them in “in-depth problem investigations” and give them the opportunity to “explor[e] possible ways to solve [each] problem.” Consistent with these ideas, she structures her lessons around one or sometimes two meticulously selected problems, distributing manipulatives prepared in advance to facilitate students' explorations. She asks students to first work individually, and then to share their ideas and consider different ways to approach the assigned problem(s).

At the beginning of the study, Noelle had 19 years of experience. Although she received her bachelor's in teaching with a major in geography, Noelle felt unprepared to teach mathematics. She recalled that most of her preservice training was centered on “theoretical stuff” with few practical applications. To compensate, Noelle joined several professional development seminars, used various ancillary materials, and even read research on teaching mathematics. Noelle's mathematical knowledge, as measured at the beginning of the study, was strong. From the subsample of ten teachers whose lessons were videotaped, she ranked third on the MKT measure with a score of 1.21, and she was in the 89th percentile among the larger sample of teachers.

The mathematical quality of Noelle's teaching excelled in several respects, as might be inferred from her average overall lesson score (see Figure 1). To illustrate the convergent aspects of Noelle's instruction, we elaborate three features of her practice: her careful use of mathematical language; her construction of a setting that supports rich mathematical thinking; and her ability to respond flexibly to students. We then move to a central area in which Noelle's instruction diverges from expectations set up by her MKT score: in the lack of telos—an end (closure) and a purpose (directionality). This area of divergence helps explain Noelle's disparate performance in our quantitative and qualitative analyses, and also suggests an area of concern for mathematics educators and policy-makers.

Noelle as a Convergent Case

To illustrate the ways in which Noelle's strong MKT supports the mathematical quality of her instruction, we use episodes from three connected first-wave lessons.

Cube Attributes: The Careful Use of Mathematical Language

Noelle's first lesson revolves around generating different spatial arrangements of two, three, and four cubes. To ensure that students are using correct mathematical terminology, Noelle opens the lesson by distributing solid wooden cubes and asking students to identify their attributes. Before proceeding, however, she first ensures that students are familiar with the term “attributes” by eliciting students' prior knowledge. She is careful to differentiate between student contributions that are valid and those that are not relevant; for example, she accepts students' nominations of the terms “type” and “qualities” as good descriptors, but does not accept “number.” In addition, she proposes other synonyms (“traits,” “characteristics”) to support students' access to the term.

After this exchange, students are given time to identify the attributes of a cube. Noelle listens carefully and respectfully to students' ideas, asks for more clarifications, and lists the nominated attributes on the board. From this ten-minute introductory activity, we single out two short episodes illustrative of her attention to mathematical language.

In the first episode, Noelle opens the discussion by soliciting students' ideas about cubes. One student begins:

Shaun:   It has four like edges, I mean eight.

Noelle:   Okay, would you explain what the edges are? What you're calling “edges”?

Shaun:   Like the sides or the point of a cube.

Noelle:   Okay, so you're talking about a point or the actual side where the two parts come together?

Shaun:   Like the point.

Noelle:   The point. Okay. [Turning to the rest of the class: Would you agree that there are eight points? Look at your cube. He's talking about the points on the cube. [She touches the vertices of the cube she holds in her hands.] Would you agree that there are eight points on there?

Shaun's first utterance (“It has four like edges, I mean eight”) is ambiguous. Cubes do have edges, but they have twelve edges, not eight; cubes also have eight vertices, which could be what he means. Instead of making an assumption and rushing to correct the student, Noelle prompts him to clarify his thinking. Through this short exchange, Shaun proposes another term—“point”—which indicates that he is thinking about the vertices. After asking students to verify that a cube has indeed eight “points,” Noelle introduces the correct mathematical term (vertex) and its plural form (vertices), which she writes on the board. She then returns to the term “edges” in the second episode, as students continue identifying attributes of the cube:

Carmen:   They [cubes] have twelve, these lines over there. I don't know what they're called.

Noelle:   Okay. So the lines between two what?

Carmen:   Vertex, I mean vertices.

Noelle:   Okay, so the line between the two vertices. And how many are there?

Carmen:   Twelve.

Noelle:   Okay. Anybody has an idea what those might be called? Ramona?

Ramona:   Edges.

Noelle:   Okay.

The episode above again illustrates Noelle's careful use of mathematical language. Aware of the definitions of the two terms “edge” and “vertex,” Noelle skillfully steers students' thinking toward the correct terms, honoring both the integrity of the mathematics and students' contributions (c.f. Ball, 1993). The term “edge,” which is incorrectly used by a student in the first episode, is correctly defined and used in the second episode, but even more critically, it is defined through another cube attribute. This helps students build connections between the attributes under consideration.

In her interviews, Noelle confirmed her attention to mathematical language:

To me [language is] important … but it sure requires a lot of thinking about it ahead of time to make sure that you know what you want to say and how you're going to say it and I think most people don't take the time to think about that. (emphases added)

Noelle's reference to thinking carefully about how to introduce mathematical language resonates with her instructional approach, demonstrated above in the drawing of connections between the edges and the vertices of a cube. Noelle's own highly developed knowledge of mathematical terms supported this work. Our interview data, and especially Noelle's reasoning during the clinical interview, demonstrate how. For instance, in solving a geometry problem, she confidently answered that a cube does not have eight edges, and differentiated between the edges, the vertices, and the faces of a cube. She also built on geometric definitions to reason through the test items, much as she does in this episode from her instruction.

Surprisingly, despite the deliberate and careful use of mathematical language in her lessons, Noelle scored poorly on the language density and precision scale. In fact, although Noelle ranked second after Lauren in terms of her use of appropriate general language (0.63), her ranking with respect to the density and precision of technical language (0.32) was last among the five cases examined in this article. We revisit and explicate this discrepancy later in this article, when we explain what rendered Noelle's MKT and observational scores divergent.

Cube Attributes II: Rich Mathematics and Responding to Students

The next day, Noelle begins class with another review of cube attributes. Early in the review, a student (Oscar) proposes that a cube has 24 right angles. Although this is not the focus of this lesson, Noelle elicits other students' thinking about this claim, only to find that students disagree. She asks students to take a moment and evaluate the validity of Oscar's proposal, hinting that proof may come in different forms: “See if we can figure out how many right angles there are. There might even be a better way than counting: looking for a pattern.” Using the definition of a square that was previously introduced, a student maintains that Oscar's conjecture is valid:

Allen:   I would agree that there are twenty-four [right angles] and I found that out by—since the definition of a square is four right angles … so then I multiplied four times the number of faces on the cube. So [there are] six faces … altogether that equals 24 right angles.

Noelle reiterates Allen's argument, in the process emphasizing a key mathematical element—the use of a definition to support mathematical reasoning:

Noelle:   Okay, so you thought about it as being six faces. And earlier today we looked up the definition. And so now you know the definition, [a] square [has] four right angles. And since there are six of those on the cube [points to the faces of a cube], six times four would be twenty-four, okay.

She then welcomes other student comments:

Joseph:   I disagree because if you do it that way … always one of the right angles will form another, one part of another square so it's like you can't count one layer or something, so you just have to count the top and the bottom so that four on the top and four on the bottom, so four times two is eight. So I'm pretty sure it's eight right angles.

…

Noelle:   Harold?

Harold:   There are twelve [right angles] because … if you count four on one layer then that means this one [points to an angle] on another face is already used. So you can't count that, and Joseph forgot to count the sides. So, it's twelve.

In contrast to Allen, who used the definition of a square to prove Oscar's conjecture, Joseph and Harold employ a counting method. Yet their approach is complicated by the fact that they are counting the angles (a two-dimensional trait) on a three-dimensional shape. In fact, Joseph appears to be counting the corners where three right angles come together as one right angle, a logical error given the task.

Noelle identifies Joseph's misunderstanding and appears to follow Harold's reasoning as well, no easy feat. Neither student uses standard mathematical terminology, redefining general language (layers, sides) to describe their thinking. Yet Noelle quickly deciphers their claims, then moves to bring the discussion to consensus. She explains that, where in representing three-dimensional shapes one should draw some faces “at an angle”—as her initial drawing on the board suggests (see the left panel of Figure 3)—for the purposes of their problem, it is easier to “flatten” the cube, and present its faces one next to the other. Having said that, she draws two adjacent squares, and asks a student to come to the board and identify all the right angles. After all eight right angles are identified (see right panel of Figure 3), she asks Joseph if he would like to revise his thinking, and he responds by agreeing that a cube has 24 right angles.

FIGURE 3 Noelle's drawings to support students' exploration of the number of right angles on a cube.

In this episode, students must prove or refute a conjecture proposed by one of their classmates; they use definitions and identify patterns to justify their claims (e.g., Andrew) and explain their thinking using the available manipulatives (e.g., Joseph and Harold). Noelle adroitly facilitates discussion by encouraging students to consider multiple paths to prove or refute the conjecture, reiterating their contributions and making them available to the whole class for further reflection, and intervening when students' different perceptions of “right angles” make it unlikely they can quickly resolve this discussion on their own. These moves all require knowledge of the mathematical terrain, but, we argue, not just ordinary mathematical knowledge. Instead, these are decision points where highly developed and specialized knowledge of mathematics, students and their ideas, and pedagogical possibilities can make the difference between a well-formed and ill-formed lesson (Ball & Bass, 2003).

This episode also allows us to observe the third feature of Noelle's lessons: responding to students. All students' contributions are welcomed, even those that are erroneous or do not strictly comply with the goals of the lesson. For instance, although Noelle could ignore or bracket Oscar's conjecture about the number of right angles, suggesting that it lies beyond the focus of the lesson, she instead uses his contribution to engage other students in the discussion. And while a non-teaching adult might be confused about Joseph and Harold's arguments, Noelle quickly deciphers their thinking and moves instruction forward correspondingly. Again, we argue that Noelle's practice provides examples of a kind of joint knowledge of mathematics and students held by some teachers, and that enables fluid classroom work.

In addition to the characteristics described earlier, Noelle's teaching has other admirable features, including some not captured by our coding system. Most notably, Noelle offers her students cognitively demanding tasks, and in most cases, maintains the cognitive demand of those tasks throughout the lesson. Although analysis of this hypothesis is beyond the scope of this article, we believe Noelle's use of cognitively challenging tasks is supported by her MKT. In fact, the selection and enactment of cognitively demanding activities may be examples of teaching tasks in which mathematical knowledge is most observable.

Finally, like Lauren, Noelle's encouragement of student participation also has implications for equity. In the first episode, for instance, Noelle distributed a cube to all students, so that each might connect the listing of cube attributes with a tangible example. She ensured that every student understood the meaning of the word “attribute” before beginning the task. Although not as explicit about mathematical reasoning and practices as Lauren, Noelle encourages her diverse students to engage with the mathematics, and provides the prerequisite understandings for all students to engage in the work.

Noelle as a Divergent Case: The Lack of Telos

The previous text portrays Noelle as a convergent case, an example of the correlation between high MKT and lessons of high mathematical quality. However, as shown in Table 4, Noelle's language and rich mathematics scores do not seem to reflect instruction of high mathematical quality. Noelle's 0.27 score on the mathematical language code is similar to Zoe's score on this scale. Similarly, Noelle's very low score on the “richness of the mathematics” code (0.04) suggests that she structured a mathematically impoverished learning environment. Again, comparing Noelle's and Zoe's corresponding codes, it could be inferred that students in these two teachers' classes experience mathematics of the same low quality. And yet, as the excerpts demonstrate, Noelle's teaching was by far better than Zoe's.

A closer review of Noelle's lessons provides insight into these discrepancies. With respect to language, we found that when Noelle used technical terms, she generally used them appropriately, as reflected in her modest error in language score (8% of clips). However, there were long segments of instructional time when Noelle monitored her students' work without actively interacting with them. Because she was either not talking or her talk was non-mathematical (e.g., encouraging students to continue working on a task), she had no instances of technical or general language in these clips. And although Noelle selected rich mathematical tasks for her students, she seldom brought these explorations to closure. That is, she rarely highlighted the mathematical content that these explorations were supposed to afford. In fact, in none of the nine videotaped lessons did Noelle summarize the mathematical purpose of the exploration. Thus, despite the strong aspects in Noelle's teaching discussed earlier, her lessons lacked a telos: an end (closure and synthesis of ideas) and a purpose (directionality).

This lack of closure or synthesis was manifested in at least three different levels. We demonstrate each by referring to the set of first-wave lessons described in Table 5. First, when circulating during student work time, Noelle engaged individuals or groups of students in discussions of their explorations, but only very infrequently posed questions that would help students arrive at some closure or synthesis of ideas. Consider, for instance, a lesson in which students were asked to use seven different arrangements of three and four cubes (see Figure 4) to explore different ways to construct a Soma cube (i.e., a 3 × 3 × 3 cube).

FIGURE 4 Arrangements of three and four cubes used to construct the Soma cube (Youngs & Pauls, 1999, p. 67).

TABLE 5 Noelle's First Wave Lessons

Lesson	Student Activity
No, W1-25: Different cube arrangements	Students first consider the attributes of a cube and then work collaboratively to construct different arrangements using 2, 3, and 4 cubes.
No, W1-27: The Soma cube	Students experiment with building simple 3D shapes and then the Soma cube. After sharing some solutions, they are guided to record their constructions on isomorphic grid paper.
No, W1-29: Cube nets	Students predict what a cube net might look like. Then, they are given paper cubes to cut to verify their predictions. For the next fifty minutes they work in groups to find as many cube nets as possible. During the last five minutes they are prompted to start exploring commonalities among their nets.

While monitoring students' work, Noelle encouraged them to consider more than one way to construct the cube, hinting that there exist “240 different combinations of [the] seven pieces to make the [Soma] cube.” However, she did not pose any further probes to guide students' exploration or to point their attention to the mathematical aspects of this exploration. For example, she could have helped students become more strategic in their exploration by excluding combinations that were not helpful (e.g., arrangement number 7 already has 3 cubes in a row, hence the sequence of 3 cannot be extended with any part of any other arrangement and still fit in the 3 × 3 × 3 solution).

Second, when reconvening into a whole class discussion, Noelle also failed to help students synthesize their explorations. At the conclusion of the activity described earlier, Noelle did not ask students to identify common features of their Soma cubes. For example, she could have drawn students' attention to the fact that the seven arrangements being used consisted of 27 total cubes, which is a necessary condition to construct a 3 × 3 × 3 cube. Instead, Noelle shifted to another activity, one that asked students to record three-dimensional shapes on isomorphic grid paper. The lesson ended without any closure or synthesis of this activity, either.

Finally, closure was also absent across a sequence of lessons. Although our videotaping may not have corresponded to Noelle's own unit sequencing, we found it notable that there were nearly no mathematical connections made across lessons, and no hints as to the mathematical ties binding the activities. The three lessons in Wave 1 (see Table 5), for instance, asked students to engage three related but disparate topics: arrangements of cubes, different ways of constructing a Soma cube, and different cube nets. Although these topics could have been linked in several ways, no such logic was apparent in Noelle's instruction. Instead, the activities employed in these lessons stand as compelling, but separate, activities. We observed the same pattern in the other two waves of our data collection.

Thus Noelle's lessons lack directionality. They occur as singular events and fail to contribute to a greater whole (c.f. Cooney & Wiegel, 2003) or foster the development of key mathematical ideas (Hiebert, Carpenter, Fennema, Fuson, Wearne, Murray, et al., 1997; National Research Council, 2001). A reading of Noelle's interviews and post-lesson reflections suggests a plausible cause: When planning her lessons, Noelle pays more attention to the nature of the activities she selects than to the content goals these activities serve. Her main concern is whether the activities create a working space for her students that allows mathematical exploration, not whether the activities contribute toward students learning specific content. This lack of directionality is amplified by the fact that Noelle typically consults several resources to find interesting activities, focusing on the activities per se rather than on the goals these activities could serve. Noelle, in fact, often ignores the activities and lesson goals outlined in her mandated curriculum, which could have offered her support in identifying not only the purpose of the individual activities, but also their mathematical relationship to each other.

Noelle's post-lesson reflections provide evidence on this point. She explained, for example, that she developed the sequence of the three first-wave lessons starting from an interesting activity (i.e., constructing different cube arrangements) that she found in supplemental curriculum materials, moving to another activity from this same set of materials (the Soma Cube), and closing with the cube nets activity she learned in professional development. In an interview following the third Wave 1 lesson, Noelle shared her rationale for sequencing these activities, explaining that the first two explorations offer students an opportunity to investigate different constructions with cubes, whereas in the last, students have the opportunity to deconstruct a cube. Her interview suggests these two ideas—construction/deconstruction, and arrangements—seem to have glued her Wave 1 lessons together. These links were not clearly communicated to students; doing so might have helped them see connections among the activities in which they were engaged.

Generalizability of These Themes

The positive aspects of Noelle's instruction, the moments in her lessons during which Noelle exhibited strong command of mathematical language and created rich mathematical environments for her students, generalize well to other high-MKT teachers. Lauren and others demonstrated similar characteristics. However, Noelle's lack of telos was not observed in other high-MKT teachers, although it could be seen often in lower-knowledge teachers like Zoe. In fact, linking the mathematics within and between lessons appeared as one of the most significant challenges among the lower-knowledge teachers in our video sample.

Including Noelle in our case study analysis allowed us to examine additional influences on the relationship between MKT and the mathematical quality of instruction. In particular, Noelle's failure to build important mathematical concepts within and across lessons raises issues related to teachers' use of curriculum. Like other teachers in our study, Noelle was very critical of her mandated curriculum. And like others, she invested considerable time in identifying and synthesizing activities from supplemental resource materials. Yet doing so increases the challenge inherent in mathematics teaching; teachers must hold in mind the central ideas around a particular topic, choose lessons that help build these ideas, and then enact the lessons such that they relate back to those ideas. In Lauren's case, working across different materials resulted in lessons that had these qualities; in Noelle's case, it did not. Lauren's case suggests that teachers need not follow their mandated curriculum with fidelity. However, the study of Noelle seems to suggest that even strong MKT might not be sufficient to support teachers as curriculum developers, a role which many unwittingly undertake (c.f. Ball & Feiman-Nemser, 1988).

Noelle's case also sheds light on teaching tasks not included in our coding system that nevertheless call upon a teacher's MKT. In addition to making connections to mathematical ideas within and across lessons, these MKT-intensive tasks of teaching include the selection of cognitively demanding tasks and their enactment in a manner that maintains their cognitive challenge, deciphering mathematically imprecise student statements, revoicing students' contributions and knowing when to make them the object of further exploration for the whole class, as well as stepping into student discussions before they become mathematically counterproductive. These topics provide hypotheses for further research in this area.

Anna

Anna is the second divergent case we discuss. Like Noelle, there are areas of similarity between her MKT and MQI scores, including average scores for MKT and mathematical errors. And when using her assigned textbook, Anna also appears average on other MQI scales such as the density and precision of mathematical language. Yet there are two ways in which Anna performs much lower than one would expect from her MKT scores: connecting classroom work to mathematical ideas and procedures, and richness of the mathematics. In what follows, we illustrate Anna's instruction and consider the extent to which it can inform our understanding of the links between MKT and MQI and additional factors that impinge upon those links. In particular, Anna's case suggests we must also attend to at least two contextual issues: beliefs about mathematics instruction, and the use of curriculum materials as a mediator between MKT and instruction.

Background

Anna is a committed elementary teacher with 10 years of experience and a Master's degree in curriculum and instruction. Her second-grade classroom is bright, colorful, and orderly. The walls are covered with posters, bulletin-board displays, calendars, graphs, and a huge collection of carefully displayed student work. Children's desks are arrayed in two semicircles facing the front of the room. Students know exactly what to do; off-task behaviors are rare. Anna's students have a wide range of English language fluency and come from diverse economic backgrounds. Anna is an active mathematics teacher, commanding attention from the front of the room during whole group lessons, and circulating and stopping frequently to talk with students during small group and individual work. When students are confused, Anna is quick to give direction and encouragement. It is important to Anna that all of her students are involved in activities and that they complete lesson components. The students seem to enjoy and like Anna, often smiling and laughing in response to Anna's questions, directions, jokes, and frequent compliments.

Every day the class spends at least an hour on mathematics. The school day begins with a morning calendar routine that includes tracking the number of days spent in school, graphing the weather, and tallying the number of lost teeth. These and other similar activities reinforce basic mathematical skills such as counting, place value, addition, subtraction, and recognition of simple patterns. The math period occurs later in the day. Most lessons are taken from the Harcourt mathematics textbook and begin with a regular routine. Students complete a set of review problems (e.g., listing coin combinations that total a certain value, interpreting graphs, solving word problems) and then work on one or two problems related to the lesson content for that day. Next, students take out their workbooks and systematically complete the pages for that day's lesson.

Anna wants her students to be involved in activities that they will enjoy and that will build their interest in doing mathematics. This inspires her to regularly supplement the textbook lessons with activities of her own design or from her collection of handouts and workbooks. These supplementary activities typically require cutting, pasting, or coloring, and appear to require a great deal of preparation and planning on Anna's part.

By her own account, Anna has struggled with mathematics, especially as a child. However, Anna's difficulty with mathematics content has not led her to shy away from teaching mathematics. She attends many hours of professional development in this topic each year, often with her district math coach.

Anna's mathematical knowledge for teaching falls right in the middle of the case study teachers with an MKT scale score of 0.56. In the context of the larger sample, Anna's score is in the 68th percentile. Her average MKT is confirmed by her performance on clinical interview tasks. On straightforward content questions, Anna generally answered correctly: she knew cubes have 12 edges, and she could determine the number halfway between 1.1 and 1.11. Anna's difficulty with mathematics appeared in answers to the “specialized” knowledge items, including an inability to interpret unconventional algorithms and a struggle with terminology and definitions. For instance, when presented with an algorithm that was mathematically correct although unusual, Anna was quick to say things like “the method's wrong … because that's not what you do.” When given the definition for a prism (i.e., a solid figure that has two congruent, polygon-shaped bases, where all other faces are rectangles), Anna became confused and argued that a pyramid is not a prism because “they're not congruent, the prism and the pyramid. They're not the same, they're totally different shapes.” In this example, Anna confused congruence, which is used here to define a characteristic of the prism's bases, to refer to a comparison between the prism and pyramid. This type of confusion permeated Anna's understanding of mathematics and shaped how she used her knowledge to reason about mathematical problems.

Anna as a Convergent Case

These characteristics of Anna's mathematical knowledge are reflected in the mathematical quality of her classroom practice. In some part, her MKT and MQI align well. Anna falls in the middle of the teacher range in areas such as mathematical errors, errors in language, and responding to students (see Table 4). This correlates well, we argue, with her adequate performance on the common content knowledge items. Her poorer performance on the specialized content knowledge items is mirrored by a very low score for the richness of the mathematics. And her problems with definition and use of language during the interview are reflected in poor scores on the density and precision of language scale.

Our qualitative analysis bore these quantitative results out. When Anna uses a textbook to guide her lessons, as she does in five of her nine videotaped lessons, they tend to fall squarely into the vicinity we expect in terms of the mathematical quality of instruction: they are mixed. To illustrate, we present the first part of a lesson on plane symmetry and congruence.

Anna begins this lesson like most that she teaches from the textbook. Students first work independently to complete a set of review problems. They then work as a class to complete the problem of the day, which today reads, “Mario has a picture of a circle. At what point on the circle would he start to draw a line of symmetry?” To launch their work on this problem, Anna asks the class for the definition of symmetry.

Anna:   First of all, what is symmetry?

Student:   Divided in half?

Anna:   Divided in half. Equally, right? It's symmetrical.

This brief exchange is typical of Anna's instruction. As Anna noted in the interview, she is concerned that all students understand the vocabulary and is committed to frequently reviewing mathematical terms. However, Anna's discussion of symmetry is neither complete nor fully accurate. It is actually a “line of symmetry,” not symmetry, that divides a plane figure into symmetrical regions. Furthermore, a line of symmetry does not simply divide a shape in half; the halves must also mirror one other across the line of symmetry. Missing this key condition, Anna's definition would accept the diagonal of the rectangle shown in Figure 5 as a line of symmetry, even through the reflection criteria is not met.

FIGURE 5 A line that divides this rectangle in half, but that is not a line of symmetry.

As in her clinical interview, Anna's classroom mathematical language lacks precision. And, because the language is vague, and sometimes incorrect, students could easily become confused about key mathematical features of the work.

After completing the review, Anna has her students take out their math books and start on a worksheet. Students are asked to use a line of symmetry to divide a square drawn on grid paper:

Anna:   Draw a line of symmetry. The two parts will be congruent. They need to be equal. So on number one, how are you going to do that? How are you going to draw a line to make it congruent?

Student:   From the left side of the dot in the middle.

Anna:   She says the left side, the dot in the middle, all the way across. Is that acceptable?

Students:   Yes.

Anna:   Yes. Is there any other way you can divide that to make it congruent? Betsy?

Betsy:   The top middle to the bottom middle.

Anna:   Good. What have you created? From that square what did you …

Student:   Two rectangles.

Anna:   Good job. Is there any other thing we could possibly do with number one?

Anil:   I wanted to ask a question.

Anna:   Yes, Anil?

Anil:   From corner to corner.

Anna:   Corner to corner, absolutely. What do you have if you go corner to corner?

Anil:   A triangle.

Anna:   How many?

Anil:   Two.

Anna continues to talk the class through the exercise, pointing out that a rectangle has two lines of symmetry, and the triangle and trapezoid one. She is careful to use the names of the shapes, and she recognizes students for their work. She continues, reading a question at the bottom of the worksheet:

Anna:   How can you prove that the two parts of a figure are congruent? How can you prove they're congruent? Prove to me they're congruent. Look at these examples here.

Student:   That they're the exact same shape.

Anna:   They're the exact same shape. That's what you want. Everybody accepts that? Is that what you want on this? Okay, then that's what we're going to write. Both pieces are exactly the same size. [The] key word here is EXACTLY. Right?

These short episodes are all typical of how Anna teaches using the textbook. She follows the materials closely and works hard to make sure that students are completing activities and attending to relevant vocabulary. In discussing the shapes in the aforementioned activity, Anna does use key mathematical terms: congruent, line of symmetry, triangle, and even horizontal and vertical. Moreover, in most cases, she uses these terms correctly. She is also open to multiple solutions and solution methods, as shown in the second episode. And Anna even makes an effort toward proof, although it was not enacted with complete mathematical integrity (e.g., proof requires a method for showing congruence, such as paper folding or rotating and sliding one region over another and not simply stating a definition). Whereas we repeatedly observed high-knowledge teachers, such as Lauren, taking up opportunities like this one to introduce students to mathematical ideas such as proof, Anna seemed unaware of this opportunity; instead, she held the work at the level of definition of terms. In all, Anna's instruction seemed average and matched the expectations set up by her MKT when using her textbook.

Anna as a Divergent Case

Anna, however, differs markedly from what one would expect given her MKT score in one very important way. The students in Anna's classroom spend almost a third of their time during mathematics lessons (32% of lesson clips) engaged in activities that involve no mathematics at all. Even the lower-knowledge teachers, such as Zoe, spend 90% or more of a mathematics lesson doing math. This makes Anna a divergent case, in that the mathematical quality of her lessons was far below what would be expected from one with average MKT. We offer two interconnected reasons why this divergence might occur: her beliefs about how students learn mathematics, and her use of supplemental curriculum materials.

Beliefs About Mathematics Teaching and Learning

Anna's interview passages regarding the value of professional development best illuminate her views of mathematics teaching and learning. To start, Anna sees professional development not only as a way to learn more about mathematics, but also to expand the pool of activities she has available for use with her students. When talking about the benefits of professional development, she reported that she liked bringing back “fun” activities that included “hands on” and “concrete” materials. Anna was particularly excited about a set of mathematical games she brought back from her latest professional development experience, remarking, “I can do fun stuff now.” In fact, one of Anna's primary goals for mathematics instruction is to help her students learn to love math. She elaborates by saying that most of her students arrive in her class disliking math for two reasons: many are non-native English speakers, and find mathematics difficult because of its specialized vocabulary; and the difficulty of the concepts taught at each grade has increased substantially over the last few years due to revisions in state policy, leaving even early-grade students to struggle. Anna wants to change this for her students. She was particularly enthusiastic about the materials and activities she collected from the professional development sessions because she thought they would make mathematics more accessible and fun for the students. And, in fact, many of Anna's lessons included activities from the professional development.

Making mathematics fun, interesting, and concrete for her students was a priority for Anna, as it surely is for other teachers as well. But for Anna, this led to many mathematics lessons where mathematics was barely evident. We illustrate this further as we discuss the second reason for divergence: Anna's use and non-use of textbooks.

Use of Supplemental Curriculum Materials

The mathematical quality of Anna's instruction drops dramatically when Anna departs from the textbook, which she does for most of four of nine lessons and parts of others. Most striking is that the supplemental activities, which are clearly intended to build on the topics addressed in the textbook, often have no mathematical content. Her score for “classroom work connected to mathematical ideas or procedures” for the lessons she teaches from the textbook is 0.87, which is already low in comparison to other teachers. But for the supplemental lessons, her score drops to 0.32, far lower than any of the other teachers. Even when the focus is on mathematics, these lessons or parts of lessons have problems; for instance, the density and accuracy of mathematical language is lower than for her textbook lessons, dropping from 0.26 in the textbook lessons to 0.16, again the lowest of all the teachers.

We illustrate the problems in Anna's supplemental lessons in the final segment of the aforementioned symmetry/congruence lesson. After completing the textbook portion of the lesson, Anna introduces an extension activity, a single, reproducible page titled “A Symmetrical Pet” (see Figure 6). The page is meant to be colored, cut, folded, and stood on a desk or other surface.

FIGURE 6 A symmetrical pet.

It is easy to see why Anna selected this activity. The word “symmetrical” is in the title of the worksheet, and the two rabbits are mirror reflections of one other. But this activity also differs from the textbook lesson in a number of important ways. In the textbook, a line of symmetry always divided a whole shape (e.g., square, triangle) into two congruent halves. In Anna's extension activity, the whole figure is made up of two rabbits. This is bound to be a confusing leap for young children. Further, folding and standing up the final figure both moves the activity out of the two-dimensional plane and also obscures the line of symmetry in the original plane figure. Anna, however, seems oblivious to these contradictions and complications, and moves ahead as if this activity is a direct extension of the lesson from the textbook.

Anna introduces the symmetrical pet activity saying, “The last thing we are going to do today is fun. There's always fun.” This usually means that that activity involves coloring, cutting, and ending up with some artfully designed final product.

Anna:   … What I want you to do, if this rabbit is symmetrical and this rabbit is congruent, both sides of this rabbit must be what? What's the key word?

Students:   Same.

Anna:   Same, but what kind? What's the key word? They can be the same, but they must be what?

Student:   Exactly.

Anna:   Exactly the same. So now, I don't care how many colors you take out. I don't care how you decorate this, but what are you going to do with each side? You're going to make them …?

Students:   The same.

Anna:   Exactly the same. So whatever you do to this side, you do it to this side. Does anybody have any questions or thoughts? Yes.

Student:   Can we have two—I mean if I color the rabbit brown or something, cause it would have to be brown here.

Anna:   What do you think? He says if I color this half brown, does this half have to be brown?

Students:   Yes.

Anna:   Yes, exactly. So color. I'll help you when it comes time to cut. I don't want you to cut them in half and have two rabbits. I want one rabbit with two sides. So color first and then we'll do the cutting together, the folding and the gluing.

Here, Anna flounders with the mathematical content. In introducing the activity, Anna says “if this rabbit is symmetrical and this rabbit is congruent,” but it is unclear what it means to call the drawing shown in Figure 6 symmetrical and congruent at the same time. This confusion is heightened by the fact that it is not clear whether she is referring to the whole rabbit, the two rabbits that compose the whole figure, or something else. Anna asks what characteristics the two sides of the rabbit must have in order to be congruent, and a student replies with the word “same,” close to the mathematical definition of “same size and shape.” But instead of focusing on shape and size as the key defining features, Anna elicits the word “exactly.” She goes on to explain that the two sides must have colors that are reflected across the line of symmetry. However, she never discusses whether the definition of congruent (i.e., same size and shape) also implies the same color pattern on each side of the line of symmetry. It appears that Anna is unaware that she is being imprecise in her language and has introduced new and more complex mathematical features into the lesson. It is also possible that Anna is just not attending to the mathematics. For Anna, the point of this lesson may be to provide an activity that the class will find enjoyable, and her attention is focused on describing to the students how to construct the stand-up rabbit; the mathematics is relatively peripheral.

After Anna's brief introduction, the class spends about eight minutes coloring and then another ten minutes or so cutting, folding, and gluing the rabbit, with slower students taking an additional few minutes getting help from those who are already done. Anna circulates around the room and helps students complete the project. Although the students are busy, there is no mathematical discussion, no explanation, no closure, and no reminding about what they are doing and how it relates to the topic of the lesson.

In the episode just discussed, the rabbit activity was selected by Anna to supplement the textbook lesson on symmetry and congruence. However, these supplemental activities were used not just to extend or reinforce textbook lessons; nearly half the lessons we observed were entirely from supplemental materials. These lessons are similar in many ways to the rabbit activity, with the mathematics off-target or almost entirely missing.

Generalizability of These Themes

Anna is our second divergent case. Although she had average MKT, two factors rendered her instruction of worse mathematical quality than one would expect: her beliefs about the importance of mathematics being fun, and her proclivity to use supplemental mathematical activities in place of textbook lessons. These often led her into non-mathematical activities, which then degraded the mathematical quality of her lessons.

The case of Anna raises the question about the degree to which she is a threat to our hypothesis about the relationship of MKT and MQI. Like Noelle, we did observe many similarities between her performance on these two measures, in particular the correspondence between low specialized knowledge and poor skills in navigating rich mathematics. However, Anna's case also suggests that this relationship is sensitive to teachers' beliefs about learning and the contexts within which they construct their work. Had Anna not replaced so many of her textbook lessons with fun activities, her mathematics might not have fared so poorly.

With Anna, we circle back again to the question of teachers' use and non-use of textbooks, a recurrent theme in our investigation of additional factors that intervene between MKT and MQI. While Noelle failed to make connections within and across the supplemental activities she strung together, her students were doing mathematics for a majority of the mathematics class. In Noelle's case, in other words, activities were enacted with some mathematical integrity: students were engaged in mathematical practices and work. In Anna's case, by comparison, the supplemental activities contributed little in the way of mathematical work. Anna's own modest content knowledge may not have allowed her to see or emphasize the mathematical connections inherent in these activities; or her beliefs about making mathematics “fun” might have influenced her decision to make the activities non-mathematical. Whatever the mechanism, this case again illustrates the challenge of teaching mathematically rigorous lessons from supplemental materials.

Rebecca

This next portrait illustrates our last divergent case. Rebecca is the lowest-scoring teacher in our sample, and her instruction bears this out: it is largely focused on the mechanics of procedures without corresponding explanation, and sprinkled with errors. Yet she differs from other low-scoring teachers along several key dimensions. Unlike Zoe, we never observed Rebecca trying to teach “conceptually” oriented mathematics to students. Instead, each lesson consisted of one new procedure, rendered with a minimum of explanation or meaning. Perhaps as a result, her mistakes tended to be less damaging to the mathematical content than Zoe's, and did not cloud the main mathematical issues of the lesson. Second, unlike Anna and some of the other teachers in our study, Rebecca's lessons focused on mathematics all the time. Seldom were students off-task even for a moment, and it seems likely that students left her class proficient in specific mathematical procedures. Examining the reasons for this divergence suggests several mediators between MKT and MQI, including Rebecca's views of mathematics and student learning, and her nearly complete reliance on a textbook to provide instruction.

Background

Rebecca teaches science as well as sixth-grade and eighth-grade mathematics, and is the only middle school teacher in our sample. She is also the only African-American teacher in our sample, and the only minority. When we observed Rebecca, she was in her fifth year of teaching. Rebecca reports that between mathematics and science, she prefers to teach mathematics. “I like being able to find a solution. Being able to work things out different ways, the satisfaction of knowing that when you get to the end you know you're done and being able to go back and check it.” Rebecca's classroom is arranged with groups of desks of four to six students. There are mathematics posters on the walls of the classroom and shelves filled with matching textbooks, but otherwise the room is bare, with desks and white boards predominant. Rebecca stands at the front, commanding attention, and students follow her directions, filling in her sentences when prompted and practicing the mathematical procedures she teaches each day. A visitor is struck by the composition of the student body, entirely Latino, Southeast Asian, and African American. All are dressed in school uniforms, with white-collared shirts, khaki pants or skirts, and navy sweaters or sweatshirts.

Rebecca's lessons are typical to the United States: she opens with a brief review of content from a previous lesson and launches directly into the day's new procedure, which she models. Her lessons are taken directly from her assigned textbooks, MacDougal Littell Algebra Thinking (sixth grade) and Prentice-Hall Pre-Algebra (eighth grade). Rebecca involves students in her presentations by beginning sentences that students are to complete. Students then practice the procedure while Rebecca circulates, leaning over her students' shoulders and answering their questions. She closes most lessons with a homework assignment consisting of similar exercises.

Rebecca had no teaching certificate at the time of our study and was taking classes toward certification at two different universities. She reported that in her school district she could teach for an unlimited period without a teaching certificate. Based our measures, Rebecca had very low mathematical knowledge. Her MKT score was –0.79, lower than all other teachers in our videotape sample and in the 22nd percentile in our larger sample.

Rebecca as a Convergent Case

Rebecca's teaching is in great part what one would expect from her low MKT score: mathematically thin and punctuated by errors. Across all lessons, Rebecca's “richness of the mathematics” score is 0.02, indicating that she seldom provides or elicits mathematical representations, explanations, justifications, or explicitness around mathematical practices. Rebecca's error scale score is in the middle, at 0.12; these errors range from slips of the tongue to poorly designed tasks and examples. Rebecca scores in the middle of the video study teachers on the “density and precision of mathematical language,” and at the bottom on “responding to student productions and errors.” Like Zoe, for instance, she often passes quickly over students' incorrect answers, or simply repeats the steps in the procedure under study until students have mastered them.

These patterns and others are illustrated well in a lesson on multiplying binomials. Rebecca begins by stating her goal: “So today we're going to work on multiplying, and because I'm really tired, we're multiplying binomials, not polynomials.” As she typically does, as she starts writing on the board she hearkens back to an earlier lesson:

Rebecca:   So, remember, was it Monday, we did x plus two plus x plus four (writes x + 2 + x + 4). And then we said x plus two plus x plus four. What's x plus x? x plus x is what?

Students:   Two x.

Rebecca:   Two x. And then two plus four is what?

Students:   Six.

Rebecca:   Six. So that would be our answer. Two x plus six.

Unlike Zoe, whose links back to prior lessons frequently distort the mathematics and connections between topics, Rebecca's progression through the textbook allows her to identify a recent lesson as immediately relevant to the one about to take place. This episode also illustrates typical student participation in Rebecca's classroom. Students' responses are one-word, fill-in-the-blank computational answers, with strong student participation and attention.

Rebecca then launches into the presentation of a new procedure that builds on material from the earlier lesson she has just invoked. She says, “Well, today we're going to make it a little more difficult. But we're going to multiply. This is the fun part. You guys should pick up on this easier.” She then draws an example directly from the textbook: “So everybody on your paper, x plus 4 times x minus 3. X plus 4 times x minus 3.” She continues:

Now, I'm going to make a little face. You guys ready for my face? Whatever I do on my board, you do on your paper. Everything. So x plus four times x minus three. So here's the first part of my not-so-great face. Here's the eyebrow of one part of the face. That is one eyebrow.

Rebecca draws an “eyebrow” connecting the two x's (see Figure 7), and then continues:

Rebecca:   Got the one eyebrow? Okay, so what's x times x?

Student:   One x.

Rebecca:   Not one x. x what?

Student:   Squared?

Student:   x squared.

Rebecca:   x squared. So x times x is going to give me x squared.

She continues “making a face” to multiply the binomial factors by connecting the 4 and 3 as a second eyebrow, the 4 and x as a nose, and x and 3 as a mouth, as in Figure 7.

FIGURE 7 Face drawing as mnemonic for multiplying binomials.

There are merits to this method. As in other lessons, Rebecca supplies a memorable trick by which to perform a challenging operation. The narrative structure provides a way to remember a series of mathematical acts that are, on the surface, devoid of much logic. When multiplying two binomials, each term in the first factor must be multiplied by both of the terms in the second factor. Rebecca's “face” method is a systematic way to do this and serves a mnemonic function. By the end of this lesson, it appears that all students can perform the procedure, no small feat for a middle school mathematics teacher.

Missing, however, is any understanding of this procedure as a whole, or what each step signifies. Students are given no clue as to the meaning of these quantities or the operations performed on them. While there are several ways to give/impart meaning to this procedure, one rendering, as actually suggested by her textbook, involves an area model. In this model, the two quantities being multiplied are represented as the side lengths of a rectangle; the product of these factors corresponds to the area of the resulting rectangle. For example, her book advises teachers to begin this lesson by using an area model to represent (x + 2)(x + 4) (Figure 8).

FIGURE 8 Area model for multiplying binomials.

Such a representation and its attendant explanation might have given a conceptual grounding to the procedural shorthand Rebecca showed her students. However, the initial problem Rebecca chose for her lesson, (x + 4)(x – 3), would not be ideal for introducing an area model. The subtraction in the second factor complicates the use of the area model and, in an introductory lesson, would likely increase confusion rather than understanding. This in fact points to another task of teaching that appears to be influenced by MKT—the selection of numeric examples. We saw a lack of strategic selection here and throughout Rebecca's lessons.

This lesson illustrates other areas of convergence as well. Her use of mathematical language in this episode, and in fact the entire lesson, is problematic. Not only does she repeatedly reference steps in binomial multiplication as parts of the “face,” even this becomes unclear at points in the lesson; in one comment to students, she referenced “one eyebrow, the second eyebrow, and the inside eyebrows.” And during the lesson, Rebecca responds to student confusion by repeating the steps; when one student expresses confusion, she replies “You'll get it, watch. Trust me.” In circulating during student work time, her response to student errors is to prompt students through the steps of the procedure again. This no doubt contributes to Rebecca's low score on the “responding to students appropriately” scale.

The instruction highlighted here is typical. In nearly every lesson observed, Rebecca conveyed mathematical material through a mnemonic device or metaphor rather than mathematical explanation. In adding integers, negative and positive numbers “did not like one another” and thus canceled one another out; in adding fractions with unlike denominators, the standard find-the-common-denominator procedure was supplemented by what Rebecca calls the “butterfly” method, another graphic mnemonic similar to the “face” method for multiplying binomials. These lessons were no doubt dictated not only by Rebecca's own lack of mathematical knowledge, but also by her view that mathematics is a set of rules, stories, and tricks.

Clinical and general interviews with Rebecca provide evidence on this point. On multiple occasions, Rebecca makes reference to solving problems by doing what one is told to do. In solving a division of fractions problem for herself, she says, “What I did I just, so many times we are told to do the reciprocal.” Working hard to understand meaning is to be avoided. In one interview, she explains why she teaches such tricks to her students: “I teach them the little tricks to do fractions, because there's no point to see them struggle.” This is a statement about what mathematics is for Rebecca (getting to a correct answer quickly) and about learning in general (it should go easily, without a struggle).

Rebecca as a Divergent Case

Despite these earlier illustrations of Rebecca as a convergent case, Rebecca's lessons diverge from expectations set up by her MKT score in two significant ways. First, although Rebecca's instruction is sprinkled with errors, the types of errors she makes tend not to interfere with the mathematical goals of the lesson, as Zoe's often do. For instance, in one lesson, Rebecca repeatedly says that the quantity pi is “three point one fourteen.” In the same lesson she also says “three point one four” a number of times. Combined with a correct numeric representation of 3.14 on the board during the lesson, it is likely that students walked away with little confusion, despite the slips in Rebecca's language. In a lesson on prime, composite, and square numbers, she went to great lengths to define “square,” but throughout the lesson, she incorrectly referred to square numbers as “squared numbers” and even wrote this on the overhead projector. Without knowing what exactly students took from this lesson, we cannot say with certainty the magnitude of this error for their learning. Certainly, all mathematical errors by teachers in the classroom are problematic. However, while still troubling, Rebecca's errors seem less damaging to the underlying mathematical core of the lessons than Zoe's and other low-knowledge teachers.

The second aspect of Rebecca's teaching that can be characterized as divergent from expectations is her intense focus on mathematics nearly every minute of the class period. Unlike other teachers with weak MKT (and Anna most notably), Rebecca does not fill her mathematics lessons with activities or games of dubious mathematical value. Instead, every student appears busy doing nontrivial mathematical work across every lesson we observed. Students are highly engaged even though they have limited opportunities to speak in class or carry on mathematically rich discussions.

Next, we illustrate four possible supports and explanations for these areas of divergence: Rebecca's reliance on her textbook, her views of mathematics, her strong general pedagogical skills and routines, and her beliefs about equity.

Reliance on a Textbook

Rebecca is one of two teachers in our video study sample who rely nearly exclusively on a textbook to provide the daily mathematics lesson. The lessons she presents on tape closely match the lessons in her books. In fact, the only exception is when the textbook includes a mathematical explanation for a procedure; Rebecca omits this explanation, much as she did in the binomial multiplication lesson. In this particular case, we argue that reliance on her assigned texts helps decrease the number and severity of the mathematical errors made in class. This also serves to keep her mathematics lessons purely mathematical; instead of add-on activities meant to be fun or “conceptual,” Rebecca simply taught each textbook page in sequence. And this sequencing served to allow Rebecca to make connections between lessons with some degree of facility; we did not witness the same odd mathematical pairings that Zoe exhibited. When Rebecca did reference past lessons, as we saw above, the connections seemed germane.

Views of Mathematics and Their Implications for Teaching.

Rebecca's views of mathematics as procedures, and almost exclusive teaching of procedures, also help explain why her errors are less damaging to the content of the lesson than Zoe's errors. Whereas Zoe and others downplay memorization and suggest they desire more conceptually rich instruction, Rebecca does not. In fact, in an interview she embraces what she calls “drill and skills” instruction because she believes it is what her students need to be successful. This focus on procedures circumscribes her opportunities to make mathematical errors; Zoe and others often get into trouble with exactly the meaning-oriented elements of mathematics Rebecca avoids.

General Pedagogical Skills and Routines

Rebecca has a strong rapport with students, but her demeanor is decidedly business-like. There is good-natured banter but she makes clear that math class is all about math. Notably, in Rebecca's classroom, there is very little time spent on management issues, outside distractions, or administrative demands. For instance, in the lesson on multiplying binomials, she began, as she did most days, with pre-emptive measures to focus students' attention and to ward off interruptions:

Hurry up and sit down. Chandra, you're not doing okay today? Do you have paper over there? I already told Mrs. Little anybody that can't follow directions is going straight to her office.

….

All right. We'll wait till Wendy's ready.

….

Julie, you're going to answer the phone for me. Evan, open the door when somebody knocks.

Here, we see Rebecca creating an environment in which her students can focus on mathematics and mathematics alone. She asks students to take their seats, provides a public warning about off-task behavior, and makes clear her expectation that the class get ready. In barely two minutes, Rebecca's class is ready for work. Notice too in this episode how Rebecca prepares for the constant interruptions that punctuate most class periods. Amid telephones ringing, announcements coming over the public address system, and students coming and going, Rebecca minimizes these interruptions so well that an observer barely notices them, nor Rebecca's efforts to keep them virtually invisible in the flow of instruction.

There is evidence that these management skills work. Viewing the video records, one sees virtually all students in class productively engaged in mathematics and doing the assigned tasks correctly, even in the face of Rebecca's errors. Judging from student performance observed on the tapes, students are learning the procedures that Rebecca is teaching, and are performing them competently, without error. Engagement is high, participation is widely shared, and the work is purposeful. ²

We posit that these indicators of student effort also result from well-elaborated instructional routines. Classes begin immediately with no time wasted on non-academic matters. Every class has a stated mathematical purpose that is followed doggedly throughout the lesson. Expectations are high for students to follow the lesson, answer when called on, and take notes. Students do written exercises when directed, and at least from the camera's view, every student seems to bring in homework consistently. From the opening bell to the closing bell, each period is filled with mathematics instruction that follows a predictable architecture. Although there is little richness to the mathematics, mathematics is the constant hum in the lessons we observed.

Equity in Mathematics Instruction

Finally, Rebecca is committed to equity and makes repeated references to this in her interviews:

In the class that I was being videotaped in, for this school year, a lot of them were English language learners … in all honesty, people say “I want to teach GATE [Gifted and Talented Education] students because they'll do their projects so much nicer” and I'm going, “No, I don't want to deal with them.” I would rather work with the students that I can present projects in different ways and let them go ahead at it how they want to and bring in their cultural aspects and make the whole classroom like a family.

Rebecca also commented that she has not found the professional development in mathematics terribly helpful, and that this was especially true regarding teaching to a diverse student body. Importantly, she links her approach to teaching strictly procedures to the needs of her population:

As teacher of mathematics I think I do a great job focusing on what is important for my kids to pick up and also allowing my students to sometimes work collaboratively, sometimes having them work independently, having them go back to what some people call drill and kill and I say drill and skills because that's what they need.

In fact, when Rebecca is asked in an interview about opportunities for her students to explain mathematical ideas or procedures, she says directly that she does not do so because the population she teaches is mostly minority. The implication is that minority students are best served by a skills-driven mathematics curriculum.

I didn't really ask them to explain it, what I really want them to do was just be able to understand how to multiply the fraction then that would be the procedure but I didn't go really into depth into why this works….

Rebecca's claim that minority students most need skills and procedures, with little emphasis on mathematical understanding and explanation, gives us pause. We wonder whether this works against Rebecca's intentions for equity by limiting minority students to skills-based mathematics. It would be hard to listen to Rebecca's thoughts about teaching skills to her minority students, though, without hearing echoes of Delpit's (1986) argument that minority students most need skills that they can only learn in schools, and these minority students have been ill-served by well-meaning White liberals' efforts to get them to discuss ideas, something they do quite well without schooling. It is also the case that performance of procedures is the mathematical competence that her students will be expected to demonstrate on standardized tests and college entrance examinations. Rebecca, like Delpit, argues that her students will not learn what they need to succeed anywhere else. In the face of Rebecca's significant achievements with her students, we pose this as an open question for further consideration.

Generalizability of These Themes

Rebecca represents a divergent case because although the quality of her mathematical instruction is low, it is not as low as her MKT score would have predicted. Like other divergent cases, her MKT and MQI scores are in some ways convergent, in the sense that many of the things afforded by high MKT are absent in her instruction, and in that her instruction does contain specific deficits such as errors and an inability to hear and respond to students' misunderstandings. Yet her strong general pedagogical routines, her constant focus on mathematics, and the less intrusive nature of her mathematical errors all leave the observer with the impression of unexpected strengths in her mathematics instruction.

As with the other divergent cases, we ask about the extent to which additional factors shape the relationship between MKT and MQI, and the overall conclusions we can make by balancing the convergent and divergent evidence. In this case, a bevy of additional factors, from beliefs about instruction and equity to the use of pedagogical routines and textbooks, shape the relationship under study here. Yet framed in broader terms, although these additional factors can mitigate the influence of MKT on the mathematical quality of instruction, their total effect is smaller than that of MKT itself.

CONCLUSION

This study has clear limitations. Without student achievement data, we cannot know whether the variation between teachers results in differential student performance. However, we think it is likely to be so; certainly, offering students sound mathematical explanations and representations, explicit depictions of disciplinary work, equitable access to mathematical thinking, accurate mathematics, and mathematically saturated classroom work results in increased opportunities for students to learn mathematics. We also used measures of teacher knowledge that have been linked to gains in student achievement; this study, in some ways, helps explain why those linkages might occur.

We are also cautious in making claims about causality. This is a correlational study, one in which we have demonstrated strong links between teachers' knowledge and the mathematical quality of their classroom practice. Yet without random assignment of teachers to knowledge levels—or the more realistic random assignment of teachers to programs to improve their knowledge—we cannot prove that greater knowledge results in richer instruction. However, the typical threats to social science research seem to us less compelling in this case. We employed a design that included multiple observations of teachers at different points in the year and teaching different content, a range of teacher MKT levels, and an objective and valid measure of teacher knowledge. We were able to account for differences among teachers—particularly in the use of curriculum materials and teacher beliefs—that scholars argue might pose alternative causes for the mathematical quality of instruction. And we demonstrated in numerous ways, from MKT-MQI correlations to triangulation between clinical interviews and classroom examples, the strength of the relationship between these two variables.

In fact, the inescapable conclusion of this study is that there is a powerful relationship between what a teacher knows, how she knows it, and what she can do in the context of instruction. We inspected cases for the possibility that other factors might mediate this relationship and we identified a few: teacher beliefs about how mathematics should be learned and how to make it enjoyable by students; teacher beliefs about curriculum materials and how they should be used; and the availability of curriculum materials to teachers. However, these influences paled in comparison to, and in many ways were shaped by, teachers' knowledge itself. In case after case, the quality of the modifications made to curriculum materials, the goals for student learning, and even beliefs about what mathematics is were shaped by teachers' knowledge.

At the outset of this article, we asked what mathematical knowledge provides for instruction. Does it simply help teachers avoid errors, meaningless “mathematical” activities, and other characteristics listed in the deficit literature? Or does knowledge also translate into mathematical affordances, such as strong modeling, explanations, explicitness around mathematical practices, and so forth?

The 4 high-knowledge teachers in our sample of 10, including Lauren and Noelle, suggest that the answer is both avoidance of error and denser, more rigorous mathematics in instruction. Among these four teachers, including one who was using the Saxon mathematics, we saw many examples of elegant mathematics. This is not to say the lessons were mathematically impeccable; however, they held many examples of rich mathematics, teacher skill in responding to students, and other aspects of skilled mathematics instruction, from choosing examples wisely to ensuring equitable opportunities to learn.

Among lower-knowledge teachers, these elements were much more variable. Occasionally, a lower-knowledge teacher would exhibit some of these characteristics; when she did so, it was often supported by the textbook or by professional development. They were not constant across lessons we observed, and lessons just as often went poorly as went well.

Another way to answer our initial questions is by examining the correlation of various scale scores with MKT. Mathematical errors, including errors in language, did prove the most strongly related to teacher knowledge. At −0.83, this is a remarkably high correlation, and no doubt goes some distance toward explaining the relationship between teacher knowledge and student achievement observed in other studies (e.g., Hill et al., 2005). But at the same time, several other scales, including richness of the mathematics, classroom work being connected to mathematics, and responding to students appropriately, had a moderate (roughly 0.5) relationship to teacher knowledge. Looking across the case studies, we posit that these aspects of instruction are more likely than errors to be influenced by the additional variables we identified as intervening on the MKT–MQI relationship. Anna might have taught more mathematics if it were not for her beliefs about “fun” activities; Rebecca might have taught very low-quality conceptual mathematics if not for her belief in drilling on skills. Several low-knowledge teachers occasionally provided richer mathematics based on what they learned from textbooks or professional development.

One other scale, the density of accurate mathematical language, was less related to the mathematical quality of instruction. It might be true that factors such as general verbal ability—and not mathematics knowledge—partially govern this relationship. It may also be true that we have yet to learn how to measure teachers' use of language well. Although it is easy to spot an error in definition or plain language use, it is not as easy to agree on what makes for good instruction, linguistically (Sleep, 2007). Further work on this issue seems warranted, given the importance of mathematical language in conveying mathematical ideas to children.

In addition to these scales, our study uncovered additional sites, or classroom tasks, in which teachers' mathematical knowledge plays a role in instruction. Zoe demonstrated that commonplace teaching activities—from restating textbook definitions in slightly different terms to choosing numeric examples to linking current lessons to prior knowledge—are affected by the intellectual resources a teacher has available. Lauren showed that attending to issues of equity has a strong content knowledge component in that choosing and mediating contextualized examples and making mathematical practices more explicit and apparent to all students place demands on teachers' intellectual resources. Lauren also demonstrated how carefully sequencing mathematical tasks and activities places knowledge demands on a teacher. Noelle provided an example of the mathematical work teachers must do in responding to unexpected or inarticulate student comments. We did not have adequate video-based or pencil-and-paper measures for these mathematical teaching practices; however, they seem to us a fruitful line of future research, especially because they are tasks teachers must do all the time.

One critique of these conclusions might come from one who argues that what we saw on these tapes results from teachers' general pedagogical skill, rather than their mathematical knowledge for teaching. But as our background comments about each teacher showed, the case study teachers seemed to us relatively well matched in their ability to bring order to their classrooms and to motivate students. The wide variation we saw in the mathematical quality of the lessons seemed more likely a function of what these teachers knew, mathematically.

Another critique might involve those who say that this particular sample of teachers, by virtue of the fact that they have signed up for professional development, has chosen to teach conceptually richer mathematics than others. We agree, and this constitutes another limitation to our study. In fact, we had no example of a high-knowledge teacher who adheres to a very traditional version of mathematics. Finding such teachers, and studying their instruction, would provide an interesting line of research. How such a teacher might fare on our MQI instrument depends in part, we argue, on how one defines “traditional” instruction. If one defined traditional instruction as “providing facts and procedures without explanation or meaning,” such a teacher would perform poorly on the “richness” and “responding to students” portion of the MQI instrument, although likely would perform well on other elements (e.g., errors, language, connections to mathematics). However, defining traditional instruction as “didactic” (as opposed to student-centered), one could imagine some very high-MQI traditional teachers. High-knowledge traditional teachers, in this interpretation, would provide mathematical explanations, link representations, discuss mathematical notation and the like. They may also design opportunities for themselves to learn about and respond to what students are thinking, even though the majority of instruction flows from the teacher to students. Locating such teachers and studying their practice would help illuminate one limit of the reform-traditional dichotomy/debate mathematics educators have been engaged in for nearly two decades.

Finally, we arrive at some observations about how the relationship between mathematical knowledge and the mathematical quality of instruction can be mediated. This is of particular interest to policymakers who may be searching for ways to improve teacher knowledge not only through direct programs, such as professional development or preservice coursework, but also through more ancillary activities. We discuss three such factors: the use of curriculum materials, beliefs about mathematics, and the effects of teacher professional development. Unfortunately, each of these factors can either serve to degrade the mathematical quality of instruction or improve it.

Although our study was not designed to examine the effect of the nature of curriculum materials on instruction, we can say that for most teachers in our sample, using supplemental activities and materials served to lower the quality of the mathematics in instruction. Teachers like Noelle lacked the ability to pull together big mathematical ideas across lessons; teachers like Anna lacked the ability to make even the supplemental activities mathematical in nature. By contrast, Rebecca sticks closely to her textbook and provides passable, although severely constrained, mathematics lessons. Teachers' knowledge of the curriculum—a relatively less-developed part of Shulman's original notion of pedagogical content knowledge—seems a crucial construct, and one we have not successfully tapped with either the MKT or MQI measures.

This seems to us a problem. Teachers are flooded with messages not to use their textbooks, starting with scholarly work (Ben-Perez, 1990) and continuing on to the materials thrust upon them in professional development and ending with district curriculum documents that piece together units from disparate resources. This may have been appropriate in an era when most textbooks were similar in their mathematical drabness; however, the quality of available materials has sharply improved, yet this ethos persists. And we argue that solid mathematical tasks and representations that come from a drab textbook are preferable to teacher-created math lessons in the hands of teachers with little mathematical knowledge for teaching. Without the ballast of mathematical knowledge, teachers' implementation of supplementary materials is chancy at best.

Lest one outcome from this study be for districts to instruct teachers to strictly adhere to their textbooks, we have two pieces of countervailing evidence. First, Zoe aptly illustrated that reading and copying definitions from a textbook does not ensure mathematical accuracy in classroom instruction. We also found that the use of supplementary materials can in some cases be at least neutral, and perhaps even improve, the quality of mathematics in the classroom. Lauren explicitly rejected her texts' development of probability and taught a lovely lesson from two supplemental sources she pieced together. Karen, a teacher on whom we did not focus, used a standard mathematics text, but skillfully supplemented it with meaning-oriented instructional activities based on her own professional development experiences and mathematical knowledge. Teachers' mathematical knowledge for teaching in fact appears amplified (Hill, 2007) by the choices made around curriculum materials.

Beliefs, as expected, also proved to be another factor that mediates the MKT–MQI relationship. Anna thought her students in need of liking mathematics, and adjusted her instruction to leave little mathematics for students to dislike. Rebecca had very circumscribed views of mathematics itself, and thus enacted that very circumscribed mathematics in her classroom. By contrast, the views of Lauren and Noelle were more expansive, specific, and mathematical in nature.

Professional development, unfortunately, cut both ways as well. In some cases, our evidence suggests that extensive professional development served to bolster teachers' knowledge and improve the mathematical quality of instruction. But we also saw countless examples of “new” mathematical methods and activities arriving in classrooms courtesy of the professional development institutes teachers attended, and then being implemented without meaning, or even without purpose. Zoe's superficial enactment of the partial differences method is an excellent case in point. We saw worse, too: in several cases, teachers returned to class with mathematical tasks they themselves did not understand, and then taught them to students as procedures instead of non-routine, complex problems to be solved. In some cases, the new tasks were taught without any mathematical connection at all.

Despite these myriad other influences on the mathematical quality of instruction, the bottom line remains that policymakers need to find a means to improve teacher knowledge in this content area; improvements in instruction and student learning are unlikely unless this problem can be resolved. And given what we observed in this study, the need for a solution is pressing. Even if California teachers were for some reason below the national average in knowledge and skill, “shifting up” the entire distribution one-half standard deviation would not ensure classrooms we would want our children to attend.

Given what we have observed about the mixed effects of professional development—the main method for improving the quality of the teaching force—we are not sanguine. Cohen, Raudenbush, and Ball (2003) argue that simply adding resources to schools—in this case, professional development for teachers—will not of itself improve instruction. Our study is a case in point. The quality of instruction depends instead on how such resources get used by teachers. We are also wary of approaches that suggest that recruiting disciplinary experts to teach elementary school will suffice. To start, there are few such disciplinary experts interested in becoming elementary school teachers. We also believe that there is unique knowledge for teaching, as Shulman proposed two decades ago, and that having such knowledge is key to the enactment of rich and rigorous mathematics. Our MKT measures are not simply measures of common content knowledge—the kind that disciplinary experts would possess. Instead, our measures encompass what teachers would need to know to connect mathematics and children, something disciplinary experts would not necessarily know. This suggests that, while what we have measured through both the MKT and MQI instruments is founded on strong common content knowledge, it is also comprised of additional aspects of knowledge that support teaching and learning.

Instead, we are drawn to several more novel solutions. One is to encourage schools to use more mathematically knowledgeable teachers as math specialists, teaching only mathematics. This would immediately improve the mathematical quality of instruction for many students, and also allow the concentration of professional learning resources within a smaller subset of teachers. Given that the demands for learning this material appear high (i.e., even a relatively intense content-focused program did not help teachers like Zoe), such concentration would be a great benefit.

Another solution that many have called for is to reshape the nature of the profession and professional education. This is an ambitious project, but one that may be unavoidable if we wish to see real improvement in the teaching and learning of mathematics in this country. Here we take a leaf from the Japanese book of teachers' professional development. This involves continuous, career-long professional development that is steeped in the mathematics curriculum that they teach. Teachers meet regularly—weekly and monthly—to work through the mathematics curriculum together to understand both the mathematics contained in it, and to devise ways to present ideas to children. This is not a summer mathematics teaching workshop or a few days sprinkled over the length of one's career. Instead, studying the content of the curriculum and working collaboratively to experiment with ways children learn would be the fabric of a teacher's ongoing work. A national curriculum would help in this regard—imagine if teachers nation-wide could pool resources to think about how children would best learn a slimmer and more focused mathematics curriculum—but it is not essential. What is essential is a model in which teachers' learning is anchored in the real work of instruction, with the content demands and children's learning placed front and center as the driving force of professional development. This proposal departs from current models of professional development in this country, by addressing content learning for teachers in the context of children's learning. Such changes, we think, are required if we are to make serious inroads in improving mathematics instruction.

APPENDIX A

1. Mr. Allen found himself a bit confused one morning as he prepared to teach. Realizing that ten to the second power equals one hundred (10² = 100), he puzzled about what power of 10 equals 1. He asked Ms. Berry, next door. What should she tell him? (Mark (X) ONE answer.)

   1. 0

   2. 1

   3. Ten cannot be raised to any power such that ten to that power equals 1.

   4. –1

   5. I'm not sure.

2. Imagine that you are working with your class on multiplying large numbers. Among your students' papers, you notice that some have displayed their work in the following ways (Figure 9): Which of these students would you judge to be using a method that could be used to multiply any two whole numbers?

   FIGURE 9 Three solutions to 35 × 25.

   

   Table

   	Method Would Work for All Whole Numbers	Method Would NOT Work for All Whole Number	I'm Not Sure
   Method A	1	2	3
   Method B	1	2	3
   Method C	1	2	3

3. Takeem's teacher asks him to make a drawing to compare 3/4 and 5/6. He draws the following: and claims that 3/4 and 5/6 are the same amount. What is the most likely explanation for Takeem's answer? (Mark ONE answer.)

   1. Takeem is noticing that each figure leaves one square unshaded.

   2. Takeem has not yet learned the procedure for finding common denominators.

   3. Takeem is adding 2 to both the numerator and denominator of 3/4, and he sees that that equals 5/6.

   4. All of the above are equally likely.

APPENDIX B

Mathematics errors—Any errors in the following:

Makes links among any combination of symbols, concrete pictures, diagrams, etc.: When the teacher makes explicit links among any of the above. The links must be mathematically significant—-for instance, pointing out connections between representations in ways that allow students to grasp how representations are alike or different, how pieces of one relate to pieces of another, or what one representation affords that another does not.

Mathematical descriptions (of steps): Teacher's directing of mathematical descriptions (by self or co-produced with students) provides clear characterizations of the steps of a mathematical procedure or a process (e.g., a word problem). Does not necessarily address the meaning or reason for these steps. Code I for incomplete or unclear attempts.

Mathematical explanations—-giving mathematical meaning to ideas or procedures: Teacher's directing of explanations (by self or co-produced with students) includes attention to the meaning of steps or ideas. Does not necessarily provide mathematical justification. Code I for incomplete or unclear attempts.

Mathematical justifications: Teacher's directing of explanations (by self or co-produced with students) include deductive reasoning about why a procedure works or why something is true or valid in general.

Computational errors or other mathematical oversights: Use this code when the teacher makes computational errors either in spoken or written language, or when the teacher neglects to discuss key aspects of a problem (e.g., forgetting a step, forgetting to finish the problem). If present, computational errors or oversights are always inappropriate. If not present, the segment is appropriate. Hence there are only two options for this code: P/I or N/A.

Conventional notation (mathematical symbols): Use of conventional symbols and mathematical notation, such as +, –, =, or symbols for fractions and decimals, square roots, angle notation, functions, probabilities, exponents. Inappropriate or inaccurate uses of notation might include inaccurate use of the equals sign, parentheses, or division symbol. By “conventional notation,” we do not mean use of numerals or mathematical terms.

Technical language (mathematical terms and concepts): Use of mathematical terms, such as “angle,” “equation,” “perimeter,” and “capacity.” Appropriate use of terms includes care in distinguishing everyday meanings different from their mathematical meanings. When the focus is on a particular term or definition, code errors in spelling, pronunciation, or grammar related to that term as present-inappropriate.

General language for expressing mathematical ideas (overall care and precision with language): Code general language including analogies, metaphors, and stories used to convey mathematical concepts. Appropriate use of language includes sensitive use of everyday terms when used in mathematical ways (e.g., borrow).

Connecting classroom practice to mathematics ³

Development of mathematical elements of the work (i.e., moving the mathematics along): Code here for whether the teacher's moves, questions, and statements keep the development of the mathematics moving along. Considering the content topics marked in Ib, does the content appropriately open up, develop, or solidify in this segment, or does the teacher seem to move the lesson off track (i.e., it lacks as sense of mathematical direction) without a plausible rationale about why this is happening? This is a global decision, hence, there are only two options: P/A or N/I.

Classroom work is connected to mathematical idea or procedure: Activity, task, lecture or discussion is connected to mathematical procedure or idea. Rule of thumb: can students accurately answer “what mathematics were you working on in this segment?” Code P-A if work is connected to mathematical procedure or idea. Code P-I if such connections distort the mathematics. Code NP-A in cases where connection is apparent later in the tape, but not apparent here. Code NP-I if students/teacher are completing a task, but the ways that task illustrates, solidifies, or connects to a mathematical idea or procedure is not apparent throughout segment and tape. If explained in earlier segment, carry over code into current segment. This code is intended to pick up work that teachers might endorse as part of current reform efforts, but which instead of illustrating mathematical ideas turns into students following directions to cut, paste, draw, etc.

Instructional time is spent on mathematics. Most (over 3/4 of segment) instructional time is spent on mathematics, or setting up a mathematical task, rather than on administrative/organizational matters (passing out papers), resolving student confusion over poorly presented tasks (i.e., answering the question “what do I color?”). Warrant: Ladson-Billings' advice to look at how efficiently the teacher uses instructional time.

Richness of the mathematics

Representations/manipulatives

Multiple models: Whether or not the teacher uses more than one model for the mathematical content. By multiple models, we mainly mean models across “families”—e.g., graphs, equations and tables, or pictures, numeric procedures, and stories. However, multiple models within a family can be coded here if they represent significantly different features of an idea. Do not count the model used in the problem statement unless it is also used in the solution in a significant way. For instance, if the problem is given symbolically or as a concrete scenario, but interpreted and solved using a graphical model, this does not count as using multiple models, but if the concrete situation is used to make sense of and manipulate the graphical model, this does count as using multiple models.

Makes links among any combination of symbols, concrete pictures, diagrams, etc.: When the teacher makes explicit links among any of the above. The links must be mathematically significant—-for instance, pointing out connections between representations in ways that allow students to grasp how representations are alike or different, how pieces of one relate to pieces of another, or what one representation affords that another does not.

Explanations/justifications

Mathematical explanations—-giving mathematical meaning to ideas or procedures: Teacher's directing of explanations (by self or co-produced with students) includes attention to the meaning of steps or ideas. Does not necessarily provide mathematical justification. Code I for incomplete or unclear attempts.

Mathematical justifications: Teacher's directing of explanations (by self or co-produced with students) include deductive reasoning about why a procedure works or why something is true or valid in general.

Explicitness (about mathematical practices, reasoning and language)

Explicit talk about the meaning and use of mathematical language. Teacher attends explicitly to language used (by the teacher or the students): defines terms, shows how to use them, points out specific labels or names. Code P if the teacher has made terms explicit in a previous segment, and this carries over into the segment being coded now.

Explicit talk about ways of reasoning. Teachers may highlight elements in an explanation, guide students toward more rigorous proof, or otherwise provide students opportunities to learn about mathematical reasoning itself. Explicit talk about ways of reasoning may ensure all students have access to features of mathematical reasoning and argument. Code NP if teacher simply asks students to reason, but does not make elements of that reasoning explicit. Code P when teacher points out parts of a mathematical argument, prods students to add to or change explanations, etc. Code P if the teacher has made ways of reasoning explicit in a previous segment, and this carries over into the segment being coded now.

Explicit talk about mathematical practices. Teacher is explicit about how to use representations, how to pose or use a definition, test an assertion, or respond to an argument. Code P if the teacher has made ways of mathematical practices explicit in a previous segment, and this carries over into the segment being coded now.

Responding to students appropriately (Include only instances of PA for these codes.)

Interprets student productions: Use this code to indicate whether or not the teacher tries to understand and appropriately interpret students' comments, questions, solutions, or ideas. Does the teacher appear to be processing what students are saying and is there evidence that the interpretations are reasonable? Mark (PA) if teacher appropriately interpreted student production; (PI) if teacher inappropriately interpreted student production; (NP-A) if no student productions, or if student productions were so short or perfunctory as to not require significant interpretation (e.g., recitation of answer to computational problem, fill-in-the-blank answers). (NP-I) student production was present and required interpretation, but not interpreted by teacher.

Uses students' errors: Use this code to record when teachers respond to, use, or otherwise address student errors (errors from the teacher's perspective) in some way other than simply telling the student it is wrong or ignoring the error. One compelling instance in the segment is enough to code for appropriate use of errors. Mark (PA) if teacher used a student error appropriately; (PI) if teacher used student error in a way that significantly distorted the mathematics or missed the point of the student error; (NPA) for no student errors, no teacher interpretation; (NPI) for cases when teachers should have used student errors in order for instruction to reasonably proceed.

Responding to students inappropriately (Include only instances of PI for these codes.)

Interprets student productions: Use this code to indicate whether or not the teacher tries to understand and appropriately interpret students' comments, questions, solutions, or ideas. Does the teacher appear to be processing what students are saying and is there evidence that the interpretations are reasonable? Mark (PA) if teacher appropriately interpreted student production; (PI) if teacher inappropriately interpreted student production; (NP-A) if no student productions, or if student productions were so short or perfunctory as to not require significant interpretation (e.g., recitation of answer to computational problem, fill-in-the-blank answers). (NP-I) student production was present and required interpretation, but not interpreted by teacher.

Uses students' errors: Use this code to record when teachers respond to, use, or otherwise address student errors (errors from the teacher's perspective) in some way other than simply telling the student it is wrong or ignoring the error. One compelling instance in the segment is enough to code for appropriate use of errors. Mark (PA) if teacher used a student error appropriately; (PI) if teacher used student error in a way that significantly distorted the mathematics or missed the point of the student error; (NPA) for no student errors, no teacher interpretation; (NPI) for cases when teachers should have used student errors in order for instruction to reasonably proceed.

Mathematical language

Conventional notation (mathematical symbols): Use of conventional symbols and mathematical notation, such as +, –, =, or symbols for fractions and decimals, square roots, angle notation, functions, probabilities, exponents. Inappropriate or inaccurate uses of notation might include inaccurate use of the equals sign, parentheses, or division symbol. By “conventional notation,” we do not mean use of numerals or mathematical terms.

Technical language (mathematical terms and concepts): Use of mathematical terms, such as “angle,” “equation,” “perimeter,” and “capacity.” Appropriate use of terms includes care in distinguishing everyday meanings different from their mathematical meanings. When the focus is on a particular term or definition, code errors in spelling, pronunciation, or grammar related to that term as present-inappropriate.

General language for expressing mathematical ideas (overall care and precision with language): Code general language including analogies, metaphors, and stories used to convey mathematical concepts. Appropriate use of language includes sensitive use of everyday terms when used in mathematical ways (e.g., borrow).

Explicit talk about the meaning and use of mathematical language. Teacher attends explicitly to language used (by the teacher or the students): defines terms, shows how to use them, points out specific labels or names. Code P if the teacher has made terms explicit in a previous segment, and this carries over into the segment being coded now.

ACKNOWLEDGMENTS

Research presented in this article was supported by NSF grants REC-0207649, EHR-0233456, and EHR-0335411. The authors thank two anonymous Cognition and Instruction reviewers as well as Hyman Bass, Katie Brach, Seán Delaney, Imani Masters Goffney, and Deborah Zopf for their help in developing aspects of this article. Errors remain the property of the authors.

Notes

∗Significant at the 0.05 level.

∗∗ Significant at the 0.01 level.

¹ Bear in mind that it is unlikely a teacher would use technical language in 100% of her clips. Mathematics lessons include student work time in which teacher utterances are short questions, quizzes, exams, and periods in which tasks occur (e.g., pulling cubes from a bag) that set up later mathematical work.

² We rely on what can be seen in the videotaped records of these observed lessons because we have no written records of student achievement, either in the form of test scores or students' work in class.

³ This scale is reverse scored, that is, a teacher's score is actually 1-score because the scale actually measures when connections are not being made between the classroom activities and mathematics.