Investigating the role of functional mutations in leucine binding to Sestrin2 in aging and age-associated degenerative pathologies using structural and molecular simulation approaches

Abstract

Leucine is the native known ligand of Sestrin2 (Sesn2) and its interaction with Sesn2 is particularly important, as it influences the activity of mTOR in aging and its associated pathologies. It is important to find out how leucine interacts with Sesn2 and how mutations in the binding pocket of leucine affect the binding of leucine. Therefore, this study was committed to investigating the impact of non-synonymous mutations by incorporating a broad spectrum of simulation techniques, from molecular dynamics to free energy calculations. Our study was designed to model the atomic-scale interactions between leucine and mutant forms of Sesn2. Our results demonstrated that the interaction paradigm for the mutants has been altered thus showing a significant decline in the hydrogen bonding network. Moreover, these mutations compromised the dynamic stability by altering the conformational flexibility, sampling time, and leucine-induced structural constraints that consequently caused variation in the binding and structural stability. Molecular dynamics-based flexibility analysis revealed that the regions 217–339 and 371–380 demonstrated a higher fluctuation. Noteworthy, these regions correspond to a linker (217–339) and a loop (371–380) that cover the leucine binding cavity that is critical for the ‘latch’ mechanism in the N-terminal, which is essential for leucine binding. Further validation of reduced binding and modified internal motions caused by the mutants was obtained through binding free energy calculations, principal components analysis (PCA), and free energy landscape (FEL) analysis. By unraveling the molecular intricacies of Sesn2-leucine interactions and their mutations, we hope to pave the way for innovative strategies to combat the inevitable tide of aging and its associated diseases.

Communicated by Ramaswamy H. Sarma

Keywords:

• Sestrin2
• molecular interactions
• aging
• molecular simulation
• free energy calculations

Introduction

Aging is a universal biological process that comes with a gradual decline in physiological function and an increased susceptibility to an array of diseases due to the diminished efficacy of the defense mechanisms against different types of cellular stress states (Budanov, 2015; Fatima et al., 2021). Research efforts to understand and slow down the effects of aging are not new and have long been a central theme in biomedical research, but recent years have witnessed an increased surge of interest in the molecular pathways that govern longevity and are involved in age-related pathologies. Central to this research is Sestrin2 (Sesn2), an evolutionary conserved protein, that plays an important role in cellular homeostasis, antioxidant defense, and modulation of metabolic processes (Budanov et al., 2010). Sesn2 is a leucine sensor for the mechanistic target of the rapamycin (mTOR) pathway (Wolfson et al., 2016; Zahid et al., 2023). As the mTOR pathway is a central regulator of cell growth and metabolism and lies at the heart of a molecular network of aging biology, Sesn2 functions as a crucial node in this network. Sesn2 plays a crucial part in the mTOR signaling cascade by influencing the activity of mTOR in complex 1 (mTORC1). This regulation is achieved through the interaction of mTORC1 with the RAAG family of GTPases, which form two types of heterodimers, RRAG-A/B and RAAG-C/D (Budanov, 2015). The activation of these heterodimers is contingent upon GTP and GDP binding to RRAG-A/B and RRAG-C/D, respectively. This interaction is essential for the recruitment of mTORC1 to lysosomal membranes, its subsequent activation by RHEB, and the modulation of its activity via guanine nucleotide exchange factors (GEFs) and GTPase-activating proteins (GAPs). Sesn2’s role becomes particularly significant during leucine deficiency, where it binds to GATOR2, thereby relieving GATOR1, a GAP for RAAG, from GATOR2’s suppression, culminating in the inhibition of mTORC1 (Chantranupong et al., 2014). Upon leucine binding, Sesn2 dissociates from GATOR2, inhibiting GATOR1 and leaving mTORC1 unleashed to perform anabolic activities, which come at the cost of oxidative stress. Additionally, mTORC1 activation inhibits autophagy which is one of the important mechanisms for degrading damaged macromolecules and organelles and provides defense against cellular stress (Gelino & Hansen, 2012). Stimulation of AMP-activated protein kinase (AMPK), inhibition of mTORC1 activation, and initiation of autophagic signaling have demonstrated the potential to enhance the lifespan and overall health of model organisms (Gelino & Hansen, 2012; Harrison et al., 2009; Miller et al., 2011; Wilkinson et al., 2012). Loss of Drosophila Sestrin (dSesn) resulted in early onset of aged phenotype as evidenced by skeletal and cardiac muscle degeneration, mitochondrial dysfunction, and the accumulation of triglycerides through uncontrolled activation of mTORC1 (Lee et al., 2010). The aged cardiac muscles express low levels of Sesn2 and are more prone to damage by stress (Quan et al., 2017; 2020). As Sesn2 activates AMPK, inhibits mTOTC1, and activates autophagy, modulation of Sesn2 is a viable strategy to prevent or delay the onset of age-associated pathologies (Cordani et al., 2019; Kim et al., 2015; Morrison et al., 2015). The discovery of NV-5138, a leucine-like ligand of Sesn2 to activate mTORC1, is the proof of concept that the modulation of the mTORC1 pathway is possible through Sesn2 (Sengupta et al., 2019). Sestrin 2 emerges as a pivotal target in combatting chemotherapeutic drug resistance, given its role in triggering the activation of AKT and/or AMPK pathways. Within human SCC and melanoma cells, sestrin 2 has been observed to foster chemotherapeutic drug resistance through AKT pathway activation and modulation of PTEN activity (Pasha et al., 2017).

The Sesn2 protein is composed of a singular polypeptide chain that spans 480 amino acids, with an overall molecular weight of approximately 55 kilodaltons. Structurally, Sesn2 is characterized by its globular form that solely consists of alpha-helical structures without the presence of beta sheets. The three-dimensional conformation of SESN2, as determined through X-ray crystallography and cataloged under the Protein Data Bank identifier 5DJ4, reveals distinct domain organizations: an N-terminal domain (NTD) composed of amino acids 66 to 220, a C-terminal domain (CTD) consisting of amino acids 339 to 480, and a flexible linker domain (LD) spanning amino acids 221 to 338 that connects the NTD and CTD (Saxton et al., 2016; Wolfson et al., 2016). Within the CTD lies a leucine-binding site, formed by the convergence of three alpha helices and one helix from the LD. Essential for the protein’s function, the residues GLU451 in the CTD and LEU261 in the LD are integral to leucine’s attachment to Sesn2. Furthermore, the residues SER190 in the NTD, alongside Asp406 and Asp407 in the CTD, are pivotal for Sesn2’s interaction with the protein complex GATOR2, with the latter two residues’ proximity to the leucine-binding site shedding light on the leucine-dependent modulation of Sesn2 and GATOR2's interaction. However, the comprehensive structural nuances of Sesn2’s engagements with other stress-response regulating proteins like AMPK and LKB1, particularly how leucine binding influences these interactions, remain to be fully elucidated. Unraveling these details is essential for the synthesis and optimization of small molecules that could potentially enhance SESN2's activity by reinforcing these protein-protein interactions.

Leucine is the native known ligand of Sesn2, and its interaction with Sesn2 is particularly noteworthy, as it influences the activity of mTOR (Saxton et al., 2016; Sengupta et al., 2019). Understanding the nuances of leucine binding to Sesn2, therefore, has profound implications for therapeutic strategies aimed at modulating aging and its associated pathologies. It is important to find out how leucine interacts with Sesn2 and how mutations in the binding pocket of leucine affect the binding of leucine. Mutations within the Sesn2 gene can alter the structural integrity and function of the protein, potentially affecting leucine binding and subsequent mTOR pathway signaling. The exploration of these functional mutations provides a window into the complexity of aging mechanisms, revealing how subtle genetic variations can have far-reaching effects on cellular function and organismal health. This study is committed to investigating the impact of these mutations on the binding dynamics between leucine and Sesn2. By employing state-of-the-art structural and molecular simulation approaches, we aim to dissect the dynamics of atoms and energies that dictate the affinity and specificity of this interaction. These computational analyses, grounded in empirical data, will enable us to predict the effects of specific mutations on Sesn2 structure and function. Moreover, the apo structure of Sesn2 is still elusive (Saxton et al., 2016). The differences in leucine bound and apo state of Sesn2 are of utmost importance to decipher the mechanism of binding and dissociation of mTORC1 to GATOR2.

Incorporating a broad spectrum of simulation techniques, from molecular dynamics to free energy calculations, our study is designed to model the atomic-scale interactions between leucine and mutant forms of Sesn2 already described in the literature (Kim et al., 2015; Wolfson et al., 2016). The implications of these interactions for the mTOR pathway and downstream biological effects are profound, as they may unveil novel regulatory mechanisms at play in the aging process. The translational impact of this research is significant, as it has the potential to inform the development of targeted interventions. By identifying mutation ‘hotspots’ that critically alter leucine binding, we can pinpoint potential drug targets for the modulation of the mTOR pathway. Such therapeutic agents could be instrumental in the management of metabolic diseases, cancer, and neurodegenerative disorders, thereby extending the health span and improving the quality of life for the aging population. As the global demographic shifts toward an older population, the urgency to understand and mitigate the effects of aging becomes increasingly paramount. Our research stands at the intersection of gerontology, structural biology, and computational biophysics, aspiring to contribute valuable knowledge to the scientific community. By unraveling the molecular intricacies of Sesn2-leucine interactions and their mutations, we hope to pave the way for innovative strategies to combat the inevitable tide of aging and its associated diseases.

Materials and methods

Structural modeling and preparation

The co-crystal structure of the Sesn2 in complex with leucine was downloaded from RCSB and the sequence was obtained from UniProt to model the missing residues (Consortium, 2019). The sequences were submitted to Alpha Fold 2.0 to model the structures of the WT and mutants which uses a deep neural network architecture to model the structure of a query sequence (Jumper et al., 2021). It first predicts the distances between the amino acid pairs and then refines the calculated distances to model the structure. For the calculation of distance both the convolutional and residual layers in the ANN are considered. The predicted distances are represented in a matrix form called the contact map. A new attention mechanism has been incorporated into the network to facilitate the mapping of the 3D structure, allowing the network to concentrate on the most significant aspects of the input data. This attention mechanism has been modeled on the Transformer architecture employed in the natural language processing algorithm. Given a protein sequence S, Alpha Fold first generates a multiple sequence alignment (MSA) M using a profile Hidden Markov Model (HMM). The MSA is used to compute features such as the pairwise distance matrix D. Next, the MSA and features are input into a deep residual neural network with L layers, which maps the protein sequence to a predicted 3D structure. The network consists of L residual blocks, each containing multiple convolutional layers and self-attention layers. The output of the last residual block is passed through a final layer to predict the per-residue coordinates in the 3D space (Skolnick et al., 2021). The pLDDT score was used to evaluate the quality of each structure and also subjected to further validations. Each structure was minimized for 1000 steps using the steepest descent and 100 steps of conjugate gradient algorithms embedded in Chimera software. For structural deviations, the root mean square deviation (RMSD) method was used by aligning the wild-type (WT). For the visual representation of each, PyMOL and Chimera software were used (Goddard et al., 2005; Pettersen et al., 2004; Yuan et al., 2017).

Molecular interaction analysis using an in-silico docking approach

To decipher the binding variations induced by the naturally reported mutations on the binding of leucine with the Sesn2, we performed protein–protein docking using HADDOCK online server (Dominguez et al., 2003). It is an information-driven flexible docking approach that estimates the protein interfaces by using ambiguous interaction restraints (AIRs) and uses other approaches such as NMR residual dipolar couplings to model the complex. This docking is based on generating multiple conformations and then clustering the identical conformations into their respective component. A blind docking protocol was employed to automatically search for the binding interface. All three complexes revealed similar docking sites thus showing the accuracy of the employed algorithm. The top complexes were visualized and inspected for the potential hydrogen bonding and salt-bridges interactions using the PDBsum webserver and PyMOL software for 3D interactions (Laskowski, 2001).

All-atoms simulation in explicit solvent

To perform molecular simulations of all the systems, i.e., WT apo and holo state with the mutants and along with leucine, the coordinates, and topology files were prepared using the ‘tLeap’ an integrated module in AMBER21 (Case et al., 2005; Salomon‐Ferrer et al., 2013). A solvent box (OPC) was strategically positioned around each system, followed by the addition of ions to neutralize the charge. Subsequently, the systems underwent energy minimization utilizing algorithms like steepest descent and conjugate gradient until meeting convergence criteria, such as a maximum force or energy change threshold. To facilitate temperature equilibration, a temperature couplings algorithm such as Langevin Dynamics or Berendsen thermostat gradually heated the systems from a low temperature. Long-range electrostatic interactions were computed using the Particle Mesh Ewald (PME) method, while van der Waals forces were assessed via the Lennard-Jones potential (Toukmaji et al., 2000). Each system underwent multiple stages of equilibration at the designated temperature and pressure. These stages included positional restraint, gradual heating, and unrestrained equilibration. To preserve covalent bond lengths, the SHAKE algorithm was employed to constrain both bond lengths and angles. The system pressure was regulated utilizing a barostat mechanism such as Berendsen or Andersen (Fyta, 2016). Following equilibration, each system underwent a production simulation lasting 300 ns, employing a molecular dynamics algorithm like the NPT or NVT ensemble (Salomon-Ferrer et al., 2013). In this step, simulation parameters including time step and cut-off distances were set. We then analyzed each trajectory by using CPPTRAJ or PTRAJ modules (Roe & Cheatham, 2013). For structural stability, RMSD, for residual flexibility, RMSF, for structural compactness, Rg, and hydrogen bonding for each system were calculated (Cooper, 1976; Lobanov et al., 2008; Maiorov & Crippen, 1994). (ii) $$\mathit{\text{RMSD}}=\sqrt{\frac{\sum d^{2}i=1}{N_{\mathit{\text{atoms}}}}}$$(ii) where:

The parameter ‘di’ signifies the disparity in atom positions between the original and superimposed structures, with ‘I’ representing the reference point. Meanwhile, the root mean square fluctuation (RMSF) can be derived from the B-factor, a critical parameter for gauging the flexibility of protein residues. Mathematically, RMSF is calculated using the following equation. (iii) $$\mathit{\text{Thermal}}\mathrm{ }f\mathrm{a}\mathit{\text{ctor or}}\mathrm{ }B-\mathit{\text{factor}}=\left[\right(8\pi \mathrm{*}\mathrm{*}2)/3]\left(\mathit{\text{msf}}\right)$$(iii)

The radius of gyration measures the compactness of a protein structure. (iv) $$R_{\mathit{\text{gyr}}}^2=\frac{1}{M}\mathrm{ }\sum _{i=1}^N{m}_i(r_i-R^2)$$(iv) where (v) $$M={\sum }_{i=1}^N{m}_i$$(v) is the total mass and; (vi) $$R=N^{-1}{\sum }_{i=1}^N{r}_i$$(vi) is the center of mass of the protein consisting of N atoms.

Binding-free energy estimation through MM/GBSA analysis

Understanding how proteins recognize their biologically significant ligands or small molecule inhibitors is crucial for the development of effective treatments. This method offers advantages over others due to its time efficiency and low computational cost. It is commonly employed to determine the binding free energy (BFE) for both protein-protein and protein-ligand complexes. The BFE is computed as the disparity between the free energies of the bound protein-ligand complex (G_{complex, solvated}) and the unbound states of Sesn2 (G_{protein, solvated}) and Leucine (G_{ligand, solvated}). The subsequent equation was utilized to compute each term contributing to the overall binding energy (Chen et al., 2016). (vii) $${\Delta G}_{\mathit{\text{bind}}}=G_{(\mathit{\text{complex}},\mathit{\text{solvated}})}–G_{\left(\mathit{\text{protein}},\mathit{\text{solvated}}\right)}–G_{(\mathit{\text{ligand}},\mathit{\text{solvated}})}$$(vii)

This equation can be used to determine the contribution of interaction in the complex and can be expressed as; (viii) $$G=E_{\mathit{\text{Molecular Mechanics}}}‐G_{\mathit{\text{solvated}}}–\mathit{\text{TS}}$$(viii)

This equation can be further restructured to calculate the specific energy term. (ix) $${\Delta G}_{\mathit{\text{bind}}}={\Delta E}_{\mathit{\text{Molecular Mechanics}}}+{\Delta G}_{\mathit{\text{solvated}}}–\Delta \mathit{\text{TS}}={\Delta G}_{\mathit{\text{vaccum}}}+{\Delta G}_{\mathit{\text{solvated}}}\mathrm{ }$$(ix) (x) $${\Delta E}_{\mathit{\text{Molecular Mechanics}}}={\Delta E}_{\mathit{\text{int}}}+{\Delta E}_{\mathit{\text{electrostatic}}}+{\Delta E}_{\mathit{\text{vdW}}}$$(x) (xi) $$\Delta G_{\mathit{\text{solvated}}}=\Delta G_{\mathit{\text{Generalized born}}}+\Delta G_{\mathit{\text{surface area}}}$$(xi) (xii) $$\Delta G_{\mathit{\text{surface area}}}=\gamma .\mathit{\text{SASA}}+b$$(xii) (xiii) $$\Delta G_{\mathit{\text{vaccum}}}={\Delta E}_{\mathit{\text{Molecular Mechanics}}}-T\Delta S$$(xiii)

The total binding energy, denoted as ΔG_bind, encompasses contributions from various terms. Specifically, the overall gas-phase energy, comprising ΔE_internal, ΔE_{electrostatic}, and ΔE_vdw, is encapsulated in ΔE_MM. Additionally, ΔGsol represents the summation of polar (ΔG_PB/GB) and non-polar (ΔG_SA) solvation contributions. Conformational binding entropy, often determined through normal-mode analysis, is denoted by -TΔS. The internal energy originating from molecular mechanics (MM) force fields, encompassing bonds, angles, and dihedral angles, is reflected in ΔEinternal. ΔEelectrostatic and ΔEvdw signify electrostatic and van der Waals energies computed via MM, while ΔG_PB/GB quantifies the polar solvation-free energy utilizing Poisson–Boltzmann (PB) or generalized Born (GB) methodologies. ΔG_SA denotes nonpolar solvation-free energy, typically calculated using a linear function of the solvent-accessible surface area (SASA). It’s noteworthy that conformational entropy was omitted due to computational demands and inherent inaccuracies (Nadeem et al., 2023).

Dimensionality reduction through principal component analysis (PCA)

Principal Component Analysis (PCA) is a widely used method in analyzing data from molecular dynamics simulations of biological macromolecules. It simplifies the analysis by reducing the complexity of the data while retaining important information. PCA is popular because it is easy to use and does not require extensive computational resources. It helps in removing the influence of overall motion from the data. The process involves calculating a covariance matrix from the data, determining its eigenvectors and eigenvalues, and identifying the principal components based on the highest eigenvalues. These principal components capture the most significant structural changes and movements in the system, allowing for a better understanding and visualization of the simulation results (Kurita, 2019). The subsequent mathematical equation facilitates the computation of the covariance matrix (C) based on a series of n-dimensional vectors (xi): (x) $$C=\frac{1}{N}\mathrm{ }x\mathrm{ }\sum \left(i=1\mathrm{ }\mathit{\text{to}}\mathrm{ }N\right)\left[\mathrm{ }{(x}_i-\mu \mathrm{ }x\right(x_i-\mu {)}^T]$$(x) where:

The equation enables the derivation of the eigenvectors (V) and eigenvalues (λ) from the covariance matrix C, with N representing the number of vectors, μ denoting the mean vector, and T indicating the transpose operation. (xi) $$C x V=\lambda x V$$(xi) where V represents the eigenvector matrix while the diagonal matrix of eigenvalues is represented by λ. The principal components of the system are represented by the eigenvectors with the highest corresponding eigenvalues. In our analysis, we utilized the unsupervised PCA method to calculate the two principal components, PC1 and PC2, which are essential for understanding the motions in our systems. We employed the CPPTRAJ module within the AMBER21 software package, considering the entire simulation trajectory comprising 10,000 frames per system. The spatial covariance matrix was computed using the eigenvectors and atomic coordinates, followed by an orthogonal coordinate transformation to obtain a diagonal matrix of eigenvalues. These eigenvectors and eigenvalues were then used to identify the principal components of the system, enabling us to visualize significant movements during the simulation and detect any conformational transitions.

Free energy landscape (FEL) of the molecular simulation trajectories

The free energy landscape (FEL) plays a crucial role in determining the thermodynamics and kinetics of molecular processes in solution. It is a very useful approach to interpreting and analyzing biomolecular processes such as molecular folding, aggregation, and recognition (Maisuradze et al., 2010). It is a graph of the free energy (f) plotted against the configuration space, which is defined by the collective coordinates (r) of all the atoms in the molecule. In our study, we employed the two principal components (PCs) to map the conformational transitions in each system and characterize them consequently identifying the lower energy minima and meta-states separated by energy barriers, which were depicted as deep valley plots. The free energy graph, depicting (f) against the configuration space defined by the collective coordinates (r) of all molecule atoms, illustrates the energy landscape. Our analysis utilized the two principal components (PCs) to depict conformational transitions within each system. This approach allowed us to identify lower energy minima and meta-states, separated by energy barriers, which were visualized as deep valley plots.

Results and discussion

Structures retrieval, modeling and preparation

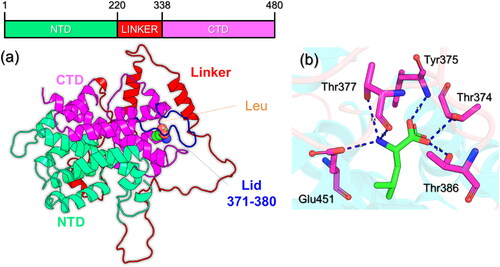
The 3D coordinates of the leucine-bound Sesn2 were retrieved from RCSD using the accession number 5DJ4. This bi-domain structure contains an NTD (N-terminal domain), CTD (C-terminal domain), and a linker that connects the two domains. The NTD spans from 1–219, the linker spans from 220–338 while the CTD space over 339–480 residues. The domain organization is given in Figure 1(a). The region 371–380 is a loop and responsible for the ‘lid-latch’ mechanism which helps in the robust binding of leucine. The structure of Sesn2 contains missing loops which correspond to a loop region that connects L1 and L2 helices in the linker, the tail of the linker, and the NTD (N2 helix). These regions were modeled using a loop modeler as both domains are required for the leucine recognition and binding. To determine the binding pattern of leucine with Sesn2, the interaction pattern was determined which reported several hydrogen bonding interactions with the key residues. For instance, six hydrogen bonds involving Thr374, Tyr375, Thr377, Thr386, and Glu451 residues are in direct contact with the leucine. The binding pattern strongly aligns with the crystallographic coordinates reported by previous literature (Saxton et al., 2016). To further decipher the impact of the aforementioned mutations the interaction pattern was revealed and compared with the WT. The interaction pattern of the WT Sesn2 and leucine is given in Figure 1(b).

Figure 1. Structural organization of Sesn2 and Leucine binding. (a) shows the domain organization of the Sesn2. The CTD is given in magenta color, NTD is given in green color while the linker is given as red. The Lid that is essential for the leucine robust interaction is given in blue color corresponding to 371-380 residues. (b) shows the interaction pattern of leucine with Sens. Hydrogen bonds are shown as dotted blue lines.

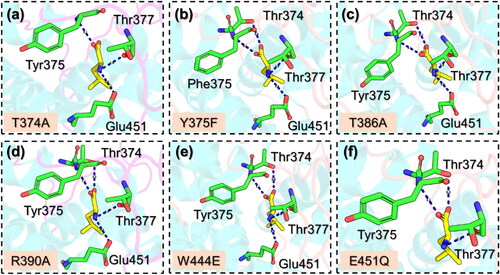
The interaction paradigm of the mutants such as T374A, Y37F, T386A, R390A, W444E, and E451Q was also explored to determine the functional impact and variations caused by these substitutions. The interaction pattern for the T374A mutant is given in Figure 2(a), which shows that upon the substitution three hydrogen bonds are lost while only three are remaining. The interactions include Tyr375, Thr377 and Glu451. It has been previously reported that this mutation functionally impairs the binding of leucine and therefore plays an essential role in the leucin binding (Saxton et al., 2016). Similarly, the Y375F reported four hydrogen bonds which were also observed in the T386A, R390A, and W444E. All these mutants determined a similar pattern of interactions and are presented in Figure 2(b–e). It can be seen that the interaction with T386 is primarily lost and, therefore, shows the essential role of T386 in leucine binding. The T386 has been reported to be one of the three conserved threonines that make hydrogen bond contacts with the carboxyl group of leucine (Saxton et al., 2016). In the E451Q, the interaction with the highly conserved residue E451 has been diminished and make is functionally impaired. The role of E451 has been described somewhere which reports the essential contribution of E451 in leucine binding (Wolfson et al., 2016). The interaction pattern for the E451Q mutant is shown in Figure 2(f). Overall, this shows that these mutations significantly affect the binding of leucine and, therefore, play an essential role and lead to a concomitant increase in the leucine concentration required for mTORC1 activation in cells.

Figure 2. Interaction patterns of Leucine with the mutants of Sesn2. (a) shows the binding pattern of T374A with Sesn2, (b) shows the binding pattern of Y375F with Sesn2, (c) shows the binding pattern of T386A with Sesn2, (d) shows the binding pattern of R390A with Sesn2, (e) shows the binding pattern of W444E with Sesn2, and (f) shows the binding pattern of E451Q with Sesn2. Hydrogen bonds are shown as dotted blue lines.

Structural dynamics-based stability assessment

The investigation of structural stability using a dynamics-based trajectory determines essential information regarding the biological mechanisms of different processes. Dynamics stability influences the efficiency of biological reactions and any perturbation in the dynamics stability influences the overall reaction rate. Moreover, it also ensures the specificity of these interactions, and effective signal transduction within the cell, and is central to regulating gene expression and cell cycle control. Considering the essential role of structural stability in deciphering many biological processes we also calculated RMSD as a function of time for each system. As shown in Figure 3(a), the RMSD for the apo state remains higher than the WT-holo state. For instance, the RMSD for the apo state was calculated to be 5.80 Å while for the WT an average RMSD remained lower and maintained a level of 3.10 Å during the simulation. No significant structural perturbation was observed, and a more rigid simulation was observed. In the context of T374A the RMSD remains similar to the apo state, however, a minor difference in the average RMSD was observed. An average RMSD for the T374A was estimated to be 4.86 Å during the simulation. As given, it can be seen that the WT bound to leucine maintains a more stable and lower RMSD level than the apo and T374A systems and, therefore, revealed that the apo state and T374A exhibit higher conformational flexibility due to the absence/reduced binding of the ligand (leucine) that consequently reduces the ligand-induced–structural constraints and allows it to sample a broader range of conformations, resulting in a higher RMSD.

Figure 3. Dynamic stability analysis of the apo, holo (WT and mutant) systems. (a) shows the RMSD results for the apo state, WT (holo) and T374A complexes, (b) shows the RMSD results for the apo state, WT (holo) and Y375F complexes, (c) shows the RMSD results for the apo state, WT (holo) and T386A complexes, (d) shows the RMSD results for the apo state, WT (holo) and R390A complexes, (e) shows the RMSD results for the apo state, WT (holo) and W444E complexes, and (f) shows the RMSD results for the apo state, WT (holo) and E451Q complexes.

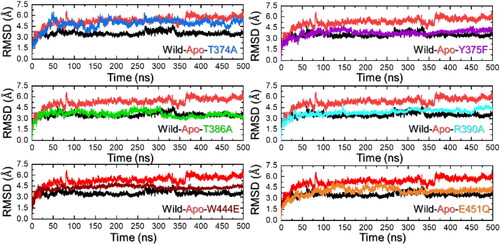
On the other hand, the Y375F reported a more similar RMSD pattern as the WT complex. The RMSD started to increase from 0 and reached a maximum of 3.5 Å at 110 ns. Then the RMSD gradually decreased and reached the lowest at 350 ns. Afterward, the RMSD started to gradually increase again and determined a pattern with no major deviation during the simulation. It can be speculated that the Y375F engages local structural changes in specific regions of the protein that are associated with the reduced binding of leucine to the leucine binding cavity of Sesn2. The RMSD results for the Y375F are given in Figure 3(b). Moreover, the T386A also reported similar RMSD levels as the WT and Y375F. The RMSD initially reported structural deviations until 320 ns and then stabilized after 320 ns and remained uniform until the end of the simulation. A similar RMSD levels does not necessarily reflect similar binding of leucine but may also determine that the defined simulation time is enough for enhanced sampling in which this complex attained stability in contrast to the others. The RMSD results for the T386A are given in Figure 3(c).

Similarly, the R390A also reported a similar level of RMSD as the WT but after 450 ns the RMSD increased again which shows that the complex is still searching for stabilized conformation and is sampling a broader range of conformations even after 400 ns of simulation time period. This shows that the mutations have induced some changes that are responsible for variations in the dynamic properties, particularly the structural stability, and cause functional variance. The RMSD results for the R390A are given in Figure 3(d). An average RMSD for the R390A complex was calculated to be 3.27 Å. The W444E mutation in the Sesn2 reported a higher RMSD than the WT complex and major perturbations were observed during the first 100 ns. The RMSD remained higher during the 1–280ns and then converged with the WT RMSD.

Similarly, the E451Q reported major perturbations during the first 300 ns and attained a stable conformation after 300 ns. An average RMSD for the W444E and E451Q were reported to be 3.50 and 3.20 Å, respectively. The RMSD results for the W444E and E451Q complexes are reported in Figure 3(e and f). In sum, these mutations compromised the dynamic stability by altering the conformational flexibility, sampling time, and leucine-induced structural constraints that consequently caused variation in the binding and structural stability.

Protein structure size measurement through Rg calculation

Quantification of the structural size through Rg calculation reveals essential knowledge regarding the binding and unbinding events. It has been a widely used approach to determine the variation in the protein size caused by the mutations acquired by it. As depicted in Figure 4(a), the apo state has an Rg lower than the WT complex. The T374A reported a lower Rg value and thus maintained a tighter structure of the protein. During the first 225 ns, the WT complex reported lower Rg, which then gradually increased and reached up to 22.80 Å. The increase in the protein size determines the conformational rearrangement that leads to optimized binding of the leucine than the mutants.

Figure 4. Structural compactness analysis of the apo, holo (WT and mutant) systems. (a) shows the Rg results for the apo state, WT (holo) and T374A complexes, (b) shows the Rg results for the apo state, WT (holo) and Y375F complexes, (c) shows the Rg results for the apo state, WT (holo) and T386A complexes, (d) shows the Rg results for the apo state, WT (holo) and R390A complexes, (e) shows the Rg results for the apo state, WT (holo) and W444E complexes, and (f) shows the Rg results for the apo state, WT (holo) and E451Q complexes.

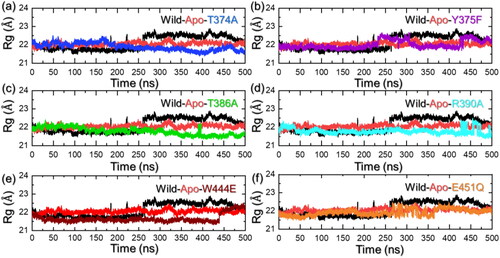
Similarly, the Rg value for the Y375F also determined a lower Rg during the first 225 ns and then increased up to 22.41 Å in the last part of the simulation. The result strongly aligns with the RMSD results where the WT and Y375F converged with each other and hence here also followed the same pattern by determining similar behavior. The Rg graph for the Y375F mutant is shown in Figure 4(b). On the other hand, the T386A started to decrease the Rg gradually and reached the lowest at 500 ns. An average Rg for this complex was calculated to be 21.85 Å. The Rg graph for the T386A mutant is shown in Figure 4(c). A more similar behavior was observed for the R390A complex but similar to RMSD the Rg increased at the end of the simulation. After 475 ns, the Rg decreased and continues to maintain a similar level. The Rg graph for the R390A mutant is shown in Figure 4(d). The W444E mutant also reported a lower Rg than the apo and the WT complex. This complex continues to report a uniform Rg level but at 440 ns an abrupt increase was observed. The Rg graph for the W444E mutant is shown in Figure 4(e). Next, the E451Q complex reported a perturbation in the Rg pattern between 250 and 350 ns, and thereafter, no significant deviation was observed. The Rg graph for the E451Q mutant is shown in Figure 4(f). This shows that upon the leucine binding a conformational expansion of the WT complex might take place therefore resulting in a larger Rg. Due to the loss of structural integrity, the mutant complex may disrupt protein folding leading to a more compact and unstable structure rendering it dysfunctional. Misfolded proteins often fail to attain their native structure, leading to functional impairment. Moreover, flexibility is essential for proteins to carry out their functions, excessive rigidity or constraints in specific regions might impair dynamic motions required for catalysis, signaling, or other biological activities. Hence, the mutants’ structure maintained more constrained dynamics and therefore could potentially lead to leucine binding impairment.

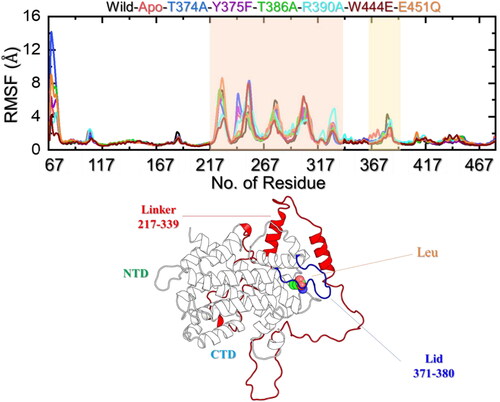
Residue’s flexibility indexing

Within the domain of molecular dynamics (MD) simulations, the root mean square fluctuation (RMSF) emerges as a valuable asset, facilitating the assessment and comparison of flexibility across diverse regions within a molecule or between molecules. It assists in pinpointing significant flexible areas pivotal in phenomena such as ligand binding or protein–protein interactions. Furthermore, RMSF plays a pivotal role in validating MD simulations, as experimental RMSF measurements offer a means to authenticate the accuracy and effectiveness of the employed force field.

An alignment between the experimental and simulated RMSF values indicates that the simulation aptly captures the biomolecule’s flexibility and dynamics. To determine the residual flexibility and decipher the role of each residue in leucin recognition, binding, and stabilization we calculated the flexibility of each residue using the simulation trajectory. All the complexes demonstrated lower fluctuations for the region between 70–216, 340–370, and 380–470. The regions 217–339 and 371–380 demonstrated a higher fluctuation. Nonetheless, these regions correspond to a linker (217–339) and a loop 371–380 that cover the leucine binding cavity that is involved in the ‘latch’ mechanism that lies in the N-terminal and makes it essential for the N-terminal involvement in leucine binding mechanism (Figure 5(a)). Three threonine residues, Thr374, Thr377, and Thr386, exhibit a high degree of conservation and are situated directly above the leucine-binding site. Mutations at these positions (T374A or T386A) lead to the disruption of the interaction with leucine, while concurrently establishing a constitutive interaction with GATOR2 (Saxton et al., 2016). This underscores the indispensable role of the lid region in mediating leucine binding. Although both the domains are required for the leucine binding CTD comes in direct interaction only while residue His86 from NTD latches the cavity and makes it accessible to the active site residues. The linker that demonstrated higher flexibility and also the loop that is responsible for the lid-latch mechanism is shown in Figure 5(b).

Figure 5. Residue’s flexibility analysis of the apo, holo (WT and mutant) systems. (a) shows the RMSF results for the apo state, WT (holo), and mutant complexes. It shows the regions that are dynamically more flexible than the others and are highlighted with the shade. (b) shows the mapped dynamically flexible regions, i.e. the linker and the lid. The linker is shown as red, the lid is given in blue while the NTD, CTD, and leucine binding are also highlighted.

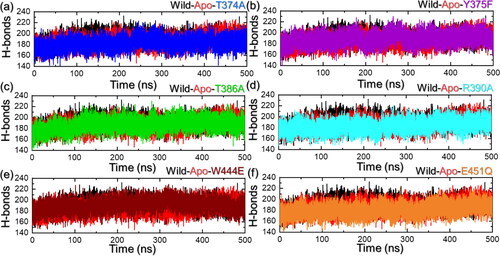
Hydrogen bonding analysis

On the other hand, hydrogen bonds particularly in the context of protein–protein interaction are important to determine the binding strength of interactions. It is an essential part of deciphering the mechanism of different biological processes, disease mechanisms, and the impact of mutations on protein coupling and molecular signaling. Considering the essential role of hydrogen bonding in various biological processes, we also estimated the hydrogen bonds in each trajectory over time. It can be observed that the average number of hydrogen bonds is higher in the WT than in the mutants, particularly in the T374A, T386A, R390A, and E451Q. This indicates a strong alignment of the current findings with the experimental reports where these residues were reported to be the most essential for leucine recognition and binding (Saxton et al., 2016). These observations also indicate that these mutations disrupt the regular hydrogen bonding patterns, reducing the ability of leucine to form hydrogen bonds leading to loss of functional integrity that consequently impacts the leucine binding. Hydrogen bonding graphs are depicted in Figure 6(a–f).

Figure 6. Hydrogen bonds (H-bonds) analysis of the apo, holo (WT and mutant) systems. (a) shows the H-bonds results for the apo state, WT (holo) and T374A complexes, (b) shows the H-bonds results for the apo state, WT (holo) and Y375F complexes, (c) shows the H-bonds results for the apo state, WT (holo) and T386A complexes, (d) shows the H-bonds results for the apo state, WT (holo) and R390A complexes, (e) shows the H-bonds results for the apo state, WT (holo) and W444E complexes, and (f) shows the H-bonds results for the apo state, WT (holo) and E451Q complexes.

Binding-free energy calculation

The validation of docking results can be effectively achieved through the utilization of binding free energy calculation methods. These approaches, namely MM/PBSA (Molecular Mechanics/Poisson-Boltzmann Surface Area) and MM/GBSA (Molecular Mechanics/Generalized Born Surface Area), are recognized for their accuracy, efficiency, and computational cost-effectiveness. Widely applied across diverse research contexts, these methods offer a robust means of determining the binding potential of various protein complexes implicated in different diseases. In light of the demonstrated efficacy of this approach, we conducted binding free energy calculations using MM/PBSA and MM/GBSA methods to further validate our docking results. The MM/PBSA results are summarized in Table 1. For the WT, the vdW was calculated to be −27.46 ± 0.19 kcal/mol while the mutants reported vdW values of −18.47 ± 0.10 kcal/mol for T374A mutant, −21.43 ± 0.18 kcal/mol for Y375F mutant, −20.47 ± 0.20 for T386A mutant, −21.39 ± 0.13 for R390A mutant, −21.84 ± 0.14 kcal/mol for W444E mutant, and −22.81 ± 0.11 kcal/mol for E451Q mutant.

Table 1. Estimation of the BFE using the MM/PBSA approach for the whole simulation trajectory. All the results are provided in kcal/mol.

MMPBSA
	Wild-type (WT)	T374A	Y375F	T386A	R390A	W444E	E451Q
VDWAALS	−27.46 ± 0.19	−18.47 ± 0.10	−21.43 ± 0.18	−20.47 ± 0.20	−21.39 ± 0.13	−21.84 ± 0.14	−22.81 ± 0.11
EEL	−151.23 ± 0.75	−136.14 ± 0.79	−130.37 ± 0.85	−129.62 ± 0.85	−134.35 ± 0.32	−128.42 ± 0.23	−130.78 ± 0.41
EPB	133.47 ± 0.49	124.630 ± 0.74	116.68 ± 0.80	117.43 ± 0.80	120.78 ± 0.24	117.27 ± 0.22	123.26 ± 0.29
ENPOLAR	−2.10 ± 0.33	−1.95 ± 0.21	−2.67 ± 0.02	−3.01 ± 0.01	−3.17 ± 0.01	−2.45 ± 0.00	−1.88 ± 0.01
EDISPER	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00	0.00 ± 0.00
DELTA G gas	−167.94 ± 0.73	−130.58 ± 0.81	−133.48 ± 0.86	−118.23 ± 1.53	−136.95 ± 0.83	−122.96 ± 1.25	−157.59 ± 1.41
DELTA G solv	131.37 ± 0.49	116.29 ± 0.52	114.22 ± 0.77	108.25 ± 1.26	112.42 ± 1.24	119.78 ± 1.27	121.38 ± 1.29
DELTA Total	−47.32 ± 0.71	−31.93 ± 0.73	−37.79 ± 0.76	−35.67 ± 0.82	−38.13 ± 0.85	−35.44 ± 0.84	−32.21 ± 0.77

On the other hand, the electrostatic energy (EEL) was calculated to be −151.23 ± 0.75 kcal/mol for the WT, −136.14 ± 0.79 kcal/mol for T374A mutant, −130.37 ± 0.85 kcal/mol for Y375F mutant, −129.62 ± 0.85 for T386A mutant, −134.35 ± 0.32 for tR390A mutant, −128.42 ± 0.23 for W444E mutant, and −130.78 ± 0.41 kcal/mol for E451Q mutant. The total binding free energy using the MM/PBSA approach was calculated to be −47.32 ± 0.71 for the WT, −31.93 ± 0.73 kcal/mol for the T374A mutant, −37.79 ± 0.76 kcal/mol for Y375F mutant, −35.67 ± 0.82 kcal/mol for T386A mutant, −38.13 ± 0.85 for R390A mutant, −35.44 ± 0.84 for W444E, and −32.21 ± 0.77 kcal/mol for the E451Q. The MM/PBSA results for each system are summarized in Table 1.

Furthermore, the total binding free energy was also calculated for each complex using the MM/GBSA, and the results are summarized in Table 2. The total binding free energy for each complex was calculated to be −53.60 ± 0.38 kcal/mol for the WT, −43.45 ± 0.10 kcal/mol for T374A, −46.55 ± 0.89 kcal/mol for Y375F mutant, −45.58 ± 0.47 kcal/mol for T386A mutant, −47.43 ± 0.18 kcal/mol for R390A mutant, −43.91 ± 1.16 kcal/mol for W444E mutant, and −44.43 ± 0.16 kcal/mol for E451Q. The total binding free energy has significantly declined which aligns with previous findings where these mutations were reported to make Sesn2 non-functional (Saxton et al., 2016; Wolfson et al., 2016). From these data, it can be observed that each system gains free energy in the gas phase but not in the solvent. These findings suggest that the leucine binding is thermodynamically favored in terms of enthalpy, primarily owing to advantageous interactions in the gas phase. However, it is disfavored in terms of entropy due to the unfavorable effects of solvation.

Table 2. Estimation of the BFE using the MM/GBSA approach for the whole simulation trajectory. All the results are provided in kcal/mol.

MMGBSA
	Wild-type (WT)	T374A	Y375F	T386A	R390A	W444E	E451Q
VDWAALS	−27.46 ± 0.19	−18.47 ± 0.10	−21.43 ± 0.18	−20.47 ± 0.20	−21.45 ± 0.13	−21.84 ± 0.14	−22.81 ± 0.11
EEL	−151.23 ± 0.75	−136.14 ± 0.39	−130.37 ± 0.85	−129.62 ± 0.85	−134.35 ± 0.32	−128.42 ± 1.23	−130.78 ± 0.41
EGB	128.51 ± 0.51	110.07 ± 0.46	108.42 ± 0.94	107.12 ± 1.26	110.90 ± 0.19	110.30 ± 1.20	116.53 ± 0.32
ESURF	−3.42 ± 0.06	−2.91 ± 0.03	−3.17 ± 0.02	−2.61 ± 0.01	−2.41 ± 0.01	−3.95 ± 0.02	−3.37 ± 0.00
DELTA G gas	−167.94 ± 0.73	−130.58 ± 0.81	−133.48 ± 0.86	−118.23 ± 1.53	−136.95 ± 1.03	−122.96 ± 1.25	−157.59 ± 0.41
DELTA G solv	125.08 ± 0.51	115.64 ± 0.64	109.82 ± 0.75	109.40 ± 1.26	118.86 ± 1.19	113.47 ± 1.27	122.16 ± 0.32
DELTA TOTAL	−53.60 ± 0.38	−43.45 ± 0.10	−46.55 ± 0.89	−45.58 ± 0.47	−47.43 ± 0.18	−43.91 ± 1.16	−44.43 ± 0.16

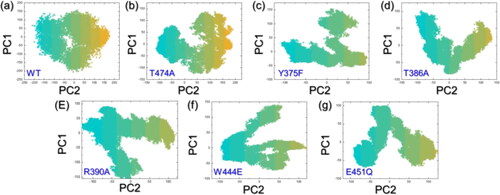
Principal components analysis (PCA)

PCA provides a simplified representation of the essential motions in an MD simulation trajectory, making it easier to interpret and understand the dynamics of the molecular system. It is a valuable tool for extracting meaningful information from the often complex and high-dimensional data generated by MD simulations. Herein, the WT protein exhibits a constrained motion in PCA suggesting that its native structure has a stable, well-defined conformation optimized for leucine recognition. The constrained motion implies limited flexibility, possibly indicating a specific binding site geometry. On the other hand, mutated proteins with spread-out motions suggest altered or dynamic binding regions, potentially affecting ligand interactions. This increased flexibility in mutants influences binding kinetics or enables the accommodation of diverse leucine conformations. Overall, the PCA results hint at the structural impact of mutations on the protein’s binding dynamics, potentially influencing ligand recognition and binding affinity. The PCA results are shown in Figure 7(a–g).

Figure 7. PCA analysis of the WT and Sesn2 mutants.

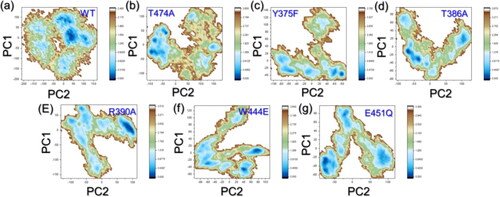
Free-energy landscape analysis (FEL)

In the case of FEL analysis, a WT protein displaying a constrained motion suggests a well-defined energy minimum in the landscape, indicating a stable native state optimized for ligand binding. The mutations, resulting in spread-out motions, imply a broader and less-defined landscape, potentially leading to multiple conformational states. This increased flexibility in mutants could result in a more dynamic and diverse FEL, affecting the energy barriers associated with ligand binding. Thus, the FEL analysis supports the idea that mutations influence the protein’s energy landscape, potentially impacting ligand binding kinetics and specificity. The FEL results are shown in Figure 8(a–g).

Figure 8. FEL analysis of the WT and Sesn2 mutants.

Conclusions

Leucine is the native known ligand of Sesn2 and its interaction with Sesn2 is particularly noteworthy, as it influences the activity of mTOR in aging and its associated pathologies. This study investigated the impact of non-synonymous mutations by incorporating a broad spectrum of simulation techniques, from molecular dynamics to free-energy calculations. Our results demonstrated that the interaction paradigm for the mutants has been altered and variations in the dynamic stability by altering the conformational flexibility, sampling time, and leucine-induced structural constraints consequently caused variation in the binding and structural stability. The regions 217–339 and 371–380 demonstrated a higher fluctuation and correspond to a linker (217-339) and a loop 371–380 that cover the leucine binding cavity that is involved in the ‘latch’ mechanism that lies in the N-terminal and makes it essential for the N-terminal involvement in leucine binding mechanism. The reduced binding and altered internal motions by the mutants were further validated by the binding free energy, PCA, and FEL methods. Research findings have indicated the significant clinical relevance of SESN2 across a spectrum of diseases. Notably, circulating levels of SESN2 have been recognized as informative markers for assessing disease severity or predicting prognosis in various conditions, including cardiovascular diseases, respiratory diseases, neurodegenerative diseases, metabolic disorders, and cancers. Given the dynamic alteration of SESN2 expression during liver pathology, we propose that SESN2 holds promise as a valuable clinical biomarker and prognostic indicator for liver diseases (Fang et al., 2020; Kishimoto et al., 2020; Pasha et al., 2017). By unravelling the molecular intricacies of Sesn2-leucine interactions and their mutations, we hope to pave the way for innovative strategies to combat the inevitable tide of aging and its associated diseases by using structure-based methods and pharmacophore design using leucine as input for the design of the features and, therefore, can be used to develop novel therapeutics considering these essential features. The only limitation of the current study is using microsecond simulations and repeated runs to ensure the replicated results that can be correlated for therapeutic purposes. Experimental validation of these mutations should be performed to guide the drugs development against SENS2 in various diseases.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

Open Access funding provided by the Qatar National Library. This work was funded by Qatar National Research Fund (Qatar Research Development and Innovation Council) [grant No. NPRP14S-0406-210150]. M.A.Z. is supported by Ph.D. graduate assistantships from the Office of Graduate Studies (Qatar University). The statements made herein are solely the responsibility of the authors.