A note on the can-order policy for the two-item stochastic joint-replenishment problem

Abstract

In this paper, a two-item continuous-review inventory system is studied. Demands for item 1 and item 2 occur at epochs generated by independent Poisson processes. In addition to the standard cost structure, there is economy of scale in joint replenishment. For the continuous joint replenishment problem, the literature proposes the can-order policy. Under this policy, an order is triggered by item 1 at its demand epoch, when its inventory position falls to its reorder level. In this situation, if the inventory position of item 2 is at or below its “can-order” level, item 2 is also included in this order and a discounted fixed ordering cost is charged for it. As a result, the inventory positions of both items are raised to their respective order-up-to levels. Reciprocally, the same procedure is valid at the demand epoch of item 2. In this study, this two-item inventory system is modeled as a semi-Markov decision process and a simple enumeration algorithm is proposed for its solution. We show that previous formulations of the problem do not necessarily converge to the best can-order policy by providing numerical examples.

Keywords:

• Inventory control
• semi-Markov decision process
• joint replenishment

1. Introduction

The joint replenishment problem requires the coordination of several products in a warehouse or the coordination of several locations for a single commodity. Consider a system where a product is supplied by a unique source, from which all locations must order. The locations could order separately, but joining their orders may reduce their transportation costs. Thus, there is economy of scale in joint replenishment. In multi-product systems, joint replenishment offers similar advantages. It allows reducing transportation and/or ordering charges by coordinated replenishment. Orders are combined when products are supplied from the same source. In this sense, multi-location systems and multi-product systems are fundamentally identical. There are distinctions in detail eventually but these are superficial. Thus, we adopt the term “multi-item model” and use it throughout the paper.

In the traditional formulation of the joint-replenishment problem, a continuous-review multi-item inventory system is considered. Demands for the items are generated by independent Poisson processes. Excess demand is backlogged and replenishment requires a known and constant leadtime. There is a major ordering cost associated with a replenishment of the family. In the procurement context, this is the fixed cost of placing an order for the family of items, regardless of the size or composition of the order. On the other hand, for each individual item included in the replenishment, an item-specific ordering cost is also added. The objective is to minimize the long-run average cost per unit time.

In this paper, we consider the same problem for two items and model the underlying dynamics as a semi-Markov decision process. Restricting attention to only two items means that we can solve for the policy parameters without decomposing the problem and hence avoid the errors that decomposition might introduce. Indeed, our aim is to be able to quantify the errors introduced by the decomposition approach. Using numerical examples, we show that this error could be significant.

Ignall (1969) discovered, through numerical experiments, the optimal coordinated ordering policy, which minimizes the sum of ordering and inventory holding costs for a two-item inventory system under a lost sales scenario. The optimal policy obtained by Ignall (1969) is parameter specific and he could not offer a generalization of the solution. Nevertheless, his results show that the form of the optimal policy fails to have a simple form and motivated other researchers to restrict their attention to classes of policies which are simple and “implementable”.

The can-order policy as a simple coordinated control rule was introduced by Balintify (1964) and Silver (1974). This control rule is characterized by three parameters, reorder level s _j , can-order level c _j , and order-up-to level S _j for item j, with s _j ≤ c _j < S _j . An order is triggered by item j when its inventory position falls to or below the reorder level. In this situation, the inventory positions of other items are inspected. Any item for which the inventory position is at or below its can-order level, is also included in the order. As a result, the inventory positions of all items included in the order are raised up to their order-up-to levels. Silver (1974) seems to be the first author to suggest a heuristic for finding can-order policy parameters by decomposing the problem into many single-item problems with normal and special replenishment opportunities under the unit Poisson demands and positive leadtimes. Thompstone and Silver (1975) extend that approach to compound Poisson demand and zero leadtimes. Silver (1981) revisits the problem of finding can-order policy parameters and describes a procedure for non-zero leadtimes.

Federgruen et al. (1984) model the can-order policy as a semi-Markov decision problem with compound Poisson demands and positive leadtimes. Consideration of the dimensionality of the state space allowed Federgruen et al. (1984) to decompose the multi-item model into single-item problems. The underlying idea in this decomposition method is that the whole system is indeed some kind of a superposition of single items. When this decomposition method is used, one searches for solutions of the single-item model and then extends this solution, to the multi-item case. We also formulate the problem similarly but we argue that the decomposition approach may introduce substantial errors and hence by restricting attention to two items, we provide a formulation without decomposition.

At this juncture, by considering unit Poisson demand and assuming quasi-convex expected inventory holding and shortage costs, Zheng (1994) shows that the single-item can-order policy is optimal. However, the result has not yet been extended to multiple items. The decomposition method of Federgruen et al. (1984) results in a near-optimal solution.

Indeed using the decomposition method to determine the can-order policy, one has to assume two distinct and independent replenishment opportunities for each item. There is the opportunity created by the demand process of the item itself and also a special replenishment opportunity at a promoted fixed order cost. Federgruen et al. (1984) assume that these special replenishment opportunities also follow a Poisson process. This is only an approximation of the real scenario.

Atkins and Iyogun (1988) question the quality of the solutions found under the can-order policy for realistically sized problems. They refer to Ignall (1969) to highlight that can-order policies are not optimal; meanwhile they accept that the performance of these policies has been good on small problems. Furthermore, they introduce a new lower bound on the cost of the optimal policy as a comparison tool. They show that the “lower bound is a long way below the cost of can-order policy”. In order to answer the questions of whether the bound is weak and whether the can-order policy can be considerably improved, they propose two “periodic” replenishment policies which are fairly easy to implement in practice. Their various numerical experiments coincide with their expectations about the can-order policy. They are able to state that the performance of their modified periodic policy compared with the can-order policy improves as the major ordering cost increases. However, the can-order policy parameters they refer to, as found by the method of Federgruen et al. (1984), are already suboptimal among all possible can-order policy parameters.

Pantumsinchai (1992) suggests another simple continuous control policy, called the QS policy, for the same problem. When the group demand exceeds Q, inventory positions of all items are raised up to S. In a numerical study, in most of the cases this policy is shown to outperform the can-order policy whose parameters are computed by the method of Federgruen et al. (1984).

Schultz and Johansen (1999) focus once again on the can-order policy. They assume that special replenishment opportunities are not distributed according to a Poisson distribution but rather the discount opportunities are a superposition of the discount opportunity processes generated by all items except item j. They also reject the assumption that discount opportunities are independent of the behavior of item j. They approximate this lack of independence by using the discount process generated by all items as the process of potential discount opportunities for item i. Evidently, the special opportunities generated by item i itself are fictive while discount opportunities that item j generates for other items are real. Under these assumptions, they propose a decomposition approach to find the parameters of the can-order policy. Specifically they assume that the waiting times between epochs of replenishment are r-Erlang distributed. They use policy iteration supported by simulation to find the can-order policy parameters.

Their numerical results show that for large values of the major fixed cost, the Atkins-Iyogun algorithm (Atkins and Iyogun, 1988) performs better than all can-order algorithms. However, the can-order policy parameters they refer to are once again computed either via their proposed decomposition algorithm or the decomposition algorithm of Federgruen et al. (1984).

Van Eijs (1994) also points out that the algorithms to determine can-order policy parameters (up to 1994 and still) are only approximate and there are better can-order parameters that the current algorithms cannot converge to. He argues that when the major ordering cost is large, can-order policy parameters will be of the type (s, S−1, S) and develops a method to find the parameters s and S under this assumption. He shows that can-order policies are at least as good as other coordinated replenishment policies (namely those of Atkins and Iyogun (1988) and Pantumsinchai (1992)) under this setting.

In this paper, for the two-item stochastic joint replenishment problem we try to find a better can-order policy than those that are reported in the literature. We also formulate the problem as a semi-Markov decision process but we do not use decomposition. In the two-item inventory system, it is clear that a special replenishment opportunity for an item in fact corresponds to the demand epoch for the other item. If one does not use decomposition, the state space in the underlying semi-Markov decision process becomes large and policy iteration becomes more complex. However, by restricting attention to only two items the problem is still tractable. We use the two-item restriction and come up with a search algorithm (instead of policy iteration) to find better can-order policy parameters under unit Poisson demands and positive leadtimes. Using numerical examples we show that our approach consistently outperforms the heuristic approach of Federgruen et al. (1984). Particularly, as the major setup cost increases the difference in expected total cost increases in our favor. A downside of our approach is that we can only solve two-item problems. Although it comes as no surprise that there are better can-order policy parameters than those that are found by various heuristics suggested in the literature, the question “how much better?” is still open and a brief highlight is provided in this paper.

The rest of the paper is organized as follows. In Section 2 we present the elements of the semi-Markov decision process and the solution method we propose. In Section 3, we present numerical results in an experimental study and we conclude in Section 4.

2. Modeling

We consider a two-item inventory system. Demand for item 1 is generated by a Poisson process with rate λ and demand for item 2 is generated by a Poisson process with rate μ. The inventory is reviewed continuously. There exist non-negative constant leadtimes (L ₁ > 0 and L ₂ > 0). Holding costs, h _j > 0 and backorder costs, p _j ≥ 0 are incurred at rates proportional to inventory on hand just after a possible replenishment. Finally, π _j ≥ 0 are one-time-incurred fixed penalty costs for each unit not delivered immediately from the inventory.

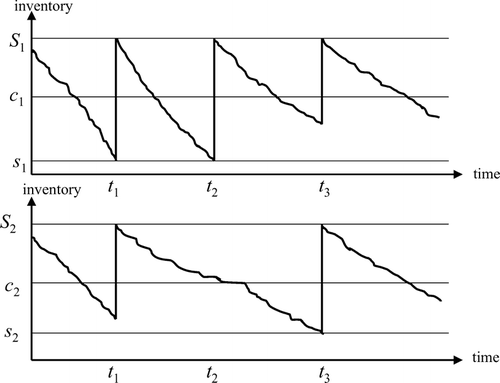
The can-order policy has three parameters (S _j ,c _j ,s _j ) for each item j. Whenever the inventory position (on hand plus in transit less backorders) of an item reaches its reorder level s _j it is ordered up to S _j at a fixed ordering cost of K > 0. During this normal replenishment opportunity, if the inventory position of another item j′ is below its can-order level, c _j′, this is a special replenishment opportunity for item j′ and it is also ordered up to S _j′ at a reduced ordering cost κ (0 ≤ κ ≤ K). Figure 1 shows a realization of the can-order policy for two items. As the system is not decomposed into two separate one-item inventory systems in this study, R = (R ₁,R ₂) denotes the can-order policy where R ₁ = (s ₁, c ₁, S ₁) and R ₂ = (s ₂, c ₂, S ₂). Note that in Fig. 1, t ₁ and t ₃ are regeneration points whereas t ₂ is not such a point.

Fig. 1 A realization of can-order policy for two-items: plot of inventory position against time.

The long-run average cost per unit time is taken as the performance measure for a given policy. For this criterion, elements of the semi-Markov decision model for the two-item joint replenishment problem are defined. Decision epochs are constituted by the demand epochs of the items. The state space is given by

Here (i ₁,i ₂) reflects the situation where a demand has just occurred leaving an inventory position of i ₁ units for item 1 and an inventory position of i ₂ units for item 2. At each decision epoch, a decision (k ₁,k ₂) is specified where (k ₁,k ₂) denotes the inventory positions of item 1 and item 2, respectively just after a possible replenishment. Note that as i ₁ and i ₂ correspond to the inventory positions for items where a demand has just occurred, the specification of the demand epoch is not important.

Since demands for items are Poisson and independent, the time between consecutive decision epochs are independent and exponentially distributed with mean (λ +μ)⁻¹. The next decision epoch is generated by a demand for item 1 with probability λ (λ +μ)⁻¹ or by a demand for item 2 with probability μ (λ +μ)⁻¹.

Let P _{(i 1,i 2)(k 1−1,k 2)}(k ₁,k ₂) be the one-step transition probability that starting at state (i ₁,i ₂), the decision (k ₁,k ₂) is specified which results in state (k ₁−1,k ₂). Similarly, P _{(i 1,i 2)(k 1,k 2−1)}(k ₁,k ₂) is the one-step transition probability that starting at state (i ₁,i ₂), the decision (k ₁,k ₂) is specified which results in state (k ₁,k ₂−1). These probabilities are given as follows:

The inventory system can be represented by a denumerable state semi-Markov decision model once the cost components are included. Let t _R (i ₁, i ₂) be the expected time until the next regeneration state if policy R is used when starting in state (i ₁, i ₂), and let k _R (i ₁, i ₂) be the total expected costs incurred until the first return to the regeneration state when starting in state (i ₁, i ₂) and using policy R. Finally, let g _R be the long-run average cost of using policy R. It is possible to use a control rule which may be quite complicated, for example, its actions may depend on the whole history of the system. However, without loss of generality, due to the memoryless property of exponentially distributed inter-arrival times (time between two successive demand epochs) and stationarity of problem parameters, we can restrict attention to stationary control rules which prescribe the same actions whenever the system is observed in state (i ₁,i ₂) at a decision epoch.

By fixing a stationary policy R, denote by X _n the state of the system at the nth decision epoch. Under policy R, the embedded stochastic process X _n is a discrete-time Markov chain with one-step transition probabilities P _{(i 1, i 2)(k 1−1, k 2)}(k ₁, k ₂) and P _{(i 1, i 2)(k 1, k 2−1)}(k ₁, k ₂).

Since excess demand is backlogged and leadtimes are constant, the inventory on hand for item j at any time t + L _j is distributed as the inventory position at time t minus the total demand during a period of length L _j . Letting {τ _n } be the sequence of the decision epochs, the inventory position just after τ _n determines the inventory on hand at time τ _n + L _j . Therefore, as in Federgruen et al. (1984), when choosing decision (k ₁, k ₂) at epoch τ _n , a fixed ordering costs of an order is charged along with c ₁(k ₁) and c ₂(k ₂) representing the expected holding and shortage costs incurred in [τ _n + L _j , τ _n+1+ L _j ].

Hence the one-step expected costs of items are

where δ (j) = 0 for j ≤ 0 and δ (j) = 1 for j ≥ 1.

To derive the one-step expected holding costs c _j (k _j ), j = 1,2, we note that the probability distribution of the total demand during the replenishment leadtime L is again the Poisson distribution which is given by {r(i), i ≥ 0}. Thus, c ₁(k ₁) can easily be computed from:

and c ₂(k ₂) can be computed similarly.

Remark 1. The cost function is a special case of the one given in Federgruen et al. (1984) for unit size demands. However, the recursive formula in that paper had a small error for k ₁ = 1 and k ₂ = 1, which is fixed here.

This completes the specification of the semi-Markov decision model. Now, we need to determine the expected costs of a given policy. For a can-order policy R, the average cost g _R has to be determined. The long-run average cost per unit time is equal to the expected total cost during one cycle divided by the expected length of one cycle by the renewal reward theorem:

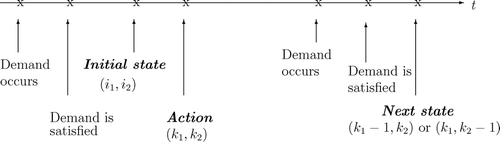
To determine these expectations, it is necessary to condition on the state of the system at the first decision epoch after time 0. This decision epoch is a demand epoch for item 1 with probability λ (λ+μ)⁻¹ and a demand epoch for item 2 with probability μ (λ+μ)⁻¹. The order of events is depicted in Fig. 2 in a general form. Note that the occurrence of the demand and the time at which the demand is satisfied are simultaneous. Thus, the state of the system (i ₁, i ₂), corresponds to the inventory position of items where a demand has just occurred (c.f. Equation (1)).

Fig. 2 Order of events.

Note that in the state where the inventory system makes the transition, the inventory position of item 1 and item 2 are compared to s ₁ and s ₂, respectively by a strict equality. As a matter of fact, when a demand occurs for an item, its inventory position cannot drop below its reorder level since the inventory system is monitored continuously and the inventory position decreases only by one unit due to Poisson demands.

Consider the case where the initial state is (s ₁+1,i ₂) with i ₂ > s ₂. As the action in that state is to do nothing, then with probability λ(λ+μ)⁻¹ the inventory position of item 1 drops by one unit and the next decision epoch is the decision epoch of item 1 (i.e., (s ₁,i ₂)). Evidently this state will not be a regeneration state if i ₂ > c ₂ in which case only an order is triggered for item 1. A symmetric argument is also valid for item 2 when the system starts at (i ₁,s ₂+1). Using these two arguments, the following two propositions are used to calculate the expected time and expected total cost until the next regeneration state.

Proposition 1.

Proof. Consider the case where i ₁ > s ₁ and i ₂ > s ₂. It clearly does not satisfy regeneration conditions and the decision is to make no replenishments. Hence it will take 1/(λ + μ) time units in expectation to the next decision epoch, which is a demand epoch for item 1 with probability λ (λ +μ)⁻¹ and a demand epoch for item 2 with probability μ (λ +μ)⁻¹. From that point on, the expected time it takes until the next regeneration state is conditioned upon the realized state ((i ₁− 1, i ₂)) or (i ₁, i ₂− 1) with the respective probabilities. The last two cases correspond to stopping conditions.

In Proposition 1, we have not specified the expected time until regeneration for states (s ₁, i ₂) [(i ₁, s ₂)] where i ₂ > c ₂ [i ₁ > c ₁]. At this state, the inventory position of item 1 [item 2] is raised up to S ₁ [S ₂] while the other item's inventory position does not change. With the specified time-line, we can safely assume that the system makes an immediate transition to the state (S ₁, i ₂) [(i ₁, S ₂)]. Therefore, we have:

The result of Equations (4), (5), (6) is a system of (S ₁−s ₁+1)(S ₂−s ₂+1) linear equations with (S ₁−s ₁+1)(S ₂−s ₂+1) unknowns and can be solved simultaneously by traditional methods of linear algebra.

The total expected cost incurred in a single regeneration cycle can be expressed as in the following:

Proposition 2.

Proof. The proof is similar to the previous one. If state (i ₁,i ₂) does not satisfy regeneration conditions, it will cost c ₁(i ₁)+c ₂(i ₂) until the next decision epoch and further costs are incurred based upon the realization of the next state. If the state satisfies regeneration conditions, then it will cost K+κ to order both items.

If item 1 [item 2] triggers a replenishment while item 2 [item 1] inventory is more than its can-order level c ₂ [c ₁], then only major ordering cost K is incurred and the system makes an immediate transition to the state (S ₁, i ₂) [(i ₁,S ₂)]: Therefore, we can write:

As a result of Equations (7), (8), (9), we also obtain (S ₁−s ₁+1)(S ₂−s ₂+1) simple linear equations with (S ₁−s ₁+1)(S ₂−s ₂+1) unknowns which are similar to the waiting time calculations. These two systems of linear equations are similar in nature and can be solved in the same way.

Therefore, for a given can-order policy, R, we can compute the long-run average expected cost g _R in a straightforward manner. We do not pursue a policy iteration approach in this paper mainly because we are not sure whether the policy iteration is going to converge to the best can-order policy. Instead, we propose an enumerative approach for all possible policies R.

Any generalization of our model to other demand functions lacking the memoryless property requires an increase in the dimension of the state space. We then need to keep track of the time spent since the last demand epoch for each item. This would rapidly increase the complexity of the problem. However, we can still extend our model to compound Poisson demands. First we redefine s _j as the inventory position of item j when it is at or below its reorder level. Furthermore, we have to modify the transition probabilities as follows:

where λ [μ] is the rate of the Poisson process which generates the demand epoch for item 1 [item 2], and r _j (n) is the discrete probability distribution of the non-negative random demand size for item j. With this argument, we can extend Propositions 1 and 2 which are fundamental to find the average cost of any policy. However, we will not further investigate this issue in this paper since we are not after a general method to find can-order policy parameters.

3. Computational results

We compare our results to those of Federgruen et al. (1984). We have coded their algorithm (hereafter referred to as the FGT algorithm) along with ours. As opposed to Federgruen et al. (1984), this paper does not propose a general algorithm to find the optimum can-order parameters. However, we do propose a direct enumeration algorithm (ENUM), which is shown in Fig. 3.

Fig. 3 Enumerative algorithm (ENUM) to find can-order policy variables.

This is a typical enumeration algorithm. For the search spaces of both items, the outer two loops are used for must-order (s _j ) and order-up-to levels, (S _j ), respectively. In the most inner loop, can-order level (c _j ) is processed from must-order level to order-up-to level minus one. In our numerical analysis we selected the bounds of the search which are a fixed percentage away from what Federgruen et al. (1984) calculate. The idea is to find whether there is a better can-order policy than the one the FGT algorithm has just found.

Thirty six experiments were conducted in this manner. In order to gain better insight about the behavior of the two algorithms when the problem parameters change, the experiment was conducted only on problems whose items have equal holding cost, leadtime and penalty cost π. The guidelines suggested by Pantumsinchai (1992) were followed in selecting the cost parameters. In all problems, μ = 1, h _j = 1, L _j = 2, π _j = 10, i = 1,2. The remaining three parameters p _j , major ordering cost K and λ were changed in three levels. The results are given in Table 1. Another set of experiments were performed by changing the minor ordering cost, κ, and these results are shown in Table 2.

Table 1 Experiment results (μ = 1, h _j = 1, L _j = 2, π _j = 10, i = 1,2)

Exp.	p 1	p 2	K	κ	λ	μ	FGT cost	FGT par.	ENUM cost	ENUM par.	% diff.
1	1	30	3	1	1	1	10.122	(2, 4, 6)	10.040	(2, 4, 6)	0.82
								(3, 5, 7)		(3, 5, 7)
2	1	30	3	1	3	1	13.971	(8, 11, 14)	13.860	(8, 11, 14)	0.81
								(3, 5, 7)		(3, 5, 7)
3	1	30	3	1	10	1	21.976	(26, 31, 36)	21.876	(26, 31, 36)	0.46
								(3, 5, 7)		(3, 4, 7)
4	1	30	10	1	1	1	12.583	(1, 5, 7)	12.225	(1, 5, 7)	2.92
								(3, 6, 8)		(3, 6, 8)
5	1	30	10	1	3	1	17.468	(7, 13, 16)	17.049	(7, 13, 16)	2.46
								(3, 6, 8)		(3, 6, 7)
6	1	30	10	1	10	1	27.805	(24, 36, 41)	27.217	(24, 36, 41)	2.16
								(3, 6, 8)		(2, 5, 7)
7	1	30	100	1	1	1	26.878	(0, 12, 14)	24.549	(0, 11, 12)	9.49
								(2, 14, 16)		(2, 12, 14)
8	1	30	100	1	3	1	37.621	(3, 27, 30)	34.394	(3, 26, 28)	9.38
								(2, 13, 15)		(2, 11, 12)
9	1	30	100	1	10	1	59.602	(20, 63, 68)	56.229	(20, 63, 67)	6.00
								(1, 11, 13)		(1, 8, 10)
10	10	30	3	1	1	1	10.463	(3, 4, 6)	10.395	(3, 4, 6)	0.65
								(3, 5, 7)		(3, 5, 7)
11	10	30	3	1	3	1	14.354	(8, 11, 14)	14.253	(9, 11, 14)	0.71
								(3, 5, 7)		(3, 5, 7)
12	10	30	3	1	10	1	22.290	(26, 31, 36)	22.185	(26, 31, 36)	0.47
								(3, 5, 7)		(3, 4, 7)
13	10	30	10	1	1	1	13.019	(2, 6, 8)	12.681	(2, 6, 7)	2.66
								(3, 6, 8)		(3, 6, 8)
14	10	30	10	1	3	1	17.925	(8, 14, 17)	17.504	(8, 14, 16)	2.40
								(3, 6, 8)		(3, 6, 7)
15	10	30	10	1	10	1	28.230	(25, 37, 42)	27.555	(25, 37, 41)	2.45
								(2, 6, 8)		(2, 5, 7)
16	10	30	100	1	1	1	27.693	(1, 13, 15)	25.321	(1, 12, 13)	9.37
								(2, 14, 16)		(2, 12, 14)
17	10	30	100	1	3	1	38.411	(5, 28, 31)	35.196	(5, 27, 29)	9.13
								(2, 13, 15)		(2, 11, 12)
18	10	30	100	1	10	1	60.182	(21, 63, 68)	56.834	(21, 63, 68)	5.89
								(1, 11, 13)		(1, 8, 10)
19	100	30	3	1	1	1	11.613	(4, 6, 8)	11.531	(4, 5, 7)	0.71
								(3, 5, 7)		(3, 5, 7)
20	100	30	3	1	3	1	15.681	(10, 13, 16)	15.571	(10, 13, 16)	0.71
								(3, 5, 7)		(3, 5, 7)
21	100	30	3	1	10	1	23.891	(28, 33, 38)	23.788	(28, 33, 38)	0.43
								(3, 5, 7)		(3, 4, 7)
22	100	30	10	1	1	1	14.155	(4, 7, 9)	13.862	(4, 7, 9)	2.11
								(3, 6, 8)		(3, 6, 8)
23	100	30	10	1	3	1	19.410	(10, 15, 18)	19.005	(10, 15, 18)	2.13
								(3, 6, 8)		(3, 6, 7)
24	100	30	10	1	10	1	29.976	(27, 38, 43)	29.335	(27, 38, 43)	2.19
								(2, 6, 8)		(2, 5, 7)
25	100	30	100	1	1	1	29.292	(3, 15, 17)	26.850	(3, 13, 15)	9.10
								(2, 14, 16)		(2, 13, 14)
26	100	30	100	1	3	1	40.445	(8, 30, 33)	37.101	(8, 29, 31)	9.01
								(1, 13, 15)		(1, 10, 12)
27	100	30	100	1	10	1	62.587	(25, 66, 71)	59.234	(25, 66, 70)	5.66
								(1, 11, 13)		(1, 8, 10)

Table 2 Experiment results (μ = 1, h _j = 1, L _j = 2, π _j = 10, i = 1,2)

Exp.	p 1	p 2	K	κ	λ	μ	FGT cost	FGT par.	ENUM cost	ENUM par.	% diff.
28	1	30	100	10	1	1	27.459	(0, 9, 14)	25.406	(0, 10, 13)	8.08
								(2, 11, 16)		(2, 11, 15)
29	1	30	100	10	3	1	38.331	(3, 22, 30)	35.547	(3, 22, 29)	7.83
								(2, 10, 15)		(2, 9, 12)
30	1	30	100	10	10	1	60.702	(20, 53, 68)	58.040	(20, 55, 68)	4.59
								(1, 9, 14)		(1, 7, 11)
31	10	30	100	10	1	1	28.268	(1, 10, 15)	26.199	(1, 10, 14)	7.89
								(2, 11, 16)		(2, 11, 15)
32	10	30	100	10	3	1	39.124	(5, 23, 31)	36.362	(5, 23, 30)	7.60
								(2, 10, 15)		(1, 9, 12)
33	10	30	100	10	10	1	61.322	(21, 54, 69)	58.654	(21, 55, 69)	4.55
								(1, 9, 14)		(1, 7, 11)
34	100	30	100	10	1	1	29.823	(3, 12, 17)	27.736	(3, 11, 15)	7.52
								(2, 11, 16)		(2, 11, 14)
35	100	30	100	10	3	1	41.145	(8, 25, 33)	38.283	(8, 25, 32)	7.48
								(1, 10, 15)		(1, 9, 12)
36	100	30	100	10	10	1	63.698	(25, 56, 71)	61.075	(25, 58, 71)	4.29
								(1, 9, 14)		(1, 7, 11)
FGT cost = optimal cost of FGT.
FGT par. = can-order policy parameters for FGT (upper one is for item 1 and the lower one is for item 2).
ENUM cost = optimal cost of ENUM.
ENUM par = can-order policy parameters for ENUM (upper one is for item 1 and the lower one is for item 2).
% diff. = percentage difference between FGT cost and ENUM cost.

We observe that ENUM consistently performs better than the FGT algorithm and the percentage difference varies from 1 to 10%. Indeed these differences can be grouped into three classes: 1, 2.5 and 9%. Further analysis reveals that these groups correspond to different levels of major ordering cost K: three, ten and 100, respectively. As the major ordering cost K increases, the difference increases significantly. This is due to the decomposition assumption used in Federgruen et al. (1984). As has been already noted in the literature, when K is large the probability of a special replenishment opportunity will be low at the start and high at the end of a cycle which contradicts the Poisson arrivals assumption (Pantumsinchai, 1992, p. 292). However, in our numerical studies, even when the major-ordering-cost to minor-ordering-cost ratio is as high as 100 we did not encounter any (s, S−1, S) policy that yields the best cost as Van Eijs (1994) would lead us to believe.

With respect to changes in penalty cost p ₁ and λ parameters, the difference between the two models is relatively minor. However, it seems that the gap closes slightly as the demand for item 1, λ, increases.

For the experiments reported in Table 1, the minor ordering cost is somewhat comparable to other parameters. The question arises of what happens if the minor ordering cost increases with respect to other parameters? Results shown in Table 2 attempt to answer this question. The ratio of κ/K is the same as in experiments 4–6, 13–15 and 22–24, where the average cost difference between the two algorithms is 3%. For experiments 28–36 the difference increases suddenly to 7% on the average. This implies that if order cost parameters are relatively higher than other parameters, then the results obtained using the FGT algorithm become significantly worse.

Another important point worth noting is that even if the FGT algorithm finds the same policy parameters as ENUM, its average cost may differ significantly to what ENUM finds! The experiments 1, 2, 4, 10, 20 and 22 in Table 1 reveal this fact. The difference can be as high as 3%. This is another drawback of the decomposition principle employed in that paper. This may be the reason for the difference in simulated costs and computed costs stated frequently in the literature about FGT's performance (Pantumsinchai, 1992; Van Eijs, 1994; Schultz and Johansen, 1999).

4. Conclusions

In this paper, a two-item inventory system with coordinated replenishment is modeled as a semi-Markov decision model and controlled by the can-order policy. The main objective here is to describe the system without decomposing it into two single-item inventory systems. Since the dimension of the state space is larger than the single-item inventory problem, the operating characteristics necessary to search for a rule that minimizes the long-run average cost per unit time are considerably more complicated than the decomposition approach.

The two-item problem is solved using an enumerative approach to investigate the best solution in the class of can-order policies. It is shown that the policy iteration algorithm of Federgruen et al. (1984) does not always converge to the best can-order policy. Furthermore, even if it does, it overestimates the cost of the policy. The cost difference can be as high as 10% in this two-item setting. The difference is likely to increase with a higher number of items.

Therefore, more research is justified to find the best parameters for the can-order policy.

Biographies

Enis Kayış received his B.S. in IE and B.A. in Mathematics degrees from Boğaziçi University in 2002. He is now a Ph.D. candidate at Stanford University's Management Science and Engineering Department.

Taner Bilgiç received his B.S. and M.S. degrees from Middle East Technical University in 1987 and 1990, respectively. He completed his Ph.D. at the University of Toronto in 1995 and worked as a Research Associate in the same university before joining Boğaziçi University in 1997.

Deniz Karabulut received her M.S. in IE from Boğaziçi University in 2000. She is currently working for Arçelik in Istanbul.

Acknowledgement

This research is supported by Boğaziçi University Research Project 01A302.