Approximate mean waiting time in a GI/D/1 queue with autocorrelated times to failures

Abstract

In this paper, we study process completion time and propose an accurate approximation for the mean waiting time in queues with servers experiencing autocorrelated times to failure, which include only busy periods from a repair completion until the next failure. To do this, we employ a three-parameter renewal approximation that represents the stream of autocorrelated times to failure. The approximation gives rise to a renewal interruption process with two-state Hyper-exponential (H2) times to failure. Then we compute the mean waiting time exactly in a queue experiencing H2 times to failure when the job arrival process is Poisson. This model provides an approximation for the mean waiting time of the original queue having an autocorrelated disruption process. We also propose an accurate approximation for queues with renewal job arrival processes when the server interruption process is general.

Keywords:

• Autocorrelation
• GI/D/1 queues with unreliable server
• mean waiting time
• process completion time

1. Introduction

The random phenomena that are observed in manufacturing systems are due to random processing times, and/or random machine failures/interruptions followed by random repair times. This randomness is the main cause of variability in manufacturing systems to which down time is a major contributor. The general approach to the analysis of the impact of machine failures on system performance involves the assumption of a constant processing time along with random interruptions and repair times. In the literature, these problems (traditionally known as machine interference problems) have received considerable attention (Dallery and Gershwin, 1992), and a queueing approach has been widely used in their analysis. In most of the published studies, the random components in manufacturing systems are assumed to be independent and identically distributed (i.i.d). However, it is not uncommon to experience stoppages with many short times to failure followed by a long time to failure, indicating positively autocorrelated time-to-failure, that is the period between the completion of a repair and the next failure occurrence excluding those periods when the server is operational yet idle. In this case, positive autocorrelation is mainly due to frequent short times to failure. The system can experience a superposition of independent time-to-failure streams originating from different sources. For example, pharmaceutical packaging lines have components (i.e., filler, cartoner, and labeler) failing independently, and stopping the line. It is well known in the literature that the superposition of independent streams is not a renewal process (Whitt, 1983; Albin, 1984; Balcıo[gtilde]lu et al., 2005). By the same token, repair times can have similar patterns as well. As indicated by Altıok and Melamed (2001), when such correlations exist in the system, ignoring them may result in serious errors in performance estimation. We refer the reader to their work for examples of autocorrelated interruption processes in real scenarios. Furthermore, even though current research in reliability assumes that a repaired system does not return to as-good-as-new condition (implying there is dependence in the failure process), analyses involving autocorrelation functions have not been employed (see Jardine and Tsang (2006, pp. 69–70)).

The existing literature on machine interference problems generally assumes i.i.d. exponential times to failure. White and Christie (1958) showed the relationship between queues with high-priority customers pre-empting low-priority customers and the server failures. While they assumed repair times to be exponential, Thiruvengadam (1963) proceeded to generalize the same model incorporating general i.i.d. service and repair times. Mitrany and Avi-Itzhak (1968) extended the analysis to the multi-server M/M/N queue by assuming that the repair process would start immediately upon a failure. This model was later revisited by Neuts and Lucantoni (1979) who considered that c crew members would carry out the repair process. Sztrik and Gál (1990) studied a computer system with multiple servers and designed a recursive algorithm to obtain system performance measures. Gray et al. (2004) considered an M/PH/1 queue, where the server consists of M modules, each of which has a finite number of components subject to random failures. These papers approach the problem from a queueing perspective and the performance measures of interest are the waiting time distributions, the mean waiting time and, in the multi-server cases, the mean number of functional/busy servers.

The machine interference problem has also been analyzed from a reliability engineering perspective. Tang (1997) analyzed an M/G/1 queue in which the up times are exponential random variables when the server is busy and renewal random variables when it is idle. Li et al. (1997) assumed exponential up times and incorporated Bernoulli vacations after each service completion. Wang et al. (2001) modeled the M/G/1 queue as a retrial queue and assumed that arrivals seeing the server either busy or down would return to the system until they were served. Sherman and Kharoufeh (2006), on the other hand, considered that customers interrupted while being serviced make retrials until the server is operational. Unlike the majority of problems that assume Poisson job arrivals, Xueming and Li (2003) assumed renewal job arrivals and used a matrix-analytic approach for a GI/PH/1 queue with the up and down times being modeled as phase-type random variables. In this second group of papers, the performance measures of interest are the system reliability, availability, expected number of failures and repairs over a given time period.

As can be seen from the literature, general times to failure have received little attention in queueing models. However, the impact of autocorrelated interarrival and service time streams on the performance of high-speed integrated telecommunication networks has been demonstrated by Fendick et al. (1989). Also Livny et al. (1993) showed that positive lag-1 autocorrelation in the service process leads to an increased mean waiting time. More recently, Altıok and Melamed (2001) simulated an M/G/1 workstation with a deterministic processing time and autocorrelated times to failure. They demonstrated that the existence of a dependence on the times to failure dramatically degrades the performance measures of interest, such as flow times, customer service levels, and finished product levels. Thus, models ignoring autocorrelation (should it exist) in the underlying stochastic processes often poorly approximate the behavior of real systems.

In this paper, we focus on autocorrelated times to failure at a work station with general repair times, and Poisson subsequently, general job arrival processes. We propose to approximate a positively autocorrelated interruption process by a three-parameter renewal process. These parameters summarize the important statistics concerning the autocorrelation information, and help the approximating renewal process represent the original process with some degree of accuracy. This technique was first proposed by Jagerman et al. (2004) in approximating a single-source autocorrelated arrival process offered to workstations having i.i.d. service times following general distributions. This approach was extended by Balcıo[gtilde]lu et al. (2005) so as to be able to handle the superposition and splitting of autocorrelated arrival processes. In this paper, we will assume that the i.i.d. interarrival times of jobs arriving at the workstation are drawn from a general distribution. Hence, we will observe the extent to which the proposed approximation captures the impact of autocorrelation in the interruption process on the mean time a job spends in the queue.

The approximating renewal times to failure will enable us to carry out a process completion time analysis, first proposed by Gaver (1962) and Avi-Itzhak and Naor (1963). The process completion time is defined as the total time a job spends on a machine until its process is completed. During this time, the machine may experience stoppages. This approach allows us to incorporate failures into the process completion time and eliminate them from the analysis. This can make the analysis more tractable in many scenarios. The majority of the existing literature on the process completion time assumes exponential times to failure, (with possibly general i.i.d. processing and repair times) even though this may not reflect the actual behavior of many real scenarios. This compromise, at the cost of possibly having inaccurate predictions about the system, has been made due to analytical tractability, whereas incorporating general i.i.d. times to failure was considerably difficult.

Federgruen and Green (1986, 1988) provided two prominent models with general i.i.d. times to failure in single-server queueing systems with Poisson job arrivals. Federgruen and Green (1986) derived approximations for the mean waiting time, the probability of delay and the steady-state distribution of the number of jobs in the system for general i.i.d. times to failure. Federgruen and Green (1988) proceeded to provide the exact solution for this system when the times to failure follow a phase-type distribution. Since the renewal approximation we use yields a 2-state Hyper-exponential (H2) random variable, we propose an alternative model to obtain the steady-state distribution of the number of jobs in the queue. Federgruen and Green (1988) considered repair time distributions that are closed under convolutions such as Normal and Gamma. The approach we use accommodates more general repair time distributions.

We propose an approximating renewal service time distribution, that is a function of the server utilization, which is used to accurately capture the mean waiting time in queueing systems with renewal job arrival streams. The contributions of this paper may be summarized as follows: (i) the use of a renewal approximation to model autocorrelated times to failure data and using it in a queueing setting to obtain the mean waiting time; and (ii) the modeling of queues with general times to failure with general repair times when jobs arrive according to a general renewal process. The problem we study with our approach addressing autocorrelation in the process completion time sequence further provides insight on the case with general autocorrelated service times.

The remainder of this paper is organized as follows. In Section 2, queueing systems experiencing autocorrelated times to failure with Poisson job arrivals are investigated. Modeling the time to failure with an approximating H2 random variable, we obtain the steady-state distribution of the queue length process. The corresponding numerical examples are provided in Section 3. In Section 4, on the other hand, we propose an approximate analysis of systems receiving general independent arrival processes. In doing this, we propose an approximating renewal service time distribution, which is a function of the server utilization. Section 5 includes numerical examples showing the accuracy of the approximation proposed in Section 4. We conclude in Section 6.

2. The M/D/1 case

In this section, we consider a single-server queueing system receiving Poisson job arrivals with rate λ and fixed processing time x. The server encounters interruptions with autocorrelated times to failure provided that it has jobs. It stays out of service throughout the repair time that starts immediately after a failure. Repair times are assumed to be i.i.d. random variables that are independent of the failure process with general distributions with a density function f _D(d). We assume that the server can fail only while it is busy and that it resumes operation from the point of interruption once a repair is completed. Our objective is to compute the mean waiting time in the M/D/1 queue with an unreliable server experiencing autocorrelated times to failure. This analysis consists of two stages:

1.	Approximating the autocorrelated times to failure stream by a renewal process with H2 times to failure as summarized in Section 2.1.
2.	Computing the exact mean waiting times in the M/D/1 queue with an unreliable server experiencing H2 times to failure as presented in Section 2.2. Note that the parameters of the H2 random variable are obtained at the first step. The mean waiting time computed at this step provides an approximation for the original queue with the autocorrelated interruption process.

2.1. Renewal approximation

We will start our analysis by first constructing a renewal process approximation of the autocorrelated interruption process. This can be achieved by estimating three parameters, γ _X , A _E , α _E , after analyzing the autocorrelated times to failure data in line with Jagerman et al. (2004) and Balcıo[gtilde]lu et al. (2005). The three-parameter renewal approximation is designed for a second-order stationary or weakly stationary process, X = {X _n } _{n = 0} ^∞, where X _n denotes the time between the nth and (n−1)st event occurrences. In other words, the finite mean m _X and the finite variance σ _X ² = Var[X _n ] of X are the same for all n, and the autocorrelation function between X _k and X _k+j , ρ _X (j) = (E[X _k X _k+j ] − m _X ²)/σ _X ²,     j = 0,1,… does not depend on k but j. X is assumed to be nonlattice.

In our problem, X is the autocorrelated stream of times to failure, in which X _n is the period between the completion of the nth repair and the next failure occurrence excluding those periods when the server is operational yet idle. The three-parameter renewal approximation results in a renewal failure rate equal to that of the autocorrelated stream, namely the parameter γ _X . In other words, in the approximating renewal process, the mean time to failure equals the mean autocorrelated times to failure. The parameter A _E captures the squared coefficient of variation, c _X ² = σ _X ²/m _X ², and the sum of all autocorrelation function coefficients as

The parameter α _E , on the other hand, captures the behavior of the original stream in the transient period (Balcıo[gtilde]lu et al., 2005). As shown by Jagerman et al. (2004), the approximating renewal times to failure will have a squared coefficient of variation, c _R ²:

Since we focus on bursty interruption processes due to positive autocorrelation at all lags, A _E turns out to be non-negative, resulting in a c _R ² > 1. This lets us express the renewal times to failure random variable as an H2 random variable with parameters p, γ₁, γ₂. Note that H2 distributions are extensively used to approximate distributions, whose squared coefficient of variation exceeds unit. An H2 (p, γ₁, γ₂) random variable is an exponential random variable with parameter γ₁ (γ₂) with probability p (1−p) (Kleinrock, 1975, p. 141; Altıok, 1997, pp. 46–47). Denoting its density function by g _R (t), the Laplace transform _R(s) = ∫₀ ^∞ e ^−st g _R(t)dt of an H2 random variable is

with its parameters expressed in terms of γ _X , A _E , and α _E being:

In the next section we use the H2 random variable defined above to model the times to failure in an M/D/1 queue.

2.2. The M/D/1 queue with H2 times to failure

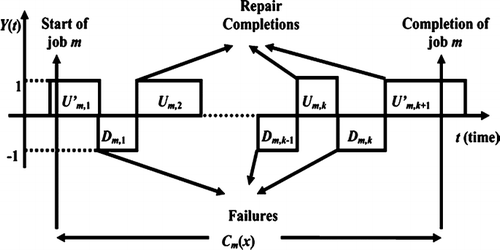
In this section, we present an exact analysis to obtain the mean waiting time in an M/D/1 queue experiencing H2 times to failure followed by general i.i.d. repair times. Let us define the Process Completion Time (PCT), C _m (x), as the total time the mth job spends on the server, possibly augmented by down times due to failures. We assume that as m→ ∞, C _m (x) converges to a random variable C(x) whose distribution is given by B(t,x)≡ P(C(x) ≤ t), where x denotes the constant processing time.

Let Y(t) denote the status of the server at time t so that:

Hence, the model will be an alternating stochastic process of the machine's up and down times, which stops when the processing of a job is completed. In this framework, the stopping rule is that the sum of the up times is equal to the processing time, x. Let K _m be the number of failures that occur during the processing time of the mth job. If K _m = k, then customer m's completion time occurs during the (k+1)st up time of the process {Y(t):t ≥ 0}. Letting D _m,i denote the duration of the ith repair time during customer m's service we note that {D _m,i :i ≥ 1} is an i.i.d. sequence of random variables with density function f _D(·). The first up time, U _m,1′, is any time leftover from the last up time of the previous job, and U _m,k+1′ is the portion of the (k+1)st up time to be spent on the current job to complete the process. Therefore, the process will be completed for the mth job when the following condition is satisfied as shown in Fig. 1:

Fig. 1 The process completion random variable, C _m (x).

When a general i.i.d. random variable models the interruption process or there exists autocorrelation in the times to failure stream, the PCTs will become autocorrelated since the first up time of each job depends on the last up time of the previous job. This is the very reason why the PCT analysis becomes more difficult when the times to failure are not i.i.d. exponential random variables.

In our model, an H2 random variable governs the times to failure, which implies that during any up time the failure process is in either of the states i,j = 1,2. During idle times, the failure process stays in the same phase of the H2 random variable until a new job arrives and initiates service. Therefore, we can use a semi-Markov approach, since the state transitions are imbedded in service completions, i.e., departure instants.

To compute the mean waiting time in the queue, we need to compute the steady-state probability of having n customers in the queue and failure process in state i, namely, π _i (n). It is clear that π(n) = π₁(n)+π₂(n) gives the steady-state probability of having n customers in the queue since Poisson arrivals see the time averages (the PASTA property).

Computing π _i (n) requires the transition probability of the queue length process, p _i,j (n), i.e., the probability of having n arrivals during the PCT of a job, if the failure process ends in state j given that it started in state i. To this end, we make use of q _i,j (k,x) defined as the conditional probability that k failures occur during the processing time x and the failure process ends in state j, given that it was in state i when the job seized machine, i,j = 1,2 and k = 0,1,2,…. Additionally, we introduce an intermediate probability, p(k,n), which is the probability of having n job arrivals when k failures are observed during processing time x. Hence,

where q _i,j (k,x) rapidly tends to zero as k increases.

Let t _m be the time of the mth departure from the system. Letting Z(t) be the number of jobs in the queue at time t, we further define N _m ≡ Z(t _m ⁺). Furthermore, S _m is the state of the failure process at the mth departure such that S _m ∈ {1,2} for all m. Then, the Discrete-Time Markov Chain (DTMC) of interest is {(S _m , N _m ):m ≥ 1}, which is completely characterized by the initial probability vector of having n customers in the queue while the failure process is in state i at time 0 ( Π ⁰) and the transition probability matrix P, which can be truncated at a sufficiently large K value (guaranteed to exist for systems with ρ = λ E[C(x)] < 1 where E[C(x)] is the mean PCT). Let Π = [π₁(0), π₂(0),…,π₁(K),π₂(K)] ^T be the 2(K+1) × 1 vector of steady-state probabilities π _i (n) of having n customers in the queue while the failure process is in state i as observed by a departing customer. Hence, the 2(K+1) × 2(K+1) transition probability matrix, P, of the DTMC is given by

If 2(K+1) × 1 Π ⁰ denotes the initial probability vector of having n customers in the queue while the failure process is in state i at time 0 (which can be assumed to be Π ⁰ = [p, 1−p,0,…,0,0] ^T , since the choice does not have an impact on Π ), we have:

subject to

hence, π(n) = π₁(n)+π₂(n), from which the mean number of customers in the queue, and via Little's formula, the mean waiting time can be computed easily. For computational purposes, matrix multiplication of P is performed a sufficient number of times. In the numerical examples we considered, K = 100 and N = 2000 were more than sufficient.

Federgruen and Green (1988) use matrix calculations to compute q _i,j (k,x), and then express p _i,j (n) in terms of infinite sums to avoid numerical integration. Finally, they employ an aggregation/disaggregation procedure to obtain π _i (n), which is reported to be time consuming for certain types of problems. When it comes to general repair times, they only consider those distributions, which are closed under convolutions such as Normal and Gamma. This requires that the sum of k repair times during a processing time maintains the original repair time distribution. This is quite a limitation under the assumption of general repair times. The approach we used accommodates general repair times.

In this paper, we propose an alternative technique to compute q _i,j (k,x), p _i,j (n) and π _i (n). First of all, it is easy to check that:

and for k > 0

It appears to be difficult to obtain q _i,j (k,x) using Equation (8). We suggest using their Laplace transforms, which can be numerically inverted to arrive at q _i,j (k,x). The Laplace transforms of interest are

and for k > 0

where _R(s) is given in Equation (2). We numerically invert Equations (9) and (10) using the technique proposed by Jagerman (1982) and compute q _i,j (k,x).

Now we are ready to compute p(k,n), which is the probability of having n Poisson arrivals when k failures happen during processing time x. Let D ^k define the total length of k repair times the machine undergoes while servicing a job if k failures are observed. Then C(x,k) = x+D ^k will be the total time (effective service time) a job spends on the machine. Let B(t,x,k)≡ P(C(x,k) ≤ t) denote the distribution function of C(x,k) and denote its Laplace-Stieltjes transform with (s,x,k) as

where _D(s) is the Laplace transform of the down/repair time density function. Then p(k,n) is given by

If v denotes the number of arrivals during C(x,k), its z-transform, namely V(z) = ∑ _{n = 0} ^∞ P[v = n]z ⁿ , can be expressed in terms of (s,x,k) (Kleinrock, 1975, p. 184):

Since (Kleinrock, 1975, p. 336):

where i = √−1, using the fact that the path is a circle around the origin given by z = re ^iθ,r < 1, the contour integral given in Equation (14) is prepared for quadrature as follows:

The integrand in Equation (15) is an analytic function and it returns back to its initial value around a circle. Hence, the trapezoidal rule is particularly accurate in the numerical inversion of the z-transform to obtain p(k, n) (Davis and Rabinowitz, 1967, p. 92):

where h = 2π/L, 0 < r < 1, a number in the unit circle, and L a sufficiently large number. Once this is done π _i (n), the steady-state probability of having n customers in the queue and failure process in state i, can be found via Equation (6).

For the case involving i.i.d. exponential times to failure (named TES⁺ A in the numerical examples), one can alternatively use (s,x), which is (Altıok, 1997, p. 94):

and computing the first and second moments, E[C(x)],E[C(x)²] of the process completion time random variable, employ the P-K formula, which is

3. Numerical examples: Poisson job arrivals

In order to assess the efficacy of the proposed method, we have used a simple Transform-Expand-Sample (TES⁺) process and also a Markov-Modulated Poisson Process (MMPP) to model autocorrelated times to failure.

The TES⁺ processes considered here have marginal exponential distributions characterized by a parameter triplet (L,R,γ _X ) (Jagerman and Melamed, 1992a, 1992b). While γ _X is the rate of the exponentially distributed times to failure, [L,R) subject to −0.5 ≤ L ≤ R < 0.5, is the support interval. The decrease in the length of the support interval induces more positive autocorrelation in the interruption process (Melamed, 1993). In particular, the lag-1 autocorrelation, ρ _X (1), of the times to failure ranges from zero (for L = −0.5 and R = 0.5) to one (for L = R = 0) (Melamed, 1991).

We have generated the following TES⁺ failure processes and estimated their respective parameters γ _X , A _E , and α _E employing the techniques due to Jagerman et al. (2004) and Balcıo[gtilde]lu et al. (2005) (or equivalently p,γ₁, γ₂ via Equation (3)) as summarized in Section 2.1.

•	TES+ A: γ X = 0.8, L = −0.5,R = 0.5 which is the stream of i.i.d exponential times to failure with rate γ X = 0.8.
•	TES+ B: γ X = 0.8, L = −0.2,R = 0.2 which is approximated by γ X = 0.8; ρ X (1) = 0.32, and A E = 1.2849 and α E = 0.54, or equivalently using Equation (3) we have p = 0.807 31, γ1 = 1.792 89, γ2 = 0.240 95.
•	TES+ C: γ X = 0.8, L = −0.11,R = 0.11 which is approximated by γ X = 0.8, ρ X (1) = 0.51, and A E = 5.2103 and α E = 0.17, or equivalently p = 0.945 05, γ1 = 1.779 32, γ2 = 0.076 43.
•	TES+ D: γ X = 0.8, L = −0.05,R = 0.05 which is approximated by γ X = 0.8, ρ X (1) = 0.69, and A E = 27.181 and α E = 0.036, or equivalently p = 0.988 79, γ1 = 1.7985, γ2 = 0.016 01.

Using the same autocorrelated interruption process, we also generated test cases via simulation to compute the reference mean waiting time values. Here, we have chosen the job arrival rate λ to have a server utilization of ρ = 0.8, while the processing time is x = 5, and the failure rate is γ _X = 0.8. The simulation model is in essence a single server queue. The failure process is modeled by a single high-priority customer that pre-empts the job in process for the duration of the repair time. Each time a repair is over, the next time to failure (time for the high-priority customer to pre-empt) is generated from a TES⁺ process as outlined by Jagerman and Melamed (1992a, 1992b). The idle periods are inserted into the times to failure appropriately. Each run had five replications with each replication taking 2000 000 time units. Then using the approximating H2 times to failure, we obtained the analytical results for the mean waiting time as discussed in Section 2.2 and compared with its reference counterpart from the simulation.

In Table 1, Table 2, Table 3, the first column displays the TES⁺ process used as the autocorrelated interruption process. In column 2, we present the lag-1 autocorrelation function of the process completion time random variable, ρ _C(x)(1), also found from simulation. Column 3 lists the mean waiting times estimated from simulation with their 95% confidence intervals given beneath each. Finally, in the last column we present our analytical approach with its approximation error. A comparison of the approximation method to the reference values obtained by simulation reveals the following facts.

1.	Higher positive autocorrelation levels in the times to failure process induces more positive autocorrelation in the PCT.
2.	Table 1 displays the results obtained when the repair times are drawn from a Uniform(0.5, 1) distribution yielding an overall 30% system down time probability. This table shows the impact of positive autocorrelation most dramatically. The mean waiting time increases by 125% from the i.i.d exponential times to failures case (TES+ A) to the most positively autocorrelated case (TES+ D). The renewal approximation performs consistently well in predicting the mean waiting times of the original problem.
3.	Table 2 displays the results obtained when the repair times are drawn from a Uniform(0.34, 0.5) distribution yielding an overall 20% system down time probability. The mean waiting time increases by 54% from the i.i.d exponential times to failures case (TES+ A) to the most positively autocorrelated case (TES+ D). The renewal approximation performs consistently well in predicting the mean waiting times of the original problem.
4.	Table 3 displays the results obtained when the repair times are drawn from a Uniform(0.1, 0.26) distribution yielding an overall 10% system down time probability. This table shows the cases where the impact of autocorrelation is reduced. Yet, the mean waiting time increases by 13% from the i.i.d exponential times to failures case (TES+ A) to the most positively autocorrelated case (TES+ D). The renewal approximation performs consistently well in predicting the mean waiting times of the original problem.

Table 1 Mean waiting times in M/D/1 systems with λ = 0.1, a TES⁺ times to failure process and f _D(d) = Uniform(0.5, 1), with d ₁ = 0.75, d ₂ = 0.5833, and a 30% down time

TES^+	ρ C(x) (1)	Simulation	Approximation
A	0.00	16.15	16.58
		(+/− 0.62)	(2.68%)
B	0.24	17.86	17.93
		(+/− 0.1)	(0.38%)
C	0.45	21.17	21.46
		(+/− 0.13)	(1.38%)
D	0.62	36.63	36.91
		(+/− 0.78)	(0.76%)

Table 2 Mean waiting times in M/D/1 systems with λ = 0.119 76, a TES⁺ times to failure process and f _D(d) = Uniform(0.34, 0.5), with d ₁ = 0.42, d ₂ = 0.178 54, and a 20% down time

TES^+	ρ C(x)(1)	Simulation	Approximation
A	0.00	13.576	13.575
		(+/− 0.393)	(−0.01%)
B	0.24	14.12	14.08
		(+/− 0.03)	(−0.27%)
C	0.45	15.25	15.39
		(+/− 0.08)	(0.92%)
D	0.62	20.48	20.71
		(+/− 0.11)	(1.12%)

Table 3 Mean waiting times in M/D/1 systems with λ = 0.1399, a TES⁺ times to failure process and f _D(d) = Uniform(0.1, 0.26), with d ₁ = 0.18, d ₂ = 0.034 54, and a 10% down time

TES^+	ρ C(x)(1)	Simulation	Approximation
A	0.00	11.378	11.493
		(+/− 0.284)	(1.01%)
B	0.24	11.58	11.61
		(+/− 0.06)	(0.27%)
C	0.44	11.83	11.89
		(+/− 0.04)	(0.52%)
D	0.61	12.82	12.94
		(+/− 0.06)	(0.92%)

In order to assess the performance of our analytical model, we have also considered MMPPs to induce different positive autocorrelation structures in the failure process (we refer the reader to Fischer and Meier-Hellstern (1992) for a thorough investigation of the MMPP).

An m-state MMPP is a doubly stochastic Poisson process whose arrival rate at a certain time t depends on the state of an m-state modulating Markov process. It is defined by an m × m infinitesimal generator Q of the underlying process and an m × m diagonal matrix Λ with diagonal elements λ _i , i = 1,…,m. When the modulating Markov chain is in state i, arrivals will follow a Poisson process with rate λ _i . The length of time that the Markov process spends in state i before making a transition out of that state is exponentially distributed with rate −Q _ii . The probability that the Markov process enters state j after leaving state i is given by −Q _ij /Q _ii .

We have generated the following MMPPs and estimated their respective parameters γ _X , A _E , and α _E employing the techniques due to Jagerman et al. (2004) and Balcıo[gtilde]lu et al. (2005) (or equivalently p,γ₁, γ₂ via Equation (3)):

•	MMPP A: This is the stream of i.i.d exponential times to failure with rate γ X = 0.8.
•	MMPP B: This is a two-state MMPP with: which yields γ X = 0.8, ρ X (1) = 0.33, and A E = 12.632 and α E = 0.23 or equivalently using Equation (3) we have p = 0.952 44, γ1 = 3.888 04, γ2 = 0.047 32.
•	MMPP C: This is a three-state MMPP with: which yields γ X = 0.8, ρ X (1) = 0.317, and A E = 10.1297 and α E = 0.29 or equivalently using Equation (3) we have p = 0.940 79, γ1 = 3.969 16, γ2 = 0.058 45.
•	MMPP D: This is a four-state MMPP with: which yields γ X = 0.8, ρ X (1) = 0.36, and A E = 21.155 and α E = 0.143 or equivalently using Equation (3) we have p = 0.970,86, γ1 = 3.939 12, γ2 = 0.029 04.

Similar to the previous examples with TES⁺ interruption processes, we have generated another set using MMPPs to induce positive autocorrelation in the times to failure as presented in Table 4. Here the repair times are drawn from a Uniform(0.5, 1) distribution yielding an overall 30% system down time probability. The mean waiting time increases by 121% from the i.i.d exponential times to failures (MMPP A) case to the MMPP D case. The renewal approximation performs consistently well in predicting the mean waiting times of the original problem.

Table 4 Mean waiting times in M/D/1 systems with λ = 0.1, an MMPP times to failure process and f _D(d) = Uniform(0.5, 1), with d ₁ = 0.75, d ₂ = 0.5833, and a 30% down time

MMPP	ρ C(x)(1)	Simulation	Approximation
A	0.00	16.15	16.58
		(+/− 0.62)	(2.68%)
B	0.5	30.71	29.51
		(+/− 0.94)	(−3.9%)
C	0.48	27.86	27.07
		(+/− 0.68)	(−2.82%)
D	0.59	37.52	37.8
		(+/− 1.21)	(0.76%)

The results indicate that if the repair times are lengthy, the existence of positive autocorrelation in the interruption process increases the mean waiting time significantly.

4. The GI/D/1 case

The exact analysis presented in Section 2 for servers experiencing H2 times to failure is based on the assumption of Poisson job arrivals. In this section, we extend our analysis to GI/D/1 queues with an unreliable server experiencing autocorrelated times to failure. To test the performance of the renewal approximation, clearly one can simulate the system with H2 times to failure and compare the results to those from the simulation of the original queue with autocorrelated times to failure. Even though this is a simple and valid approach, our motivation in this section is to propose an analytic approximation to be able to study the autocorrelated PCTs and service times.

After directly collecting the autocorrelated PCT data, one could also apply the three-parameter renewal approximation and obtain an approximating renewal service time random variable Y, in line with Equation (1), having c ² _Y = 2A _Y + 1. In systems with moderate to high utilizations, we can exploit the heavy-traffic formula (see Shantikumar and Buzacott (1980) and the references therein) to compute the mean waiting time:

where c ² _A is the squared coefficient of the renewal job interarrival times.

However, renewal approximations of the autocorrelated service times, and therefore, the PCTs, appear to be dependent on the server utilization. Our numerical analysis further verifies this observation. Whitt (1983) and Albin (1984) make a similar observation in a different setting for the interarrival time renewal approximations.

Consequently, in this study, we propose to index our approximating service time distribution on ρ. The approximation algorithm we propose is as follows:

• Step 1. Approximate the autocorrelated times to failure stream in the GI/D/1 queue with server utilization ρ by a renewal process with H2 times to failure as summarized in Section 2.1.

• Step 2. Using the model in Section 2.2, obtain the queue length distribution of an M/D/1 queue with server utilization ρ and H2 times to failure, the parameters of which are obtained at the first step. As will be discussed later, construct an M/G/1 queue that has the same steady-state queue length distribution as the M/D/1 queue. Let 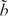(s,ρ) denote the Laplace transform of the service-time density function in the M/G/1 queue.

• Step 3. Since a direct use of 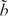(s,ρ) is difficult for computational purposes, approximate it by an appropriate PHase-type (PH) distribution having a Laplace transform of 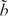(s), using its first three moments.

• Step 4. Let 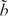(s) obtained from the previous step be the Laplace transform of the service time of a GI/G/1 queue, which has the same renewal arrival process as in the original GI/D/1 queue with the unreliable server experiencing autocorrelated times to failure. The exact mean waiting time of the GI/G/1 queue (Riordan, 1962, pp. 50–52) provides an approximation for the mean waiting time in the original GI/D/1 queue.

Let us next present details of the algorithm. In the approximating M/G/1 queue, the Laplace transform (s,ρ) of the service-time density function satisfies the P-K transform equation (Kleinrock, 1975, p. 194):

which can be rewritten as

where Q(z) = ∑ _{n = 0} ^∞π(n) z ⁿ is the z-transform of the queue length process. Then after a change of variable, one can express (s,ρ) of the M/G/1 queue as

where π(n) comes from Equation (6) ensuring that the M/G/1 queue has the same steady-state queue length distribution π(n) as the M/D/1 queue. Now we propose to use (s,ρ) from Equation (22) to approximate the PCT in the GI/D/1 queue with the same server utilization and whose autocorrelated times to failure process are approximated by the same H2 random variable.

For numerical computations, Equation (22) is not easy to use. However, one can compute the moments of (s,ρ) and choose PH random variables that match the first two moments exactly, and the third moment with the least error. The rationale behind incorporating the third moment is due to Balcıo[gtilde]lu et al. (2005), who demonstrate that two-moment matching techniques could incur larger errors. Clearly, moment approximations will increase the error with respect to the GI/D/1 queue with autocorrelated times to failure. In the moment approximations (Altıok, 1997, pp. 52–56), if (s,ρ) yields a squared coefficient of variation, c ²(ρ) < 1, we choose a Generalized-Erlang random variable, GE(μ,p,k), which has the following density function Laplace transform:

In the case where c ²(ρ) > 1, we will choose an H2 random variable, H2(p,μ₁, μ₂), whose Laplace transform is presented in Equation (2). Note that for the i.i.d. exponential times to failure case (TES⁺ A or MMPP A), the analysis is still exact due to Equation (17).

5. Numerical examples: Renewal job arrivals

In order to assess the efficacy of the method proposed in Section 4, we have used a simple TES⁺ process and MMPP to model autocorrelated times to failure. In numerical examples to be presented in Table 6, Table 7, Table 8, the down times are uniformly distributed over (0.5, 1), since this is the case in which the impact of a positively autocorrelated interruption process is felt most dramatically when job arrivals are Poisson. Here, independently of the TES⁺ process or MMPP used to generate the autocorrelated times to failure, the first moment of the process completion time is E[C(x)] = 8. The first column in Table 5 lists the TES⁺ and MMPP interruption processes used. For each case, we obtain (s,ρ) of the approximating PCT random variable via Equation (22), which have the second and third moments that are displayed in columns 2 and 3, respectively. The distributions given in column 4 match the first two moments, exactly, and approximate the third moment with the least possible error. Their third moments are listed in the last column.

Table 5 PH distributions approximating the PCT in the G/D/1 queue

Failure process	E[C(x)^2]	E[C(x)^3]	PH-distribution	E[C(x) PH ^3]
TES^+ B	71.71	730.5	GE(μ = 1.115,p = 0.99,k = 9)	707.6
TES^+ C	85.9	1325.5	GE(μ = 0.372,p = 0.987,k = 3)	1154
TES^+ D	148.15	6478.7	H2(μ1 = 0.13113, μ2 = 0.0286, p = 0.9863)	6125.37
MMPP B	118.04	3329.3	GE(μ = 0.171,p = 0.37,k = 2)	2521
MMPP C	108.28	2596.3	GE(μ = 0.206,p = 0.646,k = 2)	2024
MMPP D	151.21	6531.8	H2(μ1 = 0.13204, μ2 = 0.0284, p = 0.98457)	6607.29

Table 6 Mean waiting times in GI/D/1 systems with GE(0.2, 1,2) interarrival times with c ² _A = 0.5, TES⁺ times to failure and f _D(d) = Uniform(0.5, 1), with d ₁ = 0.75, d ₂ = 0.5833, and a 30% down time

TES^+	ρ C(x) (1)	Simulation	Approximation	c ^2 Y	Heavy traffic
A	0.00	7.68	7.78	0.036	8.58
		(+/− 0.18)	(1.30%)		(11.67%)
B	0.24	8.70	9.05	0.126	10.02
		(+/− 0.24)	(4.07%)		(15.13%)
C	0.45	12.37	12.47	0.41	14.56
		(+/− 0.56)	(0.8%)		(17.70%)
D	0.62	26.82	27.78	1.93	38.88
		(+/− 2.38)	(3.58%)		(44.97%)

Table 7 Mean waiting times in GI/D/1 systems with H2(0.888 89, 0.2, 0.02) interarrival times with c ² _A = 5, TES⁺ times to failure and f _D(d) = Uniform(0.5, 1), with d ₁ = 0.75, d ₂ = 0.5833, and a 30% down time

TES^+	ρ C(x) (1)	Simulation	Approximation	c ^2 Y	Heavy traffic
A	0.00	78.854	78.63	0.036	80.58
		(+/− 0.84)	(−0.28%)		(2.18%)
B	0.24	80.958	80.25	0.126	82.02
		(+/− 1.59)	(−0.88%)		(1.31%)
C	0.45	83.172	84.43	0.41	86.56
		(+/− 1.97)	(1.51%)		(4.07%)
D	0.62	103.24	101.79	1.93	110.88
		(+/− 3.59)	(−1.4%)		(7.40%)

Table 8 Mean waiting times in GI/D/1 systems with GE(0.2, 1,2) interarrival times with c ² _A = 0.5, MMPP times to failure and f _D(d) = Uniform(0.5, 1), with d ₁ = 0.75, d ₂ = 0.5833, and a 30% down time

MMPP	ρ C(x)(1)	Simulation	Approximation	c ^2 Y	Heavy traffic
A	0.00	7.68	7.78	0.036	8.58
		(+/− 0.18)	(1.30%)		(11.67%)
B	0.5	20.42	20.64	0.92	22.72
		(+/− 0.55)	(1.04%)		(11.25%)
C	0.48	18.06	17.77	0.77	20.32
		(+/− 0.53)	(−1.61%)		(12.54%)
D	0.59	28.89	28.54	1.5	32
		(+/− 0.93)	(−1.23%)		(10.75%)

Table 6, Table 7, Table 8 have similar structures to those of Table 1, Table 2, Table 3, Table 4 with two additional columns. We have used the same simulation model discussed in Section 3, this time with renewal job arrivals to obtain the reference mean waiting times (column 3) in the GI/D/1 queue where the server encounters the autocorrelated times to failure listed in column 1. The analytical solution presented in column 5 is obtained from the algorithm we propose where the renewal service time approximation is indexed on ρ. The last two columns are for the alternative approach ignoring the utilization dependence, for which we have collected the PCT data from the original queues with autocorrelated times to failure. We have computed the c ² _Y = 2A _Y + 1 for the approximating renewal service time, which is presented in column 6. In the last column, we present the heavy-traffic result computed from Equation (19).

A comparison of the approximation methods to the reference values obtained by simulation reveals the following facts.

1.	Table 6 displays the results obtained when the job arrival process has GE(0.2, 1,2) interarrival times (see Equation (23)) with a lower c 2 A = 0.5 than that of the Poisson job arrival process analyzed in Section 3. Although the mean waiting times are shorter than the ones presented in Table 1, this measure increases by 249% from the i.i.d exponential times to failure case (TES+ A) to the most positively autocorrelated case (TES+ D). The GI/G/1 approximation performs consistently well, but yet, for the cases with TES+ B and TES+ D, the error is bigger than their counter parts in Table 1. The two additional error sources on top of the renewal approximation become influential when the job/customer arrival process has a squared coefficient of variation of less than one. Yet, compared to the errors one incurs (as presented in the last column) when the dependence of the renewal service-time approximation on server utilization is ignored, our proposed approximation performs quite accurately.
2.	Table 7 displays the results obtained when the job arrival process has interarrival times following H2 with parameters (0.888 89, 0.2, 0.02) (see Equation (2)), with a squared coefficient of variation equal to five. The mean waiting time increases by 31% from the i.i.d exponential times to failure case (TES+ A) to the most positively autocorrelated case (TES+ D). In these cases, the high variability in the job/customer arrival process becomes the more dominant factor on the mean waiting time. As can be seen from the last column, ignoring server utilization in the renewal service-time approximation still incurs much higher errors.
3.	Table 8 displays the results obtained when the job arrival process has GE(0.2, 1,2) interarrival times (see Equation (23)) with a lower c 2 A = 0.5 than that of the Poisson job arrival process. The fundamental difference in this table is that the failure processes in reference cases are generated using MMPPs. Although the mean waiting times are shorter than the ones presented in Table 4, this measure increases by 276% from the i.i.d exponential times to failure case (MMPP A) to the MMPP D. The GI/G/1 approximation indexed by ρ performs consistently well.
4.	Although it has additional sources of error, the results indicate that the GI/G/1 approximation indexed by ρ can be used to analyze the GI/D/1 queues where servers experience autocorrelated times to failure.

6. Conclusions

In this paper, we have introduced a PCT analysis for a workstation that encounters autocorrelated times to failure with general i.i.d. repair times. To do this, we employed a three-parameter renewal approximation, where the approximating times to failure are modeled using a H2 distribution. When the arrival process is Poisson, an exact computation of the mean waiting time in a single server queue with H2 times to failure is possible as shown in Section 2.2. This model can also be extended to other forms of phase-type times to failure.

When the server experiences general and/or autocorrelated times to failure, PCT, i.e., the total time a job spends on the machine (effective service time), also becomes autocorrelated. We have observed that directly applying the three-parameter renewal approximation on the autocorrelated service-time sequence will not be sufficient to reflect the intricate behavior of the original system. Therefore, we propose indexing the approximating renewal service-time distribution on the system utilization of the original system. Hence, in the case of renewal job arrivals, an approximate yet accurate approach is developed in Section 4. This approximation works on the principle of computing the mean waiting time in a GI/G/1 queue by making use of the results from the M/G/1 queue that has the same server utilization as that of the former.

Numerical examples demonstrate that the autocorrelation in times to failure should be incorporated in the analysis of real-time scenarios in case it exists. Especially in queues with renewal job arrivals showing less variability, increased levels of positive autocorrelation degrade system performance significantly. In all the cases considered, the three-parameter renewal approximation proved to be accurate in capturing the behavior of the autocorrelated interruption processes.

Biographies

Barış Balcıo[gtilde]lu is an Assistant Professor in the Department of Mechanical and Industrial Engineering at the University of Toronto. He received his Ph.D. in Industrial and Systems Engineering from Rutgers University in 2003. His research and teaching activities are in the areas of queueing theory, discrete-event simulation, performance analysis of call centers and production/inventory systems, and reliability and maintenance engineering. His research has been supported by the Natural Sciences and Engineering Research Council of Canada.

David Jagerman is a mathematical consultant at Rutgers Center for Operations Research (RUTCOR) at Rutgers, The State University of New Jersey. He received his Ph.D. in Mathematics from New York University in 1962. He worked as a mathematical consultant at the AT&T Bell Laboratories, Holmdel, NJ, between 1963 and 1989. He was a Professor of Electrical Engineering and Computer Science at the Stevens Institute of Technology between 1984 and 1991. His research and teaching activities are in the areas of mathematics, electrical engineering, queueing theory, and computer applications stemming from industrial-military requirements. He has numerous publications including a book entitled Difference Equations with Applications to Queues published in 2000 by Marcel Dekker, New York.

Tayfur Altıok is a Professor and the Chairman of the Department of Industrial and Systems Engineering at Rutgers, The State University of New Jersey. He received his Ph.D. in Industrial Engineering at North Carolina State University at Raleigh. His research and teaching activities are in the areas of queueing systems, simulation modeling, performance analysis and design of manufacturing systems, marine ports, computer information systems, and supply chain logistics. His research has been supported by the National Science Foundation, DHS and industry for a number of years. He has numerous publications including two books in the areas of performance analysis and simulation.

Acknowledgements

This work was supported in part by NSF grants DMI-9812858 and DMI-0085659. We wish to thank Professor Georgia-Ann Klutke and the anonymous referees for their suggestions.