An effective methodology for the stochastic project compression problem

Abstract

In this paper, we consider the problem of planning a complex project when task durations are random. Specifically, we consider the problem of deciding how much to compress tasks in order to minimize the expected total cost that is defined by the sum of direct, indirect, and incentive costs. We initially consider this problem under the assumption that task durations can be modeled by a negative exponential distribution although we later relax this assumption and show that our methodology can be applied to any general distribution. To solve this problem, we develop an effective heuristic algorithm that we call the Stochastic COmpression Project (SCOP) algorithm; the SCOP algorithm is straightforward to implement and our numerical tests indicate that the algorithm performs significantly better than previously reported heuristics. In addition, we compare our approach to solutions found using expected values embedded in a deterministic approach (an approach that is frequently used to solve this problem in practice). Using our results, we show that the deterministic approximation approach, such as the classic PERT model, provides biased results and should be avoided.

Keywords:

• Project management
• project scheduling
• stochastic compression/crashing
• time-cost trade-offs

1. Introduction

In this paper, we consider a project planning problem that focuses on the trade-off between project cost and makespan when task time durations are random. That is, given a set of tasks, precedence constraints, and assumptions about the relationship between task times and direct labor costs, we develop an effective methodology to find optimal task durations that minimize the expected total cost that is defined by the sum of direct, indirect, and incentive (e.g., penalty) costs. We refer to this problem as the stochastic project compression problem (also known as the stochastic time-cost trade-off problem).

Project planning and optimal timing, especially for new product development projects, is extremely critical for many organizations. In a recent Business Week article (Hamm, 2006), the author noted that some new cell phone development times have been reduced from 12–18 months to 6–9 months, and noted that the Nissan Motor Company has reduced their new car development times from 21 months to 10.5 months. Clearly, these reduced new product development projects require very careful planning. Recently, there has been considerable discussion about the value of managerial flexibility in R&D projects (Santiago and Vakili, 2005). Having an effective algorithm for solving the stochastic project compression problem will give project managers a significant tool for replanning project allocation decisions in response to previous events and outcomes. As a result, the uncertainty associated with such risky projects should be reduced.

An effective algorithm for calculating optimal activity compressions would accrue benefits for “standard” as well as R&D projects. In several large construction projects, the authors have observed firms that have earned significant returns by optimally managing the time-cost trade-off decisions needed to exploit incentive payments or avoid penalties associated with delaying the successful completion of a project beyond a client-imposed due date. Alternatively, Szmerekovsky (2005) presented a deterministic methodology for scheduling tasks and timing payments to maximize the net present value of the project; the algorithm presented in this paper could be applied to the stochastic version of this problem. The overall importance of the stochastic project compression problem has been noted in much of the Project Management (PM) literature as well as many PM texts (e.g., Klastorin (2004)).

The deterministic project compression problem is well known (Elmaghraby, 1977; Klastorin, 2004). To describe this problem, we represent a project by a directed acyclic graph G = (N,A,W) with a set of nodes N = {1,…,n } that represent tasks or activities, a set A of directed arcs {(i,j) _{i,j ∈ N} } that represent finish-to-start precedence relationships, and a set of node weights W = {t _i }. We assume that tasks i ∈ N are lexicographically ordered such that i < j and have processing times t _i = t” _i − x _i fori = 2,…,n − 1 where t” _i denotes a maximum or uncompressed (e.g., normal) duration and x _i denotes the compression time (we also assume that x _i ≤ t” _i − t′ _i where t′ _i denotes the minimum allowable duration of task i). Without loss of generality, we assume that tasks 1 and n are dummy tasks representing the starting and ending tasks, respectively, such that t ₁ = t _n ≡ 0. In the deterministic problem, we assume that the direct cost of performing task i ∈ N is a linear function of the task compression x _i with constant marginal compression cost c _i . The deterministic problem of finding the optimal project plan that minimizes total costs is given by problem (P1) where C” _i denotes the cost of performing task i ∈ N at its maximum or normal time, C _I denotes the indirect costs charged to the project per time period, and C _P denotes the penalty cost per time unit given a due date D. The decision variables in problem (P1) are T _i (the starting time of task i), Γ (tardiness of the project given due date D) and the compression quantities x _i :

Problem (P1) can be easily solved by any general Linear Programming (LP) algorithm or by algorithms that exploit the specialized structure of the problem (Fulkerson, 1961). More recently, Phillips (1996) developed an optimization approach based on a cut search procedure, and Demeulemeester et al. (1998) developed an exact procedure for a discrete version of problem (P1) that constructs the complete time-cost profile subject to the availability of a single limited resource. We will refer to problem (P1) as the standard project compression problem.

When task times are stochastic, managers frequently use the expected durations to estimate the values of t” _i and t′ _i and solve problem (P1) to find the level of resources (e.g., hours from project staff, additional labor resources that should be hired, etc) to assign to each task. The solution in this case, however, can be far from optimal as we will show in this paper. The need to find better solutions to the general stochastic project planning problem provides the motivation for this research. Specifically, we develop a new algorithm for solving the stochastic project compression problem under the initial assumption that task duration times are exponential ¹ but later relax this assumption to consider general distributions. Our algorithm, which is easily implemented, determines compression strategies that minimize the sum of a project's direct costs, indirect and overhead costs, and penalty costs. We initially consider the case when C _P = 0 but later relax this assumption and consider the case when C _P > 0.

The remainder of this paper is organized as follows. In the following section, we review the previous work in this area and define the stochastic project compression problem explicitly. In Section 3, we discuss the stochastic compression problem with series and parallel networks and show how these cases can be efficiently solved when task times are exponential. In the fourth section, we extend our results for series and parallel subnets and exponential task times to general activity networks, and develop an effective heuristic that we denote as the Stochastic COmpression Project (SCOP) algorithm. In the fifth section, we compare the performance of the SCOP algorithm to previously proposed methods; in Section 6, we show how our algorithm can be extended to the case where C _P > 0. Finally, we summarize our results and discuss the implications of our findings.

2. Literature review and problem description

The literature addressing the stochastic project compression problem is very limited (Herroelen and Leus, 2005). As noted by Elmaghraby (1977), the assumption that activity times are stochastic adds a considerable element of difficulty to the stochastic compression problem as we must solve this problem as a network problem without the benefit of a simplifying aggregate cost function. To the best of our knowledge, the only published research on this problem when task times are defined by continuous random variables was the paper by Johnson and Schou (1990), who suggested three rules for a project manager to use when selecting tasks to compress. While their rules appear sensible, the only test of their approach was based on a simulation study of a single small sample project. When task durations follow discrete distributions and a limited set of compression strategies exist, Wollmer (1985) applied a stochastic programming approach to the stochastic compression problem. Gutjahr et al. (2000) described a branch-and-bound algorithm for solving a discrete version of this problem when activity times must be either normal or crashed (i.e., a binary state).

A number of researchers, including Van Slyke (1963), used Monte Carlo simulation to find a project's expected makespan and related distribution. Indeed, some largely analytical research projects (e.g., Hartley and Wortham (1966)) relied on simulation to resolve problems when no analytical result could be obtained directly.

The development of our approach is related to the work of Martin (1965) who showed that any series-parallel activity network can be reduced to a single arc with an associated density function that represents the distribution of time through the original network. A series-parallel activity network is an acyclic network with a single starting and ending node that consists entirely of series and parallel subnets. A series subnet consists of tasks arranged only in series such that each task in the subnet, with the exception of the first and last tasks, has exactly one predecessor and one successor. A parallel subnet consists of a subnet with a single starting and ending node, between which there exist two or more parallel paths, each consisting of one or more tasks in series. The key feature of such an activity network is the absence of interdicting arcs (e.g., arcs joining two paths within a network) that introduce dependence among paths in a network.

Although Martin (1965) extended his procedure for series-parallel networks to accommodate dependent paths, his procedure is computationally infeasible for project networks of any significant size. Other work related to the problem of determining the expected project makespan with stochastic task durations includes papers by Dodin (1985a) who developed a procedure for finding an approximate makespan Cumulative Density Function (CDF), Kleindorfer (1971), Robillard and Trahan (1976) and Dodin (1985b) who obtained bounds for the makespan CDF, Kulkarni and Adlakha (1986) who developed the makespan distribution for a project network with exponentially distributed task times using Markov Pert Networks (MPNs), and Buss and Rosenblatt (1997) who used an MPN approach similar to Kulkarni and Adlakha (1986) to determine the optimal activity delay in a stochastic project network. Many of these, including Dodin (1985a), developed approximations using discretization of CDFs that simplified calculating the convolutions of task densities. Dodin's approximation was based on the assumption of path independence; his results showed that the discretization granularity is the primary source of error in the approximation. When the independence assumption was the only source of error, Dodin's approximation produced a distribution function that was very close to the distribution found using an approach based on Monte Carlo simulation that was similar to the approach suggested by Van Slyke (1963). Dodin (as well as Kleindorfer (1971)) noted that a distribution function developed on the assumption of path independence bounds the true makespan distribution from below.

Kulkarni and Adlakha (1986), assuming exponential task durations, developed the concept of a MPN that yields the exact makespan distribution for independent, exponentially distributed tasks. Their approach, however, suffers from the significant limitation that the Markov state space quickly became overwhelmingly large and therefore computationally infeasible.

Hagstrom (1990) developed a recursive algorithm for finding the CDF or moments of the project makespan distribution by introducing an arc for every possible duration of an activity. In a separate paper, Hagstrom (1988) discusses the computational complexity of PERT problems and showed that computing the makespan distribution is NP-complete while computing the expected makespan is at least as difficult.

2.1. Definition of the stochastic project compression problem

We initially assume that activity times for all tasks i ∈ N are exponentially distributed with a Probability Density Function (PDF) of f _i (t) = λ _i e ^{− λ _i t} where t” _i = 1/λ _i is the mean (and normal) duration of task i. The assumption that task times are exponentially distributed is consistent with much prior work (e.g., Kulkarni and Adlakha (1986), Buss and Rosenblatt (1997), and Elmaghraby (2005)) as noted in the previous section. To “compress” a task in this case implies that we reduce the mean task duration (as well as the variance). Given the values of λ _i , we wish to find the optimal compression strategy x* = (x ₁*,…,x _n *) that minimizes the expected total cost E[TC(x)] defined as

where β _i (x _i ) represents the compression costs for tasks i ∈ N, E[M(x)] denotes the expected project makespan that is uniquely determined by the compression strategy, and E[L(x| D)] denotes the expected tardiness of the project given a due date D. We assume that the marginal costs of compression are monotonically nondecreasing [∂ β _i (x _i )/∂ x _i ≥ 0] and convex with respect to compression amounts [∂ ²β _i (x _i )/∂ x _i ² ≥ 0] for all functions β _i (x) ∀ i ∈ N. Note that the (constant) direct costs associated with performing tasks i ∈ N at their normal durations/costs are omitted from Equation (1) without loss of generality.

To motivate and explain the development of the SCOP algorithm, we initially consider only series and parallel subnets with exponential task durations and no penalty costs (i.e., C _P = 0). We then extend these results to general networks and other probability distributions. Extensive numerical tests indicate that our approach is very effective for general network configurations and activity time distributions.

3. Solving series and parallel subnets with exponential task times

We first consider a project network G with two tasks {a,b} in series. Given exponential activity times, the expected total cost of the project is

where E[M _{a + b} ] = (t” _a + t” _b ) − (x _a + x _b ) defines the expected project makespan. Using the First-Order Conditions (FOCs) of Equation (2), we can show at optimal compression that:

Given our assumption about the nature of the compression cost functions (i.e., that ∂ β _i (x _i )/∂ x _i ≥ 0 and ∂²β _i (x _i )/∂ x _i ² ≥ 0 ∀ i ∈ N, Equation (3) implies that:

for i = a,b where t′ _i is the minimum allowable task duration for task i. Equation (4) implies that a greedy algorithm can be used to identify the cost minimizing compression to achieve any feasible target makespan for a series subnet with exponential task times. For a series subnet of n tasks, the optimal compression for a series subnet is easily found by fully compressing all tasks for which ∂ β_i(x _i )/∂ x _i ≤ C _I; otherwise, x _i * = 0.

3.1. Parallel subnets

If we consider an activity network G with two tasks in parallel whose activity times are exponential, the expected makespan of this subnet (Mitchell, 2005) is defined as

and the expected total cost becomes:

Assuming that β _i (x _i ) = c _i x _i , we find that x _a and x _b are interrelated as follows:

Using Equation (6) and second-order conditions, we can derive a set of conditions (see Table 1) that define the values of x _a * and x _b * that minimize Equation (5).

Table 1 The compression conditions

Compression strategy	Compression condition
x a * = 0 x b * = 0	C I < (t” a + t” b )^2min [c a /(t” a )^2 + 2t” a t” b , c b /(t” b )^2 + 2t” a t” b ]
x a * = 0 x b * > 0	c b (t” a + t” b )^2/(t” b )^2 + 2t” a t” b ≤ C I < c a (t” a + t” b )^2/(t” a )^2 + 2t” a t” b
x a * > 0 x b * = 0	c a (t” a + t” b )^2/(t” a )^2 + 2t” a t” b ≤ C I < c b (t” a + t” b )^2/(t” b )^2 + 2t” a t” b
x a * > 0 x b * > 0	(t” a + t” b )^2max [c a /(t” a )^2 + 2t” a t” b , c b /(t” b )^2 + 2t” a t” b ] ≤ C I

Alternatively, we can use these results to define a set of threshold values, _a and _b , as follows:

If c _a ≤ _a or c _b ≤ _b , then task a or task b, respectively, should be compressed for a given C _I. To find the values of _a and _b when no compression should occur, we set x _a and x _b equal to zero in Equation (7) and solve for _a and _b respectively.

Since x _a * is a function of x _b (and vice versa), Equation (6) implies that:

From Equation (8), we observe that x _a * and x _b * are monotonically increasing in each other for all values of c _i ≤ C _I, i = a, b. Extending this observation, we can show that Equation (5) is jointly convex in x _a and x _b ; thus, an iterative procedure for finding the optimal values of x _a * and x _b * will converge to some arbitrary level of precision, ϵ > 0.

We can generalize these results to an n-task parallel subnet; the expected total cost in this case is defined as follows:

where E[M(x ₁,…,x _n )] defines the expected makespan. Using the FOCs of Equation (9) with respect to (w.r.t.) x _i , we find that:

that is, the minimum expected total cost occurs where the marginal costs of overhead and compression are equal. From Equation (10), we know that the expected total cost will be decreased by increasing compression in task i as long as

where (Mitchell, 2005)

Λ _jk is the sum of λ _i for tasks in the jth combination of n tasks taken k at a time, where λ _i ^{− 1} = t” _i − x _i . Using Equation (12), we can show that:

where Λ _ijk is equal to λ _i plus the sum of λ _l for tasks in the jth combination of n − 1 tasks taken k at a time from N\ {i}, where U\ u = U ∩ u ^c and, by convention, Λ _ijk = 1 for k = 0. For example, in a three-task parallel subnet, the value of Equation (13) w.r.t. x ₁ is

Using the results in Equations (11), (12) and (13), we can construct an efficient algorithm for the n-task parallel subnet that minimizes the expected total cost defined by Equation (9). To clarify the description of this algorithm, we will use the following notation:

During each rth iteration, the algorithm finds the minimum compression amount x _i ^r ≤ _i given x ^{r − 1} for which χ _i ^r ≥ C _I− ϵ, where ϵ > 0 is a small positive number. The algorithm for solving the parallel subnet problem proceeds as follows:

• Step 1. Let r denote the iteration index and initialize r = 0 and x _i ^r = 0 ∀ i ∈ N.

• Step 2. Set r = r + 1 andx _i ^r = x _i ^{r − 1} ∀ i ∈ N, and compute χ _i ^r for i ∈ N using Equation (11).

• Step 3. If x _i ^r ≥ _i , then set χ _i ^r = ∞.

• Step 4. If max _{i ∈ N} | x _i ^r − x _i ^{r − 1}| ≤ ϵ, then STOP.

• Step 5. Otherwise, let χ _p ^r = min {χ _i ^r } _{i ∈ N} .

• Step 6. Set x _p ^r equal to the smallest value in the interval (x _p ^{r − 1}, _p ] for which χ _p ^r ≥ C _I.

• Step 7. Go to Step 2.

The algorithm reduces the expected total cost in each iteration by selecting the compression variable based on the direction of steepest descent. The algorithm is terminated when no further movement in the direction of steepest descent reduces the total project cost (i.e., the chosen compression variable is increased as much as possible during an iteration). Since the compression variables are bounded, 0 ≤ x _j ≤ _j and monotonically nondecreasing, the algorithm is finite with order complexity O(n ²log n).

When n > 3, we cannot prove that the solution is globally optimal due to the difficulty of proving joint convexity of the expected total cost function in this case (we can prove joint convexity, and therefore global optimality, when n ≤ 3). However, our extensive numerical tests in larger subnets (when n > 3) indicate that the algorithm does find global optimality.

4. Solving the general stochastic project compression problem

To develop an effective methodology for the general stochastic project compression problem, we extend our (previously described) results for series and parallel subnets using exponential distributions to general networks with any probability distributions. Given the well-known difficulty associated with determining the makespan distribution under continuous stochastic activity times (Martin, 1965; Dodin, 1985a, 1985b; Hagstrom, 1988, 1990), we discretize the (continuous) task duration distributions and proceed in an analogous manner to our previously described approach. To calculate the starting and ending time distributions for all tasks, we extend Dodin's procedure (Dodin, 1985a). Using this approach to find the makespan distribution, we then extend the condition defined by Equation (11) to form the basis of a general stochastic activity network compression condition for the SCOP algorithm.

The probability of completing task i by time t is defined by the convolution of the start time and activity time distributions for task i. Let S _i (t), F _i (t) and A _i (t) be the start time, completion time and activity time CDFs respectively for task i, and let a _i (t) = dA _i (t)/dt. Then

where P _j is the set of immediate predecessors of j. Assuming, without loss of generality, a lexicographic ordering of tasks in network G, we proceed sequentially from task 1 through task n, determining F _i (t) for every activity in the network. Upon completion, S _i (t) and F _i (t) have been determined for all tasks, and F _n (t) gives the project makespan distribution.

In each iteration, the SCOP algorithm reduces the expected total project cost by increasing the compression in the task that indicates the direction of steepest descent. Execution terminates either when all tasks are maximally compressed or no additional compression will reduce the total project costs.

The form of the compression decision in the general case is derived from the parallel subnet approach described in Section 3.1. We denote Δ _i E[M] (analogous to ∂ E[M]/∂ x _i ) as the first difference of the expected makespan with respect to compression in task i:

where δ > 0 is a nondivisible unit of compression. Extending Equation (11) to the general case, we compress task i when the following condition holds:

or, alternatively, when

The left-hand side of the inequality in Equation (18) has an intuitively appealing interpretation; it is the overhead cost saved per compression dollar. At any point during the algorithm, a compressible task is one for which 0 ≤ x _i < _i . During each iteration, the compressible task chosen for compression is that with the largest value of χ _i ^r ≥ 1. Increasing compression for task i necessitates recalculating its ending time distribution, and doing so recursively for all successors of task i. We will refer to this recursive recalculation of distributions as adjusting the activity distributions.

The SCOP algorithm, to find optimal compression amounts, x _i *, is described as follows:

• Step 1. Discretize activity time probability distributions.

• Step 2. Initialize iteration index r = 0, and set x _i ^r = 0 ∀ i ∈ N.

• Step 3. Let r = r + 1 and x _i ^r = x _i ^{r − 1} ∀ i ∈ N.

• Step 4. Determine N _r ^C = {i ∈ N | 0 ≤ x _i ^r < _i } where N _r ^C = set of potential compressible tasks in iteration r.

• Step 5. If N _r ^C = ∅ then STOP; there are no compressible tasks.

• Step 6. Compute χ _i ^r for i ∈ N _r ^C using Equation (18).

• Step 7. If χ _i ^r < 1 ∀ i ∈ N _r ^C, then STOP as x ^r is locally optimal and no further compression is justified (where x ^r = {x ₁ ^r ,…,x _n ^r } as previous defined).

• Step 8. Find χ _p ^r = max {χ _i ^r } _{i ∈ N} where ties are broken arbitrarily.

• Step 9. Set x _p ^r = 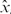_p and adjust the activity distributions for all successors of task p.

• Step 10. If C _I(Δ _p E [M(x ^r )]) ≥ c _p δ, then go to Step 3; otherwise, find by interval bisection search, the smallest value of x _p ^r ∈ (x _p ^{r − 1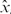}, _p ] such that χ _p ^r ≥ 1 − ϵ.

• Step 11. Go to Step 3.

The algorithm reduces the expected project cost in every iteration by increasing each compression variable through a line search in the direction of steepest descent. Compression is monotone nondecreasing in each iteration. The line search is terminated when further compression will not reduce the expected total cost (i.e., the chosen compression variable is increased as much as possible during an iteration). Since compression variables are bounded, 0 ≤ x _i ≤ _i ; execution terminates when either no compressible task remains (N _r ^C = ∅) or additional compression yields no reduction in the expected total cost. The order complexity of the algorithm is O (Q{n + k ² n + log Q }), where Q = max ( _i )/ϵ, k equals the cardinality of the discretized distributions, and n = | N |.

5. Numerical results

We conducted extensive numerical studies to test the efficacy of the SCOP algorithm with different activity networks, activity time distributions, and cost parameters. Within each numerical study, we held the uncompressed activity costs and marginal compression costs constant, and measured the effectiveness of the SCOP algorithm by varying the indirect cost rate, C _I, or the due date, D (if appropriate). We then compared the results from the SCOP algorithm to the project cost and makespan determined by other methods (i.e., deterministic compression via LP, and the heuristics proposed by Johnson and Schou (1990)).

Each numerical study consisted of several experiments. For each experiment, we randomly generated a set of activity networks with n = 30 tasks ² using the procedure described in Mitchell (2005). For each task in the network, we randomly generated an activity time distribution as described in Section 5.1; in this way, we were able to isolate the impact of network topology on the SCOP algorithm's performance. For each network that was generated, we then applied the SCOP algorithm and each of the comparison methods. To evaluate the cost and makespan performance of the SCOP algorithm relative to the comparison methods, we randomly generated 5000 activity time realizations ³ and calculated the total cost and project makespan, comparing the results of the SCOP algorithm to each of the comparison methods.

We compared the solutions found by the SCOP algorithm to three other heuristics: (i) no compression; (ii) deterministic compression (that is, we solved problem (P1) using a deterministic equivalent activity network); and (iii) the minimum-cost solution found by the three rules suggested by Johnson and Schou (1990).

Within each numerical experiment, we held the (normal) costs of uncompressed tasks and the marginal compression costs constant. To evaluate the impact of the indirect cost rate, we varied C _I to achieve predetermined ratios of C _I/max {c _i }. Similarly, for studies evaluating the impact of the due date, we varied D to achieve predetermined ratios of D/E[M]. Finally, for each value of C _I or D, we computed descriptive statistics for the expected cost and makespan across activity networks within an experiment, and across experiments within a numerical study. In this way, we were able to measure the interaction of activity network topology and indirect cost rate on the effectiveness of our algorithm.

5.1. Generating activity time distributions

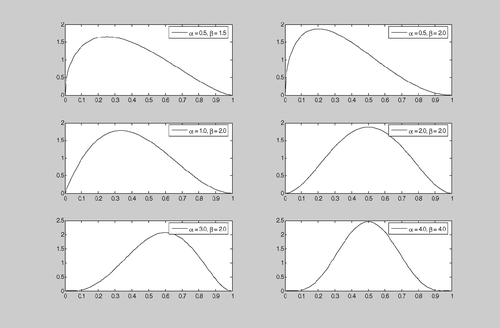
Activity time distributions were generated from beta, exponential, and uniform distributions as well as a random mix of these distributions (i.e., the selection was drawn uniformly from among the three distributions). The selection of the beta and exponential distributions was based on their widespread use in previous PM research (e.g., the classic PERT model is based on a beta distribution; see Klastorin (2004); we chose the uniform distribution based on the assumption that a project manager may have no a priori information about a task's activity time distribution. Overall, these three distributions presented a variety of symmetric and asymmetric distributions and variances for testing the SCOP algorithm. Since a beta distribution is characterized by two shape and two location parameters, we set these values to achieve a desired mean uncompressed activity time (i.e., t” _i ). Rather than allowing the shape parameters to be implicitly determined by choice of location parameters and a target mode (as is done in the classic PERT approach), we randomly selected a shape (and hence the shape parameters α and β) from among the set of shapes indicated in Fig. 1. This approach offers a more robust assessment of our stochastic compression algorithm's effectiveness on a variety of distributions. The mean, mx, and variance, vx, of the beta distribution are completely determined by the two shape parameters, α and β.

Fig. 1 Beta distribution shape parameter sets.

After setting the shape parameters, we randomly generated the lower support, A, and mean, t” _i , for the beta distribution from which we calculated the remaining location parameter, B, that specifies the upper support, and t′, the minimum value activity time under maximum compression:

where

To define exponential distributions (that are, of course, completely determined by the mean t” _i = 1/λ _i ), we generated values for t” _i and t′ _i as follows:

We defined uniform distributions by generating the lower support, A, and the mean, t” _i , from which the upper support was calculated:

We utilized the procedure described in Mitchell (2005) to randomly generate the cost parameters for the numerical studies such that project costs were characterized by C _i ′ ′∼ U [4,25] and c _i = s (C” _i /t” _i ), s∼ U [1.2, 3.0], where t” _i is the mean activity time calculated from a randomly generated activity distribution.

5.2. Numerical study results

Table 2 compares the results from the SCOP algorithm to those found using deterministic compression (that is, solving problem (P1)) for experiments ⁴ using beta, exponential, uniform and mixed activity time distributions with 30 different randomly generated network structures, n = 30 nodes, and ten different ratios of (C _I/max {c _i }) ∈ {1,2,…,10 }. The results in Table 2 indicate that for most values of the indirect cost rate ratio C _I/max {c _i }, the SCOP algorithm yielded significantly lower expected costs than deterministic compression. Instances of lower costs produced by deterministic compression are almost entirely limited to very small values of C _I relative to the marginal compression costs. In practice, indirect cost rates as a percentage of marginal compression costs are typically larger than the smaller ratios we tested. Moreover, instances of deterministic compression producing the lower cost were eliminated in our tests when the cardinality for the discrete probability distributions was increased (albeit at longer execution times). Further tests indicated that cost reductions continued to improve with increasing values of C _I and varying values of the ratio C _I/max {c _i }. A few instances of over-compression by a standard time-cost trade-off linear program were noted as indicated by positive percentage cost changes and negative percentage makespan changes.

Table 2 Expected cost comparison between the SCOP algorithm and the deterministic compression (n = 30)

		Ratio of C I max {c i }
Distribution type		1	2	3	4	5	6	7	8	9	10
Beta	Mean (%)	c0.62	c0.85	c1.18	c1.40	c1.79	c2.01	c2.25	c2.43	c2.60	c2.73
	Stdev (%)	0.33	0.47	0.52	0.54	0.58	0.67	0.73	0.80	0.84	0.86
Exponential	cMean (%)	c1.20	c1.89	c2.74	c3.43	c3.99	c4.34	c4.67	c4.98	c5.16	c5.34
	Stdev (%)	0.46	0.47	0.74	0.86	1.01	1.04	1.12	1.17	1.24	1.23
Uniform	cMean (%)	c0.26	c0.39	c0.85	c1.12	c1.42	c1.69	c1.87	c2.08	c2.24	c2.37
	Stdev (%)	0.07	0.26	0.30	0.41	0.50	0.52	0.55	0.56	0.57	0.62
Random	cMean (%)	c2.01	c4.29	c5.25	c6.05	c6.46	c6.90	c7.19	c7.46	c7.65	c7.80
	Stdev (%)	2.48	4.94	5.78	6.21	6.40	6.56	6.69	6.79	6.86	6.87
Overall	cMean (%)	c1.02	c1.86	c2.50	c3.00	c3.41	c3.74	c4.00	c4.24	c4.41	c4.56
	Stdev (%)	1.35	2.76	3.23	3.53	3.64	3.75	3.82	3.90	3.93	3.95

Table 3 indicates the makespan differences between solutions found by the SCOP algorithm and those found by deterministic compression. These results show that in most cases, the SCOP algorithm yielded significantly lower project makespan values. In addition, the SCOP algorithm produced greater makespan reduction in activity networks that had a greater variance (as demonstrated by the largest percentage reductions in the exponential distribution experiments, the second largest reductions in the mixed-distribution experiments, etc). This observation was consistent with the results we observed in series and parallel subnets. In series subnets, stochastic and deterministic compression algorithms yield the same results. In parallel subnets, however, the savings yielded by stochastic compression over deterministic compression increases with the variance of the parallel subnet that is directly related to the number of parallel tasks.

Table 3 Expected makespan comparison between the SCOP algorithm and the deterministic compression (n = 30)

		Ratio of C I max {c i }
Distribution type		1	2	3	4	5	6	7	8	9	10
Beta	cMean (%)	c0.20	c2.17	c3.11	c3.58	c3.88	c4.00	c4.08	c4.14	c4.18	c4.21
	Stdev (%)	1.00	1.13	1.16	1.15	1.08	1.07	1.07	1.08	1.09	1.08
Exponential	cMean (%)	c1.82	c5.10	c5.90	c6.34	c6.58	c6.74	c6.85	c6.96	c6.99	c7.03
	Stdev (%)	0.81	1.36	1.32	1.40	1.44	1.48	1.52	1.54	1.54	1.54
Uniform	cMean (%)	c0.15	c2.23	c3.00	c3.37	c3.53	c3.64	c3.70	c3.74	c3.77	c3.80
	Stdev (%)	0.66	0.92	0.85	0.90	0.90	0.91	0.93	0.93	0.93	0.94
Random	cMean (%)	c5.22	c7.54	c8.43	c8.92	c9.13	c9.33	c9.42	c9.51	c9.57	c9.61
	Stdev (%)	6.48	7.28	7.33	7.36	7.35	7.34	7.33	7.36	7.35	7.33
Overall	cMean (%)	c1.85	c4.26	c5.11	c5.55	c5.78	c5.93	c6.01	c6.09	c6.13	c6.16
	Stdev (%)	3.71	4.15	4.17	4.21	4.20	4.22	4.23	4.25	4.25	4.25

To the best of our knowledge, the paper by Johnson and Schou (1990) is the only other research that has considered rules for compressing a general activity network with stochastic activity times. We therefore compared the effectiveness of our stochastic compression algorithm to their suggested heuristic rules (J&S rules) that are summarized in Table 4.

Table 4 The stochastic project compression heuristics of Johnson and Schou (1990)

Rule	Statement	Comments
1	Select the lowest cost activity or activities that will reduce the expected critical path (based on classic PERT analysis)	Deterministic equivalent. Assumes the PERT-identified critical path is the only critical path
2	Select the activity with the highest criticality index (probability of being on the critical path)	Recognizes the existence of multiple critical paths in a stochastic activity network by introducing the criticality index
3	Compute a weighted ranking factor: r = (C j ^C− C j ^N)/(t” j − t′ j ) Pr {j ∈ CP} where C j ^C is the fully compressed cost for task j, C j ^N is the uncompressed cost for task j and CP is the critical path. Choose the task with the smallest value of r first	Combines compression cost per unit time with existence of multiple critical paths

Compression results for small parallel subnets suggest that the J&S heuristics may significantly undercompress parallel subnets, and consequently general networks, because they do not adequately account for the effect of multiple stochastic paths on makespan variance. This hypothesis was supported by our numerical results. Table 5, Table 6, and Table 7 present the cost difference percentages between solutions determined by the SCOP algorithm and six other methods:

•	UNCOMP – no compression.
•	DETCOMP – compression determined by a standard time-cost trade-off linear program (i.e., solving the deterministic equivalent problem).
•	RULE 1 – J&S rule 1 (see Table 4).
•	RULE 2 – J&S rule 2 (see Table 4).
•	RULE 3 – J&S rule 3 (see Table 4).
•	BEST OF J&S – The best results obtained from the three J&S rules.

Although the five alternative compression methods (UNCOMP, DETCOMP, J&S rules 1 through 3, and Best of J&S) reduced project costs compared to no compression, our stochastic compression heuristic outperformed all six methods in all cases. In addition, we observed that:

1.

The percentage cost improvements of stochastic compression over the other methods generally increases as a function of C I.

2.

The performance of the J&S rules relative to the SCOP algorithm varies as a function of variance and C I. For example, when C I = 1.0 and tasks have beta or uniform activity times, rule 3 provides the greatest cost reduction among the J&S rules, followed by rules 2 and 1 in that order. However, for C I∈ {5.5,10.0}, rule 1 offers the greatest cost reduction, followed by rules 2 and 3 in that order. Under exponential and mixed activity times, the best performance among the J&S rules is obtained by rules 1, 2 and 3, in that order, for all values of C I (due to the larger makespan variability).

We believe the SCOP algorithm outperformed the J&S rules for the following reasons:

1.	Under the J&S rules, tasks are either uncompressed or maximally compressed. Nothing in their heuristic allows for tasks to be compressed between the normal and crash times. Thus, in many cases, these rules result in under or overcompression of tasks.
2.	Rule 1 evaluates only the marginal cost of compression. Hence, tasks with low compression cost coefficients will be compressed first, even though they may have little effect on expected makespan due to low variability, and those with large compression costs coefficients may not be compressed, even though they might have a large impact on expected makespan.
3.	Rule 2 evaluates only the criticality index. Although this at least recognizes the possibility of multiple critical paths, it does so in an incomplete way, introducing a potential to make poor compression choices. A task may be on a critical path 100% of the time while contributing nothing to the makespan variance (e.g., it could be a predecessor to all paths but have an activity time distribution characterized by little to no variance).
4.	Rule 3 attempts to recognize marginal cost of compression and the possibility of multiple critical paths by combining aspects of rules 1 and 2. However, this appears simply to increase rule 3's tendency to make poor compression decisions.

It is important to note that the performance of all three J&S rules can be improved by changing their respective stopping rules. However, due to the simplicity of the J&S heuristics, this improves their effectiveness in some cases while worsening their effectiveness in other cases.

Table 5 Average percent cost reduction using the SCOP algorithm (C _I/max {c _i } = 1)

	Solution methodology
Distribution type	UNCOMP	DETCOMP	Rule 1	Rule 2	Rule 3	Best of J&S
Beta	5.17	0.13	7.55	5.17	4.95	4.60
Exponential	6.87	0.83	4.28	4.46	5.61	3.73
Uniform	5.24	0.31	10.50	6.23	6.02	5.39
Random	5.13	0.43	2.47	3.09	3.32	2.16

Table 6 Average percent cost reduction using the SCOP algorithm (C _I/max {c _i } = 5.5)

	Solution methodology
Distribution type	UNCOMP	DETCOMP	Rule 1	Rule 2	Rule 3	Best of J&S
Beta	19.24	2.14	3.04	8.30	9.91	3.04
Exponential	26.06	7.86	6.64	15.55	18.66	6.55
Uniform	22.80	2.32	1.65	10.94	14.45	1.65
Random	16.64	3.53	2.81	7.91	10.39	2.76

Table 7 Average percent cost reduction using the SCOP algorithm (C _I/max {c _i } = 10)

	Solution methodology
Distribution type	UNCOMP	DETCOMP	Rule 1	Rule 2	Rule 3	Best of J&S
Beta	21.35	2.97	3.25	9.59	10.70	3.25
Exponential	28.30	9.12	7.34	17.00	20.38	7.08
Uniform	25.53	3.28	1.57	13.16	15.82	1.57
Random	18.05	4.13	3.14	9.21	11.16	3.10

6. Stochastic compression with a due date

If we include a due date (denoted by D) and a late completion penalty, C _P, the expected total cost for the project is then defined by

where x = {x ₁,…,x _n } is the compression strategy and f _n (z|x) is the PDF of the ending time of task n given x. In this case, we can modify the compression rule in Equation (18) by the following:

where

Equation (20) indicates that we compress task i when the expected savings in overhead and penalty costs from such compression is greater than the marginal cost of compression. We compress the task that has the largest value of C _IΔ _i E[M] + C _PΘ _i /δ c _i . The partial expectations (i.e., expected days late given T _n ≥ D) in Equation (21) can be estimated using the discretized distributions utilized in the SCOP algorithm:

where T _n is the ending time of task n, y _i is the ith discrete realization of T _n , and m(y| x ) is the conditional probability mass function for the discretized distribution corresponding to compression strategy x. Using Equation (22), we may approximate Equation (21) as follows:

We conducted additional numerical studies to test the effectiveness of the SCOP algorithm when there exists a due date and penalty cost. These studies compare the efficacy of the stochastic compression algorithm with due date extensions to stochastic compression without due date extensions and a standard time-cost trade-off linear program with due date. These numerical studies were structured as described in Section 5 in all other respects.

Table 8 and Table 9 present the mean additional percentage cost reduction of the stochastic compression algorithm with due date extensions compared to the standard stochastic compression algorithm. The due date extensions consistently deliver additional cost reductions over the standard algorithm, with the amount of additional reduction increasing and then decreasing within an experiment as the due date ratio increases from a half to one. Significantly, additional cost reduction continues even when the ratio of due date to expected makespan is greater than one. This is clearly due to the uncertainty associated with the stochastic activity times. For values of the due date ratio less than one, the late delivery penalty dominates the compression decision (i.e., the project is so far into the penalty it is probable a penalty will be incurred regardless of the actual activity time realizations). However, as the due date ratio approaches a value of one, less compression is warranted as the probability of incurring the penalty becomes smaller. This results in a lowering of the additional cost reduction achieved compared to standard stochastic compression.

Table 8 Percent cost reduction (SCOP with versus without due date extensions) for 30 task activity networks

	Ratio: Due date E[M]
Distribution type		0.5	0.6	0.7	0.8	0.9	1	1.1	1.2	1.3	1.4
Beta	cMean (%)	c2.35	c2.74	c3.01	c2.02	c0.78	c0.31	c0.11	c0.06	c0.01	c0.02
	Stdev (%)	1.02	1.19	1.26	0.71	0.30	0.18	0.11	0.09	0.02	0.04
Exponential	cMean (%)	c3.80	c4.15	c4.37	c4.26	c3.52	c2.61	c1.77	c1.11	c0.60	c0.18
	Stdev (%)	0.88	0.96	1.02	1.08	1.02	0.97	0.88	0.69	0.37	0.13
Overall	cMean (%)	c3.07	c3.44	c3.69	c3.14	c2.15	c1.46	c0.94	c0.59	c0.31	c0.10
	Stdev (%)	1.18	1.26	1.30	1.46	1.61	1.38	1.06	0.72	0.40	0.13

Table 9 Percent makespan reduction (SCOP with versus without due date extensions) for 30-task activity networks

	Ratio: Due date E[M]
Distribution type		0.5	0.6	0.7	0.8	0.9	1	1.1	1.2	1.3	1.4
Beta	cMean (%)	c2.97	c2.97	c2.97	c2.50	c1.11	c0.47	c0.23	c0.17	c0.14	c0.06
	Stdev (%)	1.30	1.30	1.30	0.91	0.40	0.29	0.25	0.23	0.19	0.12
Exponential	cMean (%)	c4.54	c4.54	c4.54	c4.54	c4.16	c3.25	c2.25	c1.61	c0.97	c0.34
	Stdev (%)	0.78	0.78	0.78	0.78	0.73	0.75	0.75	0.88	0.61	0.30
Overall	cMean (%)	c3.75	c3.75	c3.75	c3.52	c2.64	c1.86	c1.24	c0.89	c0.56	c0.20
	Stdev (%)	1.31	1.31	1.31	1.34	1.70	1.56	1.19	0.97	0.61	0.26

7. Conclusions and extensions

In this paper, we developed an effective algorithm (the SCOP algorithm) for compressing general networks with stochastic activity times; the development of our algorithm was based on results we found for series and parallel subnets when task time durations are described by negative exponential distributions. We evaluated the effectiveness of our algorithm on randomly generated activity networks with 30 tasks when activity times were distributed according to beta, exponential, uniform and mixed distributions. We found that the SCOP algorithm performed well, obtaining greater cost reductions than those yielded by comparison methods. In most cases, project makespan reductions were realized concurrently with lower project costs.

We observed that the effectiveness of the SCOP algorithm, relative to comparison methods, improved as a function of C _I. We had originally hypothesized that the performance differential between the SCOP and deterministic compression would decrease as values of C _I increased relative to marginal compression costs, and that at some very large values of C _I, the differential would be zero (due to the fact that all tasks would be set to their maximum compression). However, we did not observe this trend in our numerical tests. In fact, the observed difference was always increasing in favor of stochastic compression, albeit at a slower rate, even when C _I/max (c _i ) = 200.

We developed an algorithm for compressing general stochastic activity networks and compared its performance against a standard time-cost trade-off linear program and three rules for determining compression in stochastic activity networks suggested by Johnson and Schou (1990). Although all of the compression rules yielded compression strategies that lowered costs compared to an uncompressed project, our stochastic compression algorithm consistently yielded the lowest costs. The narrowest margin of difference was more than 1.5%, as compared to the J&S rule 1, when activity times were uniformly distributed. In all other cases (i.e., beta, exponential and a randomly generated set of beta, exponential and uniform distributions), our stochastic compression algorithm lowered expected total costs by a margin of at least 3% (and as high as 20%) over comparison methods.

Finally, we extended our algorithm to the due date case (i.e., C _P > 0). We conducted extensive numerical studies, comparing the expected total costs from our algorithm with those for the standard stochastic compression (no due date case) and a standard time-cost trade-off linear program enhanced for a due date and late delivery penalty. Our algorithm performed well against both benchmarks, yielding cost reductions over standard stochastic compression and deterministic compression with a due date. We observed additional cost reductions even when the ratio of due date to expected makespan was greater than one, as a result of the variance of the project makespan. As expected, the additional cost and makespan reductions, versus the comparison methods, decreased for due date ratios over one. For values of the due date ratio in the range [0.4, 0.7], the algorithm compressed projects maximally and we observed cost reductions increasing over the range. This reflected the maximal compression, in the due date ratio range, and decreasing likelihood of the project's being in penalty as the due date ratio approached 0.7.

The stochastic compression algorithms presented in this paper appear to be effective methods for planning cost-reducing task compression. In most cases this will also reduce project makespan and makespan variability. In context, this means a project manager can reduce a major source of uncertainty risk in a project, specifically makespan uncertainty, while simultaneously lowering total project costs.

Our results clearly indicate that simple heuristics for determining project compression with stochastic task durations do not account for the extent of the effects in parallel subnets, where a task's optimal compression is an increasing function of the compression levels of other tasks in the subnet. Our findings demonstrate that compression decisions under stochastic task durations are very different from those in deterministic activity networks.

The development of an effective algorithm for the stochastic project compression problem (the SCOP algorithm) introduces a number of important related questions and extensions. Further testing of the SCOP algorithm could be useful, especially tests based on the well-known project network generator, ProGen (Kolisch et al., 1995). Identifying other algorithms for the stochastic compression problem, including optimization approaches, represents another important area. We have also begun to investigate the implications of slack measures in stochastic activity networks. Finally, an empirical study relating types of tasks with activity time distributions would be of great value to practicing project managers as well as researchers.

Biographies

Gary Mitchell is an Assistant Professor of Operations Management at the University of Portland, Portland, OR. He holds a B.S. (1984) and MBA (1988) from the University of California at Riverside, and a Ph.D. from the University of Washington (2005). His research focuses on project management, the impact of potential disruptions on operations, new product development projects, and supply chain and inventory management under imperfect information. He has been active in information systems development and project and supply chain management consulting since 1981. He founded a successful supply chain management software and consulting company in 1993 from which he retired in 1998 to pursue his academic interests.

Ted Klastorin is the Burlington Northern/Burlington Resources Professor of Operations Management at the University of Washington Business School, Department of Information Systems and Operations Management (formerly Management Science), as well as Adjunct Professor in the Department of Health Services (School of Public Health and Community Medicine), and Adjunct Professor of Industrial Engineering (College of Engineering) at the University of Washington, Seattle, WA. He holds a B.S. degree from Carnegie-Mellon University (1969) and a Ph.D. from the University of Texas at Austin (1973). His research focuses on new product development projects, project management, and the impact of potential disruptions on operations. He is an active consultant and the author of numerous articles as well as the book Project Management: Tools and Trade-offs, John Wiley & Sons, 2004.

Acknowledgements

The authors gratefully acknowledge helpful comments from Professors K. Moinzadeh and T. Rockefellar as well as the Burlington Northern/Burlington Resources Foundation that provided support for the second author. The authors gratefully acknowledge the assistance of several anonymous referees whose comments have significantly improved this paper.

Notes

¹This assumption has been widely used in previous research, including papers on PM by Buss and Rosenblatt (1997) and also Kulkarni and Adlakha (1986).

²We conducted studies with as few as ten, and as many as 100, tasks per activity network. In all cases, the results were consistent with those presented here for 30-task networks.

³We conducted experiments with a variety of simulated trials from 100 to 25 000 activity time realizations per activity. The results were consistent with those reported here for 5000 simulated trials.

⁴Each experiment represents the results of 5000 randomly generated combinations of activity networks and indirect cost rates.