Location and allocation of service units on a congested network

Abstract

We consider the problem of locating facilities and allocating servers on a congested network (LASCN). Demands for service that originate from the nodes are assumed to be Poisson distributed and the servers provide a service time that is exponentially distributed. The objective is to minimize the total cost of the system which includes a fixed installation cost, a variable server cost, a cost associated with travel time and a cost associated with the waiting time in the facility for all the customers. The problem is formulated using non-linear programming and subsequently analyzed. Results for exact and approximate solution approaches are reported. We also show that we can modify the approaches to solve the LASCN with constraints limiting both the travel time to the servers and the waiting time of customers.

Keywords:

• Location
• multiple servers
• congested network

1. Introduction

This paper belongs to the family of median-type location models on congested networks with fixed facilities. In median location problems the focus is on the average behavior of the system. Congestion occurs when requests for service are generated in a probabilistic fashion and when the capacity of the service facilities is limited. When facilities are fixed, customers travel to the closest facilities to obtain service.

Wang et al. (2002) studied the problem of locating facilities modeled as M/M/1 queuing systems. Their objective was to minimize the total cost of the system that consists of the travel cost and waiting time cost of customers subject to service level constraints on the maximum waiting time in all facilities. Customers were assumed to travel to the closest facility to obtain service. Berman et al. (2006) considered a similar model. Their objective was to minimize the total number of facilities and they included an additional constraint on the demand that is lost due to congestion and insufficient coverage.

In a recent paper, Berman and Drezner (2007) introduced a model in which they generalized the type of facilities considered by Wang et al. (2002) by modeling the facilities as M/M/k (k ≥ 1) queuing systems. Given p homogenous servers, the problem is to find locations for the service facilities and to allocate the p servers among them. It is assumed that there is a finite set of potential locations for the facilities (e.g., nodes) and customers travel to the closest facility to obtain service.

Given p facilities, the objective function in Wang et al. (2002) and in Berman and Drezner (2007) is to minimize the sum of the travel cost and waiting time cost for all customers. In this paper, while the number of servers is also a decision variable, we consider a more realistic objective function which, in addition to travel and waiting time costs, also includes the fixed cost of opening facilities and the variable cost of the servers.

The new objective function introduces more trade-offs. With just the cost of travel and the cost of waiting, the trade-off is between the effect of pooling servers to reduce waiting time (for a discussion see Drezner (1988)) and thus having fewer facilities with more servers in each, and the effect of travel which is reduced when locating more facilities in different locations. With the new objective function, there is also a trade-off between the fixed cost of facilities that gets smaller with fewer facilities, which also reduces the waiting time because of pooling and the variable cost of the servers that declines when we use fewer servers and thus more facilities which also reduces the cost of travel time.

A recent paper by Castillo et al. (2002) considers a similar problem to the one discussed in this paper. The difference is that in Castillo et al. (2002) there is a centralized assignment of customers to facilities and approximations are used for the probability of queuing delay, whereas in this paper customers are assigned to the closest facility and an exact queuing delay formula for the M/M/k is used. As a result the analysis is completely different from that in Castillo et al. (2002).

This paper is different from Berman and Drezner (2007) in that: (i) as mentioned earlier, in this paper the number of facilities is not limited and in the objective function the fixed cost of facilities and the variable cost of servers are also considered; (ii) whereas in Berman and Drezner (2007) the focus in solving the problem is on heuristics, in this paper, following a detailed analysis of the model, we propose an exact solution approach that is shown to be quite efficient in our computational analysis; and (iii) the solution procedures introduced in this paper can be modified to solve an extended model with service level constraints.

Applications of the model introduced in this paper include location of bank branches where the number of teller stations at each branch is an important decision variable and the location of ATM machines where at each location one or more ATMs are built.

Finally, we note that in Aboolian, Berman and Drezner (2006), a minimax-type model of the same problem as that discussed in Berman and Drezner (2007) is introduced (i.e., the objective is to minimize the maximum sum of the travel cost and waiting time cost to customers).

Related location problems with congestion include: the median problem with mobile servers (see for example, Berman et al. (1990)); covering-type models (see for example Marianov and Serra (1998) and Marianov and Rios (2000)); models where demand is a decreasing function of distance and possibly of waiting time (see for example Berman and Drezner (2006)).

This paper is organized as follows. In the next section the problem is formulated. In Section 3 the problem of allocating servers given a facility location is discussed. In Section 4 we discuss solution procedures and in Section 5 computational results are reported. In the last section we conclude with a summary and suggestions for future research.

2. Problem formulation

Let G = (N,L) be a network with a set of nodes N (|N| = n) and a set of links L. We assume that demand is generated at the nodes at a rate of λ _i per unit of time for each i ∈ N. The service rate for all servers is μ customers per unit of time. We also assume that the demand and service rates are both Poisson distributed. Let M⊂ N (|M| = m) be a set of potential locations for service facilities. We assume that there is no limit on the number of servers that can be allocated to each facility. Let d _ij be the shortest distance between i, j ∈ N.

We will use S⊂ M to denote the set of facilities selected. We assume here that customers do not have any information on waiting times at the facilities and therefore they travel to the closest facility in S. For the time being we assume that there are no ties among closest facilities to a customer point. Later we show that with the exact algorithm we develop we can handle the situation when there are several facilities in S with closest equal distance to a customer point. In that case the demand in that point can be divided equally among the tying facilities. If a facility is located at site j, we call it facility j.

Define λ _j (S) to be the arrival rate to facility j∈ S. Then (for simplicity of presentation we assume that there are no tying distances):

where E _j (S) is the set of demand points in N that are closer to facility j than to any other facility in S. The objective function is to minimize the total system cost including the cost of opening a facility (fixed and variable), a customer's travel time, and a customer's waiting time spent at the facilities.

The expected waiting time for service at a facility is a function of the arrival rate, service rate and the number of servers at that facility. Let W _q(λ, μ, k) be the expected waiting time spent at a facility with k servers each having a service rate of μ, when the arrival rate is λ . We denote by k _j (S) the number of servers assigned to facility j∈ S and by vector K(S) = {k _j (S) | j∈ S}, an assignment of servers to the facilities in S.

Let ƒ _j be the fixed cost of installing servers in facility j∈ S, h be the variable server cost, g be the customer's traveling cost per unit of distance per unit of demand, and v be the customer's waiting cost per unit of time per unit of demand. Then, the problem is:

Consider the following decision variables

and k _j is an integer variable representing the number of servers in facility j∈ M.

Note that each facility j∈ S acts as a M/M/k _j (S) queuing system. Let γ _j = ∑ _{i∈ N} λ _i y _ij be the demand rate at facility j∈ M, and let W _q(γ _j ,μ,k _j ) be the waiting time spent at facility j∈ M, which can be computed (see e.g., Winston (1994)), by the following equation:

where ρ _j = γ _j /μ k _j , and P(γ _j ,μ,k _j ) is defined to be the probability that all the k _j servers are busy, and is calculated by

An efficient way for calculating W _q(γ _j ,μ,k _j ) is given in Pasternack and Drezner (1998) and was applied in Berman and Drezner (2007) and in Aboolian, Berman and Drezner (2006).

Given the above definitions, the problem (LASCN) can be formulated as follows:

subject to

Constraints (3) forbid assigning a demand to a non-existent facility. Constraints (4) guarantee that each demand is assigned to a facility. Constraints (5) are to ensure that a customer will visit the facility with the smallest traveling time. In constraints (5), ℒ is a large-enough positive number (e.g., ℒ = max _{j∈ M, i∈ N} {d _ij }). In constraints (8) we ensure that the expected waiting time cannot be negative (it cannot be infinite because the objective function is a minimization). Note that (LASCN) is a highly non-linear integer program because of its objective function. To solve this problem we develop metaheuristics to find near-optimal solutions and a special purpose algorithm to find the optimal solution. In the next section, we show how to find the optimal assignment vector K*(S) = {k _j *(S) | j∈ S} given S.

3. Optimal assignment of servers given a set of facilities

Given S, the objective function can be written as

or

or

where k _j ^min is the minimum number of servers required to serve the demand λ _j (S) for every j∈ S, using

The following property is a direct result of Dyer and Proll (1977).

Property 1. W _q(λ _j (S),μ,k _j ) is decreasing and convex in k _j , i.e., W _q(λ _j (S),μ,k _j +1)−W _q(λ _j (S),μ,k _j ) is increasing.

Define K*(S) to be the optimal server assignment vector given S and F(K*(S)) to be the minimum total cost of the waiting and server costs. For simplicity, throughout the paper we refer to F(K*(S)) as the server assignment cost and K as the server assignment vector.

We can find K*(S) and F(K*(S)) using the following result.

Lemma 1. F _j (k _j ) = hk _j +vλ _j (S)W _q(λ _j (S),μ,k _j ) is convex in k _j , and k _j * (the number of servers which minimizes the cost function F _j (k _j )) can be found by

Proof. F _j (k _j ) is a sum of linear and convex functions and is thus convex.

We now introduce the following algorithm which finds an optimal assignment for a given set of server sites S.

Algorithm 1

• Step 1. Follow Steps 1.1 through 1.5 ∀ j∈ S.

  • 1.1. Find E _j (S) the set of demand points in N such that facility j∈ S is the closest in S. Then set λ _j (S) = ∑ _{i∈ E j (S)}λ _i .

  • 1.2. Find k _j = k _j ^min = int[λ _j (S)/μ] +1.

  • 1.3. If F _j (k _j +1)−F _j (k _j ) ≥ 0 then go to Step 1.5.

  • 1.4. Set k _j = k _j +1 and go to Step 1.3.

  • 1.5. Set k _j *(S) = k _j and F _j (k _j *(S)) = hk _j *(S)+v λ _j (S)W _q(λ _j (S),μ,k _j *(S)).

• Step 2. Stop. K*(S) = {k _j *(S)|j∈ S} is an optimal server assignment and F(K*(S)) = ∑ _{j∈ S} F _j (k _j *(S)) is the optimal server assignment cost found by Algorithm 1.

4. Solution approaches

In this section we present several solution approaches, exact and approximate. First we present a special-purpose methodology which finds the optimal solution. This methodology is based on a location-allocation procedure where in each iteration the sum of the fixed cost of locating facilities and travel cost of customers is minimized to provide the location of facilities. Given the location of facilities, Algorithm 1 provides the optimal assignment cost by minimizing the sum of the variable cost of servers and waiting times of customers. We note that this general idea was also used recently in a competitive location problem (Aboolian, Sun and Koehler (2007)). However, the problem as well as the approaches used to solve the location and allocation problems in our paper and those in Aboolian, Sun and Koehler (2007) are completely different.

4.1. An exact solution approach

By ignoring the server assignment cost in the (LASCN), we immediately obtain the classical Uncapacitated Facility Location Problem (UFLP), for which many effective solution approaches are available even when the dimensionality is large (see e.g., Cornuejols et al. (1990)) and which is formulated as follows:

(UFLP)

subject to

Note that (UFLP) is a special case of (LASCN) where the server assignment cost is not considered. Consider Problem (UFLP(l)) as follows:

(UFLP(l))

subject to Equations (9), (10), (11), (12)

where S*(r) is defined to be the optimal set of server sites for (UFLP(r)). Therefore, to solve (UFLP(l)), we need to solve (UFLP(r)) for r = 1,2,…,l − 1. Also we note that (UFLP(1)) does not include constraints (13). Therefore, (UFLP(1)) is the classical (UFLP) by definition. As explained in Theorem 1 below, constraints (13) ensure that none of the optimal solutions for (UFLP(r)) for r = 1, …, l−1 can be obtained. Therefore, the solution derived in problem (UFLP(l)) is the lth best solution of (UFLP).

Consider the following result.

Theorem 1. Define Z _UFLP(l)* to be the optimal value for the objective function of (UFLP(l)). Then: (i) Z _(UFLP(l))* is non-decreasing in l; and (ii) problem (UFLP(l)) provides the lth best solution of (UFLP).

Proof. We first prove that the role of constraints (13) in (UFLP(l)) is to avoid solutions S*(1), S*(2),…, and 𝒮*(l−1), without forcing any other solution to become infeasible. For any k = 1,2,¨,l−1; consider the following exhaustive cases:

• Case 1. (∑ _j∈S*(r) x _j = |S*(r)|): In this case constraints (13) will result in ∑ _{j∈ M−S*(r)} x _j ≥ 1, which guarantees that the optimal server site location for (UFLP(l)) will never be S*(r).

• Case 2. (∑ _j∈S*(r) x _j < |S*(r)|): In this case constraints (13) will lead to ∑ _{j∈ M−S*(r)} x _j ≥ a _r , where a _r = ∑ _j∈S*(r) x _j −|S*(r)|+1 ≤ 0, which guarantees that any solution other than S*(r) is feasible for (UFLP(l)) and from the condition of the case it is obvious that the optimal server site location for (UFLP(l)) will never be S*(r).

Therefore, we conclude that for any positive integer values p and q where 1 ≤ p < q, the feasible region of (UFLP(q)) is a subset of the feasible region of (UFLP(p)), and since both of these problems have identical values of the objective function, we obtain Z _UFLP(p)* ≤ Z _UFLP(q)* and S*(l) is the lth best solution of (UFLP) and Z*_UFLP(l) is its value. Hence, the proof is complete.

We note that by Theorem 1, we can define Z _UFLP(l)* to be the lth best solution for the (UFLP), which can be found solving (UFLP(l)).

We note that for a given S*(l) (the optimal set of server sites in (UFLP(l))), we can use Algorithm 1 to find K*(S*(l)) = {k _j *(S*(l)) | j∈S*(l)} the optimal server assignment and F(K*(S*(l))) = ∑ _{j∈ S} hk _j *(S*(l))+vλ _j (S*(l))W _q(λ _j (S*(l)),μ,k _j *(S*(l))), the optimal server assignment cost given S*(l). Note that λ _j (S*(l)) = ∑ _{i∈ E j (S*(l))}λ _i .

Denote F ^min to be the minimum server assignment cost, such that F ^min ≤ F(K*(S)) for any S⊂eqN. To find F ^min consider the following results.

Lemma 2. If ρ = γ/μ k, = /μ , ρ ≤ and < k, then P(γ,μ,k) < P(,μ,).

Proof. From Equation (2) we have:

Then,

Since

and

then (P(γ, μ, k))⁻¹− (P(,μ, ))⁻¹ > 0 or P(γ, μ, k) < P(,μ,).

Thus, the proof is complete.

Lemma 3. If ρ = γ/μ k, = /μ , ρ ≤ and < k, then γ W _q(γ,μ,k) < W _q(,μ,).

Proof. From Lemma 2 we have P(γ,μ,k) < P(,μ, ). Since 0 < ρ ≤ , then:

From Equation (1), we obtain γ W _q(γ, μ, k) < W _q(, μ, ).

Thus, the proof is complete.

Theorem 2. Suppose for a given S, we have γ = ∑ _{j∈ S} λ _j (S) and = ∑ _{j∈ S} k _j . Then:

Proof. Let ρ = γ/μ and ρ _j = λ _j (S)/μ k _j , ∀ j∈ S. Consider the following exhaustive cases:

• Case 1. (|S| = 1): In this case γ = λ _j (S) and 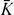= k _j , therefore γ W _q(γ, μ, 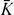) = λ _j (S) W _q(λ _j (S), μ, k _j ).

• Case 2. (|S| > 1 and ρ > ρ _j ∀ j∈ S): By definition 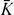= γ/μ ρ = (∑ _{j∈ S} λ _j (S))/μ ρ = ∑ _{j∈ S} (λ _j (S)/μ ρ) < ∑ _{j∈ S} (λ _j (S)/μ ρ _j ) = ∑ _{j∈ S} k _j · This contradicts 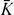= ∑ _{j∈ S} k _j , therefore this case is impossible.

• Case 3. (|S| > 1 and ∃ r∈ S: such that ρ ≤ ρ _r ): Since ρ ≤ ρ _r and 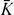> k _r then from Lemma 3, we have γ W _q(γ,μ,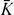) < λ _r (S)W _q(λ _r (S),μ,k _r ), therefore γ W _q(γ,μ,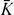) < ∑ _{j∈ S} λ _j (S)W _q(λ _j (S),μ,k _j ).

This concludes the proof.

Theorem 3. Define γ = ∑ _{i∈ N} λ _i , and k** = arg min _{k ≥ int[γ/μ]+1}{hk+vγ W _q(γ,μ,k)}. Then:

Proof. For a given S, we have γ = ∑ _{i∈ N} λ _i = ∑ _{j∈ S} λ _j (S). We also have F(K*(S)) = h∑ _{j∈ S} k _j *(S)+v∑ _{j∈ S} λ _j (S)W _q(λ _j (S),μ,k _j *(S)) ≥ h∑ _{j∈ S} k _j *(S)+vγ W _q (γ,μ,∑ _{j∈ S} k _j *(S)) ≥ hk**+vγ W _q(γ,μ,k**) = F ^min. The first inequality is from Theorem 2, and the second inequality is from the definition of k**. Hence, the proof is complete.

Notice that F ^min is the sever assignment cost when S is a singleton.

Theorem 4. Denote 𝒵 _LASCN* to be the optimal total cost for the (LASCN). Then Z _UFLP(1)*+ F ^min is a lower bound for 𝒵 _LASCN* such that 𝒵 _LASCN* ≥ Z _UFLP(1)*+ F ^min.

Proof. Z*_UFLP(l) is the minimum of the sum of the travel cost and fixed cost, and F ^min is the minimum of the sum of the waiting cost and variable cost. Therefore, Z*_UFLP(l)+ F ^min is a lower bound for the problem.

Now we present the exact algorithm.

Algorithm 2

• Step 0. Set l = 1, and Z ^A = ∞. Find F ^min using Theorem 3.

• Step 1. Solve (UFLP(l)) and find S*(l), the optimal set of server sites in problem (UFLP(l)), and set Z _UFLP(l)* = ∑ _j∈S*(l)(ƒ _j +g∑ _{i∈ E j (S*(l))}λ _i d _ij ). If Z ^A < Z _UFLP(l)*+F ^min then go to Step 4. Otherwise, go to Step 2.

• Step 2. ∀ j∈S*(l), find K*(S*(l)) = {k _j *(S*(l))|j∈S*(l)} using Algorithm 1. Set F(K*(S*(l)) = h∑ _j∈S*(l) k _j *(S*(l))+v∑ _j∈S*(l)λ _j (S*(l))W _q(λ _j (S*(l)),μ,k _j * (S*(l))).

• Step 3. If Z ^A > Z _UFLP(l)*+F(K*(S*(l)), then set Z ^A = Z _UFLP(l)*+F(K*(S*(l)), S ^A = S*(l), K ^A = K*(S*(l)). To find the next best solution for problem (UFLP), set l = l+1 and go to Step 1.

• Step 4. Stop. Output location set is S ^A, output allocation set is K ^A = K*(S ^A) = {k _j *(S ^A) | j∈S ^A}, and the objective function value is Z ^A.

Intuitively, Algorithm 2 starts solving (UFLP(l)) (for l = 1) to find 𝒮*(l), the lth best location for server sites, ignoring the server assignment cost. In Step 1 it also checks to see if this solution may be possibly improved over the current best solution. If it does not, then it stops the algorithm going to Step 4. Otherwise, in Step 2, using Algorithm 1, it finds the optimal server assignment given S*(l). In Step 3, if the total cost of the new solution (including installation, traveling and server assignment costs) is less than the total cost of the current best solution, then the new solution is assumed to be the current best solution. Next, Algorithm 2 looks for the next best solution for (UFLP) (this is done by solving (UFLP(l+1)) in Step 1). This continues until Algorithm 2 reaches a solution in Step 1, for which Z ^A ≤ Z _UFLP(l)*+F ^min.

Note that the S*(l) and Z*_UFLP(l) found when solving (UFLP(l)) will not change whether or not (UFLP(l)) assigns a customer's demand to a single facility or fractions of it to several facilities with equal distances. Therefore, when there are two or more facilities closest to a demand point we can divide the demand equally among the tying facilities in Step 1.1 of Algorithm 1. Therefore, Algorithm 2 can handle the situation when such ties exist.

The following results proves the exactness of Algorithm 2.

Theorem 5. Let Z ^A be the objective function value produced by Algorithm 2. Then Z ^A ≤ Z _UFLP(l)*+F(K*(S*(l)) for l ≥ 1.

Proof. Define = arg min {Z ^A ≤ Z _UFLP(l)*+F ^min} to be the value of l, when Algorithm 2 stops. Consider the following exhaustive cases.

• Case 1. (l < ): In this case by the definition of Step 3 in Algorithm 2 we obtain Z _UFLP(l)*+ F(K*(S*(l))) ≥ Z ^A.

• Case 2. (l ≥ ): In this case by definition of and F ^min, we obtain Z _UFLP(l)*+F(K*(S*(l)) ≥ Z _UFLP(l)*+F ^min ≥ Z _UFLP()*+F ^min ≥ Z ^A. This concludes the proof.

Theorem 6. Let Z ^A be the objective function value produced by Algorithm 2. Let Z*be the optimal objective function value for problem(LASCN). Then Z ^A = Z*.

Proof. Note that given the definition of problem (UFLP(l)), it is easy to verify that ∀ S ⊂eqM, ∃ l integer such that S = S* (l). Now, Theorem 6 follows directly from Theorem 5.

Next we present heuristic algorithms to find approximate solutions for larger problems.

4.2. Approximate approaches

The heuristic approaches are based on the observation that once the set S is selected, the number of servers assigned to each node in S can be found by Algorithm 1. Consequently, the problem is converted to finding the best set S. The proposed metaheuristic approaches are similar to those suggested in Berman and Drezner (2007).

4.2.1. The descent approach

We first define the neighborhood of a set S. Since the cardinality of S is not fixed, we consider in the neighborhood of S: (i) subsets with an additional node; (ii) subsets with one node removed from S; and (iii) adding a node to S and removing another node from S (exchange of nodes). The cardinality of the neighborhood is n+|S|(n−|S|) where |S| is the cardinality of S. Once the neighborhood is well defined, the descent algorithm is straightforward: randomly generate a starting subset S; evaluate the change in the value of the objective function for all the subsets in the neighborhood; if an improved subset exists in the neighborhood, move the search to the best subset in the neighborhood. Repeat the process with the new subset until no improved subset exists in the neighborhood. The last subset is the solution.

Note that adding and removing a node from S can be calculated in two steps, first adding a node and then removing a node. The calculation can be streamlined by evaluating the value of the objective function by adding nodes not in S in order. The value of the objective function for the subset S′ (including an extra node) is calculated. The subset S′ is in the neighborhood. As a second phase, a removal of all the nodes in S from S′ are evaluated. The evaluation of the value of the objective function for subsets with one node from S removed, completes the evaluation of all the subsets in the neighborhood.

4.2.2. Simulated annealing

The simulated annealing approach (Kirkpatrick et al., 1983) simulates the cooling process of melted metals. The variant used in this paper depends on three parameters: the starting temperature T ₀; the number of iterations iter; and the factor α < 1 by which the temperature is reduced every iteration.

Algorithm 3: Simulated annealing

• Step 1. Start with a randomly generated S and calculate F(S). Set the temperature T to T ₀.

• Step 2. Select randomly a move in the neighborhood of S. The move defines S′.

• Step 3. Calculate F(S′).

• Step 4. If F(S′) < F(S) change S to S′ and go to Step 6.

• Step 5. Otherwise,

  	•	Calculate δ = (F(S′)−F(S))/T.
  	•	Change S to S′ with probability e−δ.

• Step 6. Set T = α T and go to Step 2 unless the predetermined number of iterations is reached.

• Step 7. The best encountered solution throughout the process is the resulting solution.

For our test problems the following parameters were used following extensive experimentations: T ₀ = 1000, iter = 2000n, and α = 1− (5/iter).

5. (LASCN) with maximum traveling and waiting time constraints

In practice we may want to limit the customer traveling times to the server sites and the waiting time at a server site. Including the waiting time and traveling time constraints in (LASCN) will result in the following mathematical formulation:

(LASCN2)

where α and β are respectively the maximum traveling distance and the maximum waiting time at the server sites. Note that Equation (16) can be presented in an aggregate fashion ∑ _j y _ij d _ij ≤ α     ∀ i ∈ N.

In this section we show that all methodologies developed in Section 4 can be simply modified to handle constraints (16) and (17). Because of constraints (17), the value of k _j ^min (the minimum number of servers required to serve the demand λ _j (S)) is now computed by

The exact approach for (LASCN) with maximum traveling and waiting time constraints is similar to the one presented in Section 4.1 with the following modifications.

1.	In (UFLP(l)) when y ij d ij > α, replace d ij with a very large number to ensure that y ij * = 0 when solving (UFLP(l)).
2.	Solving Algorithm 1 to find K*(S*(l)) and F(K*(S*(l)), k j min is found using Equation (18).

The approximate approaches for (LASCN) with maximum traveling and waiting time constraints is similar to the approach in Section 4.2 with the following modifications.

1.	When searching for a given set of server sites, S, accept only those assignments which are feasible considering constraints (16).
2.	Solving Algorithm 1 to find K*(S) and F(K*(S), k j min is found using Equation (18).

6. Computational results

We tested the algorithms on the set of 40 Beasley problems which are networks designed for the solution of the p-median problems (Beasley, 1990). The parameters used are: ƒ _j = 1000, ∀ j; λ _i = 1, ∀ i; μ = n/p; v = 1; and h = 50. Two values of g were tested g = 1 and g = 3.

The exact algorithm was coded in C⁺⁺ and we used CPLEX LP/IP Version 9.0 to solve (UFLP(l)). The program was run on a 2.8 GHz laptop computer with a 256 MB RAM. The descent and simulated annealing algorithms were coded in Fortran, compiled by Intel Fortran 9.0, and run also on a 2.8 GHz laptop computer with a 256 MB RAM.

6.1. Experiments with the exact algorithm

The results for the exact algorithm are summarized in Table 1. The third (the seventh) column of the table is the lower bound Z*_UFLP(1)+ F ^min for g = 1 (g = 3). The Best Found Solution (BFS), percent of BFS over the lower bound when the BFS is not known to be optimal and the CPU time are given respectively in the fourth, fifth and sixth columns (eighth, ninth and tenth) for g = 1 (g = 3). Recall that each iteration of the algorithm consists of one set of (UFLP) and the server cost assignment associated with it. We limited the time of an iteration to 30 minutes. Therefore, once a completed iteration took more than 30 minutes the test was terminated and the BFS (which is not known to be optimal) is recorded.

Table 1 Results for the 40 Beasley problems obtained using the optimal algorithm

		g = 1				g = 3
n	p	LB	†	‡	Time ^#	LB	†	‡	Time^#
100	5	10 248.94	10 253.45*		1.67	22 257.94	22 339.20*		33.21
100	10	10 320.82	10 366.95*		9.69	21 945.82	22 556.30*		171.61
100	10	10 715.82	10 770.17*		8.57	22 487.82	22 613.85*		149.33
100	20	11 843.21	11 904.96*		12.71	24 394.21	24 568.71*		231.66
100	33	10 391.79	10 439.79*		4.03	20 968.64	21 136.17*		59.05
200	5	12 488.94	12 499.77*		280.32	28 173.94	28 239.32*		5553.42
200	10	11 425.82	11 439.42*		3.66	26 380.82	26 499.82*		51.69
200	20	13 086.21	13 108.95*		61.23	29 224.21	29 394.23*		1196.54
200	40	13 411.92	13 507.53*		267.76	28 977.92	29 163.62*		5303.65
200	67	12 807.60	12 864.50*		74.87	25 378.60	25 582.60*		1467.79
300	5	11 468.94	11 474.36*		46.73	28 390.94	28 446.28*		908.19
300	10	12 998.82	13 055.52*		235.99	29 780.82	29 896.41	0.388	1824.33
300	30	13 213.97	13 261.76*		127.35	30 078.97	30 187.21*		2011.42
300	60	16 031.15	16 105.54*		1750.56	33 771.15	33 997.11	0.669	1924.02
300	100	16 413.33	16 458.97*		33.15	32 436.33	32 675.89	0.739	1969.05
400	5	12 207.94	12 218.34*		313.34	29 631.94	29 738.04	0.358	2376.85
400	10	13 103.82	13 112.09*		623.15	30 951.82	31 161.63	0.678	2643.19
400	40	15 766.92	15 835.44	0.435	2141.23	35 322.92	35 519.32	0.556	2041.23
400	80	17 395.65	17 502.55	0.615	1878.09	35 737.65	35 976.73	0.669	1973.89
400	133	20 371.45	20 490.53*		1911.96	39 691.45	39 883.52	0.484	2248.62
500	5	13 532.94	13 583.66*		290.20	32 618.94	32 735.81	0.358	2495.08
500	10	15 066.82	15 095.43	0.190	2923.76	35 976.82	36 157.01	0.501	3012.99
500	50	16 719.99	16 796.79	0.459	2173.40	36 222.99	36 432.99	0.580	1987.84
500	100	18 959.33	19 055.31	0.506	1960.25	38 498.33	38 723.70	0.585	2309.71
500	167	21 382.10	21 449.70*		246.79	40 997.71	41 176.87	0.437	2130.55
600	5	14 061.94	14 068.93*		972.44	34 820.94	34 951.78	0.376	1943.57
600	10	13 989.82	13 998.43*		622.91	34 341.82	34 448.27	0.310	1840.19
600	60	16 650.15	16 675.90	0.155	2057.23	36 866.15	37 047.70	0.492	2623.44
600	120	20 241.67	20 357.27	0.571	2318.22	41 074.67	41 330.07	0.622	2217.29
600	200	25 212.69	25 458.00	0.973	1844.18	47 310.69	47 682.25	0.785	22 373.45
700	5	14 497.94	14 550.46	0.362	1843.29	35 112.94	35 179.81	0.190	2168.83
700	10	16 191.82	16 258.24	0.410	12 445.66	38 100.82	38 353.97	0.664	2831.38
700	70	18 885.37	19 009.70	0.658	4889.10	40 727.37	40 975.59	0.609	9837.42
700	140	21 896.57	21 966.78	0.321	5241.08	43 475.57	43 751.41	0.634	9974.75
800	5	14 863.94	14 875.15	0.075	8101.60	36 329.94	36 414.17	0.232	15 436.94
800	10	16 757.82	16 786.73	0.173	13 813.20	40 053.82	40 265.54	0.529	59 143.81
800	80	20 902.65	21 001.32	0.472	7015.04	45 450.65	45 731.96	0.619	17 808.69

The following conclusions are drawn from the table.

1.	When n ≤ 300 and g = 1 (n ≤ 200 and g = 3) the exact algorithm was able to find the optimal solution in a reasonable time for all problems.
2.	When n ≥ 700 and g = 1 (n ≥ 400 and g = 3) the algorithm failed to find an optimal solution in a reasonable time for all problems.
3.	Even when the optimal solution is not found the best solution is very close to the lower bound (results in columns 5 and 9 are less then 1% away from the lower bound).
4.	When n = 900 for all problems, CPLEX ran out of memory and even the first iteration could not be computed.

We also performed sensitivity analysis on the parameters of the problem. In Table 2, for the first Beasley problem with n = 100 and p = 5 we let μ, h, v, g, ƒ _j and λ _i change respectively in rows 1–4, 5–9, 10–14, 15–19, 20–24 and 25–28.

Table 2 Varying parameters for the first Beasley problem (n = 100, p = 5)

							Optimal algorithm		Descent
ƒ j	h	g	v	λ i	μ	LB	BFS	Time ^#	BFS	†	Time ^#
1000	50	1	1	1	1	15 084.33	15 130.20*	8.87	15 130.20*	1000	5.14
1000	50	1	1	1	5	11 011.21	11 039.78*	5.91	11 039.78*	1000	4.80
1000	50	1	1	1	10	10 502.82	10 513.68*	1.72	10 513.68*	1000	4.64
1000	50	1	1	1	20	10 248.94	10 253.45*	1.67	10 253.45*	1000	4.61
1000	50	1	1	1	20	10 248.94	10 253.45*	1.67	10 253.45*	1000	4.50
1000	250	1	1	1	20	11 448.94	11 453.45*	1.68	11 453.45*	1000	4.98
1000	500	1	1	1	20	12 948.94	12 953.45*	1.68	12 953.45*	998	5.66
1000	750	1	1	1	20	14 448.94	14 453.45*	1.71	14 453.45*	940	6.44
1000	1000	1	1	1	20	15 948.94	15 953.45*	1.67	15 953.45*	931	6.62
1000	50	1	1	1	20	10 248.94	10 253.45*	1.67	10 253.45*	1000	4.69
1000	50	1	5	1	20	10 260.69	10 283.27*	3.59	10 283.27*	1000	4.59
1000	50	1	10	1	20	10 275.38	10 320.53*	8.86	10 320.53*	1000	4.55
1000	50	1	15	1	20	10 290.06	10 347.55*	8.79	10 347.55*	1000	4.58
1000	50	1	20	1	20	10 304.75	10 364.74*	8.93	10 364.74*	1000	4.64
1000	50	1	1	1	20	10 248.94	10 253.45*	1.67	10 253.45*	1000	4.53
1000	50	2	1	1	20	16 940.94	16 986.30*	9.63	16 986.30*	1000	9.83
1000	50	3	1	1	20	22 257.94	22 339.26*	33.21	22 339.26*	1000	18.19
1000	50	4	1	1	20	27 006.94	27 156.23*	1059.32	27 156.23*	891	28.78
1000	50	5	1	1	20	31 232.94	31 492.67	1801.57	31 492.67	471	32.80
100	50	1	1	1	20	5149.94	5750.04	1811.38	5639.65	98	49.39
250	50	1	1	1	20	6978.94	7110.07	1806.41	7110.07	997	26.44
500	50	1	1	1	20	8621.94	8651.30*	51.65	8651.30*	1000	9.67
750	50	1	1	1	20	9637.94	9651.30*	9.85	9651.30*	822	7.09
1000	50	1	1	1	20	10 248.94	10 253.45*	1.67	10 253.45*	1000	4.67
1000	50	1	1	1	20	10 248.94	10 253.45*	1.67	10 253.45*	1000	4.67
1000	50	1	1	2	20	17 194.82	17 284.55*	55.88	17 284.55*	1000	10.88
1000	50	1	1	3	20	22 765.95	22 900.74*	343.61	22 900.74*	1000	18.44
1000	50	1	1	4	20	27 769.21	27 990.59	1802.36	27 990.59	831	27.64

We make the following observations.

1.	The computational time is a decreasing function in μ.
2.	The computation time is a non-increasing function in ƒ j (looks convex), in fact when ƒ j ≤ 250, the optimal solution is not attainable in a reasonable amount of time. Note that this is for n = 100, the smallest size problem in Beasley's samples.
3.	The computational time is a non-decreasing function in v (looks concave).
4.	The exact method's computational time is a non-decreasing function (looks convex) in g and λ. In fact when g ≥ 5 or λ i ≥ 4, the optimal solution is not attainable in a reasonable amount of time.
5.	The exact method's computational time is independent of h.

6.2. Experiments with the heuristic algorithms

The results of the heuristic algorithms are listed in Table 3 and Table 4. The descent algorithm was repeated 1000 times from 1000 randomly generated starting solutions. The simulated annealing was repeated ten times for each instance so as to require a comparable run time. The BFS (including all known optimal solutions) were found by the descent algorithm and simulated annealing for all problems.

Table 3 Results for the 40 Beasley problems for g = 1 using the heuristic algorithms

				Descent			Sim. annealing
n	p	LB	BFS	†	‡	Time ^#	†	‡	Time ^#
100	5	10 248.94	10 253.45*	1000	0.000	4.77	10	0.000	4.02
100	10	10 320.82	10 366.95*	1000	0.000	4.50	10	0.000	3.94
100	10	10 715.82	10 770.17*	1000	0.000	6.08	10	0.000	5.06
100	20	11 843.21	11 904.96*	1000	0.000	6.88	10	0.000	5.08
100	33	10 391.79	10 439.79*	1000	0.000	4.77	10	0.000	4.30
200	5	12 488.94	12 499.77*	772	0.181	21.30	10	0.000	20.38
200	10	11 425.82	11 439.42*	1000	0.000	15.53	10	0.000	16.33
200	20	13 086.21	13 108.95*	918	0.062	16.78	10	0.000	16.72
200	40	13 411.92	13 507.53*	1000	0.000	21.66	10	0.000	20.83
200	67	12 807.60	12 864.50*	723	0.021	16.94	9	0.008	17.16
300	5	11 468.94	11 474.36*	1000	0.000	35.16	10	0.000	37.59
300	10	12 998.82	13 055.52*	1000	0.000	51.09	10	0.000	48.12
300	30	13 213.97	13 261.76*	1000	0.000	39.73	10	0.000	38.52
300	60	16 031.15	16 105.54*	806	0.077	47.98	8	0.080	50.06
300	100	16 413.33	16 458.97*	1000	0.000	40.52	10	0.000	40.11
400	5	12 207.94	12 218.34*	1000	0.000	70.81	10	0.000	79.14
400	10	13 103.82	13 112.09*	1000	0.000	72.25	10	0.000	79.91
400	40	15 766.92	15 835.44	495	0.020	78.94	5	0.020	90.44
400	80	17 395.65	17 494.36	1000	0.000	82.70	10	0.000	82.47
400	133	20 371.45	20 490.53*	1000	0.000	84.48	10	0.000	97.17
500	5	13 532.94	13 583.66*	1000	0.000	124.69	10	0.000	160.44
500	10	15 066.82	15 095.43	385	0.047	124.59	6	0.031	157.83
500	50	16 719.99	16 796.79	1000	0.000	131.41	10	0.000	162.36
500	100	18 959.33	19 055.31	1000	0.000	150.31	10	0.000	170.05
500	167	21 382.10	21 449.70*	1000	0.000	104.62	10	0.000	137.39
600	5	14 061.94	14 068.93*	1000	0.000	158.58	10	0.000	225.17
600	10	13 989.82	13 998.43*	1000	0.000	154.39	10	0.000	227.48
600	60	16 650.15	16 675.90	1000	0.000	155.55	10	0.000	232.47
600	120	20 241.67	20 357.27	1000	0.000	186.61	10	0.000	268.59
600	200	25 212.69	25 289.25	1000	0.000	175.02	10	0.000	240.75
700	5	14 497.94	14 503.09	1000	0.000	229.64	10	0.000	333.41
700	10	16 191.82	16 239.71	165	0.061	234.98	4	0.036	352.80
700	70	18 885.37	18 958.39	494	0.121	252.22	7	0.068	384.91
700	140	21 896.57	21 966.78	442	0.294	224.25	5	0.289	382.88
800	5	14 863.94	14 875.15	670	0.017	291.75	6	0.021	547.02
800	10	16 757.82	16 785.41	735	0.056	314.59	9	0.018	526.94
800	80	20 902.65	20 996.60	478	0.010	323.42	5	0.009	535.72
900	5	15 477.77 ^$	15 707.14	1000	0.000	388.62	10	0.000	677.59
900	10	15 664.60 ^$	15 684.45	1000	0.000	351.64	10	0.000	673.50
900	90	21 379.10 ^$	21 553.17	1000	0.000	466.33	10	0.000	766.88
Average:				877	0.024	131.65	9.1	0.015	198.04

Table 4 Results for the 40 Beasley problems for g = 3 using the heuristic algorithms

				Descent			Sim. annealing
n	p	LB	BFS	†	‡	Time ^#	†	‡	Time^#
100	5	22 257.94	22 339.20*	1000	0.000	19.06	10	0.000	8.78
100	10	21 945.82	22 556.30*	365	0.137	21.33	7	0.066	9.30
100	10	22 487.82	22 613.85*	1000	0.000	21.59	10	0.000	9.28
100	20	24 394.21	24 568.71*	1000	0.000	19.86	10	0.000	8.14
100	33	20 968.64	21 136.17*	973	0.034	16.89	10	0.000	8.12
200	5	28 173.94	28 239.32*	738	0.063	80.44	9	0.024	36.33
200	10	26 380.82	26 499.82*	1000	0.000	59.73	10	0.000	31.34
200	20	29 224.21	29 394.23*	979	0.019	84.94	10	0.000	35.77
200	40	28 977.92	29 163.62*	137	0.037	62.33	3	0.026	30.45
200	67	25 378.60	25 582.60*	960	0.035	59.22	10	0.000	32.23
300	5	28 390.94	28 446.28*	1000	0.000	114.30	10	0.000	64.94
300	10	29 780.82	29 896.41	496	0.024	169.88	6	0.019	84.75
300	30	30 078.97	30 187.21*	715	0.032	93.69	8	0.022	61.67
300	60	33 771.15	33 997.11	228	0.199	212.52	3	0.155	92.50
300	100	32 436.33	32 675.89	1000	0.000	162.97	10	0.000	84.22
400	5	29 631.94	29 738.04	847	0.050	313.97	9	0.033	162.81
400	10	30 951.82	31 161.63	269	0.019	347.17	6	0.011	171.58
400	40	35 322.92	35 519.32	325	0.097	316.14	6	0.047	156.70
400	80	35 737.65	35 976.73	360	0.065	328.36	6	0.022	157.69
400	133	39 691.45	39 983.53	1000	0.000	391.69	10	0.000	166.09
500	5	32 618.94	32 735.81	1000	0.000	394.42	10	0.000	234.61
500	10	35 976.82	36 150.49	675	0.067	596.70	9	0.012	278.23
500	50	36 222.99	36 432.99	774	0.041	557.12	8	0.025	279.38
500	100	38 498.33	38 723.70	728	0.113	461.42	8	0.085	243.62
500	167	40 997.71	41 176.87	1000	0.000	281.73	10	0.000	202.33
600	5	34 820.94	34 929.27	711	0.076	733.22	9	0.032	402.30
600	10	34 341.82	34 448.27	623	0.116	502.39	6	0.123	341.89
600	60	36 866.15	37 047.70	977	0.010	658.02	10	0.000	386.80
600	120	41 074.67	41 330.07	373	0.015	673.19	5	0.015	400.61
600	200	47 310.69	47 682.25	583	0.056	980.81	7	0.027	459.94
700	5	35 112.94	35 179.81	685	0.048	955.45	9	0.013	595.80
700	10	38 100.82	38 353.97	1000	0.000	1338.22	10	0.000	658.64
700	70	40 727.37	40 965.91	445	0.035	1155.12	6	0.024	646.98
700	140	43 475.57	43 751.41	1000	0.000	1151.42	10	0.000	620.45
800	5	36 329.94	36 414.17	1000	0.000	1340.23	10	0.000	781.94
800	10	40 053.82	40 265.54	520	0.035	1707.34	9	0.006	870.75
800	80	45 450.65	45 731.96	986	0.007	2396.27	10	0.000	972.11
900	5	37 489.60 ^$	38 240.57	525	0.029	1789.77	5	0.035	1075.17
900	10	37 960.32 ^$	38 588.05	271	0.063	1622.61	2	0.063	1147.20
900	90	45 638.67 ^$	46 002.87	1000	0.000	2236.08	10	0.000	1242.75
Average:				731.7	0.038	610.69	8.15	0.022	331.35

For g = 1 (Table 3) we draw the following conclusions.

1.	The descent algorithm found the BFS at least 165 times out of 1000 replications for each problem.
2.	It found the BFS in all 1000 replications for 28 of the 40 problems.
3.	It found the BFS in 87.7% of the runs and the average solution was 0.024% over the BFS.
4.	The simulated annealing found the BFS at least four times out of ten replications.
5.	It found the BFS in all ten runs for 30 of the 40 problems.
6.	It found the BFS in 91% of the runs and the average solution was only 0.015% over the BFS.

For g = 3 (Table 4) we draw the following conclusions:

1.	The descent algorithm found the BFS at least 137 times out of 1000 replications for each problem.
2.	It found the BFS in all 1000 replications for 13 of the 40 problems.
3.	It found the BFS in 73.17% of the runs and the average solution was 0.038% over the BFS.
4.	The simulated annealing found the BFS at least twice out of ten replications.
5.	It found the BFS in all ten runs for 18 of the 40 problems.
6.	It found the BFS in 81.5% of the runs and the average solution was only 0.022% over the BFS.

Both heuristic algorithms performed extremely well. The g = 3 problems are somewhat harder to solve by the heuristic algorithms compared to the case when g = 1.

7. Conclusions and future research

In this paper we discussed the problem of locating facilities and allocating p servers to the facilities where the facilities behave as M/M/k queueing systems. The objective is to minimize the total cost of the system that is comprised of the fixed cost of opening facilities, the variable cost of servers, the travel cost and the waiting cost of customers.

The paper includes an exact algorithm and heuristics to solve the problem. The exact algorithm is a location allocation procedure. Given a set of facilities the problem of minimizing the server assignment costs is easy since it is proved that the server assignment cost for each facility is convex in the number of servers. Ignoring the server assignment cost the problem is a (UFLP). The overall algorithm is to solve in each iteration a (UFLP) that provides the facilities locations and for each set of locations Algorithm 1 is used to minimize the server assignment cost.

Two heuristic approaches are suggested in the paper: the descent approach and simulated annealing. Both heuristics performed very well (better for a small travel cost) in terms of CPU time and solution quality.

The exact algorithm performs well in terms of CPU time for medium (small) sized problems when the cost of travel is not large (large) and therefore not many (relatively many) facilities are required. The solution quality of the exact algorithm when the time for iterations is limited to 30 minutes is very good. Also, the exact algorithm becomes less efficient when the (waiting cost + variable cost) is not a small portion of the total cost. We see this point in Table 2, where it takes much more time to solve the problem when the fixed cost is small (100 and 250). Therefore, we suggest for future research to develop an exact algorithm to solve the problems more efficiently when the total waiting and variable cost is a significant part of the total cost. We believe that a promising direction is to obtain a tighter lower bound. We know that F ^min, the lower bound for server assignment cost, is based on the case when |S| = 1. Note that we can get tighter lower bounds based on |S| > 1 but finding those values seems to be quite hard. If we can come up with some theoretically sound lower bounds based on any given |S| (and note that as |S| gets larger, the bounds get tighter), we would be able to avoid a lot of solutions for (UFLP(l)) by enforcing the flowing constraint:

where F ^min(p) is defined to be the lower bound for server assignment cost when we locate p facilities.

Other suggestions for future research are:

i.	to study the problem discussed in the paper when there are bounds on the number of servers and on the number of facilities;
ii.	to study the problem discussed in the paper when locating facilities on the plane; and
iii.	to extend the problem to consider also finding optimal pricing for a monopolist when customer demand is a function of price, distance and waiting times.

Biographies

Robert Aboolian is an Assistant Professor of Operations and Supply Chain Management at the College of Business at the California State University San Marcos. He received his PhD (2002) in Operations Management from the Joseph L. Rotman School of Management at the University of Toronto. His main research interests include location theory, supply chain management and discrete optimization. He has published several articles in refereed journals such as European Journal of Operational Research, Annals of Operations Research, and Journal of Operational Research Society.

Oded Berman is the endowed Sydney Cooper Chair in Business and Technology and the former Associate Dean of Programs at the Joseph L. Rotman School of Management at the University of Toronto. He received his PhD (1978) in Operations Research from the Massachusetts Institute of Technology. He had been with the Electronic Systems Lab at MIT, the University of Calgary, and the University of Massachusetts at Boston, where he was also the Chairman of the Department of Management Science. He has published over 170 articles and has contributed to several books in his field. His main research interests include operations management in the service industry, location theory, network models, and software reliability. He is an Associate Editor for Management Science and Transportation Science, and a member of the Editorial Board for Computers and Operations Research.

Zvi Drezner is a Professor of Information Systems and Decision Sciences at California State University, Fullerton. He received his BSc in Mathematics and PhD in Computer Science from the Technion, Israel Institute of Technology. His research interests are in location theory, metaheuristics and computational statistics. He edited two books and published over 200 articles in refereed journals such as Operations Research, Management Science, IIE Transactions, Naval Research Logistics and others.

Acknowledgements

This paper was partially supported by a NSERC grant awarded to the second author. We would like to thank the referees and associate editor for valuable comments.

Notes

*Optimal.

^†The BFS (or optimal solution).

^‡Percent of BFS over the lower bound.

^#Time in seconds.

*Optimal.

^†Number of times BFS found (out of 1000 replications).

^#Time in seconds (for all 1000 runs for descent).

*Optimal.

^$Lower bound by solving the continuous (UFLP).

†Number of times BFS found (out of 1000 for Descent, ten for simulated annealing).

‡Percent of average solution over the BFS.

^#Total time in seconds for all runs.

*Optimal.

^$Lower bound by solving the continuous (UFLP).

†Number of times BFS found (out of 1000 for Descent, ten for simulated annealing).

‡Percent of average solution over the BFS.

^# Total time in seconds for all runs.