Decentralized multi-product multi-stage systems with backorders

Abstract

A multi-stage production/inventory system with decentralized two-card kanban control policies producing multiple product types is considered. The system involves one-at-a-time processing at each stage, finite target levels in the buffers and batch transfers between production stages. The demand process for each product is assumed to be Poisson and excess demand is backordered. Products have a priority structure and the processor at each stage is shared according to a switching rule. Our objective is to obtain steady-state performance measures such as the average inventory and service levels for each product type. We propose an approximation algorithm based on: (i) characterization of the delay by a product type before receiving the processor's attention at each stage; and (ii) creation of subsystems for all the storage activity and phase-type modeling of the remaining system's behavior. Numerical examples are presented to show the accuracy of the method and its potential use in system design.

Keywords:

• Decentralized systems
• multi-product
• multi-stage
• pull-type
• backorders

1. Introduction

Pull systems have become quite common in manufacturing industries, particularly in large-scale companies and in repetitive manufacturing environments (White et al., 1999; Fullerton and McWatters, 2001). The kanban mechanism that is the backbone of pull systems provides a simple way of implementing a pull control policy by transferring information from a downstream stage to an upstream one in a production/inventory system (Buzacott and Shantikumar, 1992; Monden, 1993; Bonvik et al., 1997; Karaesmen and Dallery, 2000).

Existing pull-type multi-stage systems rely on the application of either one-card or two-card kanban systems. One-card systems are used in industrial settings that consist of a flow line within a single location with production stages close enough to each other to ignore material handling. It is assumed that products are processed one at a time at each stage and that once the production of a part is completed, it is immediately transferred to the next stage. Two-card systems, on the other hand, control both production and material handling operations. Typically, they involve not only moving materials in batches but also producing in batches, mainly due to high set up costs and/or set up times associated with delivering products to buffers.

Neither system seems adequate to address current trends in the manufacturing industry. First, with the spread of distributed/decentralized manufacturing, the concept of periodic material transfer has become quite widespread in many supply chain systems, where semi-finished units are transferred from one facility to another in fixed lot sizes and/or in fixed time intervals. Tax advantages, lower labor costs or the availability of high tech processes and laboratories promote this type of manufacturing even within the same enterprise. Second, production line designers are increasingly using reconfigurable manufacturing equipment to achieve rapid and low cost changeovers between different product types allowing processing of parts one at a time.

The production/inventory system we have considered is a combination of one-card and two-card kanban systems, and involves unit production at each stage with the transportation of material from one stage to another being in fixed lot sizes. The system corresponds to a serial chain of centers involving production, procurement and inventory holding activities. Two buffers, one for input and the other for output, are located at each stage to control production and procurement operations. The system is market driven in the sense that the actual customer demand triggers final stage production and then information is transmitted upstream initiating production and procurement at each stage. The system is decentralized since the production and the procurement decisions at each stage are solely based on the state of that stage. Each stage produces and makes the procurement according to the demand generated by the immediate downstream stage. At each stage, production starts as the inventory level drops below the reorder level r and it continues until the target inventory level R is achieved. This two-level control policy is known as the continuous-review (R, r) policy, which is a generalized case of a base stock policy with r = R − 1 (Gavish and Graves, 1980).

Procurement operations are performed periodically based on a fixed-quantity, non-constant withdrawal cycle (Q, q) policy (De Bodt and Graves,1985). When the inventory level in the input buffer at a stage drops to q, an order of size Q is transferred from the immediate upstream stage. There is another material handling policy discussed in the literature, called the fixed-withdrawal cycle, variable-order quantity policy, in which accumulated units are withdrawn at fixed time intervals with the number of units withdrawn being a variable (Savsar, 1996). Following common practice in the just-in-time literature we did not consider this approach.

For single-product one-card systems, exact solutions were obtained for networks of small size using numerical techniques. Motivated by difficulties in the exact analysis, a number of approximation methods were developed. These studies typically analyze multi-stage systems using state space decompositions of the underlying Markov chains. Mitra and Mitrani (1990, 1991) decomposed a multi-stage, single-product system into semi-autonomous subsystems, each consisting of a single kanban cell supplied with raw parts from the upstream and with demands from the downstream. Fujiwara et al. (1998) extended this analysis to systems in which a number of raw parts are procured from different suppliers that are then assembled to produce a single product. Both studies considered two buffers at each production stage, as do we in this paper, but parts were transferred from one stage to another one at a time. Hence, their kanban system is equivalent to a system of buffers in tandem working under the minimal blocking policy (Bonvik et al., 1997). In another approach, Di Mascolo et al. (1996) applied product-form approximations with load-dependent service times to solve the subsystems. Baynat et al. (2001) showed how to extend the earlier product-form approximation methods to more general kanban systems such as assembly and disassembly systems, but still with only one type of product.

In all the aforementioned studies the upstream stage was assumed to respond immediately to a demand coming from the downstream stage. However, in many multi-stage production/inventory systems, either due to set up times or the presence of multiple product types, production at a stage may be deferred until a sufficient number of orders accumulate. This necessitates an (R, r) continuous-review control policy, which we also assume in this paper. The magnitude of R − r at each stage depends on the existence and the magnitude of the set up time or the set up cost. Chaouiya et al. (2000) and Dallery and Liberopoulos (2000) introduced an extended kanban control system that combines classical kanban system with a base stock policy.

Even though pull systems in practice involve the production of several products (Anupindi and Tayur, 1998), the literature on multi-product, pull-type systems with finite target inventory levels is rather limited. In a multi-product setting the underlying stochastic process is quite intricate due to random delays that may occur when the processor is occupied with other product types at the point at which a product requests attention. This high level of interaction among the products can be expressed in terms of delays they experience prior to production. Altiok and Shiue (1994, 2000) related this delay phenomenon to “server vacations” and split a multi-product system into several single-product systems that were analyzed as M/G/1 queues with vacations. Krieg and Kuhn (2002, 2004) also used the vacation analogy in a one-card system with a fixed switching sequence among product types. All these analytical studies on multi-product one-card kanban systems are confined to single-stage settings.

Simulation studies have been extensively performed on two-card kanban systems (Abdou and Dutta, 1993; Berkley, 1996; Savsar, 1996). Blocking caused by finite capacity buffers and periodic procurement makes the analytical modeling of two-card multi-stage systems a challenging task. Two-card systems using batch sizes of one in transporting material between stages are equivalent to one-card systems and can be analyzed as tandem queues. However, when material transport is periodic, and consequently the batch size is greater than one, kanban systems differ from a tandem queue and the analyses of such systems becomes a lot more involved. Gurgur and Altiok (2004) have used a two-node decomposition method to analyze single-product, multi-stage pull systems with a two-card control policy. The present paper extends this scenario to the case with multiple products.

The main contribution of this paper is to show how interdependencies among the products can be characterized by analyzing the delay periods they experience before being processed. Characterization of delay periods helps us unravel the interactions among different product types competing for a single processor. This enables us to split the original system into several single-product, multi-stage systems (one for each product) by treating the delay period as an additional phase a processor has to go through before being assigned to a product type. The analysis of each single-product system originates from the decomposition approach discussed in Gurgur and Altiok (2004), and involves the creation of subsystems for all the storage activities and phase-type modeling of the remaining system behavior. However, due to interactions among the products in the evaluation of delay parameters, the characterization of subsequent subsystems is different from that of Gurgur and Altiok (2004). A subsystem of a particular product interacts with subsystems of all the other products in the evaluation of delay parameters. Since the delay period of a product involves conditional probabilities belonging to other products, its calculation requires an iterative characterization of the subsystems of all the products involved in the output buffer at that stage. We show that the proposed analytical method is quite efficient and yields near-exact approximations for system-wide performance measures, such as average inventory levels, probability of backordering and consequently service levels for each product type.

Note that our analytic approach can be also used to analyze a one-card system in a multi-product, multi-stage setting, when the lead time in material handling operations is negligible and the batch size in transportation is equal to one. In that case the input and output buffers between two stages operate as a single buffer controlled by an (R*, r*) policy, where R* = R + q + 1 and r* = r + q + 1, and a two-card system is transformed into a one-card system.

In the next section, a description of a decentralized, multi-stage, multi-product, market-driven system is described in detail. The analytical approach and the approximation technique are presented in Section 3. Numerical examples in Section 4 evaluate the accuracy of the approximation by comparing its estimates against simulation results. We present an optimization problem in Section 5 and discuss how the approximation algorithm can be embedded with a numerical search technique to find optimal production and procurement control parameters. Section 6 concludes the paper.

2. Description of the production/inventory system

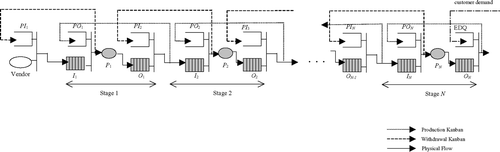
The production/inventory system we consider involves a vendor at the upstream and M product types processed in N stages arranged in series as shown in Fig. 1. Stage j has a processor P _j , an input buffer I _j and an output buffer O _j . Each product retains a preallocated space in I _j and O _j at stage j. Demand for a single unit of product i arrives at the warehouse O _N , following a Poisson process with rate λ (i). It is assumed that unsatisfied customer demand is backlogged. Processor P _j can process several different product types, one at a time. Furthermore, the processing time of product i at stage j is assumed to be exponentially distributed with rate μ _j (i).

Fig. 1 A multi-stage, decentralized, market-driven system.

Two types of kanban cards are used to facilitate information flow within the system: (i) a production kanban that serves as the work release order at each stage; and (ii) a withdrawal kanban that serves as the transfer order between consecutive stages. Production kanbans are attached to finished products residing in the output buffers, whereas withdrawal kanbans are attached to work-in-process parts waiting in the input buffers. The number of kanbans represents the maximum inventory that can be carried by a buffer.

When a part departs from O _j , the associated production kanban is sent back to the production order pool, PO _j at stage j. Similarly, once a semi-finished product i is taken from I _j to be processed at P _j , the withdrawal kanban of product i is dispatched to the procurement order pool, PI _j at stage j − 1. A kanban placed in PO _j or PI _j becomes active signaling a demand from the downstream. The accumulation of a sufficient number of active kanbans initiates a production or a transportation operation, as explained below.

When to start and stop producing a product at each stage is handled by an (R, r) continuous-review policy. Stage j has R _j (i) production kanbans for product i . Once R _j (i) − r _j (i) production kanbans of product i pile up in PO _j , a request is made to P _j to resume production of product i. At this point r _j (i) units of product i reside in O _j . When the production starts, it continues until all production kanbans of product i in PO _j are cleared. Note that the production order pool PO _j and the input buffer I _j work as assembly queues, i.e., production starts only if a semi-finished good in I _j is combined with a production kanban from PO _j . The magnitude of R −r at each stage depends on the existence and the magnitude of the set up time or the set up cost. Since we assume quick processor set ups, we do not explicitly model set up times. It is, however, our intention to assume the more general (R, r) policy to accommodate a stage's involvement in production of other product types.

In a multi-product setting, since a processor pays attention to many product types, a delay is inevitable in diverting production from one product to another. If the processor is busy, then the production order of product i has to wait until it receives the processor's attention. We assume product 1 has the highest priority and product M has the lowest priority in the entire system. We have employed a dynamically changing priority structure to restrict the number of switchovers among higher priority products. Under this priority structure, a production order of product i cannot be delayed more than once by the orders of another product that has a higher priority. Consequently, low-priority products are not ignored for long periods.

To gain more insight about the working of this priority structure, consider a three-product system. Suppose that product B is being processed at the moment and product C is in the queue waiting to be processed. Then, a production order for product A is received. Since product A has a higher priority, product C slips into second place in the queue. When the machine finishes its work with product B, product A will take its place and start being processed. Product C keeps on waiting. If during that time another order for product B arrives, this time product C will not give up its place. Instead, product B will wait in the queue behind product C.

Procurement from one stage to another is made according to a fixed-quantity, non-constant withdrawal cycle, which is also known as a (Q, q) policy. Stage j has Q _j (i) + q _j (i) withdrawal kanbans for product i . Once Q _j (i) withdrawal kanbans of product i accumulate in procurement order pool PI _j , an order is given to O _{j − 1} to transfer Q _j (i) units of product i to I _j . At this point q _j (i) units of product i reside in I _j . The procurement order is fulfilled once Q _j (i) units accumulate in O _{j − 1}. Hence, the procurement order pool PI _j and output buffer O _{j − 1} work as assembly queues, i.e., a shipment to I _j occurs only if semi-finished goods from O _{j − 1} are combined with withdrawal kanbans at PI _j . The transportation time from O _{j − 1} to I _j for product i is exponentially distributed with rate γ _j (i). The same procurement policy is also used to provide raw material from the vendor at the upstream. The vendor lead time of product i is also assumed to be exponentially distributed with rate γ ₁(i).

3. Analytical approach

We first address the interdependencies among the products, which are expressed in terms of the delay periods they experience before they start being processed. Once the delay periods are characterized, we model them as exponentially distributed random variables. This is an approximation since the delay periods do not necessarily have an exponential distribution. We treat each delay period as an additional phase a processor has to go through before processing each product type. This enables us to reduce the original system into a set of multi-stage, single-product systems, which can be analyzed in isolation.

After partitioning the system into M multi-stage, single-product systems (one for each product), we decompose each multi-stage, single-product system into 2N subsystems, resulting in 2NM subsystems in total. Each subsystem consists of a storage activity (an input or an output buffer) and two pseudo-processors around the storage activity representing the remaining view of the original system. Phase-type modeling of processing times of the pseudo-processors gives rise to a tractable analysis based on Continuous-Time Markov Chains (CTMCs). The analysis of subsystems is carried out in isolation and then integrated using a fixed-point iteration algorithm.

We used several assumptions and approximations in the analytical approach. Some of them are the result of mathematical necessity, i.e., the underlying (conditional) probabilistic expressions were too complicated to offer exact analytical solutions. When this was the case we used certain simplifying assumptions (most commonly, independence of product types from each other) to solve these expressions.

In other cases, we used approximations to increase the speed of the algorithm. For example, we modeled the delay period as a single-phase random variable, even though it may have thousands of phases depending on the location of the corresponding processor).

These assumptions and approximations, naturally, caused our analytical model to express different characteristics than the actual system. To quantify the magnitude of this deviation in system behavior, we compared performance metrics obtained from the analytical approach with those obtained from simulation. Numerical results in Section 4 quantify the cumulative loss in the accuracy of the analytical approach caused by approximations and assumptions.

The simulation model truly reflects the model described in Section 2; thus, the performance measures obtained from simulation provide true values of the performance metrics (within a certain confidence interval) at the steady state. Since none of these approximations were included in the simulation model, they did not affect the simulation results.

We introduce the following notation.

Ω j (i)	=	subsystem of product i involving I j ;
Ω ′ j (i)	=	subsystem of product i involving O j ;
ō j (i)	=	throughput of subsystem Ω j (i);
ō′ j (i)	=	throughput of subsystem Ω ′ j (i);
M′ j (i)	=	pseudo-processor modeling the procurement of product i to I j ;
N′ j (i)	=	pseudo-processor modeling the production of product i to O j ;
M″ j (i)	=	pseudo-processor modeling the demand arrival process of product i at I j ;
N″ j (i)	=	pseudo-processor modeling the demand arrival process of product i at O j ;
U′ j (i)	=	processing time at M′ j (i), i.e., the time needed to procure Q j (i) units of product i to I j ;
U″ j (i)	=	processing time at M″ j (i), i.e. the time between two successive departures of product i from I j ;
V′ j (i)	=	processing time at N′ j (i), i.e., the time between two successive arrivals of product i at O j ;
V″ j (i)	=	processing time at N″ j (i), i.e., the time between two successive departures of batches of size Q j (i) of product i from O j ;
NI j (i)	=	inventory level of product i at I j ;
NO j (i)	=	inventory level of product i at O j .

3.1. Characterization of delay periods

The delay period experienced by a product when it requests a processor's attention depends on two factors: (i) the characteristics of the product type being produced at that time; and (ii) the additional delay that may occur if the processor switches to a higher priority product. We express the delay period of a product in terms of the parameters of the other products.

At the point an incoming demand for product i sees NO _j (i) = r _j (i) + 1 units in O _j , it depletes the inventory level to r _j (i) and a production order is placed for product i. The production of product i is delayed if P _j is working on another product type. Let Pr (P _j = m| NO _j (i) = r _j (i) + 1) be the probability that P _j is processing product m at the point product i requests attention and D _j (i|m) be the associated delay of product i at stage j due to product m. Then, the expected delay D _j (i) of product i at stage j is given by

D _j (i|m) consists of two parts: (i) the time W _j (i, m) needed for P _j to bring the inventory level NO _j (m) of product m in O _j to the target level R _j (m); and (ii) the delay S _j (i, m) due to the switching of P _j (after processing product m) to products with a higher priority than product i:

W _j (i, m) is the sum of the residual processing time _j (i, m) of one unit of product m at stage j at the time product i makes the request, and the processing time of the remaining units of product m, where each has a processing time of X _j (m). Let Pr( NO _j (m) = k|P _j = m, NO _j (i) = r _j (i) + 1) be the probability that at the point product i requests P _j , there are k units of product m (for k = 0, 1, …, R _j (m) −1) in O _j given that P _j is busy processing product m. Then, E [W _j (i,m)] can be written as

where

and

The term 1/(1 − ρ _j (m)) comes from the busy-period analysis of stage j (Kleinrock, 1975). It represents the expected number of offspring of product m at stage j that are expected to arrive during the production of one unit of product m. The term R _j (m) − 1 − E[ NO _j (m)|.] represents the number of production kanbans of product m waiting in the production order pool, i.e., the number of units needed to bring the inventory level of product m at stage j to the target level.

Now let us explain the delay S _j (i, m) due to switching, which is the second term on the left-hand side of Equation (2). After NO _j (m) reaches R _j (m), P _j may switch to a product type other than product i. Let K(i) = {1, …, i − 1} be the set of products with a higher priority than product i. We define p _j (n|i, m) as the probability that P _j switches to product n ∈ K(i) after finishing product m, given that products i and n are waiting; S _j (n|i, m) as the associated delay period due to this switching and p _j ( NO _j (n) = k|i,m) as the probability that the inventory level of product n at stage j at the time of switchover is k:

where E[ NO _j (n)|.] = ∑ _{k = 0} ^{R _j (n) − 1} kp _j ( NO _j (n) = k|i, m) and R _j (n) − E[NO _j (n)|.] is the expected number of production kanbans of product n waiting in the production order pool PO _j at the time P _j switches from product m to product n while both product n and product i are waiting. Note that due to the restricted priority scheme employed in the system, P _j would not switch product n ∈ K(i) more than once while product i is waiting in the queue. Hence, we do not need to consider a second switchover to a higher priority product in the calculation of the delay period.

Since the conditional probabilities in Equations (1), (3), (4) and (5) involve more than one product type, their exact solutions are quite complicated as one needs to keep track of inventory levels of different product types and the status of the processor at the same time. We therefore approximate these conditional probabilities assuming that the products are independent of each other. The approximation makes sure that each conditional probability involves only one product type.

We start with approximating the conditional probability in Equation (1) which involves the status of product m as well as the inventory level of product i. We first partition this probability into two by conditioning on the busy status of P _j :

Then, using the assumption on the independence of products, we approximate the first term as

The second term on the right-hand side of Equation (6) already contains a single product type (i.e., product type i) and therefore there is no need to approximate that probability.

Next we move to the approximation of the conditional probability used in Equation (3):

The approximation in Equation (8) implies that the inventory level of product m at O _j at the time it is being processed at stage j is independent of the inventory levels of the other products. Thus, if P _j is busy with product m when its attention is requested, then the remaining processing time of product m at P _j would be independent of the event that another request is made for the processor. In a single-resource environment there is likely to be a negative correlation between the inventory levels of different product types, but our approximation does not capture this correlation.

Equation (4) involves a conditional probability on the switching of P _j from product m to product n although product i has requested attention before product n. We approximate this as

Equation (9) states that the probability of switching from product m to product n at stage j is independent of the product type that is being processed at stage j and the products that are waiting in the queue for the processor's attention. Since switching to product n means that: (i) the processing of product n is delayed until P _j finishes the job; and (ii) P _j was previously busy with processing another product, we approximate the probability of switching to product n at stage j by conditioning the delay of product n on the status of P _j . Since this approximation does not differentiate among the priorities of different product types, it is likely to overestimate (underestimate) the probability of switching to a lower (higher) priority product.

Finally, the conditional probability in Equation (5), the inventory level of product n at O _j at the time of a switchover from product m to product n while product k is waiting, is also assumed to be independent of both the product type being processed at stage j and the product types waiting to be processed by P _j :

3.2. Characterization of subsystems

The previous analysis shows that the average delay of a product type at any stage is simultaneously determined by the characteristics of all other product types. In this section we present the characterization of the subsystems constructed around each storage activity for each product type. Since a delay event is related to the output buffer, we calculate the conditional probabilities in Equations (6), (7), (8), (9), (10) for each product from the characterization of the subsystems that involve output buffers. Then, these conditional probabilities are used to find the delay periods formulated in Equations (1), (2), (3), (4), (5) for a particular product type.

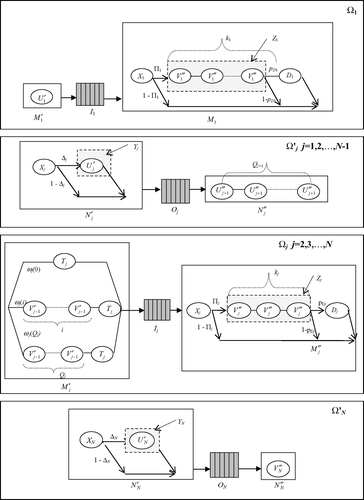
The processing times of the pseudo-processors at each subsystem are modeled using phase-type distributions leading to a Markovian analysis (Neuts, 1981). The underlying CTMC in each subsystem involves a three-tuple stochastic process keeping track of the service phases at each pseudo-processor and the number of parts in the associated buffer. The characterization of each subsystem is shown in Fig. 2 where product indices are suppressed for simplicity.

Fig. 2 Phase-type modeling of the processing times of the pseudo-processors in each subsystem.

We begin with the procurement process in Ω _j (i) of product i at stage j. The processing time at pseudo-processor M′₁ (i) is simply the vendor lead time. Therefore, U′₁ (i) has an exponential distribution with parameter γ₁ (i). The processing time at M′ _j (i), j = 2, …, N, on the other hand, is more involved. Whenever NI _j (i) drops to q _j (i), an order is given to O _{j − 1} to deliver Q _j (i) units of i to I _j . At that moment, if NO _{j − 1}(i) ≥ Q _j (i), a shipment of size Q _j (i) from O _{j − 1} is sent to I _j instantaneously. The transportation time T _j (i) of product i from stage j − 1 to j is exponentially distributed with rate γ _j (i). Otherwise, the shipment has to be delayed until NO _{j − 1}(i) reaches Q _j (i). The length of this delay is proportional to the level of NO _{j − 1}(i). Let ω _j (i, k) be the conditional probability that there are k units (k = 0, 1, …, Q _j (i)) missing in O _{j − 1} at the time a procurement request for product i is dispatched from I _j . Then, the processing time at M′ _j (i) becomes:

where the V′ _{j − 1,v} (i) are independent random variables with the same distribution as V′ _{j − 1}(i).

Next, we look at the demand arrival process in Ω _j (i) of product i at stage j. The processing time at M″ _j (i) consists of the processing time X _j (i), the blocking time Z _j (i), and the delay period D _j (i) of product i at stage j:

where p _j ^D(i) is the probability that product i is delayed at stage j when it requests the attention of processor P _j . Let Π _j (i) be the conditional probability that there is only one space available in O _j for product i at the time a unit of product i is about to finish processing on P _j . Then, the blocking time, Z _j (i) is defined by

where the V″ _{j − 1,v} (i) are independent random variables with the same distribution as V″ _{j − 1}(i), and

note that ⌈ ⌉ rounds to the next largest integer.

We now move to subsystem Ω ′ _j (i) of product i at stage j and start with the production process. The processing time at N′ _j (i) consists of the processing time X _j (i) and the starvation period Y _j (i) of product i at stage j, that is V′ _j (i) = X _j (i) + Y _j (i). Let Δ _j (i) be the conditional probability that there is no product i in I _j at the time a unit of product i is about to finish processing on P _j . Then, Y _j (i) can be written as

Finally, we analyze the demand arrival process at Ω ′ _j (i) of product i at stage j. The processing time at N″ _N (i) is simply the customer inter-arrival time of product i. Thus, V″ _N (i) has an exponential distribution with parameter λ(i). The processing time at N″ _j (i), j = 1, …, N − 1, on the other hand, is equal to the demand inter-arrival time at O _j . The demand arrival process at O _j is initiated by I _{j + 1} whenever NI _{j + 1}(i) drops to q _{j + 1}(i). Thus, there are Q _{j + 1}(i) units of product i leaving O _j between any two consecutive transfer requests from I _{j + 1} for product i. Also, V″ _j (i) = ∑ _{v = 1} ^{Q _{j + 1}(i)} U″ _{j + 1,v} (i), where the U″ _{j + 1,v} (i) are assumed to be independent random variables with the same distribution as U″ _{j + 1}(i).

3.3. Approximation algorithm

The analysis of each subsystem requires the solution of the steady-state probabilities in the underlying Markov chain. Although it is possible to use a more accurate representation of the processing time distributions of the pseudo-processors in the analysis such an approach would enlarge the state space to a level where tractability is lost even in a single-product case, as shown in Gurgur and Altiok (2004). For instance, the distribution of V″ _j (i) in subsystem Ω ′ _j (i) involves Q _{j + 1}(i) phases, each denoted by U″ _{j + 1}(i) with (k _N (i) … k _{j + 1}(i)) (Q _N (i) … Q _{j + 2}(i)) phases. In a reasonably small system that includes five stages and ten kanbans, there could be more than 100 000 phases in the distribution of some pseudo-processors . In the analysis of Ω ′ _j (i) we model U″ _{j + 1}(i) as an exponential random variable. This assumption changes the distribution of V″ _j (i) to an Erlang distribution with Q _{j + 1} (i) phases. Numerical examples provided in the next section show that this assumption does not cause a significant deterioration in the accuracy of our algorithm, while maintaining its tractability.

We obtain the flow-balance equations from the state transition diagram of each subsystem, and solve the steady-state probabilities using a matrix-recursive algorithm (Herzog et al., 1975; Buzacott and Kostelski, 1987). The solution of subsystems is available in Gurgur and Altiok (2006). The subsystems are linked with each other through the unknown parameters of the system, namely Δ _j (i), Π _j (i), ω _j (i,k), p _j ^D(i) and D _j (i), for i = 1, …, M. j = 1, …, N, k = 0, 1, …, Q _{j + 1}(i). Each subsystem updates a subset of parameters while taking the others as given as shown in Table 1. Interactions between the subsystems of different product types occur through the delay events, whereas interactions between the subsystems of a given product occur through blocking and starvation events of the processors. Since the starvation of a processor is related to the lack of input parts, the conditional starvation probabilities Δ _j (i) are computed using the steady-state probabilities of Ω _j (i), i.e., the subsystems involving input buffers. The blocking of a processor, on the other hand, is related to the lack of space in the output buffer, and therefore conditional blocking probabilities Π _j (i) are computed in Ω ′ _j (i), the subsystems involving output buffers.

Table 1 Parameter use and update

	Unknown parameters
	Δ j (i)	∏ j (i)	ω j (i,k)	p j ^D(i),D j (i)
Used in	Ω ′ j (i)	Ω j (i)	Ω j (i)	Ω j (i), Ω ′ j (n) n = 1, …, M
Updated in	Ω j (i)	Ω ′ j (i)	Ω ′ j − 1(i)	Ω ′ j (n) n = 1, …, i−1, i + 1, …, M

The following computations of Δ _j (i) and Π _j (i) are due to Little's Law (Kleinrock, 1975):

Throughputs of subsystems around input and output buffers are obtained using:

Since the conditional probability ω _j (i, k) involves the inventory level in O _{j − 1}, it is calculated and updated using the steady-state probabilities of Ω′ _{j − 1}(i):

The delay event is related to the output buffer. Hence, the probability of a delay of product i at stage j is calculated and updated using the steady-state probabilities of Ω ′ _j (i):

The delay periods D _j (i) are found using Equations (1), (2), (3), (4), (5) as discussed in Section 3.1.

We now present the approximation algorithm.

Approximation algorithm for multi-product, multi-stage systems

	Step 1. Initialize Δ j (i), Π j (i), ω j (i,k), p j D(i) and D j (i) for i = 1, …, M; j = 1, …, N; k = 0, 1, …, Q j + 1(i).
	Step 2. Set j = 1.
	Step 3. Analyze Ω j (i) for i = 1, …, M, obtain steady-state probabilities, update Δ j (i) using Equation (15).
	Step 4. Perform several iterations (three to five for instance) of the following subprogram: 4.1 Set i = 1 4.2 Analyze Ω ′ j (i), obtain steady-state probabilities, update Π j (i), ω j (i,k) D j (n) and p j D(n), for n = 1, …, i − 1, i + 1, …, M and k = 0, 1, …, Q j + 1(n) using Equations (1), (2), (3), (4), (5) and Equations (16), (17), (18), (19), (20), (21) 4.3 Repeat step 4.2 for i = 2., …, M.
	Step 5. Stop if the relative difference between the current value and the previous value of each unknown parameter is less than ε, else set j = 1 + (j mod N) and go to Step 2.

The algorithm starts with the input buffer of the first stage, solving the underlying CTMC of the associated subsystem for each product type separately and updating Δ₁(i) in isolation. Next, it moves to the output buffer of the first stage. The subsystem of a particular product interacts with the subsystems of all the other products in the evaluation of delay parameters. Since the delay period of a product involves conditional probabilities belonging to other products, the calculation of the delay period of each product at a particular stage requires an iterative characterization of the subsystems of all products involving the output buffer at that stage. Hence, using Δ₁(i) from Ω₁(i), the algorithm executes a few iterations (three to five for instance) among all subsystems Ω ′₁(i)     i = 1, …, M to update p ₁ ^D(i), D ₁(i), Π₁(i) and ω ₁(i, k). The updated ω ₁(i,k) is used in the solution of Ω₂(i), whereas p ₁ ^D(i), D ₁(i) and Π₁(i) are used later in Ω₁(i) during the next iteration of the algorithm. The algorithm ends when the current value and the previous value of each unknown parameter are sufficiently close to each other in successive iterations.

4. Accuracy of the approximation algorithm

In this section, we provide numerical examples to evaluate the accuracy of the approximation by comparing its estimates against simulation results. The simulation model is developed using the ARENA® simulation tool. Each run consists of ten replications with approximately 50 000 000 total job departures to provide point estimates and 95% confidence intervals for various performance measures of our interest. The replication length is chosen to be long enough to ensure that a confidence interval is always less than 0.1% of the point estimate. The convergence criterion is chosen to be ε = 0.01. The CPU time of the approximation method ranges between 3 and 270 seconds, whereas it takes approximately 60 to 350 minutes to finish a simulation run in a computer operating at 1 GHz. In all numerical experiments the algorithm converged in five or fewer iterations.

The following performance measures are estimated on a per product basis: (i) average level of raw material inventory; (ii) average work-in-process inventory; (iii) average finished goods inventory; and (iv) customer service level. In the base model, the system parameters are chosen as follows:

where ρ represents the system load (defined as the ratio of total demand arrival rate to processing rate of the slowest processor). The buffer capacities are chosen to be proportional to the target level of O ₁ using the following:

The initial value of R ₁(i) is chosen as 30 for i = 1, …, M. Note that as R ₁(i) increases, the values of all control parameters, and thus the scale of the system, increases as well. In the base model, three products are considered.

We have conducted six sets of experiments.

1.	Number of stages: two, five and eight.
2.	Number of products: five and eight.
3.	R 1(i): 20 and 50 for i = 1, …, M.
4.	System workload: 0.80 and 0.90.
5.	Processing rates at processors: 0.45 + 0.1(j − 1)/(N − 1) for processor j = 1, …, N, and 0.55 – 0.1(j − 1)/(N − 1) for processor j = 1, …, N. Note that, in the first case, processing rates are higher in the downstream stages whereas the second case has the opposite arrangement.
6.	Demand arrival rates of products: λ i = (0.220, 0.165, 0.083) and λ i = (0.083, 0.165. 0.220).

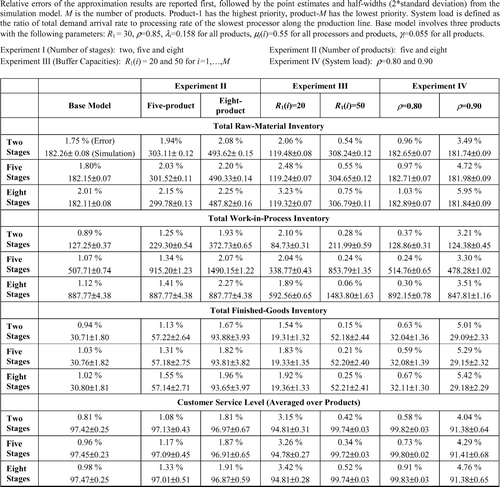
In each experiment, we changed one parameter at a time while keeping all the others constant. Simulation results are reported in the tables presented in Fig 3, Fig 4, Fig 5. We have first analyzed whether the analytical procedure retains its accuracy, as the scale of the system gets larger. For that purpose we have increased the number of stages, the number of product types and the values of production and procurement control parameters. As the table in Fig. 3 shows, the accuracy does not deteriorate in large-scale systems. When the capacity of the system is reduced, approximation tends to overestimate the average inventory levels and customer service levels. Looking at the impact of the system load (ratio of the arrival rate of the total customer demand to the processing rate of the slowest processor), we have observed that the demand arrival process has a significant impact on all performance measures. As the customer inter-arrival times decrease, the rate of backlogging intensifies, which is captured less accurately by the approximation.

Fig. 3 Accuracy of approximating performance measures in multi-product, multi-stage systems.

Fig. 4 Average total inventory levels at each stage.

Fig. 5 Per product performance measures.

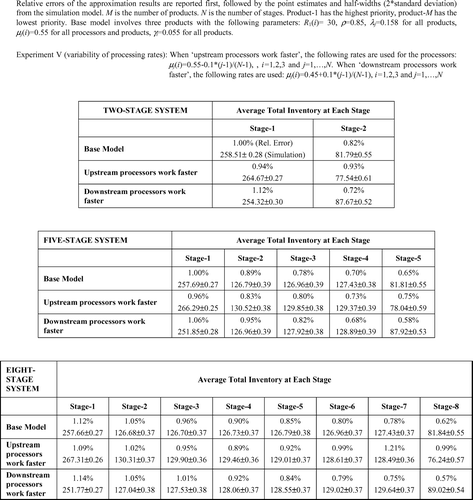
The tables in Fig. 4 summarize the impact of line balance on the accuracy of the approximation. In addition to the base model, we have considered an unbalanced system where processing rates differ from upstream to downstream. The magnitude of the deviation is slightly higher in the upstream stages. This is due to the fact that in pull systems customer information propagates from the downstream end to the upstream end and decomposition techniques transmit this information with some error. When the upstream (downstream) processors work faster this deterioration decreases (increases). Lower processing rates in the downstream stage reduce the workload of the upstream stages and allow more accurate approximations at the upstream stages.

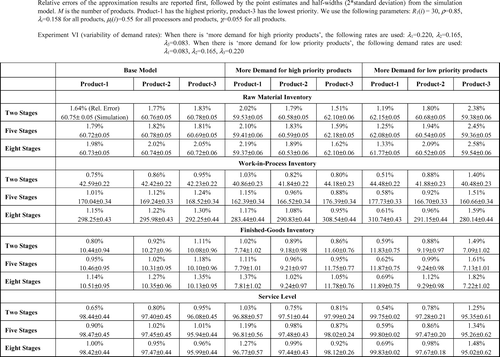
Finally, in the table in Fig. 5 we summarize how the approximation fares in estimating the performance metrics of each product. We look at the impact of demand variability (that is, one product type has a higher demand rate than others) in the base model that includes three product types. In general, the estimates of the lowest priority product (product 3) are approximated with a larger error than those associated with the highest priority product (product 1), provided that each product type has the same set of parameters (i.e., demand inter-arrival rates, processing rates, transportation rates, production and procurement control parameters). Since product 3 also has the lowest service level, we attribute this result to the difficulty in predicting the behavior of systems overloaded with customer demand.

The deviation of the approximation results from the simulation results varies from 0.06 to 5.95%. Two factors that cause the largest deterioration in the approximation are small buffer capacities and high workloads, which are symptoms of frequent backlogging and low customer service levels. The number of stages, number of product types, demand variability and processing time variability along the production stages do not have any significant adverse effect. A common feature of many decomposition-based approximation methods proposed for kanban systems is that the accuracy of the algorithm is closely linked to the service level of the system defined as the probability of satisfying customer demand upon arrival (So and Pinault, 1988; Albino et al., 1995; Krieg and Kuhn, 2002). In this study, we have also observed a similar pattern: the accuracy of the approximation improves when the product service levels are higher.

5. Designing the production/inventory system

A potential use of our analytical approach, other than performance evaluation, is to design the pull production/inventory system analyzed in this paper. The common desire in the operation of a production/inventory system is to maintain a customer service level with the minimum inventory holding cost. Therefore, the decisions involved in such a design problem include production and procurement control parameters for each product type at each stage. The problem can be formulated as

where S _i (·), i = 1, …, M is the customer service level of product i, z _i ⁰ ∈ (0, 1) is a constant representing the threshold customer service level of product i that has to be satisfied by the system on the average, and c _ij > 0 and c′ _ij > 0 are the unit inventory holding costs of product i at input buffer j and output buffer j, respectively. In a possible scenario, the unit costs may increase as we move towards the downstream, i.e., c _{i,j + 1} ≥ c _ij , c′ _{i,j + 1} ≥ c′ _ij , c′ _ij ≥ c _ij and high-priority products may require a higher service level than low-priority products, i.e., z _i ⁰ ≥ z _{i + 1} ⁰.

As Singh and Smith (1997) stated “… identifying the optimal buffer vectors is an NP-hard optimization problem with no closed form objective function”. Moreover, the possible configurations of design parameters increase rapidly with the number of stages and the number of products. Since the functional relationship between the response variables (inventory and service levels) and the system parameters are not explicitly known, the design problem cannot be solved analytically and the only alternative is a numerical search technique. Our approximation method provides values of responses (inventory and services levels) for a given level of design parameters. An optimization approach that incorporates our method in a numerical search technique can be easily implemented to design the production/inventory system. Even though a simulation tool can be used for the same purpose, it would require a much larger effort to solve the optimization problem. The relative speed and accuracy of the approximation algorithm developed in this paper makes it a potentially powerful tool that can be used in system design.

6. Conclusions

In this paper, we have considered a multi-product, multi-stage and market-driven production/inventory system with decentralized control policies. The system involves finite target levels in buffers, production of different product types one at a time and batch transfers between production stages. Due to complexity of the underlying stochastic processes modeling interactions among products and stages, we have proposed an approximation algorithm to study interdependencies among the products in terms of the delay periods they experience. Once the delay periods are characterized and added into the process completion times of each product type, the original system is reduced to a set of multi-stage, single-product systems. We have decomposed each multi-stage, single-product system into two-node subsystems, which are analyzed in isolation using a matrix-recursive approach capitalizing on phase-type modeling of blocking, starvation and delay periods in the original system. A fixed-point algorithm integrates the subsystems together and obtains system-wide performance metrics by iteratively solving them. Numerical examples are provided to show the accuracy of the approximation and its speed relative to simulation. We have also provided guidance to the reader on how our approximation algorithm can be incorporated with a numerical search technique to find the optimum production and procurement control parameters in designing the production/inventory system.

Biographies

Cigdem Gurgur is an Assistant Professor of the Division of Economics and Business at Colorado School of Mines. She received her Ph.D. in Industrial and Systems Engineering from Rutgers, The State University of New Jersey. Her research and teaching activities and interests are in the areas of simulation and stochastic modeling with applications in performance analysis and design of manufacturing systems, supply chains, energy and logistics and the management of financial risk. She is a member of IIE, INFORMS, and POMS.

Tayfur Altiok is a Professor and the Chairman of the Department of Industrial and Systems Engineering at Rutgers, The State University of New Jersey. He received his Ph.D. in Industrial Engineering at North Carolina State University at Raleigh. His research and teaching activities are in the areas of queueing systems, simulation modeling, performance analysis and design of manufacturing systems and supply chains, marine port logistics and security and computer information systems. His research has been supported by the National Science Foundation, DHS, NJDOT and industry for a number of years. He has numerous publications including two books in the areas of performance analysis and simulation.