Performance evaluation of two-stage multi-product kanban systems

Abstract

We propose an approximate evaluation procedure for a kanban-controlled production system with two stages and multiple products. In the first stage, single-product manufacturing facilities produce items that are the input material for a single multi-product manufacturing facility in the second stage. Each manufacturing facility is controlled by a distinct kanban loop with a fixed number of kanbans. Processing and setup times are exponentially distributed, demand arrivals at the output store of the second stage are Poisson and independent for each product. If a customer's demand cannot be met from stock, the customer either waits or leaves the system, depending on the admissible number of backorders and the current number of waiting customers (partial backordering). We describe a new decomposition-based approximation method for the evaluation of such systems in steady state. We focus on the performance measures average fill rate, average fraction of served demand, and average inventory level. We report the results of several numerical tests. The results indicate that the approximation is sufficiently accurate for a large variety of systems. We also illustrate the effects of increasing the maximum number of backorders on the performance of the system.

Keywords:

• Kanban system
• performance evaluation
• Markov chain
• queueing system
• production/inventory system
• stochastic modeling

1. Introduction

Several empirical studies document that kanban control bears great potential to significantly improve operations (e.g., White et al. (1999), Fullerton and McWatters (2001) and White and Prybutok (2001)). The main advantage of a kanban control system is its simplicity. Although there is not the kanban system, one principle is common to all variants: production, or some other kind of operation, may only take place if there is a deficit, that is, if less containers with processed items are at hand than desired.

In the classic kanban system, the number of full containers that should be on stock determines the number of cards, or “kanbans”, that circulate in the system (e.g., Monden (1998)). Since full containers must always have a kanban attached to them and since those kanbans must be removed when a container is depleted, the number of free, or “active”, kanbans signals the current deficit. Active kanbans are usually collected at one place (for example, a scheduling board) that is close to the person responsible for the operation. As a result, that person always has all the information necessary to decide whether to continue processing without the need to receive explicit orders from a planning department and without running the risk of producing unwanted surplus. In the literature many different versions of kanban systems or pull control policies are described (e.g., Buzacott and Shanthikumar (1993), Gershwin (2000) and Dallery and Liberopoulos (2000)). However, most of them are very similar and only differ in their details.

Determining the appropriate number of kanbans is crucial for the performance of the system. If this number cannot be found by trial and error during the first days of operation, then procedures are needed to evaluate the performance of the system for any number of cards that might be optimal. Simulation models could be used to determine the system's performance, but optimizing a system using a simulation model as the evaluation tool is cumbersome. Fast analytical procedures are needed, even if they may only be able to approximate the true performance of the system.

A number of analytical procedures have been proposed for single- and multi-stage kanban systems with one type of product (single-stage: Jordan (1988), Wang and Wang (1990, 1991), Di Mascolo (1996), Kim and Tang (1997), Nori and Sarker (1998) and Seki and Hoshino, 1999; multi-stage: So and Pinault (1988), Deleersnyder et al. (1989), Karmarkar and Kekre (1989), Berkley (1990, 1991, 1992), Mitra and Mitrani (1990, 1991), Di Mascolo et al. (1992, 1996), Buzacott and Shanthikumar (1993), De Araújo et al. (1993), Di Mascolo et al. (1993), Tayur (1993), Schmidbauer and Röesch (1994), Siha (1994), Albino et al. (1995), Gstettner and Kuhn (1996), Fujiwara et al. (1998), Bonvik et al. (2000) and Baynat et al. (2001)).

Some approaches are available for single-stage multi-product kanban systems (Askin et al. 1993; Krieg and Kuhn, 2002, 2004). In the context of stochastic lot scheduling problems, Federgruen and Katalan (1996) and Markowitz et al. (2000) analyze systems very similar to the single-stage multi-product kanban systems studied by Krieg and Kuhn (2002). Altiok and Shiue (1994, 1995, 2000) analyze stochastic “multi-product pull-type production/ inventory systems,” which are equivalent to single-stage multi-product kanban systems with a shared manufacturing facility (see also Altiok, 1997).

In this paper, we extend the procedure given in Krieg and Kuhn (2004) for the analysis of single-stage multi-product kanban systems to kanban-controlled systems with multiple products and two stages. We also consider the possibility of partial backordering. In future research, the new procedure proposed here is also expected to prove instrumental as a building block for the analysis of multi-product kanban systems with an arbitrary number of stages.

The rest of this paper is organized as follows. In Section 2, we give a detailed description of the considered system. In Section 3, we show that although the system could be modeled exactly by a continuous-time Markov chain, the size of the state space prohibits the construction and solution of the exact model for most system sizes. We then develop a decomposition-based procedure to approximate the performance of the system in steady state (Section 4). We focus on the performance measures average fill rate, average fraction of served demand and average inventory level. The accuracy of the approximation is indicated in Sections 5 and 6 via comparisons with results from exact analysis and simulation. In Section 7, we illustrate the effects of increasing the maximum number of backorders on the performance of the system. We conclude with a short summary and suggestions for future research.

2. Description of the system

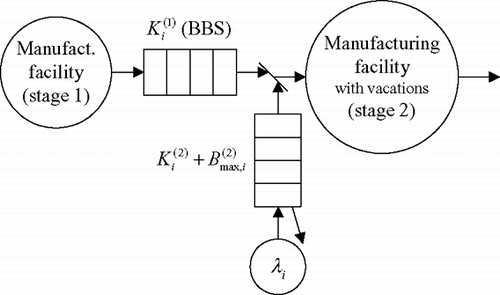
In this paper, we consider a production system with two stages. In stage 1, r single-product manufacturing facilities process items of r different products (one product per manufacturing facility). These items are processed further in a single multi-product manufacturing facility in stage 2 (Fig. 1:model_Mitra_Mitrani_like depicts such a system with three different products). Each manufacturing facility is controlled by a distinct kanban loop with a fixed number of kanbans, K _i ⁽¹⁾ and K _i ⁽²⁾, i = 1,…,r (in Fig. 1, the kanban loops are indicated by dashed lines). Processed items of both stages are carried, stored and requested in standard containers with a fixed, product-specific filling quantity (in Fig. 1, the flow of products is indicated by arrows with regular lines). The filling quantity is the minimum manufacturing lot size for a product, and any other lot size is an integer multiple of this filling quantity.

Fig. 1 Model of a kanban system with two stages and three different products (adapted from Mitra and Mitrani (1990, Fig. 3)).

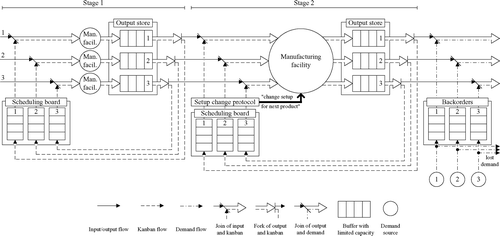
Customers arrive to the output store of stage 2 according to Poisson processes with rate λ _i , i = 1,…,r (in Fig. 1, the demand sources are depicted by the numbered circles in the bottom right-hand corner, the demand flow is indicated by arrows with alternately dashed and dotted lines). Each customer demands one container of a single product. Should no full container be available to fill the customer's demand, then this demand is backordered (in Fig. 1, backordered demand accumulates in the buffers on the right-hand side). For each product i, the maximum number of backorders is restricted by B _i ^max. A customer who arrives at the system when the maximum number of backorders is reached leaves the system immediately and satisfies his or her demand elsewhere.

Input material for the first stage is always available in the required quantities. After a container in stage 1 has been filled, it is transferred to the output store of the stage. Each manufacturing facility in stage 1 can only process items of one specific product. We define that manufacturing facility i always produces items of product i. No setup activities are required in stage 1. The time to fill a container in stage 1 is exponentially distributed with mean 1/μ _i ⁽¹⁾, i = 1,…,r.

The items processed in stage 1 are the input material for stage 2. Just before the manufacturing facility of stage 2 starts processing items, it removes the required input material from the output store of stage 1. The time to fill a container in stage 2 is exponentially distributed with mean 1/μ _i ⁽²⁾, i = 1,…,r. The time to set up the manufacturing facility in stage 2 for product i is exponentially distributed with mean s _i ⁽²⁾, i = 1,…,r.

The condition for a setup is that at least one active kanban and one container with input material must be available. Once the manufacturing facility in stage 2 has been set up for a product, it processes items of this product until either the number of active kanbans is zero, that is, all empty containers for the product are filled, or the number of containers with input material is zero (exhaustive processing with limited input material). Then the manufacturing facility is being set up for the next product that meets the setup condition. The order in which products are considered for production is stipulated by a predetermined fixed setup sequence. For ease of presentation, we only consider setup sequences that result from a rotation cycle, that is, a setup cycle with one setup change per product. Without loss of generality, we use the setup cycle (1, 2, …, r).

Should no product meet the setup condition at the end of a production run, then the manufacturing facility idles until there is at least one active kanban and one container with input material for a product. During an idle period the current setup of the manufacturing facility is preserved, that is, if the first product to meet the setup condition is the same product that was manufactured last, then no additional setup activities are required and production can resume instantly.

3. Exact model

The pieces of information that must be represented in an exact model of this system are the current state of the manufacturing facility in stage 2 and, for each product, the number of full containers in the output store of stage 1 and the number of active kanbans and backorders in stage 2. It is not necessary to explicitly represent the number of active kanbans for a product in stage 1 because this number can be derived directly from the number of full containers and the total number of kanbans in stage 1. It is also not necessary to explicitly represent the number of full containers in the output store of stage 2 because this number can be derived directly from the number of active kanbans and the total number of kanbans in stage 2. Lastly, it is also not necessary to explicitly represent the current state of each manufacturing facility in stage 1 because this state can be derived directly from the number of kanbans for the respective product in stage 1. If this number is greater than zero, then the facility is busy, otherwise, it idles.

A Continuous-Time Markov Chain (CTMC) can be constructed to accurately model the considered system. We did this to obtain reference values for the small systems evaluated during the numerical tests described in Section 5 and Section 6. The state vector of this CTMC contains two elements for each product (the number of full containers in stage 1 and the number of active kanbans and backorders in stage 2) and one element for the current state of the manufacturing facility in stage 2. After the state vector has been defined, the formulation of the balance equations of this CTMC is time consuming, but straightforward. We therefore omit a detailed description of the balance equations.

Unfortunately, the size of the state space grows so rapidly with increasing number of products and kanbans that this modeling approach is impractical for most system sizes. If denotes the state space of the CTMC and || the number of elements in this set, then the number of states is

where

If K _i ⁽¹⁾ = K ⁽¹⁾ and K _i ⁽²⁾+B _i ^max = K ⁽²⁾ for all i = 1,…,r, then:

where | _I (r)| is the number of states with z = I. For systems with two and three products, respectively, this number, for example, is

For a system with three different products and five kanbans for each product in each of the two stages, the CTMC consists of 217 833 states. For a system with three different products and ten kanbans each, the number of states is 9 251 613. Because of this state space explosion, construction and analysis of the CTMC is mathematically intractable for most system sizes. We therefore propose a decomposition-based approximation method that generates sufficiently accurate values for the performance measures of interest for systems of practically any size. A general approach to developing decomposition-based methods can be found in Gershwin (1994).

4. Decomposition into subsystems

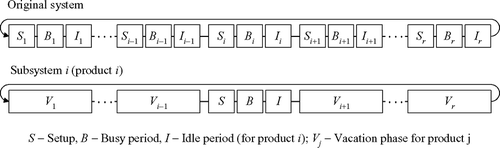
The explosive growth of the state space of the exact model stems from the necessity to increase the state vector by two elements for each additional product. Therefore, we decompose the original system into single-product subsystems for which the state vector always, that is, for any number of products, consists of only three elements: one for the number of active kanbans and backorders in stage 2, n ⁽²⁾+b, one for the number of full containers in the output store of stage 1, y ⁽¹⁾, and one for the current state of the manufacturing facility in stage 2, z. The different states of this manufacturing facility in a subsystem will be discussed in the following subsection.

4.1. Description of a subsystem

In each subsystem, only one product, for example, product i in subsystem i, is considered explicitly. The other products, however, must also be included in some way because they also determine the behavior of the manufacturing facility in stage 2. We propose the use of server vacation phases to solve this problem. This approach will be explained in detail in the following paragraphs.

A queueing model of subsystem i is given in Fig. 2. The join symbol on the left-hand side of the manufacturing facility with vacations (depicted by the right circle) represents that at least one container with input material (manufactured in stage 1) and one active kanban for stage 2 must be present before production may start in stage 2. To correctly capture the kanban control mechanism in stage 1, the size of the queue following the first manufacturing facility is set equal to the number of kanbans for product i in stage 1, K _i ⁽¹⁾, and it is assumed that production stops in stage 1 as soon as the queue is filled to capacity (blocking before service). Alternatively, the assumption blocking after service could be used here as well. Then, however, the queue size would have to be set equal to K _i ⁽¹⁾−1.

Fig. 2 Queueing model of subsystem i (product i); BBS = Blocking Before Service.

From the start of the setup activities until the end of the busy period for product i, that is, when either all active kanbans or all containers with input material have been fully depleted, the behavior of the manufacturing facility in stage 2 depends only on product i. Therefore, these time periods can be captured exactly in the model of the single-product subsystem for product i. At the end of the busy period, however, the complete state of the system, that is, the number of active kanbans and containers with input material for the other products, too, must be known to decide whether the manufacturing facility in stage 2 will idle or be set up for one of the other products. If the manufacturing facility in stage 2 turns its attention to a different product, then the time until its return to product ialso depends on the other products. Thus, in a model of subsystem i, the length of the period in which the manufacturing facility in stage 2 attends to some product j (j≠ i) must be based on information derived from subsystem j.

Even if products may be skipped in a specific cycle, thus causing a sojourn time of zero for some states, the general sequence of states of the manufacturing facility in stage 2 is always identical (Fig. 3). For each of these states, there is a long-run average time length. These averages can be used in the model of a subsystem to represent the lengths of the time periods when the manufacturing facility in stage 2 is not available for the explicitly modeled product without knowing the current status of the other products.

Fig. 3 States of the manufacturing facility in stage 2 in the original system and in subsystem i.

We use one state for each of the products that are not explicitly modeled in a subsystem and determine the long-run average length of each of these states by analyzing the model of the subsystem that explicitly considers the respective product (the details will be given in Section 4.6). Following classical queueing theory, we call the time period when the manufacturing facility in stage 2 is not available for product i in subsystem i during a cycle a “vacation”. In addition, we call the time period when the manufacturing facility in stage 2 is not available for product i (because it is being set up for processing, or being idle after processing product j) a “vacation phase for product j”. Thus, a vacation in subsystem i consists of r−1 vacation phases, one vacation phase for each product j, j = 1,…,r; j≠ i (Fig. 3). In summary, we have 3+(r−1) different states of the manufacturing facility in stage 2 in the model of each subsystem. For subsystem i, these states are: setup (S), busy period (B), and idle period (I) for product i and one vacation phase (V _j ) for each product j, j = 1,…,r; j≠ i.

4.2. Definition of stochastic processes

For each subsystem, we define three elementary stochastic processes. To simplify the notation, we use n instead of n ⁽²⁾+b to denote the number of active kanbans and backorders in stage 2, y instead ofy ⁽¹⁾ to denote the number of full containers in the output store of stage 1, and z instead of z ⁽²⁾ to denote the state of the manufacturing facility in stage 2.

Let N ⁽ⁱ⁾(t) denote the number of active kanbans and backorders in stage 2 in subsystem i at time t (i = 1,…,r; t ≥ 0). Then {N ⁽ⁱ⁾(t), t ≥ 0} is a stochastic process over state space {0,…,K _i ⁽²⁾+B _i ^max}, where K _i ⁽²⁾ is the number of kanbans for product i in stage 2 and B _i ^max is the maximum number of backorders for product i.

Let Y ⁽ⁱ⁾(t) denote the number of full containers in the output store of stage 1 in subsystem i at time t. Then {Y ⁽ⁱ⁾(t), t ≥ 0} is a stochastic process over state space {0,…,K _i ⁽¹⁾}, where K _i ⁽¹⁾ is the number of kanbans for product i in stage 1. Note that due to the rules in a kanban system, the number of kanbans for a product in a stage defines the maximum number of full containers for this product in the output store of this stage.

Let Z ⁽ⁱ⁾(t) denote the state of the manufacturing facility in stage 2 in subsystem i at time t. We abbreviate the possible states of the manufacturing facility by S (setup), B (busy period), I (idle period), and V _j , j = 1, …, r; j ≠ i (vacation phase for product j). Then {Z ⁽ⁱ⁾(t), t ≥ 0} is a stochastic process over state space ⁽ⁱ⁾ = {S;B;I;V _j , j = 1,…,r;j≠ i }.

4.3. Approximate model of a subsystem

The triple [N ⁽ⁱ⁾(t), Y ⁽ⁱ⁾(t), Z ⁽ⁱ⁾(t)]completely defines the state of subsystem i at time t. Unfortunately, the combined stochastic process {[N ⁽ⁱ⁾(t), Y ⁽ⁱ⁾(t), Z ⁽ⁱ⁾(t)], t ≥ 0 } is not a Markov process because the length of a vacation phase is generally not exponentially distributed. To make it a Markov process, we substitute an exponential distribution with parameter t _SBI ^(j) for the (unknown) true distribution of the length of vacation phase V _j , j = 1,…,r; j≠ i (an equation for parameter t _SBI ^(j) will be developed in Section 4.6). If, for example, {Ñ⁽ⁱ⁾(t), t ≥ 0} is defined analogously to {N ⁽ⁱ⁾(t), t ≥ 0} for the resulting approximate model of subsystem i, then the combined stochastic process {Ñ⁽ⁱ⁾(t), Ỹ⁽ⁱ⁾(t), [Ztilde]⁽ⁱ⁾(t)],t ≥ 0} is a CTMC on state space ⁽ⁱ⁾ = {(n,y,S), n = 1,…,K _i ⁽²⁾+B _i ^max;y = 1,…,K _i ⁽¹⁾; (n,y,B),n = 1,…,K _i ⁽²⁾+B _i ^max; y = 0,…,K _i ⁽¹⁾;(0,y,I), y = 0,…,K _i ⁽¹⁾; (n,0,I),n = 1,…,K _i ⁽²⁾+B _i ^max; n,y,V _j ),n = 0,…,K _i ⁽²⁾+B _i ^max; y = 0,…,K _i ⁽¹⁾;j = 1,…,r; j ≠ i }.

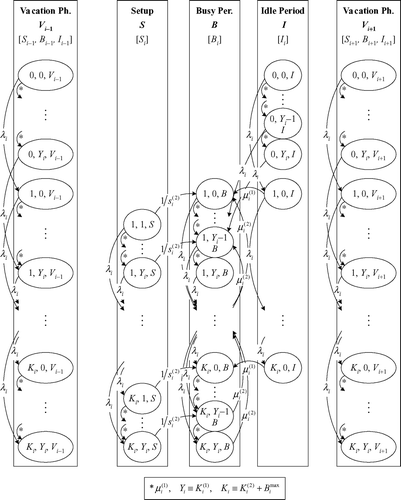
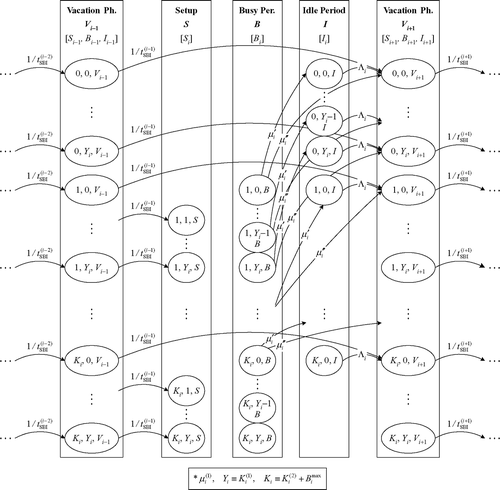
Figure 4 and Figure 5 show the main part of a generalized state-transition rate diagram of this CTMC (divided into two layers to improve readability). To simplify the notation in these figures, we substitute Y _i for K _i ⁽¹⁾, the number of kanbans for product i in stage 1, and K _i for K _i ⁽²⁾+B _i ^max, the number of kanbans plus the maximum number of backorders for product i in stage 2. Symbol Y _i may be read as the maximum number of full containers with items of product i in the output store of stage 1. The significance of transition rates μ′ _i , μ” _i and Λ _i will be explained in Sections 4.7 and 4.9.

Fig. 4 State-transition rate diagram of the CTMC for subsystem i (product i): layer 1.

Fig. 5 State-transition rate diagram of the CTMC for subsystem i (product i): layer 2.

A decomposition approach can only be successful if it is possible to quickly analyze the subsystems. For Markov chains, the size of the state space is the critical factor for the computation time. The number of states of the CTMC for any subsystem i is

This number is much smaller than the number of states of the CTMC for the original system (compare to Equation (3)). For example, for a system with three different products and five kanbans for each product in each of the two stages, the CTMC of a subsystem consists of 138 states (compared to 217 833). For a system with three different products and ten kanbans each, the CTMC of a subsystem consists of 473 states (compared to over 9000 000).

4.4. Steady-state probability distributions

Next, we define steady-state probability distributions for the stochastic processes {Ñ⁽ⁱ⁾(t), t ≥ 0}, {Ỹ⁽ⁱ⁾(t), t ≥ 0}, and {[Ztilde]⁽ⁱ⁾(t), t ≥ 0}, and for several combined stochastic processes. We also give equations for computing the values of these distributions.

Let [Ptilde]⁽ⁱ⁾(n) = lim _t→∞ P[Ñ⁽ⁱ⁾(t) = n], n = 0,…,K _i ⁽²⁾+B _i ^max, be the steady-state probability distribution of {Ñ⁽ⁱ⁾(t), t ≥ 0}.

Let [Ktilde]⁽ⁱ⁾(y) = lim _t→∞ P[Ỹ⁽ⁱ⁾(t) = y], y = 0, …, K _i ⁽¹⁾, be the steady-state probability distribution of {Ỹ⁽ⁱ⁾(t), t ≥ 0}.

Let [gtilde]⁽ⁱ⁾(z) = lim _t→∞ P[[Ztilde]⁽ⁱ⁾(t) = z], z ∈ ⁽ⁱ⁾, be the steady-state probability distribution of {[ztilde]⁽ⁱ⁾(t), t ≥ 0}.

Let [Gtilde]⁽ⁱ⁾(n,z) = lim _t→∞ PÑ⁽ⁱ⁾(t) = n,[Ztilde]⁽ⁱ⁾(t) = z], (n,z)∈ {[(n,S), (n,B)], n = 1,…,K _i ⁽²⁾+B _i ^max; [(n,I), (n,V _j )], n = 0,…,K _i ⁽²⁾+B _i ^max; j = 1,…,r; j ≠ i }, be the steady-state probability distribution of{Ñ⁽ⁱ⁾(t),[Ztilde]⁽ⁱ⁾(t)], t ≥ 0}.

Let [htilde]⁽ⁱ⁾(y,z) = lim _t→∞ P[ỹ⁽ⁱ⁾(t) = y,[Ztilde]⁽ⁱ⁾(t) = z], (y,z)∈ {(y,S), y = 1,…,K _i ⁽¹⁾; [(y,B),(y,I),(y,V _j )],y = 0,…,K _i ⁽¹⁾; j = 1,…,r; j ≠ i }, be the steady-state probability distribution of {[Ỹ⁽ⁱ⁾(t),[Ztilde]⁽ⁱ⁾(t)], t ≥ 0}.

Let õ⁽ⁱ⁾(n,y,z) = lim _t→∞ P[Ñ⁽ⁱ⁾(t) = n,Ỹ⁽ⁱ⁾(t) = y, [Ztilde]⁽ⁱ⁾(t) = z], (n,y,z)∈ ⁽ⁱ⁾, be the steady-state probability distribution of {[Ñ⁽ⁱ⁾(t),Ỹ⁽ⁱ⁾(t),[Ztilde]⁽ⁱ⁾(t)], t ≥ 0}.

We can determine distribution õ⁽ⁱ⁾ by solving the balance equations for the rate of probability inflows and outflows of each state of the CTMC. Using distribution õ⁽ⁱ⁾, we can then calculate distribution [qtilde]⁽ⁱ⁾,

and distribution [htilde]⁽ⁱ⁾,

Distributions [Ptilde]⁽ⁱ⁾ and [gtilde]⁽ⁱ⁾ can be derived from distribution [qtilde]⁽ⁱ⁾,

Distribution [ktilde]⁽ⁱ⁾ can be derived from distribution [htilde]⁽ⁱ⁾,

4.5. Performance measures

The steady-state probability distributions defined above can be employed to determine performance measures for the approximate model of subsystem i. These values can then be used as estimates for the respective performance measures of the original system.

The fill rate is a measure of the service level of a system. It is the fraction of demand that is filled immediately (off-the-shelf service, type-1 service). An estimate for the long-run average fill rate of product i in the original system is

If demands may be backordered, then the fraction of served demand (backordered and immediately served demand) is another measure of the service level. An estimate for the long-run average fraction of served demand of product i in the original system is _SD,i = 1−ᵱ⁽ⁱ⁾(K _i ⁽²⁾+B _i ^max).

If we measure the inventory level of a product in a stage by the number of full containers in the output store of that stage, then _i ⁽¹⁾ = ∑ _{y = 1} ^{K _i (1)} y × [Ktilde]⁽ⁱ⁾(y)is an estimate for the long-run average inventory level of product iin stage 1 in the original system and _i ⁽²⁾ = ∑ _{n = 0} ^{K _i (2)−1}(K _i ⁽²⁾−n)ᵱ⁽ⁱ⁾(n)is an estimate for the long-run average inventory level of product i in stage 2 in the original system.

4.6. Equation for parameter t _SBI ⁽ⁱ⁾

Let t _S ⁽ⁱ⁾ (t _B ⁽ⁱ⁾, t _I ⁽ⁱ⁾) be the long-run average amount of time that the manufacturing facility in the model of subsystem ispends in state S (B, I) between two vacations. Also, let t _SBI ⁽ⁱ⁾ be the long-run average total amount of time between two vacations in the model of subsystem i. Since the manufacturing facility of a subsystem can only be in states S, B, or I between two vacations, we know that t _SBI ⁽ⁱ⁾ = t _S ⁽ⁱ⁾+t _B ⁽ⁱ⁾+t _I ⁽ⁱ⁾ (Krieg and Kuhn, 2004).

We define T ⁽ⁱ⁾ as the long-run average amount of time from the end of a vacation until the end of the next vacation in subsystem i. If t _V ⁽ⁱ⁾ denotes the long-run average length of a vacation in the model of subsystem i, then T ⁽ⁱ⁾ = t _SBI ⁽ⁱ⁾+ t _V ⁽ⁱ⁾. Note thatt _V ⁽ⁱ⁾ = ∑ _{j = 1;j≠ i} ^r t _SBI ^(j).

From distribution [gtilde]⁽ⁱ⁾, we get the long-run average fraction of time of a vacation in the model of subsystem i: [gtilde] _V ⁽ⁱ⁾ = ∑ _{j = 1;j≠ i} ^r [gtilde]⁽ⁱ⁾(V _j ). Since[gtilde] _V ⁽ⁱ⁾ T ⁽ⁱ⁾ = t _V ⁽ⁱ⁾, we can now calculate T ⁽ⁱ⁾with T ⁽ⁱ⁾ = t _V ⁽ⁱ⁾/[gtilde] _V ⁽ⁱ⁾.Finally, we can determine t _SBI ⁽ⁱ⁾ with t _SBI ⁽ⁱ⁾ = T ⁽ⁱ⁾−t _V ⁽ⁱ⁾.

At the beginning of the algorithm of the proposed decomposition method (Section 4.10), we need rough estimates for t _S ⁽ⁱ⁾, t _B ⁽ⁱ⁾, i = 1,…,r, and for t _SBI ⁽ⁱ⁾, i = 1,…,r; i ≠ 2. A rough estimate for t _SBI ⁽²⁾ is not required because the algorithm starts with the analysis of the CTMC for subsystem 2 and this CTMC does not contain transition rate t _SBI ⁽²⁾. Simplifying greatly, we pretend that the sequence of states of the manufacturing facility in the original system is S ₁, B ₁, S ₂, B ₂, …, S _r , B _r , S ₁, B ₁, S ₂, B ₂, …, S _r , B _r , …, that is, always at least one active kanban and one container with input material for the product that is to be produced next, so that no setup of the setup sequence is skipped and the manufacturing facility never idles. Based on this scenario, rough estimates for t _S ⁽ⁱ⁾ and t _I ⁽ⁱ⁾ are t _S ^i:est = s _i ⁽²⁾ and t _I ^i:est = 0.

The number of active kanbans and backorders at the beginning of a busy period, say B _i , must be between one and the sum of the total number of kanbans and the maximum number of backorders for product i in stage 2, K _i ⁽²⁾+B _i ^max. Thus, the long-run average number of active kanbans at the beginning of B _i may be (very) roughly estimated as (K _i ⁽²⁾+B _i ^max)/2. A busy period ends when either the number of active kanbans or the number of containers with input material is down to zero. We estimate the long-run average time to reduce the number of active kanbans in subsystem i by one unit as (μ _i ⁽²⁾−λ_{eff, i} ^M/M/1/N )⁻¹, where λ_eff,i ^M/M/1/N is the effective arrival rate in an M/M/1/N queueing system with λ = λ _i , μ = μ _i ⁽²⁾ and N = K _i ⁽²⁾+B _i ^max (N = system capacity including service position). Assuming that input material is always available, we get as a rough estimate for t _B ⁽ⁱ⁾: t _B ^i:est = (K _i ⁽²⁾+B _i ^max)/2 × (μ _i ⁽²⁾−λ_{eff, i} ^M/M/1/N )⁻¹, where, with ρ _i = λ _i /μ _i ⁽²⁾:

Finally, since t _I ^i:est = 0, we have t _SBI ^i:est = t _S ^i:est+t _B ^i:est.

4.7. Equations for transition rates μ′ _i and μ″; _i

Transition rates μ _i ′ and μ _i ″ result from splitting transition rate μ _i ⁽²⁾, the average processing rate for product i containers in stage 2. At the end of the busy period, the manufacturing facility in stage 2 either switches into the idle state or it starts a vacation (Fig. 5). If no product meets the setup condition in stage 2, that is, if there is not at least one active kanban and one container with input material for any product, then the manufacturing facility in stage 2idles. If E _i denotes the event that no product meets the setup condition at the end of a busy period in stage 2 of subsystem i and P(E _i ) denotes the probability of this event, then μ′ _i = P(E _i )μ _i ⁽²⁾and μ” _i = [1−P(E _i )]μ _i ⁽²⁾.

4.8. Approximation of probability P(E _i )

The probability that no product meets the setup condition at the end of a busy period in stage 2 of subsystem i, P(E _i ), depends on the individual probabilities that each of the products does not meet the setup condition at this point in time. Let P(E _ij ) denote the probability that product j, j = 1,…,r, does not meet the setup condition at the end of a busy period for product i in stage 2. If it is true that all events E _ij for the same value of i are mutually independent, then P(E _i ) = ∏ _{j = 1} ^r P(E _ij ).

There is no reason to believe that the events E _ij for a fixed i and j = 1,…,r are stochastically dependent. The demand arrival processes that determine the availability of active kanbans for all products j = 1,…,r run independently, and the same is true for the product-specific manufacturing facilities in stage 1 that determine the availability of containers with input material for stage 2. Hence, the fact that some product j does not meet the setup condition at the end of a production run for product i in stage 2 does not contain any information about the availability of active kanbans and input material for the other products.

It remains to determine the probabilities P(E _ij ). Clearly, the probability that product i does not meet the setup condition at the end of a busy period for product i in stage 2 is one because the busy period is terminated as soon as the setup condition is breached. That is, P(E _ii ) = 1. To approximate probability P(E _ij ) for all j = 1,…,r; j≠ i, note that P(E _ij ) = P(E _ij ^{n _j = 0 ∨ y _j = 0}) = P(E _ij ^{n _j = 0 ∧ y _j > 0}) + P(E _ij ^{n _j > 0 ∧ y _j = 0}) + P(E _ij ^{n _j = 0 ∧ y _j = 0}), if n _j denotes the number of active kanbans and backorders for product j in stage 2, y _j denotes the number of full containers in the output store of stage 1 for product j, E _ij ^{n _j = 0 ∨ y _j = 0} denotes the event that n _j = 0 or y _j = 0 (inclusive or) at the end of a busy period for product i and, for example, E _ij ^{n _j = 0 ∧ y _j > 0} denotes the event that n _j = 0 and y _j > 0 at the end of a busy period for product i. To simplify the notation, we substitute P(E _ij ⁿ ), P(E _ij ^y ) and P(E _ij ^n,y ) for P(E _ij ^{n _j = 0 ∧ y _j > 0}), P(E _ij ^{n _j > 0 ∧ y _j = 0}) and P(E _ij ^{n _j = 0 ∧ y _j = 0}).

Consider probability P(E _ij ⁿ ). The conditional probability that input material is available, but no kanban is active for product j given that the manufacturing facility is dedicated to product i, may serve as an approximation for the probability that both conditions are met at the end of a busy period for product i. This conditional probability for the approximate model of subsystem i is equal to [[qtilde]^(j)(0,V _i )−õ^(j)(0,0,V _i )]/[gtilde]^(j)(V _i ). Hence, P(E _ij ⁿ ) ≈ [[qtilde]^(j)(0,V _i )−õ^(j)(0,0,V _i )]/[gtilde]^(j)(V _i ).

Equivalently, P(E _ij ^y )≈ [[htilde]^(j)(0,V _i )−õ^(j)(0,0,V _i )]/[gtilde]^(j)(V _i )andP(E _ij ^n,y )≈ õ^(j)(0,0,V _i )/[gtilde]^(j)(V _i ).

Since no values are available for the steady-state probability distributions for the model of subsystem j until after the first analysis of subsystem j, different approximations are required for probabilities P(E _ij ⁿ ), P(E _ij ^y ) and P(E _ij ^n,y )at the beginning of the algorithm.

If P(E _ij ^{n _j = 0}) denotes the probability that no kanban is active for product j at the end of the busy period for product i (regardless of the number of containers with input material) and if t _ji is an estimate for the long-run average time from the last busy period for product j until the end of the busy period for product i, then, assuming that n _j was zero at the end of the last busy period for product j, a (very rough) estimate for P(E _ij ^{n _j = 0}) is P ^est(E _ij ^{n _j = 0}) = e^{−λ _j t _ji} , where

By similar argument, we getP ^est(E _ij ^{y _j = 0}) = e^{−μ _j (1) t _ji} . Then, using basic probability calculus, we obtain P ^est(E _ij ⁿ ) =P ^est(E _ij ^{n _j = 0}) [1−P ^est(E _ij ^{y _j = 0})]= e^{−λ _j t _ji} −e^{−(λ _j +μ _j (1))t _ji} ,P ^est(E _ij ^y ) = [1−P ^est(E _ij ^{n _j = 0})]P ^est(E _ij ^{y _j = 0}) = e^{−μ _j (1) t _ji} − e^{−(λ _j +μ _j (1))t _ji} , and P ^est(E _ij ^n,y ) = P ^est(E _ij ^{n _j = 0})P ^est(E _ij ^{y _j = 0})= e^{−(λ _j +μ _j (1))t _ji} .

4.9. Equation for transition rate Λ _i

The idle period in subsystem i ends as soon as one product meets the setup condition. If this product is product i, then the manufacturing facility immediately resumes production, that is, the manufacturing facility switches back into state B. If, however, the first product that satisfies the setup condition in one of the other products, then a vacation starts, that is, the manufacturing facility switches into state V _i+1.

The transition rate for transitions (0,y,I)→ (0,y,V _i+1), y = 0,…,Y _i , and transitions (n,0,I) → (n,0,V _i+1), n = 1,…,K _i , must be the reciprocal of the mean of an exponentially distributed random variable that stands for the time from the beginning of the idle period until the first of the other products meets the setup condition. We denote this reciprocal by Λ _i . Ifl _ij denotes the long-run average time from the beginning of the idle period after processing items of product i until product j meets the setup condition and if the actual time followed an exponential distribution, then Λ _i = ∑ _{j = 1;j≠ i} ^r 1/l _ij , since the minimum of independent exponential random variables is an exponential random variable, and the parameter of this random variable is the sum of the parameters of the individual random variables.

The averages l _ij can only be approximated since no information is available in the model of subsystem i on the number of active kanbans and full containers with input material for product j, j = 1,…,r;j≠ i. It is known that product j needs an average of 1/λ _j time units to meet the setup condition if input material is available in the output store of stage 1, but no kanban is active (n _j = 0). It is also known that product j needs an average of 1/μ _j ⁽¹⁾ time units to meet the setup condition if the number of active kanbans is greater than zero, but no input material is available in the output store of stage 1 (y _j = 0). Finally, it is known that product j needs an average of 1/λ _j +1/μ _j ⁽¹⁾−1/(λ _j +μ _j ⁽¹⁾) time units to meet the setup condition if the number of active kanbans and the number of containers with input material are both zero. The average time needed in this last case is equal to the average value of the maximum of the two exponential random variables that stand for the time until a container of input material is filled in stage 1 and the time until a kanban is activated in stage 2. Weighting these three average times with the (approximate) probabilities that each of the three different situations prevails at the beginning of the idle period after processing items of product i, we get

4.10. Algorithm

The algorithm consists of two parts. In the first part (Steps 1–3), initial values are determined, in the second part (Steps 4–6), the models of subsystems 1 through r are analyzed one by one repeatedly until the performance measures change by less than 100ε percent.

Algorithm of the decomposition method

(Initialization)

	Step 1. Compute t S i:est and t B i:est for all i = 1,…,r.
	Step 2. Compute t SBI i:est for all i = 1,…,r; i ≠ 2.
	Step 3. (The “zeroth” rotation, starting with i = 2) For i = 2 to r 1. Approximate P(E ij n ), P(E ij y ) and P(E ij n,y ) for all j = 1,…, r; j≠ i, and determine P(E ij ) for all j = 1,…,r; j≠ i. 2. Approximate P(E i ) and calculate μ′ i and μ” i . Compute l ij for all j = 1,…,r; j≠ i, and determine transition rate Λ i . 3. Solve the balance equations of the CTMC for subsystem i to obtain probability distribution õ(i). Then determine probability distributions [qtilde](i) and [htilde](i). 4. Compute probability distribution [gtilde](i) and parameters t V (i), T (i) and t SBI (i). Next i (Convergence process)
	Step 4. Set k = 1.
	Step 5. (The kth rotation) For i = 1 to r 1. Approximate P(E ij n ), P(E ij y ) and P(E ij n,y ) for all j = 1,…, r; j≠ i, and determine P(E ij ) for all j = 1,…,r; j≠ i. 2. Approximate P(E i ) and calculate μ′ i and μ” i . Compute l ij for all j = 1,…,r; j≠ i, and determine transition rate Λ i . 3. Solve the balance equations of the CTMC for subsystem i to obtain probability distribution õ(i). Then determine probability distributions [qtilde](i) and [htilde](i). 4. Compute probability distributions ᵱ(i) and [ktilde](i). Then calculate the current values (rotation k) for the performance measures of interest. 5. if k > 1, then: if for all performance measures |currentvalue − lastvalue|currentvalue < ε, then stop, else continue the computations. 6. Compute probability distribution [gtilde](i) and parameters t V (i), T (i) and t SBI (i). Next i
	Step 6. Set k = k+1. Go to Step 5.

5. Tests without backorders

We conducted a series of test sets to determine the accuracy of the proposed approach (Table 1). In each test set, one characteristic of the base system (Table 2) was systematically increased by a given increment (the traffic intensity for manufacturing facility i in stage 1 was defined as ρ _i ⁽¹⁾ = λ _i /μ _i ⁽¹⁾, the total traffic intensity for stage 2 was defined as ρ⁽²⁾ = ∑ _{i = 1} ^r ρ _i ⁽²⁾ = ∑ _{i = 1} ^r λ _i /μ _i ⁽²⁾ and the parameter values for products 2,…,r−1 were chosen to obtain equal differences between the parameter values of consecutive products, for example, s ₂−s ₁ = s ₃−s ₂ = … = s _r −s _r−1). This experimental design was chosen to detect critical system properties that may significantly impact the approximation quality of the decomposition method.

Table 1 Test sets (tests without backorders)

Test set	Modified parameter	Range	Increment
1a	Total traffic intensity stage 2, ρ^(2)	0.10–0.90	0.10
1b	Traffic intensities stage 1, ρ i ^(1) (i = 1,…,r) [ρ^(2) = 0.80]	0.10–1.00	0.10
1c	Traffic intensities stage 1, ρ i ^(1) (i = 1,…,r) [ρ^(2) = 0.30]	0.10–1.00	0.10
2a	Traffic intensity ratio ρ1 ^(2)/ρ r ^(2) [ρ^(2) = 0.80]	2–20	2
2b	Traffic intensity ratio ρ1 ^(2)/ρ r ^(2)	2–20	2
	[ρ i ^(1) = 0.30 (i = 1,…,r), ρ^(2) = 0.30]
2c	Spread of traffic intensities stage 1, ρ1 ^(1)−ρ3 ^(1)	0.0–0.9	0.1
	[ρ^(2) = 0.80; ρ2 ^(1) = 0.50, ρ1 ^(1)−ρ2 ^(1) = ρ2 ^(1)−ρ3 ^(1)]
3	Setup to processing time ratio of product 1, s 1 ^(2)μ1 ^(2)	0.5–4.0	0.5
4	Setup time ratio s 1 ^(2)/s r ^(2)	0.3–1.0	0.1
5	Number of products, r	3–10	1

Table 2 Parameter values and ratios of the base system

Stage 1:
Traffic intensities, ρ i ^(1) (i = 1,…,r)	0.80
Stage 2:
Total traffic intensity, ρ^(2)	0.80
Traffic intensity ratio ρ1 ^(2)/ρ r ^(2)	1.60
Average processing rate of product 1, μ1 ^(2)	2.00
Processing rate ratio μ1 ^(2)/μ r ^(2)	0.90
Setup to processing time ratio of product 1, s 1 ^(2)μ1 ^(2)	2.00
Setup time ratio s 1 ^(2)/s r ^(2)	0.80
Required fill rates, f i ^min (i = 1,…,r)	0.95

As basis for comparison, we took either the results of the exact model (for small systems) or the results of a discrete-event simulation. Simulation results were gathered with the replication/deletion approach (e.g., Law and Kelton (2000)). Warmup periods and observation periods (replication length−warmup period) were generally set generously to obtain observations representative of steady-state behavior (warmup periods:200 000 or 300 000 time units, observation periods: from 3000 000 up to 6000 000 time units). We selected a maximum relative error of 0.1% for each point estimate at an individual confidence level of (approximately) 99%. When the point estimates did not satisfy this condition after 25 replications, additional replications were performed until either the maximum relative errors of the point estimates were satisfactory, or 80 replications had been performed. For some performance measures, the maximum relative error still exceeded the desired relative precision after 80 replications (test set 1b, ρ _i ⁽¹⁾ = 1.00, y ₁ ⁽¹⁾: max. rel.error 0.102%, ₂ ⁽¹⁾: 0.123%, ₃ ⁽¹⁾: 0.125%; 1c, ρ _i ⁽¹⁾ = 0.90, ₂ ⁽¹⁾: 0.127%, y ₃ ⁽¹⁾: 0.123%; 1c, ρ _i ⁽¹⁾ = 1.00, ₁ ⁽¹⁾: 0.213%, ₂ ⁽¹⁾: 0.261%, ₃ ⁽¹⁾: 0.276% ₂ ⁽²⁾: 0.111%, ₃ ⁽²⁾: 0.112%; 2a, ρ₁ ⁽²⁾/ρ _r ⁽²⁾ = 12, ₃ ⁽¹⁾: 0.111%; 2a, ρ₁ ⁽²⁾/ρ _r ⁽²⁾ = 14, ₃ ⁽¹⁾: 0.104%; 2a, ρ₁ ⁽²⁾/ρ _r ⁽²⁾ = 16, ₃ ⁽¹⁾: 0.129%; 2a, ρ₁ ⁽²⁾/ρ _r ⁽²⁾ = 18, ₃ ⁽¹⁾: 0.127%; 2a, ρ₁ ⁽²⁾/ρ _r ⁽²⁾ = 20, ₃ ⁽¹⁾: 0.170%).

The proposed evaluation algorithm was implemented with Visual Basic 5.0 and run on a PC with a Pentium III processor at 733 MHz. It converged for all test instances. We report for each test instance the number of rotations and the computation time (ε = 10⁻⁴). For many test instances the number of rotations is non-integer. This indicates that for these test instances the stopping criterion was met before the last rotation was completed.

Instead of reporting every single relative approximation error we reduced the amount of data by calculating for each stage and performance measure the Mean Absolute relative Deviation (MAD) and the Maximum relative Deviation (MaxD) of the estimates over all products. Let the relative Deviation (D) of an estimate be D = (estimate−exact value)/exact value. Then,

Note that if MaxD is negative (positive), then the decomposition method underestimated (overestimated) the true performance measure.

In test sets 1a–1c, we varied the total traffic intensity for stage 2 and the traffic intensity for each product in stage 1, respectively. As for all other test sets, the kanban configuration for each test instance, that is, the number of kanbans for each product in stages 1 and 2, was determined with a heuristic optimization procedure very similar to the one described in Krieg and Kuhn (2001). In this optimization procedure, a kanban configuration is considered optimal if there is no other kanban configuration that achieves given average fill rates with less average total inventory holding cost per unit of time. Out of pocket costs for setup changes are assumed to be negligible and identical inventory holding costs per container and unit of time are used for both stages and all products.

The results for test sets 1a–1c (Table 3, Table 4, Table 5) indicate that the approximation is only moderately sensitive to changes in the (total) traffic intensity. It appears that the estimation errors tend to increase for higher traffic intensities.

Table 3 Test set 1a

					^(1)		^(2)		f
ρ^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.10 ^e	3,3,3	5,5,5	7.7	1.782	0.79	0.72	-0.78	0.77	-0.11	0.11
0.20 ^e	4,3,3	4,5,5	6.7	0.902	0.94	0.66	-1.24	1.14	-0.20	0.17
0.30 ^e	5,5,4	4,4,5	7.3	0.872	-0.53	0.34	-0.94	0.79	0.13	0.09
0.40 ^e	5,5,4	5,5,6	5.7	0.831	-0.83	0.55	0.45	0.24	0.49	0.28
0.50	6,5,5	6,7,6	5.7	1.072	-1.17	0.88	1.65	1.22	0.71	0.48
0.60	6,7,6	9,7,7	6.0	1.703	-1.14	1.02	1.94	1.27	0.46	0.33
0.70	8,8,7	11,10,9	7.0	3.575	-1.31	1.27	0.47	0.41	-0.28	0.27
0.80	11,11,11	15,14,12	7.7	9.804	-1.89	1.84	-0.63	0.57	-1.15	1.10
0.90	18,19,16	23,22,21	8.0	44.985	-2.80	2.59	0.67	0.34	-2.09	1.83

Table 4 Test set 1b

					^(1)		^(2)		f
ρ^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.10	3,4,4	13,12,11	7.0	1.272	0.05	0.05	0.65	0.49	-0.96	0.85
0.20	4,6,5	14,12,11	7.0	1.823	0.12	0.12	1.09	0.55	-1.04	0.80
0.30	6,7,6	13,12,11	7.0	2.373	0.22	0.21	1.20	0.54	-1.06	0.87
0.40	7,7,6	13,13,12	7.0	2.904	0.27	0.18	1.59	0.65	-1.30	0.90
0.50	8,8,8	13,13,11	7.0	3.585	-0.16	0.11	0.39	0.28	-1.07	1.00
0.60	10,8,8	13,14,12	7.0	4.987	-0.69	0.52	0.61	0.45	-1.43	1.07
0.70	9,10,9	15,13,12	7.3	6.609	-1.25	1.14	-0.74	0.47	-1.36	1.15
0.80	11,11,11	15,14,12	7.7	9.824	-1.91	1.84	-0.57	0.51	-1.14	1.09
0.90	14,12,12	15,16,14	8.0	16.294	-2.38	2.34	-0.38	0.36	-1.01	0.93
1.00	18,18,16	20,19,18	9.7	43.883	-2.14	1.99	1.15	1.10	-0.49	0.43

Table 5 Test set 1c

					^(1)		^(2)		f
ρ^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.10 ^e	1,1,1	4,3,3	7.7	0.080	-0.12	0.09	1.45	0.70	1.08	0.86
0.20 ^e	2,2,1	3,3,4	7.7	0.110	-0.26	0.20	-1.22	0.79	0.42	0.26
0.30 ^e	2,2,2	3,3,3	7.3	0.120	-0.35	0.34	-1.77	1.32	0.32	0.20
0.40 ^e	3,2,2	3,4,3	7.3	0.201	-0.41	0.35	-1.87	1.30	-0.31	0.20
0.50 ^e	2,3,2	4,3,4	7.7	0.241	-0.37	0.27	-1.67	1.22	0.27	0.19
0.60 ^e	3,3,2	4,4,5	7.3	0.381	-0.34	0.27	-1.39	1.00	-0.18	0.12
0.70 ^e	4,3,3	4,5,4	7.3	0.541	-0.43	0.18	-1.29	0.85	-0.19	0.12
0.80 ^e	5,5,4	4,4,5	7.3	0.892	-0.53	0.34	-0.94	0.79	0.13	0.09
0.90	6,5,5	6,7,7	7.3	2.484	-0.31	0.19	-0.43	0.20	-0.06	0.04
1.00	11,10,10	10,11,11	7.7	15.672	0.49	0.25	-0.16	0.09	-0.03	0.01

In test sets 2a–2c (Table 6,Table 7, Table 8), the test instances were increasingly unbalanced with respect to the per product traffic intensities in stage 2 (test sets 2a, 2b) and in stage 1 (test set 2c). For that purpose, the ratio of the traffic intensity of the first product and the traffic intensity of the third product in stage 2 was systematically enlarged (the mean of the resulting intensities was used for product 2). For test set 2c, the traffic intensity of product 2 in stage 1, ρ₂ ⁽¹⁾ = λ₂/μ₂ ⁽¹⁾, was fixed at 0.50 and the spread of the traffic intensities for products 1 and 3 was systematically increased (while ρ₁ ⁽¹⁾ ≥ ρ₃ ⁽¹⁾ and ρ₁ ⁽¹⁾−ρ₂ ⁽¹⁾ = ρ₂ ⁽¹⁾−ρ₃ ⁽¹⁾). The results of these test sets suggest that the approximation is insensitive to changes of the traffic intensity ratio in stage 2 and moderately sensitive to drastically different average processing rates for the products in stage 1. Note that in the last instance of set 2c μ₁ ⁽¹⁾ = 0.69 and μ₃ ⁽¹⁾ = 9.12.

Table 6 Test set 2a

					^(1)		^(2)		f
ρ^(2)/ρr^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
2	12,10,10	14,15,11	7.3	8.933	-1.84	1.70	-0.55	0.41	-1.14	1.08
4	11,11,7	16,14,9	7.3	8.503	-1.76	1.57	-0.73	0.56	-1.32	0.91
6	10,13,9	17,13,6	7.3	8.913	-1.66	1.24	1.71	0.92	-1.43	0.73
8	10,11,6	16,14,6	7.3	7.631	-1.77	1.30	1.62	0.84	-1.23	0.63
10	10,11,6	16,14,5	7.3	7.621	-1.79	1.25	1.64	0.91	-1.14	0.53
12	12,12,5	14,13,5	7.3	7.661	-1.74	1.34	1.25	0.63	-0.95	0.43
14	11,12,5	14,13,5	7.3	7.230	-1.79	1.33	1.40	0.72	-0.97	0.39
16	10,11,6	15,13,4	7.3	6.830	-1.74	1.19	1.56	0.83	-0.94	0.37
18	10,11,5	15,13,4	7.3	6.740	-1.78	1.20	1.46	0.79	-0.89	0.35
20	10,11,5	15,13,4	7.3	6.770	-1.77	1.20	1.43	0.76	-0.83	0.34

Table 7 Test set 2b

					^(1)		^(2)		f
ρ^(2)/ρr^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
2 ^e	2,2,2	4,3,3	7.3	0.150	-0.37	0.35	-1.83	1.15	0.46	0.24
4 ^e	2,2,2	4,3,2	7.3	0.130	-0.36	0.26	-2.30	1.48	-0.83	0.57
6 ^e	1,2,2	5,3,2	7.7	0.151	-0.46	0.29	-3.25	2.13	1.12	0.88
8 ^e	1,2,2	4,3,2	7.3	0.130	-0.49	0.30	-3.45	1.92	1.26	0.90
10 ^e	1,2,1	4,3,2	7.3	0.120	-0.47	0.38	-3.63	2.09	1.19	0.98
12 ^e	1,2,1	4,3,2	7.3	0.130	-0.46	0.36	-3.74	2.04	1.16	0.94
14 ^e	1,2,1	4,3,2	7.3	0.130	-0.45	0.35	-3.81	1.99	1.14	0.91
16 ^e	1,2,1	4,3,2	7.3	0.131	-0.44	0.33	-3.86	1.95	-1.14	0.89
18 ^e	1,2,1	4,3,2	7.3	0.140	-0.44	0.33	-3.90	1.92	-1.15	0.87
20 ^e	1,2,1	4,3,2	7.3	0.160	-0.43	0.32	-3.92	1.89	-1.17	0.86

Table 8 Test set 2c

					y ^(1)		y ^(2)		f
ρ1 ^(1)−ρ r ^(1)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.00	8,8,8	13,13,11	7.0	3.705	-0.15	0.11	0.33	0.24	-1.07	1.01
0.10	9,7,8	13,14,11	6.7	3.905	-0.10	0.05	1.43	0.65	-1.25	1.00
0.20	10,7,6	13,14,12	7.0	4.086	-0.40	0.18	1.29	1.11	-1.57	0.96
0.30	10,8,7	13,13,11	7.0	4.196	-0.63	0.29	0.65	0.46	-1.19	1.00
0.40	10,10,5	14,12,12	7.0	4.747	-1.10	0.43	2.49	1.31	-1.38	0.94
0.50	10,7,6	15,14,11	7.3	5.147	-1.45	0.57	1.35	0.92	-1.28	1.03
0.60	12,9,5	14,12,11	7.0	5.478	-1.79	0.65	0.93	0.78	-1.25	0.97
0.70	11,7,5	16,14,11	7.7	6.459	-1.92	0.69	1.73	1.24	-1.34	1.01
0.80	14,6,3	15,15,12	7.7	8.312	-1.64	0.61	3.22	1.81	-1.46	0.90
0.90	15,6,3	17,15,11	7.7	10.365	-1.49	0.57	3.64	2.03	-1.46	0.99

In test sets 3 and 4 (Table 9 and Table 10), the setup times were changed. First, they were simultaneously enlarged for all products, then, the ratio of the setup times for product 1 and 3 was varied (s ₂ ⁽²⁾ = (s ₃ ⁽²⁾−s ₁ ⁽²⁾)/2). The results indicate a relatively high sensitivity of the approximation to changes in the setup times. The errors are most pronounced for the estimates of the average inventory levels in stage 2.

Table 9 Test set 3

					y ^(1)		y ^(2)		f
s 1 ^(2)μ1 ^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.5	6,5,4	6,7,7	6.7	1.172	-1.89	1.39	5.67	3.98	1.88	1.65
1.0	6,7,8	10,9,7	8.3	2.784	-1.70	1.46	3.29	2.37	0.94	0.77
1.5	8,9,8	13,11,11	8.3	5.558	-1.65	1.58	1.03	0.64	-0.49	0.32
2.0	11,11,11	15,14,12	7.7	9.964	-1.90	1.83	-0.62	0.56	-1.15	1.10
2.5	14,14,12	17,16,15	7.0	16.123	-2.12	2.08	-1.32	1.27	-1.77	1.68
3.0	14,15,14	22,20,18	7.3	27.019	-2.62	2.45	-2.83	2.67	-2.26	2.14
3.5	16,17,14	25,22,22	7.0	38.796	-2.73	2.58	-4.05	3.55	-2.77	2.52
4.0	20,19,16	26,25,24	6.3	55.419	-2.89	2.75	-3.97	3.42	-2.82	2.73

Table 10 Test set 4

					y ^(1)		y ^(2)		f
s 1 ^(2)/s r ^(2)	K ^(1)	K ^(2)	Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.3	18,17,18	27,25,20	6.7	49.031	-2.68	2.54	-4.02	2.87	-2.71	2.52
0.4	16,15,15	21,20,17	6.7	27.339	-2.31	2.24	-2.47	1.91	-2.31	2.10
0.5	14,14,13	19,17,15	7.0	18.517	-2.24	2.10	-1.96	1.49	-1.83	1.78
0.6	13,12,12	17,16,14	7.3	14.180	-2.07	2.02	-1.44	1.17	-1.58	1.51
0.7	12,12,11	15,14,13	7.3	10.715	-1.90	1.82	-0.72	0.68	-1.33	1.29
0.8	11,11,11	15,14,12	7.7	9.804	-1.90	1.83	-0.62	0.56	-1.15	1.10
0.9	12,10,11	13,14,11	7.3	8.502	-1.81	1.73	-0.20	0.16	-0.98	0.91
1.0	9,9,10	15,14,11	7.7	7.881	-1.78	1.69	-0.58	0.39	-1.06	0.87

Finally, the number of products was systematically increased from three to ten (test set 5, shown in Table 11). The results show no significant changes in the approximation quality when more products are added to the system.

Table 11 Test set 5

r	K ^(1)	K ^(2)
3	11,11,11	15,14,12
4	11,13,11,10	15,13,13,12
5	11,12,10,12,10	16,14,15,12,12
6	12,12,12,10,11,11	15,14,13,14,12,11
7	13,11,11,10,12,9,11	14,15,14,15,12,14,11
8	11,11,11,10,12,11,9,10	16,15,14,15,12,12,13,11
9	11,11,13,12,10,11,11,11,10	16,15,13,13,14,13,12,11,11
10	11,11,11,12,10,12,11, 12,11,8	16,15,14,13,15,12,12,11,11,14
		y ^(1)		y ^(2)		f
Rotations	Time(seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
7.7	9.794	-1.89	1.84	-0.63	0.57	-1.15	1.10
7.3	17.064	-1.76	1.74	-0.90	0.78	-1.43	1.25
7.2	29.363	-1.81	1.73	-1.29	1.16	-1.43	1.28
5.8	39.356	-1.74	1.60	-1.06	0.93	-1.30	1.20
3.9	51.283	-1.56	1.47	-1.33	1.09	-1.35	1.16
5.1	71.833	-1.41	1.32	-1.34	1.14	-1.29	1.13
6.2	105.001	-1.38	1.26	-1.05	0.85	-1.16	1.02
5.5	131.770	-1.25	1.13	-1.23	0.87	-1.11	0.98

6. Tests with backorders

In this section, we give results of tests in which the maximum number of backorders, B _i ^max, is greater than zero (partial backordering). All reference values, except for the two instances of the first test set, were obtained from simulation. In the simulation experiments for the first test set (warmup periods: 300 000 time units, observation periods: 6000 000 time units), additional replications were made until each point estimate had a relative error of at most 0.1% at an individual confidence level of (approximately) 99%. In the simulation experiments for the second test set (warmup periods: 400 000 time units, observation periods: 8000 000 time units), additional replications were made until each point estimate had a relative error of at most 0.2% at an individual confidence level of (approximately) 99%. Only for B _i ^max = 18, did the maximum relative errors of the estimates for the average inventory levels in stage 2 for products 1 and 2 still exceed this value after 80 replications ₁ ⁽²⁾: 0.205%, ₂ ⁽²⁾: 0.205%).

First, we ran test set 1a with B _i ^max = 1 for all i = 1,…,r to determine if increasing the total traffic intensity in stage 2 has the same effect on the approximation quality when B _i ^max > 0, that is, larger errors for ρ⁽²⁾ > 0.70.

The results (Table 12) are almost identical to the ones for B _i ^max = 0 (Table 3). Only for total traffic intensities above 0.70, do the relative errors appear to increase systematically. The relative errors, however, are still very moderate, even for ρ⁽²⁾ = 0.90.

Table 12 Test set 1a with backorders

					y ^(1)		y ^(2)		f		f SD
ρ^(2)	K ^(1)	K ^(2)	Rotations	Time (seconds)	MaxD (%)	MAD (%)	MaxD (%)	MAD(%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0.10 ^e	3,3,3	5,5,5	9.3	2.654	0.80	0.73	-0.86	0.84	-0.12	0.12	-0.08	0.08
0.20 ^e	4,3,3	4,5,5	6.7	1.342	0.95	0.67	-1.36	1.24	-0.21	0.16	-0.15	0.13
0.30	5,5,4	4,4,5	8.0	1.322	-0.48	0.27	-0.69	0.46	0.30	0.16	0.11	0.07
0.40	5,5,4	5,5,6	7.7	1.301	-0.62	0.47	1.14	0.73	0.81	0.53	0.40	0.24
0.50	6,5,5	6,7,6	6.7	1.493	-0.93	0.71	2.20	1.66	0.98	0.75	0.53	0.38
0.60	6,7,6	9,7,7	7.3	2.413	-1.07	0.97	2.45	1.60	0.77	0.55	0.41	0.26
0.70	8,8,7	11,10,9	9.0	4.737	-1.40	1.37	0.48	0.40	-0.24	0.22	-0.30	0.28
0.80	11,11,11	15,14,12	9.7	12.448	-2.10	2.05	-0.81	0.74	-1.23	1.16	-1.11	1.06
0.90	18,19,16	23,22,21	10.3	53.767	-3.00	2.79	0.64	0.36	-2.18	1.87	-2.06	1.80

We also investigated if increasing the maximum number of backorders has any effect on the accuracy of the approximation (test set 6). For that purpose, we used a completely balanced system with three products and ρ⁽²⁾ = 0.80, ρ _i ⁽¹⁾ = 0.80 and s _i ⁽²⁾μ _i ⁽²⁾ = 2, i = 1,2,3 (μ _i ⁽²⁾ = 2, λ _i = 0.53, s _i ⁽²⁾ = 1 and μ _i ⁽¹⁾ = 0.67). We set the number of kanbans to K _i ⁽¹⁾ = 7 and K _i ⁽²⁾ = 9 to yield average fill rates of about 0.90 for B _i ^max = 0. Then B _i ^max was increased from zero to 18 in increments of two (Table 13).

Table 13 Test set 6

					y ^(1)		y ^(2)		f		f SD
ρ^(2)	K ^(1)	K ^(2)	Rotations	(seconds)Time	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)	MaxD (%)	MAD (%)
0	7,7,7	9,9,9	6.3	2.163	-0.80	0.79	0.26	0.25	-0.81	0.81	-0.81	0.81
2	7,7,7	9,9,9	8.0	3.565	-0.97	0.95	0.39	0.35	-0.66	0.64	-0.89	0.88
4	7,7,7	9,9,9	8.7	5.218	-1.13	1.11	-0.04	0.03	-0.65	0.64	-0.94	0.94
6	7,7,7	9,9,9	8.7	7.290	-1.27	1.25	-0.79	0.74	-1.01	0.98	-0.95	0.95
8	7,7,7	9,9,9	9.0	10.265	-1.41	1.39	-2.13	2.04	-2.02	1.95	-0.99	0.98
10	7,7,7	9,9,9	9.3	13.800	-1.51	1.50	-3.39	3.33	3.09	3.04	-0.98	0.98
12	7,7,7	9,9,9	9.3	18.016	-1.60	1.59	-4.89	4.85	-4.43	4.40	-0.99	0.99
14	7,7,7	9,9,9	9.3	22.773	-1.71	1.68	-6.61	6.56	-5.99	5.95	-1.00	0.99
16	7,7,7	9,9,9	9.3	28.390	-1.74	1.74	-8.24	8.21	-7.55	7.53	-1.00	1.00
18	7,7,7	9,9,9	9.7	35.001	-1.80	1.80	-9.87	9.86	-9.13	9.11	-1.01	1.00

In this example, increasing the maximum number of backorders leads to a very moderate rise of the relative approximation errors of the average inventory levels in stage 1 and the average fractions of served demand. The increase of the relative errors of the average fill rates and the average inventory levels in stage 2, however, is more pronounced. Starting at under 1% the values rise to almost 10% for B _i ^max = 18.

7. Analysis of system behavior

For a completely balanced two-stage kanban system with three products and no or a limited number of backorders (λ _i = 0.53, μ _i ⁽²⁾ = 2, s _i = 1, i = 1,2,3; ρ⁽²⁾ = 0.80), we explored the effects of increasing the maximum number of backorders on the performance measures average fraction of served demand, average fraction of immediately served demand (average fill rate) and average inventory level, first, when stage 1 is the bottleneck of the system (μ _i ⁽¹⁾ = 0.67, hence, ρ _i ⁽¹⁾ = 0.80), and, second, when stage 1 is not the bottleneck (μ _i ⁽¹⁾ = 5.3, hence, ρ _i ⁽¹⁾ = 0.10). Since the performance measures are identical for all three products, we only report the values for product 1.

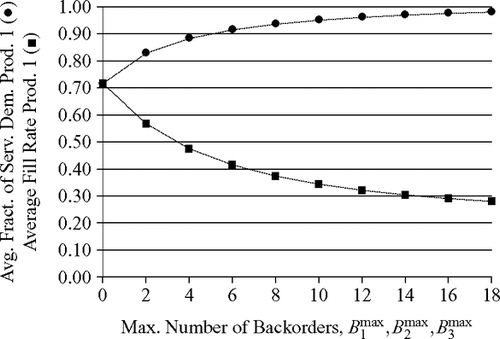
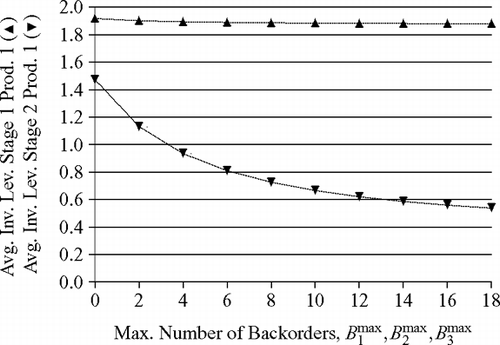
For the first experiment, the approximations are depicted in Fig. 6 and Fig. 7. We increased the maximum number of backorders simultaneously for each product from zero to 18 in increments of two, while we kept the number of kanbans in stages 1 and 2 constant at K ₁ ⁽¹⁾ = K ₂ ⁽¹⁾ = K ₃ ⁽¹⁾ = 3 and K ₁ ⁽²⁾ = K ₂ ⁽²⁾ = K ₃ ⁽²⁾ = 4, respectively, to yield average fill rates of about 0.70 forB ₁ ^max = B ₂ ^max = B ₃ ^max = 0. The results depicted in Fig. 6 indicate that the average fraction of served demand hardly changes, whereas the average fraction of immediately served demand (average fill rate) drops sharply. At the same time, the average inventory level in stage 1 remains almost constant, while the average inventory level in stage 2 falls drastically (Fig. 7).

Fig. 6 Increasing the maximum number of backorders when stage 1 is the bottleneck (ρ⁽¹⁾ = 0.80, ρ⁽²⁾ = 0.80); • = average fraction of served demand for product 1, ▪ = average fraction of immediately served demand for product 1 (average fill rate).

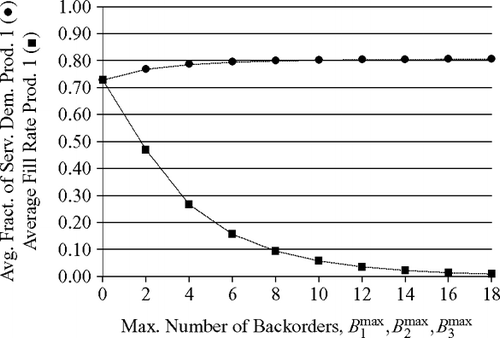
Fig. 7 Increasing the maximum number of backorders when stage 1 is the bottleneck(ρ⁽¹⁾ = 0.80, ρ⁽²⁾ = 0.80); ▵ = average inventory level in stage 1 for product 1, ▪ = average inventory level in stage 2 for product 1.

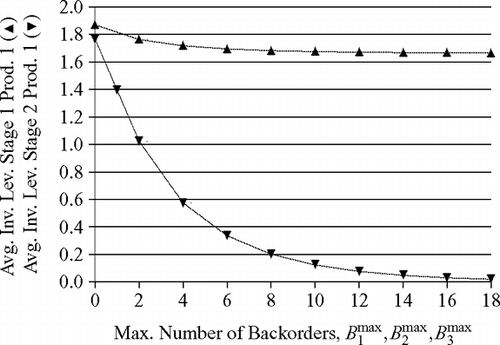
One would expect the average fraction of served demand to rise faster when the maximum number of backorders is increased. The production runs in stage 2 should become longer because more orders may accumulate between production runs since the maximum number of orders at the start of a production run is K _i ⁽²⁾+B _i ^max,2 for product i. Longer production runs mean that the fraction of time that the manufacturing facility in stage 2 actually produces items increases and a smaller fraction of time is used for changing the setup. Consequently, the average production rates for each product should increase, which would then translate directly into larger fractions of served demand. In this example, however, stage 1, which is clearly the bottleneck of the system, sabotages the described mechanism. Production runs in stage 2 must be terminated before all production orders have been processed because stage 1 cannot keep up with the production of the input material for stage 2. As a consequence, the production runs in stage 2 hardly expand when the number of backorders is raised. Average inventory levels in the output store of stage 2 drop sharply because filled containers are often withdrawn instantly to satisfy accumulated backorders.

For comparison, we conducted a second experiment in which stage 1 was not the bottleneck of the system. Again, we increased the maximum number of backorders for each product simultaneously from zero to 18 in increments of two. We held the number of kanbans constant at K ₁ ⁽¹⁾ = K ₂ ⁽¹⁾ = K ₃ ⁽¹⁾ = 2 and K ₁ ⁽²⁾ = K ₂ ⁽²⁾ = K ₃ ⁽²⁾ = 3 to yield average fill rates of about 0.70 for B ₁ ^max = B ₂ ^max = B ₃ ^max = 0. Figure 8 illustrates that in this experiment the average fraction of served demand increases much faster and the average fill rate falls significantly slower. Moreover, the average inventory levels in both stages clearly decrease at a lower pace (Fig. 9).

Fig. 8 Increasing the maximum number of backorders when stage 1 is not the bottleneck (ρ⁽¹⁾ = 0.10, ρ⁽²⁾ = 0.80); • = average fraction of served demand for product 1,▪ = average fraction of immediately served demand for product 1 (average fill rate).

Fig. 9 Increasing the maximum number of backorders when stage 1 is not the bottleneck (ρ⁽¹⁾ = 0.10, ρ⁽²⁾ = 0.80); ▵ = average inventory level in stage 1 for product 1, ▪ = average inventory level in stage 2 for product 1.

8. Conclusions

In this paper, we have presented a decomposition method for the evaluation of two-stage multi-product kanban systems. The proposed procedure is an extension of the decomposition method described in Krieg and Kuhn (2004). The general principle used is the decomposition of a system with r products into r single-product subsystems. The results of several test sets suggest that the approximation is sufficiently accurate for a large variety of systems.

In future research, an approach should be developed for the evaluation of multi-product kanban systems with an arbitrary number of stages in series. The decomposition method presented here is expected to be an important building block in the construction of a suitable and effective procedure.

Biographies

Georg N. Krieg received his Ph.D. in Business Administration from the Catholic University of Eichstaett-Ingolstadt, Germany. He holds a degree in Business Administration from the University of Cologne, Germany, and an M.B.A. from Eastern Illinois University, Charleston, IL, USA. He was an Assistant Professor at the Chair of Production and Operations Management of the Catholic University of Eichstaett-Ingolstadt (2003–2006). Before that, he was a Teaching and Research Assistant at the same chair (1998–2003). He is the author of the research monograph Kanban-Controlled Manufacturing Systems published by Springer (Berlin, 2005).

Heinrich Kuhn is a Full Professor of Production and Operations Management at the Catholic University of Eichstaett-Ingolstadt, Germany and a Contract Professor for Production and Logistics at the Free University of Bozen, Italy in the Faculty of Business Administration and Economics. Before that, he was an Assistant Professor at the University of Cologne, Germany (1994–1997) and a Teaching and Research Assistant at the Technical University of Brunswick, Germany (1990–1994). He received his Ph.D. (1990) in Industrial Engineering from the Technical University of Darmstadt, Germany, and the degree of Habilitation (1997) in Business Administration from the University of Cologne, Germany. He is a co-author of the textbook Flexible Manufacturing Systems – Decision Support for Design and Operation, published by Wiley (New York, NY, 1993). His research interest are in operations management, logistics, lot sizing, scheduling and stochastic models.

Acknowledgements

We are grateful for the helpful comments of the editor, Dr. Stanley B. Gershwin, and two anonymous reviewers.

Notes

^eComparison based on exact values.

^eComparison based on exact values.

^eComparison based on exact values.

^eComparison based on exact values.