An economic comparison of CUSUM and Shewhart charts

Abstract

This paper compares the economic performance of CUSUM and Shewhart schemes for monitoring the process mean. We develop new simple models for the economic design of Shewhart schemes and more accurate ways to evaluate the economic performance of CUSUM schemes. The results of the comparative analysis show that the economic advantage of using a CUSUM scheme rather than the simpler Shewhart chart is substantial only when a single measurement is available at each sampling instance, i.e., only when the sample size is always n = 1, or when the sample size is constrained to low values.

Keywords:

• Economic design
• CUSUM chart
• Shewhart chart

1. Introduction

For many years the research community has allocated a considerable part of its effort to the design of effective quality control charts. The effectiveness of the charts is usually evaluated from a statistical point of view, but it is increasingly recognized that since it is the bottom line that matters, the control chart design must be primarily evaluated using economic criteria. The objective of this paper is to provide a thorough economic comparison between the most frequently used control charts, i.e., the standard Shewhart chart and the CUSUM chart for monitoring the mean of a quality characteristic.

Many researchers have developed and proposed models for the economic optimization of control chart design since the seminal work of Duncan (1956), who was the first to introduce an economic model for the design of the Shewhart-type chart. In Duncan's model the process is represented as a series of stochastically identical cycles, ending with the restoration of the process after the detection of an actual occurrence of some assignable cause. The average cost per time unit is computed as the ratio of the average cost per cycle to the average duration of a cycle. The optimal chart parameters, i.e., sampling interval h, sample size n and control limit coefficient k, are those that minimize the average cost per time unit. This general approach has been extended, with variations, to more complex charts. The economic design of the CUSUM chart was first studied by Taylor (1968). He developed a model similar to that of Duncan (1956) but without optimizing the sample size and the sampling interval. Goel and Wu (1973) and Chiu (1974) proposed similar models and algorithms for determining the economically optimum design of CUSUM charts and reported some results of sensitivity analyses.

A general model for the economic design of control charts has been proposed by Lorenzen and Vance (1986). Their approach may be used for the selection of the optimal parameters of a variety of charts, including Shewhart, CUSUM and EWMA, as long as certain statistical measures of performance, for example the Average Run Length (ARL), can be computed for any combination of chart parameters. Simpson and Keats (1995) used two-level fractional factorial designs to identify highly significant parameters in the economic model of Lorenzen and Vance (1986) as applied in the case of a CUSUM chart.

All the above papers and the majority of the literature about economic control chart design use the expected cost per time unit as the optimality criterion. An alternative approach, which was followed by Knappenberger and Grandage (1969) and Saniga (1977) among others, adopts the expected cost per item as the optimality criterion. However, both approaches lead to almost identical optimal chart designs (Montgomery, 1980).

Over the years there have been only a few papers that compare Shewhart and CUSUM charts on economic grounds. Arnold and Von Collani (1987) developed a method to determine a near-optimal economic design and then used it to make comparisons between Shewhart and non-Shewhart charts such as CUSUM charts. They used a loss-per-item cost function, found the optimal design parameters of the Shewhart chart and then followed a three-step procedure to determine a near-optimal non-Shewhart design: in step 1 they use the optimal sample size of the Shewhart chart as the sample size of non-Shewhart charts; in step 2 they determine the reference value and the control limit of the non-Shewhart chart by minimizing the out-of-control ARL _δ, keeping the value of the in-control ARL ₀ equal to that of the Shewhart chart; and finally in step 3 for the sample size of step 1 and the reference value and the control limit of step 2, they find the sampling interval that minimizes the loss function. They concluded that, under certain assumptions, Shewhart charts perform very well and cannot be improved significantly by other, more complicated charts, such as CUSUM charts.

Nantawong et al. (1989) performed an experiment to evaluate the effect of three factors (sample size, sampling interval and magnitude of the shift) on three control charts, namely Shewhart chart, CUSUM and geometric moving average charts, using profit as the evaluation criterion but without optimizing any of the three charts.

Keats and Simpson (1994) used designed experiments to identify the cost and model parameters that have a significant impact on the average cost of CUSUM and Shewhart charts. They concluded that CUSUM charts are significantly more economical than Shewhart charts, especially for monitoring processes subject to small shifts. Ho and Case (1994) have also undertaken a brief economic comparison between Shewhart, CUSUM and EWMA charts and they concluded that both CUSUM and EWMA charts have a much better economic performance than Shewhart charts.

From the above exposition it appears that the results of the previous investigations regarding the relative economic effectiveness of Shewhart and CUSUM charts are inconclusive. For example, although Arnold and Von Collani (1987) state that Shewhart charts cannot be improved significantly by other, more complicated charts, Ho and Case (1994) and Keats and Simpson (1994) conclude that the anticipated savings from using a CUSUM chart rather than a Shewhart one are substantial. This contradiction may be partially explained by the fact that most models for the economic evaluation of CUSUM schemes use approximations of the ARLs in the respective cost functions. Specifically, most models use the zero-state ARL for detecting a δ-shift in the mean (ARL _δ), which is computed assuming that at the time of the shift, the value of the CUSUM statistic is equal to zero. However, when a shift occurs, the process under study has been typically operating for some time and the value of the CUSUM statistic may not be zero. In fact, the CUSUM statistic at the time of the shift is a random variable with a steady-state distribution. Therefore, the cost function of the CUSUM chart is computed more accurately using the steady-state ARL _δ, which is the weighted average of all the ARL _δ values given the value of the CUSUM statistic when the shift occurs, with the weights being the probabilities of the steady-state distribution of the CUSUM values (see Crosier (1986)). This is a difficult computation, which the model presented in this paper avoids by using a somewhat different approach in formulating the cost functions.

The purpose of this paper is to resolve the existing ambiguity regarding the relative economic effectiveness of Shewhart and CUSUM charts. The vehicle is a new, accurate model for the computation of the average quality-related cost for the case of monitoring a process mean using a CUSUM chart. Using this tool the paper proceeds to a systematic numerical investigation of the conditions (problem characteristics) under which it is worth monitoring the process mean with a CUSUM chart instead of the simpler Shewhart chart. The main finding of this investigation is that the economic superiority of the CUSUM scheme is significant only when the sample sizes are restricted to be unitary, i.e., when rational grouping of observations is infeasible, or when they are restricted to be very small.

The next section describes the problem in detail and presents the proposed models for the economic design of Shewhart and CUSUM charts. Section 3 presents and discusses the results of the numerical investigation and Section 4 summarizes the conclusions of this research.

2. Problem setting and cost models

We consider a production process that operates indefinitely. There is a single quality characteristic X that must be monitored on-line, which is assumed to be a normally distributed random variable with target value μ₀ and variance σ². Note that the variance of X is not known in reality but we assume that it can be accurately estimated by sufficient past data. Also note that the assumption of the normality of X, which is typical in the majority of the related literature, is practically innocuous when the sample sizes are not too small because then the sample means are anyway approximately normally distributed by the central limit theorem. However, if the distribution of X exhibits substantial departures from normality and the sample sizes are small or unitary, then the analysis of the relative economic performance of CUSUM and Shewhart charts must be modified accordingly and is beyond the scope of this paper.

The process starts in a state of statistical control (“in control”) with E(X) = μ₀ and is subject to the occurrence of two assignable causes (cause 1 and cause 2) that bring the process to an out-of-control state by shifting the mean of the quality characteristic to μ₁ = μ₀ + δ σ or to μ₂ = μ₀ − δ σ without affecting the standard deviation. The times until the occurrence of assignable cause 1 and 2 are assumed to be independent exponentially distributed random variables with means 1/λ₁ and 1/λ₂ time units respectively. Therefore, the expected time until the occurrence of any assignable cause is 1/λ where λ = λ₁ + λ₂. The probability that an assignable cause occurs in an interval of h time units, given that the interval starts in statistical control, is a function of h but for simplicity it will be denoted by γ:

The probability that assignable cause j (j = 1 or 2) occurs before the other cause in an interval h that starts in control is

It is assumed that after the occurrence of assignable cause j the process mean will stay at μ _j until it is restored to μ₀.

At each sampling instance a sample of size n is taken, the sample mean is computed and, depending on its value and the chart statistic, an alarm may be issued. If the chart issues no alarm, no action is taken and the next sampling instance is after exactly h time units. If an alarm is issued, it is followed by an investigation and then restoration to the in-control state, if an assignable cause is detected. The process may either continue operating or be shut down during search and repair. It is assumed that the time to sample and investigate after a false alarm is less than h. Consequently, the sampling process stops during investigation and restoration because sampling is useless when the process is known to operate in the out-of-control state. After the detection and removal of an actual assignable cause the process resumes its operation with μ = μ₀; the next sample is then taken after h time units.

The sampling and inspection cost is c per unit and the fixed cost per sample is b. The cost of a false alarm is L ₀, and the cost of restoring the process after a true alarm is L ₁ ≥ L ₀. The additional expected cost per time unit of operation when the process operates in an out-of-control state is M. Table 1 contains the notation that has been introduced so far, as well as the other notation that is used in this paper.

Table 1 Nomenclature

Notation	Description
λ	Average rate of occurrence of the assignable causes
λ j	Average rate of occurrence of assignable cause j (j = 1, 2)
τ	Expected time of occurrence of the assignable cause within an interval of length h
γ	Probability that an assignable cause will occur in an interval of h time units
γ j	Probability that assignable cause j will occur in an interval of h time units
n	Sample size
h	Sampling interval
k s	Control limit for the Shewhart chart
k c	Reference value for the CUSUM chart
H	Control limit for the CUSUM chart
σ	Standard deviation of the quality characteristic
μ0	Target mean of the quality characteristic
δ	Magnitude of the shift in the mean, measured in standard deviations
μ1	Mean of the quality characteristic when the first assignable cause has occurred
μ2	Mean of the quality characteristic when the second assignable cause has occurred
δ1	Index variable indicating whether production continues during searches (1-yes, 0-no)
δ2	Index variable indicating whether production continues during repairs (1-yes, 0-no)
L 1	Cost of restoring the process after a true alarm
L 0	Cost of a false alarm
c	Sampling and inspection cost per unit
b	Fixed cost per sample
M	Additional expected cost per time unit of operation when the process is out of control
C ij	Expected cost between two successive samples associated with departure from state (Y t = i, a t = j)
T ij	Expected time between two successive samples associated with departure from state (Y t = i, a t = j)
ARL 0	ARL while the process is in control
ARL δ	ARL while the process operates out of control with mean μ1 or μ2
α	Probability of a type I error at each sample when using a Shewhart chart
β	Probability of a type II error at each sample when using a Shewhart chart
T 0	Expected search time when a false alarm is issued
T 1	Expected search time to uncover an existing assignable cause
T 2	Expected time to repair the process
g	Time to sample and chart one item
Y t	Actual state of the process when sample t is taken
C t ^h	CUSUM statistic for detecting upward shifts
C t ^l	CUSUM statistic for detecting downward shifts
C t	Unique CUSUM statistic for use when following the approach of Crosier (1986)
m	Number of subintervals (from zero to H and from −H to zero)
w	Width of subintervals (from −(m − 1) to m − 1)
p ij ^kl	Transition probabilities of CUSUM scheme during a sampling interval where i, j (= − m, …, m) represent the value of C t and k, l (= 0, 1, 2) represent the state of the process
π ij	Steady-state probabilities where i (= 0,1,2) represents the state of the process and j (= 0, 1) represents the decision whether to overhaul (1) or not (0) (for Shewhart charts) or j (= –m, …, m) represents the value of C t (for CUSUM charts)
z t	Standardized observation at sample t
φ (z)	Density function of the standard normal distribution

Lorenzen and Vance (1986) have developed a general economic model that is representative of a large class of models, which express the process operation and monitoring as a succession of stochastically identical cycles and compute the expected cost per time unit as the ratio of the expected cycle cost to the expected cycle length using the renewal-reward theorem. An alternative modeling approach is to express the evolution of the process by means of Markov chains as in the works of Knappenberger and Grandage (1969), Saniga (1977) and Nikolaidis et al. (1997). These papers deal with the economic minimization of the expected cost per unit of output. They use the steady-state probabilities that the process is in each particular state at the time of a sample, and the fractions of time spent in each particular state during a sampling interval.

In this paper we also employ Markov chains to develop the models for the economic optimization of both Shewhart and CUSUM charts. Specifically, we use a two-dimensional discrete-time Markov chain that describes: (i) the actual state of the process (operation under statistical control or under the effect of an assignable cause); and (ii) the decision that is made at each sampling instance (for Shewhart charts) or the actual value of the statistic of the CUSUM charts (in case of CUSUM charts). We start by describing the Markov model for the Shewhart chart.

2.1. Shewhart-type chart

For the case of a Shewhart chart with control limits μ₀ ± k _sσ/√n, the probability of a type I error at each sample is α = 2Φ (− k _s) whereas the probability of a type II error is β = Φ (k _s− δ √n) − Φ (− k _s− δ √ n).

Let Y _t denote the actual state of the process at sampling instance t, prior to investigation and restoration if needed, where Y _t = 0 denotes the in-control state (μ = μ₀), Y _t = 1 refers to the out-of-control state where μ = μ₁ = μ₀ + δ σ and Y _t = 2 refers to the out-of-control state where μ = μ₂ = μ₀ − δ σ. If at sampling instance t the absolute value of the standardized sample mean z _t = ( − μ₀) √n/σ exceeds the control limit k _s, then a signal is issued and the process is investigated; this action/decision is indicated by a _t = 1. Otherwise (|z _t | < k _s), no action is taken: a _t = 0. The discrete-time stochastic model for the process and its monitoring scheme is based on the combination of the actual state of the process Y _t and the value of a _t at every t. The pair (Y _t , a _t ) constitutes the state of a two-dimensional Discrete-Time Markov Chain (DTMC) with the special feature that each step may have a different duration when measured in actual time units. There are six possible states and the transition probability matrix is as follows:

The steady-state probabilities of (Y _t = i, a _t = j), denoted π _ij (i = 0, 1, 2, j = 0, 1), are obtained by solving the respective system of linear steady-state equations and can be used to evaluate the long-run expected cost per time unit as the ratio of the average cost of a transition step over its average duration; if C _ij is the expected cost and T _ij is the duration of a transition step from state (Y _t = i, a _t = j) of the DTMC to some other or the same state at the next sampling instance, then the long-run expected cost per time unit is

More specifically, the expected costs C _ij between two successive sampling epochs associated with the departure from each of the six possible states of the Markov chain are

The respective time lengths T _ij are given in Fig. 1. If the chart issues no signal (Y _t = 0, 1, 2 and a _t = 0) the time until the next sampling instance is just h. If there is a signal the time length is increased by the times of investigation and restoration, unless the alarm is false and the process continues its operation during the investigation (δ₁ = 1); in that case T ₀ becomes part of h, assuming it does not exceed h − gn.

Fig. 1 Time between two successive sampling instances associated with the departure from each of the six states of the Markov chain.

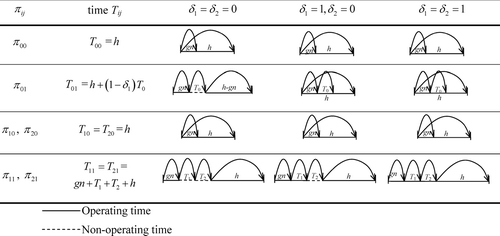
Note that the term cn + b appears in all the above cost expressions C _ij because the sampling cost is the same regardless of the state (Y _t = i, a _t = j). The cost of a false alarm, L ₀, appears only in C ₀₁ because state (0, 1) is the only one associated with a false alarm. Similarly, the cost of restoring the process after a true alarm, L ₁, appears only in C ₁₁, C ₂₁.

The expected additional cost of operating under the effect of an assignable cause during an interval T _ij is somewhat less obvious as it depends on the expected time that the process operates in an out-of-control state during that interval. This cost is Mh in intervals starting from states (Y _t = 1, a _t = 0) and (Y _t = 2, a _t = 0) of the DTMC because these states signify a type II error of the chart and consequently out-of-control operation for the entire interval of length h until the next sample. Cost M (gn + δ₁ T ₁ + δ₂ T ₂) is incurred during the operational time before the removal of an existing assignable cause when (Y _t = 1, a _t = 1) or (Y _t = 2, a _t = 1). Finally, M (h − γ/λ) is the expected cost of out-of-control operation within an interval of length h, given that the interval starts with the process in control, i.e., when the DTMC is in state (Y _t = 0, a _t = 0) or (Y _t = 0, a _t = 1), as well as after the removal of an existing assignable cause when (Y _t = 1, a _t = 1) or (Y _t = 2, a _t = 1); see Fig. 1. In particular, if τ denotes the conditional expected time of the occurrence of an assignable cause within an interval, given that there is such an occurrence within that interval, then the process will operate under its effect for an expected time h − τ. Consequently, the unconditional expected time of out-of-control operation within an interval of length h where the process begins its operation in the in-control state is γ(h − τ). From Duncan (1956) it is known that τ = [1 − (1 + λ h)exp (− λ h)]/[λ (1 − exp (− λ h))] and since γ = 1 − exp (− λ h) we get that γ (h − τ) = γ h − γ ((γ − λ h + γ λ h)/γ λ) = h − γ/λ. Thus, the corresponding expected cost of out-of-control operation is M (h −γ/λ).

By grouping similar cost terms together, Equation (4) can be simplified as follows:

In the special case where λ₁ = λ₂ = λ/2, which implies γ₁ = γ₂ = γ/2, the steady-state probabilities of (Y _t = i, a _t = j) are

If we substitute for the above π _ij in Equation (5), we get:

The above expression is almost identical to the corresponding one in Lorenzen and Vance (1986). There is only a small difference in the sampling cost term, which is due to the different assumption in their model, namely that sampling never stops as long as the process operates.

2.2. CUSUM chart

For the case of the monitoring of the process mean using a CUSUM chart, the usual approach is to use two separate CUSUM statistics, i.e., C _t ^h for detecting upward shifts and C _t ^l for detecting downward shifts:

where z _t = (− μ₀) √n/σ is the standardized sample mean and k _c is the reference value of the CUSUM chart. A signal is issued when either of the two statistics exceeds the control limit H. An alternative approach, which was proposed by Crosier (1986), uses a single statistic C _t that can take either positive or negative values:

and C ₀ = 0. A signal is issued when C _t ≥ H or C _t ≤ − H. Whichever approach is used, the ARLs are computed by one of the methods suggested in the literature, i.e., integral equations, Markov chain approximations and simulation (Hawkins and Olwell, 1998).

We conducted a numerical investigation which showed that the use of the two separate CUSUM charts with the same k _c > 0 always leads to slightly better economic results than the use of a single statistic. More specifically, the optimal k _c tends to be higher in the single-statistic approach compared to the optimal value of k _c when two separate CUSUM charts are used, in order to avoid positive or negative values of the statistic when no assignable cause is present. Moreover, to counterbalance the higher value of k _c, the optimal value of the control limit H in the single CUSUM chart approach is lower so as to detect the assignable causes relatively fast. However, in all cases examined the cost reduction resulting from the use of two separate CUSUM charts, compared to the single-statistic approach, was less than 0.5%. Hence, we adopt the single statistic C _t here because it is easier to formulate, faster to optimize and simpler to implement in practice.

The Markov chain that describes the evolution of the process when monitored by a CUSUM chart is {(Y _t , C _t ), t = 0, 1, 2…} where Y _t is again the actual state of the process and C _t is the value of the CUSUM statistic at sampling instance t. For practical purposes C _t is discretized into 2m + 1 values following the approach of Brook and Evans (1972).

Specifically, we partition the interval [− H, H] into 2m − 1 subintervals and we define w, the width of each subinterval, as follows:

Then, the real value of C _t is transformed to an integer between −(m − 1) and m − 1 by rounding the actual value of C _t /w to the closest integer in the set {− (m − 1), …, m − 1}. When the real value of C _t is such that C _t ≤ − (m − (1/2)) w = − H, then its value is transformed to − m, whereas when the real value of C _t exceeds (m − (1/2)) w = + H, then its value is transformed to m. Thus, with the addition of the “− m” and “+ m” states that correspond to the decisions to issue a signal, the total number of states increases to 2m + 1.

Using the above discretization of C _t , the Markov chain has 3× (2m + 1) possible (Y _t , C _t ) states, with transition probabilities defined as follows:

Thus, the transition probability matrix takes the following form:

The elements of the above matrix are divided into nine parts which contain, respectively, the probabilities of moving from C _{t − 1} to C _t for each of the nine possible combinations of Y _{t − 1} and Y _t . The exact expressions for the transition probabilities p _ij ^kl are given in the Appendix.

Similarly to the case of Shewhart charts, the steady-state probabilities π _ij of (Y _t = i, C _t = j) (i = 0, 1, 2, j = − m, …, m) are used to evaluate the expected cost per time unit function, which can be written as follows:

The ECT ₂ cost function is the exact analog of ECT ₁ for the case of CUSUM charts and the explanation of all terms is similar to the explanation of the terms of ECT ₁. Note that this Markovian model does not require the explicit computation of ARLs and thus Equation (11) avoids any inaccuracies generated by such a computation.

3. Numerical investigation and comparisons

We undertook a numerical investigation to explore the potential savings from monitoring a process with a CUSUM chart instead of using the standard Shewhart chart. The numerical investigation entails 48 cases, covering a broad range of cost parameters (c, b, M, L ₀, L ₁) and process parameters (λ, δ), as shown in Table 2. In all 48 cases, certain parameters were kept constant: instantaneous sampling g = 0, restoration cost L ₁ = 200 and negligible times to search for an assignable cause and restore the process: T ₀ = T ₁ = T ₂ = 0. Although the models are flexible enough to accommodate non-negligible times for search and restoration, our numerical investigation has shown that the effect of these times on the optimal process parameters and cost is minimal and thus, for the sake of parsimony, we have kept their values equal to zero. We also assume that the process is stopped for investigation whenever the chart issues an alarm (δ₁ = 0) as well as when the process is being restored to the in-control operation after a true alarm (δ₂ = 0). Finally, we set λ₁ = λ₂ = λ/2 in all cases.

Table 2 Parameter sets of the 48 numerical examples (c = 1 or 4, L ₁ = 200, g = 0, T ₀ = T ₁ = T ₂ = 0, δ₁ = δ₂ = 0)

Case	b	M	L 0	λ	δ
1	0	100	100	0.01	0.5
2	0	100	200	0.01	0.5
3	0	1000	100	0.01	0.5
4	0	1000	200	0.01	0.5
5	5	100	100	0.01	0.5
6	5	100	200	0.01	0.5
7	5	1000	100	0.01	0.5
8	5	1000	200	0.01	0.5
9	0	100	100	0.1	0.5
10	0	100	200	0.1	0.5
11	0	1000	100	0.1	0.5
12	0	1000	200	0.1	0.5
13	5	100	100	0.1	0.5
14	5	100	200	0.1	0.5
15	5	1000	100	0.1	0.5
16	5	1000	200	0.1	0.5
17	0	100	100	0.01	1
18	0	100	200	0.01	1
19	0	1000	100	0.01	1
20	0	1000	200	0.01	1
21	5	100	100	0.01	1
22	5	100	200	0.01	1
23	5	1000	100	0.01	1
24	5	1000	200	0.01	1
25	0	100	100	0.1	1
26	0	100	200	0.1	1
27	0	1000	100	0.1	1
28	0	1000	200	0.1	1
29	5	100	100	0.1	1
30	5	100	200	0.1	1
31	5	1000	100	0.1	1
32	5	1000	200	0.1	1
33	0	100	100	0.01	2
34	0	100	200	0.01	2
35	0	1000	100	0.01	2
36	0	1000	200	0.01	2
37	5	100	100	0.01	2
38	5	100	200	0.01	2
39	5	1000	100	0.01	2
40	5	1000	200	0.01	2
41	0	100	100	0.1	2
42	0	100	200	0.1	2
43	0	1000	100	0.1	2
44	0	1000	200	0.1	2
45	5	100	100	0.1	2
46	5	100	200	0.1	2
47	5	1000	100	0.1	2
48	5	1000	200	0.1	2

For any particular set of parameters we first determine the economically optimal design and cost of the Shewhart chart from Equation (5) and then compare them with the optimal parameters and cost of the CUSUM chart obtained from Equation (11). To expedite the optimization procedure we allowed k _s and k _c to be integer multiples of 0.1 and, by setting w = 0.1, we used the same discretization step for the control limit H of the CUSUM chart with an initial value of 0.05 (m = 1). Note that the number of states used to discretize the Markov chain of CUSUM charts, given w = 0.1, depends on the actual value of H in each case. The sampling interval h was allowed to vary in 0.01 increments within the range (0, 0.1); for h ≥ 0.1 the increment was set equal to 0.1, i.e., h = 0.1 or 0.2 or 0.3 etc.

Table 3 presents the optimal Shewhart and CUSUM parameters and costs for the 48 cases of Table 2 with the variable sampling cost per unit c = 1. The percentage profit resulting from using the optimal CUSUM chart rather than the optimal Shewhart chart is shown in the final column of Table 3.

Table 3 Shewhart charts compared with CUSUM charts (c = 1)

	Optimal Shewhart				Optimal CUSUM
Case	h	n	k s	ECT 1	h	n	k c	H	ECT 2	Percentage cost improvement (%)
1	7.2	24	1.6	11.76	6.9	23	1.1	0.6	11.72	0.4
2	8.3	32	1.9	12.64	7.8	30	1.3	0.7	12.59	0.4
3	2.2	24	1.6	33.92	2.1	23	1.1	0.6	33.77	0.4
4	2.5	34	2.0	36.81	2.4	31	1.3	0.7	36.64	0.5
5	8.3	27	1.6	12.41	8.0	26	1.1	0.6	12.39	0.2
6	9.1	34	1.9	13.22	9.0	34	1.4	0.6	13.19	0.2
7	2.6	28	1.6	36.01	2.5	27	1.2	0.5	35.94	0.2
8	2.8	35	1.9	38.69	2.7	34	1.4	0.6	38.58	0.3
9	2.8	21	1.5	45.46	2.6	20	0.9	0.7	45.32	0.3
10	3.2	28	1.8	47.70	3.0	26	1.1	0.8	47.53	0.4
11	0.7	23	1.6	117.66	0.7	23	1.1	0.6	117.18	0.4
12	0.8	31	1.9	126.46	0.8	31	1.3	0.7	125.90	0.4
13	3.3	23	1.4	47.13	3.2	22	0.9	0.6	47.05	0.2
14	3.6	31	1.8	49.17	3.5	30	1.2	0.7	49.08	0.2
15	0.8	26	1.6	124.09	0.8	26	1.1	0.6	123.86	0.2
16	0.9	34	1.9	132.18	0.9	34	1.4	0.6	131.86	0.2
17	4.4	10	2.2	7.82	4.4	10	1.5	0.8	7.79	0.4
18	4.7	12	2.5	8.20	4.7	12	1.7	0.9	8.16	0.5
19	1.4	10	2.2	20.82	1.3	10	1.6	0.7	20.72	0.5
20	1.6	13	2.5	22.03	1.4	12	1.7	0.9	21.90	0.6
21	5.9	12	2.2	8.78	5.8	12	1.7	0.6	8.77	0.1
22	6.3	14	2.4	9.09	6.2	14	1.9	0.6	9.08	0.2
23	1.8	12	2.2	23.91	1.8	12	1.7	0.6	23.89	0.1
24	1.9	14	2.5	24.93	1.9	14	1.9	0.6	24.88	0.2
25	1.7	10	2.2	35.90	1.5	9	1.4	0.9	35.80	0.3
26	1.9	12	2.4	36.90	1.7	11	1.6	0.9	36.78	0.3
27	0.5	11	2.2	78.39	0.4	9	1.5	0.8	77.95	0.6
28	0.5	13	2.5	81.97	0.5	12	1.7	0.8	81.66	0.4
29	2.2	11	2.1	38.48	2.2	11	1.6	0.6	38.45	0.1
30	2.3	13	2.4	39.30	2.3	13	1.8	0.6	39.27	0.1
31	0.6	12	2.2	87.81	0.6	12	1.7	0.5	87.75	0.1
32	0.6	14	2.5	90.96	0.6	13	1.8	0.7	90.82	0.2
33	2.7	4	2.8	5.31	2.2	3	1.7	1.1	5.29	0.4
34	2.8	4	2.9	5.46	2.7	4	2.0	1.0	5.44	0.5
35	0.9	4	2.7	12.64	0.7	3	1.7	1.1	12.57	0.6
36	0.9	4	2.9	13.14	0.8	4	2.0	1.1	13.05	0.7
37	4.6	5	2.7	6.71	4.5	5	2.2	0.6	6.71	0.0
38	4.5	5	2.9	6.81	4.6	5	2.3	0.6	6.81	0.0
39	1.4	5	2.7	17.13	1.4	5	2.2	0.6	17.12	0.1
40	1.4	5	2.9	17.47	1.4	5	2.3	0.6	17.46	0.0
41	1.0	4	2.8	29.26	0.8	3	1.7	1.1	29.16	0.3
42	1.0	4	2.9	29.66	1.0	4	2.0	1.0	29.59	0.2
43	0.3	4	2.7	53.17	0.2	3	1.7	1.2	53.02	0.3
44	0.3	4	2.9	54.75	0.3	4	2.0	1.0	54.52	0.4
45	1.7	5	2.7	33.11	1.6	4	2.0	0.6	33.11	0.0
46	1.7	5	2.9	33.38	1.7	5	2.2	0.7	33.36	0.0
47	0.5	5	2.7	67.26	0.5	5	2.2	0.5	67.26	0.0
48	0.5	5	2.8	68.34	0.5	5	2.2	0.7	68.29	0.1

Table 3 shows that the optimal sampling interval and sample size of the CUSUM scheme do not differ significantly from the respective optimal values of the Shewhart scheme. In particular, in most cases both the optimal h and n of the CUSUM scheme are marginally smaller than the respective optimal h and n when the Shewhart chart was used.

The cost improvement of the CUSUM scheme over the standard Shewhart scheme is less than 0.7% in all 48 cases we have examined. Consequently, it is obvious that from an economic point of view the CUSUM scheme is not significantly superior to the standard Shewhart chart, even when the magnitude of the shift is small. Note that Ho and Case (1994) concluded that the CUSUM chart is much better than the standard chart even though their numerical results are very similar to ours. More importantly, our results contradict those obtained by Keats and Simpson (1994), who found CUSUM charts to significantly outperform Shewhart charts. We conjecture that this contradiction may be due to the inaccuracy resulting from the computation and use of the ARLs in the model for the economic optimization of the CUSUM scheme.

The results of Table 2 are surprising, considering the widespread understanding that CUSUM charts are far more effective than Shewhart charts, at least in detecting small shifts in the mean. In addition, there was a concern (expressed clearly by one of the referees) about the appropriateness of the range of parameters used in the experimentation, given that the optimal values of the sample sizes n were found to be much larger than what is usual in practice, especially when the anticipated shifts in the mean are small (δ = 0.5, cases 1–16). Taking the above observations and concerns into account we first validated the results of Table 3 by simulation and then expanded the numerical investigation in order to reinforce our findings. More specifically, we obtained the optimal designs of the Shewhart and CUSUM charts for the 48 cases of Table 2 increasing the per unit cost of inspection from c = 1 to c = 4. The results are shown in Table 4. The optimal sample sizes decreased, as expected; for example in the cases with δ = 0.5 the optimal n ranges between 14 and 18 when c = 4, down from optimal values as high as n = 35 when c = 1. However, the percentage reduction in the average cost from the use of the CUSUM rather than the Shewhart chart remained negligible and did not exceed 0.6% in any case. Furthermore, in many of the 16 cases where δ = 0.5 it is better not to sample at all if c = 4 but to search regularly for assignable causes and restore the process if needed. This type of policy, which resembles preventive maintenance, is justified when the potential savings from monitoring the process are small and consequently insufficient to counterbalance the relatively high sampling costs. We have also tried various other combinations of parameters and the conclusion stayed invariably the same, i.e., that the differences between the optimum costs of CUSUM and Shewhart charts are negligible for all sets of process and cost parameters and even for very small magnitudes of the shift when the sample sizes are unrestricted.

Table 4 Shewhart charts compared with CUSUM charts (c = 4)

	Optimal Shewhart				Optimal CUSUM
Case	h	n	k s	ECT 1	h	n	k c	H	ECT 2	Percentage cost improvement (%)
1	14.9	0	*	14.73	14.9	0	*	*	14.73	0.0
2	12.6	15	1.2	18.94	11.9	14	0.7	0.6	18.86	0.4
3	4.5	0	*	45.37	4.5	0	*	*	45.37	0.0
4	3.8	17	1.3	58.68	3.6	16	0.8	0.6	58.42	0.4
5	14.9	0	*	14.73	14.9	0	*	*	14.73	0.0
6	13.4	16	1.2	19.32	12.7	15	0.7	0.6	19.26	0.3
7	4.5	0	*	45.37	4.5	0	*	*	45.37	0.0
8	4.0	18	1.3	59.97	3.8	17	0.8	0.6	59.79	0.3
9	5.7	0	*	48.94	5.7	0	*	*	48.94	0.0
10	8.2	0	*	56.15	8.2	0	*	*	56.15	0.0
11	1.5	0	*	147.34	1.5	0	*	*	147.34	0.0
12	1.3	16	1.2	189.41	1.2	14	0.7	0.6	188.57	0.4
13	5.7	0	*	48.94	5.7	0	*	*	48.94	0.0
14	8.2	0	*	56.15	8.2	0	*	*	56.15	0.0
15	1.5	0	*	147.34	1.5	0	*	*	147.34	0.0
16	1.4	17	1.2	193.23	1.3	16	0.7	0.6	192.60	0.3
17	7.2	6	1.6	11.76	7.1	6	1.1	0.6	11.72	0.4
18	8.3	8	1.9	12.64	8.1	8	1.3	0.7	12.59	0.4
19	2.2	6	1.6	33.92	2.2	6	1.1	0.6	33.78	0.4
20	2.5	8	1.9	36.82	2.5	8	1.4	0.6	36.65	0.5
21	8.5	7	1.6	12.41	8.4	7	1.2	0.5	12.39	0.1
22	9.5	9	1.9	13.22	8.6	8	1.3	0.7	13.19	0.2
23	2.6	7	1.6	36.01	2.5	7	1.2	0.5	35.95	0.2
24	2.9	9	1.9	38.69	2.8	9	1.4	0.6	38.59	0.3
25	2.7	5	1.5	45.47	2.6	5	0.9	0.7	45.32	0.3
26	3.2	7	1.8	47.70	3.1	7	1.2	0.7	47.54	0.3
27	0.7	6	1.6	117.68	0.7	6	1.1	0.6	117.21	0.4
28	0.8	8	1.9	126.49	0.8	8	1.3	0.7	125.96	0.4
29	3.2	6	1.5	47.13	3.3	6	1.0	0.5	47.07	0.1
30	3.7	8	1.8	49.18	3.5	7	1.1	0.7	49.09	0.2
31	0.9	7	1.6	124.23	0.8	6	1.1	0.5	123.95	0.2
32	0.9	8	1.9	132.36	0.9	8	1.3	0.7	132.00	0.3
33	4.9	3	2.3	7.86	3.7	2	1.4	0.9	7.82	0.4
34	4.7	3	2.5	8.20	4.7	3	1.7	0.9	8.16	0.5
35	1.5	3	2.3	20.90	1.1	2	1.4	0.9	20.85	0.3
36	1.5	3	2.5	22.03	1.4	3	1.7	0.9	21.90	0.6
37	5.9	3	2.2	8.78	5.8	3	1.7	0.6	8.77	0.1
38	6.7	4	2.5	9.13	5.7	3	1.7	0.8	9.11	0.2
39	1.8	3	2.2	23.91	1.8	3	1.7	0.6	23.89	0.1
40	2.0	4	2.5	25.03	2.0	4	2.0	0.6	25.00	0.1
41	1.5	2	2.1	36.03	1.4	2	1.3	1.0	35.84	0.5
42	1.9	3	2.4	36.90	1.8	3	1.7	0.8	36.81	0.2
43	0.5	3	2.3	78.60	0.4	2	1.3	1.0	78.44	0.2
44	0.5	3	2.4	82.04	0.5	3	1.7	0.8	81.66	0.5
45	2.3	3	2.1	38.50	2.3	3	1.6	0.6	38.47	0.1
46	2.3	3	2.3	39.35	2.2	3	1.7	0.7	39.29	0.2
47	0.6	3	2.2	87.81	0.6	3	1.7	0.5	87.75	0.1
48	0.7	4	2.5	91.36	0.6	3	1.7	0.7	91.17	0.2

On the other hand, CUSUM charts for monitoring the process mean are often based on samples of n = 1, since there are several applications where only one observation is available at each sampling instance (Hawkins and Olwell, 1998). It is therefore interesting to investigate the potential savings of using a CUSUM chart under the restriction that n = 1 and see whether or not the conclusions are similar to those of the unrestricted n case. Table 5 presents the results of the numerical investigation for the same 48 cases with c = 1, exactly in the same way as in Table 3 but with the restriction n = 1.

Table 5 Shewhart charts compared with CUSUM charts for n = 1 (c = 1)

	Optimal Shewhart			Optimal CUSUM
Case	h	k s	ECT 1	h	k c	H	ECT 2	Percentage cost improvement (%)
1	14.9	*	14.73	0.3	0.2	6.6	12.57	14.7
2	21.5	*	19.32	0.3	0.2	8.0	13.77	28.7
3	4.5	*	45.37	0.09	0.2	6.7	36.72	19.1
4	6.5	*	62.58	0.07	0.2	9.1	40.46	35.3
5	14.9	*	14.73	14.9	*	*	14.73	0.0
6	21.5	*	19.32	21.5	*	*	19.32	0.0
7	4.5	*	45.37	4.5	*	*	45.37	0.0
8	6.5	*	62.58	6.5	*	*	62.58	0.0
9	5.7	*	48.94	0.1	0.2	7.1	47.44	3.1
10	8.2	*	56.15	0.1	0.2	8.5	49.75	11.4
11	1.5	*	147.34	0.03	0.2	6.6	125.68	14.7
12	2.1	*	193.26	0.03	0.2	8.0	137.72	28.7
13	5.7	*	48.94	5.7	*	*	48.94	0.0
14	8.2	*	56.15	8.2	*	*	56.15	0.0
15	1.5	*	147.34	1.5	*	*	147.34	0.0
16	2.1	*	193.26	2.1	*	*	193.26	0.0
17	0.7	2.2	12.46	0.4	0.5	4.5	8.43	32.3
18	0.5	2.5	15.21	0.4	0.5	5.1	8.91	41.4
19	0.2	2.2	36.65	0.1	0.5	4.9	23.14	36.9
20	0.2	2.4	46.07	0.1	0.5	5.5	24.46	46.9
21	14.9	*	14.73	1.8	0.4	2.3	13.78	6.5
22	2.9	1.7	18.77	1.4	0.4	3.3	15.23	18.9
23	4.5	*	45.37	0.5	0.4	2.4	40.89	9.9
24	0.7	1.8	58.72	0.4	0.4	3.5	45.80	22.0
25	0.3	2.2	46.38	0.2	0.4	4.5	37.45	19.2
26	0.3	2.4	52.24	0.2	0.4	5.3	38.94	25.5
27	0.07	2.2	124.56	0.04	0.5	4.5	84.34	32.3
28	0.05	2.5	152.11	0.04	0.5	5.1	89.14	41.4
29	5.7	*	48.94	5.7	*	*	48.94	0.0
30	8.2	*	56.15	0.7	0.4	2.8	52.88	5.8
31	1.5	*	147.34	0.2	0.4	2.1	138.05	6.3
32	0.3	1.7	187.83	0.2	0.4	2.7	155.09	17.4
33	0.8	2.6	6.79	0.7	1.0	2.6	5.61	17.4
34	0.7	2.8	7.65	0.6	1.0	3.1	5.82	24.0
35	0.3	2.5	17.57	0.2	1.0	2.7	13.61	22.6
36	0.2	2.8	20.42	0.2	1.0	3.0	14.28	30.0
37	2.8	2.0	9.64	2.4	0.9	1.6	9.12	5.3
38	2.6	2.2	10.89	2.0	0.9	2.1	9.78	10.2
39	0.9	2.0	26.93	0.7	0.9	1.6	25.16	6.6
40	0.8	2.2	31.09	0.6	0.9	2.1	27.31	12.1
41	0.3	2.6	33.04	0.3	0.9	2.6	30.06	9.0
42	0.3	2.7	35.31	0.2	1.0	3.1	30.65	13.2
43	0.08	2.6	67.89	0.07	1.0	2.6	56.05	17.4
44	0.07	2.8	76.54	0.06	1.0	3.1	58.18	24.0
45	1.2	1.9	40.11	1.0	0.8	1.6	39.02	2.7
46	1.2	2.1	43.11	0.9	0.9	1.9	40.67	5.7
47	0.3	1.9	96.40	0.2	0.9	1.8	91.88	4.7
48	0.3	2.1	109.24	0.2	0.9	2.1	97.77	10.5

The optimal sampling interval of the CUSUM chart is now much smaller than the respective one of the Shewhart chart. Indeed, the restriction on the sample size and the cumulative nature of the CUSUM scheme leads to a large number of samples, in order for the chart to be maximally effective. Thus, the optimal h of the CUSUM chart is much shorter especially when the magnitude of the shift (δ) is small.

There are even more cases now (when b is large while δ and L ₀ are small) in which it is optimum to investigate regularly for possible occurrence of assignable causes without prior sampling because the chart detection power is very limited when n = 1. This phenomenon is observed mainly in the case of Shewhart charts, since these charts are not typically meant to operate with individual measurements but with rational subgroups (Reynolds and Stoumbos, 2004). There are some cases, though, where this preventive-maintenance-type policy is better even than monitoring with a CUSUM chart.

If we exclude the cases where preventive maintenance outperforms both Shewhart and CUSUM charts, the potential savings from using a CUSUM chart with n = 1 are great, especially when b and δ are small while M and L ₀ are large. Table 5 shows that the cost reduction often exceeds 20% and it may be as high as almost 50% (46.9% in case 20). Nevertheless, a side-by-side comparison of the costs in Tables 3 and 5 reveals that in all cases where some SPC-type monitoring is desirable, the minimum expected cost with n = 1 is substantially higher than the minimum cost when the sample size is unrestricted, for both CUSUM and Shewhart charts. Thus, although it is commonly argued that CUSUM charts have better statistical performance when using unitary samples (see for example Hawkins and Olwell (1998) and Reynolds and Stoumbos (2004)), our numerical investigation shows that their economic performance when n = 1 is inferior to that of CUSUM charts with larger sample sizes.

Finally, it should be emphasized that there are many practical applications where the sample sizes are not necessarily unitary but they are constrained to relatively low values for rational subgrouping purposes or other reasons. Constraining the value of the sample size to, say, n ≤ 5 would result in a CUSUM chart significantly outperforming the respective Shewhart chart, unless of course the optimum unconstrained sample size would anyway be not much larger than five. The difference in the economic performance of the two charts if there is a restriction on the sample size will be somewhere between the observed differences in the cases of unconstrained n and n = 1. Consider for example case 1 of Table 2 with c = 1. If there is no restriction in the sample size, from Table 3 we see that the two charts have relatively large sample sizes and almost identical average costs: ECT ₁ = 11.76 with n = 24 for the Shewhart chart, ECT ₂ = 11.72 with n = 23 for the CUSUM. If the sample size is constrained by n ≤ 5 for rational subgrouping purposes, then the average costs of the two constrained–optimal chart designs (with n = 5) are ECT ₁ = 14.12 and ECT ₂ = 12.39 (a 12.3% cost difference). If the restriction n = 1 is imposed on the sample size then we see from Table 5 that ECT ₁ = 14.73, ECT ₂ = 12.57 and the economic advantage of the CUSUM increases to 14.7%.

4. Summary and conclusions

We have presented simple and accurate Markov chain models for the economic optimization of Shewhart and CUSUM charts for monitoring the mean of a normally distributed quality characteristic. Our numerical investigation has led to the following conclusions.

1.	CUSUM charts are economically far superior to Shewhart charts only if process monitoring must be performed on the basis of individual measurements (sample size n = 1). If there are no restrictions on the size of each sample, the economic performance of the optimal CUSUM chart is almost identical to the performance of the optimal Shewhart chart even when the magnitude of the anticipated shift is small. In between these two extreme cases, namely if the sample size is restricted to low values for reasons such as the need for rational subgrouping, the CUSUM chart may significantly outperform the Shewhart chart when the shifts in the mean are small.
2.	From a pure economic perspective and if there are no restrictions on the sample size n, the common choice of n = 4 or n = 5 is always inferior to larger sample sizes when the magnitude of the shift is small, both for Shewhart and CUSUM charts. Sample sizes n ≤ 5 may be economically optimal only if the magnitude of the anticipated shift is moderate to large and the sampling cost is not very low.
3.	When the sample size is by necessity restricted to n = 1 and/or when the sampling cost is high and the magnitude of the shift is small, it is often optimal not to monitor the process through sampling but to control it by means of a preventive-maintenance-type policy. Consequently, this option should always be considered as an alternative to the usual SPC procedures.

Appendix
Derivation of the transition probabilities p _ij ^kl of the CUSUM scheme

The exact values of the transition probabilities (9) are computed from the following relationships, where ϕ (z) is the density function of the standard normal distribution.

Note that p _ij ⁰² is computed based on the set of equations for p _ij ⁰¹, by setting γ₂ instead of γ₁ and +δ √n instead of –δ √n. On the other hand, p _ij ²² is computed based on the set of equations for p _ij ¹¹, by setting +δ √n instead of − δ √n.

Biographies

George Nenes is a Research Associate in the Department of Mechanical Engineering at Aristotle University of Thessaloniki (A.U.Th.). He has obtained a Diploma (5-year degree) in Mechanical Engineering, an M.Sc. in Management of Production Systems and a Ph.D. in Mechanical Engineering from the same university. His main research interest is in the area of statistical process control.

George Tagaras is Professor of Mechanical Engineering at A.U.Th., where he teaches and conducts research in quality assurance, inventory distribution systems and stochastic models in production and operations management. He holds a Diploma in Mechanical Engineering from A.U.Th. and an M.S. and Ph.D. in Industrial Engineering from Stanford University. He has held faculty positions at the Wharton School of the University of Pennsylvania and at INSEAD in France. He has also taught at the University of Thessaly and in the graduate program of the University of Macedonia in Greece. He has published many technical papers in a variety of journals, including Management Science, Operations Research, IIE Transactions, International Journal of Production Research, European Journal of Operational Research and Journal of Quality Technology. He is currently Associate Editor of Management Science, Senior Editor of Production and Operations Management and on the Editorial Board of IIE Transactions. He is a member of INFORMS and ASQ.

Acknowledgements

We thank the anonymous referees for their comments that contributed significantly to the improvement of the paper. The present study has been co-funded by European Union—European Social fund and National fund–PYTHAGORAS-EPEAEK II.

Notes

*Preventive maintenance is optimal (n = 0).

*Preventive maintenance is optimal (n = 0).