A binomial approximation of lot yield under Markov modulated Bernoulli item yield

Abstract

The existing literature that models item-by-item production yield as a Bernoulli process assumes that the intraperiod likelihood of producing an acceptable item is stationary. We investigate the stochastic process that results from relaxing this assumption to account for system deterioration during each production run. More specifically, we consider a Bernoulli yield model with a non-stationary parameter that depends on the deterioration level of the system, which evolves according to a discrete-time Markov chain. For tractability reasons, we construct a simple binomial approximation of the non-stationary process, and compare the two yield distributions both analytically and numerically. Our results suggest that the approximation performs well, even when the deterioration occurs relatively fast, which serves to validate existing (and future) decision models that impose the stationarity assumption.

Keywords:

• Random yield
• Markovian deterioration
• production

1. Introduction

This paper addresses the mathematical modeling of yield uncertainty. As Yano and Lee (1995) explain, because the modeling of random yields involves an inherent trade-off between accuracy and tractability, yield uncertainty is modeled in several ways in the lot sizing literature. The three most common models are the binomial/Bernoulli, stochastically proportional and interrupted geometric. In terms of simplicity, Yano and Lee explain that the binomial model is the most attractive due to the fact that given a lot size, the binomial distribution requires the specification of only one parameter, p, the probability of generating a good unit of output from one unit of input.

Many papers in the lot sizing literature model yield as a Bernoulli process (see Yano and Lee (1995)). More recently, Braha (1999), DePuy and Usher (2001) and Grosfeld-Nir (2005), for example, study single-period, multi-stage production problems in which the yield at each stage is binomial with a success probability that depends on the stage. Sloan (2004), on the other hand, studies a multi-period, single-stage problem in which the yield in each period is binomial with a success probability that depends on the current state of the production equipment. All of these papers assume, however, that the success probability is stationary within each stage or period, respectively. That is, they assume that the yield depends only on the state of the production process at the beginning of each stage/period, as opposed to the intermediate state(s) of the production process during each stage/period.

We investigate the stochastic process that results from relaxing this assumption. More specifically, we consider a Markov modulated Bernoulli process model (see Ozekici (1997) for a general treatment of this stochastic process) of the yield. That is, we model the within-lot deterioration process as a discrete-time Markov chain, and assume that the yield from each item produced is a Bernoulli random variable, the parameter of which depends on the current deterioration state.

Again, and as Yano and Lee (1995) point out, although this type of non-stationary stochastic process can be used to model yields for repetitive processes, it is not widely used, undoubtedly due to its intractability. The focus of this paper, therefore, is to assess the potential to approximate this Markov modulated Bernoulli yield process with a more tractable, stationary process. Specifically, we develop a stationary binomial approximation whose first moment matches that of the non-stationary process, and compare the behavior of the two processes both analytically and numerically.

In Section 2, we describe the within-lot deterioration and yield processes, and derive an expression for the corresponding probability mass function of the yield for a given lot size. In Section 3, we construct a stationary binomial approximation to the process described in Section 2. In Section 4, we analytically establish common characteristics of the two processes under intuitive conditions on the problem parameters. In Section 5, we implement a large numerical experiment to facilitate further comparisons of the two processes, including moment comparisons and statistical hypothesis testing of simulated data sets. Section 6 summarizes our work, draws conclusions and identifies directions for future work.

2. Lot yield under item-by-item deterioration

Consider a unit of production equipment (henceforth referred to as “the machine”) that deteriorates stochastically as it produces. The set of possible wear states for the machine is {1, 2, …, w _max{, and machine condition is non-improving in wear state, i.e., wear state 1 corresponds to a “new” machine condition and wear state w _max corresponds to the “most worn” machine condition. The machine produces items sequentially (one at a time), and deteriorates according to a discrete-time Markov chain. Specifically, let p _w,w′ denote the probability that, given the machine is in wear state w immediately before production of an item, the machine will be in wear state w′ immediately after production of the item. We assume that:

and

Suppose that the machine is scheduled to produce a lot of q items, and denote the wear state of the machine at the beginning of the production run by w ₀. Not every item produced will be of adequate quality, i.e., some will be defective. Let p _d (w) denote the probability that, given the machine is in wear state w immediately before production of an item, the produced item will be defective.

Next, let Ψ denote the yield from the production lot, i.e., the number of non-defective items produced. Because of the stochastic nature of machine deterioration and the probabilistic nature of product quality, Ψ is a random variable with range {0, 1, …, q}. (Although Ψ is a function of w ₀, w _max, q, p _w,w , w = w ₀, w ₀+ 1, …, w _max− 1, and p _d(w), w = w ₀, w ₀ + 1, …, w _max, we do not denote the functional dependence for notational convenience.) Ozekici (1997) presents a recursive expression for the probability mass function of Ψ under a general Markov chain structure. To facilitate the computation of this probability distribution in our setting, we derive a non-recursive form of the probability mass function of Ψ, which requires that we first derive the joint distribution of the sojourn times in each wear state.

We denote the number of items produced when the machine is in wear state w (the sojourn time in state w) by N _w . Furthermore, let the number of items produced in wear states w ₀ through w be given by

Since the machine begins the production lot in state w ₀, the distribution of the sojourn time in this state is given by

Now consider some w ∈ {w ₀ + 1, w ₀ + 2, …, w _max− 1}. Given some realization of _{w − 1}, say _{w − 1}, we have that:

For the case in which the lot is completed before wear state w is reached, i.e., _{w − 1} = q:

We do not need to consider the distribution of N _{w max} since it is determined by _{w max− 1}, that is

Finally, let N = [N _{w 0} , N _{w 0 + 1},…, N _{w max} ], and let n = [n _{w 0} , n _{w 0 + 1},…, n _{w max} ]. Then the joint sojourn time distribution is given by

Next, we derive the joint distribution of the yields generated in each wear state, conditional on the collection of sojourn times. Let Y _w denote the number of non-defective items produced with the machine in wear state w. Given a realization of N _w , say n _w , Y _w is a binomial random variable with sample size n _w and probability of success 1 −p _d(w), in which case

If Y = [Y _{w 0} , Y _{w 0 + 1}, …, Y _{w max} ], and y = [y _{w 0} , y _{w 0 + 1}, …, y _{w max} ], then the conditional joint distribution of the yields is given by

Finally, we can express the probability mass function of Ψ as

3. A stationary binomial approximation

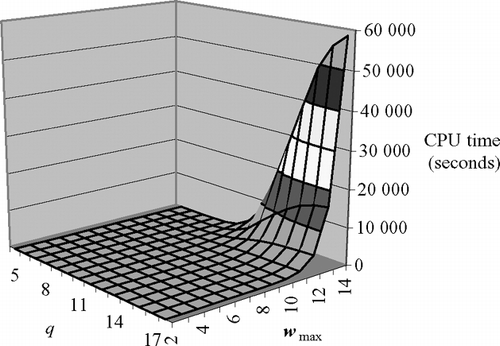
In Section 2, we present an exact expression (1) for the probability mass function of the Bernoulli yield from a finite-sized production lot on a machine subject to item-by-item Markovian deterioration. However, there are two primary shortcomings of this function. First, embedding this probability distribution in a production and/or maintenance decision-making model is analytically unwieldy. Second, the computational effort associated with just the numerical evaluation of this probability distribution is burdensome. Figure 1 plots the CPU time required to compute the probability mass function of Ψ using Visual C++ code executed on a personal computer with a 2.8 GHz processor and 1 GB of RAM. In general, the computational complexity of computing the probability of a particular yield outcome is O(q ^{2(w _max− 1)}).

FIG. 1 CPU time required to compute the yield distribution.

Because the computational effort required to compute the probability mass function of Ψ for medium to large lot sizes (q ≥ 15) is prohibitive, we propose an approximation to this probability mass function with less demanding computational requirements. Let denote the approximation of Ψ . We model as a binomial random variable with sample size q and probability of success 1 − [pcirc], derived below. We choose this form because of its intuitive appeal for production yield modeling, and because the existing literature often models the lot yield as a binomial random variable.

Let W _t denote the wear state of the machine after t items have been produced, t = 0, 1, …, q. Based on our previous assumptions, {W _t , t = 0, 1, …, q} is a discrete-time Markov chain with state space {w ₀, w ₀+ 1, …, w _max{, and W ₀ = w ₀. Let p _w,w′ ⁽ⁿ⁾ denote the n-step transition probability from state w to state w′, that is

Next, let

Then,

which implies that:

Furthermore,

which implies that:

To complete the construction of the approximation, we equate the expected values of and Ψ . Since is a binomial random variable:

and equating expressions (3) and (4) yields:

As a result, we approximate the probability mass function (1) with:

4. Analytical comparison of Ψ and Ψ

In this section, we establish conditions under which Ψ exhibits intuitive monotonic behavior, and then show that inherits this behavior under the same conditions. This result supports the validity of the approximation since it demonstrates that the two distributions have common analytical properties, which can be useful in establishing the optimal policy structure in a decision-making framework.

Clearly, Ψ and are stochastically non-decreasing, in the sense of first-order stochastic dominance, in q for all w ₀. That is, all else held constant, if more items are attempted, then the resulting yield tends to be larger. Furthermore, as shown in Theorem 1 and the subsequent corollary, if both the probability of deteriorating by one wear level and the probability of producing a defective item increases in the wear state, then Ψ and are stochastically non-increasing in w ₀ for all q.

Theorem 1. If

and

then Ψ is stochastically non-decreasing in w ₀ for all q.

Proof. Under condition (6), P exhibits an Increasing Failure Rate (IFR), i.e., its rows are in increasing stochastic order. It follows directly from Barlow and Proschan (1976) that if P has an IFR, then so does P ^(m) for all m, or

By Lemma 4.7.2 in Puterman (1994), it follows that,

which because of the upper triangularity structure of the Markov chain, is equivalent to

which implies that:

where ≻_st denotes first-order stochastic dominance. Clearly then, by Equation (2):

As shown in Corollary 1, the approximation constructed in Section 3 preserves these intuitive properties of Ψ .

Corollary 1. If conditions (6) and (7) hold, then is stochastically non-increasing in w ₀ for all q.

Proof. It is well known (Ross, 1996) that binomial random variables are stochastically non-decreasing in both of their parameters. Therefore, the result holds based on Equation (5) and Equation (8).

Note that the proof of Theorem 1 relies on the fact that P is IFR, not the restriction that p _{w,w + 1} = 1 − p _w,w for all w < w _max nor the fact that w _max < ∞ . That is, the theorem and corollary hold for P matrices with more general structures than the one considered here, provided they possess the IFR property.

5. Numerical comparison of Ψ and Ψ

5.1. Experimental design

Since our ability to analytically compare and Ψ is limited to the results in Section 4, we use a designed experiment to foster a thorough numerical comparison of the approximate and exact probability distributions of the yield. Without loss of generality, we set w ₀ = 1 in all of our experiments. We consider all values of w _max in the set {2, 4, 6, 8,10, 12, 14, 16}, and all values of q in the set {10, 25, 50, 75, 100, 150, 200}. Our remaining four experimental factors parameterize the deterioration process. The first of these factors is p _d(1); we consider all values of p _d(1) in the set {0.005, 0.01, 0.02, 0.05, 0.1}. The second of these factors is δ ₁ where:

We consider only situations in which δ ₁ > 1, or the probability of producing a defective item increases in the machine's wear state (Fig. 2). We consider all values of δ ₁ in the set {1.5, 2, 5, 10}. The third of these factors is p _1,2; we consider all values of p _1,2 in the set {0.001, 0.005, 0.01, 0.02, 0.05}. The fourth of these factors is δ ₂ where:

FIG. 2 Changes in item yield probability as the machine deteriorates.

We consider only situations in which δ ₂ ≥ 1, or the machine deterioration is IFR (Fig. 3). We consider all values of δ ₂ in the set {1, 1.5, 2, 5, 10}.

FIG. 3 Changes in the probability of additional deterioration as the machine deteriorates.

Specification of the values of these experimental factors dictates values for p _d(1), p _d(w _max) and p _1,2. To specify the intermediate values of p _d(w) and p _{w,w + 1} for w = 2, 3, …, w _max−1, we consider three cases: linear deterioration, exponential deterioration, logarithmic deterioration. Under linear deterioration, for any w ∈ {2, 3, …, w _max−1};

and

Under exponential deterioration, for any w ∈ {2, 3, …, w _max−1}:

and

where

Under logarithmic deterioration, for any w ∈ {2, 3, …, w _max−1}:

and

where

For each case of deterioration (linear, exponential, logarithmic), we consider all combinations of the values of the six experimental factors, resulting in 28 000(3) = 84 000 individual realizations of machine behavior.

5.2. Comparison of moments

We first compare the second, third, and fourth moments of Ψ and , excluding the first since E[Ψ] = E[] by construction. These higher moments of the binomial approximation are given by

and

For the exact distribution of yield, we calculate these higher moments using the probability generating function derived in Ozekici (1997), namely:

where Z is the w _max× w _max matrix with (i, j)th element [α (1 − p _d(i)) + p _d(i)]p _i,j . It is well known that given this generating function, the second, third and fourth moments are given by

and

Computing the higher moments of the exact distribution, although simpler than computing the entire probability mass function, becomes exponentially more difficult as q and w _max increase. Therefore, we initially limit our attention to those experiments with q ≤ 25. For each of these 24 000 experiments, we compute:

which we refer to as the percent error in the nth moment, and

which we refer to as the absolute percent error in the nth moment. For the experiments with q > 25, we take an alternative approach, addressed subsequently.

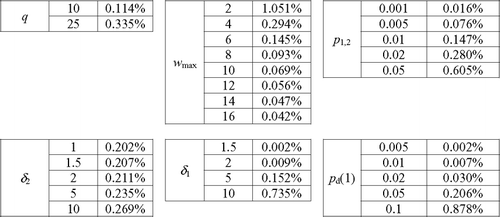
Our first noteworthy result is that the binomial approximation underestimates all three moments in all 24 000 experiments with q ≤ 25. This behavior is intuitive in light of the fact that our approximation is a Bernoulli process with a yield probability that is smaller than that of the initial state of the true process, coupled with the fact that the initial state of the process corresponds to the slowest rate of machine deterioration. This result also allows us to focus exclusively on absolute percent error. Table 1, Table 2, Table 3 present our results for this metric with respect to each moment and the type of deterioration. The values in Table 1, Table 2, Table 3 correspond to the average, maximum and median absolute percent error across the relevant subset of experiments.

Table 1 Average absolute percent error for the numerical comparison of the approximate yield moments to the exact yield moments

Moment	Exponential	Linear	Logarithmic
Second	0.07	0.08	0.13
Third	0.15	0.20	0.32
Fourth	0.24	0.32	0.52

Table 2 Maximum absolute percent error for the numerical comparison of the approximate yield moments to the exact yield moments

Moment	Exponential	Linear	Logarithmic
Second	24.8	24.8	24.8
Third	47.9	47.9	47.9
Fourth	64.7	64.7	64.7

Table 3 Median absolute percent error for the numerical comparison of the approximate yield moments to the exact yield moments

Moment	Exponential	Linear	Logarithmic
Second	0.000 06	0.000 21	0.001 00
Third	0.000 18	0.000 58	0.002 78
Fourth	0.000 34	0.001 07	0.005 17

The results in Table 1, Table 2, Table 3 suggest that the higher moments of the binomial approximation closely match those of the true yield distribution; the average absolute percent error ranges from 0.07 to 0.52%. However, motivated by the fact that the median absolute percent errors range from 0.0006 to 0.00517%, closer inspection of the results suggests that the notably small averages are actually inflated by a small number of cases with very large errors. These cases correspond to situations in which the number of wear states is two (w _max = 2) and the difference in equipment performance in these two wear states is large (δ ₁ = 10). Indeed, when w _max = 2 and δ ₁ = 10, the average absolute percent error in the second moment is 1.6%, the average absolute percent error in the third moment is 3.5% and the average absolute percent error in the fourth moment is 5.2%.

The results in Table 1, Table 2, Table 3 also suggest that the quality of the approximation tends to degrade as the order of the moment increases. This result is expected since the approximation is formed by matching only the first moment. Finally, the approximation performs best in the exponential case and worst in the logarithmic case. This behavior is intuitive since machine deterioration and the corresponding yield degradation occur relatively slowly (quickly) in the exponential (logarithmic) case.

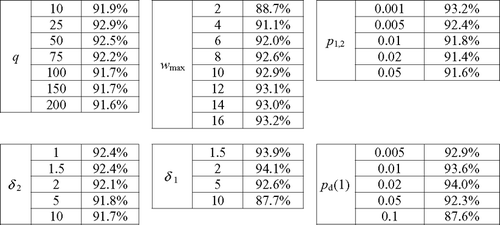
Figure 4 summarizes the results of our numerical moment comparisons with respect to the experimental parameters q, w _max, p _d(1), δ ₁, p _1,2 and δ ₂. The values in the tables in Fig. 4 correspond to the average absolute percent error across the relevant subset of experiments. These values highlight the intuitive result that the quality of the approximation tends to degrade as the degree of non-stationarity increases. As q increases, the true process has more opportunity to change deterioration states. As w _max decreases, each change in deterioration state results in a larger marginal change in equipment performance. As p _d(1) or δ ₁ increases, there is greater absolute disparity between the equipment performance in each deterioration state. Finally, as p _1,2 or δ ₂ increases, the likelihood of changing deterioration states increases.

FIG. 4 Numerical comparison of the approximate yield moments to the exact yield moments by average absolute percent error.

Since the higher moments of the exact distribution cannot be computed in a reasonable amount of time when q > 25, we take an alternative approach in these cases. Our alternative approach is similar in spirit to that of simulation researchers who evaluate random number generators by subjecting their output to statistical tests of randomness, although the generators are known to be only “pseudo-random.” In particular, we simulate yields from the exact distribution and use the resulting data to test the hypothesis that the higher moment of the exact distribution is equal to the higher moment of the approximate distribution. Because these tests are sensitive to sample size, we introduce this factor, m, into the experimental design at five levels, {30, 50, 75, 100, 250}. For each of the 84 000 realizations of machine behavior, we simulate independent data sets for each of the experimental values of m. Adding m to the set of experimental factors results in 420 000 sets of three statistical tests (second moment comparison, third moment comparison, fourth moment comparison). We use a significance level of 0.05 for all tests.

Table 4 summarizes the results of these hypothesis tests with respect to each moment, type of deterioration and sample size. The values in the table correspond to the percentage of the tests that result in the conclusion to not reject the null hypothesis. These results are consistent with the non-simulated, numerical results presented in Table 1, Table 2, Table 3. First, note the high percentages throughout the table, particularly since a perfect approximation would only result in a “pass rate” of 95% under a 0.05 significance level. Second, the quality of the approximation tends to degrade slightly as the order of the moment increases. Third, the quality of the approximation is worst under logarithmic deterioration. However, the reduction in quality observed in Table 1, Table 2, Table 3 with the change from the exponential to the linear case is not apparent in Table 4 (perhaps due to the probabilistic nature of the simulation output).

Table 4 Pass rates (in percent) for simulation-based higher moment comparison

		Simulated sample size
	Moment	30	50	75	100	250
	Second	92.4	93.3	93.4	93.6	93.0
Exponential	Third	92.0	92.6	92.5	92.4	91.4
	Fourth	91.6	92.0	91.6	91.5	90.0
	Second	92.4	93.4	93.6	93.7	93.4
Linear	Third	92.0	92.9	92.8	92.9	92.2
	Fourth	91.7	92.4	92.2	92.1	91.2
	Second	92.4	93.1	93.2	93.1	92.3
Logarithmic	Third	91.8	92.1	91.8	91.5	89.8
	Fourth	91.2	91.2	90.6	89.9	87.8

Figure 5, analogous to Fig. 4, summarizes the results of these simulation-based tests with respect to the experimental parameters q, w _max, p _d(1), δ ₁, p _1,2 and δ ₂. Again, the values in the tables correspond to the percent of the tests that result in the conclusion to not reject the null hypothesis. These results are consistent with the results presented in Fig. 4 in that the quality of the approximation tends to degrade as w _max decreases, as δ ₁ increases, as p _1,2 increases, and as δ ₂ increases. However, the trends observed in Fig. 4 with respect to q and p _d(1) are not apparent in Fig. 5.

FIG. 5 Pass rates for simulation-based higher moment comparison.

5.3. Comparisons of simulated yield data

As another means of comparing the exact and approximate distributions of yield, we use both a chi-squared contingency test of homogeneity and a chi-squared goodness-of-fit test (Montgomery and Runger, 2003). For the former, we simulate yields from both distributions and subject the resulting data to a chi-squared contingency test, which tests the hypothesis that both data sets are realizations of the same distribution. For the latter, we simulate yields from the exact distribution and subject the resulting data to a chi-squared goodness-of-fit test, which tests the hypothesis that the data set is actually a realization of the approximate distribution.

Because these tests are sensitive to sample size, we again include the factor m in the experimental design at the five levels in the set {30, 50, 75, 100, 250}. For each of the 84 000 realizations of machine behavior, we simulated independent data sets for each of the experimental values of m resulting in 420 000 pairs of statistical tests. We use a significance level of 0.05 for both tests, and enforce the general rule that every bin's expected value exceeds five. Because of this rule, 3–4% of the experiments in each case resulted in zero degrees of freedom. One can argue, however, that these instances constitute failures to reject the null hypothesis, since in these instances all of the observations fall in a single bin. For this reason, we report the percentage of experiments in which we reject the null hypothesis for each of the three cases, rather than the percentage in which we fail to reject (Table 5).

Table 5 Reject rates (in percent) for the goodness-of-fit and homogeneity tests

Case	Goodness-of-fit test	Homogeneity test
Exponential	15	13
Linear	19	16
Logarithmic	24	21

These results further suggest that the approximation performs best in the exponential case and worst in the logarithmic case. In all three cases, however, the stationary Bernoulli process seems to well approximate the non-stationary process. In the worst case, the goodness-of-fit test in the logarithmic case, we reject the null hypothesis in only 24% of the experiments (and we would expect a 5% rejection rate even if the approximation were perfect). In all three cases, the approximation passes the test of homogeneity more easily than the goodness-of-fit test. This result seems intuitive since the goodness-of-fit test requires that the simulated non-stationary data match the given binomial distribution, whereas the homogeneity test only requires that the simulated non-stationary data match the simulated binomial data set.

6. Summary and conclusions

We considered a Markov modulated Bernoulli production yield process with a non-stationary parameter, p. This success parameter is a function of the deterioration level of the system, which evolves according to a discrete-time Markov chain on an item-by-item basis. This model captures the effects of intraperiod deterioration, as opposed to the existing literature which assumes that yield depends only on the condition of the equipment at the beginning of each production run. Because of the computational complexity and analytical intractability of this type of model, and in an attempt to validate the existing literature which uses stationary binomial yield models, we formulated a simple binomial approximation of the non-stationary process by matching first moments.

Analytically, we established common characteristics of the true and approximate yield processes under reasonable conditions. More specifically, we showed that if the yield success probability is non-increasing in the wear level and the deterioration process is IFR, then both the true and approximate yield distributions are stochastically non-increasing in the wear state at the beginning of the production run. This result easily generalizes to the case in which the deterioration process is neither upper triangular nor limited to the case in which increases in the wear level are unit valued. Whether the numerical results generalize similarly is left for future research.

Numerically, we designed a large experiment to test the performance of the approximation over many parameter value combinations. For the subset of 24 000 experiments in which the true yield moments are tractable, we numerically compared the second, third and fourth moments of the exact and approximate yield distributions. We found that the moments of the approximate distribution are reasonably close to the true yield moments. Indeed, across the experiments considered, the median absolute percent error is 0.0006%. We also found that the quality of the approximation tends to degrade as the amount of non-stationarity in the process degrades. For all 84 000 experiments, we both test the hypotheses that the second, third and fourth moments of the true yield distribution match the corresponding moments of the approximate yield distribution and also use simulated yield data to compare the exact and approximate yield distributions. Including sample size in the experimental design increases the number of parameter combinations by a factor of five. Over the resulting 420 000 parameter combinations, we obtained a 92% pass rate in testing the hypotheses that the higher moments of the exact yield distribution match the higher moments of the approximate distribution. For the tests designed to compare the exact and approximate probability distributions, we reject the null hypothesis between 13 and 24% of the time, depending on the type of test administered and the characteristics of the deterioration process.

Based on these results, it seems that the stationary binomial approximation is a good surrogate for the true, non-stationary Bernoulli yield process. This conclusion serves to validate existing literature that assumes the success probability is constant during each production run, and suggests that this assumption is worth imposing for analytical and/or numerical tractability in future work in the area of joint production and maintenance decision making in the presence of random yield.

Biographies

Lisa Maillart is an Assistant Professor in the Industrial Engineering Department at the University of Pittsburgh. Prior to joining the faculty at Pitt, she served on the faculty at Case Western Reserve University. She received her M.S. and B.S. in Industrial and Systems Engineering from Virginia Tech, and her Ph.D. in Industrial and Operations Engineering from the University of Michigan. Her primary research interest is in sequential decision making under uncertainty, with applications in medical decision making, maintenance optimization and entrepreneurship. She is a member of INFORMS, SMDM and IIE.

Richard Cassady is Associate Professor of Industrial Engineering at the University of Arkansas. Prior to joining the faculty at the UofA, he was on the faculty at Mississippi State University. He received his Ph.D., M.S. and B.S. all in Industrial and Systems Engineering from Virginia Tech. His primary reliability research interests are in repairable system modeling and preventive maintenance optimization. He is a senior member of IIE and a member of ASEE, ASQ, INFORMS and SRE. He is also a member of the RAMS Management Committee.

Jason Honeycutt received his B.S. and M.S. in Industrial Engineering from the University of Arkansas. He is a full-time engineer in the transportation logistics industry.