Simultaneous optimization of [Xbar] control chart and age-based preventive maintenance policies under an economic objective

Abstract

The economic design of control charts and the optimization of preventive maintenance policies have separately received a tremendous amount of attention in the quality and reliability literature over the years in an attempt to reduce the costs associated with operating manufacturing processes. Not until recently has the proposal been made to integrate these two fields and utilize the relationship between quality and equipment performance to improve the productivity of a manufacturing process. In this paper, we extend the initial preliminary investigation of this idea of using an chart in conjunction with an age-replacement preventive maintenance policy. We formulate a partially observable, discrete-time Markov decision process in order to obtain the near-optimal combined preventive maintenance/statistical process control policy that minimizes the costs associated with maintenance, sampling, and poor quality. We develop transition probabilities for the various states of the infinite horizon problem and a solution algorithm for finding the best policy in polynomial time by finding a control limit on the sampling policy. We also perform sensitivity analysis on the decision variables for each of the various input parameters. It is shown that in every case a combined PM and SPC policy is the most cost efficient.

Keywords:

• Quality control
• control limit
• partially observable Markov decision processes
• preventive maintenance

1. Introduction

The economic design of control charts has recently received a tremendous amount of attention in the statistical process control literature. Designing control charts with an economic objective refers to the cost model optimization practice of selecting control chart parameters in order to minimize the “cost of quality”. Keats et al. (1997) provide an overview of both historical and modern techniques of economic design in the literature.

The optimization of maintenance planning and maintenance models via mathematical modeling has been increasingly reported in the literature (Dekker and Scarf, 1998). This literature is summarized by McCall (1965), Pierskalla and Voelker (1976), Valdez-Florez and Feldman (1989), Dekker (1996) and Garg and Deshmukh (2006). More recent work by Juang and Anderson (2004), Maillart (2006) and Wang (2006) demonstrate adaptive maintenance policies, combined maintenance policies with production quantity and maintenance policies for systems with condition monitoring, respectively.

In spite of the fairly intuitive relationship between product quality and equipment maintenance, very little research has been conducted to integrate these fields. The relationship has been recognized (Tsuchiya, 1992; McKone and Weiss, 1998), but almost all research has been limited to either quality control or equipment maintenance as detailed above, but not both. The logical link between equipment maintenance and product quality operates as follows. Equipment maintenance, either corrective or preventive in nature, has a direct impact on the reliability of the equipment, and thus the performance of the equipment. Under the assumption that the equipment is used to manufacture some type of product, with improved performance of the equipment comes increased product quality.

Furthermore, the effectiveness of quality control and the tremendous cost burden of equipment maintenance are clear in industry. Over the past 25–30 years quality improvement methodologies have spawned increased industrial productivity in the range of 15–25% (Cassady and Nachlas, 1998; Yang and Rahim, 2005, 2006; Batson et al., 2006; Zhang et al., 2006), and in 1988 alone, the combined services of the United States spent approximately $10 billion on programmed depot maintenance (Joint Logistics Commanders, 1988).

Several authors have suggested that the incorporation of proactive improvements to a system based on process monitoring techniques can lead to improved performance. Barros et al. (2005) apply the hazard rate process to multi-unit systems when imperfect information is known about the state of the system. They examine the situation when it is not possible or is prohibitively expensive to perfectly and continuously monitor a system. Therefore, the condition of the system must be determined based on a monitoring process that can fail and non-detected events can occur. Barros et al. (2005) suggest the use of their observed hazard rate process to optimize a preventive maintenance policy, but do not actually do so in their study. Weheba and Nickerson (2005) develop a proactive approach to the economic design of charts. They introduce a proactive cost function that accounts for the cost of process improvement. This along with a reactive function, allows process improvement alternatives to be evaluated on their economic worth, however, they do not propose any specific improvement or maintenance policies.

To our knowledge, Tagaras (1988) was the first to develop a model for the integration of process control and maintenance. Ben-Daya and Rahim (2000) study the effect of maintenance on the economic design of an control chart. Ben-Daya (1999) adds the economic production quantity as an additional optimization parameter. These models do not consider corrective maintenance, only preventive actions. Linderman et al. (2005) develop a model to demonstrate the economic benefit of integrating statistical process control and equipment maintenance. They demonstrate the use of an adaptive maintenance policy wherein the scheduling of maintenance actions adapts to the stability of the process. They include a corrective maintenance action in their model. All of the previously mentioned papers utilize some type of non-linear search technique such as a direct grid search with a combination of golden section and Fibonacci lattice search (Tagaras, 1988) or Hooke and Jeeves (Ben-Daya, 1999; Ben-Daya and Rahim, 2000; Linderman et al., 2005) for their optimization procedure.

Cassady et al. (2000) perform a preliminary investigation to model and analyze the relationship between maintenance and quality by combining existing models of Preventive Maintenance (PM) and Statistical Process Control (SPC). They use a simulation-based optimization approach in conjunction with a genetic algorithm to minimize the average cost per hour of the manufacturing process. They present a single numerical example to show that the combined policy can achieve greater productivity than either policy in isolation or not performing corrective maintenance actions.

In this work, we modify the model suggested by Cassady et al. (2000) (henceforth referred to as the original model) of using an chart to monitor the output of the production process and to determine when to perform corrective, conditioned-based maintenance. This is also the basis for establishing an age-based PM policy. If the control chart signals that the process is out of control, then corrective maintenance will be performed. Furthermore, if a specified time has elapsed since the last maintenance action, then PM will be performed. The goal of this research is to simultaneously optimize both policies to determine how often to sample for the control chart, the optimal control chart parameters and the optimal interval for performing PM.

We formulate a Partially Observable, discrete-time Markov Decision Process (POMDP) to determine the long-run cost of implementing a combined PM and SPC policy. Cassady et al. (2000) have already shown that the combined policies can be better; however, we develop a solution algorithm to find a near-optimal policy without simulation and demonstrate the characteristics of the combined policy, the cases in which it is effective, as well as its sensitivity to the various input parameters.

The remainder of this paper is organized as follows. First, we define the problem statement and our modifications to the original model of Cassady et al. (2000). Then, we present our assumptions and POMDP formulation. Next, we define structural properties of the transition probability matrix and outline our solution algorithm. We demonstrate our solution approach through a numerical example, and present our designed experiment to perform a sensitivity analysis study on the decision variables to the various input parameters. Finally, we conclude with the characteristics of our near-optimal policies and sensitivity analysis.

2. Problem statement

Consider a manufacturing process that operates continuously (i.e., 24 hours a day, 7 days a week) and can be best evaluated by measuring a key quality characteristic of the finished products. An chart can be used to monitor the process in order to determine whether the process is in or out of control. If the process is determined to have gone out of control, a Corrective Maintenance (CM) action is required to restore the process to an in-control condition. Furthermore, this maintenance action can be performed in a preventive manner. A PM action may be conducted when the process is in control to restore the equipment to its optimal condition in order to decrease the likelihood that the process will transition to an out-of-control state. We seek to solve the problem of determining the combined PM and SPC policy that simultaneously optimizes the parameters of both policies under an economic objective. Namely, reducing the costs associated with sampling, PM and CM. This policy would detail when to implement the control chart along with the optimal sample size and control limits for the chart. The policy would also determine the age replacement interval at which to perform a PM action.

3. Model assumptions

The previous model elements retain most of the original aspects of the original model; however, several key exceptions are made in order to eliminate the necessity for simulation. Let X denote the measurement of the key quality characteristic for a given product, and suppose that X is a normal random variable having mean μ and standard deviation σ. The value of μ is referred to as the process mean, and the value of σ is referred to as the process standard deviation. When the process is In Control (IC), or operating properly, the process mean is μ = μ₀ and the process standard deviation is σ = σ₀.

Suppose that the manufacturing process is such that the process standard deviation does not change. However, the process mean is subject to one type of instantaneous shift, and this particular type of shift can be attributed to an equipment failure. After a shift has occurred, the new process mean is given by

where η is some non-zero real number. After the shift, the process is said to be Out Of Control (OOC). Unfortunately, the equipment failure is subtle and cannot be recognized without shutting down the process and performing close inspection of the equipment.

The two maintenance actions, CM and PM, are considered to occur instantaneously. We justify our assumption of instantaneous maintenance by assuming that the time required to perform maintenance is very small relative to the time periods into which time is discretized. We acknowledge that in reality maintenance times are not instantaneous and are time consuming in nature. Furthermore, we realize that maintenance times are random in nature and do add uncertainty to maintenance decision making. However, for the reasons previously stated, we feel that the negligible maintenance time assumption is justified in the context of our model. Note that these maintenance actions also restore the equipment to an “as good as new” condition.

Cassady et al. (2000) assume that the time from process start-up until a shift occurs is governed by a Weibull probability distribution with an Increasing Failure Rate (IFR). However, we assume that process shifts can only occur at the end of equal length, discrete time periods. We assume that the rate of production is fast relative to the rate of equipment deterioration. This assumption simultaneously allows us to set the length of the time period to be sufficiently small to justify discretization of time while still allowing ample production to occur within a time period. Let i denote the number of discrete time periods since the last maintenance action (CM or PM). Let p(i) denote the probability that (given the process is an IC condition) a shift occurs immediately before the ith period since the last maintenance action, i = 1, 2, …. Similarly, let q(i) denote the probability that (given the process is in an IC condition) a shift does not occur immediately before the ith period since the last maintenance action, i = 1, 2, …. It follows that:

We do assume that the unit of equipment is subject to an IFR which implies that:

We assume that PM is performed on the equipment using a modified age replacement policy, τ. Our age replacement policy is denoted modified, because it is implemented as follows: if the unit of equipment functions without a detected failure (detected process shift) for τ time periods (τ > 0), then PM is performed. Traditional age replacement policies assume that equipment failures are easy to detect, however, this is not the case for our model. The value of τ is referred to as the age replacement period.

Due to the fact that the process is subject to shifts in the mean that are subtle, and these shifts may occur before the expiration of the age replacement period, an chart can be used to monitor the process. If the chart is implemented, then sampling and charting take place at some subset of discrete points in time. The SPC policy is captured by the vector s = (s ₁, s ₂, …, s _{τ − 1}). Let s _i denote a binary decision variable indicating whether or not sampling occurs at the beginning of the ith time period since the last maintenance action where s _i = 1 if sampling occurs and s _i = 0 otherwise, i = 1, 2, …, τ − 1. For each evaluation of the process, the sample size is given by n, and the number of standard deviations between the center line and the control limits is given by k. Therefore, the control limits of the chart are given by

The chart operates as follows. At the beginning of any given period, if s _i = 1, then a sample of n finished products is taken from the process, and the quality characteristic of each finished product is measured. The sample mean quality characteristic is then computed and plotted on the control chart. If the sample mean falls within the range (LCL, UCL), then the conclusion is drawn that the process is in an IC state, i.e., no equipment failure has occurred. The process is therefore allowed to continue operating. If the sample mean falls outside of the control limits, a signal of an OOC condition is made. In other words, the conclusion is drawn that an equipment failure has occurred and the process mean has shifted; thus, the process is shut down and a maintenance action is initiated. Note that we assume that all of this takes place instantaneously.

Since only a sample is taken from the process, the control chart can lead to both Type I errors (OOC signals when IC) and Type II errors (no signals when actually OOC). Let α denote the probability of a Type I error, let β denote the probability of a Type II error, and let Φ denote the cumulative distribution function of the standard normal random variable. Then, α and β are given by

This is the situation in which Type I or Type II errors can occur that was previously investigated by Barros et al. (2005) for an imperfectly monitored system.

The objective of this research is to develop the most cost efficient policies that utilize the chart in conjunction with the modified age replacement PM policy to simultaneously improve the performance of a manufacturing process. Specifically, we seek to choose values of s, n, k and τ such that the costs of inspection, maintenance and poor quality are minimized. Cassady et al. (2000) were forced to use simulation-based optimization in conjunction with a genetic algorithm in order to evaluate such policies, however, with our modifications to the original model, we are able to formulate a PODMP to evaluate the long-run expected cost associated with values of s, n, k and τ and develop an algorithm that minimizes cost over all such values.

4. Model formulation

As in Cassady et al. (2000), we follow the current trend in the maintenance optimization and SPC literature of optimizing the performance of the manufacturing process under an economic objective. Let c _s denote the cost of inspecting a single item, let c _m,OOC denote the cost of performing maintenance when the process is in an OOC state, let c _{m, IC} denote the cost of performing maintenance when the process is in an IC state, and let c _q denote the cost of poor quality. We assume that the cost of poor quality is a fixed value that occurs when the process spends an entire time period in an OOC state. Furthermore, we assume that:

This relationship states that the cost of maintenance is always less than or equal to the cost of poor quality, and the total cost of sampling (c _s n) is always less than or equal to the cost of maintenance. Furthermore, this relationship dictates that there is always at least some cost associated with these three actions (i.e, they are always greater than zero).

Given these costs, the long-run expected cost per time period of the manufacturing process is given by

Since we are evaluating the performance of our manufacturing process under an economic objective in Equation (9), the expected cost of being in each state must be calculated as required by Equation (9). The expected cost of being in an IC state, (1, IC), (2, IC), …, (τ − 1, IC), is given by

Note that a cost is only occurred in Equation (10) if sampling occurs (i.e, s _i = 1). If sampling occurs, a cost will be incurred for each item in the sample (c _s n) in addition to the expected cost of maintenance should a false alarm occur (c _m,ICα).

The expected cost of being in an OOC state, (1, OOC), (2, OOC), …, (τ − 1, OOC), is

If sampling does not occur, there will be a cost associated with poor quality (c _q). If sampling does occur, there will be a cost incurred for sampling (c _s n) along with an expected cost of maintenance (c _m,OOC(1 − β)) and an expected cost of poor quality should a Type II error occur (c _q β).

The expected cost of being in state τ is c _m,OOC regardless of whether the process is in an IC or OOC state. A complete overhaul of the equipment is assumed to be performed if state τ is reached; thus, the cost is assumed to be the same as when the process is in an OOC state.

Also in Equation (9), Pr(i, IC) is the limiting probably of being in state (i, IC), Pr (i, OOC) is the limiting probability of being in state (i, OOC), and Pr(τ) is the limiting probability of being in state τ. These limiting probabilities are derived in the remainder of this section.

Suppose that the process is initially in an IC state. After some amount of time, a process shift occurs due to the failure of a unit of equipment. The process remains in an OOC condition until maintenance is performed (either due to a signal on the control chart or the expiration of the PM policy). Furthermore, since maintenance restores the unit of equipment to an “as good as new” condition, the initiation of a maintenance action is a renewal point for the process.

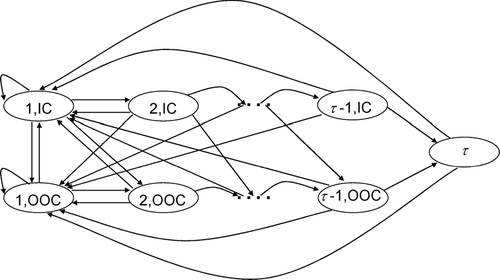
We model the process as a discrete-time, discrete-valued stochastic process where the discrete points in time correspond to the opportunities for SPC or PM. The state space includes 2(τ − 1) + 1 possible states. These states are denoted by (1, IC), (1, OOC), (2, IC), (2, OOC), …, (τ − 1, IC), and (τ − 1, OOC), and finally, τ. The process is in state (i, IC) if it has been i discrete time periods since the last maintenance action and the process is still in an IC condition, i = 1, 2, …, τ − 1. The process is in state (i, OOC) if it has been i periods since the last maintenance action and the process has shifted to an OOC condition, i = 1, 2, …, τ − 1. The process is in state τ if it has been τ periods since the last maintenance action. The distinction between IC and OOC conditions is unnecessary at state τ since the PM policy dictates that maintenance will be initiated. The stochastic process is a Markov decision process since the next state of the process and the expected value of the costs incurred at the current time depend only upon the current state of the process and the action regarding SPC or PM. Note that the Markov decision process is only partially observable because it is impossible to determine with absolute certainty whether the process is in an IC or OOC condition. At state (i, IC) or (i, OOC), i = 1, 2, …, τ − 1, the set of possible actions is comprised of “do nothing” (s _i = 0) and “initiate SPC” (s _i = 1). At state τ, the only possible action is “initiate PM”. Figure 1 captures the possible state transitions for the POMDP.

Fig. 1 State transition diagram.

There are two ways in which the process may transition from state (i, IC) to state (i + 1, IC), i = 1, 2, …, τ − 2. The first is the result of choosing the do nothing action and no equipment failure (process shift) at the end of the subsequent time period. The second is the result of choosing the initiate SPC action, no false alarm, and no equipment failure at the end of the subsequent time period. The probability of transitioning from state (i, IC) to state (i + 1, IC) is given by

Transitioning from state (i, IC) to state (1, IC) is only possible if the initiate SPC action is chosen, a false alarm occurs (resulting in maintenance and equipment renewal), and no process shift occurs at the end of the subsequent time period. The probability of transitioning from state (i, IC) to state (1, IC) is given by

The process may transition from state (i, IC) to state (i + 1, OOC) as a result of either the do nothing or the initiate SPC action. Under the do nothing scenario, a shift must occur at the end of the subsequent time period. If SPC is initiated, then a false alarm must not occur, and there must be a process shift at the end of time period i. This transition probability is given by

The transition from state (i, IC) to state (1, OOC) occurs if SPC is initiated, a false alarm occurs, and a shift to an OOC condition occurs at the end of the subsequent time period. The probability of transitioning from state (i, IC) to state (1, OOC) is given by

Transitions may also occur from an OOC state, the first such instance being from state (i, OOC) to state (1, IC), i = 1, 2, …, τ − 2. This transition occurs if SPC is initiated, a signal occurs (implying that maintenance is performed on the equipment), and there is no process shift at the end of the subsequent time period. This transition probability is given by

The process transitions from state (i, OOC) to state (i + 1, OOC) if either the do nothing option is chosen or the initiate SPC action is chosen and a signal does not occur. This transition probability is given by

Finally, the process transitions from state (i, OOC) to state (1, OOC) if SPC is initiated, a signal occurs, and a process shift occurs at the end of the subsequent time period. The resulting transition probability is given by

Recall that an OOC process remains in an OOC condition until maintenance is performed. Therefore, it is impossible to transition from state (i, OOC) to state (i + 1, IC).

Transitioning to state τ can only occur from states (τ − 1, IC) or (τ − 1, OOC). This transition occurs if SPC is initiated and no signal occurs or if SPC is not initiated. The probability of transitioning from state (τ − 1, IC) to τ is given by

The probability of transitioning from state (τ − 1, OOC) to τ is given by

The Markov decision process is renewed at state τ and therefore may only transition to state 1, however, at the end of state 1 the process may either be in an IC or an OOC condition. The probability of transitioning from state τ to (1, IC) is simply the probability that a shift does not occur from when the process is renewed after PM to the end of time period 1, that is

Likewise, the probability of transitioning from state τ to (1, OOC) is simply the probability that a shift occurs from when the process is renewed after PM to the end of time period 1, that is,

The transition probabilities associated with moving to and from each state are also summarized in the transition probability matrix in Fig. 2 of the next section when we demonstrate the structural properties. The probabilities of being in each state are the limiting probabilities found by solving the system of equations formed by the transition probability matrix (Fig. 2).

Fig. 2 Structural properties of the transition probability matrix for the PM policy τ.

Note that manufacturing process performance is defined as a function of the parameters of the age replacement policy and the chart. These variables, s, n, k and τ are our decision variables. All other defined parameters (c _s, c _m,IC, c _m,OOC, c _q, η) are treated as input parameters. Our objective is, given a set of input parameters, to minimize Equation (9) over all decision variables.

5. Structural properties of the POMDP

In this section we establish some structural properties of the POMDP. These properties allow us to easily expand and update the transition probability matrix as increases in τ are evaluated. These structural properties offer tremendous computational benefit in constructing our solution algorithm presented in the next section.

The dimensions of each transition probability matrix are γ by γ where:

The size of the transition probability matrix increases as τ increases. The matrix also changes in composition, however, we are able exploit the structural properties of the transition probability matrix as it expands in size. Entries in the matrix shift in fixed patterns that allow us to easily build a matrix for any value of τ. For every increase in τ, the dimensions of the transition probability matrix increase by two and the first γ − 1 rows and columns of the original matrix remain unchanged. These structural properties are demonstrated in Fig. 2 for a matrix of PM policy τ.

Figure 2 then transitions to Fig. 3 for τ + 1.

Fig. 3 Transition probability matrix for the PM policy τ + 1.

The boxed equations with arrows in Fig. 2 indicate the position shift in the number of rows and columns in terms of a Cartesian coordinate system. Column numbers represent points on the horizontal axis, and row number represent points on the vertical axis. A “Copy” action indicates the equations are “copied” to their indicated position and their indices are incremented by one. Likewise, a “Move” action indicates the equations are removed from the matrix, replaced by zeros, “moved” to the indicated location, and their indices are incremented by one. For example, Move (2, -2) denotes moving the boxed equations two columns to the left, and two rows down.

6. Solution procedure

In order to obtain a policy that simultaneously optimizes the SPC and PM policy, we have developed a polynomial-time algorithm which provides near-minimum cost performance. It may be summarized as follows:

	Begin with τ = 2. Iterate over specified values of s, n and k. Record best C(s, n, k, τ = 2).
	Build matrix for τ + 1.
	Iterate over all possible values of s, n and k. Record best C (s, n, k, τ + 1).
	If C(s, n, k, τ + 1) < C(s, n, k, τ), then return to Step 2. Else, the best solution is C(s, n, k, τ).

We begin by iterating over τ. Due to the cost relationship we assume in Equation (8), performing PM every time period (τ = 1) will never be optimal, and thus the algorithm begins with τ = 2. For each value of τ, we evaluate C (s,n,k,τ) in Equation (9) by formulating the transition probability matrix and solving for the limiting probabilities. We evaluate solutions using a total enumeration approach for specified ranges of k and n and all possible permutations of s. The decision variables k and n were not tested for all possible values, but rather the most probable and practical values. For each τ, the k values were evaluated from k = 0.25 to 4 in increments of 0.25, and n was evaluated for one to seven, ten, 15 and 30. This encompasses what Cassady et al. (2000) termed “Textbook SPC” (k = 3, n = 5). Due to the fact that we do not evaluate every possible value of k and n we denote the solution of our algorithm as near optimal, instead of optimal.

To solve the infinite-horizon problem, τ must be iterated over until the cost objective function begins to increase. Our cost function behaves similar to a convex function of τ, and will decrease until the optimal maintenance policy is reached, and subsequent values of τ will cause the cost to increase. This is why our solution algorithm stops when C(s, n, k, τ + 1) > C(s, n, k, τ).

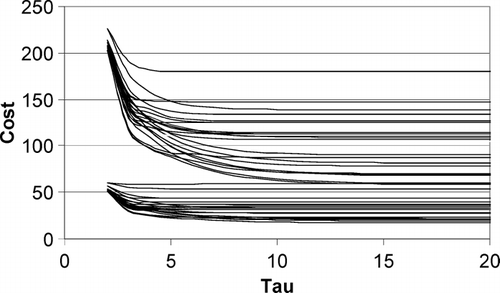
In order to empirically demonstrate the convex properties of the objective function, we perform a study on a subset of the experimental design that will be presented in Section 7. These values are chosen to represent roughly the 25th and 75th percentile values of the experimental design to be presented in Section 7. Rather than terminating the algorithm after τ begins to increase, we continue to evaluate the objective function to τ = 45 in order to show that once the function increases it will never again decrease. Figure 4 shows a plot of 48 objective functions for the experimental design given in Table 1.

Fig. 4 Plot of objective functions.

Table 1 Empirical convexity study

Factor	Levels	Level description
Cost of IC maintenance (c m,IC) ($)	2	50, 200
Cost of OOC maintenance (c m,OOC) ($)	1	2c m,IC
Cost of quality (c q) ($)	2	2c m,OOC, 10c m,OOC
Size of process shift (η)	3	0.5σ, 1.5σ, 2σ,
Initial probability of failure (p 0)	2	0.01, 0.03, 0.05, 0.10
δ	2	0.85, 0.97

It is shown in Fig. 4 that in every case the cost objective never decreases again, once it begins to decrease. It is interesting to note that the increase in the objective function once the minimum value has been reached is very slight and becomes horizontally asymptotic. This is due to the fact that as time increases, the probability of a failure approaches unity and the probability that the failure is eventually detected also approaches unity. Thus, as time increases, the probability of a CM action occurring is so likely that the positioning of a PM action is moot and the cost reaches a steady state.

We are also able to ensure the existence of a control limit policy on the best s policy. A control limit policy is of the simplest form: sample the product produced by the equipment if and only if the observed state is one of the states ψ, ψ + 1, ψ + 2, … for some state ψ called the control limit (Barlow and Proschan, 1965). Knowing that the optimal policy is of the control limit type allows the problem to be solved much more efficiently as we can dramatically reduce the permutations of the s vector that must be evaluated. Puterman (1994) also notes that control limit policies are easier to implement in practice.

The sampling rule is a control limit rule if the underlying Markov chain with transition probability matrix (p _ij ) is IFR (Barlow and Proschan, 1965). As noted above, one of the assumptions of our manufacturing process is an IFR.

definition 1. (Barlow and Proschan, 1965).

i.	A discrete distribution {p k } k = 0 ∞ is IFR if p k /∑ i = k ∞ p i is non-decreasing in k = 0, 1, 2, ….
ii.	A Markov chain is said to be IFR if its rows are in increasing stochastic order, that is is non-decreasing in i for all k = 0, 1, …, m.

This condition is very intuitive: the higher the state of the equipment, the greater the deterioration. This definition is also equivalent to the idea of stochastic dominance. Once sampling becomes effective in reducing cost for a given τ, sampling will be effective for all subsequent increases in the value of τ. The impact of this finding cannot be overstated as it allows our algorithm to solve in polynomial time rather than exponential time if all permutations of s must be evaluated. Without the advantage of the control limit policy, all possible permutations of s must be realized in the solution algorithm. For example, when τ = 18, the solution algorithm would have to evaluate 2¹⁸ = 262 144 possible permutations of s, taking an average of 5.7 hours to compute. However, when making use of the control limit, we are able to only evaluate 18 + 1 = 19 total permutations (e.g., … 0000, … 0001, … 0011, …) yielding an average solution time of a mere 13.8 seconds. Without the control limit we were only able to solve a maximum problem size of τ = 19, which took over 15 hours to compute. Making use of the control limit, we are able to solve problems of size τ = 19 in an average of only 15.3 seconds. From our experimental design detailed in a later section, we are also able to easily solve problems of size τ = 55 in only 7.5 minutes.

7. Numerical experimentation

7.1. Example

In this section we present a numerical example to demonstrate the implementation of our methodology. A function is needed to generate the probability of failure in each time period. This function needs to be monotonically increasing (for IFR and to guarantee the existence of a control limit policy) and horizontally asymptotic at p(i) = 1 to ensure probabilities of failure generated by the function do not exceed unity. The following function was formulated to model the probability of failure for our experiment:

where p ₀ is the initial probability of failure and δ is a constant, 0 < δ < 1. Higher values of δ lead to more gradual failure rates. Figure 5 shows the plot of p(i) for various values of δ with p ₀ = 0.05. As δ increases, the function also becomes more linear in nature. The value of p ₀ has little effect on the shape of the curve, but determines the starting position of the probability failure curve (Fig. 5).

Fig. 5 Plot of p(i).

Consider an example with the following inputs:

The probabilities given for each time period are given by the function in Equation (25). We evaluate k and n for the values specified in the algorithm description above. The results are displayed in Table 2.

Table 2 Numerical example

Cost (å)	τ	k	n	s 1	s 2	s 3	s 4	s 5	s 6
50.00	1	—	—	—	—	—	—	—	—
27.50	2	—	—	0	—	—	—	—	—
22.36	3	1	3	0	1	—	—	—	—
20.95	4	1.25	4	0	1	1	—	—	—
20.61	5	1.25	4	0	1	1	1	—	—
20.57	6*	1.25	4	0	1	1	1	1	—
20.58	7	1.25	4	0	1	1	1	1	1

The optimal PM policy is τ = 6 (marked with an * in Table 2) with sampling occurring in all but the first time period. For τ = 1, maintenance occurs every time period and therefore the process is always in state 1. Thus, the cost of τ = 1 is the cost of a complete overhaul (c _m,OOC = $50). Since under a τ = 1 policy sampling never occurs, k and n are not relevant. Increasing τ to two, the cost per time period is almost cut in half to $27.50, but SPC is still not cost effective. As τ is iterated to a value of three the cost again decreases to $22.36 and SPC becomes effective at time 2. At τ = 4, the cost continues to decrease to $20.95 with SPC effective at times 2 and 3, but not time 1. The cost continues to decrease in this manner with SPC being effective for every time period except the first. However, at τ = 7 the cost increases. Since we know the cost will not decrease again after increasing due to its convex behavior, we know the optimal policy was found at τ = 6.

7.2. Experimental design

A full factorial experiment was conducted over the various input parameters. A summary of the experiment is presented in Table 3.

Table 3 Experimental design

Factor	Levels	Level description
Cost of IC maintenance (c m,IC) ($)	6	31, 50, 100, 150, 200, 500
Cost of OOC maintenance (c m,OOC) ($)	1	2c m,IC
Cost of quality (c q) ($)	6	1.05c m,OOC, 1.5c m,OOC, 2c m,OOC, 5c m,OOC, 10c m,OOC, 50c m,OOC
Size of process shift (η)	4	0.5σ, 1σ, 1.5σ, 2σ,
Initial probability of failure (p 0)	4	0.01, 0.03, 0.05, 0.10
δ	7	0.8, 0.85, 0.90, 0.95, 0.96, 0.97, 0.98

Without loss of generality the cost of sampling a single item was set at $1 for all experiments and all maintenance and quality costs are defined proportionally. The cost of maintenance was evaluated over five values: $31, $50, $100, $150, $200 and $500. The minimum c _m,IC value of 31 was selected to be the smallest value above the highest possible cost of sampling (i.e., n = 30). The cost of maintenance on an OOC process (c _m,OOC) was considered to be twice that of c _m,IC in all cases. The cost of quality was tested at multiples of the cost of maintenance on the OOC process specifically, 1.05, 1.5, 2, 5, 10 and 50 times. The size of the shift was tested at four different multiples of σ : 0.5, 1, 1.5 and 2. As previously mentioned, the experiment was full factorial for (6)(6)(4)(4)(7) = 4032 total experiments.

A subset of the experimental design in Table 3 (576 experiments) was also used without using the control limit policy as further verification of its existence. The experiment used limited the size of c _m and c _q as well as the size of the deterioration parameter δ in order to keep τ ≤ 19 (the largest size problem that could be solved). All 576 experiments in the subset exhibited the control limit.

7.3. Results and sensitivity analysis

Whereas Cassady et al. (2000) tested combinations of no SPC, “Textbook” SPC, optimal SPC, no PM and optimal PM and reported their impact on cost, we simultaneously evaluate all possible combinations and report the best policy. Our model implicitly evaluates the PM-only and SPC-only policies as it seeks the best overall policy. It is shown that in all cases, a combined PM/SPC policy is more effective than either in isolation, or not applying a policy. If this were not the case, τ would be infinity in some instances, or the s vectors would contain all zeros. If only an SPC-only policy was effective there would be cases in which the s vector was non-zero and τ was infinity. An infinite τ would mean that it is never optimal to perform PM, but no such results were found over the entire experimental design. If a PM-only policy was optimal, then the policy would consist of some τ for PM and the s vector would contain all zeros. Likewise, all cases showed SPC to be effective for at least one time period. In the 61.2% of cases, SPC is cost effective for all time periods, and it is effective in 93.9% of cases from the third time period on where τ ≥ 4. SPC is always optimal from the fourth time period on where τ ≥ 5.

As expected, the value of τ for the best PM policy increases as c _m increases or the deterioration of equipment is very slow (i.e., high δ values). The largest τ value obtained over the experimental design is 55 (16 cases). These occur when c _m,IC is in the upper half of its range, the c _q multiple is small (≤ 2) and δ is at its highest level (0.98). Obviously, the average cost per time period is most affected by the respective costs of performing maintenance and the cost of poor quality. The highest cost ($545.31) occurs when the costs factors are at their highest levels, and τ is low (i.e., costly maintenance must be performed often). The least costly policy had an average cost per time period of $9.53 with a τ = 39. The cost factors were at the lowest levels in this case, and the deterioration rate was at its slowest (p ₀ = 0.01, δ = 0.98).

Table 4 shows the impact of the parameters p ₀ and δ for the probability function p(i) (25) on cost and the three decision variables τ, k and n. c _m,IC, c _q and η are held constant at their median values $100, $400 and 1.5, respectively. As expected, the slower the equipment deteriorates (higher levels of δ) the longer PM actions will be delayed (higher τ values) and thus smaller maintenance costs will be incurred. Increasing the initial probability of failure (p ₀) leads to a steady increase in the cost of the best policy, however, it has very little effect on τ or the sampling parameters k and n. In fact, k and n remain very stable for all levels of p ₀ and δ when the costs remain unchanged.

Table 4 Sensitivity to p ₀ and δ

	p 0
	0.01				0.03				0.05				0.1
δ	τ	å	k	n	τ	å	k	n	τ	å	k	n	τ	å	k	n
0.80	11	60.74	1	5	11	65.08	1.25	6	9	67.85	1.75	7	9	72.95	1.75	7
0.85	14	55.68	1.25	6	12	59.86	1.5	6	12	62.47	1.75	7	12	67.89	1.75	7
0.90	17	49.03	1.5	6	17	53.05	1.5	6	14	55.71	2	7	14	61.52	2	7
0.95	24	39.46	1.75	6	24	43.31	2	7	24	45.78	2	7	25	52.29	2	7
0.96	29	36.75	1.75	6	29	40.55	2	7	29	43.10	2	7	31	49.83	2	7
0.97	36	33.60	1.75	6	36	37.33	2	7	37	39.98	2	7	39	46.98	2	7
0.98	50	29.78	1.75	6	38	33.36	2	6	53	36.19	2	7	51	43.58	2	7

Table 5 shows the impact of the cost parameters, c _m,IC, c _m,OOC and c _q, on cost and the three decision variables τ, k and n. p ₀, δ and η are held constant at 0.03, 0.95 and 1.5, respectively. The most important result of this table is that the cost of quality relative to the cost of maintenance has very little impact on the overall cost of the policy; the primary cost driver is only the cost of maintenance (i.e., setting c _q = 50c _m only changes the cost of the policy by a few dollars as compared to c _q = 1.05c _m). As expected, as c _m increases, the cost of the best policy increases. There is also a steady increase in the sample size (n) as c _m increases as well as when c _q increases for each level of c _m. However, the k value associated with sampling remains relatively unchanged for each level of c _m despite varying levels of c _q. Moreover, as c _m increases, the frequency of PM (τ) decreases. With an increase in c _m, it will be optimal to delay maintenance actions as long as possible. It is also interesting to note that increasing c _q for a particular level of c _m does not have a tremendous effect on τ as one might expect.

Table 5 Sensitivity to c _m and c _q

	c m,IC (å)
	31				50				100				150				200				500
c q× c m,OOC ((å))	τ	(å)	k	n	τ	å	k	n	τ	$	k	n	τ	å	k	n	τ	å	k	n	τ	å	k	n
1.05	19	14.88	1.25	3	21	22.45	1.50	4	25	41.36	1.75	5	31	59.62	2.0	7	33	77.59	2.0	7	54	181.66	2.5	10
1.50	17	15.42	1.25	3	19	23.17	1.50	4	27	42.32	1.75	6	29	60.88	2.0	7	30	78.84	2.0	7	54	182.59	2.5	10
2.0	15	16.01	1.25	3	22	23.82	1.50	5	24	43.31	2.0	7	26	61.46	2.0	7	35	79.32	2.25	10	40	183.31	2.25	10
5	14	18.09	1.50	5	19	25.95	1.75	7	23	44.90	1.75	7	27	62.91	2.25	10	29	80.55	2.25	10	46	184.92	2.75	15
10	14	19.01	1.50	6	20	26.92	1.50	7	25	45.82	2.0	10	28	63.73	2.0	10	30	81.64	2.0	10	38	185.60	2.5	15
50	14	21.08	1.25	7	16	29.01	1.75	10	21	48.02	1.75	10	28	66.88	2.25	15	32	84.17	2.25	15	37	187.92	2.25	15

Table 6 shows the impact of the size of the shift (η) on cost and the three decision variables. The equipment deterioration parameters (p ₀, δ) are held constant as in the above cases. c _m was evaluated at its minimum, median and maximum. As η increases, the length of the optimal PM policy τ increases. Thus, as the optimal PM policy increases, the amount of maintenance being performed decreases and the overall cost of the policy decreases. The results also show intuitively that as η gets larger, the size of the shift becomes less subtle and easier to detect. Therefore, the best k value will increase and the best sample size n will decrease. As the size of the shift increases, the cost of the policy will decrease because an OOC process becomes easier to detect and there are less quality costs incurred. It follows that cost savings become more dramatic as c _q increases which is evident in the results.

Table 6 Sensitivity to η with varying costs

		c m, IC (å)
		31				100				500
η	c q× c m, OOC	τ	å	k	n	τ	å	k	n	τ	å	k	n
0.5	1.05	8	16.15	0.25	1	8	51.26	0.25	1	18	222.29	1.5	30
0.5	1.5	7	17.78	0.25	1	11	56.24	0.25	4	21	231.17	1.25	30
0.5	2	7	19.48	0.25	1	9	60.86	0.75	10	18	239.26	1.25	30
0.5	5	5	24.30	0.25	1	11	72.93	0.5	15	12	278.21	1.25	30
0.5	10	5	31.34	0.25	5	9	85.45	1	30	11	307.46	1	30
0.5	50	3	43.79	0.25	10	6	103.75	0.75	30	7	400.19	0.75	30
1	1.05	12	15.87	0.25	1	16	45.77	1.5	7	32	192.80	2	15
1	1.5	11	17.34	0.25	1	20	47.17	1.5	10	29	195.90	2	15
1	2	12	18.29	1	5	19	48.51	1.5	10	25	198.34	2	15
1	5	12	21.56	1	7	17	53.42	1.75	15	35	201.00	2.5	30
1	10	9	24.73	1	7	18	55.37	1.5	15	32	202.20	2.5	30
1	50	7	29.15	1	10	14	61.66	1.25	15	34	206.41	2	30
1.5	1.05	19	14.88	1.25	3	25	41.36	1.75	5	54	181.66	2.5	10
1.5	1.5	17	15.42	1.25	3	27	42.32	1.75	6	54	182.59	2.5	10
1.5	2	15	16.01	1.25	3	24	43.31	2	7	40	183.31	2.25	10
1.5	5	14	18.09	1.5	5	23	44.90	1.75	7	46	184.92	2.75	15
1.5	10	14	19.01	1.5	6	25	45.82	2	10	38	185.60	2.5	15
1.5	50	14	21.08	1.25	7	21	48.02	1.75	10	37	187.92	2.25	15
2	1.05	19	13.75	1.5	2	33	39.15	2	4	54	176.84	2.75	7
2	1.5	21	14.24	1.75	3	30	39.85	2	4	39	177.26	2.75	7
2	2	24	14.58	1.5	3	30	40.07	2.25	5	38	177.63	2.5	7
2	5	20	15.70	1.75	4	29	40.90	2	5	38	178.93	2.5	7
2	10	16	16.26	1.75	4	32	41.46	2	6	40	179.31	2.75	10
2	50	19	17.40	1.5	5	29	42.66	2	7	37	180.38	2.5	10

Table 7 shows the sensitivity of the decision variables to η with varying equipment deterioration parameters. The costs are fixed as in Table 4 above. It is again shown that an increase in η causes a significant drop in cost as well as causing k to increase and n to decrease. Moreover, increases in p ₀ exhibit only minimal increases in the cost of the policy and decreases in τ. Table 7 shows little impact on k and n for increases in p ₀.

Table 7 Sensitivity to η with varying equipment deterioration

		p 0
		0.01				0.03				0.05
η	δ	τ	$	k	n	τ	$	k	n	τ	$	k	n
0.5	0.8	5	68.62	0.25	7	5	74.29	0.25	7	5	79.93	0.25	7
0.5	0.85	6	64.60	0.25	5	6	70.52	0.25	6	6	76.35	0.25	7
0.5	0.9	6	60.09	0.25	3	6	66.36	0.25	4	7	72.48	0.25	5
0.5	0.95	11	51.91	0.25	5	9	60.86	0.75	10	12	66.60	0.75	15
0.5	0.96	11	49.16	0.25	4	11	58.74	0.75	10	11	64.61	1	15
0.5	0.97	10	46.26	0.25	2	14	56.06	1	15	14	61.96	1	15
0.5	0.98	18	43.06	0.75	10	19	52.31	1	15	19	59.01	1	15
1	0.8	9	63.89	0.5	6	8	68.70	0.75	7	9	73.37	1	10
1	0.85	11	59.29	0.75	7	11	64.02	1	10	10	68.51	1.25	10
1	0.9	13	53.37	1.25	10	13	57.67	1.25	10	14	62.08	1.25	10
1	0.95	18	44.35	1.5	10	19	48.51	1.5	10	19	52.85	1.5	10
1	0.96	21	41.72	1.5	10	22	45.91	1.5	10	23	50.29	1.5	10
1	0.97	27	38.71	1.5	10	28	42.94	1.5	10	21	47.19	1.75	10
1	0.98	37	34.68	1.5	10	28	39.17	1.75	10	29	43.22	1.75	10
1.5	0.8	11	60.74	1	5	11	65.08	1.25	6	9	67.85	1.75	7
1.5	0.85	14	55.68	1.25	6	12	59.86	1.5	6	12	62.47	1.75	7
1.5	0.9	17	49.03	1.5	6	17	53.05	1.5	6	14	55.71	2	7
1.5	0.95	24	39.46	1.75	6	24	43.31	2	7	24	45.78	2	7
1.5	0.96	29	36.75	1.75	6	29	40.55	2	7	29	43.10	2	7
1.5	0.97	36	33.60	1.75	6	36	37.33	2	7	37	39.98	2	7
1.5	0.98	50	29.78	1.75	6	38	33.36	2	6	53	36.19	2	7
2	0.8	13	59.16	1.25	4	11	62.67	2	5	11	64.57	2	5
2	0.85	15	53.74	1.5	4	14	57.13	2	5	14	59.15	2	5
2	0.9	19	46.95	1.75	4	20	50.16	2	5	20	52.31	2	5
2	0.95	34	37.07	1.75	4	30	40.07	2.25	5	31	42.44	2.25	5
2	0.96	32	34.40	2	4	37	37.32	2.25	5	37	39.76	2.25	5
2	0.97	40	31.14	2	4	47	34.11	2.25	5	54	36.64	2.25	5
2	0.98	53	27.14	2	4	51	30.17	2.25	5	54	32.82	2.25	5

8. Conclusions

We have modified the model presented by Cassady et al. (2000) and formulated the problem as a PODMP. We have evaluated the probability of all possible transitions and formulated the generic transition probability matrix that is expandable for all values of τ due to our ability to exploit the structural properties of the matrix. We have created an enumerative algorithm for finding the near-optimal combined PM and SPC policy for an economic objective. The algorithm makes use of a control limit on the s policy as well as convex-like behavior of the cost function. Finally, we have conducted an experiment to perform sensitivity analysis on the decision variables for the various input parameters. Whereas Cassady et al. (2000) only showed that a combined policy can be effective, through simulation-based optimization (and they only show a single numerical example), we show that a combined policy is effective in every case over an entire full factorial experimental design.

Using our model, managers wishing to both reduce production cost and improve product quality now have the ability to accurately and efficiently simultaneously optimize their quality control and maintenance policies. Rather than attempting to separately formulate policies for maintenance and quality, managers can take advantage of the symbiotic relationship between the two and utilize quality control procedures to determine when maintenance should be performed. Our analysis shows that managers would be best served by focusing their attention on improving mean time to failure of their equipment and improving their ability to detect a shift in the process should one occur. These areas show the greatest potential for cost reduction. It is also shown that, despite the intuitive thinking of many managers, the cost of producing a poor quality product has very little impact on the overall cost of production, and is not an area to which management needs to devote extensive efforts.

The formulation of the model as a POMDP has tremendous research implications in addition to its managerial implications. The POMDP formulation eliminates the necessity for simulation-based optimization and allows managers to obtain an exact near-optimal solution rather than a simulation-based approach in conjunction with a genetic algorithm in which the quality of the solution is unknown. Furthermore, the discovery of both the convex and control limit properties of the model provide a breakthrough in understanding optimal SPC policies (control limit type) and tremendously speed up the solution procedure algorithm. The increased speed allows managers to determine the optimal combined policy in real time so that they can easily be applied to a wide range of products and processes and may be quickly adapted to changing conditions.

Biographies

Thomas Yeung is an Assistant Professor in the Department of Industrial Engineering & Automatic Control at the Ecole des Mines de Nantes and he is also a member of the Institut de Recherche en Communications et Cybernétique de Nantes (IRCCyN Research Lab). He received his Ph.D. in Industrial Engineering from the University of Arkansas. His primary research interests are in optimization under uncertainty with application to maintenance optimization and finance. He is a member of IIE and INFORMS.

Richard Cassady is an Associate Professor in the Department of Industrial Engineering at the University of Arkansas. Prior to joining the faculty at the University of Arkansas, he was on the faculty at Mississippi State University. He received his Ph.D. in Industrial and Systems Engineering from Virginia Tech. His primary reliability research interests are in repairable systems modeling and preventive maintenance optimization. He is a Senior Member of IIE, and a member of ASEE, INFORMS and SRE. He is also a member of the RAMS Management Committee.

Kellie Schneider is the Freshman Engineering Instructor at the University of Arkansas and a Ph.D. student in the Department of Industrial Engineering. She received both her BSIE and MSIE from the University of Arkansas.