Optimal specifications for degrading characteristics

Abstract

In this article, we show that the manufacturing target for a product characteristic affected by degradation is not the value that maximizes the quality of the product. By sacrificing some quality at the manufacturing stage it is possible to increase the product's lifetime and thus reduce the quality loss over a long period. We propose a procedure for finding the optimal manufacturing target that maximizes both quality and reliability of the product.

Keywords:

• Manufacturing target
• product design
• quality
• reliability

1. Introduction

Many characteristics of a product are subject to degradation. During the product usage, those characteristics degrade, resulting in the deterioration of the product's performance. How should we set the manufacturing specifications for such characteristics? Traditionally they have been chosen to maximize the quality of the product. However, if the characteristic is affected by degradation, then this may not be the optimal choice with respect to the performance of the product over time. By sacrificing the quality at the initial stage of the product's usage, we might be able to improve the reliability of the product and increase its lifetime. Therefore, the specifications for degrading characteristics should be chosen to maximize the quality as well as the reliability. The idea of integrating quality and reliability into product design is not a new concept (see, e.g., Chen et al. (2004) and Joseph and Yu (2006)), however, a formal and scientific approach for developing manufacturing specifications seems to be lacking. In this article we attempt to develop this approach.

As an example consider the problem of determining the ball diameter in a roller-ball bearing. Suppose we find the target for the diameter to maximize the quality of the bearing. Note that here quality is defined in terms of loss to society as in Taguchi (1986) (see also Joseph (2004)). If we can manufacture bearings with the target ball diameter, then we have the best quality. Even in a hypothetical situation, where we can achieve this with zero variation, the reliability of the bearing can be poor. This is because during usage the ball will wear out, thereby deviating from the ideal target leading to inferior performance. It is intuitively clear that if we shift the target for the ball diameter at the manufacturing stage to a value above the ideal value, then the reliability can be improved.

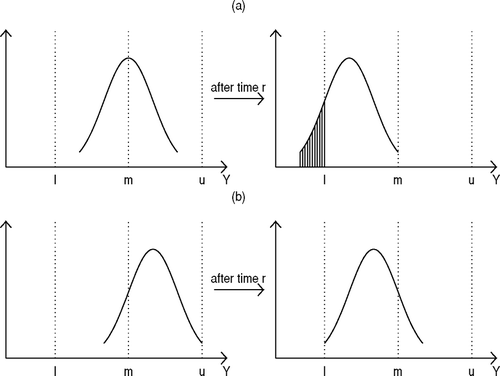
The idea is pictorially depicted in Fig. 1. Here m denotes the ideal value of the characteristic that maximizes the quality, and l and u denote the lower and upper specification limits for the characteristic beyond which the product is considered as failed. The figure shows two situations. In Fig. 1(a), the products are manufactured aiming at the target m, whereas in Fig. 1(b), the manufacturing target is above m. It can be seen that after time r, the second situation produces a smaller proportion of products below l. Thus, even though the quality is relatively poor at the beginning, over time the second process has a much better performance than the first process in terms of the proportion failed.

Fig. 1 Effect of shifting manufacturing target: (a) without shift; and (b) with shift.

It is clear from the example that the target for a characteristic should be chosen based on both quality and reliability. This can be achieved by extending the concept of quality loss to include reliability. To achieve this, we can define the total loss by integrating the quality loss over time. Then we can determine the manufacturing target by minimizing the total loss. This is what we propose to do in this article. Taguchi (1993, p. 427) has proposed some methods for determining tolerances for deteriorating characteristics based on integrated loss functions, but has not considered the possibility of shifting the manufacturing target (see also Creveling (1997, pp. 241–244)).

The problem of determining the optimal target for the degrading characteristics resembles another problem studied in manufacturing and process control. In machining processes, the machined dimension can change over time due to tool wear; in chemical processes, concentration can decrease over time due to the depletion of the chemical, and so on. In such cases the characteristic is set above or below the target depending on whether the characteristic is decreasing or increasing over time (see Drezner and Wesolowsky (1989), Jeang and Yang (1992), Makis (1996), Pakkala and Rahim (1999) and Joseph (2001)). Our problem formulation differs from theirs in many aspects and is explained in the next section.

2. Problem formulation

Consider a product characteristic Y _t that degrades over time t. Let m be the value of the characteristic that minimizes the quality loss and let T be the manufacturing target for the characteristic. As discussed in the Introduction, T should be less than m if Y _t increases over time and more than m if Y _t decreases over time. The following Brownian motion model is widely used for modeling a degradation characteristic (Doksum and Hoyland, 1992; Whitmore, 1995; Joseph and Yu, 2006):

where B _t is a standard Brownian motion, ε∼ N(0,σ² _ε), and β has some distribution with mean β and variance σ_β ². The model assumes the mean degradation path to be linear, which may not be true for some product characteristics. However, this assumption significantly simplifies the problem. If the path is non-linear, then we assume that there exists a transformation, so that the mean of the transformed characteristic is approximately linear. We have used a random degradation rate β, because the rate can vary between units. The variations introduced during the usage of the product is captured by the Brownian motion B _t (see Joseph and Yu (2006)). The error term ε represents variations in the product characteristic at the manufacturing stage, because at t = 0, Y ₀ = T + ε.

The performance of the product at any time t can be evaluated using a quality loss function. The choice of loss function depends on the type of characteristic: smaller the better, larger the better, or Nominal the Best (NTB). In this article, we only consider the case of NTB characteristics. The quadratic loss function for an NTB characteristic is given by (Taguchi, 1986):

where K is a cost coefficient that is used for converting the squared deviations into dollar amounts per unit time. For example, suppose the target for a product dimension is m = 100 centimeters and a loss of $180 is incurred if a product with dimension 106 centimeters is used for a year. Then, K = 180/6² = 5 with units of dollars per squared centimeter per year.

The foregoing loss can be integrated over the usage period of the product to obtain the total quality loss. Many products have a periodic replacement policy. Let r be the replacement period, which means that the product will be replaced after every r units of time. In some cases, the product may fail before time r and has to be replaced or repaired immediately. Let τ be the failure time of the product. Then the total quality loss is given by

where r ∧ τ is used to denote the minimum of the two values. Let d be the down time due to the failure or the replacement time and let C be the cost of replacement/repair. C should actually be an increasing function of d, but by assuming d to be much smaller than r we take it as a constant. The total loss is the sum of the quality loss and C which is incurred in a time r∧τ+d. Thus, the average loss per unit time is given by

Our objective is to find T and r that minimize AL(T,r).

Assume that the product meets its intended function only when Y _t is within the specification limits [l,u]. Thus, the failure time can be defined as the time at which Y _t is below l or above u. For simplicity, assume that the degradation characteristic increases monotonically with time t. Then model (1) approximately satisfies this assumption if the degradation rate is larger than σ. We have P(Y ₀ < l) = Φ((l−T)/σ_ε), where Φ denotes the standard normal distribution function. Noting that τ = 0 when Y ₀ < l, we can simplify Equation (3) to

where φ is the standard normal density function and AL ₊(T,r) is given by

Here the expectation is taken over the distribution specified by model (1) but with ε truncated to {ε > l−T}. Note that, because we only need to consider the cases with T < (l+u)/2, the probability of Y ₀ > u is negligibly small and thus truncating ε to {ε < u−T} does not help simplify the objective function.

Before explaining how to perform optimization, we would like to point out the differences between our problem formulation and that of the optimal process control problem. First, model (1) is different from the models used in process control due to the random degradation rate and Brownian motion term. Second, the objective function in Equation (3) is different from that used in the process control literature (Jeang and Yang, 1992; Pakkala and Rahim, 1999; Joseph, 2001):

A similar objective function is also used in the literature on maintenance policies (see Chen and Jin (2006)). The objective function that we have proposed is more realistic to the present problem and is more challenging to solve. Interestingly our formulation can be applied to a slightly different control problem. If the quality characteristic is measured on-line, then the adjustment can be made when Y _t reaches u, which makes the replacement cycle random similar to our case.

3. Optimization

Because τ is random, the expectation in Equation (4) cannot be taken inside the integral and thus the objective function cannot be simplified. This makes the optimization difficult. Here we propose a simple algorithm using stochastic optimization methods.

The problem can be solved using the Sample Average Approximation method (SAA) (see, e.g., Ruszczynski and Shapiro (2003)). To do this, generate N Monte Carlo samples. Suppose that N _T of the samples satisfy the condition ε > l−T. Then approximate Equation (4) by the sample average:

Thus, the expected loss can be approximated by

This can be minimized with respect to T and r. For T > l, we have:

Hence, when N is large, the solution will be close to the solution of the original problem.

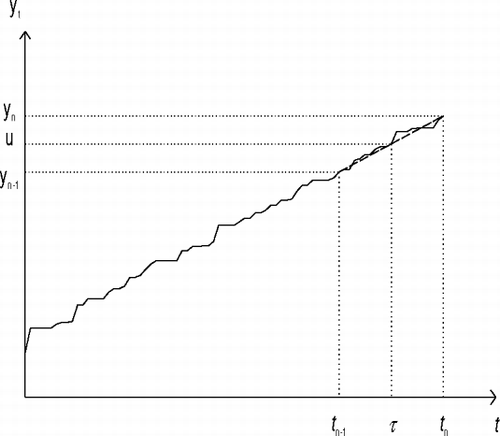
The minimization of Equation (6) is still complicated; here we propose a simple algorithm. First we explain the details of the Monte Carlo simulations and the evaluation of AL ₊ (T,r) in Equation (5). Choose some time points with equally spaced intervals as t _j = jh for j = 0,1,2,…. Generate y _ij by

where (B _i1, B _i2,…) is drawn from N (0, Σ) with Σ = (σ _st ) and σ _st = hmin (s,t); β _i is sampled independently from N (β,σ² _β); and ε _i is sampled independently from N(0,σ² _ε). Note that sampling from N(0,Σ) can be done by multiplying a sample from a standard normal distribution by the square root of Σ . Recall that for each T, we only use the samples with ε _i > l−T.

The next step is to find the failure time. Because Y ₀ > l and Y _t is increasing, an approximate estimate of the failure time from the simulated data is given by

As can be seen in Fig. 2, this is an overestimate of the failure time. Interpolating with the time point t _{n i −1}, we can obtain a better estimate. We obtain:

provided y _{i,n i} > y _{i,n i −1}.

Fig. 2 The estimation of the failure time.

Suppose that r∧τ _i = τ _i . Let I _i = ∫₀ ^{τ _i} L(Y _i,t )dt. For the interval [t _j ,t _j+1], j = 0, …,n _i −2, the integral can be approximated by

and for the interval [t _{n i −1},τ _i ], the integral can be approximated by

Thus, I _i can be approximated by

When r ∧τ _i = r, the integral can be computed in the same way with some minor modifications. First, t _{n i} in Equation (7) should be defined as

The integrals over the interval [t _j ,t _j+1], j = 0, …,n _i −2, are approximated as before. However, for the interval [t _{n i −1},r], the integral is approximated by

where

Then I _i is given by

Thus, we obtain:

and

This is a function of T and r and can be minimized using a standard optimization package. We note that the Monte Carlo simulations are done only once, which makes the SAA algorithm run fast. Most optimization algorithms require a starting point. A good starting point for the above problem can be obtained as follows.

Consider the following modified objective function:

where λ is a constant (not random). This expression can be simplified. From the Brownian motion model in Equation (1), we have:

and

Thus, using the quadratic loss function in Equation (2), we obtain:

Let Δ = T−m. Then from Equation (9) and assuming λ ≫ d, we obtain:

Differentiating AL(T,lambda;) with respect to T and lambda;, and equating to zero, we obtain the following two equations:

and

Substituting Equation (10) in Equation (11), we obtain

This cubic polynomial can be easily solved to find the optimal value of λ. In most practical cases, the first term dominates the second term and thus an approximate solution is given by

We can see that decreases with: (i) decrease in the replacement cost; (ii) increase in the quality loss coefficient; and (iii) increase in the mean and variability of the degradation rate. It is also easy to see that the actual solution to Equation (12) decreases with increase in σ². These results agree with intuition. The optimal solution can be substituted into Equation (10) to obtain the optimal solution of Δ. We can see that it is half of the change in the mean value of the characteristic during the replacement cycle, which is expected because of the symmetric loss function. The optimal manufacturing target is then given as = m− /2.

We can use and as starting values of r and T in the optimization procedure. In fact, it is possible to obtain better starting values as shown below. The original objective function contains the term Φ((l−T)/σ_ε)C/d, which can be large if T is close to or below l. To ensure the probability of this to be small (say, less than 2.5%), we let T > l+2σ_ε. Thus, we take the starting value of T to be

If T ⁽⁰⁾ = l+2σ_ε, then we reduce r by (l+2σ_ε−). Thus, take the starting value of r to be

We also note that in some special cases the optimization can be greatly simplified. If we know that we are going to do a periodic replacement, then τ from the objective function in Equation (3) can be removed and can be easily optimized as done for Equation (9). Similarly if we know that we are going to replace the product only after it fails, then r from Equation (3) can be removed and thus Equation (8) needs to be optimized only with respect to T. These cases arise quite naturally in practical applications. For example, we may wish to replace the brake pad in an automobile periodically, because if it fails, it can damage the disk brake rotor and other components of the braking system which can be very costly, whereas in the case of a vacuum cleaner, we may wish to replace the belt only when it breaks. These two cases arise when the ratio of the cost of replacement to the cost of quality (C/K) is low or high. They can be identified using the solutions to the modified problem in Equation (9). After time , the mean and variance of the characteristic are and σ² _β ²+σ² +σ² _ε respectively. Thus, if

then with high probability (≈97.5%) the product will be replaced before it fails. Similarly, if

then with high probability the product will be replaced only after it fails.

4. An example

Consider an example adapted from Taguchi et al. (2005, pp. 208–210) with some minor modifications. The mean wear rate per year (), the standard deviation of random error (σ_ε) and the price of three materials (C) are given in Table 1. The objective is to select the material and its manufacturing target to maximize both quality and reliability. It is given that if the dimension changes by 6%, there will be a problem in the market, resulting in a loss of $180. Thus, we have l = −6, u = 6 and K = 180/6² = 5.

Table 1 Material characteristics and optimal solutions

				With shift			Without shift
Material	(%)	σε(%)	C($)	T*	r*	AL*	T	r*	AL*
1	0.15	1.20	36	−0.931	12.42	11.535	0	7.82	14.079
2	0.06	0.45	70	−0.857	28.57	4.685	0	18.00	6.842
3	0.05	0.15	126	−0.981	39.25	4.926	0	24.72	7.753

First assume that σ = σ_β = 0 and d = 0.01. We chose h = 1 and sampled N = 1500 values of ε _i fromN(0,σ² _ε). We implemented the optimization using the nlmin function in S-plus. Note that the random values are generated only once and used in every iteration of the optimization algorithm. This reduces the total time needed for optimization.

The optimal solutions (T*, r*) are given in Table 1. We can see that material 2 is the best in terms of minimizing the average loss. For this material, the manufacturing target is shifted by −0.857% and the product is replaced every 28.6 years. In all the three cases, Equation (13) is satisfied and thus the product is replaced periodically before it fails. For comparison, we also computed the optimal solutions if no shift were applied at the manufacturing stage. The results are again given in Table 1. We can see that the average loss is much higher than that with shift. Note that shifting the manufacturing target does not cause any additional expense. This clearly shows the advantage of the proposed strategy.

Now we study the effect of σ and σ_β. Note that in real applications, σ and σ_β can be estimated from degradation data (Joseph and Yu, 2006). Table 2 shows the results for material 2 with different values of σ and σ_β. We can see that the average loss increases with increase in the two values. However, the effect of σ is negligibly small and thus model (1) could be simplified by ignoring the Brownian motion term. To see the effect of C/K, we increased it from the current value of 70/5 = 14. The results are given in Table 3 for the case σ_β = σ = 0 (for calculating AL*, we took K = 5). Note that when C/K = 10 000, the condition in Equation (14) is satisfied and thus a product is replaced only after it fails. This is expected because when the replacement cost is high compared to the quality loss, it is better to use the product as long as possible.

Table 2 Effect of σ and σ_β (material 2)

σ	σβ	T*	r*	AL*
0.00	0.00	−0.857	28.57	4.685
0.00	0.01	−0.828	27.58	4.817
0.01	0.00	−0.856	28.54	4.693
0.01	0.01	−0.827	27.56	4.824

Table 3 Effect of C/K (material 2)

C/K	T*	r*	AL*
14	−0.857	28.57	4.685
100	−1.651	55.03	14.638
1000	−3.557	118.56	64.265
10000	−3.800	—	356.055

5. Conclusions

The manufacturing target for a quality characteristic is usually determined as the value that minimizes the quality loss. However, when the characteristic is subjected to degradation, it is better to shift the manufacturing target depending on the direction of degradation. This approach increases the reliability of the product at the expense of some quality at the initial stages of its life cycle. The optimal shift is determined by minimizing the integrated quality loss over the product's life cycle.

We have used a quadratic function for the quality loss, which may not be appropriate for all cases. For example, a roller-ball bearing may have more serious quality problems when the diameter is above target than when the diameter is below target. In such cases, asymmetric loss functions should be used (see, e.g., Taguchi (1986) and Joseph (2004)). A main difficulty in the practical implementation of the approach is in obtaining the cost coefficients C and K. Therefore, it is a good idea to perform a sensitivity analysis using the ratio C/K and make a cautious decision based on engineering judgments.

Biographies

V. Roshan Joseph is an Assistant Professor in the School of Industrial and Systems Engineering at the Georgia Institute of Technology. He received his Ph.D. degree in Statistics from the University of Michigan, Ann Arbor in 2002. His research interests are in quality engineering and statistics. He is a recipient of a CAREER Award from the National Science Foundation in 2005 and the Jack Youden Prize from the American Society for Quality in 2005.

I-Tang Yu is an Assistant Professor in the Department of Statistics at Tunghai University, Taiwan, ROC. He received his Ph.D. and M.S. degrees in Statistics from the National Chengchi University, Taiwan. His research interests focus on reliability issues.

Acknowledgements

The research of Joseph was supported by the US National Science Foundation grant DMI-0448774 and the research of Yu was supported by the National Science Council of the Republic of China.