Holistic reliability analysis of weighted voting systems from a multi-state perspective

Abstract

The computation of the reliability of weighted voting systems is an important problem in reliability theory due to its potential application in security, target identification, safety and monitoring areas. Voting systems are used in a wide variety of applications where an acceptance or rejection decision has to be made about a binary proposition presented to the system. For these systems, it is of interest to obtain the probability so that based on the vote of decision-making units, the system aggregates these votes into the right decision when presented with such a proposition. This paper presents a holistic work on weighted voting system reliability by presenting modeling, computation, estimation and optimization techniques. The modeling part takes advantage of the structure of weighted voting systems to present a model of its reliability as a multi-state system. Next, based on the multi-state view of the system, an exact computational approach based on multi-state minimal cut and path vectors is introduced. The paper then acknowledges the computational complexity of the problem and provides a Monte Carlo simulation approach that estimates system reliability accurately and in an efficient computational time. Finally, an optimization heuristic that generates quasi-optimal solutions is presented that is able to solve the problem of maximizing the reliability of a weighted voting system based on a specified number of decision-making units with known reliability characteristics.

Keywords:

• Multi-state reliability
• voting systems
• simulation
• optimization

1. Introduction

Decision-making systems have recently become an area of intense activity because of their potential for application to areas such as security, target identification, and safety and monitoring (Kam et al., 1991; Viswanathan and Varshney, 1997; Nordmann and Pham, 1999; Levitin, 2002a, 2002b). Nordmann and Pham (1999) provide an example concerning target identification and pattern recognition in which an object needs to be identified based on some of its attributes. Similarly, for safety, security and monitoring different units may be used to observe some proposition and make a decision about its criticality. In summary, Levitin (2002a, 2002b) notes application to areas as diverse as data handling and multi-channel signal processing.

The problem of obtaining the reliability of decision-making systems has received considerable attention during recent years. Within this area of research, one of the systems analyzed is known as the Weighted Voting System (WVS) (Nordmann and Pham, 1999; Levitin and Lisnianski, 2001; Levitin, 2002a, 2002b, 2005). A WVS is comprised of a specified number of units that independently exercise a decision (vote) about a proposition presented to the system. For each unit, the outcome of a decision can be one of three different choices: (i) the unit accepts the proposition; (ii) the unit rejects the proposition; or (iii) the unit abstains from exercising a decision. Moreover, for each vote a unit exercises, a weight is assigned depending on the choice made. Once all the units have exercised their votes, the associated weights are aggregated based on a known function of the WVS so that a final decision is made.

For a WVS, reliability can be defined as the probability that when the system is given a proposition, it makes the right decision. As discussed, the decision of the WVS is based on the aggregated votes of the units. Each unit has reliability characteristics that represent their ability to exercise the right vote when a given proposition is presented. It is relevant to mention that Kam et al. (1991) and Viswanathan and Varshney (1997) have studied a similar problem but from the perspective of data fusion. The notation used in the remainder of this paper is presented in Table 1.

Table 1 Notation

Variable	Definition
j	The jth decision-making unit, j = 1,…,n
I	Binary proposition for WVS
d j (I)	Decision from the jth decision-making unit
D(I)	Decision from the WVS
w j ^0	Weight associated with d j (I) = 0
w j ^1	Weight associated with d j (I) = 1
τ	WVS threshold
R	WVS reliability
q im ^j	P (d j (I) = m|I = i), i = 0,1; m = 0, x, 1
Q im	P (D (I) = m|I = i)
p i	P (D(I) = I)
x j	Current state of the jth decision-making unit
x	System state vector, x = (x 1, x 2,…,x n )
q i ^j	Probability vector of the jth decision-making unit associated with I = i
d i	Demand for case I = i.
b j	State vector for the jth decision-making unit
b jm	The mth state of the jth decision-making unit
ϕ	WVS structure function
Q i	Failure counter
Γ	Simulation runs
G	Index for optimization heuristic

Based on the definition of WVS reliability, Levitin (2002b) has modeled a WVS by considering that the same binary proposition I is presented to each of the units of the system. The value of the proposition is either zero if the proposition should be rejected or one if the proposition should be accepted. The units independently exercise their vote, d _j (I), which can then be translated into the following errors.

1.	Reject a proposition that should be accepted (i.e., d j (1) = 0).
2.	Accept a proposition that should be rejected (i.e., d j (0) = 1).
3.	Abstain from exercising a vote (i.e., d j (I) = x).

Historical data on units that incur these types of error can be used to define their reliability characteristics. That is, q ₁₀ ^j , q ₀₁ ^j , and q _1x ^j and q _0x ^j define respectively the probability that unit j incurs the errors defined in 1, 2 and 3. Once all units have exercised their votes, the system decision is represented by a binary function, D(I). This function aggregates the unit votes in terms of weights and as defined by Levitin (2002b) generates an outcome as follows:

The weights w _j ⁰ and w _j ¹ in Equation (1), represent the importance given to the individual vote exercised by decision unit j. For example, Nordmann and Pham (1999), discuss that in target identification, some aspects of the target play a key role in the identification while others do not. Thus, a higher weight should be given to the detection of those key aspects. Moreover, in Equation (1) the threshold value, τ, determines what fraction of the weight given to the aggregate unit votes should be taken into account for making an overall system decision. It is worth mentioning that if there exists a non-zero probability that the system may abstain from voting (i.e., the system does not make a decision) it may be the result of one of two possible cases.

1.	Each and every voting unit does not exercise its vote. This case corresponds to situations where a time constraint for voting is imposed on the voting unit. That is, if the voting unit does not make a decision within a given time frame then it is assumed that no vote is obtained from that particular unit.
2.	The sum of the weights associated with the vote of the voting units equals zero.

Thus, the reliability of the WVS is a function of the unit weights and the threshold value and can be obtained as

Based on the reliability model presented in Equations (1) and (2), exact computational techniques for WVS reliability have been proposed. They can be classified into one of the following two categories: state enumeration techniques (Nordmann and Pham, 1999) and Universal Generating Function (UGF)-based techniques (Levitin and Lisnianski, 2001; Levitin, 2002a, 2002b, 2005). Although these studies have significantly contributed to the development of methods for WVS reliability analysis they have some drawbacks. The enumeration technique presented by Nordmann and Pham (1999) requires the weights to be integers in order to reduce the computation time. For a large WVS, both of these techniques require an extensive computational time because of the need to enumerate an exponential number of combinations of potential unit votes. Similarly, none of these methods provide insights into how component interactions trigger system failure or system success. In summary, current WVS computational techniques have to be complemented with computational procedures that better represent and account for these types of systems and component behavior.

The aim of this paper is to address this problem. In summary, the paper presents a holistic study on the reliability analysis of a WVS by addressing three related areas: modeling, computation and optimization. For modeling purposes, the WVS is transformed into a capacitated multi-state system with multi-state components (Ramirez-Marquez and Coit, 2005a) under the rationale that the original system can be viewed as a parallel configuration of the units where each unit can have three states dictated by the weights and the threshold value. It should be noted that Lisnianski and Levitin (2003) and Li and Zuo (2008) have proposed a multi-state representation of WVS via the UGF and a multi-stated weighted k-out-of-n system, respectively.

The transformation proposed in this paper allows for the implementation of exact and approximation computational methods based on multi-state reliability theory (Ramirez-Marquez and Coit, 2005b; Ramirez-Marquez, Coit and Tortorella, 2006; Ramirez-Marquez, Rocco, Assefa, Coit and Tortorella, 2006). That is, the paper provides a technique to compute the multi-state minimal path and cut vectors (the equivalent of minimal cut and paths set in the binary case) for the WVS. These vectors are important since they can provide critical information about the interactions of the units with respect to the system reliability (Ramirez-Marquez, Rocco, Assefa, Coit and Tortorella, 2006).

The paper also discusses that for a large WVS, the exact computation of reliability will not be efficient due to the enumerative nature of the approaches currently in existence. Thus, the paper introduces a Monte Carlo (MC) simulation approach that takes into account the parallel structure of the newly transformed WVS to generate an estimate of WVS reliability. These techniques are then implemented into a numerical search method to solve the reliability optimization problem for the WVS presented by Levitin and Lisnianski (2001) and Levitin (2002b).

•	A vector y is said to be less than x, or y < x, iff for every y i (the i th entry of vector y) and x i (the ith entry of vector x), y i ≤ x i and for some y k (the kth entry of vector y), and x k (the kth entry of vector x), y k < x k .
•	A vector y is said to be greater than x, or y > x, iff for every y i (the ith entry of vector y) and x i (the ith entry of vector x) y i ≥ x i and for some y k (the kth entry of vector y) and x k (the kth entry of vector x), y k > x k .
•	A vector y is said to be equal to x, or y = x, iff for every y i (the ith entry of vector y) and x i (the ith entry of vector x), y i = x i .

The remainder of the paper is organized as follows. Section 2 presents the transformation of WVS into a multi-state system. Section 3 describes a technique to obtain WVS reliability based on Multi-state Minimal Cut Vector (MMCV) and Multi-state Minimal Path Vector (MMPV) approaches. Section 4 presents a simulation approach to estimate WVS reliability. This section also presents results on the accuracy and efficiency of the approach. Section 5 presents the heuristic for the optimization of WVS reliability along with examples for comparison with current approaches. Finally, Section 6 presents conclusions.

2. Multi-state reliability modeling, computation and simulation of WVS

A system whose components are operating in a degraded state but is still able to provide an acceptable level of service is known as a multi-state system (Ramirez-Marquez, Coit and Tortorella, 2006). For these systems, the theory of multi-state system reliability evaluation can offer modeling and computational procedures that better represent and account for the probability of system functioning.

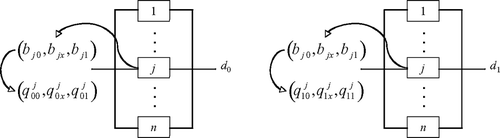
The WVS described in the introductory section can be transformed and modeled as a Multi-State system with Multi-state Components (MSMC) as follows. Let j = 1,…, n represent the jth decision-making unit of a WVS. The set of decision-making units constitutes a parallel system configuration of n components. The random current state (capacity) of decision-making unit j is represented by x _j that takes values from b _j . The vector b _j represents the state space vector of decision-making unit j. Therefore, based on the possible votes that unit j can exercise, the weight associated with such a vote and the WVS value τ, x _j can take values b _j0 = − τ w _j ⁰, b _jx = 0, b _j1 = (1 − τ)w _j ¹, where b _jm ∈ ℜ. The system state vector x = (x ₁, x ₂, …, x _n ) denotes the current state of all the decision-making units of the system. The function ϕ : ℜ ⁿ → ℜ is the multi-state structure function. It maps the system state vector x, into a system state. That is, ϕ (x) is the available system capacity under system state vector x.

Based on this description, a WVS can be modeled as a MSMC where demand varies (Ramirez-Marquez and Coit, 2004). For capacitated multi-state systems, the Loss Of Load Probability (LOLP) index is commonly used as a system reliability metric (Lisnianski et al., 1996). This index is understood as the probability that the system cannot supply a given demand load for an operating period that is divided into k operating intervals. The wth entry of vectors d = (d ₁,…,d _k ) and T = (T ₁,…,T _k ) defines the duration T _w and demand level d _w during the wth interval. Lisnianski et al. (1996) define the LOLP as

In order to model the WVS as a multi-state system, two cases for system demand, d _i , must be considered, namely d ₀ (which implies that d < 0) and d ₁(which implies that d > 0). Similarly, two time intervals T ₀ = p ₀ and T ₁ = p ₁ must be considered. Finally, the vectors q ₀ ^j = (q ₀₀ ^j , q _0x ^j , q ₀₁ ^j ) and q ₁ ^j = (q ₁₀ ^j , q _1x ^j , q ₁₁ ^j ) represent the probability associated with each of the values taken by x _j for the cases d ₀ and d ₁, respectively. That is, q _im ^j = P(x _j = b _jm |d _i ).

For a WVS, multi-state reliability can be understood as the probability that for each time interval T _i , the system can satisfy the conditions set by d _i (for i = 0, 1) through the multi-state components. Thus:

It is important to note that when i = 0, the probability of the WVS functioning, P(ϕ (x) < 0), is equivalent to Q ₀₀, the first term in Equation (2). Similarly, when i = 1, the probability of the WVS functioning, P(ϕ (x) > 0), is equivalent to Q ₁₁, the second term in Equation (2).

A graphical description of the multi-state model for a WVS is presented in Fig. 1 for both d ₀ and d ₁.

Fig. 1 Multi-state parallel system model for a WVS.

3. Exact method for reliability computation of a WVS

For each of the cases defined by d _i , success (failure) of a WVS can be completely characterized by the set containing all MMCVs and MMPVs. For a WVS, the definitions of the MMCV and MMPV can be given as

•	For the case d 0 (ϕ (x) < 0). A vector x is said to be a MMPV if ϕ (x) < 0 and for every other y > x, ϕ (y) ≥ 0. A vector x is said to be a MMCV if ϕ (x) > 0 and for every other y < x, ϕ (y) ≤ 0.
•	For the case d 1 (ϕ (x) > 0). A vector x is said to be a MMPV if ϕ (x) > 0 and for every other y < x, ϕ (y) ≤ 0. A vector x is said to be a MMCV if ϕ (x) < 0 and for every other y > x, ϕ (y) ≥ 0.

To clarify these concepts, consider the WVS depicted in Fig. 1, under condition d ₁ (the discussion is equivalent for the case d ₀). The system has n voting units and under condition d ₁ for the system to be considered functioning, the system capacity must be strictly greater than zero (i.e., D(I) = 1|I = 1). That is, for the system to satisfy condition d ₁, the sum of the weights associated with the units exercising a vote must be strictly positive (i.e., ϕ (x) = ∑ _{j = 1} ⁿ x _j > 0). In this respect, the problem of obtaining the MMPV reduces to: (i) enumerating the vectors x that satisfy condition d ₁; and (ii) from these vectors identify the ones that comply with the definition of the MMPV.

On the other hand, under condition d ₁, for the system to be considered failed, system capacity must be less than zero (i.e., [D(I) = 0 | I = 1] or [D(I) = x | I = 1]). That is, for the system not to satisfy condition d ₁, the sum of the weights associated with the units exercising a vote must be non-positive (i.e., ϕ (x) = ∑ _{j = 1} ⁿ x _j ≤ 0). In this respect, the problem of obtaining the MMCV reduces to: (i) enumerating the vectors x that do not satisfy condition d ₁; and (ii) from these vectors identifying the ones that comply with the definition of the MMCV.

It should be mentioned that computing WVS reliability by obtaining the MMPV/MMCV via enumeration is not more or less efficient than via the UGF method. However, techniques such as those described in Rocco and Muselli (2005) and Ramirez-Marquez and Assefa (2006) can be used to obtain these vectors without resorting to complete enumeration. In summary, the purpose of this part of the manuscript is not to detract or discard the UGF approach (a very valuable approach) but to provide an alternative technique that extends the state of the art and allows a reliability engineer to choose from a different array of computational tools for this problem.

3.1. Reliability computation

Based on the obtained vectors, the reliability of a WVS can be computed through the inclusion/exclusion formula. For each d _i , R _{d i} can be obtained with the following modification of the inclusion/exclusion formula:

where L _i is the number of MMCV and MMCV _li is the lth MMCV for case d _i .

The difference in the structure of the formula is because for the case where the condition d ₀ must be satisfied, a failure of the system is guaranteed when ϕ (x) ≥ 0. For the case where the condition d ₁ must be satisfied, a failure of the system is guaranteed when ϕ (x) ≤ 0. Thus, the structure of the inclusion/exclusion formula changes for each of the cases considered (i.e., d ₁ and d ₀).

To compute each of the terms in the formulas:

The remaining terms in the formula are obtained as follows:

where x _j , z _j , y _{j 0} , v _{j 1} , w _{j 0} and u _{j 1} correspond to the jth entry of vectors x, z, MMCV _{l 0} , MMCV _{l 1} , MMCV _{h 0} and MMCV _{h 1} , respectively.

Equivalently when the MMPVs, are obtained:

where T _i is the number of MMPV and MMPV _li is the lth MMPV for case d _i .

Similar to the case of MMCV, the difference in the structure of the formula is because for the case where the condition d ₀ must be satisfied, the system is considered working if ϕ (x) < 0. For the case where the condition d ₁ must be satisfied, the system is considered working if ϕ (x) > 0. Thus, the structure of the inclusion/exclusion formula changes for each of the cases considered (i.e., d ₁ and d ₀).

To compute each of the terms in the formulas:

The remaining terms in the formula are obtained as follows:

where z _j , x _j , y _{j 0} , w _{j 0} , v _{j 1} and u _{j 1} correspond to the jth entry of vectors z, x, MMPV _{l 0} , MMPV _{h 0} , MMPV _{l 1} and MMPV _{h 1} , respectively.

3.2. Example

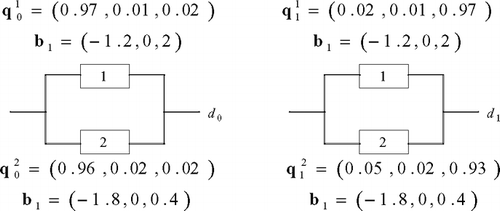
The WVS presented by Levitin (2002b) can be viewed as a security detection system where a visual detector and a heat radiation detector provide the system with their individual decisions. These individual decisions have to be merged into a single decision about some security-related proposition presented to the system. Data regarding the reliability characteristics of the detectors along with their individual unit weights are given in Table 2. A threshold of τ = 0.6 and p ₀ = p ₁ = 0.5 have been assumed to obtain system reliability. Figure 2 provides a graphical representation of the security detection system from a multi-state perspective.

Fig. 2 Transformation of WVS security system into a multi-state system.

Table 2 Data for security detection system

Detector	q 10 ^j	q 1x ^j	q 11 ^j	q 00 ^j	q 0x ^j	q 01 ^j	w j ^1	w j ^0
^1Visual	0.02	0.01	0.97	0.97	0.01	0.02	5	2
^2Heat	0.05	0.02	0.93	0.96	0.02	0.02	1	3

The transformation of the WVS into a multi-state system allows for the computation of its reliability. Table 3 illustrates the cut vectors associated with each of the cases of d _i .

Table 3 Cut vectors for WVS under case d _i

Case d 0				Case d 1
x	x 1	x 2	ϕ (x)	X	x 1	x 2	ϕ (x)
1	2	−1.8	0.2	1	−1.2	0.4	−0.8
2	0	0	0	2	0	0	0
3	2	0	2	3	−1.2	0	−1.2
4	0	0.4	0.4	4	0	−1.8	−1.8
5	2	0.4	2.4	5	−1.2	−1.8	−3

For both cases, the corresponding first and second vectors give the MMCV associated with the WVS. The computation of the reliability based on these vectors yields R = 0.979 45 where:

This is the first time the MMCV and MMPV for WVS are obtained. Although the previous approaches (Nordmann and Pham (1999), Levitin and Lisnianski (2001) and Levitin (2002a, 2002b, 2005)), can be used to obtain the same reliability value they cannot account for the MMCV and MMPV which can be helpful in developing: (i) importance measures for reliability prioritization purposes (Ramirez-Marquez, Rocco, Assefa, Coit and Tortorella, 2006); and (ii) confidence bounds around the WVS reliability estimate (Ramirez-Marquez and Jiang, 2006). These two advantages will be investigated as part of future research work.

4. Simulation of WVS reliability

Once the MMCV or MMPV for the transformed WVS have been generated, the computation of the exact reliability based on the inclusion/exclusion formula can be avoided by applying the simulation approach proposed by Ramirez-Marquez and Coit (2005a). However, the number of computations required to obtain the MMCV in a WVS is a function, g, of both n the number of decision-making units and c _i the number of vectors that comply with the case dictated by d _i . That is, g(n,c ₀,c ₁) = 3 ⁿ + [(c ₀ (c ₀ + 1))/2] + [(c ₁ (c ₁ + 1))/2] and thus, g(n, c ₀, c ₁) ∈ O(3 ⁿ ) (the complexity analysis for the computation of MMPV is equivalent and thus not presented). Since the number of computations to obtain the MMCV increases exponentially with the number of units, an accurate and efficient technique for the approximation of WVS reliability becomes relevant.

4.1. Description of the MC simulation approach

The MC simulation approach proposed in this paper allows for fast and accurate estimation of WVS reliability without resorting to enumerative techniques or computation of MMCV or MMPV. The approach can be summarized as follows: for each case d _i , a specified number, Γ, of state vectors x are generated as dictated by: (i) the WVS threshold value τ; (ii) each unit state space vector b _j ; and (iii) the vector q _i ^j . Then, for each vector, the sum of its entries is checked against the condition established by d _i . Whenever one of the vectors does not satisfy the condition, a counter Q _i increases its value by one unit. At the end of the simulation, the reliability of the WVS can be estimated as R = (1 − Q ₀/Γ)p ₀ + (1 − Q ₁/Γ)p ₁.

MC simulation approach

For (i ← 0; i + +; i < 2){γ ← 0; While (γ < Γ) { While (j < n){ Generate a random number r from U(0,1); If (q _i0 ^j > r);{x _j → b _j0}; Else-If ({q _i0 ^j < r ≤ ({q _i0 ^j + q _ix ^j ));{x _j ← b _jx }; Else {x _j → b _j1}; j ← j+1;} If ∑ _{j = 1} ⁿ x _j does not comply with d _i , Q _i ← Q _i +1; Else Q _i ← Q _i ; γ ← γ+1;} = (1 − Q ₀/Γ)p ₀ + (1 − Q ₁/Γ)p ₁

The simulation approach provides an estimate of WVS reliability by computing estimates of _{d 0} = (1 − (Q ₀/Γ)) and _{d 1} = (1 − (Q ₁/Γ)). As described in Ramirez-Marquez and Coit (2005a), when the sample Γ is large, the variance associated with these estimates can be obtained by

To compute the variance associated with the estimate of WVS reliability, define events E and F as: E = {D(I) = 0|I = 0} and F = {D(I) = 1|I = 1}. Notice that events E and F are independent and that _{d 0} = (E) and _{d 1} = (F). Thus, when the sample Γ is large, the variance of the estimate of the reliability of the WVS can be computed as

4.2. Comparison and efficiency

To test the MC simulation approach, four WVSs available in the literature have been analyzed considering two perspectives: computational effort and quality of results. The first two considered systems were taken from Levitin (2002b) and the remaining two from Levitin and Lisnianski (2001) and Levitin (2002a).

For each of these systems, figures of merit are presented to compare the MC simulation against the enumeration techniques available. Table 4 presents data for each of the considered examples. To measure the efficiency of the MC simulation approach, statistics concerning computational usage time were recorded. For each of the examples, Table 5 presents the figures of merit associated with ten repetitions of 1000 000 MC runs using a Pentium M laptop at 1500 MHz and 512 MB of RAM along with the results for each repetition.

Table 4 Data for WVS

Unit	q 10 ^j	q 1x ^j	q 11 ^j	q 00 ^j	q 0x ^j	q 01 ^j	w j ^1	w j ^0
System 1 p 0 = 0.5
1	0.020	0.010	0.970	0.970	0.010	0.020	5.000	2.000
2	0.050	0.020	0.930	0.960	0.020	0.020	1.000	3.000
System 2 p 0 = 0.5
1	0.287	0.025	0.688	0.567	0.209	0.224	0.402	0.372
2	0.219	0.106	0.675	0.680	0.077	0.243	1.796	0.124
3	0.103	0.197	0.700	0.719	0.073	0.208	2.848	0.031
4	0.197	0.014	0.789	0.751	0.249	0.000	0.526	2.693
5	0.133	0.067	0.800	0.628	0.168	0.204	0.557	0.65
System 3 p 0 = 0.5
1	0.150	0.200	0.650	0.900	0.080	0.020	2.486	2.486
2	0.180	0.000	0.820	0.940	0.000	0.060	1.878	1.878
3	0.070	0.050	0.880	0.880	0.050	0.070	2.403	2.403
4	0.120	0.160	0.720	0.760	0.160	0.080	1.685	1.685
5	0.160	0.120	0.720	0.700	0.120	0.180	1.547	1.547
System 4 p 0 = 0.5
1	0.35	0	0.65	0.65	0.35	0	2.759	2.759
2	0.23	0.1	0.67	0.56	0.1	0.34	0.172	0.172
3	0.36	0.06	0.58	0.82	0.07	0.11	3.060	3.060
4	0.07	0	0.93	0.58	0.12	0.3	4.009	4.009

Table 5 Results for WVS reliability simulation

	System 1 (p 0 = 0.5, τ = 0.60, R = 0.9795)			*System 2 (p 0 = 0.5, τ = 0.3, R = 0.7616)			System 3 (p 0 = 0.5, τ = 0.412, R = 0.9816)			System 4 (p 0 = 0.5, τ = 0.58, R = 0.891)
	Q 11 = 1	Q 00 = 0		Q 11 = 1	Q 00 = 0		Q 11 = 1	Q 00 = 0		Q 11 = 1	Q 00 = 0
Mean	0.9793	0.9796	0.9795	0.9806	0.5427	0.7617	0.9819	0.9813	0.9816	0.8345	0.9477	0.8911
MAPE	—	—	0.0001	—	—	0.0003	—	—	0.0001	—	—	0.0001
CPU time	3.5720	1.4150	4.9870	7.7610	5.0670	12.828	7.8810	4.0850	11.966	5.9800	4.3210	—

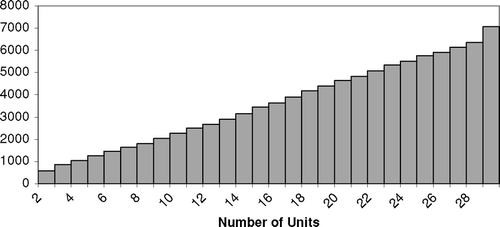
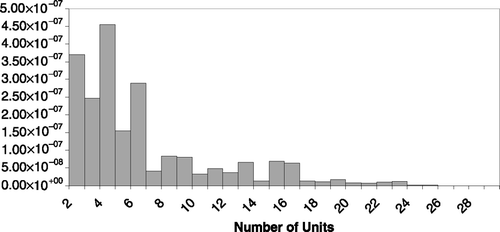
From the statistics presented in Table 5, it is evident that for a WVS, the MC simulation presents a fast reliability estimation alternative when compared to the enumeration approach. The minimum and maximum CPU times per simulation run are 1.4150 and 7.8810 seconds, respectively. It is important to note that these times are associated with the whole run (i.e., ten repetitions of 1000 000 runs). With respect to the quality of results, the accuracy of the MC approach has been compared to the real value of the WVS reliability. Table 5 also illustrates the estimates for Q ₁₁, Q ₀₀ and R. For each of the systems analyzed, the Mean Absolute Percentage Error (MAPE) has been computed; the minimum and maximum MAPE related to this approach equals 0.0001 and 0.0004.

The purpose of including the previous WVS is to illustrate how the MC approach compares against the exact values of reliability obtained via the UGF. For these small WVS the use of MC simulation and UGF techniques would not be considered. For this size of problems, complete enumeration would suffice.

However, for some applications the number of voting units (sensors) that the system may contain could be significantly higher (Kam et al., 1991; Viswanathan and Varshney, 1997) and the proposed MC simulation technique can provide an accurate time-saving alternative to enumerative approaches. To illustrate this point, Fig. 3 and Fig. 4 show how the number of units in the WVS impact: (i) the CPU time (in milliseconds) in the MC simulation; and (ii) the variance of the reliability estimate. The results used to obtain each of these figures were obtained from ten independent repetitions of 100 000 simulation runs from a WVS consisting of two and up to 29 units.

Fig. 3 MC CPU time as a function of number of units in the WVS.

Fig. 4 WVS reliability estimate variance as a function of number of units in the WVS.

5. Heuristic for the optimization of the WVS reliability

The reliability optimization problem for a WVS was initially introduced by Levitin and Lisniaski (2001) and can be described as follows. The reliability of a WVS must be maximized based on a specified number, n, of decision-making units with known reliability characteristics q _im ^j . That is, the weights (w _j ⁰ and w _j ¹) and the threshold value (τ) must be obtained so that the reliability of the WVS is a maximum.

The general mathematical model for the reliability optimization of the WVS problem is presented in model 1. It is important to note that in model 1 the reliability of the WVS is expressed as a function of the vectors w ⁰ = (w ₁ ⁰, …, w _j ⁰, …, w _n ⁰), w ¹ = (w ₁ ¹, …, w _j ¹, …, w _n ¹) and τ, the threshold value. Finally, for some applications the values of the weights may be restricted to have the same values (i.e., w _j ⁰ = w _j ¹). Such a WVS is known as the symmetric case for WVS.

Model 1

subject to

5.1. Description of the heuristic

The rationale behind the WVS reliability optimization heuristic is that the reliability characteristics of the components can be used to obtain the weights associated with vectors w ⁰ and w ¹.

For the symmetric weights problem, the sum of the values of q ₁₀ ^j and q ₀₁ ^j can be viewed as the percentage of decisions wrongly made by decision unit j. Thus, the decision unit with the highest percentage of wrong decisions should be assigned the least weight in the overall decision and this weight should be used as a benchmark to establish the weights of the remaining decision-making units. Mathematically:

That is, the weight assigned to the decision made by unit j is the ratio of the maximum percentage of decisions wrongly made by any of the decision-making units in the WVS to the percentage of decisions wrongly made by unit j.

For the special case where K _j = 0 for some j, the WVS decision should be made solely on the outcome of such unit. Thus, w _j ⁰ = w _j ¹ = ∑ _{l ≠ j} w _l ⁰+ 1 if K _j = 0.

Similarly, for the asymmetric weights problem, the values of q ₁₀ ^j and q ₀₁ ^j can be viewed as the percentage of decisions wrongly made by decision unit j when the proposition was zero and one, respectively. Thus, for each of the propositions, the decision unit with the highest percentage of wrong decisions should be assigned the least weight in the specific decision and this weight should be used as a benchmark for establishing the weights of the remaining decision-making units.

Mathematically:

There are two special cases which occur under the following conditions:

1.	Both q 10 j = 0 and q 01 j = 0, for some j. Then the WVS decision should be made solely on the outcome of such a unit. Mathematically, w j 0 = w j 1 = ∑ l ≠ j w l 0+ w l 1 if q 10 j = 0 and q 01 j = 0.
2.	Either q 10 j = 0 or q 01 j = 0, for some j. Without loss of generality, assume that q 01 j = 0, then w j 1 = ∑ l ≠ j w l 0+ 1

Once the weights are obtained, the reliability of the WVS becomes a function of the threshold value τ. Thus, the problem reduces to finding the value of τ that maximizes R(w ⁰,w ¹,τ). Based on the simulation approach the optimal value of τ can be obtained through a numerical search method. In summary, in Steps 1 and 2, the method generates different values of τ in the interval (a _t , c _t ) as dictated by Δ. Then in Step 3, for each of these τ values, the reliability of the WVS is computed and followed by Step 4 where the interval (a _t , c _t ) is updated based on the optimal value of τ obtained in loop t, this procedure is repeated for a specified number of loops dictated by G. The pseudo-code of the numerical search follows:

	Step 1. Initialize t = 0, N, G, a t = 0, c t = 1, Δ = N − 1, τ = 0, w 0, w 1.
	Step 2. From t = 1 to G do
	Step 3. While l ≤ N. Based on the simulation approach compute:
	Step 4. Obtain: α = max l {R l (w 0, w 1,a t + τ)}

If t ≤ G, go to Step 3.

Else τ*← α.

5.2. Examples

For the different WVSs presented in Table 4 it has been assumed that the decision-making units' weights and the WVS threshold are unknown. The problem is to identify the values of these variables so that the reliability of the WVS is maximized. Table 6 and Table 7 present the values obtained by the heuristic assuming parameter values G = 4 and N = 10 for the four WVSs with data presented in Table 4.

Table 6 Quasi-optimal weights and threshold for symmetric WVS

System
	1	2	3	4
τ	0.4300	0.5270	0.4104	0.464
Q 00	0.9799	0.9553	0.9775	0.8444
Q 11	0.9794	0.9077	0.9837	0.9274
R	0.9796	0.9315	0.9806	0.8859
w	(1.75, 1)	(1, 1.106, 1.643, 2.594, 1.516)	(2, 1.417, 2.429, 1.70, 1)	(1.628, 1, 1.213, 1.541)
CPU (seconds)	1.994	4.940	4.750	4.3200
R GA	0.9796	0.9360	0.9815	0.8910
APE (%)	0.00	0.48	0.09	0.57

Table 7 Quasi-optimal weights and threshold for asymmetric WVS

	System
	1	2	3	4
τ	0.3740	0.552 80	0.5928	0.504
Q 00	0.9796	0.967 89	0.9785	0.8525
Q 11	0.9796	0.921 77	0.9751	0.9328
R	0.9796	0.945 00	0.9768	0.8927
w 1	(1, 1)	(1.085, 1, 1.168, 8.255, 1.191)	(9, 3, 2.571, 2.250, 1)	(8.708, 1, 3.091, 1.133)
w 2	(2.5, 1)	(1, 1.311, 2.786, 1.457, 2.158)	(1.2, 1, 2.571, 1.5, 1.125)	(1.029, 1.565, 1, 5.143)
CPU (seconds)	1.89	5.46	4.67	4.29
R GA	0.979 45	0.954 00	NA	NA
(APE%)	0.02	0.94	NA	NA

As evidenced by these results, the minimum and maximum Absolute Percentage Error (APE) of the optimization technique proposed with respect to the Genetic Algorithm (GA) presented by Levitin and Lisnianski (2001) and Levitin (2002b) equals 0% and 0.94%. These quasi-optimal solutions can be immediately obtained without the need to set up tuning parameters that are problem specific as in GA techniques. Furthermore, as the reliability of the voting units change, the weights associated with their decisions and the threshold value τ of the system can be immediately updated to maintain a pseudo-optimally reliable system.

6. Conclusions and future research

In this paper a holistic approach to WVS reliability has been presented. In summary, the study has presented modeling, computation, estimation and optimization techniques for these types of systems. For the modeling part, the traditional perspective of a WVS was changed by taking advantage of the structure of a WVS and to develop a new model of its reliability as a multi-state system. This multi-state view of the system allows the development of an exact computational approach based on MMCV and MMPV, which is not restricted to integer weights. These vectors are currently being further investigated as part of work focused on developing a confidence interval around the estimate of the reliability of the WVS that will be tied with the impact of component reliability in such an interval.

The paper then acknowledged the computational complexity of enumeration approaches and thus developed a new MC simulation approach that estimates system reliability accurately and in an efficient computational time. Finally, the optimization heuristic developed presented a clear and straightforward method for solving the problem of maximizing the reliability of a WVS based on its reliability characteristics. The heuristic developed weights based on the reliability characteristics of the voting units and a threshold value to maximize WVS reliability. Contrary to GA-based heuristics, the proposed approach is independent of parameter tuning and the generation of good initial solutions to provide near optimal solutions.

Biography

Jose E. Ramirez-Marquez is an Assistant Professor at Stevens Institute of Technology in the School of Systems and Enterprises. His research interests include system reliability and quality assurance, uncertainty modeling, advanced heuristics for system reliability analysis, applied probability and statistical models and applied operations research. He has authored more than 20 articles in leading technical journals and has conducted funded research for both government and commercial organizations on these topics. He obtained his Ph.D. at Rutgers University in Industrial and Systems Engineering and received his B.S. degree in Actuarial Science from the UNAM in Mexico City in 1998. He also holds M.S. degrees in Industrial Engineering and Statistics from Rutgers University. He is a member of IIE, IFORS and INFORMS.

Notes

*Due to a misprint in Levitin (2002b), values for w ⁰ and w ¹ should be interchanged to obtain the results published.