Variability monitoring of multistage manufacturing processes using regression adjustment methods

Abstract

The recent trends in manufacturing toward modularity and flexibility result in complex multistage manufacturing processes that consist of many interrelated workstations. In such processes, it is highly desirable to differentiate between local and propagated variations, and implement process variability monitoring and reduction. In this paper, attention is focused on the properties of a widely used regression-adjustment-based method in the monitoring of variation propagation in multistage manufacturing processes. Particularly, the impacts of measurement errors and regressor selection on the monitoring scheme are investigated, and conclusions which can help guide the use of this method are summarized. Numerical examples are also presented to validate the analysis.

Keywords:

• Measurement errors
• multistage processes
• regression adjustment
• regressor selection
• variation propagation

1. Introduction

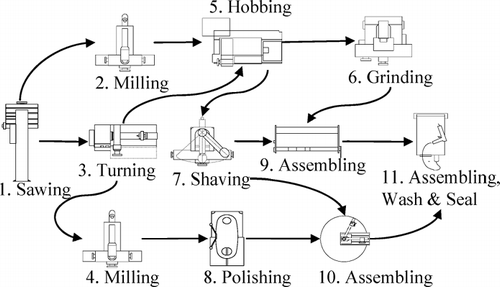
The growing demand for products with both an improved functionality and a shorter time to market in order to be successful in today's fiercely competitive marketplace places an enormous strain on production systems. Manufacturing paradigms such as modular production systems (Rogers and Bottaci, 1997), cellular manufacturing (Hyer and Wemmerlov, 2002) and reconfigurable manufacturing (Koren et al., 1999) have been developed and adopted in recent years and they are able to achieve unprecedented levels of flexibility and responsiveness. As a result, it is increasingly common to find many complex and modularized workstations linked together to create the final product in a manufacturing environment. Figure 1 illustrates a manufacturing system consisting of 11 stations and capable of producing five different types of motor reducers. Because fabrication errors are carried by the product from one station to the next station, the outgoing product quality at a particular station is determined not only by various local disturbances at that station, such as thermal error cutting-force induced error and machine geometric error, but also by the propagated variations from previous stations such as the datum error due to preceding cutting operations. The final product variation is the accumulation of variations from all manufacturing stations.

Fig. 1 A multistage process for motor reducers.

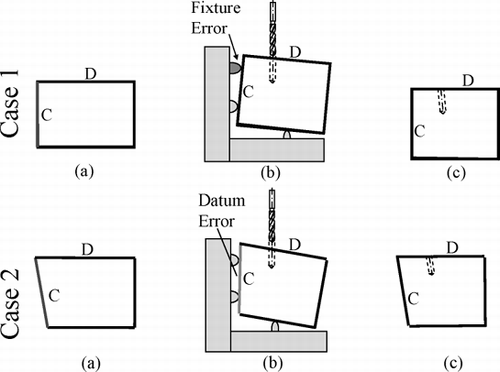
The local and propagated quality variations can be illustrated by a simple two-step machining example, as shown in Fig. 2. The workpiece is a cube of metal (the front view is shown). Surface C of the workpiece is milled in the first step (Fig. 2(a)). A hole is drilled on surface D using surface C as the primary datum (Fig. 2(b)) in the second step. Clearly, the resulting hole is not perpendicular to surface D (Fig. 2(c)). In case 1 illustrated in Fig. 2, the geometric error associated with the hole is caused by the local fixture error in the drilling operation. However, in case 2, the error associated with the hole is not caused by the drilling operation, but by the propagated error from the milling operation in the first step. In general, the Quality Characteristics (QCs) at a certain stage can be influenced not only by the errors at the current stage, but also by its preceding QCs in a multistage manufacturing process. One can imagine that process variation will propagate along the physical process topology and form a network of variation flow.

Fig. 2 A two-step maching process: (a) front view of the workpiece; (b) drilling of the hole; and (c) non-perpendicular nature of the hole.

The variation propagation poses significant new challenges for process variability monitoring and reduction. Without considering the variation propagation conventional statistical monitoring methods are not able to differentiate between local and propagated variations. Thus, a significant number of false alarms can be generated at a given stage, i.e., the monitoring scheme can mistake the propagated variation as a local variation and then generate an alarm that is due to other stages. An effective statistical monitoring scheme for variability monitoring and reduction should be able to pinpoint the variation sources to a particular stage.

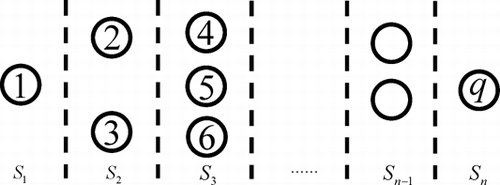
Due to rapid developments in information and sensing technologies, an abundance of data is now readily available in manufacturing processes. Total inspection for discrete processes at each intermediate operation and very high sampling rates are no longer rare in practice. For example, in autobody assembly processes, 100% dimensional inspection has been achieved through in-line optical coordinate measurement machines (Ceglarek and Shi, 1995). With these measurements at intermediate stages, if we define the QCs as nodes, a general multistage manufacturing process has a physical layout as shown in Fig. 3, where q QCs, Q _j , j = 1, 2, …, q, are distributed at n stages.

Fig. 3 Layout of a general multistage process.

This profusion of process/product measurement data provides an opportunity for effective process control of multistage manufacturing processes. In fact, some research efforts have already been made to conquer this problem. These methods can be roughly classified as being either analytical methods, those based on an off-line physical model of the process, or as data-driven techniques, those based on the statistical analysis of historical process data. The analytical method approach is represented by the recently developed “stream of variation” methodologies which focus on dimensional variation analysis of sequential discrete machining (e.g., Huang et al. (2000), Djurdjanovic and Ni (2001) and Zhou et al. (2003)) and assembly processes (e.g., Ding et al. (2000) and Jin and Shi (1999)). They are effective in describing the interactions between different units but require a thorough physical understanding of the process that might not be generally available. The existing data-driven techniques include the regression control chart of Mandel (1969) and its updated version, the cause-selecting control chart (Zhang, 1985; Wade and Woodall, 1993), where the outgoing quality is monitored after adjustment for the effect of the incoming quality. As an extension, Hawkins (1991, 1993) proposed the methodology and studied the design of the related procedures for monitoring correlated QCs based on regression adjustment in cascade processes. It was suggested that every QC is monitored by a corresponding regression-adjusted chart which is built based on the (standardized) residual, Z _j = Q _j − Q _j , j = 1, …, q, called regression-adjusted variables, which occur when Q _j is regressed on all its preceding QCs. Then Z _j being out of control can be directly interpreted as faults occurring on QC j. The idea of regression adjustment has been widely accepted as a good way to deal with multistage quality control problems and is the basis of several papers in the literature. For example, Zantek et al. (2002) measured the impact of each stage's performance on the variation in intermediate and final product quality. Hauck et al. (1999) considered process monitoring and diagnosis based on regression adjustment in multivariate cases, and Fong and Lawless (1998), Agrawal et al. (1999) and Lawless et al. (1999), analyzed the variation transmission in key characteristics as discrete parts move through a multistage production process.

Despite the general effectiveness of the regression-adjustment-based method shown in the existing studies, its properties in the monitoring of variability in practice are not comprehensively studied. There are two potential issues involved.

1.

In most of the data-driven methods, the QCs Q j , j = 1, …, q, are often assumed to be directly observable. However, in practice, the QCs can never be measured exactly and thus the observed value, X j , is actually a combination of Q j and a non-zero measurement error ε j . It has been pointed out that the least squares estimate in the presence of measurement errors is inconsistent (Fuller, 1987). As a result, the diagnostic capability of the quality control procedures based on least squares regression may be degraded by the bias of estimation. Actually the existence of measurement errors has been highlighted in the literature (Agrawal et al., 1999; Lawless et al., 1999), but the influence of these errors on the monitoring of QCs in multistage manufacturing processes has not been explored.

2.

For a complex process consisting of many QCs, regressor selection and its impact on the monitoring scheme are also very important issues. However, little work has been reported on this topic. In most cases, for every QC j, people just monitor its residual that is resulted from the adjustment of all its preceding QCs (e.g., Hawkins (1993) and Zantek et al. (2006)) without the pre-examination of the subset of QCs that really influences j. Thus, it is necessary to investigate the possible advantages or disadvantages if a regressor selection procedure, which is usually an indispensable part in the application of regression, is added into the regression adjustment method.

This article focuses on the properties of a regression-adjustment-based method in the monitoring of variability in multistage manufacturing processes. Particularly, we investigate the impacts of measurement errors and regressor selection on the existing monitoring scheme. It is found that with the measurement errors, the regression-adjusted control chart of every QC responds not only to the change of its local variation, but also to that of its preceding local variations. As a result, the preceding local variations become sources of false alarms and misdetection of the monitoring scheme. Furthermore, we find that the impacts of measurement errors and regressor selection are actually mingled together in that without measurement errors, regressor selection (either with or without) will not affect the monitoring procedure. However, when measurement errors exist, regressor selection will come into play and influence the performance of the monitoring scheme. We compare the performances of two adjustment methods, that is, adjustment for all preceding QCs and that for only the subset identified through some regressor selection procedures (called the “all-adjustment” method and “subset-adjustment” method respectively). It is shown that the monitoring procedure using the subset-adjustment procedure corresponds with fewer false alarm sources, whereas the all-adjustment procedure potentially has a lower misdetection rate. Some conclusions are drawn based on the comparison, which can be used to guide the application of regression-adjustment monitoring procedures.

The reminder of the paper is organized as follows. Section 2 introduces the conventional variability monitoring procedure based on regression adjustment. Section 3 points out the impact of measurement errors in general and compares such impacts when the all-adjustment procedure and subset-adjustment procedure are used. In Section 4, two numerical examples are used to demonstrate the analysis in Section 3. The paper concludes in Section 5.

2. Variability monitoring procedure based on regression adjustment

2.1. Process model and assumptions

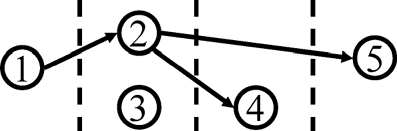
For j = 1, …, q, define _j = {1, 2, …, p} as the set of QCs in the preceding stages of QC j. For example, in Fig. 3, P ₅ is {1, 2, 3}, while _q includes all the QCs except q. In our study, we assume that QC j can be influenced by the QCs in _j . Also, let U _j and U _i , i ∈ _j , be the local variation sources of QC j and QC i respectively. The local variation sources represent the quantities which are related to a specific QC and are often not directly observable. They have different physical meanings in different processes. For example, in the simple machining process shown in Fig. 2, they denote the local fixture errors. For the sake of simplicity, we assume that every QC in the process has a different local variation source in this paper. However, the conclusions we get here are feasible for more general cases where the QCs at the same stage could share the same local variation sources. The linear model between Q _j and Q _i , i ∈ _j , is

where β = [β₁, β₂, …, β _p ]′ and Q = [Q ₁, Q ₂, …, Q _p ]′. Note that if j = 1, Equation (1) becomes Q ₁ = U ₁. Q also satisfies a linear model:

where U = [U ₁, U ₂, …, U _p ]′ is the vector of all the preceding local variation sources, D is a p × p matrix, and the superscript “′” represents vector or matrix transpose. Here, D is assumed to have a general form because one local variation source could influence multiple QCs through propagation. One point worth mentioning is that the purpose of assuming D as a square matrix is only for the convenience of notation. A rectangular D matrix will not change later results.

Because of measurement errors, the observed quantities are (Y, X) which satisfy:

where ε = [ε₁, ε₂, …, ε _p ]′, X = [X ₁, X ₂, …, X _p ]′ and X _i = Q _i + ε _i , i = 1, …, p. e is the measurement error of QC j and ε _i is that of QC i.

The following assumptions can be made based on the characteristics of most manufacturing processes.

1.	All local variation sources and measurement errors follow a normal distribution. Due to the existence of various disturbances, the variation sources and measurement errors are often a result of combined random disturbances. Thus, a normal distribution is often a reasonable assumption due to the central limit theorem. Furthermore, in this article, we focus on the detection of variance change instead of mean shift. For the sake of simplicity, we also assume that the local variation sources and the measurement errors have zero means.
2.	All local variation sources and measurement errors are independent of one another. Because the variation sources are in the process and measurement errors are in the measurement systems that are physically independent of the process, it is natural to assume that the variation sources are independent of the measurement errors. Furthermore, the local variation sources are often the result of different physical root causes and/or different manufacturing stages, so it is also reasonable to assume that they are independent of one another. Based on this assumption, the variance-covariance matrix of U, Σ U , and that of ε , Σ ε , are diagonal, i.e., Σ U = diag(σ U i 2,i = 1, …,p) and Σ ε = diag(σε i 2,i = 1,…,p), where σ U i 2 and σε i 2 are the variances of U i and ε i respectively.
3.	The process is stable, meaning that β, D, σ e 2 and σε i 2, i ∈ j are fixed.

It should be highlighted that the model described by Equations (1),(2), (3),(4) and assumptions 1–3 are consistent with the analytical models developed for multistage manufacturing processes (e.g., Zhou et al. (2003)) and have been adopted as the basis for several recently developed variability monitoring and diagnosis methodologies (e.g., Apley and Shi (2001) and Zhou et al. (2003)). In this article, we focus on the following problem: knowing Y and X and the model structures (the model parameters are unknown), how do we develop an effective statistical monitoring scheme to detect the local variation change? Before answering this question we briefly review the conventional regression-adjusted variability monitoring procedure.

2.2. The regression-adjusted variability monitoring procedure

The variability monitoring procedure based on regression adjustment has two steps.

Phase I analysis: Assume that the historical data set includes m subgroup samples, each consisting of n (p + 1)-dimensional multivariate observations. The data of the hth, h = 1, 2, …, m, subgroup are denoted by (y _h , χ _h ), where y _h = [y _h1, y _h2, …, y _hn ]′ is an n-dimensional vector in which y _ht , t = 1,2, …, n, represents the tth observation of Y and χ _h = [x _h1,x _h2, …, x _hn ]′ is an n × p matrix in which x _ht represents the tth observation of X. The following needs to be done in sequence:

	Step 1. Obtain the least squares estimate of the coefficient β by where y and χ are the stacked vector and matrix, respectively, of y h and χ h , h = 1, 2, …, m, i.e., y = [y′1, y′2, …, y′ m ]′ and χ = [ χ 1′, χ 2′, …, χ m ′]′.
	Step 2. Calculate the residuals and their standard deviations for each subgroup sample. For the hth subgroup, the residuals and corresponding standard deviation are where z h = [z h1, z h2, …, z hn ]′ and z h = ∑ t = 1 n z ht /n.
	Step 3. Calculate the control limits for the S chart of the residuals: where S = (1/m) ∑ h = 1 m S h , and B 3 and B 4 are constants which are tabulated for various sample sizes to construct the three-sigma limits (e.g., Montgomery (2001)).

Phase II analysis: When a new subgroup sample, (y ₀, χ₀), is obtained, the residuals using the estimate from Equation (5) are calculated by

and monitored by the S chart established in Phase I analysis. If it is found that this sample is out of control, it means that the local variation of QC j, i.e., σ _{U 0j} ², is out of control.

The two-step analysis above will be conducted iteratively for j = 1, 2., q. In this way, we can find the root causes of the variability change in the process.

It should be highlighted that the chart we used here is different from that used by Zhang (1985), Hawkins (1991, 1993) and Zantek et al. (2006). They respectively used a chart, a CUSUM chart and a T² chart to monitor the residuals because they were mainly interested in mean shifts, whereas in our study we select the S chart for the purpose of monitoring variability/variance changes. Later, we focus on the impacts of measurement errors and regressor selection on the monitoring performance. Although the simple S chart is used here, the conclusions should generally hold for any variability monitoring chart.

3. Impacts of measurement errors and regressor selection

3.1. Impact of measurement errors

Under assumptions (1–3), when the sample size (say, mn in the procedure) is large, the least squares estimate β → ( Σ _X )^{− 1} Σ _{X Y} , where Σ _X denotes the (variance-) covariance matrix of X, while Σ _{X Y} denotes that between X and Y (Whittaker, 1990). According to Equations (1), (3) and (4), Σ _X = Σ _Q + Σ _ε and Σ _{X Y} = cov(Q, β ′Q) = Σ _Q β , where Σ _Q is the covariance matrix of Q. Consequently,

and thus

where I _p is the p-dimensional identity matrix. Equation (9) shows that when measurement errors exist, i.e., Σ _ε ≠0 _{p× p} , β is not consistent, where 0 _{p× p} denotes the p× p empty matrix. Actually this is a well-known fact that has been pointed out by Fuller (1987).

Let (Y ₀, X ₀) be the new measurement in Phase II analysis, then the residual based on least squares estimate in Phase I analysis is Z ₀ = Y ₀− β ′ X ₀, which is essentially the prediction error of the model built on the estimate. By substituting into Equations (1)(2),(3),(4), we can get:

Since is determined in Phase I analysis, it is a constant here. So the variance of Z ₀ is

According to Equation (11), if there is no measurement error or it is negligible, i.e., Σ _ε ≈0 _{p× p} , by Equation (9), β − ≈0 _p and consequently var(Z ₀) ≈ σ _{U 0j} ² + σ _e ², where 0 _p denotes the p-dimensional empty vector. Since σ _e ² is assumed to be fixed (by assumption 3), var(Z ₀) is only determined by σ _{U 0j} ² and so if σ _{U 0j} ² changes it can be detected using the monitoring procedure introduced in Section 2.2. In fact, this is what makes regression adjustment an effective way to monitor the local variations.

However, if the measurement error is not negligible, by Equation (11), var(Z ₀) is related not only with σ _{U 0j} ², but also with Σ _{U 0} , or more specifically, σ _{U 01} ², σ _{U 02} ², …, σ _{U 0p} ². Consequently, two detrimental effects would occur.

1.

The False Alarm Rate (FAR) or the Type I error probability of the monitoring procedure will increase. Here, FAR is defined as the probability that σ U 0j 2 is declared to be out of control when in truth it is in control. This point is easy to understand: since the change of var(Z 0) in Equation (11) may be not from σ U 0j 2, but from some σ U 0i 2, i ∈ j , σ U 0j 2 may be declared to be out of control when it actually experiences no change.

2.

Likewise, the misdetection rate (MDR), or the Type II error probability, which is defined as the probability that σ U 0j 2 is declared to be in control when in truth it is out of control, will also increase. In the presence of σ U 0i 2, the proportion between the change of σ U 0j 2 and var (Z 0) will decrease and thus the monitoring procedure will have a larger Type II error probability as illustrated by the operation characteristic curves of a typical S chart (Montgomery, 2001).

In other words, the diagnostic capability of the monitoring procedure will degrade in the presence of measurement errors.

To provide more insight on the impact of measurement errors, we will use a two-stage process as an example to get a specific expression of Equation (11). Assume there is one QC in each stage and the true model of the QCs are Q ₁ = U ₁ and Q ₂ = β Q ₁ + U ₂, while the measurements are X ₁ = Q ₁ + ε andY = Q ₂ + e. Also assume that σ _{U 1} ² = σ _{U 2} ², σ _ε ² = σ _e ² and the Phase I signal-to-noise ratio σ _{U 1} ²/σ_ε ² = κ. Then by Equation (9), we can get:

From Equation (11) we obtain:

So the influence of σ _{U 01} ² is

Clearly, the smaller the κ or the larger the β, the larger the influence of σ _{U 01} ² on var(Z ₀). This means that the more substantial the measurement errors (indicated by κ) and the stronger the correlation between the QCs (indicated by β), the more serious will be the detrimental effects.

3.2. Impact of regressor selection

In regression model building, the set of regressors can be often reduced through a selection of relevant factors in the model. Accordingly, there are two ways to conduct regression adjustment, namely, the all-adjustment procedure that regresses Y on all the preceding QCs and the subset-adjustment procedure that regresses Y on only a selected subset of the preceding QCs. In this section, these two adjustment methods are compared. Firstly, a graph representation of regressor selection results is introduced.

3.2.1. Graph representation of regressor selection results

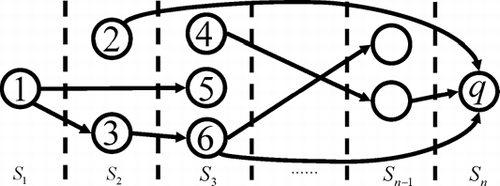
For ease of comparison of the two regression adjustment methods, a graph can be constructed as shown in Fig. 4, to show the interactions among the QCs in a process. In this graph, if there is a directed line from QC i to QC j, it means that the coefficient of i is non-zero in the multiple regression of j, i.e., β _i ≠ 0 in Equation (1). This selection can be done through physical analyses of the process or data-driven statistical selection procedures. For example, if we can identify that i is physically independent of j, then there should not be a line between i and j. For a simple process, physical analysis might be a viable way to establish such a graph. However, for a complex process involving many QCs, data-driven methods have to be used. The data-driven techniques to build such graphs include both the conventional model selection techniques (Seber and Lee, 2003) and the recent statistical testing methods based on graphical models (Drton and Perlman, 2005; Zeng and Zhou, 2006). In this article, however, we will not investigate the model building technique; instead, we assume that a graphical model is given.

Fig. 4 The graph representation of regressor selection results.

Based on this graph, _j can be divided into two subsets, _j1 and _j2, such that for every i ∈ _j1, β _i ≠ 0 there is a directed line from i to j, and for every i ∈ _j2, β _i = 0 or there is no line between i and j. For example, in Fig. 4, let j = 5, then ₅₁ = {1} and ₅₂ = {2, 3}. Correspondingly, the regressors and parameters in Equations (1) (2), (3),(4) can be divided into two parts, that is, Q = [Q′_I,Q′_II]′, X = [X′_I,X′_II]′, ε = [ ε ′_I, ε ′_II]′, β = [ β ′_I, β ′_II]′ and D = [D′_I, D′ _II]′, where the quantities with subscript “I” are related with QCs in _j1 and those with subscript “II” are related with QCs in _j2. Then model (1) becomes.

where β _I≠0, β _II = 0 _p and Q _I = D _I U, Q _II = D _II U. Accordingly, the regressors are

In later discussion, subset adjustment means that Y is regressed on X _I, while all adjustment means that Y is regressed on X. The two sets of regressors can be easily identified from Fig. 4. For example, for j = 5, the regressor is X ₁ in subset adjustment and they include X ₁, X ₂ and X ₃ in all adjustment.

3.2.2. Subset adjustment compared to all adjustment

The two adjustment methods can be compared in terms of the FAR and MDR of the procedure resulted when they are used respectively.

3.2.2. FAR comparison If the subset-adjustment procedure is used, by Equation (8), the least squares estimate:

where Σ _{Q I} denotes the covariance matrix of Q _I. Accordingly, by Equation (11):

Instead, if the all-adjustment procedure is used, the estimate:

Consequently,

Let

It can be proven that:

where A = D _I Σ _U D′_I+ Σ _{ε I} , B = D _II Σ _U D′_II+ Σ _{ε II} , C = D _IΣ _U D′_II, and d _1i and d _2i are the ith columns of D _I and D _II respectively. Note that here Σ _U is the covariance matrix of U under normal conditions, which can be assumed to be constant. The proof is given in Appendix 1.

According to Equations (20)(21)(22)(23), the coefficients of σ _{U 0i} ², f _i ^s and f _i ^a, are all non-negative and can be viewed as the measures of the influence of σ _{U 0i} ² on the monitored quantity in subset-adjustment and all-adjustment methods, respectively. The larger this measure, the larger the FAR resulting from a certain change of σ _{U 0i} ². In other words, if f _i ^s > f _i ^a, such an influence is larger in subset adjustment than in all adjustment and thus the latter is a better choice in terms of reducing the effect of σ _{U 0i} ²; and vice versa.

Considering the general assumptions in our study, it is difficult to further simplify Equations (22) and (20). However, the following facts can be drawn about the comparison between f _i ^s and f _i ^a: Fact 1: If Q _I and Q _II are independent, then f _i ^s = f _i ^a for all i ∈ _j .

This is a direct result. If Q _I and Q _II are independent, C = D _IΣ _U D′_II = Σ _{Q I Q II} = 0 _{p 1 × p 2} , where p ₁ and p ₂ are the numbers of QCs in _j1 and _j2 respectively, Σ _{Q I Q II} is the covariance matrix between Q _I and Q _II. Thus, by Equations (22) and (22), f _i ^s = f _i ^a = (β ′_I Σ _{ε I} A ^{− 1} d _1i )², meaning that the influence of σ _{U 0i} ² is the same in both methods.

Fact 2: For those i ∈ _j such that d _1i = 0 _{p 1} , f _i ^s = 0 and f _i ^a ≥ 0.

This is also direct from Equations (22) and (23). It means that for the preceding local variations satisfying this condition, their changes will not influence the monitored quantity at all if subset adjustment is used, but may have influence if all adjustment is used.

Fact 3: In general, the magnitudes of f _i ^s and f _i ^a depend on D and the values of the local variations and measurement errors. For some i, f _i ^s > f _i ^a, and for others, f _i ^s ≤ f _i ^a. In other words, there is no uniform conclusion in general cases.

Fact 3 tells us that the subset-adjustment method and the all-adjustment method are not uniformly better than the other. This point can be shown specifically by the three-stage example represented by Fig. 5.

Fig. 5 A three-stage process.

In this example, assume the true model is Q ₁ = U ₁, Q ₂ = b ₁ Q ₁ + U ₂ and Q ₃ = β₂ Q ₂ + U ₃, where b ₁, β₂≠ 0. The measurements are X ₁ = Q ₁ + ε₁, X ₂ = Q ₂ + ε₂ and Y = Q ₃ + e. So the matrix D can be written as

Following Equations (20)(21)(22)(23), we can get:

Considering a special case where σ _{U 1} ² = σ _{U 2} ², σ_ε1 ² = σ_ε2 ² and σ _{U 1} ²/σ_ε1 ² = κ, it can be shown that.

The proof is given in Appendix 2. Equation (25) shows that the influence of σ _{U 01} ² using subset adjustment is larger than that using all adjustment, while the case for the influence of σ _{U 02} ² is the reverse.

From the three facts, we can see that when the QCs in _j1and _j2 are independent, there is no difference between the two adjustments since the monitoring procedures using them will suffer the same influences from the preceding local variations. When the QCs in the two sets are correlated, depending on the correlation structure between them and the specific local variation, the performances of the subset-adjustment and all-adjustment methods are different. For the local variations which satisfy the condition in fact 2, subset adjustment can completely eliminate their influences on the monitoring procedure, but all adjustment may not do so.

3.2.2.2. MDR comparison In this part, we consider those cases where all preceding local variations are kept in normal status, i.e., σ _{U 0i} ² = σ _{U i} ² for i ∈ _j , and only the local variation of QC j increases. MDR is the probability that the change in σ _{U 0j} ² is missed by the monitoring scheme.

Consider Phase I analysis of the monitoring procedure in Section 2.2. According to the linear least square theory, the variance of Y can be decomposed into that of Y, the predictor, and that of Y − Y, the residual (Whittaker, 1990, Proposition 5.3.4). Consequently, we have that:

where var(Z ^s) and var(Z ^a) are the variances of the residual produced by the subset-adjustment method and by all-adjustment method respectively, while |Y _I(X _I)) and |Y _II(X _I, X _II)) are the variances of the corresponding predictors. Here, the parentheses are used to emphasize the regressors in these two adjustments. The variance of the predictor is also referred to as the explained variation. It can be proved that (please refer to Appendix 3)

We now perform the Phase II analysis. Assume the local variation of QC j increases by δ _j , i.e., σ _{U 0j} ² − σ _{U j} ² = δ _j . According to Equations (17) and (19), var(Z ₀ ^s) = var(Z ^s) + δ _j and var(Z ₀ ^a) = var(Z ^a) +δ _j . Thus, the ratios between the variation change, δ _j , and the background variations are

From the properties of an S chart, it is easy to see that if this ratio is larger, then the MDR (or Type II error) of the chart will be smaller. Thus, according to Equations (28) and (29), two facts can be obtained: Fact 4: If Q _I and Q _II are independent, r ^s = r ^a, implying that the subset-adjustment method is as sensitive to the change of j's local variation as the all-adjustment method. Thus, these two methods will have the same MDR.

Fact 5: Generally, r ^s < r ^a, meaning that the subset-adjustment method is less sensitive to the change of j's local variation than the all-adjustment method and thus it will yield a higher MDR.

3.2.3. Summary of the impact of regressor selection

Using the five facts obtained from the comparison, some conclusions that are helpful in the use of a regression-adjusted monitoring procedure can be summarized as follows.

1.	By fact 1 and fact 4, all the QCs in j2 that are independent of the QCs in j1 can be removed from the regressors to simplify the monitoring procedure because these QCs have no influence on the FAR and MDR.
2.	As far as the FAR is concerned, by fact 3, there is no clear advantage to using either the subset-adjustment method or the all-adjustment method. Generally they depend on the correlation structure of the QCs in the process and specific local variations. However, we can safely conclude that procedures using the all-adjustment method will suffer the influences from all preceding local variations, whereas those using the subset-adjustment method can eliminate the influences from some local variations satisfying the condition in fact 2. In other words, the subset-adjustment method corresponds with fewer false alarm sources.
3.	In terms of reducing the MDR, by fact 4 and fact 5, the all-adjustment method is a better choice or at least performs as well as the subset-adjustment method.

As such, there is generally no uniform priority between these two adjustment methods. In practice, which one to choose depends on the specific situation and people's preference on FAR and MDR. If a low FAR is important, then the subset-adjustment method should be seriously considered, whereas if MDR is critical, the all-adjustment method should be used.

4. Numerical study

4.1.4. A two-stage process to illustrate the impact of measurement errors

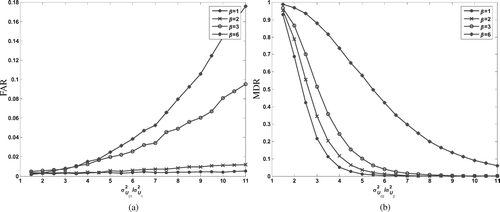
In this example, we apply the monitoring procedure in Section 2.2 on the two-stage process as described in Section 3.1. In Phase I analysis, assume σ _{U 1} ² = σ _{U 2} ² = 1, m = 200 and n = 25. Three-sigma limits are used to construct the S chart. In phase II analysis (the sample size is again 25), we consider two scenarios: in scenario 1, β is fixed at 2, while κ can be 5, 7, 10 or 20, and in scenario 2, κ is fixed at 10, while β can be 1, 2, 3 or 6. The FAR and MDR values of the procedure in these two scenarios are calculated by changing the two ratios, σ _{U 01} ²/σ _{U 1} ² and σ _{U 02} ²/σ _{U 2} ², respectively.

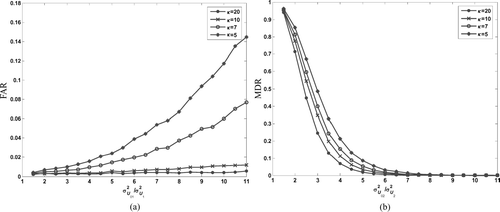
Table 1 and Table 2 list the Phase I analysis results including β and estimated control limits in scenarios 1 and 2 respectively. It is clearly seen that, as indicated by Equation (12), the difference between β and β becomes larger when κ is smaller or β is larger. FAR against σ _{U 01} ²/σ _{U 1} ² and MDR against σ _{U 02} ²/σ _{U 2} ² in scenario 1 are shown in Fig. 6, and those in scenario 2 are in Fig. 7, where every result is obtained through 20 000 Monte Carlo simulations. According to Fig. 6, we know that, as indicated by Equation (13):

1.

A larger σ U 01 2 or smaller κ corresponds with a larger FAR. We can also note that the value of κ is a very important factor in that FAR is almost unchanged and also very small when κ is large (e.g., > 20).

2.

A smaller σ U 02 2 or smaller κ corresponds with a larger MDR. Moreover, as σ U 02 2 becomes very large, MDRquickly reduces to around zero. This suggests that MDR is influenced by measurement errors especially when the change of σ U 02 2, which is supposed to be detected by the monitoring procedure, is small. Also, the impact of measurement errors becomes larger when β increases, as shown in Fig. 7.

Fig. 6 (a) FAR for different values of κ; and (b) MDR for different values of κ.

Fig. 7 (a) FAR for different values of β; and (b) MDR for different values of β.

Table 1 Phase I analysis results under different values of κ β= 2)

κ		UCL	CL	LCL
20	1.8993	1.5985	1.1140	0.6294
10	1.8440	1.7290	1.2049	0.6808
7	1.7443	1.8175	1.2666	0.7156
5	1.6891	1.9224	1.3396	0.7569

Table 2 Phase I analysis results under different values of β (κ = 10)

β		UCL	CL	LCL
1	0.8991	1.5663	1.0915	0.6167
2	1.8440	1.7290	1.2049	0.6808
3	2.7174	1.9430	1.3540	0.7650
6	5.4660	3.0158	2.1016	1.1874

4.2. A four-stage process to illustrate the impact of regressor selection

In this example, consider the monitoring of QC 5. Assume we have obtained the graph representing the interactions in the process, which is exactly as shown in Fig. 8, using a regressor selection technique. Accordingly, assume the true relationships are Q ₁ = U ₁, Q ₂ = b ₁₂ Q ₁ + U ₂, Q ₃ = U ₃, Q ₄ = b ₂₄ Q ₂ + U ₄ and Q ₅ = β₂ Q ₂ + U ₅, while the measurements are X ₁ = Q ₁ + ε₁, X ₂ = Q ₂ + ε₂, X ₃ = Q ₃ + ε₃, X ₄ = Q ₄ + ε₄ and Y = Q ₅ + e. In the simulation, let b ₁₂ = 1, b ₂₄ = 2, β₂ = 5, κ = 10. In Phase I analysis, σ _{U 1} ² = σ _{U 2} ² = σ _{U 3} ² = σ _{U 4} ² = σ _{U 5} ² = 1, m = 200 and n = 25. The sample size in Phase II is also 25. Table 3 lists the Phase I analysis results when subset adjustment, Y∼ X ₂, and all adjustment, Y∼ X ₁+ X ₂+ X ₃+ X ₄, are used. The FAR against σ _{U 01} ²/σ _{U 1} ², σ _{U 02} ²/σ _{U 2} ², σ _{U 03} ²/σ _{U 3} ² and σ _{U 04} ²/σ _{U 4} ² are shown in Fig. 9(a), Fig. 9(b), Fig. 9(c) and Fig. 9(d) respectively, where the two lines in each figure denote the results obtained in these two adjustments.

Fig. 8 A four-stage process.

Fig. 9 FAR for the two considered adjustments: (a) FAR plotted against σ _{U 01} ²/σ _{U 1} ²; (b) FAR against σ _{U 02} ²/σ _{U 2} ²; (c) FAR against σ _{U 03} ²/σ _{U 3} ²; and (d) FAR against σ _{U 04} ²/σ _{U 4} ².

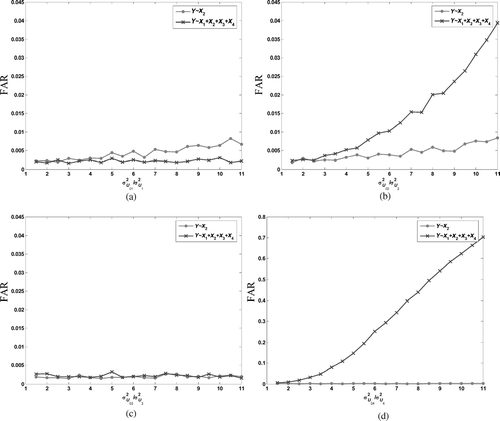
Table 3 Phase I analysis results for the two adjustment methods

Method	1	2	3	4	UCL	CL	LCL
Subset adjustment	—	4.7500	—	—	2.6374	1.8379	1.0384
All adjustment	0.3144	3.3971	−0.0193	0.6426	2.3479	1.6362	0.9244

It's easy to find that QC 3 is independent of QC 2. Thus, by fact 1, the influences of σ _{U 03} ² in subset adjustment and all adjustment are the same, as validated by Fig. 9(c). Also, we can find that d₁₄ = 0, and consequently, by fact 2, the change of σ _{U 04} ² will not cause a false alarm when the subset-adjustment method is used. This is shown by Fig. 9(d), where the FDR resulting from the change of σ _{U 04} ² is very high (> 0.5) in all adjustment, but around zero in subset adjustment. So subset adjustment is, as expected, a quite advantageous choice to eliminate the possible serious FAR caused by σ _{U 04} ². Figure 9(a) indicates that the influence of σ _{U 01} ² using all adjustment is smaller than that using subset adjustment, whereas Fig. 9(b) gives the contrary conclusion. This is as suggested by Equation (25).

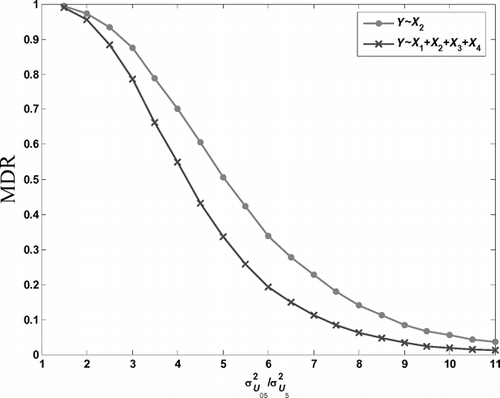
Figure 10 shows the MDR against σ _{U 05} ²/σ _{U 5} ² for the two adjustment methods when the FAR is maintained at around 0.0027. As expected, the all-adjustment method has a lower MDR and as the change in σ _{U 05} ² becomes large, the MDR for both methods quickly reduces to zero.

Fig. 10 MDR for the two adjustment methods.

5. Summary and discussion

This paper investigates the impacts of measurement errors and regressor selection on the regression-adjustment-based monitoring scheme of variability in multistage processes. It is shown that the existence of measurement errors will result in higher FAR and MDR levels, and the complexity of the impact of regressor selection is actually a byproduct of the measurement error impact. We also compare the performances of the subset-adjustment method and all-adjustment method and find that the monitoring procedure using the subset-adjustment method is more robust to the change of some preceding local variations than that using the all-adjustment method, however the all-adjustment method has a lower MDR. Thus, the choice of which of these methods to use is dependent on the characteristics of the process and preference about the FAR and MDR of the monitoring procedure.

In the analysis, asymptotical performances under large sample conditions are considered. However, similar results can be verified through further numerical studies when sample sizes are much smaller. Thus, the results of this study can be viewed as a general reflection of multistage manufacturing processes where a large number of samples are often readily available due to advances in sensing and information technologies. Consequently, the conclusions summarized in this paper possess wide applicability in practice. Another point worth mentioning is that the detrimental influences of measurement errors in regression-adjusted methods can be optimally reduced if we replace the ordinary least squares regression with a modeling technique which is known as Total Least Squares (TLS) in computational mathematics and engineering, or as Errors-In-Variables (EIV) modeling in statistics (Van Huffel and Lemmerling, 2002). By TLS/EIV, a consistent estimate can be obtained and thus the influence of measurement errors is minimized. However, these techniques are computational intense and are not easy to apply in practice. Moreover, one of the four conditions (i) σ _e ²/σ _{ε i} ² is known; (ii) σ _e ² is known; (iii) σ_{ε i} ² is known; (iv) both of σ _e ² and σ_{ε i} ² are known, is required to get the solution (Van Huffel, 2004), which sets another obstacle for TLS/EIV techniques to be applied widely. Thus, in many practical cases, least squares regression is still an efficient choice.

Appendices

Appendix 1. Proof of Equations (22) and (23)

According to Equation (9):

Let A, B and C be as defined in Equations (22) and (23), then.

By partitioned matrix property (Seber and Lee, 2003),

where E = − (A−CB ^{− 1} C′)^{− 1} CB ^{− 1} and F = B ^{− 1}+B ^{− 1} C′ (A−CB ^{− 1} C′)^{− 1} CB ^{− 1}.

Substituting Equation (A4) into Equation (A2) yields:

From Equations (20) and (21):

where d _i = denotes the ith column of D. Substituting (A1) into (A6) and (A5) into (A7) yields Equation (22) and Equation (23) respectively.

Appendix 2. Proof of Equation (25)

Let σ _{U 1} ² = σ _{U 2} ² = κ σ_ε1 ² = κ σ_ε2 ², κ > 0, substituting them into Equation (24) yields:

Equation (25) is easy to obtain by comparing the two denominators in Equations (A8) and (A9).

Appendix 3. Proof of Equations (28) and (29)

By the additivity of the explained variation (Whittaker, 1990, Proposition 5.6.1):

where _II( _I) denotes the least square predictor of X _II from X _I. Essentially, Equation (A10) indicates that the amount of variation explained by X _I and X _II is the sum of that explained by only X _I and that explained by X _II adjusted for X _I. Furthermore, the part |Y( _II− | _II( _I))) can be simplified to

where cov(Y,X _II|X _I) is the partial covariance of Y and X _II given X _I, while |(X _II|X _I) is the partial variance of X _II given X _I.

By Proposition 5.5.1 in Whittaker (1990):

Substituting Equations (3) and (15) into Equation (A13) yields:

According to assumption (2), Equation (A14) can be simplified as

Another important fact is that according to Proposition 10.5.1 in Whittaker (1990), β_II = 0 in Equation (14) is equivalent to cov(Q _j ,Q _II|Q _I) = 0.

Thus, comparing Equations (A11), (A12) and (A15), we can get:

1.	If Q I and Q II are independent, i.e., cov(Q I,Q II) = 0, cov (Y,X II|X I) = cov(Q j ,Q II|Q I) = 0, and consequently:
2.	Generally, since var εI) ≠0, cov(Y,X II|X I) ≠cov(Q j , Q II|Q I) and thus cov(Y,X II|X I) ≠0. Consequently: By Equations (26), (27) and (A10), Equations (28) and (29) hold.

Biographies

Li Zeng is a Ph.D. student in the Department of Industrial and Systems Engineering at the University of Wisconsin-Madison. Her research interests are statistical modeling and variation source diagnosis in large complex systems.

Shiyu Zhou is an Associate Professor in the Department of Industrial and Systems Engineering at the University of Wisconsin-Madison. He was awarded his B.S. and M.S. degrees in Mechanical Engineering by the University of Science and Technology of China in 1993 and 1996 respectively. He received his Master's degree in Industrial Engineering and Ph.D. in Mechanical Engineering at the University of Michigan in 2000. His research focus is on creating in-process quality and productivity improvement methodologies by integrating statistics, system and control theory, and engineering knowledge. The objective is to achieve automatic process monitoring, diagnosis, compensation, and their implementation in various manufacturing processes. His research is sponsored by National Science Foundation, Department of Energy, NIST-ATP, and industries. He is a recipient of the CAREER Award from the National Science Foundation in 2006. He is a member of IIE, INFORMS, ASME and SME.

Acknowledgements

The financial support of this work is provided by NSF grant CMMI-0545600. The authors gratefully appreciate the editor and the referees for their valuable comments and suggestions.