A shift-based sequencing method for twin-shuttle automated storage and retrieval systems

Abstract

The continuing need for high-throughput Automated Storage and Retrieval Systems (AS/RS) has lead to the introduction of storage/retrieval machines that can carry more than one unit-load. However, this technology involves a large capital investment so careful operating methods are desired to make the most of its capabilities. In this paper, we study a shift-based sequencing problem for twin-shuttle AS/RS, where depletion (retrieval operations) and replenishment (storage operations) of items occur over different shifts. For example, certain warehouses or distribution depots deplete their items in stock during morning shifts and replenish during later shifts. We show that this problem can be transformed into the minimum-cost perfect matching problem and present an efficient polynomial-time optimum method that can achieve a large throughput gain over other methods. We also provide average-case and lower bound analyses for this problem.

Keywords:

• Automated storage and retrieval systems
• retrieval sequencing

1. Introduction

Automated Storage and Retrieval Systems (AS/RS) were originally introduced in the 1950s to eliminate the walking that accounted for 70% of manual retrieval time. Today, AS/RS are widely used as alternatives to traditional warehouses, as part of advanced manufacturing systems, and as an important link in supply chain systems supporting manufacturing, distribution and retailing. The advantages of AS/RS include savings in labor costs, improved material flow and inventory control, improved throughput levels, high floor-space utilization, increased safety and increased stock rotation.

Unit-load AS/RS are considered a generic form while other AS/RS represent variations of the unit-load AS/RS (Groover, 2001). Typically, unit-load AS/RS consist of a series of storage aisles each of which is served by a single Storage and Retrieval (S/R) machine or crane. Each aisle is supported by a Pickup and Delivery (P/D) station customarily located at the end of the aisle and accessed by the S/R machine and external handling systems such as conveyor interfaces. The S/R machine carries one unit-load and operates in two modes.

1.	Single Command Cycle (SC): either storage or retrieval occurs in an SC. The S/R machine starts at the P/D station, either stores or retrieves a load, and returns to the P/D station to complete a cycle.
2.	Dual Command Cycle (DC): both storage and retrieval occur in a DC. The S/R machine picks up a load from the P/D station, travels to a storage location to store it, continues to another location to retrieve a new load, and returns with it to the P/D station to complete a cycle.

Twin-shuttle (or double-shuttle) AS/RS expand the carrying capacity of the S/R machine to two unit-loads and thereby increase the throughput capacity of AS/RS. Meller and Mungwattana (1997) reported the successful application of this technology by a large textile manufacturer.

This enhanced capability leads to more versatile operating modes for the S/R machine. These include (Malmborg, 2000):

	EDC (Expanded DC) type E1: two storages and no retrieval in one cycle;
	EDC type E2: two retrievals and no storage in one cycle;
	EDC type E3: two storages and one retrieval in one cycle;
	EDC type E4: two retrievals and one storage in one cycle; and
	EDC type E5: two storages and two retrievals in one cycle, which is called a Quadruple Command Cycle (QC) or a four-command cycle. In a QC, a twin-shuttle S/R machine transfers two unit-loads from the P/D station onto the S/R machine, and then moves to the first storage location and places a unit-load in that rack position. After this, it moves to the first retrieval location, retrieves the load from the storage rack, and places the second storage load into the vacated rack position. Finally, it moves to the second retrieval position in the storage rack, retrieves the load, and returns to the P/D station where the two retrieved loads are transferred from the S/R machine into outbound material handling interfaces such as conveyors or forklift trucks.

This technology upgrade, however, involves a large capital investment and thus system users are interested in operating methods that make the most of its capabilities. Given storage bin openings and retrieval requests (i.e., retrieval items and their bin locations), Sarker et al. (1991), Keserla and Peters (1994) and Meller and Mungwattana (1997) presented sequencing methods for the twin-shuttle S/R machine performing QCs. These methods determine where to store and which items to retrieve for each QC. The objective is to minimize the total travel time taken by the twin-shuttle S/R machine to process those storage and retrieval requests, thus maximizing throughput. Their methods are based on greedy-style sequencing heuristics. With these heuristic methods for the twin-shuttle performing QCs, they observed throughput improvement in the range of 40–45% relative to performing DCs with a single-shuttle S/R machine. Potrc et al. (2004) presented heuristic travel time models for twin-shuttle systems using a random sequencing method where QCs are performed when storage locations and retrieval loads are randomly selected among the available ones. They use their travel time models to quickly estimate the approximate throughput. Literature on the sequencing problem for a single-shuttle S/R machine performing DCs can be found in Lee and Schaefer (1996). Sarker and Babu (1995) and Malmborg (2001) presented a literature review on different travel time models for various types of AS/RS including the twin-shuttle system. In a similar spirit to increase the system throughput, Hwang et al. (1999) studied a sequencing problem of QCs of the twin-shuttle carousel system where the twin-shuttle moves in a vertical direction only and the carousel storage rack rotates.

Malmborg (2000) developed a stochastic model for twin-shuttle AS/RS operating in the above various cycle modes and derived steady-state probabilities and performance measures such as queue lengths and waiting times. This extended the stochastic model analysis for the single-shuttle system studied by Lee (1997) and Bozer and Cho (2005). These stochastic analysis studies mainly assume First-Come First-Served (FCFS) operation although such models can allow travel times derived from different sequencing rules.

In this paper, we address a new sequencing problem for the twin-shuttle system operating in either EDC type E1 or E2. This occurs for some warehouse or distribution depots, such as Associated Grocers or Department Stores Distribution Centers, where AS/RS operate on a shift basis. For example, during a morning shift, the twin-shuttle S/R machines replenish AS/RS, performing storage operations, while during an afternoon shift, they deplete AS/RS, performing retrieval operations to load the trucks which will restock rural stores overnight. Thus, the problem for EDC type E2 operation can be stated as: given a set of retrieval requests, find a retrieval sequence of these requests (i.e., which pairs of retrieval requests are processed for each EDC type E2) that minimizes the total travel time taken by the twin-shuttle S/R machine. It can be similarly stated for EDC type E1 operations by replacing retrieval with storage.

Our study differs from the previous twin-shuttle AS/RS sequencing studies of Sarker et al. (1991), Keserla and Peters (1994), Meller and Mungwattana (1997) and Potrc et al. (2004). These previous studies addressed sequencing QCs, whereas our study addresses sequencing EDCs of type E2 or E1 in the shift-based operation of AS/RS. The previous solution methods relied on greedy-style or random heuristics, whereas our study presents an efficient Polynomial Optimum method. We will also show that significant throughput improvement is possible for the shift-based operation when a twin-shuttle system is used in place of a single-shuttle system and when the proposed optimum method is used in place of commonly used sequencing heuristic methods such as the FCFS and nearest neighbor heuristics.

The rest of this paper is organized as follows. In Section 2, we present the mathematical formulation of this problem and the Optimum solution method. In Section 3, we transform the problem into a graph matching problem and give the average-case and lower bound analyses of the problem. In Section 4, we introduce two heuristic methods that can be used for this problem and give an example to illustrate the proposed Optimum method and two heuristic methods taken from the literature. In Section 5, we present experimental results using these three methods and compare the twin-shuttle system using the proposed Optimum method with the single-shuttle system in terms of travel time reduction and throughput gain. In Section 6, we conclude this paper with a summary of the findings and future research issues.

2. Problem statement and mathematical formulation

In this paper, we address a sequencing problem for twin-shuttle AS/RS that perform either EDC type E2 or E1 operations. The problem is stated for EDC type E2 as follows: given a set of even-numbered retrieval requests, find a retrieval sequence of these requests that minimizes the total travel time taken by the twin-shuttle S/R machine to process these requests. Finding the retrieval sequence is equivalent to pairing retrieval requests for each EDC type E2 operation. We call this problem the Shift-Based Sequencing Problem (SBSP) for the twin-shuttle system. For the problem for EDC type E1, we simply replace the word “retrieval” with “storage”. We will show below that the SBSP can be transformed into a known graph matching problem with a polynomial algorithm. We will also show that the problem can be relaxed for odd-numbered requests.

We first give a list of notation used in this paper.

	R = the set of retrieval requests {R i = (x i , y i ) | i = 1 to n}, which are retrieval items and their bin locations;
	n = the number of retrieval requests in R;
	z = the total travel time to process all retrieval requests;
	X ij = an assignment variable which is set to one if retrieval i and retrieval j are made during the same cycle and zero otherwise for i, j = 1 to n;
	C ij = the travel time to perform one EDC of type E2 processing retrievals i and j for i ≠ j;
	= the average C ij when processing n requests with n/2 cycles of EDC type E2 = 2z/n;
	T r(j) = the travel time between the origin (P/D station) and retrieval j;
	T ij = the travel time between retrieval i and retrieval j;
	= the average T ij when processing n requests with n/2 cycles of EDC type E2;
	b = the normalized rack shape of AS/RS, 0 < b ≤ 1.

We can model the SBSP as a graph matching problem by assigning the retrieval items to the vertices of a graph, where the weight of an edge in the graph will be the cost of matching the vertices connected by that edge. A perfect matching in graph G will be a set of edges, S, in which each vertex in G is adjacent to exactly one of the edges in S. A minimum-cost perfect matching in G is a perfect matching in which the sum of the weights of the edges in S is minimal. In our problem (SBSP), retrieval i and retrieval j will be matched if they are retrieved on the same cycle in which the twin-shuttle system performs one EDC of type E2. The cost of this matching will be the travel time of the shuttle necessary to perform the cycle, C _ij . For any distance metric which obeys the triangle inequality, any solution that has two SC retrievals can be improved by replacing them with an EDC of type E2. One common distance metric used in AS/RS is the Chebyshev distance, in which the travel time from location i to location j = max {horizontal travel time from i to j, vertical travel time from i to j}. This is because most S/R machines move simultaneously in both horizontal and vertical directions. The Chebyshev distance obeys the triangle inequality. Thus, an optimal solution to this matching problem will be an optimal solution of (SBSP). Stating this more formally, we first give the following mathematical formulation for (SBSP).

subject to

where C _ij follows its definition when i ≠ j. When i = j, C _ii takes on a very large positive value for i = 1, …, n, forcing X _ii = 0. This is because each EDC type E2 retrieves two loads from two different locations. Note that the above formulation without constraint (4) becomes identical to the one for the assignment problem. Constraint (4) forces each vertex in G to be adjacent to exactly one of the edges in S.

3. Analysis

In this section, we formally relate (SBSP) to the minimum-cost perfect matching problem. We also derive the expected time analysis for a heuristic to (SBSP) and the lower bound analysis for (SBSP).

When n is even, (SBSP) is equivalent to the minimum-cost perfect matching problem with graph G = {V,C = {C _ij foredge (i, j)}}, where V, the vertices of a graph, are the retrieval items and the weight of edge (i,j) is C _ij .

Because the cost to travel between the origin and each retrieval location is fixed, while only the cost to travel between the two retrievals in a cycle varies, we have the following.

Property 1. (SBSP) with the objective of minimizing total travel time (1/2) ∑ _i,j X _ij C _ij is equivalent to (SBSP) with the objective of minimizing the total travel-between time (1/2)∑ _i,j X _ij T _ij .

If we have an odd number of retrievals, one of them must be fetched in an SC retrieval, which is equivalent in cost to a E2 retrieval with the second retrieval at the origin, which is the P/D station. Thus, we have the following.

Property 2. When n is odd, (SBSP) is equivalent to the minimum-cost perfect matching problem with graph G′ = {V′, C′}, where V′ = VU {0} and C′ = CU {C _0j = 2T _r(j) for j = 1, …, n}.

There are existing polynomial algorithms in the literature to solve the minimum-cost perfect matching problem. We used Blossom4 by Cook and Rohe (1999) which is an efficient implementation of Edmonds' matching algorithm (Edmonds, 1965). The time complexity of this algorithm is O(n ³) (Cook and Rohe, 1999). Since Blossom4 requires integer values, we began by scaling the travel times by a factor of 10⁶. For comparison with this optimal algorithm we implemented two other heuristic algorithms that are often used in industries. One heuristic algorithm always chooses the retrieval item closest to the current retrieval item. This heuristic is called the Nearest Neighbor (NN) algorithm in the literature (Han et al., 1987; Sarker et al., 1991; Meller and Mungwattana, 1997). This heuristic requires a smaller amount of computation, O(n ²). The other algorithm (FCFS) simply retrieves the items in the order they occur in the list, and requires no computation. Some industries use a FCFS approach because of its simplicity or because of limitations imposed by the configuration of the material handling interface to the AS/RS, for example, incoming and outgoing conveyors tied to the AS/RS.

Next we discuss the expected and lower bound analyses for (SBSP). We will make the following assumptions about AS/RS that are commonly used in the literature (Bozer and White, 1984; Lee, 1997). The S/R machine is assumed to move simultaneously in the horizontal and vertical directions with constant speeds. The P/D station is located in the lower-left corner of the rack. We use the same normalized rack of size 1.0 × b without loss of any generality, where b is called the shape factor and 0 < b ≤ 1. A continuous randomized rack is assumed, implying that each bin location is equally utilized.

Property 3. For (SBSP), the expected travel time of EDC type 2 for any method is equal to the sum of the expected travel-between time of EDC type 2 of that method plus the expected single-cycle time by the single-shuttle system, E (SC).

With 2n retrieval requests, there will be n trips. Taking the expected value of the objective z of SBSP and dividing it by n results in the following desired equation:

Bozer and White (1984) showed E(SC) = 1 + b ²/3. Han et al. (1987) studied the NN algorithm for the sequencing problem with a single-shuttle system performing n DCs when there are m open storage locations and n retrieval requests. They showed that the expected travel-between time taken by NN, E(TB _n,m ^NN), is closely approximated by the following equation:

where E(Z _i ) is the expected travel time between a pair of randomly selected locations such that this pair has the smallest travel time among i such pairs and is written as

where

and

Denoting E( TB _2n ^NN) as the expected travel-between time for the NN algorithm to solve (SBSP) with 2n retrievals, we state the following relation.

Theorem 1.

Proof. When 2i of 2n items remain to be retrieved, after choosing one of the retrieval points as the first retrieval, NN chooses the second retrieval that is the closest of the remaining 2i − 1 points. After performing this EDC type E2, NN repeats the process with 2i − 2 remaining retrievals. With a similar application of the above reasoning of Han et al. (1987) to NN for (SBSP) with 2n retrievals, we have the stated result.

We can find a lower bound for (SBSP) as follows. First we find a lower bound on the travel-between time. The smallest travel-between time for any pair of retrievals has to be at least that of the travel-between time to the nearest retrieval. Thus, when we denote E(TB _2n ^LB) as the lower bound for the expected travel-between time for any algorithm to solve (SBSP) with 2n retrievals, we make the following statement.

Corollary 1.

Property 1 shows that minimizing the travel-between distance minimizes the total travel time, which give us the following statement.

Corollary 2.

We will provide numerical results of Equations (9) to (11) in Section 5 where we report the results from experiments conducted with different parameter values.

4. Example

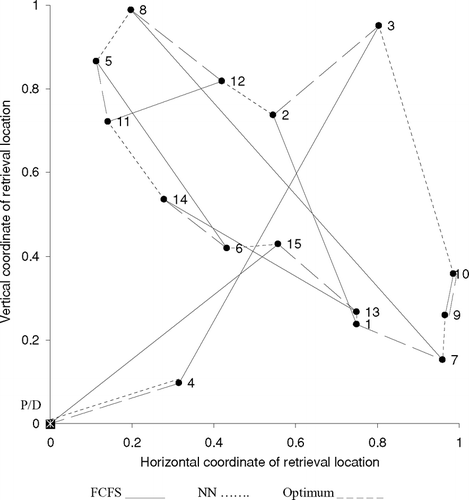
In order to illustrate the proposed Optimum and the two heuristic methods, FCFS and NN, we use an example with 15 retrieval requests. These requests are listed in Table 1 and their locations in the rack are depicted in Fig. 1. The P/D station is located at (0, 0), which is the lower-left corner of the rack. To compute the travel time taken by the twin-shuttle system, we use the Chebyshev distance.

Fig. 1 The 15 retrieval locations and retrieval pairings by three methods.

Table 1 An example problem with 15 retrievals

	x-coordinate	y-coordinate
1	0.749 29	0.237 26
2	0.545 95	0.737 50
3	0.803 17	0.951 08
4	0.314 16	0.096 72
5	0.112 62	0.865 70
6	0.431 87	0.418 52
7	0.959 01	0.151 22
8	0.197 77	0.987 17
9	0.965 15	0.259 69
10	0.984 85	0.358 16
11	0.140 94	0.720 50
12	0.420 41	0.817 62
13	0.748 93	0.267 58
14	0.278 07	0.535 66
15	0.557 41	0.428 08

FCFS performs these retrievals in the order 1, 2, 3, …, 15. This leads to the set of matches shown with the solid lines in Fig. 1. Its total travel time is 15.369 84. The total travel-between time is 4.043 94. The optimal matching is shown with the dashed lines in Fig. 1. Its total travel time is 12.918 63, while its total travel-between time is only 1.592 73. The dotted lines in Fig. 2 illustrate the solution pairs chosen by NN. NN picks up the fictitious retrieval at point 4 in the first cycle. This is also part of the optimal matching. In the subsequent cycles, it matches points 6 with 15, 14 with 11, 2 with 12, 13 with 1, 5 with 8, 3 with 10 and 7 with 9. Although it pairs the two closest points, 1 and 13, it eventually is forced to pair points 3 and 10, which causes it to be worse than optimal. The optimal matching pairs points 1 with 7, 9 with 10, 2 with 3, 8 with 12, 5 with 11, 6 with 14 and 13 with 15, and avoids pairing 3 with 10. NN's total travel time is 12.929 16, and its total travel-between time is 1.603 26.

Fig. 2 Travel-between time by different methods when b = 0.6.

5. Experimental results

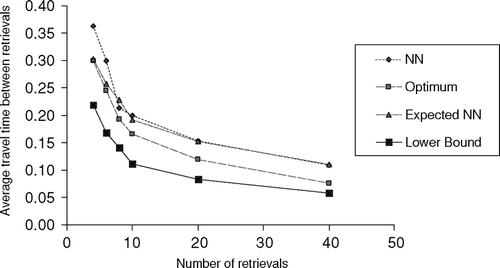
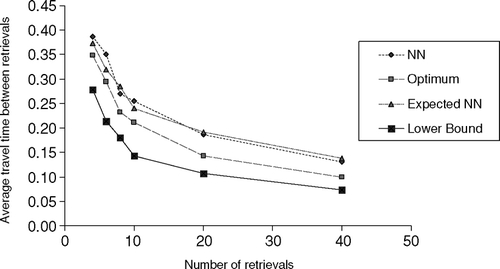
We conducted experiments for the optimal method (Optimum) and the two heuristic methods (FCFS and NN). All these methods were implemented in C++. We used two independent parameters, rack shape b and the number of retrievals n, when generating test problems. In data set I, we used a normalized square rack (i.e., b = 1), in which the time to travel from the bottom to the top of the rack was the same as the time to travel from the left to the right side of the rack. These results are reported in Table 2. In data set II, the vertical travel time was 0.6 times that of the horizontal (i.e., b = 0.6) and these results are reported in Table 3. In data set III, the vertical travel time was 0.2 times that of the horizontal (i.e., b = 0.2) and these results are reported in Table 4. In each of these data sets, we chose the bin position (x, y) coordinates of the n retrieval items randomly from a uniform distribution such that 0 < x ≤ 1 and 0 < y ≤ b. This resembles the randomized storage policy commonly used in AS/RS. The number of retrievals n ranged from four to 320. We generated 15 problems for each combination of b and n. To each problem generated, we applied the three methods and collected the following results for the solution that each method found: average cycle time of EDC type E2, , and average travel-between time, . Table 2, Table 3, Table 4 summarize the average results of 15 problems for each b and n. In Table 5, we give the results of the 15 individual problems for the case when b = 0.2 and n = 10.

Table 5 Comparison of Optimum, NN and FCFS with 15 individual problems when b = 0.2 and n = 10

Optimum		NN		FCFS
0.0992 98	0.8602 60	0.1106 68	0.8716 30	0.1185 50	0.8795 12
0.1242 04	1.1761 90	0.1242 04	1.1761 90	0.1960 26	1.2480 10
0.1137 82	0.8781 84	0.1171 82	0.8815 84	0.3739 70	1.1383 70
0.0952 28	1.2269 80	0.1252 32	1.2569 80	0.3896 12	1.5213 60
0.1056 88	1.2827 20	0.1564 22	1.3334 50	0.4157 70	1.5928 00
0.0899 80	0.9238 30	0.1030 70	0.9369 20	0.2352 90	1.0691 40
0.1341 90	1.3677 50	0.2526 54	1.4862 10	0.3214 22	1.5549 80
0.1466 64	1.4029 30	0.1744 20	1.4306 80	0.2925 66	1.5488 30
0.1173 28	1.1668 70	0.1247 56	1.1743 00	0.5100 56	1.5596 00
0.1176 46	1.0477 90	0.1176 46	1.0477 90	0.4983 78	1.4285 20
0.1026 50	1.1909 90	0.1563 76	1.2447 10	0.3989 88	1.4873 20
0.1261 26	1.6762 30	0.1313 34	1.6814 40	0.2494 82	1.7995 80
0.0994 14	1.0662 60	0.0994 14	1.0662 60	0.3581 04	1.3249 50
0.0994 74	1.2611 30	0.0994 74	1.2611 30	0.3303 38	1.4919 90
0.1153 58	1.0392 60	0.2439 08	1.1678 10	0.4080 68	1.3319 70

NN and FCFS took less than 0.1 second to run on a Pentium-4 PC, even for the largest data set (i.e., n = 320). Optimum took less than 5 seconds to run for the largest data set, and under 1 second for all other data sets.

For very small data sets (n = 4), FCFS found an optimal solution for 12 problems, but found at least a 12% larger for the other 33 problems. As n increased to 320, the FCFS value remained more or less unchanged because of its FCFS processing, while the Optimum value decreased. This caused the FCFS performance to become relatively worse as n increased. When n = 320, the FCFS value was at least 12 times larger than the Optimum value and the FCFS value was at least 28% larger than the Optimum value.

As n → ∞, the FCFS value converges to the expected DC time of a single-shuttle S/R machine, E(DC), by Bozer and White (1984), which is E(DC) = 4/3 + b ²/2 − b ³/30. This is expected because both the opening and retrieval locations of DC are randomly selected from the storage rack. This complies with our experimental results. For example, when n = 320 and b = 1, E(DC) = 1.8 while those 15 results of FCFS range between 1.728 24 and 1.856 83 with an average of 1.791 39.

Optimum outperformed NN for all n. For small n < 10, NN found an optimal solution about half of the time. In one problem with b = 0.2 and n = 10, however, the NN value was 110% larger than the Optimum value. On average of 15 replicates at n = 40, the NN value was 30% larger than the Optimum value for data sets I and III and 44% larger for data set II. In terms of , however, the difference between NN and Optimum tends to decrease as n increases. For example, when n = 320, the NN value was 0.81% larger for data set I, 0.72% larger for data set II and 0.44% larger for data set III. This is because as n increases, the average travel time between a retrieval location and the P/D remains the same, while the average travel time between two retrieval points decreases for both NN and Optimum.

As n → ∞, the value of both NN and Optimum converges to the expected SC time of the single-shuttle system, E(SC) = 1 + b ²/3. Both the travel time between the close-neighbor retrieval pair found by NN and the travel time between the matched pair found by Optimum tend to decrease as n increases. Consequently, converges to zero and E( TB _2n ^LB) approaches zero as n → ∞. From property 3, E(SC) serves as an asymptotic lower bound on for NN and Optimum as n → ∞. Optimum converges faster than NN since it finds a better solution. Our experimental results show that when n ≥ 80, the Optimum value is close to the asymptotic lower bound E(SC). For example, when n = 80, Optimum = 1.376, 1.144 and 1.044 while E(SC) = 1.333, 1.120 and 1.013, for b = 1, 0.6 and 0.2, respectively (see Table 2, Table 3, Table 4).

Table 2 Comparison of Optimum, NN and FCFS when b = 1 (square rack)

	Optimum		NN		FCFS
Number of retrievals
4	0.347 59	1.742 20	0.386 42	1.781 04	0.539 62	1.934 23
6	0.294 16	1.683 42	0.350 52	1.739 78	0.490 22	1.879 48
8	0.231 92	1.627 65	0.270 13	1.665 86	0.495 01	1.890 74
10	0.211 56	1.611 49	0.254 74	1.654 66	0.486 13	1.886 05
20	0.143 26	1.463 54	0.186 80	1.507 08	0.432 52	1.752 80
40	0.099 03	1.417 10	0.130 51	1.448 58	0.430 85	1.748 92
80	0.065 94	1.376 12	0.087 82	1.398 00	0.451 66	1.761 85
160	0.046 90	1.369 28	0.061 13	1.383 51	0.455 76	1.778 14
320	0.032 35	1.361 15	0.043 39	1.372 19	0.462 58	1.791 39

Table 3 Comparison of Optimum, NN and FCFS when b = 0.6

	Optimum		NN		FCFS
Number of retrievals
4	0.299 66	1.361 33	0.362 51	1.424 18	0.403 56	1.465 23
6	0.245 05	1.273 24	0.299 17	1.327 36	0.387 05	1.415 23
8	0.192 75	1.249 23	0.213 15	1.269 63	0.382 00	1.438 48
10	0.165 21	1.259 72	0.199 78	1.294 30	0.392 48	1.486 99
20	0.119 40	1.222 47	0.153 42	1.256 49	0.413 12	1.516 19
40	0.075 61	1.186 50	0.109 09	1.219 98	0.387 95	1.498 85
80	0.051 88	1.143 83	0.075 81	1.167 77	0.388 46	1.480 42
160	0.035 22	1.146 65	0.049 22	1.160 64	0.393 24	1.504 67
320	0.024 56	1.136 67	0.032 77	1.144 88	0.393 31	1.505 41

Table 4 Comparison of Optimum, NN and FCFS when b = 0.2

	Optimum		NN		FCFS
Number of retrievals
4	0.228 55	1.286 08	0.233 85	1.291 38	0.362 18	1.419 71
6	0.149 77	1.224 00	0.159 62	1.233 85	0.330 08	1.404 32
8	0.132 23	1.198 05	0.150 81	1.216 64	0.339 48	1.405 30
10	0.112 47	1.171 16	0.142 45	1.201 14	0.339 77	1.398 46
20	0.067 60	1.110 37	0.088 26	1.131 03	0.353 82	1.396 59
40	0.044 81	1.064 26	0.059 02	1.078 47	0.353 70	1.373 15
80	0.030 42	1.044 29	0.040 22	1.054 10	0.353 97	1.367 84
160	0.020 98	1.034 68	0.026 77	1.040 47	0.352 69	1.366 39
320	0.014 54	1.022 32	0.019 02	1.026 80	0.344 09	1.351 88

Next we discuss how this reduction in travel time can be translated into a throughput increase, where the throughput is the number of retrievals per unit time processed by the twin-shuttle AS/RS performing EDC type 2 operations. We compute the throughput R as R = 2 M / ( + 4r), where M is the number of aisles and r is the pickup or deposit time of a unit-load. The largest throughput improvement by Optimum observed among all individual problems was 27% over NN and 39% over FCFS when r is negligible (r ≪ ). In the average of 15 replicates, the largest throughput improvement by Optimum was 5% over NN and 32% over FCFS. This improvement over NN occurred when n is small, while the best improvement over FCFS occurred when n is large.

We look at the throughput improvement with twin-shuttle AS/RS using Optimum over single-shuttle AS/RS for the shift-based operation. Single-shuttle AS/RS perform SCs in the shift-based operation so its system throughput R _s is computed as R _s = M/ (E(SC) + 2r). The twin-shuttle system using Optimum significantly improves the throughput. In the average of 15 replicates, it achieved at least a 36% improvement over the single-shuttle system for any b even when n = 4 and r = 0.2, and at least a 43% improvement when n = 10 and r = 0.2. As n increases and r decreases, the improvement increases towards 100%. With this improvement, the twin-shuttle system using Optimum can meet the throughput requirements with a smaller number of aisles M, which can result in a potential cost saving over single-shuttle systems.

In Section 4, we gave analytical equations for E(TB _2n ^NN) and E(TB _2n ^LB). We now compare them with our experimental results. When n ≥ 10, the value of NN was close to the predicted approximation of E(TB _2n ^NN) from Equation (9). As Table 6 and Figures 2 and 3 show, when n was at least eight, the value of NN was within 7% of the predicted value. Applying Property 3, the percent deviation between the experimental and predicted values of NN was far less. The deviation between the two was within 3.5%. As Fig. 2 and Fig. 3 show, the value of Optimum was between that predicted value and the theoretical lower bound E( TB _2n ^LB) of Equation (10). As Table 7 shows, the optimal value was consistently over 30% above the lower bound. Applying Corollary 2, this corresponds to a difference of less than 7% over the lower bound on .

Fig. 3 Travel-between time by different methods when b = 1.0.

Table 6 Percentage difference between NN T and predicted E(TB _2n ^NN)

	b
Number of retrievals	1	0.6
4	3.77	19.86
6	9.64	16.20
8	−5.15	−6.59
10	6.17	4.53
20	−2.29	0.68
40	−5.76	−0.37

Table 7 Percentage difference between optimal T and lower bound E(TB _2n ^LB)

	b
Number of retrievals	1	0.6
4	24.99	36.96
6	37.26	46.30
8	28.77	37.29
10	48.57	49.10
20	33.77	43.51
40	34.19	31.95

6. Conclusions

The continuing need for high-throughput AS/RS resulted in the introduction of an S/R machine that can carry more than one unit-load. However, this technology involves a large capital investment so careful operating methods are desired to make the most of its capabilities. The previous research performed on the twin-shuttle sequencing problem has focused on sequencing QCs using greedy-style heuristics. In this paper, we introduced the SBSP for twin-shuttle AS/RS where replenishment and depletion occur during different shifts. We presented the efficient Optimum method with an O(n³) running time by transforming (SBSP) into the minimum-cost perfect matching problem, where n is the number of retrievals. To our knowledge, this is the first polynomial optimal method in the literature on multi-shuttle AS/RS sequencing methods. We compared the proposed Optimum method with two heuristic methods that are often used in industrial practice; the FCFS and NN heuristics. Experimental results with various test problems of different rack shapes and up to n = 320 show that FCFS took up to a 12 times longer average travel-between time than Optimum while NN took up to 1.1 times longer. With this reduction of travel time by Optimum, a throughput improvement of about 40 and 20% is possible over FCFS and NN, respectively. In comparison with a single-shuttle system, the results show that the twin-shuttle system using the proposed Optimum method improves throughput by at least 36% for n values as small as n = 4, with larger improvements for larger n. We also presented an analytical model for the expected performance of NN which is reasonably accurate in comparison with experimental results. Meller and Mungwattana (1997) reported a case study on triple-shuttle AS/RS used in a textile manufacturing firm. We leave for future research the problem of developing solution methods for triple or higher-shuttle AS/RS.

Biographies

Daniel R. Dooly is an Assistant Professor of Computer Science at Southern Illinois University Edwardsville. He holds a B.A. in Mathematics from Greenville College, an M.S. in Mathematics from Southern Illinois University Edwardsville and a D.Sc. in Computer Science from Washington University in St. Louis. His current research interests are in algorithms and machine learning. He is a member of ACM, IEEE Computer Society and IIE. His papers have appeared in Journal of Machine Learning Research, Journal of the ACM, Naval Research Logistics, and0 Telecommunication Systems.

Heungsoon Felix Lee is Professor of Industrial and Manufacturing Engineering at Southern Illinois University Edwardsville. He holds a B.S. in Industrial Engineering from Hanyang University in Korea, an M.S. in Industrial Engineering and Management from Oklahoma State University and a Ph.D. in Industrial and Operations Engineering from the University of Michigan. His current research interests are in applications of OR and IT to manufacturing systems. He is a member of IIE, SME, Tau Beta Pi and Phi Kappa Phi. He has authored a book and his papers appear in numerous journals including International Journal of Flexible Manufacturing Systems, Journal of Manufacturing Systems, Performance Evaluation, Expert Systems with Applications, IIE Transactions, Naval Research Logistics, International Journal of Production Research, and Telecommunication Systems.

Acknowledgements

We thank the Department Editor and anonymous referees for their helpful comments and suggestions that improved the quality and presentation of this paper.