Minimum Bucket and Car Battery Problems

Abstract

A solar car needs 5 fully charged batteries to run, and it depletes those batteries in 5 hours. The batteries are rechargeable, and solar panels on the car are able to charge 3 batteries simultaneously. It takes 3 hours for the solar panels to finish charging 3 batteries. Furthermore, batteries cannot be charging and in use at the same time. If the car always starts running as soon as 5 full batteries are available, and the solar panels can only operate if 3 empty batteries are available, how many batteries are needed so that the car can eventually run without stopping? We investigate this resource optimization problem and its different variations.

Systems often have inputs and outputs that utilize the same resources, and it is a common problem to minimize the amount of resources needed to reduce costs. For example, consider the following problem about a solar car. The car needs 5 fully charged batteries to run, and it depletes those batteries in 5 hours. The batteries are rechargeable, and solar panels on the car are able to charge 3 batteries simultaneously. It takes 3 hours for the solar panels to finish charging the batteries. Furthermore, batteries cannot be charging and in use at the same time. If the car always starts running as soon as 5 full batteries are available, and the solar panels can only operate if 3 empty batteries are available, how many batteries are needed so that the car can eventually run without stopping?

As a model for this rechargeable car battery problem, we consider a system of buckets that handle a certain kind of flow (electricity in the case of batteries, but the flow could also represent water, work, etc). The size of each bucket is 1. Each bucket has an inlet and outlet, and at most one of them is active at any moment; this corresponds to the restriction that the batteries cannot be in use and also be charging at the same time. Additionally, there is an inflow and outflow in the system, which each have a constant total flow speed of 1 per time unit. In the car battery problem, the solar panels correspond to the inflow (charging the batteries), running the car corresponds to the outflow (depleting the batteries), and the time units are measured in hours.

Let I and O be two positive integers dictating how the inflow and outflow of the system operate, respectively. When a bucket inlet is active, the inflow speed to the bucket is $\frac{1}{I}$; and when the outlet is active, the outflow speed is $\frac{1}{O}$. The total input flow speed is 1; hence, I buckets are needed to accommodate the inflow. Similarly, the total output flow speed is 1; hence, O buckets are needed to produce the output flow. The inflow would therefore fill up I buckets in I time units, and the outflow would deplete O buckets in O time units. The system runs as follows.

• At time 0, all buckets are empty. This is the initial bucket condition.

• The input flow starts filling up I empty buckets at time 0 (the inlets of these I buckets are activated). When these I buckets are filled up (after I time units), another set of I empty buckets (if available) will immediately be allocated to take the input flow. If there are not I empty buckets, then the input flow stops until there are I empty buckets again.

• At some point when there are O full buckets, the output flow initiates; the outlets of these O buckets activate and the output flow continues until they become empty (after O time units). Note that the initial output flow starts after $\lceil \frac{O}{I}\rceil ·I$ time units (when at least O full buckets become available for the first time). When these O buckets are completely emptied (at which point they can again be reused for input flow), then the output flow initiates on another set of O full buckets (if available). If there are not O full buckets, then the output flow stops until O full buckets become available again.

Definition

(Stable Flow). Given enough buckets, both the inflow and outflow will eventually run continuously, since the inflow and outflow speeds match (both are 1). We will call flow with nonstop inflow and outflow stable flow.

We would like to find $B_{\mathrm{\text{min}}}$, the minimal number of buckets needed in the system such that a stable flow can eventually be reached.

We consider the following problems:

1. The base case (as described above): given I and O, find $B_{\mathrm{\text{min}}}$.

2. The case with a threshold T for initiating the output flow. In the base case, the output flow starts as soon as there are O full buckets. For this case, the output flow only activates when there are T full buckets, where $T\ge O$ (in the base case, T = O). Given I, O, and T, find $B_{\mathrm{\text{min}}}$.

3. The case with F₀ initially full buckets at time 0. In the base case, there are 0 full buckets at time 0. For this case, there are F₀ full buckets at time 0, where $O>F_0\ge 0$ (in the base case, $F_0=0$). Given I, O, and F₀, find $B_{\mathrm{\text{min}}}$.

4. The case with both a threshold T and F₀ initially full buckets. This is the most general case, combining the two above cases. In this case, we relax the restraint on F₀ to be $T>F_0\ge 0$. Given I, O, T, and F₀, find $B_{\mathrm{\text{min}}}$.

It will be enough to solve case 4, since the other problems are special cases of case 4.

Example

For the car battery problem, the solar panels charge 3 batteries in 3 hours, so I = 3. The car runs on 5 batteries and depletes them in 5 hours, so O = 5. The car is able to run as soon as there are 5 fully charged batteries, so T = 5. Finally, there are no initially charged batteries, so $F_0=0$. The system progresses as follows.

• At time 0: the input flow starts filling buckets 0, 1, 2.

• At time 1: buckets 0, 1, 2 are $\frac{1}{3}$ filled.

• At time 2: buckets 0, 1, 2 are $\frac{2}{3}$ filled.

• At time 3: buckets 0, 1, 2 are completely filled; not enough full buckets are available for the output flow, while the input flow starts filling buckets 3, 4, 5.

  ⋮

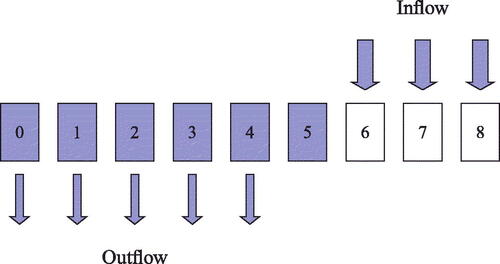
• At time 6: buckets 0, 1, 2, 3, 4, 5 are completely filled; the output flow starts draining buckets 0, 1, 2, 3, 4, while the input flow moves on to buckets 6, 7, 8.

Figure 1 shows the system at time 6.

Fig. 1 The example system at time 6. The input flow activates on buckets 6, 7, 8, and the output flow begins draining buckets 0, 1, 2, 3, 4.

Solution

It is clear that having an unlimited number of buckets would eventually allow the system to have both flows run nonstop. So, we first assume that there are an unlimited number of buckets, and then find the maximum number of the buckets that are in use at once, which would be $B_{\mathrm{\text{min}}}$.

Definition

(States). Given P_O such that $0\le P_O<O$ and P_I such that $0\le P_I<I$, we represent the state of the system where F buckets are full, O buckets are $\frac{P_O}{O}$ full, and I buckets are $\frac{P_I}{I}$ full by $S(F,P_O,P_I)$. In such a state, the output flow has been running on its current set of O buckets for $O-P_O$ time units, and the input flow has been running on its current set of I buckets for P_I time units.

According to rules described by the problem statement, the state $S(F,P_O,P_I)$ transitions to a new state after 1 time unit as follows.

• If P_O = 0 and $F\ge T$, then in the next state F decreases by O and P_O becomes O – 1.

• If P_O = 0 and F < T, then the outward flow stops, so P_O stays at 0.

• If $P_O\ne 0$, then P_O becomes $P_O-1$.

• If $P_I=I-1$, then in the next state F increases by I and P_I becomes 0.

• If $P_I\ne I-1$, then P_I becomes $P_I+1$. Even if P_I = 0, the input flow will still be guaranteed to continue because we assume there are an unlimited number of buckets; so, there will always be enough empty buckets to accommodate the input flow.

• In the case where both P_O = 0 and $P_I=I-1$, F would transition to $F+I-O$.

By definition, stable flow consists of nonstop outward and inward flows. Therefore, when the stable flow first starts, the output flow must have previously been stopped, and the input flow must have just finished completely filling enough buckets to allow the output flow to activate. This corresponds to a state of the form $S(n,0,0)$ at the beginning of the stable flow (for some positive integer n).

Definition

(Stable States). Call a state $S(F,P_O,P_I)$ stable if using this as the initial state allows the output flow to never stop (the input flow already runs continuously because of our assumption that there are an unlimited number of empty buckets). In other words, any stable state induces stable flow.

Note that all states that appear in the stable flow would be stable. Since the outward flow never stops, then P_O iterates through the numbers $0,O-1,O-2,\dots ,1$, while P_I loops through the numbers $0,1,2,\dots ,I-1$. Consequently, the cycle of states during stable flow has length $\text{lcm}(I,O)$. Furthermore, for each state $S(F,P_O,P_I)$ that follows, the sum $F+P_O+P_I$ is invariant, since the inward flow rate matches the outward flow rate, and both flows never stop.

The progression of states in the car battery problem is shown in the following tables.

Table

Time	F	PO	PI
0	0	0	0
1	0	0	1
2	0	0	2
3	3	0	0
4	3	0	1
5	3	0	2
6	6	0	0
7	1	4	1
8	1	3	2
9	4	2	0
10	4	1	1
11	4	0	2
12	7	0	0
13	2	4	1
14	2	3	2
15	5	2	0
16	5	1	1
17	5	0	2
18	3	4	0
19	3	3	1
20	3	2	2
21	6	1	0
22	6	0	1
23	1	4	2
24	4	3	0
25	4	2	1
26	4	1	2
27	7	0	0

In this example, the stable flow starts with $S(7,0,0)$ at time 12, and $S(7,0,0)$ reappears at time 27, so the stable flow has cycle length $27-12=15=\text{lcm}(3,5)$. We can see that $S(7,0,0)$ and $S(3,3,1)$ are stable states, but $S(6,0,0)$ is not stable because the outward flow stops between time 11 and 12.

Throughout the rest of the proof we let $d=\mathrm{\text{gcd}}(I,O)$.

Lemma 1.

Let x be a positive integer and k be a nonnegative integer. If the state $S(x-k,0,k)$ appears after $S(x,0,0)$, then $d|k$.

Proof.

First, we claim that both the inflow and outflow do not stop in the time between $S(x,0,0)$ and $S(x-k,0,k)$. Although $S(x,0,0)$ need not be a stable state, the fact that $(x-k)+0+k=x+0+0$ means that both inward and outward flows do not stop during the time between the 2 states. Suppose it takes t time units to get from $S(x,0,0)$ to $S(x-k,0,k)$. As both the inflow and outflow do not stop for the time between the 2 states, then P_O and P_I cycle in the manner mentioned earlier, so we have $$t\equiv 0\hspace{1em}\left(\mathrm{\text{mod}}O\right)\hspace{1em}\text{and}\mathit{\hspace{1em}t}\equiv \mathit{k\hspace{1em}}\left(\mathrm{\text{mod}}I\right).$$

Let t = aO and $t=\mathit{\text{bI}}+k$, so that $k=\mathit{\text{aO}}-\mathit{\text{bI}}$. We have $d|\mathit{\text{aO}}$ and $d|\mathit{\text{bI}}$; therefore $d|\mathit{\text{aO}}-\mathit{\text{bI}}$, i.e., $d|k$. □

Lemma 2.

$S(x,0,0)$ is stable if and only if $x\ge T+I-d$.

Proof.

Consider the states of the form $S(x-k,0,k)$ that appear after $S(x,0,0)$. By Lemma 1 we have $d|k$. Combined with $d|I$ and $0\le k<I$, we get $0\le k\le I-d$.

If $S(x,0,0)$ is stable, we know that the output flow never stops. Thus, at any state $S(x-k,0,k)$, we must have $x-k\ge T$ so that there are enough full buckets to accommodate the output flow. Conversely, if we have $x-k\ge T$ for all possible states $S(x-k,0,k)$ that come after $S(x,0,0)$, then the output flow never stops so we know $S(x,0,0)$ is stable.

If $x\ge T+I-d$, then for all possible k, $x-k\ge (T+I-d)-(I-d)=T$, so the state $S(x,0,0)$ is stable.

Now assume $S(x,0,0)$ is stable. By Bézout’s lemma [1, p.7–11], there exist integers m, n such that mO + nI = d. Since $\mathit{\text{mO}}+\mathit{\text{nI}}=d\iff (m+I)O+(n-O)I=d$, we can stipulate without loss of generality that m > 0 by repeatedly adding I to m and subtracting O from n as needed. Now we have $$\frac{(I-d)m}{d}O+\frac{(I-d)n}{d}I=\frac{I-d}{d}(\mathit{\text{mO}}+\mathit{\text{nI}})=I-d.$$

If we let $t=\frac{(I-d)m}{d}O$, then $t\equiv 0\hspace{1em}(\mathrm{\text{mod}}O)$ and $t\equiv I-\mathit{d\hspace{1em}}(\mathrm{\text{mod}}I)$. Then the state at $t=\frac{(I-d)m}{d}O$ after $S(x,0,0)$ is $S(x-I+d,0,I-d)$, since the inflow and outflow run continuously. By our earlier work we must have $x-I+d\ge T$; hence, $x\ge T+I-d$. This concludes the proof of Lemma 2. □

Lemma 3.

If $x<T+I-d$, then $S(x,0,0)$ is eventually followed by the state $S(x\prime ,0,0)$, where $x<x\prime <T+I$ and $x\equiv x\prime \hspace{1em}(\mathrm{\text{mod}}d)$.

Proof.

By Lemma 2, $x<T+I-d$ means $S(x,0,0)$ is not stable, so by the definition of a stable state, the output flow stops at some point. Thus, there exists a state $S(x-k,0,k)$ that appears after $S(x,0,0)$ such that $x-k<T$. From here, the output flow ceases, so $S(x-k,0,k)$ is followed by $$S(x-k,0,k+1),S(x-k,0,k+2),\dots ,S(x-k+I,0,0).$$

Let $x\prime =x-k+I$. From k < I we have $x<x\prime$, and we also have $x\prime =(x-k)+I<T+I$. Finally, by Lemma 1, $d|k$. This, combined with $d|I$, yields $x\prime =x-k+I\equiv \mathit{x\hspace{1em}}(\mathrm{\text{mod}}d)$. This completes the proof of Lemma 3. □

Lemma 4.

Let y represent the unique number such that $y\equiv F_0\hspace{1em}(\mathrm{\text{mod}}d)$ and $T+I-d\le y<T+I$. Then starting from the initial state, eventually the stable state $S(y,0,0)$ is reached.

Proof.

Let $x_0=F_0<T\le T+I-d$, so that the initial state is $S(x_0,0,0)$. For any nonnegative integer i, we let the next state after $S(x_i,0,0)$ (in chronological order) that is of the form $S(x,0,0)$ be $S(x_{i+1},0,0)$. By Lemma 3, we know the sequence $\left\{x_i\right\}$ exists and is strictly increasing until we have some x_N such that $T+I-d\le x_N<T+I$ for the first time. At this point $S(x_N,0,0)$ is stable by Lemma 2, so it starts the stable flow, and $\left\{x_i\right\}$ becomes constant. Also by Lemma 3, the sequence $\left\{x_i\right\}$ is constant modulo d, so $x_N\equiv x_0\equiv F_0\hspace{1em}(\mathrm{\text{mod}}d)$. This implies y = x_N, so $S(y,0,0)$ is a stable state that is eventually reached. □

Remark.

Because $I\equiv d\equiv 0\hspace{1em}(\mathrm{\text{mod}}d)$, we can find $$y=T+I-d+\left((F_0-T)\hspace{1em}\left(\mathrm{\text{mod}}d\right)\right),$$where the remainder is nonnegative and less than d.

Solution to original problem

Finally, we will answer the original problem. Let y be defined as in Lemma 4. As mentioned earlier, finding $B_{\mathrm{\text{min}}}$ is equivalent to finding the maximum number of buckets that are required for any individual state to continue in the repeating cycle induced by $S(y,0,0)$.

First let us suppose $P_O\ne 0$. At any state $S(F,P_O,P_I)$ with $P_O\ne 0$, there are F full buckets, O buckets required to accommodate the outward flow, and I buckets required to accommodate the inward flow (even if P_I = 0, there must be I empty buckets available for filling). Therefore, for $P_O\ne 0$ it suffices to maximize F. Since $F+P_O+P_I=y$ is invariant, then we must minimize $P_O+P_I$. Let the state $S(F,P_O,P_I)$ occur t time units after $S(y,0,0)$. Then $$t\equiv O-P_O\hspace{1em}\left(\mathrm{\text{mod}}O\right)\hspace{1em}\text{and}\mathit{\hspace{1em}t}\equiv P_I\hspace{1em}\left(\mathrm{\text{mod}}I\right).$$

Suppose $t=\mathit{\text{aO}}-P_O$ and $t=\mathit{\text{bI}}+P_I$. Then $P_O+P_I=\mathit{\text{aO}}-\mathit{\text{bI}}$, so since $d|\mathit{\text{aO}}$ and $d|\mathit{\text{bI}}$, then $d|P_O+P_I$. Since $P_O\ne 0$ then $P_O+P_I>0$, so $P_O+P_I\ge d$. Therefore, $F\le y-d$.

We now show this maximum is achievable. By Bézout’s lemma [1, p.7–11], there exist integers m, n such that mO + nI = d, so $$\frac{(O-d)m}{d}O+\frac{(O-d)n}{d}I=\frac{O-d}{d}(\mathit{\text{mO}}+\mathit{\text{nI}})=O-d.$$

If we let $t=\frac{(O-d)n}{d}I$ then we get P_O = d and P_I = 0, so $P_O+P_I=d$ and $F=y-d$ achieves the maximum possible value of F. This yields a total of $y-d+I+O$ buckets as the maximum amount of buckets in use at once (for the case of $P_O\ne 0$). In the example presented earlier, $(y,d,I,O)=(7,1,3,5)$. The state requiring the most buckets is $S(6,1,0)$, which uses $7-1+3+5=14$ buckets.

Now suppose P_O = 0. At any state $S(F,0,P_I)$, F + I buckets are necessary to allow both flows to continue running. However, $F+I\le y+I\le y-d+I+O$, so at most $y-d+I+O$ buckets are in use for all of these cases as well.

Therefore, $B_{\mathrm{\text{min}}}=y-d+I+O$. However, recall that $y=T+I-d+((F_0-T)\hspace{1em}(\mathrm{\text{mod}}d))$. The following theorem sums up all of our work.

Theorem 1

(Minimum number of buckets required for stable flow). Let a bucket system be defined by the input flow parameter I, output flow parameter O, threshold $T\ge O$, and initial number of full buckets $0\le F_0<T$, and let $d=\mathrm{\text{gcd}}(I,O)$. The minimum number of buckets required to eventually allow the system to have both input and output flows run nonstop is $$B_{\mathrm{\text{min}}}=2I+O+T-2d+\left((F_0-T)\hspace{1em}\left(\mathrm{\text{mod}}d\right)\right).$$

The remainder modulo d should be interpreted as nonnegative and less than d.

Using our theorem, we can simplify the expression for $B_{\mathrm{\text{min}}}$ for the 4 proposed problems as shown in the following table (with even more simplification when d = 1).

Table

Conditions	d = 1	d > 1
$T=O,F_0=0$	$2I+2O-2$	$2I+2O-2d$
$T\ge O,F_0=0$	$2I+T+O-2$	$2I+O+T-2d+(-\mathit{T\hspace{1em}}(\mathrm{\text{mod}}d))$
$T=O,O>F_0\ge 0$	$2I+2O-2$	$2I+2O-2d+(F_0\hspace{1em}(\mathrm{\text{mod}}d))$
$T\ge O,T>F_0\ge 0$	$2I+T+O-2$	$2I+O+T-2d+((F_0-T)\hspace{1em}(\mathrm{\text{mod}}d))$

As in the theorem, all the remainders modulo d should be interpreted as nonnegative and less than d.

Going back to the car battery problem, which has $(I,O,T,F_0)=(3,5,5,0)$ and $d=\mathrm{\text{gcd}}(3,5)=1$, the theorem tells us that $2·3+2·5-2=14$ batteries are necessary to allow the car to eventually run without stopping.

Additional information

Notes on contributors

Raymond Feng

Raymond Feng ([email protected]) is currently a second year undergraduate studying Computer Science and Mathematics at MIT. He is most interested in combinatorics, number theory, and theoretical computer science. In his free time, he enjoys playing ultimate frisbee with MIT’s Grim Beavers.