Invariant tests based on M-estimators, estimating functions, and the generalized method of moments

ABSTRACT

We study the invariance properties of various test criteria which have been proposed for hypothesis testing in the context of incompletely specified models, such as models which are formulated in terms of estimating functions (Godambe, 1960) or moment conditions and are estimated by generalized method of moments (GMM) procedures (Hansen, 1982), and models estimated by pseudo-likelihood (Gouriéroux, Monfort, and Trognon, 1984b,c) and M-estimation methods. The invariance properties considered include invariance to (possibly nonlinear) hypothesis reformulations and reparameterizations. The test statistics examined include Wald-type, LR-type, LM-type, score-type, and C(α)−type criteria. Extending the approach used in Dagenais and Dufour (1991), we show first that all these test statistics except the Wald-type ones are invariant to equivalent hypothesis reformulations (under usual regularity conditions), but all five of them are not generally invariant to model reparameterizations, including measurement unit changes in nonlinear models. In other words, testing two equivalent hypotheses in the context of equivalent models may lead to completely different inferences. For example, this may occur after an apparently innocuous rescaling of some model variables. Then, in view of avoiding such undesirable properties, we study restrictions that can be imposed on the objective functions used for pseudo-likelihood (or M-estimation) as well as the structure of the test criteria used with estimating functions and generalized method of moments (GMM) procedures to obtain invariant tests. In particular, we show that using linear exponential pseudo-likelihood functions allows one to obtain invariant score-type and C(α)−type test criteria, while in the context of estimating function (or GMM) procedures it is possible to modify a LR-type statistic proposed by Newey and West (1987) to obtain a test statistic that is invariant to general reparameterizations. The invariance associated with linear exponential pseudo-likelihood functions is interpreted as a strong argument for using such pseudo-likelihood functions in empirical work.

KEYWORDS:

• C(α) test
• estimating function
• generalized method of moment (GMM)
• hypothesis reformulation
• invariance
• Lagrange multiplier test
• likelihood ratio test
• linear exponential model
• M-estimator
• measurement unit
• nonlinear model
• pseudo-likelihood
• reparameterization
• score test
• testing
• Wald test

JEL CLASSIFICATION:

• C3
• C12

1. Introduction

Model and hypothesis formulation in econometrics and statistics typically involve a number of arbitrary choices, such as the labelling of independent and identically distributed (i.i.d.) observations or the selection of measurement units. Further, in hypothesis testing, these choices often do not affect the interpretation of the null and the alternative hypotheses. When this is the case, it appears desirable that statistical inference remain invariant to such choices; see Hotelling (1936), Pitman (1939), Lehmann (1983, Chapter 3), Lehmann (1986, Chapter 6), and Ferguson (1967). Among other things, when the way a null hypothesis is written has no particular interest or when the parameterization of a model is largely arbitrary, it is natural to require that the results of test procedures do not depend on such choices. This holds, for example, for standard t and F tests in linear regressions under linear hypothesis reformulations and reparameterizations. In nonlinear models, however, the situation is more complex.

It is well known that Wald-type tests are not invariant to equivalent hypothesis reformulations and reparameterizations; see Cox and Hinkley (1974, p. 302), Burguete et al. (1982, p. 185), Gregory and Veall (1985), Vaeth (1985), Lafontaine and White (1986), Breusch and Schmidt (1988), Phillips and Park (1988), and Dagenais and Dufour (1991). For general possibly nonlinear likelihood models (which are treated as correctly specified), we showed in previous work (Dagenais and Dufour, 1991, 1992; Dufour and Dagenais, 1992) that very few test procedures are invariant to general hypothesis reformulations and reparameterizations. The invariant procedures essentially reduce to likelihood ratio (LR) tests and certain variants of score [or Lagrange multiplier (LM)] tests where the information matrix is estimated with either an exact formula for the (expected) information matrix or an outer product form evaluated at the restricted maximum likelihood (ML) estimator. In particular, score tests are not invariant to reparameterizations when the information matrix is estimated using the Hessian matrix of the log-likelihood function evaluated at the restricted ML estimator. Further, C(α) tests are not generally invariant to reparameterizations unless special equivariance properties are imposed on the restricted estimators used to implement them. Among other things, this means that measurement unit changes with no incidence on the null hypothesis tested may induce dramatic changes in the conclusions obtained from the tests and suggests that invariant test procedures should play a privileged role in statistical inference.

In this article, we study the invariance properties of various test criteria which have been proposed for hypothesis testing in the context of incompletely specified models, such as models which are formulated in terms of estimating functions (Godambe, 1960)—or moment conditions—and are estimated by generalized method of moments (GMM) procedures (Hansen, 1982), and models estimated by M-estimation (Huber, 1981) or pseudo-likelihood methods (Gouriéroux et al., 1984b,c; Gouriéroux and Monfort, 1993). For general discussions of inference in such models, the reader may consult White (1982), Newey (1985), Gallant (1987), Newey and West (1987), Gallant and White (1988), Gouriéroux and Monfort (1989, 1995), Godambe (1991), Davidson and MacKinnon (1993), Newey and McFadden (1994), Hall (1999), and Mátyás (1999); for studies of the performance of some test procedures based on GMM estimators, see also Burnside and Eichenbaum (1996) and Podivinsky (1999).

The invariance properties we consider include invariance to (possibly nonlinear) hypothesis reformulations and reparameterizations. The test statistics examined include Wald-type, LR-type, LM-type, score-type, and C(α)-type criteria. Extending the approach used in Dagenais and Dufour (1991) and Dufour and Dagenais (1992) for likelihood models, we show first that all these test statistics except the Wald-type ones are invariant to equivalent hypothesis reformulations (under usual regularity conditions), but all five of them are not generally invariant to model reparameterizations, including measurement unit changes in nonlinear models. In other words, testing two equivalent hypotheses in the context of equivalent models may lead to completely different inferences. For example, this may occur after an apparently innocuous rescaling of some model variables.

In view of avoiding such undesirable properties, we study restrictions that can be imposed on the objective functions used for pseudo-likelihood (or M-estimation) as well as the structure of the test criteria used with estimating functions and GMM procedures to obtain invariant tests. In particular, we show that using linear exponential pseudo-likelihood functions allows one to obtain invariant score-type and C(α)-type test criteria, while in the context of estimating function (or GMM) procedures it is possible to modify a LR-type statistic proposed by Newey and West (1987) to obtain a test statistic that is invariant to general reparameterizations. The invariance associated with linear exponential pseudo-likelihood functions can be viewed as a strong argument for using such pseudo-likelihood functions in empirical work. Of course, the fact that Wald-type tests are not invariant to both hypothesis reformulations and reparameterizations is by itself a strong argument to avoid using this type of procedure (when they are not equivalent to other procedures) and suggest as well that Wald-type tests can be quite unreliable in finite samples; for further arguments going in the same direction, see Burnside and Eichenbaum (1996), Dufour (1997), and Dufour and Jasiak (2001).

In Section 2, we describe the general setup considered, while the test statistics studied are defined in Section 3. The invariance properties of the available test statistics are studied in Section 4. In Section 5, we make suggestions for obtaining tests that are invariant to general hypothesis reformulations and reparameterizations. Numerical illustrations of the invariance (and noninvariance) properties discussed are provided in Section 6. In Section 7, we consider linear stochastic discount factor model as an empirical example and show that noninvariant procedures may yield drastically different outcomes depending on the identifying restrictions imposed. We conclude in Section 8.

2. Framework

We consider an inference problem about a parameter of interest 𝜃∈Θ⊆ℝ^p. This parameter appears in a model which is not fully specified. In order to identify 𝜃, we assume there exist a m×1 vector score-type function where is a n×k stochastic matrix such that

(2.1)

is a mapping from Θ onto ℝ^m such that

(2.2)

so the value of 𝜃 is uniquely determined by Furthermore, we assume

(2.3)

(2.4)

where I(𝜃₀) and J(𝜃₀) are m×m and m×p full-column rank matrices.

Typically, such a model is estimated by minimizing with respect to 𝜃 an expression of the form

(2.5)

where W_n is a symmetric positive definite matrix. The method of estimating functions (Durbin, 1960; Godambe, 1960, 1991; Basawa et al., 1997), the generalized method of moments (Hansen, 1982; Hall, 2004), maximum likelihood, pseudo-maximum likelihood, M-estimation and instrumental variable methods may all be cast in this setup. Under general regularity conditions, the estimator so obtained has a normal asymptotic distribution

(2.6)

where

(2.7)

, ; see Gouriéroux and Monfort (1995, Ch. 9). Note also that “asymptotic estimation efficiency” arguments suggest one to use as weighting matrix, where I_n is consistent estimator of I₀.¹

If we assume that the number of equations is equal to the number of parameters (m = p), a general method for estimating 𝜃 also consists in finding an estimator which satisfies the equation

(2.8)

Typically, in such cases, is the derivative of an objective function which is maximized (or minimized) to obtain so that

(2.9)

In this case, is asymptotically normal with zero mean and asymptotic variance

(2.10)

Obviously, condition (2.8) is entailed by the minimization of M_n(𝜃) when m = p. It is also interesting to note that problems with m>p can be reduced to cases with m = p through an appropriate redefinition of the score-type function , so that the characterization (2.8) also covers most classical asymptotic estimation methods. A typical list of methods is the following one.

1. ML. In this case, the model is fully specified with log-likelihood function and score function

   (2.11)

2. GMM. 𝜃 is identified through a m×1 vector of conditions of the form: Then one considers the sample analogue of this mean,

   (2.12)
   and the quadratic form
   (2.13)
   where W_n is a symmetric positive definite matrix. In this case, the score-type function is
   (2.14)

3. M-estimator. is defined by minimizing (or maximizing) an objective function of the form

   (2.15)

   The score function has the following form:

   (2.16)

3. Test statistics

Consider now the problem of testing

(3.1)

where ψ(𝜃) is a p₁×1 continuously differentiable function of 𝜃, 1≤p₁≤p and the p₁×p matrix

(3.2)

has full row rank (at least in an open neighborhood of 𝜃₀). Let be the unrestricted estimator obtained by minimizing M_n(𝜃), and the corresponding constrained estimator under H₀.

At this stage, it is not necessary to specify closely the way the matrices I(𝜃₀) and J(𝜃₀) are estimated. We will denote by and or by and the corresponding estimated matrices depending on whether they are obtained with or without the restriction ψ(𝜃) = 0. In particular, if

(3.3)

standard definitions of and would be

(3.4)

where 𝜃 can be replaced by an appropriate estimator. For M-estimators, we have the derivative of the (pseudo-)likelihood associated with an individual observation.

For , other estimators are also widely used. Here, we shall consider general estimators of the form

(3.5)

where is a n×n matrix of weights (which depend on the sample size n and, possibly, on the data) and

(3.6)

For example, a “mean corrected” version of may be obtained on taking where I_n is the identity matrix of order n and which yields

(3.7)

where Similarly, so-called heteroskedasticity-autocorrelation consistent (HAC) covariance matrix estimators can usually be rewritten in the form (3.5). In most cases, such estimators are defined by a formula of the type

(3.8)

where is a kernel function, B_n is a bandwidth parameter (which depends on the sample size and, possibly, on the data), and

(3.9)

For further discussion of such estimators, the reader may consult Newey and West (1987), Andrews (1991), Andrews and Monahan (1992), Hansen (1992), and Cushing and McGarvey (1999).

In this context, analogues of the Wald, LM, score, and C(α) test statistics can be shown to have asymptotic null distributions without nuisance parameters, namely distributions. On assuming that the referenced inverse matrices do exist, these test criteria can be defined as follows:

(a) The Wald-type statistic,

(3.10)

where , , and ;

(b) The score-type statistic,

(3.11)

where and

(c) The LM-type statistic,

(3.12)

where and is the LM in the corresponding constrained optimization problem;

(d) The C(α)-type statistic,

(3.13)

where is any root-n consistent estimator of 𝜃 that satisfies and

with , and

The above Wald-type and score-type statistics were discussed by Newey and West (1987) in the context of GMM estimation, and for pseudo-maximum likelihood estimation by Trognon (1984). The C(α)-type statistic is given by Davidson and MacKinnon (1993, p. 619). Of course, LR-type statistics based on the difference of the maxima of the objective function have also been considered in such contexts:

(3.14)

It is well known that, in general, this difference is distributed as a mixture of independent chi-square with coefficients depending upon nuisance parameters; see, for example, Trognon (1984) and Vuong (1989). Nevertheless, there is one LR-type test statistic whose distribution is asymptotically pivotal with a chi-square distribution, namely the D statistic suggested by Newey and West (1987):

(3.15)

where

(3.16)

is a consistent estimator of I(𝜃₀), minimizes without restriction, and minimizes under the restriction ψ(𝜃) = 0. Note, however, that this LR-type statistic is more accurately viewed as a score-type statistic: if D_n is the derivative of some other objective function (e.g., a log-likelihood function), the latter is not used as the objective function but replaced by a quadratic function of the “score” D_n.

Using the constrained minimization condition,

(3.17)

we see that

(3.18)

i.e., the score and LM statistics are identical in the present circumstances. Further, it is interesting to observe that the score, LM, and C(α)-type statistics given above may all be viewed as special cases of a more general C(α)-type statistic obtained by considering the generalized “score-type” function

(3.19)

where is consistent restricted estimate of 𝜃₀ such that and is asymptotically bounded in probability,

(3.20)

and W_n is a symmetric positive definite (possibly random) m×m matrix such that

(3.21)

Under standard regularity conditions, we have

(3.22)

where

(3.23)

and This suggests the following generalized C(α) criterion:

(3.24)

where Under general regularity conditions, the asymptotic distribution of ; ψ,W_n) is under H₀.² ψ,W_n) can be viewed as the extension of the classical procedure of Neyman (1959) to general estimating functions and GMM setups, and it includes as special cases various other C(α)-type statistics proposed in the statistical and econometric literatures.³ On taking as suggested by asymptotic estimation efficiency arguments, ψ,W_n) reduces to ψ) in (3.13). When the number of equations equals the number of parameters (m = p), we have and ψ,W_n) does not depend on the choice of W_n:

In particular, this will be the case if is the derivative vector of a (pseudo) log-likelihood function. Finally, for m≥p, when is obtained by minimizing subject to ψ(𝜃) = 0, we can write and ψ,W_n) is identical to the score (or LM)-type statistic suggested by Newey and West (1987). Since the statistic ψ,W_n) is quite comprehensive, it will be convenient for establishing general invariance results.

4. Invariance

Following Dagenais and Dufour (1991), we will consider two types of invariance properties: (1) invariance with respect to the formulation of the null hypothesis, and (2) invariance with respect to reparameterizations.

4.1. Hypothesis reformulation

Let

(4.1)

and Ψ be the set of differentiable functions such that

(4.2)

A test statistic is invariant with respect to Ψ if it is the same for all ψ∈Ψ. It is obvious the LR-type statistics LR(ψ) and D_NW(ψ) (when applicable) are invariant to such hypothesis reformulations because the optimal values of the objective function (restricted or unrestricted) do not depend on the way the restrictions are written. Now, a reformulation does not affect , and The same holds for and provided the restricted estimator used with C(α) tests does not depend on which function ψ∈Ψ is used to obtain it. However, , and change. Following Dagenais and Dufour (1991), if we have

(4.3)

where and P₁ are two invertible functions and G(𝜃) is a p₁×p full row-rank matrix. Since where and is the Lagrange multiplier associated with we deduce that all the statistics, except the Wald-type statistics, are invariant with respect to a reformulation. This leads to the following proposition.

Proposition 4.1 (Invariance to Hypothesis Reformulations).

Let Ψ be a family of p₁×1 continuously differentiable functions of 𝜃 such that has full row rank when ψ(𝜃) = 0 (1≤p₁≤p), and

(4.4)

Then, where T stands for any one of the test statistics S(ψ), LM(ψ), ψ), LR(ψ), D_NW(ψ), and ψ,W_n) defined in (3.11)–(3.15) and (3.24).

Note that the invariance of the S(ψ), LM(ψ), LR(ψ), and D_NW(ψ) statistics to hypothesis reformulations has been pointed out by Gouriéroux and Monfort (1989) for mixed-form hypotheses.

4.2. Reparameterization

Let ḡ be a one-to-one differentiable transformation from Θ⊆ℝ^p to . ḡ represents a reparameterization of the parameter vector 𝜃 to a new one, 𝜃_∗. The latter is often determined by a one-to-one transformation of the data as occurs for example when variables are rescaled (measurement unit changes). But it may also represent a reparameterization without any variable transformation. Let k = ḡ⁻¹ be the inverse function associated with ḡ:

(4.5)

Set

(4.6)

Since k[ḡ(𝜃)] = 𝜃 and we have by the chain rule of differentiation

(4.7)

Let

(4.8)

Clearly,

(4.9)

and is an equivalent reformulation of H₀:ψ(𝜃) = 0 in terms of 𝜃_∗. We shall call the canonical reformulation of ψ(𝜃) = 0 in terms of 𝜃_∗. Other (possibly more “natural”) reformulations are of course possible, but the latter has the convenient property that If a test statistic is invariant to reparameterizations when the null hypothesis is reformulated as , we will say it is canonically invariant.

By the invariance property of Proposition 4.1, it will be sufficient for our purpose to study invariance to reparameterizations for any given reformulation of the null hypothesis in terms of 𝜃_∗. From the above definition of it follows that

(4.10)

We need to make an assumption on the way the score-type function changes under a given reparameterization. We will consider two cases. The first one consists in assuming that as in (3.3) where the values of the scores are unaffected by the reparameterization, but are simply reexpressed in terms of 𝜃_∗ and z_t∗ (invariant scores)

(4.11)

where and 𝜃_∗ = ḡ(𝜃). The second one is the one where can be interpreted as the derivative of an objective function.

Under condition (4.11), we see easily that

(4.12)

Further the functions and in (3.4) are then transformed in the following way:

(4.13)

If and are defined as in (3.4), if and if is equivariant with respect to ḡ [i.e., ], it is easy to check that the generalized C(α) statistic defined in (3.24) is invariant to the reparameterization 𝜃_∗ = ḡ(𝜃). This suggests the following general sufficient condition for the invariance of C(α) statistics.

Proposition 4.2 (C(α) Canonical Invariance to Reparameterizations: Invariant Score Case).

Let and suppose the following conditions hold:

1. ;

2. Z_n);

3. and ;

4. .

Here , and W_n are defined as in (3.24), and is invertible. Then

where , and

It is clear that the estimators and satisfy the equivariance condition, i.e., and Consequently, the above invariance result also applies to score (or LM) statistics. It is also interesting to observe that This holds, however, only for the special reformulation not for all equivalent reformulations On applying Proposition 4.1, this type of invariance holds for the other test statistics. These observations are summarized in the following proposition.

Theorem 4.3 (Test Invariance to Reparameterizations and General Hypothesis Reformulations: Invariant Score Case).

Let be any continuously differentiable function of such that ψ_∗(ḡ(𝜃)) = 0⇔ψ(𝜃) = 0, let m = p, and suppose:

1. ;

2. and .

Here Then, provided the relevant matrices are invertible, we have

(4.14)

where T stands for any one of the test statistics S(ψ), LM(ψ), LR(ψ), and D_NW(ψ). If we also have

(4.15)

If the Wald statistic is invariant:

Cases where (4.12) holds only have limited interest because they do not cover problems where D_n is the derivative of an objective function, as occurs for example when M-estimators or (pseudo) maximum likelihood methods are used

(4.16)

In such cases, one would typically have

where κ(Z_n∗) may be a function of the Jacobian of the transformation To deal with such cases, we thus assume that m = p, and

(4.17)

From (2.3) and (4.17), it then follows that

(4.18)

where and

(4.19)

Further,

(4.20)

where , i = 1,…,p, are the coordinates of and

(4.21)

By a set of arguments analogous to those used in Dagenais and Dufour (1991), it appears that all the statistics (except the LR-type statistic) are based upon H_n and so they are sensitive to a reparameterization, unless some specific estimator of J is used. At this level of generality, the following results can be presented using the following notations : are the estimated matrices for a parameterization in 𝜃 and are the estimated matrices for a parameterization in 𝜃_∗. The first proposition below provides an auxiliary result on the invariance of generalized C(α) statistics for the canonical reformulation while the following one provides the invariance property for all the statistics considered and general equivalent reparameterizations and hypothesis reformulations.

Proposition 4.4 (C(α) Canonical Invariance to Reparameterizations).

Let , and suppose the following conditions hold:

1. ;

2. Z_n);

3. , ;

4. .

Here , and W_n are defined as in (3.24), and Then, provided the relevant matrices are invertible,

Theorem 4.5 (Test Invariance to Reparameterizations and General Equivalent Hypothesis Reformulations).

Let be any continuously differentiable function of such that ψ_∗[ḡ(𝜃)] = 0⇔ψ(𝜃) = 0, let m = p, and suppose:

1. ;

2. ;

3. .

Here Then, provided the relevant matrices are invertible, we have

(4.22)

where T stands for any one of the test statistics S(ψ), LM(ψ), LR(ψ), and D_NW(ψ). If we also have

(4.23)

and, in the case where

It is of interest to note here that condition (a) and (b) of the latter theorem will be satisfied if and each individual “score” gets transformed after reparameterization according to the equation

(4.24)

where D_n∗(ḡ(𝜃); z_t∗). Consequently, in such a case, any estimator of the general form (3.5) will satisfy (b) provided the matrix W_I(n) remains invariant under reparameterizations. This will be the case, in particular, for most HAC estimators of the form (3.8) as soon as the bandwidth parameter B_n only depends on the sample size n. However, this may not hold if B_n is data-dependent (as considered in Andrews and Monahan, 1992).

Despite the apparent “positive nature” of the invariance results presented in this section, the main conclusion is that none of the proposed test statistics is invariant to general reparameterizations, especially when the score-type function is derived from an objective function. This is due, in particular, to the behavior of moment (or estimating function) derivatives under nonlinear reparameterizations. As shown in Dagenais and Dufour (1991), this type of problem is already apparent in fully-specified likelihood models where LM statistics are not invariant to general reparameterizations when the covariance matrix is estimated through the Hessian of the log-likelihood function (i.e., derivatives of the score function). When the true likelihood is not available, test statistics must be modified to control the asymptotic level of the test. Reparameterizations involve derivatives of score-type function (or pseudo-likelihood second derivatives), even in the case of LR-type statistics (see Theorem 4.5). In other words, the adjustments required to deal with an incompletely specified model (no likelihood function) make invariance more difficult to achieve, and building valid invariant test procedures becomes a challenge.

5. Invariant test criteria

In this section, we propose two ways of building invariant test statistics. The first one is based on modifying the LR-type statistics proposed by Newey and West (1987) for GMM setups, while the second one exploits special properties of the linear exponential family in pseudo-maximum likelihood models.⁴

5.1. Modified Newey–West LR-type statistic

Consider the LR-type statistic

where proposed by Newey and West (1987, hereafter NW). In this statistic, is any consistent estimator of the covariance matrix I(𝜃₀) which is typically a function of a “preliminary” estimator of The minimized value of the objective function is not invariant to general reparameterizations unless special restrictions are imposed on the covariance matrix estimator

However, there is a simple way of creating the appropriate invariance as soon as the function is a reasonably smooth function of 𝜃. Instead of estimating 𝜃 by minimizing estimate 𝜃 by minimizing For example, such an estimation method was studied by Hansen et al. (1996). When the score vector D_n and the parameter vector 𝜃 have the same dimension (m = p), the unrestricted objective function will typically be zero Z_n) = 0], so the statistic reduces to When m>p, this will typically not be the case.

Suppose now the following conditions hold:

(5.1)

(5.2)

Then, for 𝜃_∗ = ḡ(𝜃),

(5.3)

Consequently, the unrestricted minimal value and the restricted one so obtained will remain unchanged under the new parameterization, and the corresponding J and the LR-type statistics, i.e.,

(5.4)

(5.5)

are invariant to reparameterizations of the type considered in (4.17)–(4.19). Under standard regularity conditions on the convergence of and as n→∞ (continuity, uniform convergence), it is easy to see that D and D_NW are asymptotically equivalent (at least under the null hypothesis) and so have the same asymptotic distribution.⁵

5.2. Pseudo-maximum likelihood (PML) methods

PML methods

Consider the problem of making inference on the parameter which appears in the mean of an endogenous G×1 random vector y_t conditional on an exogenous random vector x_t

(5.6)

where f_t(𝜃) is a known function and 𝜃 is the parameter of interest. (5.6) provides a nonlinear generalized regression model with unspecified variance. Even if a likelihood function with a finite number of parameters is not available for such a semiparametric model, 𝜃 can be estimated through a pseudo-maximum likelihood technique (PML) which consists in maximizing a chosen likelihood as if it were the true undefined likelihood; see Gouriéroux et al. (1984c).⁶ In particular, it is shown in the latter reference that this pseudo-likelihood must belong to the specific class of linear exponential distributions adapted for the mean. These distributions have the following general form:

(5.7)

where μ∈ℝ^G and C(μ) is a row vector of size G. The vector μ is the mean of y if

Irrespective of the true data generating process, a consistent and asymptotically normal estimator of 𝜃 can be obtained by maximizing

(5.8)

or equivalently through the following equivalent program:

(5.9)

The class of linear exponential distributions contains most of the classical statistical models, such as the Gaussian model, the Poisson model, the Binomial model, the Gamma model, the negative Binomial model, etc. The constraint in the program (5.9) ensures that the expectation of the linear exponential pseudo-distribution is μ. The pseudo-likelihood equations have an orthogonal condition form

(5.10)

The PML estimator solution of these first order conditions is consistent and asymptotically normal and we can write

(5.11)

(5.12)

These matrices can be estimated by

(5.13)

(5.14)

where

(5.15)

Since and are invariant to reparameterizations, and are modified only through Further,

(5.16)

and

(5.17)

The Lagrange multiplier, score and C(α)-type pseudo-asymptotic tests are then invariant to a reparameterization, though of course Wald tests will not be generally invariant to hypothesis reformulations. Consequently, this provides a strong argument for using pseudo true densities in the linear exponential family (instead of other types of densities) as a basis for estimating parameters of conditional means when the error distribution has unknown type.

The estimation of the J matrix could be obtained through direct second derivative calculus of the objective function. For example, when y_t is univariate (G = 1), we have

The first two terms of this estimator behave after reparameterization as , but the last term is based on second derivatives of f_t(𝜃) and so leads to noninvariance problems [see (3.4) and (4.20)]. The two last terms of J vanish asymptotically, and they can be dropped as in the estimation method proposed by Gouriéroux et al. (1984c). For the invariance purpose, to discard the last term is the correct way to proceed.

Quasi generalized PML (QGPML) methods

Gouriéroux et al. (1984c) pointed out that some lower efficiency bound can be achieved by a two-step estimation procedure, when the functional form of the true conditional second order moment of y_t given x_t is known:

The method is based on various classical exponential families (negative-binomial, gamma, normal) which depend on an additional parameter η linked with the second order moment of the pseudo-distribution. If μ and Σ are the expectation and the variance-covariance matrix of this pseudo-distribution: η = Ψ(μ, Σ), where Ψ defines for any μ, a one-to-one relationship between η and Σ.

The class of linear exponential distributions depending upon the extra parameter η is of the following form:

If we consider the negative binomial pseudo distribution and C(μ,η) = ln(μ∕(η+μ));  if otherwise we use the Gamma pseudo distribution: A(μ,η) = −ηln(μ) and . In the former case, , and in the latter

With preliminary consistent estimators , of α, 𝜃 where and are equivariant with respect to ḡ, computed for example as in Trognon (1984), the QGPML estimator of 𝜃 is obtained by solving a problem of the type

The QGPML estimator of 𝜃 is strongly consistent and asymptotically normal: with

I₀ and J₀ can be consistently estimated by

where

Since , and are invariant to reparameterizations if and are equivariant, we face the same favorable case as before

and the Wald, Lagrange, score pseudo-asymptotic tests are invariant to a reparameterization. These quasi-generalized pseudo-asymptotic tests are locally more powerful than the corresponding pure pseudo-asymptotic tests under local alternatives, see Trognon (1984).

Furthermore the quasi-generalized LR statistic (QGLR) is invariant provided, the first-step estimators and are equivariant under reparameterization. And as shown in Trognon (1984), the QGLR statistic is asymptotically equivalent to the other pseudo-asymptotic statistic under the null and under local alternatives.

6. Numerical results

In order to illustrate numerically the (non)invariance problems discussed above, we consider the model derived from the following equations:

(6.1)

where , x_it>0 with for λ = 0, and the explanatory variables x_1t and x_2t are fixed. The null hypothesis to be tested is

(6.2)

The log-likelihood associated with this model is

(6.3)

(6.4)

It is easy to see that changing the measurement units on x_1t and x_2t leaves the form of model (6.1) and the null hypothesis invariant. For example, if both x_1t and x_2t are multiplied by a positive constant k, i.e.,

(6.5)

(6.1) can be reexpressed in terms of the scaled variables x_1t∗ and x_2t∗ as

(6.6)

where the power parameter λ remains the same and

(6.7)

Table 1. Test statistics for H₀:λ = 1 for different measurement units five moment model.

	Two-step GMM				CUP-GMM				Pseudo ML
k	D	Wald	Score	C(α)	D	Wald	Score	C(α)	LR	Mod. score
0.2	0.001	44.750	84.810	33.972	5.771	44.750	5.771	5.066	66.408	31.060
0.4	0.000	44.746	47.692	16.726	5.771	44.746	5.771	0.922	66.408	31.060
0.6	0.001	44.745	42.983	14.106	5.771	44.745	5.771	4.482	66.408	31.060
0.8	0.010	44.744	39.161	12.369	5.771	44.744	5.771	5.282	66.408	31.060
1.0	0.056	44.743	35.676	10.593	5.771	44.743	5.771	5.3838	66.408	31.060
3.0	34.629	44.743	118.876	42.124	5.771	44.743	5.771	0.6720	66.408	31.060
5.0	1.641	44.743	62.195	34.746	5.771	44.743	5.771	2.5545	66.408	31.060
7.0	0.282	44.742	61.766	34.953	5.771	44.742	5.771	3.9336	66.408	31.060
10.0	0.068	44.739	61.147	34.465	5.771	44.739	5.771	4.5010	66.408	31.060

On interpreting model (6.1) as a pseudo-model and (6.3) as a pseudo-likelihood, we will examine the effect of rescaling on GMM-based and pseudo-likelihood tests. Moment equations can be derived from the above model by differentiating the log-likelihood with respect to model parameters and equating the expectation to zero. This yields the following five moment conditions:

(6.8)

(6.9)

These equations provide an exactly identified system of equations. To get a system with six-moment equations (hence overidentified), we add the equation

(6.10)

To get data, we considered the sample size n = 200 and generated y_t according to Eq. (6.1) with the parameter values γ = 10, β₁ = 1.0, β₂ = 1.0, λ = −1.0, and σ² = 0.85. The values of the regressors x_1t and x_2t were selected by transforming the values used in Dagenais and Dufour (1991).⁷

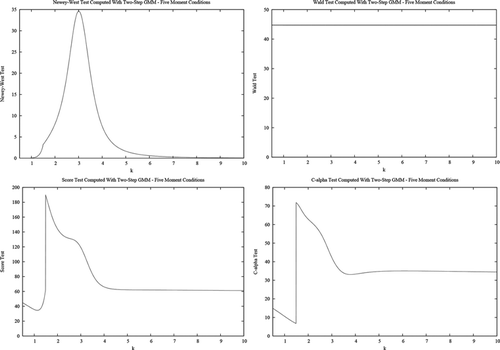
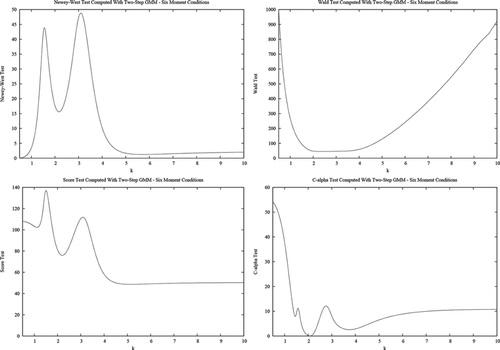
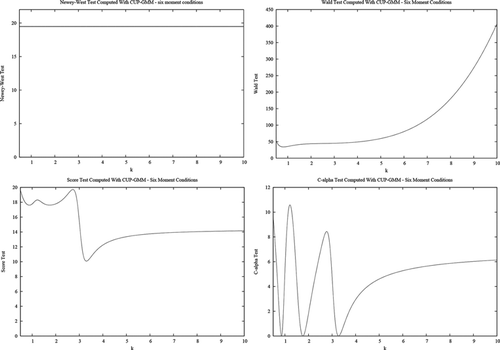
Numerical values of the GMM-based test statistics for a number of rescalings are reported in Table 1 for the five moment system (6.8)–(6.9) and in Table 2 for the six-moment system (6.8)–(6.10). Results for the pseudo-likelihood tests appear in Table 1 . Graphs of the noninvariant test statistics are also presented in Figs 1 – 3 . In these calculations, the first-step estimator of the two-step GMM tests is obtained by minimizing in (2.5) with (equal weights), while the second step uses the weight matrix defined in (3.4). No correction for serial correlation is applied (although this could also be studied).

Table 2. Test statistics for H₀:λ = 1 for different measurement units six moment models.

	Two-step GMM				CUP-GMM
k	D	Wald	Score	C(α)	D	Wald	Score	C(α)
0.2	0.016	416.546	106.734	54.462	19.480	359.380	11.107	3.189
0.4	0.036	221.829	108.142	54.852	19.480	83.743	16.296	7.318
0.6	0.248	213.918	107.764	52.818	19.480	40.481	18.637	7.063
0.8	1.068	178.757	106.053	47.539	19.480	34.101	17.678	0.661
1.0	3.562	139.364	103.364	37.915	19.480	35.580	17.769	5.215
3.0	47.490	46.214	110.751	7.960	19.480	45.146	15.250	4.650
5.0	1.651	129.698	48.704	6.518	19.480	59.667	13.367	4.611
7.0	1.511	384.944	49.719	9.978	19.480	118.911	13.937	5.639
10.0	2.031	905.870	50.264	10.747	19.480	406.974	14.162	6.136

These results confirm the theoretical expectations of the theory presented in the previous sections. Namely, the GMM-based test statistics [D(ψ), Wald, score, C(α)] are not invariant to measurement unit changes and, indeed, can change substantially (even if both the null and the alternative hypotheses remain the same under the rescaling considered here). Noninvariance is especially strong for the overidentified system (six equations). In contrast, the D(ψ) and score tests based on the continuously updated GMM criterion are invariant. The same holds for the LR and adjusted score criteria based on linear exponential pseudo likelihoods.

Figure 1. Two-step GMM tests based on five moment conditions.

Figure 2. Two-step GMM tests based on six moment conditions.

Figure 3. CUP GMM tests based on six moment conditions.

7. Empirical illustration: Linear stochastic discount factor models

In the context of linear stochastic discount factor model, it is shown that procedures based on noninvariant test statistics could lead to drastically different results depending on the form of identifying restrictions imposed. While an in-depth analysis of this problem is provided by Burnside (2010) from the perspective of model misspecification and identification, we aim to shed light on this issue from invariance considerations. The linear stochastic discount factor model is described by the following two equations:

(7.1)

(7.2)

where m_t is the stochastic discount factor (SDF); f_t is a k×1 vector of factors; is the excess return (the difference between the gross asset return and the risk free rate); and a and b are scalar and p×1 vector of unknown parameters, respectively; E[⋅] is an expectation operator conditional on information up to time t−1. Equations (7.1) and (7.2) can equivalently be written as

(7.3)

Since the unknowns a and b are not identified individually, we consider the following two normalizations (see Burnside, 2010; Cochrane, 2005):

By applying the normalizations to (7.3), we have

(7.4)

where , 𝜃 = b∕a, and . The implied two sets of sample moments are

It is clear that the sample moments satisfy

with K[ḡ(𝜃)] = diag{a∕E[m_t],1}; one set of moments can be derived from the other by affine transformation of f_t. Let be the HAC estimator of I(𝜃_∗) with Bartlett kernel and be defined similarly. Then we have

Therefore, by virtue of Eq. (5.3), the continuously updated GMM (CUP-GMM) objective function and the statistic D are invariant to affine transformation of f_t, i.e., they are not affected by the form of normalization employed. The model is estimated using the observed returns on five stocks: Weis Markets (WMK), Unisys Corporation (UIS), Orbital Sciences Corporation (ORB), Mattel (MAT) and Abaxis (ABAX), and the three factors Rm-Rf, Small [market capitalization] Minus Big (SMB), and High [book-to-market ratio] Minus Low (HML), from the Fama–French data set over the period from January 5th, 1993–March 16th, 1993. All calculations were carried out in R Version 3.0.2 (R Development Core Team (2013)) using the package gmm developed by Pierre Chaussé (Chaussé, 2010). The data we use are readily available in the Finance data set contained in gmm. The estimation methods are two-step GMM and CUP-GMM with covariance matrix estimated with Bartlett and Quadratic Spectral (QS) kernels. Table 3 reports the values of J statistic for testing the validity of the restrictions (7.4). For the two-step GMM, it is clear that the values of test statistics differ greatly across the normalizations, and are sensitive to the choice of kernels. Furthermore, the test rejects the null of correct specification under Normalization 2 with QS kernel, but the conclusion is reversed under Normalization 1. In the case of CUP-GMM with Bartlett kernel, though there is a small incongruity in the values of test statistics (possibly due to an optimization error), the model is not rejected under both normalizations. The difference between test statistics under the CUP-GMM with QS kernel may be attributed to the noninvariance of the objective function with QS kernel. The main message of this exercise is that procedures based on noninvariant test statistics can be quite sensitive to the identifying restrictions employed and may result in conflicting conclusions. For a thorough discussion on the effect of normalizations on estimation and inferences, we refer the reader to Hamilton et al. (2007).

Table 3. J statistic for the validity of (7.4) under different identifying restrictions (p-values in parentheses).

Two-step GMM				CUP-GMM
Normalization 1		Normalization 2		Normalization 1		Normalization 2
QS	Bartlett	QS	Bartlett	QS	Bartlett	QS	Bartlett
0.218	0.106	17.214	5.670	1.235	1.774	1.759	1.866
(0.897)	(0.949)	(0.000)	(0.059)	(0.539)	(0.412)	(0.415)	(0.393)

8. Conclusion

In this article, we have studied the invariance properties of hypothesis tests applicable in the context of incompletely specified models, such as models formulated in terms of estimating functions and moment conditions, which are usually estimated by GMM procedures, or models estimated by pseudo-likelihood and M-estimation methods. The test statistics examined include Wald-type, LR-type, LM-type, score-type, and C(α)-type criteria. We found that all these procedures are not generally invariant to (possibly nonlinear) hypothesis reformulations and reparameterizations, such as those induced by measurement unit changes. This means that testing two equivalent hypotheses in the context of equivalent models may lead to completely different inferences. For example, this may occur after an apparently innocuous rescaling of some model variables.

In view of avoiding such undesirable properties, we studied restrictions that can be imposed on the objective functions used for pseudo-likelihood (or M-estimation) as well as the structure of the test criteria used with estimating functions and GMM procedures to obtain invariant tests. In particular, we showed that using linear exponential pseudo-likelihood functions allows one to obtain invariant score-type and C(α)-type test criteria, while in the context of estimating function (or GMM) procedures it is possible to modify a LR-type statistic proposed by Newey and West (1987) to obtain a test statistic that is invariant to general reparameterizations. The invariance associated with linear exponential pseudo-likelihood functions is interpreted as a strong argument for using such pseudo-likelihood functions in empirical work. Furthermore, the LR-type statistic is the one associated with using continuously updated GMM estimators based on appropriately restricted weight matrices. Of course, this provides an extra argument for such GMM estimators.

Acknowledgements

The authors thank Marine Carrasco, Jean-Pierre Cotton, Russell Davidson, Abdeljelil Farhat, V. P. Godambe, Christian Gouriéroux, Stéphane Grégoir, Hervé Mignon, Denis Pelletier, Mohamed Taamouti, Pascale Valéry, three anonymous referees, and the Editor Esfandiar Maasoumi for several useful comments.

Notes

¹This “optimal” choice may be infeasible (or far from “efficient”) in finite samples when I₀ (or I_n) is not invertible or “ill-conditioned” (close to noninvertibility). For this reason, we consider here the general formulation in (2.5), though the weighting matrix is allowed as a special case. Note also that “efficiency” from the estimation viewpoint is not in general equivalent to efficiency from the testing viewpoint (in terms of power), so it is not clear is an optimal choice for the purpose of hypothesis testing.

²The regularity conditions and a rigorous proof of the latter assertion appear in the working paper version of this article Dufour et al. (2013); see also Dufour et al. (2015).

³For further discussion of C(α) tests, the reader may consult Bernshtein (1981), Basawa (1985), Ronchetti (1987), Smith (1987), Berger and Wallenstein (1989), Dagenais and Dufour (1991), Davidson and MacKinnon (1991, 1993), Kocherlakota and Kocherlakota (1991), Bera and Bilias (2001), and Dufour and Valéry (2009).

⁴The reader may note that further insight can be gained on the invariance properties of test statistics by using differential geometry arguments; for some applications to statistical problems, see Bates and Watts (1980), Amari (1990), Kass and Vos (1997), and Marriott and Salmon (2000). Such arguments may allow one to propose reparameterizations and “invariant Wald tests”; see, for example, Bates and Watts (1981), Hougaard (1982), Le Cam (1990), Critchley et al. (1996), and Larsen and Jupp (2003) in likelihood models. As of now, such procedures tend to be quite difficult to design and implement, and GMM setups have not been considered. Even though this is an interesting avenue for future research, simplicity and generality considerations have led us to focus on procedures which do not require adopting a specific parameterization.

⁵The regularity conditions and a proof of the asymptotic distribution are given in our working paper (Dufour et al., 2013).

⁶For further discussion of such methods, the reader may consult: Gong and Samaniego (1981), Gouriéroux et al. (1984a), Trognon (1984), Bourlange and Doz (1988), Trognon and Gouriéroux (1988), Gouriéroux and Monfort (1993), Crépon and Duguet (1997), and Jorgensen (1997).

⁷The numerical values of x_1t, x_1t, and y_t used are available from the authors upon request. It is important to note that this is not a simulation exercise aimed at studying the statistical properties of the tests, but only an illustration of the numerical properties of the test statistics considered.