Nonlinear autoregressive models with optimality properties

Abstract

We introduce a new class of nonlinear autoregressive models from their representation as linear autoregressive models with time-varying coefficients. The parameter updating scheme is subsequently based on the score of the predictive likelihood function at each point in time. We study in detail the information theoretic optimality properties of this updating scheme and establish the asymptotic theory for the maximum likelihood estimator of the static parameters of the model. We compare the dynamic properties of the new model with those of well-known nonlinear dynamic models such as the threshold and smooth transition autoregressive models. Finally, we study the model’s performance in a Monte Carlo study and in an empirical out-of-sample forecasting analysis for U.S. macroeconomic time series.

Keywords:

• Macroeconomic time series
• Score driven time-varying parameter models
• Smooth transition
• Treshold autoregressive models

JEL Classification codes:

• C10
• C22
• C32
• C51

1. Introduction

Many empirically relevant phenomena in fields such as biology, medicine, engineering, finance and economics exhibit nonlinear dynamics; see the discussion in Teräsvirta et al. (2010). In economics, for example, economic agents typically interact nonlinearly as implied by capital or capacity constraints, asymmetric information problems, and habit formation. Various nonlinear dynamic models have been proposed in the literature to describe such phenomena. Important examples include the threshold AR (TAR) model of Tong (1983) and the smooth transition AR (STAR) model of Chan and Tong (1986) and Teräsvirta (1994).

Consider a nonlinear AR model with additive innovations of the form (1) $$y_t=\psi (y^{t-1})+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(1) for an observed process $\left\{y_t\right\}$ and a sequence of zero-mean independent innovations $\left\{u_t\right\}$ with density $p_u(u_t),$ where ψ is a function of the vector $y^{t-1}:=(y_{t-1},y_{t-2},\dots ).$ We allow the data generating process (DGP) for ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ to be general and potentially nonparametric in nature. In particular, we only impose high-level conditions on ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ such as strict stationarity, ergodicity and bounded moments. We then focus on how to best ‘fit’ a potentially misspecified dynamic parametric model to the observed data ${\left\{y_t\right\}}_{t=1}^T,$ where T denotes the sample size. The statistical model thus adopts a specific parametric and possibly misspecified functional form for ψ. This approach of allowing for a discrepancy between the DGP and the statistical model follows the literature on misspecified parametric models dating back to White (1980, 1981, 1982) and Domowitz and White (1982), and also including the work of Maasoumi (1990) on the effects of misspecification for forecasting based on econometric models.

Given that the model is allowed to be misspecified from the outset, our main focus lies on finding good formulations for the parametric dynamic model that we use to ‘fit’ the data. We argue that despite the current general setting for the DGP, we still find some (misspecified) parametric models more suitable than others. In order to formulate our argument, we first note that (1) admits an autoregressive representation with time-varying autoregressive coefficient, (2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) where f_t is the time-varying autoregressive parameter, which can be written as a measurable function $f_t=f(y^{t-1})$ of the infinite past $y^{t-1}.$ We use the representations in (1(1) $$y_t=\psi (y^{t-1})+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(1) ) and (2(2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) ) interchangeably by setting $\psi (y^{t-1})=f(y^{t-1}) y_{t-1}.$ The parameter f_t in (2(2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) ) implies the autoregressive function ψ and vice-versa. We then use the representation in (2(2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) ) and appeal to the results in Blasques et al. (2015) to obtain a parametric functional form for our model that is locally optimal in an information theoretic sense.

While the nonlinear autoregressive representation in (1(1) $$y_t=\psi (y^{t-1})+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(1) ) is more commonly used, the time-varying parameter representation in (2(2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) ) has the advantage of revealing the changing dependence in the data more clearly through the time-varying parameter f_t. For example, in econometric applications, major economic events such as the burst of the dotcom bubble in 2000, the 2008 global financial crisis, or the 2010–2011 European sovereign debt crisis can lead to temporary changes in the dependence structure of economic time series and thus lead to time-variation in the coefficients of standard linear time series models. The representation in (2) reveals these changes directly.

Some earlier contributions have also considered time-varying parameters in (vector) autoregressive models. Doan et al. (1984) explored the estimation of time-varying coefficients in AR models via the model’s representation in state space form and the application of the Kalman filter. More elaborate Markov chain Monte Carlo methods were explored by, for instance, Kadiyala and Karlsson (1993) and Clark and McCracken (2010).

Here we adopt the time-varying parameter representation in (2) to find a nonlinear specification for the nonlinear AR model in (1) that possesses particular optimality properties. We do so by studying how to select the function $f(y^{t-1}).$ Specifically, we extend the results in Blasques et al. (2015) and Creal et al. (2018) to dynamic autoregressive models. This allows us to find a parametric functional form for ψ that at each time point t is guaranteed to improve the local Kullback-Leibler divergence between the true unknown conditional density of y_t and the conditional density implied by the fitted parametric model. The notion of optimality we work with is thus information-theoretic in nature. The original results in Blasques et al. (2015) do not cover our current setting, as they do not allow for y_t to depend on $y^{t-1}$ conditional on f_t. The parameters of our time-varying autoregressive parameter model can be estimated by maximum likelihood (ML), and we formulate conditions under which the ML estimator (MLE) has the usual asymptotic properties, such as consistency and asymptotic normality. We also analyze the finite-sample performance of the model and its ability to recover the time-varying AR coefficient f_t in a Monte Carlo study. Our results show that the model performs well.

We illustrate the model empirically in two ways. First, we model the growth rate of U.S. unemployment insurance claims, which is an often used leading indicator for U.S. gross domestic production growth. We show how temporal dependence in this series varies over time. Second, we illustrate that our model provides better out-of-sample forecasts than most direct competitors for three important macroeconomic time series observed at different frequencies: the weekly growth rate of U.S. unemployment insurance claims, the monthly growth rate in industrial production, and the quarterly growth rate of money velocity.

The remainder of this paper is organized as follows. Section 2 introduces the model and establishes its information theoretic optimality properties, regardless of whether the model is correctly specified or not. Section 3 discusses the reduced form dynamics of the model and compares these with the properties of well-known alternatives. Section 4 establishes the asymptotic properties of the MLE. Section 5 provides our empirical analysis. Section 6 concludes. In the Supplementary Appendix, we gather supplementary material including technical proofs and extensions to the theoretical optimality results of Section 2.

2. Score driven time-varying AR coefficient

2.1. The model

We consider a generalization of the time-varying AR coefficient model in Eq. (2)(2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) , (3) $$y_t=h(f_t) y_{t-1}+u_t,$$(3) where y_t denotes the observation, and $h( · )$ is a bijective link function. Obvious choices for $h( · )$ are $h(f_t)=f_t$ as in Eq. (2)(2) $$y_t=f_t y_{t-1}+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(2) , $h(f_t)=\hspace{0.17em}\text{exp}\hspace{0.17em}(f_t)>0$ to rule out negative temporal dependence, or $h(f_t)={[1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-f_t)]}^{-1}\in (0,1)$ to rule out unit-root behavior. Other appropriate link functions can be thought of as well. If we allow $h(f_t)$ to be equal to or even exceed 1 from time to time, we can endow $\left\{y_t\right\}$ with ‘transient’ unit-root or explosive behavior during specific time periods. This does not rule out that $\left\{y_t\right\}$ is strictly stationary and ergodic (SE); see Bougerol (1993) as well as the discussions below. All results derived in this paper extend trivially to the autoregressive model with intercept $a\in \mathbb{R}$ as given by $y_t=a+h(f_t)y_{t-1}+u_t.$ For simplicity, we set a = 0 and treat the case of the de-meaned sequence of data $\left\{y_t\right\}.$

We specify the time-varying parameter f_t as an observation driven process as formally defined by Cox (1981). In particular, f_t is a function of past observations $y^{t-1},$ i.e., $f_t:=f_t(y^{t-1}).$ Observation driven models are essentially ‘filters’ for the unobserved $\left\{f_t\right\}.$ They update the parameter f_t using the information provided by the most recent observations of the process $\left\{y_t\right\}.$ In general, they take the form (4) $$f_{t+1}=\varphi (f_t,y_t,y_{t-1};\mathit{\theta }),$$(4) where $\mathit{\theta }$ is a vector of unknown static parameters. Eq. (4)(4) $$f_{t+1}=\varphi (f_t,y_t,y_{t-1};\mathit{\theta }),$$(4) implies that $f_t=f_t(y^{t-1})$ is a function of all past observations. Any function $\varphi ( · ;\mathit{\theta })$ can be considered for updating f_t to $f_{t+1},$ such as the constant function, but also the threshold or smooth transition autoregressive specifications as used in Tong (1983), Chan and Tong (1986) and Teräsvirta (1994), amongst others. Petruccelli (1992) argues that many time series models of interest can be approximated by the threshold model and therefore our theoretical results below may have wider implications.

The parameter update function in (4) can lead to both linear and nonlinear dynamic specifications. For example, if $h(f_t)=f_t$ and $\varphi ( · ;\mathit{\theta })$ is given by $$f_t=\varphi (f_{t-1},y_{t-1},y_{t-2};\mathit{\theta })=\omega +\alpha (y_{t-1}-f_{t-1}{y}_{t-2}) / y_{t-1},$$ we obtain the autoregressive moving average model $y_t=\omega y_{t-1}+u_t+\alpha u_{t-1},$ where ω and α are static unknown parameters. For a discrete update function $\varphi ( · ;\mathit{\theta })$ of the type $$f_t=\varphi (y_{t-1};\mathit{\theta })=\omega +\alpha {\mathbb{I}}_{(y_{t-1}>0)},$$ we obtain the self-exciting threshold autoregression (SETAR) of Tong and Lim (1980), $$y_t=\{\begin{array}{ccc}\omega y_{t-1}+u_t,\hfill & \text{if}\hfill & y_{t-1}<0,\hfill \\ (\omega +\alpha )y_{t-1}+u_t,\hfill & \text{if}\hfill & y_{t-1}\ge 0.\hfill \end{array}$$

In the next subsection, we introduce alternative formulations of $\varphi ( · ;\mathit{\theta })$ that lead to empirically relevant nonlinear AR models with information theoretic optimality properties.

2.2. Information theoretic optimality

As stressed in the introduction, it is important for our analysis to clearly distinguish between the data generating process (DGP) and the postulated parametric statistical model. The DGP is typically unknown and potentially highly complex. For expositional purposes, we assume the DGP is the nonlinear AR process from Eq. (1)(1) $$y_t=\psi (y^{t-1})+u_t,\hspace{1em}{u}_t\sim p_u(u_t),$$(1) with $\psi (y^{t-1})$ of unknown form. The analysis below, however, still applies if the DGP falls outside this very general class of nonlinear time series models and is only characterized by its (unknown) conditional density.

The unknown DGP in (1) gives rise to a true, unobserved time-varying parameter $f_t=h^{-1}(\psi (y^{t-1})/y_{t-1}),$ where $h^{-1}( · )$ denotes the inverse function of $h( · ).$ Next to f_t, we distinguish the filtered time-varying parameter ${\tilde{f}}_t$ as obtained from the possibly misspecified statistical model (3). The parameter ${\tilde{f}}_t$ is based on the updating equation (4)(4) $$f_{t+1}=\varphi (f_t,y_t,y_{t-1};\mathit{\theta }),$$(4) , i.e., ${\tilde{f}}_{t+1}=\varphi ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta }),$ where the link function $\tilde{h}$ used in the model may also depend on $\mathit{\theta },$ i.e., $\tilde{h}({\tilde{f}}_t;\mathit{\theta }).$ The difference between f_t and ${\tilde{f}}_t$ is similar to the difference between innovations and regression residuals. While ${\left\{f_t\right\}}_{t\in \mathbb{Z}}$ has properties that are directly implied by the DGP, the filtered sequence ${\left\{{\tilde{f}}_t\right\}}_{t\in \mathbb{N}}$ only achieves those properties in the ideal setting of correct model specification, true values for the static parameters, and correct initialization of the time-varying parameter ${\tilde{f}}_1.$ Furthermore, while ${\left\{f_t\right\}}_{t\in \mathbb{Z}}$ stretches to the infinite past and depends on the entire time series ${\left\{y_t\right\}}_{t\in \mathbb{Z}},$ the filtered path ${\left\{{\tilde{f}}_t\right\}}_{t=1}^T$ is initialized at time t = 1 and depends only on the observed sequence $y^{1:T}:=(y_1,\dots ,y_T)$ with T increasing as more data become available.

We write the true unknown joint density of the vector $y^{1:T}$ as $p(y_1,\dots ,y_T).$ This density can be factorized as $$p(y_1,\dots ,y_T)=\prod _{t=1}^{T}p(y_t|y^{t-1})=\prod _{t=1}^T{p}_t,$$ where $p_t:=p(y_t|y^{t-1})=p(y_t|f_t,y_{t-1})$ denotes the true, unknown conditional density of y_t given its infinite past $y^{t-1}$ We write the filtered conditional density based on the statistical model as $${\tilde{p}}_t:=\tilde{p}(y_t|{\tilde{f}}_t,y_{t-1};\mathit{\theta })=p_u({\tilde{u}}_t;\mathit{\theta }),$$ where ${\tilde{u}}_t=y_t-h({\tilde{f}}_t;\mathit{\theta })y_{t-1},{\tilde{f}}_1\in \tilde{\mathcal{F}},$ and ${\tilde{f}}_{t+1}=\varphi ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })$ for t > 1, with ${\tilde{f}}_2$ being a function of the first observation y₁ and the fixed starting value for the filter ${\tilde{f}}_1.$ The conditional model density ${\tilde{p}}_t$ will typically differ from the conditional true density p_t.

To estimate the static parameters $\mathit{\theta },$ we use the scaled log likelihood function (5) $$L_T(\mathit{\theta },{\tilde{f}}_1)=\frac{1}{T-1}\sum _{t=2}^T{\ell }_t(\mathit{\theta },{\tilde{f}}_1)=\frac{1}{T-1}\sum _{t=2}^T\ell ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })=\frac{1}{T-1}\sum _{t=2}^T\hspace{0.17em}\text{log}\hspace{0.17em}\tilde{p}(y_t|{\tilde{f}}_t,y_{t-1};\mathit{\theta }),$$(5) which naturally depends on the filtered parameter sequence ${\left\{{\tilde{f}}_t\right\}}_{t=1}^T$ and thus on $\mathit{\theta }$ and on the initialization ${\tilde{f}}_1,$ since ${\tilde{f}}_t:={\tilde{f}}_t(y^{1:t-1};\mathit{\theta },{\tilde{f}}_1).$ Our notation is summarized in Table 1.

Table 1. Notation.

Symbol	Description
yt	Time series variable for $-\infty <t<\infty$ and observed for $t=1,\dots ,T$
y^t	Vector $y^t:=(y_t,y_{t-1},y_{t-2},\dots ),$ toward infinite past
$y^{1:t}$	Observation set $y^{1:t}:=(y_1,\dots ,y_t),$ for $t=1,\dots ,T$
ft	Time-varying parameter implied by the DGP
${\tilde{f}}_t:={\tilde{f}}_t(y^{1:t-1};\mathit{\theta },{\tilde{f}}_1)$	Filtered time-varying parameter obtained under $\mathit{\theta }\in \Theta$ and initialization ${\tilde{f}}_1\in \tilde{\mathcal{F}}$
$\mathcal{Y}$	Domain of yt
$\mathcal{F}$ and $\tilde{\mathcal{F}}$	Domains of ft and ${\tilde{f}}_t,$ respectively, for $t=1,\dots ,T$
$p_t:=p( · |y^{t-1})$	True unknown conditional density of the data
${\tilde{p}}_t:=\tilde{p}( · |{\tilde{f}}_t,y_{t-1};\mathit{\theta })$	Parametric conditional density of yt implied by specified model given ${\tilde{f}}_t$
${\ell }_t(\mathit{\theta },{\tilde{f}}_1):=\ell ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })$	Log-likelihood contribution at time t

Note that for the definition of ${\tilde{p}}_t$ it is insufficient to conditoin on ${\tilde{f}}_t$ only, as the autoregressive specification in (2) also has $y_{t-1}$ explicitly as part of the model, even when conditioning on ${\tilde{f}}_t.$

We now proceed by showing that an update function $\varphi ( · ;\mathit{\theta })$ in (4) is only optimal in an information theoretic sense if it is based on the score of the predictive log-density for y_t, that is on $\partial \hspace{0.17em}\text{log}\hspace{0.17em}{\tilde{p}}_t/\partial {\tilde{f}}_t.$ Such an update locally results in an expected decrease in the Kullback-Leibler (KL) divergence between the true conditional density p_t and the conditional model density ${\tilde{p}}_t.$ KL divergence is an important and widely applied measure of statistical divergence in various fields; see, for example, Ullah (1996, 2002). The results we derive extend the results of Blasques et al. (2015) and Creal et al. (2018) to the context of autoregressive models with time-varying dependence parameters.

The optimality properties below hold whether or not the statistical model is correctly specified. We first define the notions of expected KL variation and expected KL optimality.

Definition 1.

(EKL Optimality) Let ${\mathcal{D}}_{\text{KL}}(p_t,{\tilde{p}}_t)$ denote the KL divergence between ${\tilde{p}}_t$ and p_t, i.e., $${\mathcal{D}}_{\text{KL}}(p_t,{\tilde{p}}_t)=\int p(y|y^{t-1})\hspace{0.17em}\text{log}\hspace{0.17em}\frac{p(y|y^{t-1})}{\tilde{p}(y|{\tilde{f}}_t,y_{t-1};\mathit{\theta })}\mathrm{d}y,$$ then a parameter update from ${\tilde{f}}_t\in \tilde{\mathcal{F}}$ to ${\tilde{f}}_{t+1}\in \tilde{\mathcal{F}}$ with Expected KL (EKL) variation (6) $${\mathbb{E}}_{t-1}[{\mathcal{D}}_{\text{KL}}(p_t,{\tilde{p}}_{t+1})-{\mathcal{D}}_{\text{KL}}(p_t,{\tilde{p}}_t)]$$(6) is EKL optimal if and only if ${\mathbb{E}}_{t-1}[{\mathcal{D}}_{\text{KL}}(p_t,{\tilde{p}}_{t+1})-{\mathcal{D}}_{\text{KL}}(p_t,{\tilde{p}}_t)]<0$ for every true density p_t. The nonlinear autoregressive model (2) with time-varying dependence parameter as in (3) is said to be EKL optimal if it admits an EKL optimal parameter update.

The EKL variation in (6) measures the change in KL divergence between the true conditional density $p( · |y^{t-1})$ and the conditional model densities $$\tilde{p}( · |{\tilde{f}}_t,y_{t-1};\mathit{\theta }),\hspace{1em}\tilde{p}( · |{\tilde{f}}_{t+1},y_{t-1};\mathit{\theta }).$$

As ${\tilde{f}}_{t+1}$ depends on y_t, it is a random variable given the information up to time t – 1 only. Therefore, the EKL variation concentrates on whether the KL divergence reduces in expectation. Any individual step from ${\tilde{f}}_t$ to ${\tilde{f}}_{t+1}$ may incidentally increase the KL divergence, but for an update to be EKL the steps should reduce the KL divergence on average, whatever the true unobserved density p_t.

For a general update function $\varphi ( · ;\mathit{\theta }),$ the parameter update from ${\tilde{f}}_t$ to ${\tilde{f}}_{t+1}$ does not necessarily have this property. For a general $\varphi ( · ;\mathit{\theta })$ the update steps may leave $\tilde{p}( · |{\tilde{f}}_{t+1},y_{t-1};\mathit{\theta })$ farther away on average from the true conditional density $p( · |f_t,y_{t-1}).$ The surprising feature of our analysis is that despite the generality of the current set-up, we can still show that a local EKL optimal time-varying parameter update actually exists. In particular, we show that only a score update (or a locally topologically equivalent of that) ensures that the observation y_t is incorporated in such a way that the parameter update provides a better approximation to the conditional density of y_t in an expected KL divergence sense. This does not hold for any other updating mechanism.

The optimality property leads to a nonlinear autoregressive model formulation that takes the form of a score driven time-varying parameter model as introduced by Creal et al. (2011, 2013) and Harvey (2013). The score driven model is defined as (7) $${\tilde{f}}_{t+1}=\varphi ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })=\omega +\alpha s_t+\beta {\tilde{f}}_t,$$(7) where ω, α and β are unknown coefficients included in $\mathit{\theta },$ and (8) $$s_t=s({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta }):=S({\tilde{f}}_t,y_t;\mathit{\theta })·{\tilde{\nabla }}_t,$$(8) is the scaled score of the predictive density, where (9) $${\tilde{\nabla }}_t=\tilde{\nabla }({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta }):=\frac{\partial \hspace{0.17em}\text{log}\hspace{0.17em}\tilde{p}(y_t|{\tilde{f}}_t,y_{t-1};\mathit{\theta })}{\partial {\tilde{f}}_t},$$(9) and with $S({\tilde{f}}_t,y_t;\mathit{\theta })$ some scaling function. For our current purposes it suffices to consider the simplified setting with $S({\tilde{f}}_t,y_t;\mathit{\theta })=1.$ The update equation (7)(7) $${\tilde{f}}_{t+1}=\varphi ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })=\omega +\alpha s_t+\beta {\tilde{f}}_t,$$(7) formulates a possibly highly nonlinear function for ${\tilde{f}}_t$ in terms of the past observations $y^{t-1}.$ The functional form is partly determined by the postulated model density ${\tilde{p}}_t,$ while the impact of past observations on ${\tilde{f}}_t$ is also determined by the coefficients ω, α and β.

To show that the update in (7) satisfies EKL optimality properties, we make the following assumptions.

Assumption 1.

1. The filtering density $\tilde{p}(y|\tilde{f},y_{t-1};\theta )$ is twice continuously differentiable in y and $\tilde{f}$ and satisfies the moment conditions $$\begin{array}{c}{\mathbb{E}}_{t-1}[{\tilde{\nabla }}_t^2]<\infty \forall ({\tilde{f}}_t,y_{t-1}),\\ \underset{\tilde{f}}{\sup }{\mathcal{I}}_{t-1}(\tilde{f},y_{t-1})=\underset{\tilde{f}}{\sup }{\mathbb{E}}_{t-1}\left[\frac{{\partial }^2\hspace{0.17em}\text{log}\hspace{0.17em}\tilde{p}(y_t|\tilde{f},y_{t-1};\theta )}{\partial {\tilde{f}}^2}\right]\le K<\infty \hspace{1em}\forall y_{t-1},\end{array}$$

where ${\mathbb{E}}_{t-1}[·]$ denotes the expectations operator with respect to the true, unknown conditional density $p( · |y^{t-1})$, and K is a constant.

1. The filtering density is misspecified in the sense that ${\mathbb{E}}_{t-1}[{\tilde{\nabla }}_t]\ne 0.$

2. $\alpha >0$ and $0<S(\tilde{f},y;\mathit{\theta })<\infty \forall (\tilde{f},y,\mathit{\theta })\in \tilde{\mathcal{F}}\times \mathbb{R}\times \Theta .$

The proofs of Lemmas 1 and 2 below are easily obtained by extending the proofs of Propositions 1–5 in Blasques et al. (2015) and Proposition 2 in Creal et al. (2018) so as to allow $y_{t-1}$ to enter the conditioning sets of both p_t and ${\tilde{p}}_t.$ The proofs can be found in the Supplementary Appendix.

Lemma 1 shows that the score update of f_t is locally EKL optimal.

Lemma 1.

Let Assumption 1 hold and let $(\omega ,\beta )=(0,1)$. Then, for α sufficiently small, the score update for f_t is EKL optimal given ${\tilde{f}}_t$ and $y_{t-1}.$

Lemma 2 shows that only a ‘score-equivalent’ update can have this optimality property. An update is said to be ‘score-equivalent’ if it is proportional to the score as a function of y_t.

Definition 2.

(Score-equivalent updates) An observation driven parameter update ${\tilde{f}}_{t+1}=\varphi ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })$ is ‘score-equivalent’ if and only if $\varphi (f,y,y\prime ;\mathit{\theta })-f=a(f,y)·\tilde{\nabla }(f,y,y\prime ;\mathit{\theta })$ for every $(f,y,y\prime ,\mathit{\theta }).$

We make the following additional assumption.

Assumption 2.

The score $\tilde{\nabla }({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })$ as a function of y_t changes sign at least once for every $({\tilde{f}}_t,y_{t-1},\mathit{\theta }).$

Assumption 2 is intuitive. The score update should be such that the fitered time-varying parameter can go up as well as down for particular (possibly extreme) realizations of y_t. Otherwise, updates will always be in one direction only. We now have the following result.

Lemma 2.

Let Assumptions 1 and 2 hold. For any given p_t, a parameter update is locally EKL optimal if and only if the parameter update is score-equivalent.

The optimality properties above can be further extended to settings where $\omega \ne 0$ and/or $\beta \ne 1;$ see Blasques et al. (2015) for examples of this in a slightly different set-up. Such results apply as long as the ‘forces away’ from the optimal direction at ${\tilde{f}}_t$ as determined by the autoregressive component $\omega +(\beta -1){\tilde{f}}_t$ are weaker than the ‘forces toward’ the optimal direction as determined by the score component $\alpha s({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta }).$ Concluding, we find that the score updates have firm foundations from the perspective of information theoretic criteria (Kullback-Leibler). In fact, in the current general set-up only score updates possess such desirabe properties.

2.3. Illustrations

We present three illustrations to provide more intuition for the main results derived in Section 2.2.

2.3.1. Model I: Affine gaussian updating

Consider the statistical model with $\tilde{h}({\tilde{f}}_t;\mathit{\theta })={\tilde{f}}_t\forall ({\tilde{f}}_t,\mathit{\theta })$ and conditional model density ${\tilde{p}}_t$ equal to a normal with mean zero and variance ${\sigma }^2,$ $$\text{log}\hspace{0.17em}\tilde{p}(y_t|{\tilde{f}}_t,y_{t-1};\mathit{\theta })=-\frac{1}{2}\text{log}\hspace{0.17em}2\pi -\frac{1}{2}\text{log}\hspace{0.17em}{\sigma }^2-\frac{{\tilde{u}}_t^2}{2{\sigma }^2},$$ where ${\tilde{u}}_t=y_t-{\tilde{f}}_t·y_{t-1}.$ The score function is given by ${\tilde{\nabla }}_t={\tilde{u}}_t·y_{t-1} / {\sigma }^2.$ For the case of unit scaling $S({\tilde{f}}_t,y_t;\mathit{\theta })=1,$ we obtain the update (10) $$\begin{array}{c}{\tilde{f}}_{t+1}=\omega +\alpha {\tilde{u}}_t \frac{y_{t-1}}{{\sigma }^2}+\beta {\tilde{f}}_t.\hfill \end{array}$$(10)

The update of ${\tilde{f}}_{t+1}$ responds to the model’s prediction error ${\tilde{u}}_t$ multiplied by the scaled leverage of the observation $y_{t-1}/{\sigma }^2.$ The score pushes the update up (down) if y_t lies above (below) its predicted mean ${\tilde{f}}_t y_{t-1},$ i.e., if ${\tilde{u}}_t=y_t-{\tilde{f}}_t{y}_{t-1}>0$ (versus ${\tilde{u}}_t=y_t-{\tilde{f}}_t{y}_{t-1}<0$). The strength of this effect is determined both by α and $y_{t-1}/{\sigma }^2.$ When ${\sigma }^2$ is large, the update sizes are mitigated because the predition errors ${\tilde{u}}_t$ are noisy signals of where ${\tilde{f}}_t$ is located. The score update balances all these features in an optimal manner.

If β = 1 and ω = 0, the score is the only determinant of the parameter update. For $0<\beta <1,$ the updating mechanism becomes more complex and the signal from the score has to off-set the autoregressive step $\omega +\beta {\tilde{f}}_t$ toward the long-term unconditional mean of ${\tilde{f}}_t,$ that is toward $\omega /(1-\beta ).$

2.3.2. Model II: Logistic updating

Consider the same setting as Model I but with link function $\tilde{h}(f_t;\mathit{\theta })={[1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-f_t)]}^{-1}$ which allows for transient (near) unit-root dynamics in y_t, but rules out negative dependence and explosive behavior. The parameter update becomes (11) $$\begin{array}{c}{\tilde{f}}_{t+1}=\omega +\alpha (y_t-\frac{y_{t-1}}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\tilde{f}}_t)})\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\tilde{f}}_t)y_{t-1}}{{\sigma }^2{(1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\tilde{f}}_t))}^2}+\beta {\tilde{f}}_t.\hfill \end{array}$$(11)

The intuition for this update is similar to Model I, with the exception that the size of the update is mitigated if $\left|{\tilde{f}}_t\right|$ is large, i.e., when $\tilde{h}({\tilde{f}}_t;\mathit{\theta })$ is close to zero or one.

2.3.3. Model III: Robust updating

Robustness to outliers and influential observations can be obtained by making alternative assumptions for the conditional model density ${\tilde{p}}_t.$ For example, we can assume that ${\tilde{p}}_t$ is fat-tailed as in Harvey and Luati (2014). Consider the same setting as Model I, but with ${\tilde{p}}_t$ a Student’s t distribution with zero mean, scale parameter σ, and degrees of freedom parameter λ, i.e., $$\text{log}\hspace{0.17em}\tilde{p}(y_t|{\tilde{f}}_t,y_{t-1};\mathit{\theta })=\hspace{0.17em}\text{log}\hspace{0.17em}\frac{\Gamma ((\lambda +1)/2)}{\Gamma (\lambda /2) \sqrt{\pi \lambda {\sigma }^2}}-\frac{\lambda +1}{2}\text{log}\hspace{0.17em}\left(1+\frac{{\tilde{u}}_t^2}{\lambda {\sigma }^2}\right),$$ where ${\tilde{u}}_t=y_t-{\tilde{f}}_t y_{t-1}.$ As a result, the score update becomes (12) $${\tilde{f}}_{t+1}=\omega +\alpha \frac{(\lambda +1){\tilde{u}}_t{y}_{t-1}}{\lambda +{\tilde{u}}_t^2/{\sigma }^2}+\beta {\tilde{f}}_t=\omega +\alpha (1+{\lambda }^{-1})\frac{(y_t-{\tilde{f}}_t{y}_{t-1})y_{t-1}}{1+{\lambda }^{-1}·{(y_t-{\tilde{f}}_t{y}_{t-1})}^2/{\sigma }^2}+\beta {\tilde{f}}_t.$$(12)

The update ${\tilde{f}}_{t+1}$ is now less sensitive to large values of ${\tilde{u}}_t$ compared to the Gaussian case (${\lambda }^{-1}=0$). In particular, the robust score update in (12) is a bounded function of ${\tilde{u}}_t.$ The intuition is as follows. When the conditional model density is fat-tailed, large realizations of ${\tilde{u}}_t$ can be attributed to either an increase of the true, unobserved conditional mean ${\tilde{f}}_t y_{t-1}$ or to the fat-tailed nature of the prediction errors. The score update again balances these two competing explanations in an information theoretic optimal way. For the limiting case ${\lambda }^{-1}=0,$ we recover Eq. (10)(10) $$\begin{array}{c}{\tilde{f}}_{t+1}=\omega +\alpha {\tilde{u}}_t \frac{y_{t-1}}{{\sigma }^2}+\beta {\tilde{f}}_t.\hfill \end{array}$$(10) .

Figure 1 compares the different updating functions for ${\tilde{f}}_t$ for Models I and III. For the Student’s t distribution (Model III), the impact of large prediction erorrs on ${\tilde{f}}_{t+1}$ is clearly bounded, in contrast to the updates for Model I. The reactions are steeper if y_t is persistently away from the zero unconditional mean, i.e., if both $y_{t-1}$ and y_t are substantially positive. For extremely large prediction errors, the update tends to zero again as the KL perspective attributes such observations to the fat-tailedness of the model distribution rather than to shifts in the conditional mean. The parameter updates with $\beta =0.5$ tend to bring ${\tilde{f}}_{t+1}$ faster to its unconditional mean compared to β = 1.

Figure 1. Shape of Normal (black) and Student’s t (red) updating functions. The updated parameter $f_{t+1}$ is plotted as a function of y_t for given f_t = 0.5 and given low initial state $y_{t-1}=0.5$ (left) high initial state $y_{t-1}=2$ (middle) and very high initial state $y_{t-1}=4$ (right). All plots are obtained with ω = 0 and $\alpha =0.1.$ Solid lines have $\beta =0.5$ and dashed lines have β = 1.

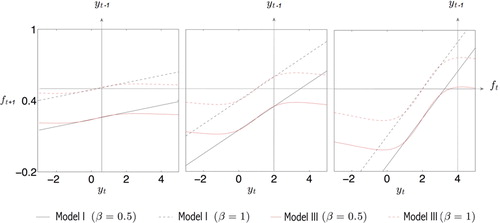
Figure 1 further reveals how the updating function uses the value $y_{t-1}$ as a crucial guidance mechanism to distinguish between changes in observed data that provide information about the conditional expectation and those that do not. For example, if the new observation is very close to its zero unconditional mean (left graph), then there is no reason to strongly update the conditional expectation, regardless of whether the realization y_t is large or small: the observation y_t does not contain much information about the dependence of the process as the mean-reverting mechanism is almost inactive in this case. By contrast, if $\left|y_{t-1}\right|$ is large, the observed y_t carries more information about ${\tilde{f}}_t.$ Consider the case where $y_{t-1}=4$ (right graph). Then, if y_t is also large, these observations provide strong evidence that the process has strong dependence and hence that f_t is large, resulting in an upward drift of ${\tilde{f}}_{t+1}.$ On the other hand, if y_t is close to zero, mean reversion apparently is fast and causes a downward pressure on ${\tilde{f}}_{t+1}.$

2.4. Estimation and forecasting

Maximum likelihood (ML) estimation of the parameter vector $\mathit{\theta }$ in the score driven AR(1) model (7) is similar to ML estimation for autoregressive moving average (ARMA) models. The conditional likelihood function (5) is known in closed-form given the explicit expressions for both the updating equation for ${\tilde{f}}_{t+1}$ and the score function s_t. The maximization of the log-likelihood function (5) with respect to $\mathit{\theta }$ is typically carried out using a quasi-Newton optimization method. The prediction errors ${\tilde{u}}_t$ evaluated at the maximum likelihood estimate ${\widehat{\mathit{\theta }}}_T$ of $\mathit{\theta }$ can be used for diagnostic checking.

Forecasting with the score driven time-varying AR model is also straightforward. The forecast for $y_{T+1}$ can be based directly on (3) with ${\tilde{f}}_{T+1}$ computed by (7) given the value for y_T. Given the nonlinearity of the model, multi-step-ahead forecasts can only be obtained via simulation. For example, to forecast $y_{T+2},$ one simulates values of $y_{T+1}$ using ${\tilde{f}}_{T+1}$ and simulated values of ${\tilde{u}}_{T+1}.$ Each simulated value of $y_{T+1}$ can be used to obtain a simulated value of ${\tilde{f}}_{T+2},$ which in turn can be combined with a simulated value of ${\tilde{u}}_{T+2}$ to produce a simulated value of $y_{T+2}.$ A series of simulated realizations $y_{T+2}$ can be used to construct the mean or median or quantile forecasts of $y_{T+2}.$ The computations are simple, fast, and can be carried out in parallel for large simulation sizes to achieve accuracy and efficiency. Forecasts of $y_{T+j},$ for $j=3,4,\dots ,$ can be obtained similarly.

3. Nonlinear AR model representations

3.1. Reduced form of time-varying AR coefficient model

It may appear difficult to compare the nonlinear autoregressive model from Section 2 with other nonlinear models such as the TAR and STAR models that are discussed in Section 1. The TAR and STAR models use lags of the dependent variable y_t itself as state variables to make the autoregressive coefficient of the AR(1) model time-varying. The score driven approach from Section 2 treats the time-varying autoregressive parameter as a time series process with innovations that are also functions of past observations. The commonalities become apparent when we consider the reduced form of the score driven model.

To obtain the reduced form, we first write Eq. (3)(3) $$y_t=h(f_t) y_{t-1}+u_t,$$(3) as $$y_t=h(f_t)y_{t-1}+u_t\iff h(f_t)=\frac{y_t-u_t}{y_{t-1}},$$ which is valid almost surely. Here we suppress the dependence of functions on $\mathit{\theta }.$ We also use f_t rather than ${\tilde{f}}_t$ as we treat the model here as the true data generating process rather than as the filter. Using $h^{-1}$ as the inverse of the link function h, we obtain $$\begin{array}{c}{f}_{t+1}=\omega +\alpha s\left(h^{-1}\left(h(f_t)\right),y_t,y_{t-1}\right)+\beta h^{-1}\left(\frac{y_t-u_t}{y_{t-1}}\right).\hfill \end{array}$$

Substituting this expression into (3), we obtain $$\begin{array}{c}{y}_t=\omega y_{t-1}+\alpha s\left(h^{-1}\left(\frac{y_{t-1}-u_{t-1}}{y_{t-2}}\right),y_{t-1},y_{t-2}\right)y_{t-1}+\beta h^{-1}\left(\frac{y_{t-1}-u_{t-1}}{y_{t-2}}\right)y_{t-1}+u_t,\hfill \end{array}$$ which reduces the model to a nonlinear ARMA model with two lags of y_t and one lag of u_t, that is a nonlinear ARMA(2, 1). This formulation of the score driven time-varying AR(1) model as a nonlinear ARMA(2, 1) model facilitates a direct comparison with the TAR and STAR models.

For Model I from Section 2.3, we have $s_t=u_t{y}_{t-1}/{\sigma }^2$ and $h(f_t)=f_t.$ The nonlinear ARMA(2, 1) specification then becomes $$y_t=\omega y_{t-1}+\alpha \frac{y_{t-1}{y}_{t-2}{u}_{t-1}}{{\sigma }^2}+\beta \frac{y_{t-1}-u_{t-1}}{y_{t-2}}{y}_{t-1}+u_t.$$

Similarly, for Model III we obtain the nonlinear ARMA representation $$y_t=\omega y_{t-1}+\alpha (\lambda +1)\frac{y_{t-1}{y}_{t-2}{u}_{t-1}}{\lambda +u_{t-1}^2}+\beta \frac{y_{t-1}-u_{t-1}}{y_{t-2}}{y}_{t-1}+u_t.$$

These highly nonlinear ARMA representations originate from a linear AR(1) model with a time-varying autoregressive coefficient based on the update function $f_{t+1}=\omega +\alpha s_t+\beta f_t.$ While the original model is relatively simple, it implies a complex but parsimonious nonlinear ARMA model. We emphasize that the current reduced form of the score driven model is only used for studying the nonlinearity of the model compared to competing model specifications, and not for the actual implementation of the model in simulations or empirical estimation. For such purposes we use the specification as presented in Section 2.

In case of Model II, the score expressions are slightly more complicated due to the chain rule for the nonidentity link function $h(f_t)={[1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-f_t)]}^{-1}$ with $h^{-1}(h(f_t))=\text{logit}(h(f_t))=\hspace{0.17em}\text{log}\hspace{0.17em}(h(f_t))-\hspace{0.17em}\text{log}\hspace{0.17em}(1-h(f_t)).$ The corresponding score function is $$s_t=h\prime (f_t) \frac{y_{t-1} u_t}{{\sigma }^2}=h(f_t)[1-h(f_t)] \frac{y_{t-1} u_t}{{\sigma }^2}=\frac{(y_t-u_t) (u_t-\Delta y_t) u_t}{{\sigma }^2 y_{t-1}},$$ with $\Delta y_t=y_t-y_{t-1},$ since $h(f_t)=(y_t-u_t) / y_{t-1}.$ The updating equation becomes (13) $$f_{t+1}=\omega +\alpha s_t+\beta \text{logit}((y_t-u_t)/y_{t-1}).$$(13) and we obtain the nonlinear ARMA model representation as $$\begin{array}{c}{y}_t={\left[1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-\omega -\alpha s_{t-1}-\beta \text{logit}((y_{t-1}-u_{t-1})/y_{t-2}))\right]}^{-1}{y}_{t-1}+u_t.\hfill \end{array}$$

We conclude that any score driven model can be represented in reduced form as a nonlinear ARMA model. To provide an intuition for the dynamic patterns described by these representations, we now compare the dynamic patterns of our model with those of TAR and STAR models.

3.2. Comparison with other nonlinear AR models

Two well-known nonlinear AR models are the threshold AR (TAR) model of Tong (1983) and the smooth transition AR (STAR) model of Chan and Tong (1986) and Teräsvirta (1994). We relate our nonlinear dynamic model with the basic versions of these two competing nonlinear AR models. We already have shown in Section 2 that our model has information theoretic optimality properties. Such optimality properties are not available for other models, including the TAR and STAR models.

We consider a standard TAR model of the following nonlinear autoregressive form, $$y_t={\gamma }_1{y}_{t-1}+{\gamma }_2 1(y_{t-2}<{\gamma }_3)y_{t-1}+u_t,$$ where $1( · )$ is an indicator function that takes the value one if the condition in the argument holds, and zero otherwise. The AR(1) coefficient switches between γ₁ and ${\gamma }_1+{\gamma }_2$ depending on whether $y_{t-2}$ is smaller or larger than γ₃. The model can be generalized in various ways.

A standard STAR model is given by $$y_t=\frac{{\gamma }_4{y}_{t-1}}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\gamma }_6 y_{t-2})}-\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\gamma }_6 y_{t-2}){\gamma }_5{y}_{t-1}}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\gamma }_6 y_{t-2})}+u_t,$$ where the AR(1) coefficient switches smoothly from γ₄ to ${\gamma }_4+{\gamma }_5$ depending on the value of $y_{t-2}.$ Both the TAR and STAR models are nonlinear ARMA(2, 0) models and have the same number of parameters as Models I and II from Section 2.3.

We visualize the differences between the models in Fig. 2 where each panel presents the response of y_t to different values of $y_{t-1}$ and $y_{t-2}$ for the TAR and STAR models, and for Model II with specific values of $u_{t-1}.$ In this visualization, the nonlinear response functions appear similar in many respects. The similarities hold even though TAR and STAR models are nonlinear AR(2) models and Model II is a nonlinear ARMA(2, 1) model.

Figure 2 Response functions for TAR, STAR, and Model II. Response functions for the TAR and STAR model (top 2 rows) are presented for different slopes in each regime. For example, in the top-left panel the TAR switches AR(1) coefficient from 0.1 to 0.55 depending on whether $y_{t-2}$ is positive or negative. The response functions for Model II (bottom 2 rows) are presented for ω = 0, $\alpha =0.05,$ different values of β (0.5 or 1.0), different values for the innovations $u_{t-1}$ (-0.5, 0 and 0.5).

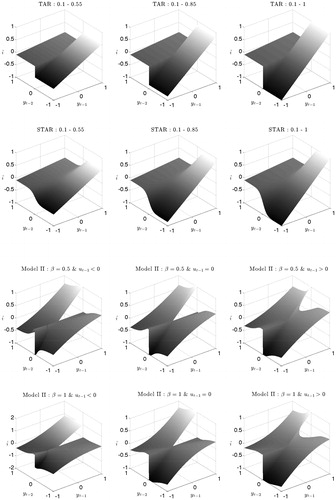
In all cases, we can distinguish two separate regimes. For the STAR model, one regime occurs for positive values of $y_{t-2}$ and has a large slope in the $y_{t-1}$ direction. Another regime with a small slope in the $y_{t-1}$ direction occurs for negative values of $y_{t-2}.$ In both the TAR and STAR models these regimes are linear in $y_{t-1},$ and hence, in each regime, the slope is constant over $y_{t-1}.$ The cross-section over the $y_{t-2}$ axis, however, shows the difference between the TAR and STAR models: the transition from one regime to the other is discontinuous for the TAR model, whereas the transition is smooth for the STAR model.

The response of Model II is similar to the TAR model given that the transition is abrupt from negative to positive values of $y_{t-2}.$ Model II is also similar to the STAR model because the response functions in $y_{t-1}$ vary continuously with the values of $y_{t-2}$ in a similar way, within each regime. The response functions for Model II are nonlinear in $y_{t-1}$ whether we have a positive or negative $y_{t-2}.$ This feature makes the nonlinearity of Model II markedly different. In particular, for negative values of $y_{t-2}$ we observe an increasing slope in $y_{t-1},$ while for positive values of $y_{t-2}$ the response function has a decreasing slope in $y_{t-1}.$ In Section 5, we investigate whether these differences improve the forecasting performance of the score driven model. The Supplementary Appendix moreover contains simulation evidence that the score driven model succeeds in uncovering the dynamics of the true f_t by the filtered ${\tilde{f}}_t$ in cases where the model is severely misspecified.

4. Statistical properties

4.1. Stochastic properties of the filter

The elements $\{\ell ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })\}$ of the log-likelihood function (5) depend on both the data $\left\{y_t\right\}$ and the filter $\left\{{\tilde{f}}_t\right\}.$ Even if the data $\left\{y_t\right\}$ are well-behaved, the stochastic properties of the likelihood function cannot be obtained without first establishing the stochastic properties of the filter $\left\{{\tilde{f}}_t\right\}$ for the unobserved time-varying parameter $\left\{f_t\right\}.$ In particular, to derive the asymptotic properties of the ML estimator (MLE) for the score driven time-varying AR parameter model of Section 2, we need to establish strict stationarity, ergodicity and bounded moments of the filter $\left\{{\tilde{f}}_t\right\}$ uniformly on the parameter space Θ, and we need to ensure that the filter is Near Epoch Dependent (NED) on a mixing sequence at ${\mathit{\theta }}_0\in \Theta$ where ${\mathit{\theta }}_0$ is the true parameter; see the treatments of Gallant and White (1988) and Pötscher and Prucha (1997) for precise definitions. The stationarity and ergodicity (SE) property and bounded moments are required to obtain the consistency of the MLE. The additional NED property is used to establish asymptotic normality.

As mentioned in the introduction, we allow the data generating process to be general and nonparametric in nature. As such we only impose high-level conditions on the data and obtain the properties of the filter and the MLE allowing for misspecification of our parametric model. In this sense, we follow the classical M-estimation literature in deriving the MLE asymptotics while imposing only high-level conditions on the data such as stationarity, fading memory and moments; see e.g. Domowitz and White (1982), Gallant and White (1988), White (1994), and Pötscher and Prucha (1997). If one wishes to work under an axiom of correct specification, then additional work should be carried out to show that the data generated by the model satisfies the desired properties.

For notational simplicity, we define the score update as $$\begin{array}{c}{\tilde{f}}_{t+1}:=\varphi ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta }):=\omega +\alpha s({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })+\beta {\tilde{f}}_t,\hfill \end{array}$$ and the supremum as $${\overline{\rho }}_t:=\underset{(f,\mathit{\theta })\in \tilde{\mathcal{F}}\times \Theta }{\sup }|\alpha \frac{\partial s(f,y_t,y_{t-1};\mathit{\theta })}{\partial f}+\beta |.$$

In many cases of interest, this supremum will prove to be bounded. We notice that ${\overline{\rho }}_t$ is a random variable due to its dependence on y_t and $y_{t-1}.$ Whenever convenient, we make the dependence of the filtered parameter ${\tilde{f}}_{t+1}$ on the initialization ${\tilde{f}}_1\in \tilde{\mathcal{F}},$ the data $y^{1:t}={\left\{y_s\right\}}_{s=1}^t,$ and the parameter vector $\mathit{\theta }\in \Theta$ explicit in our notation, for example, (14) $$\begin{array}{c}{\tilde{f}}_{t+1}(y^{1:t},\mathit{\theta },{\tilde{f}}_1)=\omega +\alpha s({\tilde{f}}_t(y^{1:t-1},\mathit{\theta },{\tilde{f}}_1),y_t,y_{t-1};\mathit{\theta })+\beta {\tilde{f}}_t(y^{1:t-1},\mathit{\theta },{\tilde{f}}_1),\hfill \end{array}$$(14) for all $t\in \mathbb{N}.$

To establish the asymptotic properties of the MLE, we require the dependence of the filter ${\tilde{f}}_{t+1}(y^{1:t},\mathit{\theta },{\tilde{f}}_1)$ on the initial condition ${\tilde{f}}_1$ to vanish in the limit. Theorem 1 below is a slight adaptation of Blasques et al. (2014) and formulates these conditions more precisely. Apart from requiring the existence of appropriate moments, the main requirements are conditions (ii), (iv), and (v), which state that (14) is contracting on average in an appropriate sense. Below we let ${\hspace{0.17em}\text{ln}\hspace{0.17em}}^{+}$ be a function satisfying ${\hspace{0.17em}\text{ln}\hspace{0.17em}}^{+}(x)=0$ for $0\le x\le 1$ and ${\hspace{0.17em}\text{ln}\hspace{0.17em}}^{+}(x)=\hspace{0.17em}\text{ln}\hspace{0.17em}(x)$ for x > 1. Additionally, $\perp$ is used to denote independence between random variables.

Theorem 1

(Blasques et al., 2014). Let $\tilde{\mathcal{F}}$ be convex, Θ be compact, ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ be SE, $s\in \mathbb{C}(\tilde{\mathcal{F}}\times {\mathcal{Y}}^2\times \Theta )$ and assume there exists a nonrandom ${\tilde{f}}_1\in \tilde{\mathcal{F}}$ such that

1. $\mathbb{E}{\hspace{0.17em}\text{ln}\hspace{0.17em}}^{+}\underset{\mathit{\theta }\in \Theta }{\sup }|s({\tilde{f}}_1,y_t,y_{t-1};\mathit{\theta })|<\infty$; and

2. $\mathbb{E}\hspace{0.17em}\text{ln}\hspace{0.17em}{\overline{\rho }}_1<0.$

Then ${\{{\tilde{f}}_t({\tilde{f}}_1,y^{1:t-1};\mathit{\theta })\}}_{t\in \mathbb{N}}$ converges exponentially fast almost surely (e.a.s.) to the limit SE process ${\{{\tilde{f}}_t(y^{t-1};\mathit{\theta })\}}_{t\in \mathbb{Z}}$; i.e. we have $$c^t \underset{\mathit{\theta }\in \Theta }{\sup }|{\tilde{f}}_t({\tilde{f}}_1,y^{1:t-1};\mathit{\theta })-{\tilde{f}}_t(y^{t-1},\mathit{\theta })|\stackrel{a.s.}{\to }0,$$ for some c > 1 as $t\to \infty$. If furthermore $\exists n_f\ge 1$ such that

1. $\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|s({\tilde{f}}_1,y_t,y_{t-1};\mathit{\theta }){|}^{n_f}<\infty$; and either

2. $\underset{\mathit{\theta }\in \Theta }{\sup }|s(f,\mathbf{y};\mathit{\theta })-s(f\prime ,\mathbf{y};\mathit{\theta })|<|f-f\prime |\forall (f,f\prime ,\mathbf{y})\in \tilde{\mathcal{F}}\times \tilde{\mathcal{F}}\times {\mathcal{Y}}^2$; or

3. $\mathbb{E}{\overline{\rho }}_1^{n_f}<1$ and ${\tilde{f}}_t({\tilde{f}}_1,y^{1:t-1};\mathit{\theta })\perp {\overline{\rho }}_{t+1}(\mathit{\theta })\forall (t,{\tilde{f}}_1,\mathit{\theta })\in \mathbb{N}\times \tilde{\mathcal{F}}\times \Theta ,$

where y is any point in ${\mathcal{Y}}^2$. It then follows that both ${\{{\tilde{f}}_t({\tilde{f}}_1,y^{1:t-1};\mathit{\theta })\}}_{t\in \mathbb{N}}$ and the limit SE process ${\{{\tilde{f}}_t(y^{t-1};\mathit{\theta })\}}_{t\in \mathbb{Z}}$ have n_f bounded moments. Hence, (15) $$\underset{t}{\sup }\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|{\tilde{f}}_t(y^{1:t-1},\mathit{\theta },{\tilde{f}}_1){|}^{n_f}<\infty ,\hspace{1em}\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|{\tilde{f}}_t(y^{t-1};\mathit{\theta }){|}^{n_f}<\infty .$$(15)

For more details on e.a.s. convergence, we refer to Straumann and Mikosch (2006). The limiting sequence ${\tilde{f}}_t(y^{t-1};\mathit{\theta })$ in Theorem 1 does not depend on the initialization condition ${\tilde{f}}_1.$ Whereas condition (ii) is key in ensuring that the initialized sequence ${\tilde{f}}_t(y^{1:t-1};\mathit{\theta },{\tilde{f}}_1)$ converges to its stationary and ergodic (SE) limit, conditions (iv) and (v) are essential for establishing the existence of an appropriate number of unconditional moments of the SE limiting sequence.

The verification of the conditions in Theorem 1 is often straightforward. Consider Model II from Section 2.3 with its updating equation (11)(11) $$\begin{array}{c}{\tilde{f}}_{t+1}=\omega +\alpha (y_t-\frac{y_{t-1}}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\tilde{f}}_t)})\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\tilde{f}}_t)y_{t-1}}{{\sigma }^2{(1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\tilde{f}}_t))}^2}+\beta {\tilde{f}}_t.\hfill \end{array}$$(11) . If ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ is SE and satisfies $\mathbb{E}|y_t{|}^{n_y}<\infty ,$ then the SE condition (ii) reduces to (16) $$\mathbb{E}\hspace{0.17em}\text{ln}\hspace{0.17em}\left|\underset{(f,\mathit{\theta })\in \tilde{\mathcal{F}}\times \Theta }{\sup }\beta +\alpha h″(f)\frac{(y_t-f y_{t-1})y_{t-1}}{{\sigma }^2}-\alpha h\prime (f)\frac{y_{t-1}^2}{{\sigma }^2}\right|<0,$$(16) with $h(f)={[1+\hspace{0.17em}\text{exp}\hspace{0.17em}(-f)]}^{-1}.$ The parameter space over which (16) is satisfied can now easily be computed, either numerically or by using upper bounds on the constituents of (16). For example, if $\left|y_t\right|$ has some bounded moment, it is easy to see that there exists a parameter space Θ with $\beta <1$ and α sufficiently close to zero for every $\mathit{\theta }\in \Theta ,$ such that (16) is satisfied for all points in the parameter space.

The presence of the supremum over $\mathit{\theta }$ in all of the expressions in Theorem 1 guarantees that we do not only obtain pointwise convergence, but that we also establish the convergence of the sequence ${\{{\tilde{f}}_t(y^{1:t-1},·,{\tilde{f}}_1)\}}_{t\in \mathbb{N}}$ with random elements taking values in the Banach space $(\mathbb{C}(\Theta ,\tilde{\mathcal{F}}),||·|{|}^{\Theta })$ for every $t\in \mathbb{N}$ to a limiting sequence ${\{{\tilde{f}}_t(y^{1:t-1},·)\}}_{t\in \mathbb{Z}},$ where $\left|\right|·|{|}^{\Theta }$ denotes the supremum norm on Θ. This more abstract convergence result in a function space allows us to relax some smoothness requirements for the likelihood in Section 4.2. In particular, we only need to put appropriate conditions on the second rather than on the third order derivatives of the likelihood; compare Straumann and Mikosch (2006) and Blasques et al. (2014).

Following Pötscher and Prucha (1997), Theorem 2 below shows that, under appropriate conditions, the NED properties of the data $\left\{y_t\right\}$ can be ‘inherited’ by the filtered sequence $\left\{{\tilde{f}}_t\right\}.$ This additional property is needed to establish the asymptotic normality of the MLE.

Theorem 2.

Let ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ be SE, have two bounded moments $\mathbb{E}|y_t{|}^2<\infty$ and be NED of size – q on some sequence ${\left\{z_t\right\}}_{t\in \mathbb{Z}}$. Furthermore, assume that $$\begin{array}{c}\left|\right|\beta (f-f\prime )+\alpha (s(f,\mathbf{y};\mathit{\theta })-s(f\prime ,\mathbf{y}\prime ;\mathit{\theta }))\left|\right|\le \hfill \\ a\left|\right|f-f\prime \left|\right|+b\left|\right|\mathbf{y}-\mathbf{y}\prime \left|\right|\hspace{1em}\forall (f,f\prime ,\mathbf{y},\mathbf{y}\prime )\in {\tilde{\mathcal{F}}}^2\times {\mathcal{Y}}^4,\hfill \end{array}$$ with $0\le a<1$ and $0\le b<\infty$. Then ${\{{\tilde{f}}_t(y^{1:t-1},\mathit{\theta },{\tilde{f}}_1)\}}_{t\in \mathbb{N}}$ is NED of size – q on ${\left\{z_t\right\}}_{t\in \mathbb{Z}}$ for every initialization ${\tilde{f}}_1\in \tilde{\mathcal{F}}.$

Theorem 2 imposes that the score $s(f,\mathbf{y};\mathit{\theta })$ is bounded by a linear function in $\mathbf{y}=(y_t,y_{t-1})$ and bounded by a contracting linear function in f. This condition is slightly more restrictive than its counterpart in Theorem 1. We use the NED property to establish asymptotic normality of the MLE for our model under misspecification: the result of the theorem allows us to use a central limit theorem for the score of the log-likelihood function.

The results in this section do not require the statistical model to be correctly specified. As the optimality results from Section 2.2 already indicate, the score based updates are optimal even if the model is severely misspecified. The Supplementary Appendix presents a number of simulated examples that demonstrate the usefulness and stability of the filter in such cases. The results of those simulations show that the score based ${\tilde{f}}_t$ track well the dynamics the time-varying f_t if the later varies sufficiently slowly over time. For a highly volatile f_t process, the data may not be sufficiently informative to allow for an accurate local estimation of the time-varying autoregressive parameter.

4.2. Asymptotic properties of MLE

To establish the strong consistency of the MLE, (17) $${\widehat{\mathit{\theta }}}_T:={\widehat{\mathit{\theta }}}_T({\tilde{f}}_1)\in \arg \underset{\mathit{\theta }\in \Theta }{\min }{L}_T(\mathit{\theta }),$$(17) with $L_T(\mathit{\theta })$ as defined in Eq. (5)(5) $$L_T(\mathit{\theta },{\tilde{f}}_1)=\frac{1}{T-1}\sum _{t=2}^T{\ell }_t(\mathit{\theta },{\tilde{f}}_1)=\frac{1}{T-1}\sum _{t=2}^T\ell ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })=\frac{1}{T-1}\sum _{t=2}^T\hspace{0.17em}\text{log}\hspace{0.17em}\tilde{p}(y_t|{\tilde{f}}_t,y_{t-1};\mathit{\theta }),$$(5) , we make the following three assumptions.

Assumption 3.

$(\Theta ,\mathfrak{B}(\Theta ))$ is a measurable space and Θ is a compact set. Furthermore, $h:\mathbb{R}\to \mathbb{R}$ and $p_u:\mathbb{R}\times \Theta \to \mathbb{R}$ are continuously differentiable in their arguments.

Assumption 4.

$\exists (n_f,f)\in [1,\infty )\times \tilde{\mathcal{F}}$ such that

1. $\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|s(f,y_t,y_{t-1};\mathit{\theta }){|}^{n_f}<\infty$ and either

2. $\underset{(f^{*},y,y\prime ,\mathit{\theta })\in \tilde{\mathcal{F}}\times \mathcal{Y}\times \mathcal{Y}\times \Theta }{\sup }|\beta +\alpha \partial s(f^{*},y,y\prime ;\mathit{\theta })/\partial f|<1$ or

3. $\mathbb{E}{\overline{\rho }}_1^{n_f}=\mathbb{E}\underset{(f^{*},\mathit{\theta })\in \tilde{\mathcal{F}}\times \Theta }{\sup }|\beta +\alpha \partial s(f^{*},y_t,y_{t-1};\mathit{\theta })/\partial f{|}^{n_f}<1$ and $${\tilde{f}}_t(y^{1:t-1},\mathit{\theta },{\tilde{f}}_1)\perp {\overline{\rho }}_{t+1}(\mathit{\theta })\forall (t,f_1,\mathit{\theta })\in \mathbb{N}\times \tilde{\mathcal{F}}\times \Theta .$$

Definition 3.

(Moment Preserving Maps) A function $H:\mathbb{R}\times \Theta \to \mathbb{R}$ is said to be n/m-moment preserving, denoted as $H\in {\mathbb{M}}_{\Theta }(n,m),$ if and only if $\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|x_t(\mathit{\theta }){|}^n<\infty$ implies $\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|H(x_t(\mathit{\theta });\mathit{\theta }){|}^m<\infty .$

Assumption 5.

$h\in {\mathbb{M}}_{\Theta }(n_f,n_h)$ and $\text{log}\hspace{0.17em}{p}_u\in {\mathbb{M}}_{\Theta }(n,n_{\hspace{0.17em}\text{log}\hspace{0.17em}{p}_u})$ with $n_{\hspace{0.17em}\text{log}\hspace{0.17em}{p}_u}\ge 1$ for $n=\min \{n_y,n_y{n}_h/(n_y+n_h)\}.$

Assumption 3 ensures the existence of the MLE as a well-defined random variable, while Assumptions 4 and 5 ensure the SE properties of the filter and the existence of the correct number of moments of the likelihood function, respectively. Moments are ensured via the notion of moment preserving maps; see Blasques et al. (2014). Products and sums satisfy all the intuitive moment preservation properties via triangle and Minkowski inequalities.

Assumption 4 is easy to verify for the robust update Model III introduced in Section 2.4. The moment bound for the score in Assumption 4(i) and the contraction condition in Assumption 4(ii) hold on a non-degenerate parameter space Θ since the score function $$s(f_t,y_t,y_{t-1};\lambda )=(\lambda +1)\frac{(y_t-{\tilde{f}}_t{y}_{t-1})y_{t-1}}{\lambda +{(y_t-{\tilde{f}}_t{y}_{t-1})}^2},$$ where λ is an element of $\mathit{\theta },$ is uniformly bounded and Lipschitz continuous.

The following theorem now establishes the consistency of the MLE. Below, ${\ell }_{\infty }$ denotes the limit likelihood function.

Theorem 3.

(Consistency) Let ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ be an SE sequence satisfying $\mathbb{E}|y_t{|}^{n_y}<\infty$ for some n_y > 0 and assume that Assumptions 3, 4 and 5 hold. Then the MLE (17) exists. Furthermore, let ${\mathit{\theta }}_0\in \Theta$ be the unique maximizer of ${\ell }_{\infty }(\mathit{\theta })$ on the parameter space Θ. Then the MLE satisfies ${\widehat{\mathit{\theta }}}_T({\tilde{f}}_1)\stackrel{a.s.}{\to }{\mathit{\theta }}_0$ as $T\to \infty$ for every ${\tilde{f}}_1\in \mathbb{R}.$

Blasques et al. (2015, Theorem 4.9) offer global identification conditions for well-specified score models which ensure that the limit log likelihood has a unique maximum ${\mathit{\theta }}_0\in \Theta .$ The assumption of a unique ${\mathit{\theta }}_0\in \Theta$ may however be too restrictive in the case of a misspecified model; see also Freedman and Diaconis (1982) for failure of this assumption in a simple location problem with iid data and Kabaila (1983) in the context of ARMA models. Remark 1 below follows Pötscher and Prucha (1997, Lemma 4.2) and highlights that if the restrictive identifiable uniqueness condition fails, then we can still show that the MLE ${\widehat{\mathit{\theta }}}_T({\tilde{f}}_1)$ converges to the set of maximizers of the limit loglikelihood function ${\ell }_{\infty }.$ In other words, we can avoid the assumption of uniqueness of ${\mathit{\theta }}_0\in \Theta ,$ stated in Theorem 3, and obtain the a set-consistency result. A simple regularity condition is required which states that the level sets of the limit loglikelihood function ${\ell }_{\infty }$ are regular (see Definition 4.1 in Pötscher and Prucha, 1997). The regularity of the level sets is trivially satisfied in our case.

Remark 1.

Let the conditions of Theorem 3 hold. Suppose that ${\ell }_{\infty }$ is maximized at a set of points. Then the MLE converges ${\widehat{\mathit{\theta }}}_T({\tilde{f}}_1)$ converges to that set as $T\to \infty$ for every ${\tilde{f}}_1\in \mathbb{R};$ see Lemma 4.2 Pötscher and Prucha (1997).

Assumption 6 below imposes the conditions used in Theorem 2 to ensure that the filter $\left\{{\tilde{f}}_t\right\}$ inherits the NED properties of the data. It also states conditions that are used to ensure that the likelihood score ${\ell }_t^{\prime }(w_t,\mathit{\theta })$ inherits the NED properties of the vector $w_t:=({\tilde{f}}_t,y_t,y_{t-1}),$ with ${\ell }_t^{\prime }(w_t,\mathit{\theta })=\ell \prime ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta }):=\partial \ell ({\tilde{f}}_t,y_t,y_{t-1};\mathit{\theta })/\partial \mathit{\theta }$ and ${\ell }_t^{″}(w_t,\mathit{\theta }):={\partial }^2{\ell }_t(\mathit{\theta })/\partial \mathit{\theta }\partial \mathit{\theta }\prime .$

Assumption 6.

For every $\mathit{\theta }\in \Theta$, it holds that

1. $|{\ell }_t^{\prime }(\mathbf{w},\mathit{\theta })-{\ell }_t^{\prime }(\mathbf{w}\prime ,\mathit{\theta })|\le c\left|\right|\mathbf{w}-\mathbf{w}\prime \left|\right|\forall (\mathbf{w},\mathbf{w}\prime )\in {\tilde{\mathcal{F}}}^2\times {\mathcal{Y}}^4$ with $\left|c\right|<\infty$

2. $\left|\right|\beta (f-f\prime )+\alpha (s(f,\mathbf{y};\mathit{\theta })-s(f\prime ,\mathbf{y}\prime ;\mathit{\theta }))\left|\right|\le a\left|\right|f-f\prime \left|\right|+b\left|\right|\mathbf{y}-\mathbf{y}\prime \left|\right|$ for all $(f,f\prime ,\mathbf{y},\mathbf{y}\prime )\in {\tilde{\mathcal{F}}}^2\times {\mathcal{Y}}^4$ with $0\le a<1$ and $0\le b<\infty .$

Conditions (i) and (ii) of Assumption 6 can be verified for the robust update Model III since, for λ bounded away from zero, the ML score function ${\ell }_t^{\prime }$ is Lipschitz continuous on w and the updating score function s is Lipschitz continuous on f and $\mathbf{y}.$ Condition (ii) in Assumption 6 allows for simple and clear results and is the same contraction condition as used in Pötscher and Prucha (1997) and Davidson (1994). A less restrictive condition can be used that allows for random coefficient autoregressive updates; see Hansen (1991).

Using Assumption 6, we obtain the asymptotic normality of the MLE in Theorem 4 by assuming that ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ is NED on an α-mixing sequence. To ease the exposition, we imposed moment bounds in Assumption 6 directly on the derivatives of the likelihood function; see also Straumann and Mikosch (2006). Alternatively, these bounds could have been derived in a similar way as in Theorem 3 from primitive conditions concerning the moment preserving properties of h and p_u; see the Supplementary Appendix.

Theorem 4.

(Asymptotic Normality) Let ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ be an SE sequence that is NED of size –1 on the $\varphi$-mixing process ${\left\{z_t\right\}}_{t\in \mathbb{Z}}$ of size $-\delta /(\delta -1)$, and let Assumptions 3, 4, 5 and 6 hold. Furthermore, let $\mathbb{E}|{\ell }_T^{\prime }(\mathbf{w}\prime ,{\mathit{\theta }}_0){|}^{\delta }<\infty \mathbb{E}|L_T^{\prime }(\mathbf{w}\prime ,{\mathit{\theta }}_0){|}^{\delta }<\infty$ for some $\delta >2,\mathbb{E}\underset{\mathit{\theta }\in \Theta }{\sup }|{\ell }_t^{″}(\mathbf{w}\prime ,\mathit{\theta })|<\infty$ and ${\mathit{\theta }}_0\in \text{int}(\Theta )$ be the unique maximizer of ${\ell }_{\infty }$ on Θ. Then the ML estimator ${\widehat{\mathit{\theta }}}_T({\tilde{f}}_1)$ satisfies $$\sqrt{T}({\widehat{\mathit{\theta }}}_T({\tilde{f}}_1)-{\mathit{\theta }}_0)\stackrel{d}{\to }\mathrm{N}(0,{\mathcal{I}}^{-1}({\mathit{\theta }}_0)\mathcal{J}({\mathit{\theta }}_0){\mathcal{I}}^{-1}({\mathit{\theta }}_0))\text{as}T\to \infty ,$$ where $\mathcal{I}({\mathit{\theta }}_0):=-\mathbb{E}{\ell }_t^{″}(\mathbf{w}\prime ,{\mathit{\theta }}_0)$ and $\mathcal{J}({\mathit{\theta }}_0):=\mathbb{E}{\ell }_t^{\prime }(\mathbf{w}\prime ,{\mathit{\theta }}_0){\ell }_t^{\prime }{(\mathbf{w}\prime ,{\mathit{\theta }}_0)}^{\top }$ are the Fisher information matrix and the expected outer product of gradients, respectively, both evaluated at ${\mathit{\theta }}_0.$

5. Empirical application

5.1. Time-varying temporal dependence in U.S. insurance claims

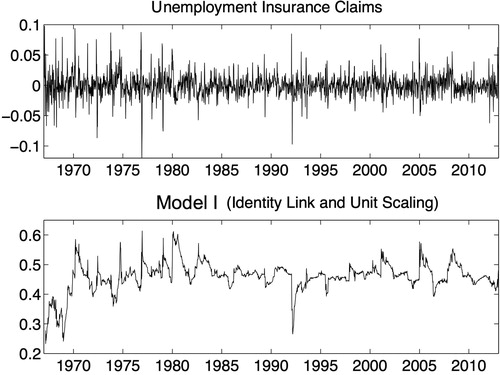
We illustrate the empirical relevance of our nonlinear autoregressive model by analyzing weekly observations of U.S. unemployment insurance claims (UIC). The empirical analysis of the time series of UIC based on dynamic macroeconomic models has received much attention in the literature; see for example McMurrer and Chasanov (1995), Meyer (1995), Anderson and Meyer (1997, 2000), Hopenhayn and Nicolini (1997), and Ashenfelter et al. (2005). The importance of forecasting weekly UIC time series data has been highlighted by Gavin and Kliesen (2002) who show that UIC is a highly effective leading indicator for labor market conditions and hence for forecasting gross domestic product growth rates. Our sample consists of weekly continuously compounded growth rates of the seasonally adjusted (four-week moving) average initial unemployment insurance claims observed from 1960 to 2013, as included in the Conference Board Leading Economic Index.

We only present the estimation results for Model I. The results for Model II are very similar. We find that the nonlinearity of the model sometimes poses challenges to the numerical optimization of the likelihood function, and that one has to use different starting values to ensure convergence to the proper maximum. If the nonlinearity of the model is combined with a density that is not log-concave, such as the Student’s t distribution in Model III, multiple local optima occur more often. Several of these local optima are not stable if the parameters are perturbed around the optimum. For example, in Model III we obtain a maximum of the likelihood function close to the one reported for Model I below, as well as a second higher local maximum for a negative value of α. A negative α does not satisfy the optimality theory developed in Section 2. The likelihood function near this second maximum is very peaked and disappears if the degrees of freedom parameter in Model III is perturbed to somewhat higher levels. Combining the properties of the different specifications, Model I presented below provides the best compromise in terms of (i) the stability of the optimum under perturbations of the parameter and the empirical interpretability of the filtered path, (ii) the optimality restriction from Section 2.2, that is $\alpha >0,$ and (iii) in-sample fit in terms of corrected Akaike’s information criterion (AICc) of Hurvich and Tsai (1991).

Figure 3 presents the UIC data together with the filtered estimates of the time-varying autoregressive parameter that fluctuate considerably over time. The parameter reaches a minimum of roughly 0.2 in the late 1960s, indicating that UIC has little temporal dependence during this time period. In the 1980s, the parameter climbs to about 0.6, indicating that the UIC may deviate persistently from its unconditional mean over an extended number of weeks. During the financial crisis of 2008 and its aftermath in 2009, we again see a rise in the level of persistence of claims, followed by a steady decline until the end of the sample.

Figure 3. Growth rate of U.S. seasonally adjusted weekly unemployment insurance claims; Filtered estimates of time-varying autoregressive parameter from Model I.

5.2. Forecasting comparison for three U.S. economic time series

We consider the one-step ahead forecasting performance of Model I and three benchmark models. We consider the weekly unemployment insurance claims series from Section 5.1 and two additional series: the U.S. monthly industrial production index from 1947 to 2013, and the U.S. quarterly money velocity M2 from 1919 to 2013. All three time series are in log-differences such that we focus on forecasting growth rates. The three series have three different seasonal frequencies: weekly, monthly and quarterly. The parameter estimates are obtained from the in-sample analysis.

Table 2 compares the forecast precision of Model I with the forecast precision of the TAR, STAR and linear AR(p) models for all three series. The order of the AR model p is chosen by the general-to-specific methodology that selects the lag length based on the minimum AICc; the optimal order is denoted by $p^{*}.$ We find that for all three macroeconomic time series Model I, the TAR, and the STAR model outperform the linear AR model in terms of root mean squared forecast error by a wide margin. Also, for all three time series, the score driven Model I has the lowest root mean squared forecast error out of the models considered. These results are consistent with the likelihood-based results: Model I also outperforms the TAR, STAR, and AR($p^{*}$) models in terms of the log-likelihood value and AICc.

Table 2. Out-of-sample forecast comparisons for three U.S. macroeconomic time series

	Model I	TAR	STAR	AR($p^{*}$)
Weekly unemployment insurance claims, $p^{*}=2$
F-RMSE	0.7502	0.7522	0.7521	0.8484
LogLik	6743.96	6736.22	6736.86	6438.89
AICc	−13477.90	−13462.41	−13463.70	−12869.76
Monthly industrial production, $p^{*}=3$
F-RMSE	0.560	0.564	0.563	0.880
Log Lik	3025.94	3020.07	3020.50	3020.84
AICc	−6041.83	−6030.09	−6030.95	−6031.62
Quarterly money velocity M2, $p^{*}=3$
F-RMSE	0.1492	0.1514	0.1514	0.2079
Log Lik	646.54	643.29	643.30	643.53
AICc	−1282.79	−1276.31	−1276.32	−1276.78

The values for the maximized log-likelihood (LogLik), Akaike’s information criterion with finite sample correction (AICc) and root mean squared errors for one-step-ahead forecasts (F-RMSE) of the logarithmic growth rates of U.S. seasonally adjusted time series for weekly unemployment insurance claims, monthly industrial production index (2007 = 100), quarterly money velocity M2; source: Federal Reserve Bank of St. Louis.

We conclude that the score driven Model I produces relatively accurate out-of-sample forecasts for the three U.S. macroeconomic time series. The reported F-RMSEs of Model I are considerably lower than those of the AR($p^{*}$) models. The nonlinear adaptation to the serial dependence parameter in Model I is therefore potentially an important feature for the forecasting of such key economic time series.

6. Conclusions

We have shown that updating the parameters in an autoregressive model by the score of the predictive likelihood results in local improvements of the expected Kullback-Leibler divergence, and thus in nonlinear autoregressive models with information theoretic optimality properties. The reduced form of the resulting model can be written as a nonlinear ARMA model that can be compared to alternative nonlinear autoregressive models such as the threshold and smooth transition autoregressive models. Estimation of the static parameters in the new model is straightforward, and the maximum likelhood estimator can be shown to be consistent and asymptotically normal. In our empirical illustration for U.S. unemployment insurance claims, and for two other key U.S. macroeconomic time series, our most basic nonlinear dynamic model outperforms well-known alternatives such as the threshold and smooth transition autoregressive models.

Additional information

Funding

Blasques and Lucas thank the Dutch National Science Foundation (NWO; grant VICI453-09-005) for financial support. Koopman acknowledges support from CREATES, Aarhus University, Denmark; it is funded by Danish National Research Foundation, (DNRF78). We thank Howell Tong and Timo Teräsvirta for helpful comments and suggestions.