INFERENCE PROCEDURES FOR FUZZY KNOWLEDGE REPRESENTATION SCHEME

Abstract

This article presents a formal model of the knowledge representation scheme based on the fuzzy Petri net (FPN) theory. The model is represented as a 13-tuple consisting of the components of the FPN, two functions that give semantic meanings to the scheme and a set of contradictions. For the scheme, called the knowledge representation scheme based on the fuzzy Petri nets theory (KRFPN) the fuzzy inheritance and fuzzy recognition-inference procedures based on the dynamical properties of the FPN, are described in detail. The upper-time complexity of both the proposed inference algorithms is O(nm), where n is the number of places (concepts) and m is the number of transitions (relations) in the scheme. Illustrative examples of the fuzzy inheritance and the fuzzy recognition algorithms for the knowledge base, designed by the KRFPN, are given.

INTRODUCTION

The crucial component of an intelligent agent is its knowledge base. Informally, a knowledge base is an abstract representation of a working environment or a world in which the agent (or agents) has to solve tasks. It contains collections of (uncertain) facts and objects (in an abstract sense) and their relationships; vocabulary definitions; disjunctive facts, and constrains; descriptions of typical situations and the agent's behavior; the rules of the world; common-sense knowledge; decision rules; hypotheses; heuristics and problem-solving methods and procedures; knowledge about states, the actions, motivations, and goals of the agent; and knowledge about knowledge (meta-knowledge).

For more than 30 years one of the central problems of artificial intelligence is the development of a sufficiently precise and efficacious notation for the knowledge representation and reasoning, called a knowledge representation scheme (KRS) (Zeigler 1987; Garcia and Chien 1991; Aiello and Nardi 1991). The major classes of KRS, according to the taxonomy based on object-relationship, the true assertion about states and state-transformations criteria, are network (Quillian 1967; Findler 1979), logical (Israel and Beranek 1983; Dahl 1983; Bobrow 1985), and procedural schemes (Newell and Simon 1972), as well as schemes based on the frame theory (Minsky 1975).

In many real-world tasks, knowledge is based on imprecise, uncertain, incomplete, or even vague, and/or fuzzy information, and agents have to deal with the information in such a form. Therefore, in order to properly represent real-world knowledge and support vague, uncertain, and fuzzy-knowledge representation, reasoning, learning, and decision-making, different knowledge schemes were developed: scheme based on subjective Bayesian probabilities (so-called Prospector approach) (Duda, Gaschnig, and Hart 1979), rule-based system with certainty factors (MYCIN approach) (Buchanan and Shortliffe 1984), Bayesian or belief networks (Pearl 1988), schemes based on Dempster-Shafer calculus (Shafer 1976), and fuzzy logic-based schemes (Zadeh 1983). Among knowledge representation schemes that support uncertain and fuzzy knowledge representation and reasoning, there is a class of schemes based on the theory of fuzzy Petri nets (FPNs) (Cardoso and Camargo 1999): Looney (1988) and Chen, Ke, and Chang (1990) proposed FPNs for rule-based decision-making; Scarpelli, Gomide, and Yager (1996) described a reasoning algorithm for a high-level FPN; Chen (2002) introduced a weight FPN model for rule-based systems; Li and Lara-Rosano (2000) proposed a model based on an adaptive FPN, which is implemented for knowledge inference, but it also has a learning ability; Looney and Liang (2003) proposed the fuzzy belief Petri nets (PNs) as a combination of the bi-directional fuzzy propagation of the fuzzy belief network and modeling flexibility of the FPN; Lee, Liu, and Chaing (2003) introduced a reasoning algorithm based on possibilistic Petri nets as a mechanism that mimics human inference; Canales, Liand, and Yu (2006) described a method of fuzzy-knowledge learning based on an adaptive FPN; Ha, Li, Li, and Wang (2005) described knowledge representation by weighted fuzzy production rules and inference with generalized FPN; and Guo-Yan (2006) proposed a hybrid of the PN and the fuzzy PN to support an inference procedure for the natural extension of fuzzy expert systems. Shen (2006) presented the knowledge representation scheme based on a high-level FPN for modelling fuzzy IF-THEN and IF-THEN-ELSE rules. Based on the high-level FPN model, an efficient algorithm is proposed to automatically reason about imprecise and fuzzy information.

The main inference procedures, as the act of automatic reasoning from factual knowledge, in the network-based knowledge representation schemas are: inheritance, intersection search, and recognition. Inheritance is a form of reasoning that allows an agent to infer the properties of a concept on the basis of the properties of its ancestors in the network hierarchical structure (Touretzky 1986). An inference procedure, called the intersection search (Quillian 1967), allows relationships to be found among facts by “spreading activities” in semantic networks. The recognition (Shastri 1988) is the dual of the inheritance problem and it can be viewed as a general form of pattern-matching.

In this article, the original inference procedures—inheritance and recognition—for a network-based fuzzy knowledge representation scheme, called KRFPN, based on the fuzzy Petri net theory, are proposed.

A KNOWLEDGE REPRESENTATION SCHEME BASED ON FUZZY PETRI NETS

A network-based fuzzy knowledge representation scheme called KRFPN uses the concepts of fuzzy Petri net theory to represent vague and/or fuzzy information obtained from modelled real-word situations. In this section, we first define a marked FPN, describe the execution of an FPN, and then introduce the graphical representation of an FPN. After that, by using additional components and functions that provide semantic interpretations, we introduce the formal definition of the knowledge representation scheme based on the fuzzy Petri nets theory (KRFPN).

A Fuzzy Petri Net

A marked fuzzy Petri net structure can be defined as 10-tuple:

where

• P = {p₁, p₂,…, p_n} is a finite set of places,

• T = {t₁, t₂,…, t_m} is a finite set of transitions,

• P ∩ T = Ø,

• I: T → P^∞ is an input function, a mapping from transitions to bags of places,

• O: T → P^∞ is an output function, a mapping from transitions to bags of places,

• M = {m₁, m₂,…, m_r}, 1 ≤ r < ∞, is a set of tokens,

• Ω: P → 𝒫(M) is a mapping, from P to 𝒫(M), called a distribution of tokens, where 𝒫(M) denotes the power set of M. Using Ω₀ we denote the initial distribution of tokens in the places of a FPN.

• μ: P → N is a marking, a mapping from places to non-negative integers, N. A mapping μ can be represented as an n-component vector μ = (μ₁, μ₂,…, μ_n), where n is a cardinality of the set P. Obviously, μ(p_i) = μ_i, and μ(p_i) denotes the number of tokens in the place p_i. An initial marking is denoted by the vector μ ₀.

• f: T → [0, 1] is an association function, a mapping from transitions to real values between zero and one.

• c: M → [0, 1] is an association function, a mapping from tokens to real values between zero and one.

The complete information about the token m_i ∊ M is given by a pair (p_j, c(m_i)), where the first component specifies the location of the token, and the second one, its value. λ ∊ [0, 1] is a threshold value related to the firing of an FPN.

Graphical Representation of an FPN

A marked FPN can be represented by a bipartite directed multi-graph containing two types of nodes: places and transitions. Graphically, the circles represent places while the bars are used for transitions. The relationships, based on input and output functions, from places to transitions and transitions to places, are represented by directed arcs. Each arc is directed from an element of one set (P or T) to the element of another set (T or P).

A generalized FPN allows multiple arcs, according to the definitions of the input and output functions, where their co-domains are bags of places (P^∞). In the case when co-domains are sets, and for all transitions t_i, i = 1, 2,…, m, is |I(t_i)| = |O(t_i)| = 1, where |.| denotes the cardinality of a set, a multi-graph is transformed into a graph called a state machine (Peterson, 1981). In our case, it is a fuzzy state machine.

The tokens in marked FPN graphs are represented by labelled dots c(m_i), where c(m_i) denotes the value of the token.

Dynamical Properties of an FPN

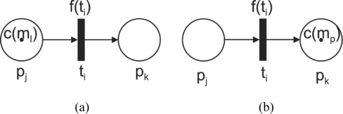
Tokens give dynamical properties to an FPN, and they are used to define its execution, i.e., by firing an enabled transition t_j, tokens are removed from its input places (elements in I(t_j)). Simultaneously, new tokens are created and distributed to its output places (elements of O(t_j)). In an FPN, a transition t_j is enabled if each of its input places has at least as many tokens in it as arcs from the place to the transition and if the values of the tokens c(m _l ), l = 1, 2,…exceed a threshold value λ ∊ [0, 1]. The number of tokens at the input and output places of the fired transition is changed in accordance with the basic definition of the original PN (Peterson, 1981). The new token value in the output place is obtained as c(m _l )f(t _i ), where c(m _l ) is the value of the token at the input place p_j ∊ I(t_i) and f(t_i) is the degree of truth of the relation assigned to the transition t_i ∊ T. Figure 1 illustrates the firing of the enabled transition of an FPN.

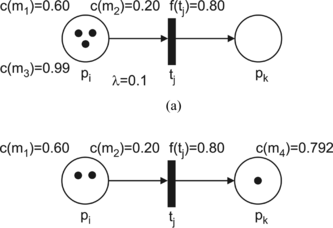
FIGURE 1 Firing an enabled transition. (a) Before firing; c(m _l ) > λ; (b) after firing; c(m_p) = c(m _l )f(t_i).

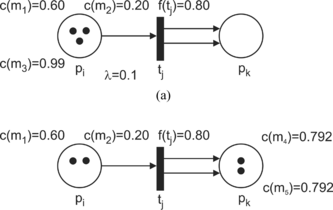
In general, if there are more tokens at an input place than arcs from the input place to the transition and if the value of each token exceeds the threshold value λ, then the selection of the token that takes the role in the firing is based on the maximum value c(m_i). For example, in Figure 2 (a), an input place p_i has three tokens {c(m₁) = 0.60, c(m₂) = 0.20, c(m₃) = 0.99}, and there is an arc directed to the transition t_j with an associated value f(t_j) = 0.80. The threshold value λ is 0.10. After firing the enabled transition t_j, a new marking is shown in Figure 2 b). The token (p_j, c(m₃)) takes place in firing the enabled transition t_j and a new token c(m₄) is generated at the output place p_k. The value of the token m₄ is 0.80·0.99 = 0.792. If there are two or more tokens with the same value c(m_i); i = 1, 2,…, then the selection is based on random criteria.

FIGURE 2 Firing an enabled transition t_j. (a) Before firing; (b) after firing the transition t_j.

Analogically, the generation of a new token at the output place p_k in configurations where there is more than one arc connected to the transition t_j with the output place, is based on the above-mentioned criteria, and it is illustrated in Figure 3. Figure 3(a) shows the situation before firing the enabled transition t_j, while Figure 3(b) depicts the state after firing the transition t_j. In this case, the tokens m₄ and m₅ are identical, i.e., the pair (p_k, m₄) is identical in terms of value to the pair (p_k, m₅).

FIGURE 3 Firing an enabled transition t_j;(case O(tj) = {p_k, p_k}). (a) Before firing; (b) after firing the transition t_j.

Note that the inheritance and recognition, as inference procedures defined for the proposed knowledge representation scheme, use the dynamical properties of a FPN.

Example 1

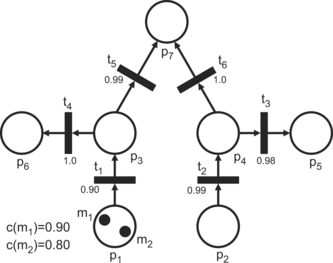
Let us illustrate an FPN graph and the execution of a fuzzy petri net, which is defined as a fuzzy state machine:

• P = {p₁, p₂, p₃, p₄, p₅, p₆, p₇},

• T = {t₁, t₂, t₃, t₄, t₅, t₆},

• I(t₁) = {p₁}, I(t₂) = {p₂}, I(t₃) = {p₄}, I(t₄) = {p₃}, I(t₅) = {p₃}, I(t₆) = {p₄},

• O(t₁) = {p₃}, O(t₂) = {p₄}, O(t₃) = {p₅}, O(t₄) = {p₆}, O(t₅) = {p₇}, O(t₆) = {p₇},

• M = {m₁, m₂, m₃,…, m_r},

• Ω₀ = {{m₁, m₂}, Ø, Ø, Ø, Ø, Ø, Ø},

• μ ₀  = (2, 0, 0, 0, 0, 0, 0},

• f(t₁) = 0.90, f(t₂) = 0.99, f(t₃) = 0.98, f(t₄) = 1.0, f(t₅) = 0.99, f(t₆) = 1.0,

• c(m₁) = 0.90, c(m₂) = 0.80,

• λ = 0.02.

The FPN graph is shown in Figure 4.

FIGURE 4 A simple FPN graph.

According to the rule that defines enabled transitions, only the transition t₁ is enabled because the number of tokens in its input place is two and there is only one arc connecting the place, and the values of the tokens exceed the threshold λ: c(m₁), c(m₂) > 0.02.

After firing the enabled transition t₁, token m₁ (based on the selection of the token that has the maximum value c(m_i)), is removed from the input place p₁ and simultaneously a new token m₃ is generated at the place p₃. The value of the token m₃ is c(m₃) = c(m₁)·f(t₁) = 0.90·0.90 = 0.81. The distribution of the tokens is now Ω ₁ = ({m₂}, Ø, {m₃}, Ø, Ø, Ø, Ø, Ø} and the marking μ ₁  = (1, 0, 1, 0, 0, 0, 0). Related to the new marking, there are now three enabled transitions in the FPN: t₁, t₄, and t₅.

Formal Definition of the Knowledge Representation scheme KRFPN

The Knowledge Representation Scheme based on the Fuzzy Petri Nets theory is defined as 4-tuple:

where FPN is a fuzzy Petri net.

• α: P → D is a bijective function that maps a set of places onto a set of concepts D. The set of concepts D consists of the formal objects used for representing objects and facts from the agent's world. The elements from D = D₁ ∪ D₂ ∪ D₃ are as follows: elements that denote classes or categories of objects and represent higher levels of abstraction (D₁), elements corresponding to individual objects as instances of the classes (D₂), and those elements representing the intrinsic properties of the concepts or values of these properties (D₃).

• β: T → Σ is a surjective function that associates a description of the relationship among facts and objects to every transition t_i ∊ T;i = 1, 2,…, m, where m is a cardinality of a set T. The set Σ = Σ₁ ∪ Σ₂ ∪ Σ₃ consists of elements corresponding to the relationships between the concepts used for partial ordering of the set of concepts (Σ₁), the elements used to specify the types of properties to which values from subset D₃ are assigned (Σ₂), and the elements corresponding to the relationships between the concepts, but not used for hierarchical structuring (Σ₃). For example, elements from Σ₃ may be used to specify the spatial relations among the objects.

The functions α and β give a semantic interpretation to the scheme.

The semantic interpretation requires the introduction of a set of contradictions C. A set of contradictions C is a set of pairs of mutually contradictory relations and/or concepts: C = {(σ_i, σ_j),…, (σ_r, σ_s), (d_k, d_l),…, (d_v, d_z)}, were σ_u;u = i, j,…, r, s are from the set Σ, and d_w;w = k, l,…, v, z are from the set D.

A set C contains elements corresponding to relations from Σ that mutually contradict each other, for example, is_a and is_not_a. Also, there are elements in the set D that are mutually contradictory if they are inherited for the same concept or object. For example, the object cannot simultaneously inherit properties such as “Quadruped” and “Biped.”

Both types of contradictions should be explicitly expressed in the KRFPN scheme.

The inverse function α⁻¹: D → P, and the generalized inverse function β⁻¹: Σ → τ; τ ⊆ T are defined in the KRFPN scheme.

Example 2

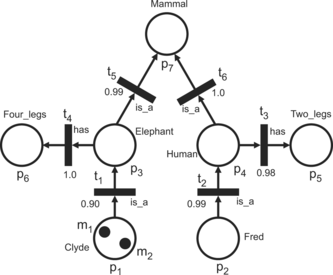
To illustrate the elementary KRFPN concepts, we use the FPN described in Example 1 as a component of the knowledge representation scheme, followed by the concepts needed for the semantic interpretation: functions α and β, and a set of contradictions C. The interpretation of the functions f and c is also needed. Example 2 is adopted from Touretzky (1986).

For α: P → D we have:

• α: p₁ → Clyde,

• α: p₂ → Fred,

• α: p₃ → Elephant,

• α: p₄ → Human,

• α: p₅ → Two_legs,

• α: p₆ → Four_legs,

• α: p₇ → Mammal.

The function β is defined as follows:

• β: t₁ → is_a,

• β: t₂ → is_a,

• β: t₃ → has,

• β: t₄ → has,

• β: t₅ → is_a,

• β: t₆ → is_a.

A set of concepts D is D₁ ∪ D₂ ∪ D₃, where a subset D₁ = {Human, Elephant, Mammal} contains concepts that represent classes, D₂ = {Clyde, Fred} is a subset consisting of concepts that correspond to individual objects as instances of the classes. A subset D₃ = {Tw o ₋ legs, Fou r ₋ legs} defines properties of the concepts.

A set of relationships Σ = Σ₁ ∪ Σ₂ ∪ Σ₃ consists of elements corresponding to the relationships between the concepts used for partial ordering of the set of concepts Σ₁ = {i s ₋ a}, the elements used to specify the types of properties to which values from subset D₃ are assigned Σ₂ = {has}, while the subset Σ₃, that contains elements corresponding to the relationships between the concepts, but not used for hierarchical structuring, in our simple example is an empty set.

A set of contradictions, C = {(Tw o ₋ legs, Fou r ₋ legs)};Tw o ₋ legs, Fou r ₋ legs ∊ D, defines that an object cannot be simultaneously a biped and quadruped.

The values defined by the function f express our confidence or our belief in the truth of the relationships. For example, the value f(t₄) = 1.0 defines our belief (or knowledge) that a human is always a mammal, while f(t₁) = 0.90 expresses our belief that Clyde is an elephant. The value f(t₁) = 0.90 can be interpreted as the statement that Clyde is a elephant is very true (see Table 1).

TABLE 1 Truth Scales and the Corresponding Numerical Intervals

Truth Scales	Numerical Intervals
Always true	[1.0, 1.0]
Extremely true	[0.95, 0.99]
Very true	[0.80, 0.94]
Considerably true	[0.65, 0.93]
Moderately true	[0.45, 0.64]
More or less true	[0.30, 0.63]
Slightly true	[0.10, 0.29]
Minimally true	[0.01, 0.09]
Not true	[0.0, 0.0]

The values c(m_i), i = 1, 2, may by interpreted as our assurance that we are really dealing with corresponding concepts. The threshold λ = 0.02 defines the relatively high sensitivity of the scheme related to the processes of inference. Figure 5 shows the graphical representation of the simple knowledge base designed by the KRFPN.

FIGURE 5 A simple knowledge base (Example 2) designed by the KRFPN.

Selection of Values f(t _i ), c(m _i ) and λ

A human's knowledge about facts from the real word is very often uncertain, ambiguous, and vague. The inference mechanism based on such facts, as well as the human interpretation of such facts and conclusions, generates uncertain and vague conclusions. There are many different approaches to representing knowledge in uncertain domains—from subjective Bayesian probabilities (Pearl 1988; Russel and Norvig 1995) through a rule-based system with certainty factors (Buchanan and Shortliffe 1984) to the fuzzy Petri net theory (Cardoso and Camargo 1999). In our approach we have used the last one, in which the uncertainty and confidence related to the facts, concepts, and the relationships between them are expressed by means of the values of f(t_i), t_i ∊ T, and c(m_i), m_i ∊ M, association functions. For example, the value of the function f, as well as the value of the function c, can be expressed by truth scales and by their corresponding numerical intervals depicted in Table 1 (Chen, Ke and Chang 1990).

The threshold value λ ∊ [0, 1] defines the “sensitivity” of the scheme during the inference procedures. By using different values for λ, the user can specify different degrees of truth for inherited concept properties or the recognized concept. The value of λ has influence on a number of levels of generated inheritance or recognition trees. Usually, λ is chosen to be small enough, for example, 0.01 or 0.1.

Example 3

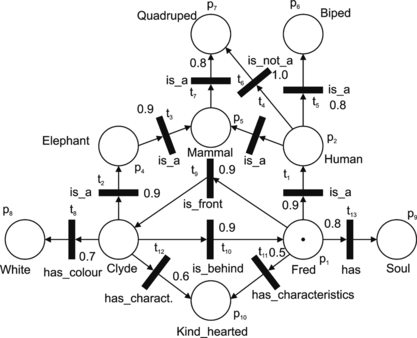
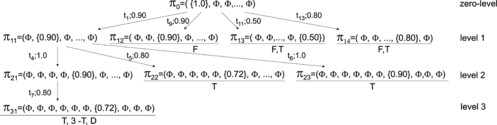
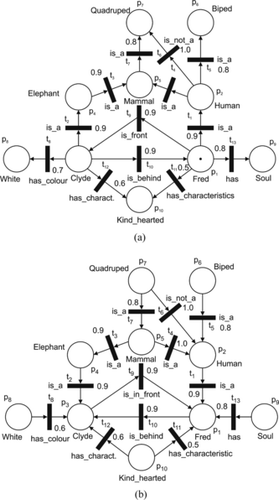
In order to illustrate the basic components of the KRFPN, a simple example (adopted from Touretzky (1986)) of the agent's knowledge base for a scene (Figure 6) is introduced. The knowledge base designed by the KRFPN = (FPN, α, β, C), where FPN is (P, T, I, O, M, Ω, μ, f, c, λ), has the following components (Figure 7): P = {p₁, p₂,…, p₁₀}; T = {t₁, t₂,…, t₁₃}; I(t₁) = {p₁}; I(t₂) = {p₃},…;I(t₁₃) = {p₁};O(t₁) = {p₂}; O(t₂) = {p₄},…; and O(t₁₃) = {p₉}. The set of tokens is M = {m₁, m₂,…, m_r}, the initial distribution of tokens is Ω₀ = {{m₁}, Ø,…Ø}, where c(m₁) = 1.0, and Ø denotes an empty set. The vector μ ₀ = (μ₁, μ₂,…, μ₁₀) = (1, 0,…, 0) denotes that there is only one token in the place p₁. The function f is specified as follows: f(t₁) = 0.9; f(t₂) = 0.9; f(t₃) = 1.0; f(t₄) = 1.0,…; f(t₁₂) = 0.6; and f(t₁₃) = 0.8 (Figure 7). f(t_i), i = 1, 2,…, m indicates the degree of our pursuance in the truth of the relation β(t_i).

FIGURE 6 A simple scene with Fred and the elephant Clyde.

FIGURE 7 The agent's knowledge base designed by the KRFPN.

The set D = D₁ ∪ D₂ ∪ D₃ is defined as follows: D₁ = {Elephant, Human, Mammal, Biped, Quadruped}, D₂ = {Fred, Clyde}, D₃ = {White, Soul, Kin d ₋ hearted}. The set Σ = Σ₁ ∪ Σ₂ ∪ Σ₃is {i s ₋ a, i s ₋ no t ₋ a} ∪ {ha s ₋ colour, ha s ₋ characteristic, has} ∪ {i s ₋ i n ₋ fron t ₋ of, i s ₋ behind}.

Functions α: P → D and β: T → Σ are (Figure 7):

Let C be a set of contradictions defined as C = {(i s ₋ a, i s ₋ no t ₋ a), (i s ₋ i n ₋ front, i s ₋ behind), (Quadruped, Biped)}.

For the initial distribution of tokens, Ω₀, the following transitions are enabled: t₁, t₉, t₁₁, and t₁₃.

Figure 7 shows the ontological complexity of even a simple example. In large examples, a graph would be too cluttered to be of much use. Therefore, the hierarchical structures of graphs have to be used. Petri nets (Petri 1962), in general, are appropriate for hierarchical system modeling, i.e., the system can be represented at the different abstract levels. In a Petri net, a subnet may be replaced by a single place or transition (the process of abstraction), or places and transitions can be replaced by subnets (the process of refinement (Peterson 1977; Ribarić 1991)).

FUZZY INHERITANCE

Inheritance can be described as the process of determining the properties of a concept d_i ∊ D, by looking up the properties that are locally attached to the concept d_i. If such local information is not available (or is insufficient), the process will continue by looking up properties attached to the concepts that lie at higher levels in the conceptual hierarchy.

K-Level Inheritance Tree

The inheritance procedure in the KRFPN is based on its dynamical properties and the determination of the inheritance set of the KRFPN. The inheritance set for the KRFPN is based on concepts similar to the reachability set of the ordinary Petri nets (PNs), where the reachability relationship is the reflexive, transitive closure of the immediately reachable relationship (Peterson 1981). In the PN, for the marking μ, a marking μ' is immediately reachable from μ if there exists a transition t_j ∊ T that can be fired, and by firing a new marking μ' is obtained. The reachability set is defined as the smallest set of all the reachable distributions of tokens stating for an initial distribution of tokens for the PN and recursively applying the firing of enabled transitions for immediately reachable distributions of tokens. The reachability set of the PN is graphically represented by a reachability tree.

The main differences between the inheritance set of the KRFPN and the reachability set of the PN (Peterson 1981) are as follows: (i) After firing all the enabled transitions for the distribution of tokens in the KRFPN, where the transitions are related to the elements in the subsets Σ₂ and Σ₃, the created tokens at the corresponding output places have to be frozen. Recall that the elements in Σ₂ and Σ₃ are used to specify the properties and the nonhierarchical structuring, respectively. A frozen token in the output place is fixed and it cannot enable a transition; (ii) An inheritance tree, as a graphical representation of the inheritance set, is bounded by k + 1 levels, where k is a predefined number of levels. Such an inheritance tree is called a k-level inheritance tree; (iii) A k-level inheritance tree has the following additional types of nodes: a k-terminal node, a frozen node, and an identical node.

A k-level inheritance tree consists of nodes (p _j , c(m_i)), j = 1, 2,…, n and i = 1, 2,…, v where n is a cardinality of the set of places P, and 0 ≤ v ≤ r, where r is a cardinality of the set of tokens M, and directed, labelled arcs. In order to simplify and make the notation uniform in the inheritance algorithm, the nodes in the tree are denoted by n-component vectors in the form π = (π₁, π₂,…π _n ). Each component π _i ; i = 1, 2,…, n of π is represented by an empty set Ø for μ(p_i) = 0, i.e., there is no token(s) at the place p_i , or by a set {c(m_k),…, c(m _l ),…, c(m _s )}, where c(m _l ) is the second component of the pair (p_i, c(m _l )) and represents the value of the token m _l at the place p _i. The number of elements in the above set is μ(p_i) ≥ 1. The vector π is called the distribution vector, or simply the distribution.

The directed arcs in a k-level inheritance tree are labelled by t_j ∊ T and f(t_j), where t_j denotes a fired transition and f(t_j) the value of its association function f, respectively. A directed labelled arc leads from the node at the ith level of the inheritance tree to the corresponding node at the i + 1th level; i = 1,2,…, k-1, where k is (pre)defined as the final level of the inheritance tree.

During the creation process of the k-level inheritance tree, each node is classified either as a frontier node, a terminal node, a k-terminal node, a frozen node, an identical node, a duplicate node, or an interior node. Frontier nodes are nodes that have not yet been processed. The special frontier node is a node that represents the initial distribution and is a root of the inheritance tree. The root node is a node at the zero-level of the inheritance tree. The frontier nodes are converted by the inheritance-tree algorithm to terminal, k-terminal, internal, frozen, duplicate, or identical nodes. A terminal node is a node corresponding to the dead distribution for which there are no enabled transitions. A k-terminal node is a node at the kth level of the inheritance tree. A frozen node corresponds to the distribution that is created by firing an enabled transition, which is related to (by means of a function β) the elements from subsets Σ₂ and Σ₃. The distributions obtained by firing such transitions become the frozen distributions. (A frozen token is fixed at the input place and cannot enable the transition). Identical nodes correspond to the distributions that have previously appeared in the tree, and for them the following is valid: Two nodes π _A and π _B are identical if π _Ai ≡ π _Bi;i = 1, 2,…, n, where π _Xi represents the ith component of π _X , where x is A or B. Duplicate nodes are nodes that have also previously appeared in the tree; they are not identical in the sense of n-tuples π, but they have the same marking μ (see a formal definition of the KRFPN): Two nodes A and B are duplicates if π _A  = π _B , where π _X represents the marking; x is A or B. In other words, two nodes are duplicate nodes if they have an equal number of tokens in each corresponding place (regardless of the values of the tokens). An interior node is an already processed frontier node that is not classified as a terminal, a k-terminal, a frozen, an identical, or a duplicate node.

The inheritance-tree algorithm for the KRFPN is presented as follows:

Input: Initial distribution as a root of the k-level inheritance tree (a frontier node at the zero-level of the tree). The depth of the tree generation k; 1 ≤ k < ∞, and the threshold value λ ∊ [0,1], which defines the firing threshold for each transition.

Output: A k-level inheritance tree with all the nodes denoted as terminal, k-terminal, frozen, interior, identical, or duplicate.

Let π _X be the frontier node to be processed.

Step 1 . If there exists another node π _Y in the inheritance tree that is not a frontier node and π _X  ≡ π _Y , the node π _X is an identical node. Denote such a node by I.

If there exists another node π _Z that is not a frontier node and π _X  = π _Z , then the node π _X is a duplicate node. Denote such a node by D.

Step 2 . If there are no enabled transitions for π _X , then π _X is a terminal node. Denote such a node by T.

If π _X lies at the kth level of the inheritance tree, then denote such a node as the k-terminal node (k-T).

Step 3 . For all transitions t_j that are enabled for π _X , create a new node π _W in the inheritance tree. The components of π _W are defined according to the firing rule of the KRFPN. An arc, labelled by t_j; f(t_j), is directed from node π _X to node π _W . After that, the node π _X is redefined as an interior node.

If π _W is the result of firing a transition that corresponds to elements from Σ₂ or Σ₃, then π _W is declared as a frozen node. Denote such a node by F.

Step 4 . If the node π _W is not classified as a frozen node, then it becomes a frontier node.

When all the nodes have been classified as terminal, k-terminal, duplicate, identical, frozen, or interior nodes, the algorithm stops.

Example 4

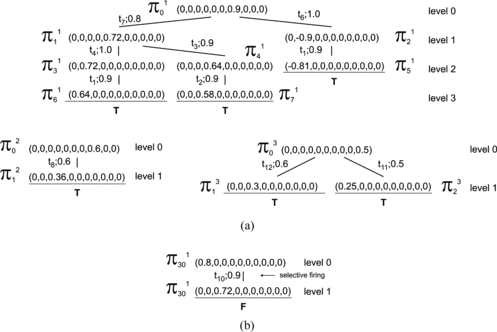
Using this example, we illustrate the inheritance-tree algorithm. Let us suppose that the initial distribution of tokens for the KRFPN scheme depicted in Figure 7 is given by Ω₀ = π ₀ = ({c(m₁) = 1.0}, Ø,…, Ø), i.e., the token m₁ is initially at the place p₁ and has a value 1.0, all other places are without tokens. Let k be the depth of the inheritance tree k = 3 and the threshold level λ = 0.1.

Input: π ₀ = ({c(m₁) = 1.0}, Ø,…, Ø), k = 3, λ = 0.1.

Output: An l-level inheritance tree (0 ≤ l ≤ k) with all the nodes denoted as terminal, k-terminal, frozen, interior, duplicate, and/or identical nodes.

The 3-level inheritance tree generated by the algorithm is shown in Figure 8.

FIGURE 8 The 3-level inheritance tree for the KRFPN scheme depicted in Figure 7.

The initial distribution of tokens π ₀ (node at the zero level) is a frontier node π _x . There are enabled transitions as follows: t₁, t₉, t₁₁, and t₁₃. By firing the enabled transitions, the following nodes at the first level are created: π ₁₁ , π ₁₂ , π ₁₃ , and π ₁₄ . The nodes π ₁₂  = (Ø, Ø, 0.9,…, Ø), π ₁₃  = (Ø, Ø,…, 0.5), and π ₁₄  = (Ø, Ø,…, 0.8, Ø) are frozen nodes. Note that the nodes π ₁₃ and π ₁₄ are also terminal nodes. The node π ₁₁ becomes a frontier node and there are three enabled transitions: t₄, t₅, and t₆. By firing the enabled transition t₄, the node π ₂₁ is generated. By firing the transitions t₅ and t₆, the nodes π ₂₂ and π ₂₃ are generated at the second level. Both these nodes are terminal nodes. The node π ₂₁  = (Ø, Ø, Ø, Ø, 0.9, Ø,…, Ø) becomes a frontier node. The transition t₇ is enabled, and after its firing, the node π ₃₁  = (Ø, Ø, Ø, Ø, Ø, Ø, 0.72, Ø, Ø, Ø) is obtained. The node π ₃₁ is a terminal node, and it is also a k-terminal node because the k = 3 level of the inheritance tree is reached. Note that π ₃₁ is also a duplicate node because π ₃₁  = π ₂₃ .

Inheritance Assertion

By using the components of the k-level inheritance tree: a node at the level i − 1, labelled arc, a node at the level i (successor of the node at level i − 1), the functions α and β, a triplet named an inheritance assertion is formed.

For example, a node π ₁₁ at the level 1, a labelled arc t₄; f(t₄) = 1.0, and the successor node π ₂₁ at the level 2, and α(p₂) = Human, β(t₄) = i s ₋ a, and α(p₅) = Mammal, define the inheritance assertion: (Human is_a Mammal). Note that the tokens are at the places p₂ (for π ₁₁) and p₅ (for π ₂₁).

The strength of the assertion is defined as the value of the token at the successor node, i.e., as a product of the token value at the node at level i − 1 and the value of the association function of the corresponding transition.

For example, the strength of the inheritance assertion (Human is_a Mammal) is 0.90 × 1.0, where 0.90 is the value of the token at place p₂(see the distribution π ₁₁ ; Figure 8).

The inheritance paths, starting from the root node of the inheritance tree and finishing at the leaves of the tree (terminal node, k-terminal node, frozen node, identical node, duplicate node) represent sequences of the inheritance assertions. An inheritance path is interpreted as the conjunction of the inheritance assertions in which the redundant concepts connected by AND are omitted. The strength of an inheritance path is defined by the value of the token at the node that is a leaf of the inheritance tree.

For example, the inheritance path defined from the root node π ₀ to the leaf node of the tree π ₂₂ (see Figure 8) is: Fred is_a Human AND is_a Biped. The strength of the inheritance path is 0.72.

In network-based knowledge representation schemes, there is the well-known problem of the conflicting multiple inheritance (Touretzky 1986). The problem of the conflicting multiple inheritance in the KRFPN scheme is expressed as follows: Two inheritance paths, represented by sequences of the inheritance assertion, are in conflict if the same concept inherits the mutually contradictory elements from D, i.e., d_k and d_n, where (d_k, d_n) ∊ C,C is a set of contradictions. Also, two inheritance paths are in conflict if the same concept inherits the concept/property α(p_k) ∊ D, but in one inheritance path it inherits the concept/property by means of β(t_r) ∊ Σ, and in another by means of β(t_s) ∊ Σ, where β(t_r) = σ_r, β(t_s) = σ_s, and(σ_r, σ_s) ∊ C.

To resolve the situations involving conflicting multiple inheritance in the KRFPN scheme, we used Touretzky's principle of inferential distance ordering PIDO (Touretzky 1986): In the situation of conflicting multiple inheritance, a concept inherits the property of the nearer individual (concept) or class. “Nearer” is defined as follows: Concept or class A is “nearer” to class B than to class C if A has an inheritance path through B to C. In many cases, the inferential distance ordering fails and reports an ambiguity (for example, see the well-known Quaker's problem) because it is based on a measure of “betweenness.” In such situations, in the KRFPN scheme, the concept inherits the property for which one can find the more direct inheritance path, i.e., the shorter path. If two or more inheritance paths have the same length the concept inherits property that corresponds to more strength in the inheritance path.

Inheritance Algorithm

The inheritance algorithm for the KRFPN is presented as follows:

Input: A concept of interest d_i ∊ D, the depth of the inheritance k; 0 ≤ k < ∞, λ ∊ [0,1].

Output: The properties of the concept d_i ∊ D, obtained by looking up the properties locally attached to the concept d_i, and the properties attached to the concepts that lie at higher levels in the conceptual hierarchy. The properties are expressed by means of semantic interpretations of the inheritance paths.

Step 1 . For a given concept of interest d_i ∊ D, by using the inverse function α⁻¹, find the corresponding place p_k:

If d_i ∉ D, stop the algorithm and send the message: “d_i is an unknown concept.”

Step 2. Define the initial marking μ ₀ = (μ₁, μ₂,…, μ _n ), where for j = 1, 2,…, n

Step 3. Define the initial distribution of tokens Ω ₀ = π ₀ = (Ø Ø Ø…{(p_j, c(m₁)},…, Ø, Ø) and set c(m₁) = 1.0.

Step 4. For the initial distribution of tokens Ω₀ = π ₀ construct k levels of the inheritance tree.

Step 5. By using the elements of the inheritance tree: a node at level i − 1, a labelled arc, a corresponding node at level i, and the functions α and β, form the inheritance assertions.

Step 6. Find the inheritance paths, starting from the root node of the inheritance tree and finishing at the leaves of the inheritance tree. Determine the strengths of each inheritance path.

Step 7. If there are situations involving conflict due to the conflicting multiple inheritance, use the inferential distance ordering concept PIDO or (if that fails) make a decision on the basis of the more direct inheritance path. If two or more inheritance paths have the same length the concept inherits the property that corresponds to the stronger path. On the basis of the above criteria, remove the inheritance assertion that is the source of conflict and all the inheritance assertions that follow it.

Example 5

For the knowledge base represented in Figure 7 infer the properties of the concept Fred (with the depth of inheritance k = 3), λ = 0.1. A set of contradictions C = {(is_a, is_not_a), (is_in_front, is_behind_of), (Biped, Quadruped)}.

Input: Fred ∊ D, k = 3, λ = 0.1.

Step 1 . α⁻¹: Fred → p₁.

Step 2. The initial marking is μ ₀ = (1, 0, 0, 0, 0, 0, 0, 0, 0, 0).

Step 3. The initial distribution of tokens is Ω ₀ = π ₀ = ({(p₁, c(m₁)}, Ø, Ø, Ø,…, Ø, Ø) and c(m₁) = 1.0.

Step 4. The inheritance tree is shown in Figure 8.

Step 5. The inheritance assertions are (see Figure 8):

Level 1:

Fred is_a Human; (α(p₁) β(t₁) α(p₂)); (strength = 0.90)

Fred is_in_front Clyde; (α(p₁) β(t₉) α(p₃)); (strength = 0.90)

Fred has_characteristic Kind_hearted; (α(p₁) β(t₁₁) α(p₁₀)); (strength = 0.50)

Fred has Soul; (α(p₁) β(t₁₃) α(p₉)); (strength = 0.80)

Level 2:

Human is_a Mammal; (α(p₂) β(t₄) α(p₅)); (strength = 0.90)

Human is_a Biped; (α(p₂) β(t₅) α(p₆)); (strength = 0.72)

Human is_not_a Quadruped; (α(p₂) β(t₆) α(p₇)); (strength = 0.90)

Level 3:

Mammal is_a Quadruped; (α(p₅) β(t₇) α(p₇)); (strength = 0.72)

Step 6. The inheritance paths and their interpretations are:

1. Fred is_a Human AND is_a Mammal AND is_a Quadruped; (0.72)

2. Fred is_a Human AND is_a Biped; (0.72)

3. Fred is_a Human AND is_not_a Quadruped; (0.90)

4. Fred is_in_front Clyde; (0.90)

5. Fred has a Soul; (0.80)

6. Fred has_characteristic Kind_hearted; (0.50).

Step 7. According to the elements of the set of contradictions C and the definition of the contradiction, the inheritance paths (i) and (ii) generate contradictions because (Biped, Quadruped) ∊ C. The paths (i) and (iii) introduce a conflicting multiple inheritance due to (is_a, is_not_a) ∊ C. There is an ambiguity about the above inheritance paths: Is Fred a quadruped or a not?

To resolve the ambiguity caused by the inheritance paths (i) and (iii), the PIDO concept is used. Conflict due to the inheritance paths (i) and (ii) is solved on the basis of the more direct inheritance path: The inheritance path (i) is a path from the concept Fred through the concepts Human and Mammal to the concept Quadruped, and simultaneously there is the inheritance subpath Human is_a_not Quadruped.

The result of resolving the conflict situation on the basis of the PIDO and a more direct inheritance path is:

• Fred is_a Human AND is_a Mammal; (0.90)

• Fred is_a Human AND is_a Biped; (0.72)

• Fred is_a Human AND is_not_a Quadruped; (0.90)

• Fred is_in_front Clyde; (0.90)

• Fred has Soul; (0.80)

• Fred has_characteristic Kind_hearted; (0.50).

Therefore, the inheritance process resulted in the following statements: Fred is a human and a biped, he has a soul, and he is kind-hearted.

The strength attached to each inheritance path has to be interpreted as the confidence of the statement. With reference to Table 1, for instance, the statement: Fred is_a Human AND is_a Mammal; (0.90) is interpreted as very true, while the statement Fred has_characteristic Kind_hearted; (0.50) is interpreted as moderately true.

FUZZY RECOGNITION

The fuzzy recognition in the KRFPN can be described as follows:

Initialization : A set of the properties S of an unknown concept X is given, where it is not necessary that X ∊ D. S = S₁ ∪ S₂, where S₁ is a set consisting of pairs (s_i, a_i), where s_i can be an element of a set of concepts D and a_i ∊ [1, 0] is the degree of a user's assurance that the unknown concept X has the property s_i. In this case the function α⁻¹ is defined for s_i, but if s_i ∉ D, then the function α⁻¹ is not defined for s_i. The elements in S₂ have the form (relationship, (s_i, a_i)). Usually the relationship is from Σ₃ and allows recognition based on the relative spatial position of concepts, but in general it is possible that relationship is not an element of Σ, because we deal with unknown concepts. Specify the threshold value λ ∊ [0, 1].

Action : Search for the concept in the KRFPN that best matches the properties in the set S. The search is based on local properties and the properties that are inherited from the higher levels of the knowledge base.

The recognition-inference procedure in the scheme KRFPN is based on an inverse scheme −KRFPN and a slightly modified definition of the enabled transition, as well as a modification of the association function c. The inverse −KRFPN = (−FPN, α, β, C) is obtained by interchanging the positions of the input I and the output O functions in the 10-tuple that defines an FPN:

where a modified association function c_r is defined as mapping: M → [−1, 1].

The main reason for the modification of the association function c is the existence of elements in Σ that have the forms of an exception or a negation of a property (for example, is_not_a). The modification of the association function c is also reflected in the execution of the −KRFPN. Firing an enabled transition t_i in the −KRFPN (where t_i corresponds to an exception in the original scheme) results in a new value of the token at the output place (Figure 9):

FIGURE 9 Firing an enabled transition that corresponds to an exception. (a) Before firing; (b) after firing: c_r(m₂) = −c_r(m_l)f(t_i) = −0.8.

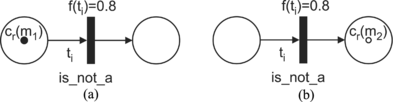
c_r(m_k) = −c_r(m_j)f(t_i), where c_r(m_j) is the value of the token at the input place p_j ∊ I(t_i) and f(t_i) is the degree of truth of the relation assigned to the transition t_i ∊ T. Such a token is graphically represented by the symbol ○ (see Figure 9).

Figure 9 illustrates the firing of such a transition and applying this modification of the association function. The initial marking is μ ₀  = (1, 0) and the initial distribution of the tokens is Ω ₀ = {{m₁}, ⊘}; c_r(m₁) = 1.0; f(t_i) = 0.8; λ = 0.1; and the transition t_i is enabled. After firing the enabled transition t_i a new marking, μ′ = (0, 1), is obtained. The token in the output place has the value c_r(m₂) = − c_r(m₁)f(t_i) = − 0.8.

The existence of the tokens with negative values in the −KRFPN also requires a redefinition of the enable transition:

• (a) if the values of the tokens, c_r(m_j) > 0, j = 1, 2,…, k ≤ m, exceed the threshold value λ ∊ [0, 1], the corresponding transition is enabled.

• (b) if the values of the tokens c_r(m_j) < 0, j = 1, 2,…,k ≤ m, the corresponding transition is enabled when |c(m_j)| exceeds the threshold value λ ∊ [0, 1]; |x| denotes the absolute value of x.

The reachability set of the −KRFPN, called the recognition set, with an initial marking μ ₀ and initial distributions of the tokens Ω₀, is defined in a similar way to the inheritance set of the KRFPN, except for two important differences:

• (c) the modification of the firing rule mentioned above is used;

• (d) the transitions corresponding to relations in the subset Σ₃ cannot be fired regardless of the states of their input places.

A graphical representation of a recognition set is called the recognition tree.

For properties having the form (relationship, (s_i, a_i)), by means of selective firing (i.e., firing of the enabled transition corresponding to the specific relationship), the recognition subtree is obtained. Note that after firing the selected transition, the token at the output place is frozen and all the subsequent firings are disabled. A subtree consists of two nodes: the initial and the terminal. There are two exceptions in the construction of a recognition sub-tree in relation to the construction of a recognition tree:

• (e) if the selected transition has the form of an exception or a negation of a property, then the value of the token in the output place is positive, i.e., c_r(m_k) = |c_r(m_j)·f(t_i)|;

• (f) the restriction expressed in (d) does not hold.

Recognition Algorithm

The recognition-inference algorithm for the KRFPN is presented as follows:

Input : A set of properties S of an unknown concept and a depth of search L, (1 ≤ L ≤ Deep < ∞; where Deep is the maximum depth of the search), expressed by levels of the recognition tree are given. The threshold value λ is selected (usually λ is chosen to be small enough, for example, 0.1).

Output : A concept from D that best matches the unknown concept X described by the set of properties S.

Step 1 . For the scheme KRFPN find the inverse scheme −KRFPN.

Step 2. For all (s_i, a_i) ∊ S₁; s_i ∊ D and a_i ∊ [0,1], i = 1, 2,…, length ≤ Card(S₁), where Card denotes a cardinality of a set, by means of the inverse function α⁻¹: s_i → p_j, determine the places p_j, 0 < j = b ≤ n. Each such place p_j becomes a place with a token (p_j, c_r(m_i)), where the token value c_r(m_i) is a_i. It defines b initial markings and initial token distributions. The initial markings are the root nodes of the recognition trees (nodes at level l = 0). The initial token values c(m_i); i = 1, 2,…, b are determined by the degrees of assurance a_i; i = 1, 2,…, b.

Step 3. For all the elements in S₂ that have the form (relationship, (s_i, a_i)), using the inverse functions, determine the initial markings and selective transitions for the construction of the recognition subtrees: α⁻¹(s_i) = p_j and β⁻¹(relationship) = τ ⊂ T.

From the set τ select such a t_i for which p_j ∊ I(t_i) in the −KRFPN. Put the token into a place p_j – this is the initial marking of the subtree. The initial token value is determined on the basis of the user's specification of a degree of assurance for the concept a_i: c_r(m_i) = a_i. If there is no such a t_i for which p_j ∊ I(t_i), the selective transition does not exist.

Step 4. Find L levels of all the recognition trees for b initial markings and initial token distributions.

Step 5. Find the recognition subtrees defined in Step 3.

Step 6. For each recognition tree, for levels l = 1, 2,…, L, compute the sum of the nodes (represented as vectors π):

where p is the number of nodes in the kth recognition tree.

Step 7. Compute the total sum of all the nodes for all the recognition trees:

where b is the number of all the recognition trees.

Step 8. Compute the sum of the terminal nodes for all the recognition subtrees:

where r is the number of all the recognition subtrees and π _s is the terminal node of a subtree.

Step 9. Compute the sum E  =  Z  +  A , where E  = (e₁, e₂,…, e _n ).

Step 10. Find:

(Note: In the case that there are several indexes i for which the same maximal value of {e_i} is obtained create the set I∗ = {i ₁∗, i ₂∗,…,}).

Step 11 . Select p_i, for every i _k ∗, k = 1, 2,…, |I∗|, k = 1,2,…, |I∗| where i = i _k ∗, from the set P, and find all d_k ∊ D using the function α: p_i → d_k. The concept(s) d_k, where k = 1, or k = 1, 2,…, |I∗|, is(are) the best match(es) to the unknown concept X described by the set of properties S.

Example 6

Let us suppose that the unknown concept X is described by the following set of properties: S = S₁ ∪ S₂, where S₁ = {(Quadruped, 0.9),(White, 0.6),(Kind_hearted, 0.5),(Royal_pet, 1.0)}, and S₂ = {(is_on, (Earth, 1.0)), (is_behind, (Fred, 0.8))}. Find the concept in the KRFPN knowledge base (Figure 7) that best matches the unknown concept X, for L = 3 levels of the recognitions trees and λ = 0.1.

Step 1. The inverse graph −KRFPN is shown in Figure 10(b). (For easy reference the graph of the original scheme is repeated in Figure 10(a)).

FIGURE 10 The KRFPN and −KRFPN inverse scheme (Example 3). (a) The KRFPN scheme; (b) the −KRFPN inverse scheme.

Step 2.

The initial markings are:  = (0, 0, 0, 0, 0, 0, 0.9, 0, 0, 0),  = (0, 0, 0, 0, 0, 0, 0, 0.6, 0, 0),  = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0.5).

Step 3. For (is_behind, (Fred, 0.8)), β⁻¹(is_behind) = {t₁₀} and α⁻¹(Fred) = p₁, and p₁ ∊ I(t₁₀) in the −KRFPN, the initial marking π _0s for a subtree is π _0s = (0.8, 0, 0, 0, 0, 0, 0, 0, 0, 0). The selected transition that will be fired is t₁₀. For (is_on; (Earth, 1.0)) the functions α⁻¹ and β⁻¹ are not defined.

Step 4. Recognition trees k = 1, 2, 3; (b = 3) for the depth of the search L = 3 are shown in Figure 11(a).

FIGURE 11 The recognition trees and the recognition subtree. (a) Recognition trees; (b) the recognition subtree.

Step 5. The recognition subtree is shown in Figure 11(b).

Step 6. Compute

For recognition tree 1, the nodes are (Figure 11(a)):

For recognition tree 2, there is only one node , and the sum is z ² (0, 0, 0.36, 0, 0, 0, 0, 0, 0, 0);

For recognition tree 3, the nodes are: ; , and their sum is z ³ = (0.25, 0, 0.30, 0, 0, 0, 0, 0, 0, 0).

Step 7. Compute the total sum of all the nodes for all the recognition trees:

Step 8. There is only one subtree (Figure 11(b)): .

Step 9. Compute the sum E  =  Z  +  A :

Step 10. Find: i∗ = arg max_i=1,…,10 {e_i} = 3.

Step 11 . Select p_i, where i = i∗, from the set P, and find d_rec ∊ D using the function α: p_i → d_rec: α: p₃ → Clyde.

According to the result of the recognition-inference procedure, the concept Clyde is the best match to the unknown concept X. Clyde is a quadruped; he is white and kind-hearted, and he is behind Fred (Figure 6). Is he a royal pet (probably yes!) or is he on the Earth (probably yes!)? We explicitly don't know.

CONCLUSIONS

Original fuzzy inference procedures for the knowledge representation scheme KRFPN based on the FPN theory are proposed. The fuzzy inheritance uses a k-level inheritance tree, which is generated on the basis of the dynamical properties of the FPN, i.e., on firing enabled transitions and changing the values of the tokens according to the association function f that specifies the degree of assurance for the relation assigned to the transitions, and according to the association function c. Recognition, as a dual of the inheritance problem, uses the inverse –KRFPN that is obtained by interchanging the positions of the output and input functions in the 13-tuple specification of the KRFPN.

The very important properties of both inference algorithms are that the inheritance and recognition trees are finite and that the upper bound of the time complexity of the fuzzy inference algorithms is O(nm), where n is the number of places (concepts) and m is the number of transitions (a total number of relations in a knowledge base designed by the KRFPN). These allow the efficient execution of both, the inheritance and recognition procedures. The KRFPN was tested on numerous examples of the agent's knowledge bases of block world scenes as well as outdoor scenes, as well as in the knowledge base in a system for determination of a mental state of a driver.

Adaptation of the knowledge representation scheme KRFPN for time-varying fuzzy knowledge and spatio-temporal reasoning are our future research directions.