GENETIC ALGORITHM MODEL FOR PROFIT MAXIMIZATION OF GENERATING COMPANIES IN DEREGULATED ELECTRICITY MARKETS

Abstract

In deregulated and rapidly changing electricity markets, there is strong interest on how to solve the new price-based unit commitment (PBUC) problem used by each generating company to optimize its generation schedule in order to maximize its profit. This article proposes a genetic algorithm (GA) solution to the PBUC problem. The advantages of the proposed GA are: 1) flexibility in modeling problem constraints because the PBUC problem is not decomposed either by time or by unit; 2) smooth and easier convergence to the optimum solution thanks to the proposed variable fitness function which not only penalizes solutions that violate the constraints but also this penalization is smoothly increasing as the number of generations increases; 3) easy implementation to work on parallel computers, and 4) production of multiple unit commitment schedules, some of which may be well suited to situations that may arise quickly due to unexpected contingencies. The method has been applied to systems of up to 120 units and the results show that the proposed GA constantly outperforms the Lagrangian relaxation PBUC method for systems with more than 60 units. Moreover, the difference between the worst and the best GA solution is very small, ranging from 0.10% to 0.49%.

In the regulated or state monopoly electricity markets, unit commitment (UC) refers to optimizing generation resources over a daily to weekly time horizon to satisfy load demand at the least operational cost while satisfying prevailing constraints, such as minimum up/down time, ramping up/down, and minimum/maximum generating capacity. Since the related objective would be to minimize the operational cost, UC is commonly referred to as a cost-based unit commitment (CBUC). The optimal solution to the CBUC problem can be obtained by complete enumeration, which is prohibitive in practice owing to its excessive computational resource requirements (Wood and Wollenberg, 1996). The need for practical, cost-effective UC solutions led to the development of various UC algorithms that produce suboptimal, but efficient scheduling for real-sized power systems comprising hundreds of generators (Sheblé and Fahd, 1994). Cost-based unit commitment methods include priority list methods (Wood and Wollenberg, 1996), dynamic programming (Snyder, Powell, and Rayburn, 1987), Lagrangian relaxation (LR) (Zhuang and Galiana, 1988), branch-and-bound (Cohen and Yoshimura, 1983), and Bender's decomposition (Baptistella and Geromel, 1980). Recently, simulated annealing (Zhuang and Galiana, 1990), expert systems (Wang and Shahidehpour, 1992), artificial neural networks (Sasaki, Watanabe, and Yokoyama, 1992), genetic algorithms (Kazarlis, Bakirtzis, and Petridis, 1996, 1996; Damousis, Bakirtzis, and Dokopoulos, 2004; Senjyu et al., 2005), and hybrid techniques (Wong and Wong, 1995; Aldridge et al., 2001; El Desouky et al., 2001) have also been used for the solution of the CBUC problem.

On the other hand, in the deregulated electricity markets, the UC used by each generating company (GENCO) refers to optimizing generation scheduling in order to maximize the GENCO's profit (Shahidehpour, Yamin, and Li, 2002). In this new paradigm, the signal that would enforce a unit's on/off status would be the price, including the fuel purchase price and the energy sales price. Increasing competition, decreasing obligations-to-serve, and enhanced futures, forwards, and spot market trading in electricity make the decision of which units to operate more complex than ever before. This UC has a different objective than that of CBUC and is referred to as price-based unit commitment (PBUC). The PBUC is a large-scale, nonconvex, nonlinear, mixed-integer optimization problem. Because electricity markets are changing rapidly, there is strong interest on how new UC models are solved and what purposes they serve (Hobbs et al., 2001). Given market prices, LR was employed to solve the PBUC problem in Shahidehpour et al. (2002). In a bilateral market, the PBUC was studied in Allen and Ilic (1999) by considering the uncertainty of market price. In a pool market, the PBUC problem was solved using LR, stochastic dynamic programming, and Bender's decomposition in Takriti, Krasenbrink, and Wu (2000). The PBUC for a price-taker thermal unit was modeled as a mixed integer programming (MIP) problem in Arroyo and Conejo (2000, 2002). Given the price quota curve, the PBUC for a price-maker participant was modeled as a MIP problem in de La Torre, Arroyo, Conejo, and Contreras (2002). The PBUC for a GENCO with thermal, combined-cycle, cascaded-hydro, and pumped-storage units is modeled as an MIP problem in Li and Shahidehpour (2005). A general probabilistic-dynamic-programming framework for the problem of self-committing units when there are multiple noncooperative producers is introduced in Correia (2006). A method for building bidding curves under price uncertainty using PBUC is proposed in Shrestha, Pokharel, Lie, and Fleten (2007).

Genetic algorithms are global optimization techniques inspired by the study of genetics (Goldberg, 1989; Michalewicz, 1996). They can be easily implemented for the solution of hard optimization problems and they provide great modeling flexibility. This article proposes a genetic algorithm (GA) model for the solution of the PBUC problem. The power of the suggested GA solution relies on the proposed variable fitness function and the problem specific operators adopted. Additional advantages of the proposed GA solution are flexibility in modeling PBUC problem constraints and easy implementation to work on parallel computers. Another benefit of using GA to generate UC schedules is that an entire population of schedules is developed, some of which may be well suited to situations that may arise quickly due to unexpected contingencies.

PBUC PROBLEM FORMULATION

Definition

The price-based unit commitment problem can be stated as follows: for a GENCO with N generating units, and given a certain market price profile of energy as well as a certain demand profile (with reserves), it is required to determine the start-up/shut-down times and the power output of all the generating units at each time interval t over a specified scheduling period T, so that the generator's total profit is maximized, subject to the unit and power balance constraints. In this article, the time interval for the considered electricity market is 1 hour.

Objective Function

For unit i at hour t, the profit is calculated by subtracting the total production cost during that hour from the revenue:

It should be noted that a negative profit, F(i, t), indicates a loss for unit i at hour t.

The revenue for unit i at hour t is calculated by multiplying its production with the forecasted market price for energy

where I(i, t) is the status of unit i at hour t (1 = ON, 0 = OFF), and p _gm (t) is the forecasted market price for energy at hour t.

The market price for energy can be forecasted using time-series models (Contreras, Espinola, Nogales, and Conejo, 2003), wavelet transform (Yao and Song, 2000), and artificial neural networks (Georgilakis, 2007).

The total production cost, Cost(i, t), for each unit at each hour is the sum of the fuel cost, start-up cost, and shut-down cost during that hour:

The fuel cost, FC(i, t), of unit i in any given hour t is a function of the power output, P(i, t), of that unit during that hour. The fuel cost function is modeled as a second-order polynomial:

The start-up cost in any given hour t depends on the number of hours a unit has been OFF prior to start-up. This cost is modeled by an exponential function of the form

where D(i) is the combined crew start-up costs and equipment maintenance costs of unit i, E(i) is the cold start-up cost of unit i, X _off (i, t) is the continuous offline time of unit i at hour t, and CT(i) is the cooling time constant of unit i.

The shut-down cost, SD(i, t), is given a constant value for each unit per shut-down.

The objective of the PBUC problem for the GENCO operating in the competitive environment is to maximize, during the scheduling horizon of T hours, the total profit for all its N generating units:

subject to constraints (7) to (14), as described in the “Constraints” subsection.

Constraints

The demand constraint for the PBUC problem is defined as follows:

where FDWR(t) is the forecasted demand with reserves for hour t.

In constraint (7), it is assumed that the buyers purchase reserves per contract; however, the algorithm could easily be modified to handle different market rules.

The coupling power-balance and reserve-requirement constraint (7) complicates the solution of the PBUC optimization problem, since the PBUC cannot be decomposed by unit.

Thermal units are subject to a variety of constraints that are described in this subsection.

1. Unit Generation Limits: Units can only generate between their minimum, P ^min(i), and maximum, P ^max(i), generation limits:

2. Unit Minimum Up Time Constraint:

   where X ^up (i, t) is the cumulative up time (i.e., time for which unit i has been ON) during hour t, and T ^up (i) is the minimum up time of unit i.

3. Unit Minimum Down Time Constraint:

   where X ^down (i, t) is the cumulative down time of unit i during hour t, and T ^down (i) is the minimum down time of unit i.

4. Unit Ramp-Up Constraint: The amount a unit's generation can increase in an hour:

   where UR(i) is the ramp-up rate limit of unit i.

   Constraint (11) applies as unit i ramps-up. The limit at start-up is given by

5. Unit Ramp-Down Constraint: The amount a unit's generation can decrease in an hour:

   where DR(i) is the ramp down rate limit of unit i.

   Constraint (13) applies as unit i ramps-down. The limit at shut-down is given by

6. Unit Status Restrictions: Certain units may be required to be online at certain hours (must run), or may become unavailable due to planned maintenance or forced outage (must not run), due to operating constraints, reliability requirements, or economic reasons.

7. Initial Conditions: The initial conditions of the units at the start of the scheduling period must be considered.

GENETIC ALGORITHM SOLUTION TO THE PBUC PROBLEM

Fundamentals of Genetic Algorithms

Genetic algorithms are optimization methods inspired by natural genetics and biological evolution. They manipulate strings of data, each of which represents a possible problem solution. These strings can be binary strings, floating-point strings, or integer strings, depending on the way the problem parameters are coded into chromosomes. The strength of each chromosome is measured using fitness values, which depend only on the value of the problem objective function for the possible solution represented by the chromosome. The stronger strings are retained in the population and recombined with other strong strings to produce offspring. Weaker ones are gradually discarded from the population. The processing of strings and the evolution of the population of candidate solutions are performed based on probabilistic rules. A comprehensive description of genetic algorithms can be found in Goldberg (1989) and Michalewicz (1996).

Chromosome Representation

A convenient binary mapping to a chromosome representation is selected in which “0” denotes the OFF state and “1” represents the ON state of a unit. A candidate solution (chromosome) is a string whose length is the product of the number of generating units and the scheduling hours.

The information available in the chromosome together with the initial state (continuous up or down time) of the units is all one needs to accurately model all time-dependent constraints of the PBUC problem. This great modeling flexibility is one of the advantages of the proposed GA solution, because the PBUC problem is not decomposed either by time or by unit.

Creation of Initial Population

The initial population of candidate solutions is created randomly. After trial and error, it was found that a population size of 50 chromosomes provides very good results.

Economic Dispatch

The economic dispatch problem at hour t is formulated as

subject to constraints (7) to (14).

For each chromosome, the unit commitment status, I(i, t), is determined and is no longer a variable. The only variable is the generation, P(i, t), of each unit i at hour t; therefore, sequential quadratic programming (SQP) (Rao, 1996) is adopted to solve the economic dispatch problem. It should be noted that in order to save computation time, the economic dispatch is only performed if the given unit commitment schedule satisfies the minimum up/down time constraints.

Evaluation of Candidate Solutions

To apply the GA to the PBUC problem that is highly constrained, the solutions (chromosomes) that violate the constraints are penalized. More specifically, the fitness value, Q, of each chromosome is calculated as follows:

where L is the number of violated constraints, is the final value of the multiplier of constraint k, g is the generation index, g ^max is the maximum number of generations the genetic algorithm is allowed to run, and V _k is the amount of violation of constraint k.

It can be seen from (16) that a variable fitness function has been adopted according to which the penalty multiplier is negligible during the first generations, while the penalty multiplier rises to its final (appropriate large) value near the end of the GA generations. The variable fitness function results in a variable search hyperspace, simpler at the beginning and more complicated at the later stages of the GA search. For the PBUC problem, this variable fitness function has been proven very efficient, since it manages to locate the exact global optimum as shown in the “Results and Discussion” section.

Reproduction

After the evaluation of the initial population, the GA begins the creation of the new generation of solutions. The chromosomes are selected in pairs (parents) using the roulette wheel parent selection algorithm that selects a chromosome with a probability proportional to the chromosome's relative fitness within the population. Then, from each two parents, two children (offspring) are produced by means of crossover and mutation operators.

Crossover Operation

The multi-point crossover operator is used. This operator is applied with a certain probability that ranges from 0.4 to 0.9 per chromosome. When crossover is applied, the parent chromosomes are combined to form two new chromosomes (children) that inherit solution characteristics from both parents. If crossover is not applied, the children are identical replications of their parents.

Mutation Operation

With a small probability, ranging from 0.004 to 0.024 per bit, randomly chosen bits of the children's chromosomes change from “0” to “1” or vice versa.

Elitism

The best two solutions of every generation are copied to the next generation so that the possibility of their destruction through a genetic operator is eliminated.

Special Operators

1. Swap-window operator: This operator is applied to all the population chromosomes with a probability of 0.3. It selects two arbitrary units u ₁, u ₂, a “time window” of width w (hours) between 1 and T, and a random window position between 1 and T − w. Then the bits of the two units (u ₁, u ₂) included in the window are exchanged.

2. Window-mutation operator: This operator is applied to all the population chromosomes with a probability of 0.3. It randomly selects one unit, a “time window” of width w (hours) between 1 and T and a random window position between 1 and T − w. Then, it mutates all the bits included in the window turning all of them to “1” or all of them to “0.”

After a thorough investigation, it was found that the above two GA special operators are very efficient for the solution of the PBUC problem.

Creation of the Next Generation

After the application of the operators adopted (crossover, mutation, elitism, and special operators), the children's population is created and the previous population is replaced by the new generation. Children are evaluated and the fitness function for each individual is calculated. The procedure is repeated until the termination criterion is met, defined by a maximum number of generations.

RESULTS AND DISCUSSION

The effectiveness of the proposed GA has been tested for six problem sets comprising 20, 40, 60, 80, 100, and 120 unit systems, respectively. Initially, a base problem set of 20 units was chosen along with a 24-hour price profile for energy as well as a 24-hour profile for the forecasted demand with reserves. For the 40-unit problem, the initial 20 units are duplicated, the forecasted demand (with reserves) is multiplied by two, while the price profile remains identical. A similar approach is followed to produce the unit and demand data for the remaining problem sets.

For each one of the six problem sets, the GA uses the advanced operators and techniques described in “Genetic algorithm solution to the PBUC problem” section. In order to avoid misleading results due to the stochastic nature of the GA, 20 runs are made for each problem set, with each run starting with different random populations.

A Lagrangian relaxation algorithm is also implemented to provide a near optimal solution for each problem set, in order to be used as a success limit for the GA, and serve as reference to judge the GA efficiency.

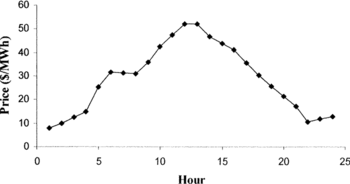
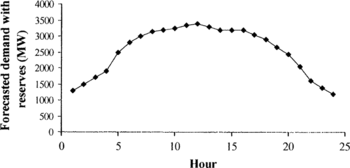
Table 1 presents the data for the 20-unit problem set, Figure 1 shows the 24-hour price profile for energy, and Figure 2 presents the 24-hour forecasted demand with reserves. In Table 1, the column X ⁰ gives the initial operational time (in hours) of each unit: if X ⁰ is positive, it means that the unit is ON for X ⁰ hours, while if X ⁰ is negative, it means that the unit is OFF for −X ⁰ hours. Table 2 presents the 20-units ON/OFF schedule

FIGURE 1 Hourly market prices of energy.

FIGURE 2 Hourly forecasted demand with reserves.

TABLE 1 Data for the 20-Unit Problem Set

Unit	Unit	P ^min(i)	p ^max(i)	A(i)	B(i)	C(i)	T ^up(i)	T ^down(i)	X ^0(i)	D(i)	E(i)	CT(i)	R ^up(i)	R ^down(i)	Shut-Down
index, i	name	[MW]	[MW]	($/MW ^2h)	($/MWh)	($/h)	(h)	(h)	(h)	($/h)	($/h)	(h)	(MW/h)	(MW/h)	cost ($)
1	U18a	3.6	18	0.04175	15.7463	19.01	0	0	−1	0	0	1	6	5	0
2	U18b	3.6	18	0.04239	15.8712	19.04	0	0	−1	0	0	1	6	5	0
3	U18c	3.6	18	0.04411	16.0311	19.27	0	0	−1	0	0	1	6	5	0
4	U18d	3.6	18	0.04513	16.1724	19.44	0	0	−1	0	0	1	6	5	0
5	U30a	6	30	0.06975	26.2541	31.72	0	0	−1	30	30	2	12	15	0
6	U30b	6	30	0.07012	26.3911	31.74	0	0	−1	30	30	2	12	15	0
7	U30c	6	30	0.07237	26.5259	31.94	0	0	−1	30	30	2	12	15	0
8	U114a	22.8	114	0.01459	20.3148	11.57	3	2	−3	75	75	3	23	23	0
9	U114b	22.8	114	0.01567	20.4512	11.59	3	2	−3	75	75	3	23	23	0
10	U114c	22.8	114	0.01704	20.6219	11.77	3	2	−3	75	75	3	23	30	0
11	U150a	37.5	150	0.01921	26.7302	15.22	4	2	−3	105	105	4	38	38	0
12	U150b	37.5	150	0.02062	26.9095	15.25	4	2	−3	105	105	4	45	45	0
13	U150c	37.5	150	0.02242	27.1341	15.49	4	2	−3	105	105	4	45	45	0
14	U230a	80	230	0.00563	15.2835	44.85	5	3	−5	225	225	6	150	150	0
15	U230b	80	230	0.00575	15.2911	44.93	5	3	−5	225	225	6	225	150	0
16	U295a	103	295	0.01088	12.8875	6.78	5	4	−4	300	300	8	290	375	0
17	U295b	103	295	0.01133	12.8913	6.89	5	4	−4	300	300	8	290	375	0
18	U350a	140	350	0.00301	10.7601	32.96	8	5	−10	300	200	8	200	300	0
19	U400a	100	400	0.01059	8.3391	64.16	8	5	−10	500	500	8	250	250	0
20	U400b	100	400	0.01123	8.4511	64.36	8	5	−10	500	500	10	250	250	0

TABLE 2 20-Units ON/OFF Schedule by Genetic Algorithm

Unit	ON/OFF Schedule for the Hours 0–24
1	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt2	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt3	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt4	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt5	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0
9.5pt6	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0
9.5pt7	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0
9.5pt8	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0
9.5pt9	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0
9.5pt10	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0
9.5pt11	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0
9.5pt12	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0
9.5pt13	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0
9.5pt14	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt15	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt16	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt17	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0
9.5pt18	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0
9.5pt19	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0
9.5pt20	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0
9.5pt

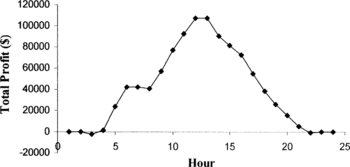
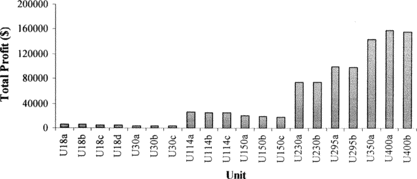
obtained by the GA and Table 3 shows the corresponding generation schedule obtained by the SQP solution to the economic dispatch problem. It is concluded from Table 2 that all 20 units are ON from hour 6 to hour 18, where the market price for energy is over 30 $/MWh, as Figure 1 shows. It is concluded from Figure 3 that the maximum profit, i.e., $107,706, is obtained during hour 12, where the energy price has its maximum value (52.2 $/MWh), while the profit is zero during hours 1, 2, 23, and 24, since all 4 units are OFF during these hours. From Figure 4 it can be seen that unit U400a produces the highest profit, i.e., $158,341, which corresponds to the 16.3% of the total profit ($972,214) of all the units during the 24-h scheduling period.

FIGURE 3 Total profit per hour for the 20-units problem set.

FIGURE 4 Total profit per generating unit for the 20-units problem set.

TABLE 3 Production (MW) Schedule for the 20-Units Problem Set

Unit Name	Production (MW) for the Hours 0–24
U18a	0	0	0	0	6	12	18	18	18	18	18	18	18	18	18	18	18	18	18	13	8	3.6	0	0	0
U18b	0	0	0	0	6	12	18	18	18	18	18	18	18	18	18	18	18	18	18	13	8	3.6	0	0	0
U18c	0	0	0	0	6	12	18	18	18	18	18	18	18	18	18	18	18	18	18	13	8	3.6	0	0	0
U18d	0	0	0	0	6	12	18	18	18	18	18	18	18	18	18	18	18	18	18	13	8	3.6	0	0	0
U30a	0	0	0	0	0	0	12	24	30	30	30	30	30	30	30	30	30	30	15	0	0	0	0	0	0
U30b	0	0	0	0	0	0	12	24	30	30	30	30	30	30	30	30	30	30	15	0	0	0	0	0	0
U30c	0	0	0	0	0	0	12	24	30	30	30	30	30	30	30	30	30	30	15	0	0	0	0	0	0
U114a	0	0	0	23	46	69	92	114	114	114	114	114	114	114	114	114	114	114	114	91	68	45	23	0	0
U114b	0	0	0	23	46	69	92	114	114	114	114	114	114	114	114	114	114	114	114	91	68	45	23	0	0
U114c	0	0	0	23	46	69	92	114	114	114	114	114	114	114	114	114	114	114	114	91	68	45	23	0	0
U150a	0	0	0	0	0	38	76	114	150	150	150	150	150	150	150	150	150	112	74	38	0	0	0	0	0
U150b	0	0	0	0	0	0	45	90	135	150	150	150	150	150	150	150	150	105	60	38	0	0	0	0	0
U150c	0	0	0	0	0	0	45	90	135	150	150	150	150	150	150	150	150	105	60	38	0	0	0	0	0
U230a	0	0	0	0	150	230	230	230	230	230	230	230	230	230	230	230	230	230	230	230	230	80	0	0	0
U230b	0	0	0	0	0	225	230	230	230	230	230	230	230	230	230	230	230	230	230	230	230	80	0	0	0
U295a	0	0	0	0	0	290	295	295	295	295	295	295	295	295	295	295	295	295	295	295	295	295	0	0	0
U295b	0	0	0	0	0	290	295	295	295	295	295	295	295	295	295	295	295	295	295	295	295	295	0	0	0
U350a	0	0	0	200	350	350	350	350	350	350	350	350	350	350	350	350	350	350	350	350	350	350	140	0	0
U400a	0	0	0	250	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	150	0	0
U400b	0	0	0	250	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	400	150	0	0

Table 4 compares the results obtained from the GA and the Lagrangian relaxation method for the six problem sets. For the GA, both the best and the worst solutions produced during the 20 runs are presented together with their difference as a percentage of the best solution. Table 4 shows that for large systems with 60 units or more, the GA constantly outperforms the LR unit commitment, since the profit calculated even by the worst GA

TABLE 4 Comparison of Lagrangian Relaxation and Genetic Algorithm Results for Up to 120-Unit Systems

		Genetic algorithm
		Total profit ($)
	Langrangian relaxation
Units	Total profit ($)	Best	Worst	Difference (%)
20	972 214	972 214	967 450	0.49
40	1 939 221	1 944 914	1 938 496	0.33
60	2 903 369	2 918 443	2 912 314	0.21
80	3 873 213	3 891 430	3 884 815	0.17
100	4 838 537	4 864 331	4 857 521	0.14
120	5 804 271	5 837 545	5 831 707	0.10

solution is always higher than the profit calculated by the LR method. Moreover, the difference between the worst and the best GA solution is very small, ranging from 0.10% to 0.49%. These very good results are attributed to the robust optimization capabilities of the GA in conjunction with the proposed variable fitness function and the problem specific operators adopted.

CONCLUSION

A GA solution to the price-based unit commitment problem has been presented. The power of the suggested GA solution relies on the proposed variable fitness function and the problem specific operators adopted. The variable fitness function not only penalizes solutions that violate the constraints but also this penalization is smoothly increasing as the number of generation increases, which significantly contributes to the smooth and easier convergence to the optimum solution. The method has been applied to systems of up to 120 units and the test results show that the proposed GA constantly outperforms the Lagrangian relaxation PBUC method for systems with more than 60 units. Moreover, the difference between the worst and the best GA solution is very small, not more than 0.49%. The obtained results show that the proposed GA approach is a very effective method for the solution of the PBUC problem.