REASONING WITH INCONSISTENT ONTOLOGIES THROUGH ARGUMENTATION

Abstract

Standard approaches to reasoning with description logics (DL) ontologies require them to be consistent. However, as ontologies are complex entities and sometimes built upon other imported ontologies, inconsistencies can arise. In this article, we present δ-ontologies, a framework for reasoning with inconsistent DL ontologies. Our proposal involves expressing DL ontologies as defeasible logic programs (DeLP). Given a query posed w.r.t. an inconsistent ontology, a dialectical analysis will be performed on a DeLP program obtained from such an ontology, where all arguments in favor and against the final answer of the query will be taken into account. We also present an application to ontology integration based on the global-as-view approach.

INTRODUCTION AND MOTIVATIONS

The semantic web (Berners-Lee, Hendler, and Lassila, 2001) is a future vision of the web where stored information has exact meaning, thus enabling computers to understand and reason on the basis of such information. Assigning semantics to web resources is addressed by means of ontology definitions. In the context of knowledge-sharing, the term ontology means a specification of a conceptualization. That is, an ontology is a description of the concepts and relationships that can exist for an agent or a community of agents (Gruber, 1993).

As proposed by the World Wide Web Consortium, ¹ ontology definitions are meant to be written in an ontology description language such as OWL (McGuiness and van Harmelen, 2004), whose semantics are based on Description Logics (DL) (Baader et al., 2003). Description logic ontologies are comprised of a terminology composed of a set of axioms defining a set of classes as well as a set of assertions about which individuals are known to be members of those classes and establishing relations/properties between individuals.

As pointed out by Wang et al. (2005), one of the advantages of logic-based ontology languages, is that reasoners can be used to compute subsumption relationships between classes and to identify unsatisfiable (inconsistent) classes. With the maturation of the tableaux algorithm based DL reasoners (such as Racer (Haarslev and Möller, 2001), FaCT (Horrocks, 1998), Pellet (Parsia and Sirin, 2004)), it is possible to perform efficient reasoning on large ontologies formulated in expressive DL. When checking satisfiability (consistency) most modern DL reasoners can only provide lists of unsatisfiable classes and offer no further explanation for their unsatisfiability. (A notable exception to is Horridge, Parsia, and Sattler (2008) discussed later in this article).

There are two main (but not incompatible) ways to deal with inconsistency in ontologies (Huang, van Harmelen, and ten Teije, 2005): one is to diagnose and repair it when it is encountered; another is to avoid the inconsistency and to apply a nonstandard inference relation to obtain meaningful answers. Although there are existing approaches for the former (e.g., identifying the minimally unsatisfiable subontologies or calculating the maximally satisfiable subontologies (Lam, Pan, Sleeman, and Vasconcelos, 2006)), performing it can be very difficult. That is, the process of “debugging” an ontology (i.e., determining why classes are unsatisfiable) is left for the user. However, when faced with several unsatisfiable classes in a moderately large ontology, even expert ontology engineers can find it difficult to work out the underlying error (Wang et al., 2005). In this work we will focus on the latter approach.

We propose to use defeasible argumentation (Chesñevar, Maguitman, and Loui, 2000; Prakken and Vreeswijk, 2002; Bench-Capon and Dunne, 2007) to reason with inconsistent ontologies. In particular, DeLP is an argumentative framework based on logic programming which is capable of dealing with possibly inconsistent knowledge bases (KB) codified as a set of horn-like clauses called DeLP programs (García and Simari, 2004). When presented with a query, DeLP performs a dialectical process in which all arguments in favor and against a conclusion are considered; arguments regarded as ultimately undefeated will be considered warranted. In this article, we propose a framework called δ-ontologies for representing and reasoning with possibly inconsistent DL ontologies. For this we interpret DL ontologies as DeLP programs adapting (Grosof, Horrocks, Volz, and Decker, 2003), which shows how a subset of DL can be effectively translated into an equivalent subset of Horn logic.

As already mentioned, traditional DL ontologies (in the sense of Baader et al. (2003)) are comprised of a terminology composed of a set of axioms defining a set of classes and a set of assertions about individuals in those classes. Thus, δ-ontologies are DL ontologies where the terminology is partitioned in such a way that conflicting axioms involved with the unsatisfiability of classes are treated specially as defeasible ones. Reasoning with such ontologies will then be carried out by means of a dialectical analysis. Our proposal involves interpreting DL ontologies as DeLP programs. That is, given a DL ontology Σ _DL , provided that it satisfies certain restrictions, it will be translated into a DeLP program Σ _DeLP . Given a query φ posed w.r.t. Σ _DL about the membership of an individual a to a concept C, a dialectical process will be performed to determine if the literal C(a) is warranted w.r.t. Σ _DeLP .

We also present an application of our framework to the problem of ontology integration. Reuse of existing ontologies is often not possible without considerable effort. When one wants to reuse different ontologies together, those ontologies have to be combined in some way. This can be done by integrating the ontologies, which means that they are merged into one new ontology, or the ontologies can be kept separate. In both cases, the ontologies have to be aligned, which means that they have to be brought into mutual agreement (Klein, 2001). A particular source of inconsistency is related to the use of imported ontologies when the knowledge engineer has no authority to correct them, and as these imported ontologies are usually developed independently, their combination could also result in inconsistencies. One kind of such integration is known as global-as-view integration (Calvanese, Giacomo, and Lenzerini, 2001), where a global ontology is used as a view of local ontologies that define the actual data. We apply our proposal to perform global-as-view integration when the involved ontologies can be potentially inconsistent.

DESCRIPTION LOGICS

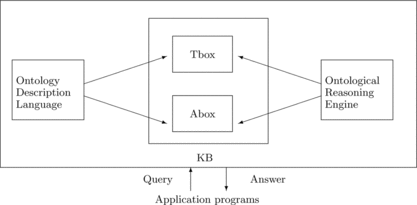
Description logics are a well-known family of knowledge representation formalisms (Baader et al., 2003). They are based on the notions of concepts (unary predicates representing classes, noted as Bird, Fly, etc.) and roles (binary relations noted as eats, isParentOf, etc.), and are mainly characterized by constructors that allow complex concepts and roles to be built from atomic ones. The expressive power of a DL system is determined by the constructs available for building concept descriptions, and by the way these descriptions can be used in the terminological (Tbox) and assertional (Abox) components of the system.

We now describe the basic language for building DL 𝒮ℋℐℱ expressions. Let C and D stand for concepts and R for a role name. Concept descriptions are built from concept names using the constructors conjunction (C ⊓ D), disjunction (C ⊔ D), negation (¬C), existencial restriction (∃R.C), and value restriction (∀R.C). Besides, the expressions⊤and⊥are shorthand for C ⊔ ¬C and C ⊓ ¬C, resp. Further extensions to the basic DL are possible including inverse and transitive roles noted as P ⁻ and P ⁺, resp. Another extension involves the possibility of allowing individual names (or nominals) in the description language; the most basic is the “set” (or one-of) constructor, written {a ₁,…, a _n } where a ₁,…, a _n are individual names.

A DL ontology Σ = (T, A) consists of two finite and mutually disjoint sets: the Tbox T which introduces the terminology and the Abox A, which contains facts about particular objects in the application domain. Tbox statements have the form C⊑D (inclusions) and C ≡ D (equalities), where C and D are (possibly complex) concept descriptions (e.g., Bird⊑Fly). Objects in the Abox are referred to by a finite number of individual names and these names may be used in two types of assertional statements: concept assertions of the type a: C (e.g., OPUS: Bird) and role assertions of the type⟨a, b⟩: R, where C is a concept description, R is a role name, and a and b are individual names (e.g., ⟨ADAM, ABEL⟩: isParentOf).

To define the semantics of concept descriptions, concepts are interpreted as subsets of a domain of interest, and roles as binary relations over this domain. An interpretation I =⟨Δ ^I , · ^I ⟩ consists of a nonempty set Δ ^I (the domain of I) and a function· ^I (the interpretation function of I) which maps every concept name A to a subset A ^I of Δ ^I , and every role name R to a subset R ^I of Δ ^I  × Δ ^I . The interpretation function is extended to arbitrary concept descriptions as follows: (¬C) ^I  = Δ ^I \C ^I ; (C ⊔ D) ^I  = C ^I ∪ D ^I ; (C ⊓ D) ^I  = C ^I ∩ D ^I ; (∃R.C) ^I  = {x|∃y s.t. (x, y)∈R ^I and y∈C ^I }, and (∀R.C) ^I  = {x|∀y, (x, y)∈R ^I implies y∈C ^I }.

The semantics of Tbox statements is as follows. An interpretation I satisfies C⊑D iff C ^I ⊆D ^I , I satisfies C ≡ D iff C ^I  = D ^I . An interpretation I satisfies the assertion a: C iff a ^I ∈C ^I , and it satisfies⟨a, b⟩: R iff (a ^I , b ^I )∈R ^I . An interpretation I is a model of a DL (Tbox or Abox) statement φ iff it satisfies the statement, and is a model of a DL ontology Σ iff it satisfies every statement in Σ. A DL ontology Σ entails a DL statement φ, written as Σ⊧φ, iff every model of Σ is a model of φ.

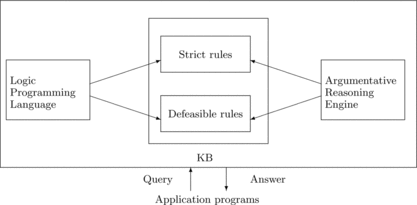
A knowledge representation system based on DL is able to perform specific kinds of reasoning, its purpose goes beyond storing concept definitions and assertions (the architecture of such a system is presented in Figure 1). As a DL ontology has semantics that makes it equivalent to a set of axioms of first-order logic, it contains implicit knowledge that can be made explicit through inferences. Inferences in DL systems are usually divided into Tbox reasoning and Abox reasoning. In this article we are concerned only with Abox reasoning, so we refer the interested reader to Baader et al. (2003).

FIGURE 1 Architecture of a knowledge representation system based on Description Logics (adapted from Baader et al. (2003), Fig. 2.1).

	Consistency: An Abox A is consistent w.r.t. Tbox T if there exists an interpretation which is a model of both A and T.
	Instance checking: Instance checking consists of determining if an assertion is entailed from an Abox. For instance, T ∪ A⊧a: C indicates that the individual a is a member of the concept C w.r.t. the Abox A and the Tbox T.
	Retrieval: If we consider a knowledge base as a means to store information about individuals, we might want to know all the individuals that are instances of a particular concept description. Given an ontology (T, A) and a concept description C, in the retrieval problem we are interested in knowing all the individuals a such that T ∪ A⊧a: C.

We now define the notion of inconsistency in DL ontologies.

Definition 2.1 (Inconsistency in DL ontologies (Baader et al., 2003))

An ontology Σ = (T, A) is inconsistent iff for every interpretation I =⟨Δ ^I , · ^I ⟩ of Σ, Δ ^I is empty.

Huang et al. (2004)Huang et al. (2005) survey several scenarios that may cause inconsistency, such as mis-presentation of defaults, polysemy (i.e., the capacity for a sign to have different meanings), ontology migration from another formalism, and use of multiple sources. We now present some inconsistent ontologies that will serve as motivating examples; they correspond to typical examples from the literature of nonmonotonic reasoning in Artificial Intelligence, and will be analyzed from an argumentative perspective in the next Section. Notice that following DL usual conventions, concepts are noted beginning with capital letters (e.g., Bird, Fly, etc.), roles with lowercase letters (e.g., in <_1>fusion, etc.), and individual names with uppercase letters (e.g., OPUS, ACME, STEEL, etc.).

Example 2.1

Let Σ_2.1 = (T, A) be an ontology, where

and

The Tbox T says that penguins are birds; birds can fly unless they have a broken wing, and superpenguins are penguins capable of flying. The Abox A asserts that it is known that Opus is a superpenguin having a broken wing.

Example 2.2

Let us consider the Nixon's diamond problem, a well-known problem in nonmonotonic reasoning (Reiter and Criscuolo, 1981). Let Σ_2.2 = (T, A) be a DL ontology where ²

and

The meaning of this ontology is as follows. If someone lives in Chicago, then he has a gun unless he is a pacifist; Quakers are pacifists, and Republicans are not pacifists. Nixon lives in Chicago and he is both a Quaker and a Republican.

Example 2.3

Let us consider the Σ_2.3 = (T, A) ontology about the stock market domain:

and

The meaning of this ontology is as described next. If some company's stock has a good price, then an investor should buy it unless that company is risky. Risky companies are those which are in the process of fusion or closing down, except for those that are in fusion with a strong company. It is known that Acme's stocks have a good price, and that Acme is in fusion with a strong company named Steel.

Example 2.4

Let Σ_2.4 = (T, A) be an ontology about the Royal African elephants (Sandewall, 1986), where:

and

It says that elephants are gray but royal elephants are not. Royal elephants are elephants; African elephants are elephants as well. It is known that Clyde is both a Royal and an African elephant.

Example 2.5

Let Σ_2.5 = (T, A) be an ontology about the adult students problem (Geffner and Pearl, 1990), with

and

It expresses that adult people are workers, and that university students do not work and are adults. It also asserts that Ken is both an adult and a university student.

Example 2.6 (adapted from Huang et al. (2004))

Let us consider the ontology Σ_2.6 = (T, A) adapted from Huang et al. (2004, Section 2.2) as an example of inconsistency caused by polysemy, with:

and

This ontology expresses that a married woman is a woman, a married woman is not a divorcee, a divorcee had a husband and has no husband. “Has_Husband” means married, “Had_Husband” also means married, and that somebody had a husband implies she does not have a husband. It is also known that Flor is a married woman and Leticia is divorced.

Notice that the concept “Divorcee” is unsatisfiable, because of the misuse of the word “Married_Woman.” Therefore, one has to carefully check if there is some misunderstanding with respect to concepts that have been used in the ontology; when an ontology is large, this kind of requirement may become rather difficult (Huang et al., 2004, p. 7).

In the next section, we will see how the above-described situations can be handled in DeLP.

DEFEASIBLE LOGIC PROGRAMMING

When a rule supporting a conclusion may be defeated by new information, it is said that such reasoning is defeasible (Pollock, 1974; Pollock, 1987; Nute, 1988; Pollock, 1995; Simari and Loui, 1992). When defeasible reasons or rules are chained to reach a conclusion, we have arguments instead of proofs. Arguments may compete, rebutting each other, so that a process of argumentation is a natural result of the search for arguments. Adjudication of competing arguments must be performed, comparing arguments in order to determine what beliefs are ultimately accepted as warranted or justified. Preference among conflicting arguments is defined in terms of a preference criterion which establishes a relation “⪯” among possible arguments; thus, for two arguments 𝒜 and ℬ in conflict, it may be the case that 𝒜 is strictly preferred over ℬ (𝒜≻ℬ), that 𝒜 and ℬ are equally preferable (𝒜⪰ℬ and 𝒜⪯ℬ), or that 𝒜 and ℬ are not comparable with each other. In the above setting, since we arrive at conclusions by building defeasible arguments, and since logical argumentation is usually referred to as argumentation, we sometimes call this kind of reasoning defeasible argumentation.

The growing success of argumentation-based approaches has caused a rich cross-breeding with other disciplines, providing interesting results in different areas such as group decision-making (Zhang, Sun, and Chen, 2005), knowledge engineering (Carbogim, Robertson, and Lee, 2000), legal reasoning (Prakken and Sartor, 2002; Verheij, 2005), and multiagent systems (Parsons, Sierrra, and Jennings, 1998; Sierra and Noriega, 2002; Rahwan et al., 2003), among others. During the last decade several defeasible argumentation frameworks have been developed, most of them on the basis of suitable extensions to logic programming (see Chesñevar et al. (2000), Prakken and Vreeswijk (2002), and Kakas and Toni (1999)). Defeasible logic programming (García and Simari, 2004) is one of such formalisms, combining results from defeasible argumentation theory (Simari and Loui, 1992) and logic programming (Lloyd, 1987). DeLP is a suitable framework for building real-world applications that have proven to be particularly attractive in that context, such as clustering (Gómez and Chesñevar, 2004), intelligent web search (Chesñevar and Maguitman, 2004b; Chesñevar, Maguitman, and Simari, 2006), knowledge management (Chesñevar et al., 2005a; Chesñevar et al., 2005b), multiagent systems (Brena, Chesñevar and Aguirre, 2006), natural language processing (Chesñevar and Maguitman, 2004a), intelligent web forms (Gómez, Chesñevar, and Simari, 2008b), among others.

Defeasible logic programming (García and Simari, 2004) provides a language for knowledge representation and reasoning that uses defeasible argumentation (Chesñevar et al., 2000; Prakken and Vreeswijk, 2002; Simari and Loui, 1992) to decide between contradictory conclusions through a dialectical analysis. The architecture of a knowledge representation system based on defeasible argumentation is shown in Figure 2 (the analogies of this architecture w.r.t. the architecture presented in Figure 1 will be considered later.

FIGURE 2 Architecture of a knowledge representation system based on defeasible argumentation.

In a defeasible logic program 𝒫 = (Π, Δ), a set Π of strict rules P←Q ₁,…, Q _n , and a set Δ of defeasible rules P − ≺Q ₁,…, Q _n can be distinguished.

Definition 3.1 (strict, defeasible, and DeLP programs)

ℒ _DeLP  = _df ℒ _{DeLP Π} ∪ℒ _{DeLP Δ} is the language of DeLP programs, where ℒ _{DeLP Π} is the language of DeLP programs formed by strict rules B←A ₁,…, A _n with (n≥1) and facts B (i.e., rules where n = 0), and ℒ _{DeLP Δ} is the language of DeLP programs formed only by defeasible rules B − ≺A ₁,…, A _n with (n≥1).

Literals can be positive or negative. The complement of a literal L (noted as ) is p if L = ∼p and ∼p if L = p. Notice that there is an extension to DeLP that allows to define presumptions (or defeasible rules without body) that model defeasible facts (see García and Simari (2004, Sect. 6.2)); however, they are outside the scope of this work.

Deriving literals in DeLP results in the construction of arguments. An argument 𝒜 is a (possibly empty) set of ground (i.e., without variables) defeasible rules that together with the set Π provides a logical proof for a given literal Q, satisfying the additional requirements of noncontradiction and minimality. Formally:

Definition 3.2 (argument)

Given a DeLP program 𝒫, an argument 𝒜 for a query Q, denoted⟨𝒜, Q⟩, is a subset of ground instances of defeasible rules in 𝒫, such that: (1) there exists a defeasible derivation for Q from Π∪𝒜; (2) Π∪𝒜 is noncontradictory (i.e., Π∪𝒜 does not entail two complementary literals P and ∼P); and (3) there is no 𝒜′⊂𝒜 such that there exists a defeasible derivation for Q from Π∪𝒜′. An argument⟨𝒜₁, Q ₁⟩ is a subargument of another argument⟨𝒜₂, Q ₂⟩ if 𝒜₁⊆𝒜₂.

The notion of defeasible derivation corresponds to the usual query-driven SLD derivation used in logic programming, performed by backward chaining on both strict and defeasible rules; in this context a negated literal ∼P is treated just as a new predicate name no<_1>P. Minimality imposes a kind of “Occam's razor principle” on argument construction. The noncontradiction requirement forbids the use of (ground instances of) defeasible rules in an argument 𝒜 whenever Π∪𝒜 entails two complementary literals. The notion of contradiction is captured by the notion of counterargument.

Definition 3.3 (counterargument. Defeat)

An argument⟨𝒜₁, Q ₁⟩ is a counterargument for an argument⟨𝒜₂, Q ₂⟩ iff there is a subargument⟨𝒜, Q⟩ of⟨𝒜₂, Q ₂⟩ such that the set Π∪{Q ₁, Q} is contradictory. An argument⟨𝒜₁, Q ₁⟩ is a defeater for an argument⟨𝒜₂, Q ₂⟩ if⟨𝒜₁, Q ₁⟩ counterargues⟨𝒜₂, Q ₂⟩, and⟨𝒜₁, Q ₁⟩ is preferred over⟨𝒜₂, Q ₂⟩ w.r.t. a preference criterion ⪯ on conflicting arguments. Such criterion is defined as a partial order ⪯⊆ Args(𝒫) × Args(𝒫). The argument⟨𝒜₁, Q ₁⟩ will be called a proper defeater for⟨𝒜₂, Q ₂⟩ iff⟨𝒜₁, Q ₁⟩ is strictly preferred over⟨𝒜, Q⟩ w.r.t. ⪯; if⟨𝒜₁, Q ₁⟩ and⟨𝒜, Q⟩ are unrelated to each other will be called a blocking defeater for⟨𝒜₂, Q ₂⟩.

Generalized specificity (Simari and Loui, 1992) is typically used as a syntax-based preference criterion among conflicting arguments, favoring those arguments which are more informed or more direct (Simari and Loui, 1992; Stolzenburg, García, Chesñevar, and Simari, 2003). For example, let us consider three arguments⟨{a − ≺b, c}, a⟩, ⟨{∼a − ≺b}, ∼a⟩, and⟨{(a − ≺b); (b − ≺ c}), a⟩ built on the basis of a program 𝒫 = (Π, Δ) = ({b, c}, {b − ≺c; a − ≺b; a − ≺b, c; ∼a − ≺b}). When using generalized specificity as the comparison criterion between arguments, the argument⟨{a − ≺b, c}, a⟩ would be preferred over the argument⟨{∼a − ≺b}, ∼a⟩ as the former is considered more informed (i.e., it relies on more premises). However, argument⟨{∼a − ≺b}, ∼a⟩ is preferred over⟨{(a − ≺b); (b − ≺c}), a⟩ as the former is regarded as more direct (i.e., it is obtained from a shorter derivation). However, it must be remarked that besides specificity, other alternative preference criteria could also be used; e.g., considering numerical values corresponding to necessity measures attached to argument conclusions (Chesñevar, Simari, Alsinet, and Godo, 2004; Chesñevar, Simari, Godo, and Alsinet, 2005) or defining argument comparison using rule priorities. This last approach is used in D-PROLOG (Nute, 1988), defeasible logic (Nute, 1992), extensions of defeasible logic (Antoniou et al., 2000; Antoniou et al., 1998), and logic programming without negation as failure (Kakas, Mancarella, and Dung, 1994; Dimopoulos and Kakas, 1995).

In order to determine whether a given argument 𝒜 is ultimately undefeated (or warranted), a dialectical process is recursively carried out, where defeaters for 𝒜, defeaters for these defeaters, and so on, are taken into account. An argumentation line starting in an argument⟨𝒜₀, Q ₀⟩ is a sequence [⟨𝒜₀, Q ₀⟩, ⟨𝒜₁, Q ₁⟩, ⟨𝒜₂, Q ₂⟩,…, ⟨𝒜 _n , Q _n ⟩…] that can be thought of as an exchange of arguments between two parties, a proponent (evenly indexed arguments) and an opponent (oddly indexed arguments). Each⟨𝒜 _i , Q _i ⟩ is a defeater for the previous argument⟨𝒜 _i−1, Q _i−1⟩ in the sequence, i>0. In order to avoid fallacious reasoning, dialectics imposes additional constraints on such an argument exchange to be considered rationally acceptable. Given a DeLP program 𝒫 and an initial argument⟨𝒜₀, Q ₀⟩, the set of all acceptable argumentation lines starting in⟨𝒜₀, Q ₀⟩ accounts for a whole dialectical analysis for⟨𝒜₀, Q ₀⟩ (i.e., all possible dialogues about⟨𝒜₀, Q ₀⟩ between proponent and opponent), formalized as a dialectical tree.

Nodes in a dialectical tree 𝒯_{⟨𝒜0, Q 0⟩} can be marked as undefeated and defeated nodes (U-nodes and D-nodes, resp.). A dialectical tree will be marked as an AND-OR tree: all leaves in 𝒯_{⟨𝒜0, Q 0⟩} will be marked U-nodes (as they have no defeaters), and every inner node is to be marked as D-node iff it has at least one U-node as a child, and as U-node otherwise. An argument⟨𝒜₀, Q ₀⟩ is ultimately accepted as valid (or warranted) w.r.t. a DeLP program 𝒫 iff the root of its associated dialectical tree 𝒯_{⟨𝒜0, Q 0⟩} is labeled as U-node.

Given a DeLP program 𝒫, solving a query Q w.r.t. 𝒫 accounts for determining whether Q is supported by (at least) one warranted argument. Different doxastic attitudes can be distinguished as follows: Yes, accounts for believing Q iff there is at least one warranted argument supporting Q on the basis of 𝒫; No, accounts for believing ∼Q iff there is at least one warranted argument supporting ∼Q on the basis of 𝒫; Undecided, neither Q nor ∼Q are warranted w.r.t. 𝒫, and Unknown, Q does not belong to the signature of 𝒫.

We present a property that will be useful for proving some results about our proposal of reasoning with δ-ontologies.

Proposition 3.1 (García and Simari, 2004)

For any program 𝒫 in DeLP, it cannot be the case that both Q and ∼Q are warranted.

In the next sections we will present a method for expressing arbitrary DL ontologies in DeLP. For now on, based on the fact discovered by Grosof et al. (2003) that DL inclusion axioms of the form “C⊑D” can be equated to PROLOG rules of the form “D(X) :- C(X)”, we will show how the application problems modeled by the ontologies presented in the previous section can be expressed in DeLP in such a way that it could be possible for an agent to automatically reason in such cases. Notice also that following PROLOG usual conventions, predicates are noted with lowercase letters (e.g., bird, fly, etc.), variable names with capital letters (e.g., X, Y, Z, etc.), and constant names with lowercase letters (e.g., opus, acme, steel, etc.).

Example 3.1

Here follows the DeLP program 𝒫_3.1 = (Π, Δ) which models the situation presented in Example 2.1:

and

In DeLP, the answer for fly(opus) is Yes, while the answer for ∼fly(opus) is No as it is shown next. It is possible to build an argument⟨𝒜₁, fly(opus)⟩, where

This argument is properly defeated by another argument⟨𝒜₂, ∼ fly(opus)⟩, with

However, argument 𝒜₁ is reinstated by another argument⟨𝒜₃, fly(opus)⟩ which is a blocking defeater for 𝒜₂, where

Example 3.2 (taken from García and Simari (2004))

Let us present the DeLP program 𝒫_3.2 = (Π, Δ) which represents the ontology presented in Example 2.2:

and

For this particular program, García and Simari (2004, Example 2.2) show that the answer for queries pacifist(nixon) and ∼pacifist(nixon) is Undecided.

Example 3.3 (taken from García and Simari (2004))

Consider the DeLP program 𝒫_3.3 = (Π, Δ) which represents the situation posed by Example 2.3, where

and

In this case, it can be shown that the answer for buy<_1>stock(acme) is Yes (see García and Simari (2004, Example 2.4) for details).

Example 3.4 (taken from Simari and Loui (1992))

Consider the DeLP program 𝒫_3.4 = (Π, Δ), with

and

This example deals with “on-path versus off-path preemption” in the context of inheritance reasoners. Among the arguments that can be built from 𝒫_3.4, ⟨{∼gray(clyde) − ≺elephant(clyde)}, ∼gray(clyde)⟩ is the most specific; therefore, the answer for the query gray(clyde) is No (Simari and Loui, 1992, p. 148).

Example 3.5 (taken from Simari and Loui (1992))

Simari and Loui (1992, p. 149) present this example that deals with “defeasible specificity.” Consider the DeLP program 𝒫_3.5 = (Π, Δ), where

and

DeLP is not able to decide whether or not Ken is a worker as the answer for the query worker(ken) is Undecided.

Example 3.6

The following DeLP program 𝒫_3.6 = (Π, Δ) codifies the ontology considered in Example 2.6, where

and

From this program, the answer for query woman(flor) is Yes, while the answer for the query divorcee(flor) is No, which are correct. However, the answer for the query has < _1 > husband(flor) is Undecided as it is not possible to build an argument for such literal. The answer for woman(leticia) is Yes and the answer for has < _1 > husband(leticia) is No.

In the next section, we will see under which constraints the translation of arbitrary DL ontologies to DeLP can be performed.

EXPRESSING DL ONTOLOGIES IN DELP

In the presence of inconsistent ontologies, traditional DL reasoners (such as Racer (Haarslev and Möller, 2001)) issue an error message and stop further processing. Thus the burden of repairing the ontology (i.e., making it consistent) is on the knowledge engineer. However, the knowledge engineer is not always available and in some cases, such as when dealing with imported ontologies, he has neither the authority nor the expertise to correct the source of inconsistency. Therefore, we are interested in coping with inconsistencies such that the task of dealing with them is automatically solved by the reasoning system.

We propose using DeLP to perform such a task by translating DL ontologies into DeLP programs. By doing so we gain the capability of reasoning with inconsistent ontologies. However, we also lose some expressiveness in the involved ontologies. As we will show in Definition 4.1, certain restrictions will have to be imposed on DL ontologies in order to be expressed in the DeLP language.

Our proposal is based in part in the work of (Grosof et al., 2003; Volz, 2004) who show that the processing of ontologies can be improved by the use of techniques from the area of logic programming. In particular they have identified a subset of DL languages that can be effectively mapped into a horn-clause logics. Given a DL ontology Σ = (T, A), we will consider the Tbox T as partitioned into two disjoint sets—a strict terminology T _S and a defeasible terminology T _D —such that T = T _S ∪ T _D and T _S ∩ T _D  = ∅.

Considering the analogies between the reasoning systems presented in Figures 1 and 2, we therefore propose translating the DL ontology Σ into a DeLP program 𝒫 = (Π, Δ) = 𝒯(Σ) by means of a mapping 𝒯 from the DL language to the DeLP language. Intuitively, the set Π of strict rules in 𝒫 will correspond to the Abox A joined with T _S in Σ, and the set Δ of defeasible rules will correspond to T _D in Σ. This translation will be achieved by two specialized functions 𝒯_Π and 𝒯_Δ, where 𝒯_Π translates from a set of DL sentences into a set of DeLP strict rules and 𝒯_Δ translates from a set of DL sentences into a set of DeLP defeasible rules, such that Π = 𝒯_Π(T _D ) ∪ 𝒯_Π(A) and Δ = 𝒯_Δ(Δ).

In the rest of this section, we will explain how to achieve the translation of DL ontologies into DeLP programs. For clarity, in spite of being incorrect according to the DeLP syntax conventions, strict rules of the form “H ← B ₁,…, B _n ” will sometimes be written as “H ← B ₁ ∧… ∧ B _n ” and defeasible rules “H − ≺ B ₁,…, B _n ” as “H − ≺ B ₁ ∧…∧ B _n .” As noted by Grosof et al. (2003), for DL sentences to be mapped into horn-logic rules, they must satisfy certain constraints. Conjunction and universal restrictions appearing in the right-hand side of inclusion axioms can be mapped to heads of rules (called ℒ _h -classes). In contrast, conjunction, disjunction, and existential restriction can be mapped to rule bodies whenever they occur in the left-hand side of inclusion axioms (called ℒ _b -classes). As equality axioms “C ≡ D” are interpreted as two inclusion axioms “C⊑D” and “D⊑C,” they must belong to the intersection of ℒ _h and ℒ _b .

Definition 4.1 (ℒ _h , ℒ _b , and ℒ _hb languages/classes (adapted from Grosof et al. (2003))

Let A be an atomic class name, C and D class expressions, and R a property. In the ℒ _h language, C ⊓ D is a class, and ∀ R.C is also a class. Class expressions in ℒ _h are called ℒ _h -classes. In the ℒ _b language, C ⊔ D is a class, and ∃ R.C is a class too. Class expressions in ℒ _b are called ℒ _b -classes. The ℒ _hb language is defined as the intersection of ℒ _h and ℒ _b . Class expressions in ℒ _hb are called ℒ _hb -classes.

We now define the mapping from DL to DeLP. Without losing generality, we assume that ontology definitions are normalized w.r.t. negation. That is, negations in class expressions are shifted inwards using De Morgan's rules and well-known relations between existential and value restrictions (for details, see the definition of the NNF function in Krötzch, Rudolph, and Hitzler (2007)). Besides, occurrences of ⊥and⊤ are not considered as they can be suitably eliminated as shown in Volz (2004, Table 4.1). These transformations of course do not change the semantics of a terminology.

First we show how to map DL axioms into defeasible rules. As previously mentioned, defeasible rules are meant to represent possibly inconsistent information. Thus DL axioms in defeasible terminologies are going to be interpreted as default class inclusions.

Definition 4.2 (𝒯_Δ mapping from DL sentences to DeLP defeasible rules)

Let A, C, D be concepts, X, Y variables, P, Q properties. The 𝒯_Δ: 2^{ℒ _DL}  → 2^{ℒ _{DeLP Δ}} mapping is defined in Figure 3. Besides, intermediate transformations that will end as rules of the form “(H ₁ ∧ H ₂) − ≺ B” will be rewritten as two rules “H ₁ − ≺ B” and “H ₂ − ≺ B” (as this is an incorrect DeLP syntax). Similarly, transformations of the form “H ₁ H ₂ − ≺ B” will be rewritten as “H ₁ − ≺ B ∧ H ₂,” and transformations of the form “H − ≺ (B ₁∨B ₂)” will be rewritten as two rules “H − ≺ B ₁” and “H − ≺ B ₂.”

FIGURE 3 Mapping from DL ontologies to DeLP defeasible rules.

Example 4.1

Consider the DL terminology

which expresses both that birds fly and that chickens do not fly unless they are scared. The application of the 𝒯_Δ mapping to T _D yields a set Δ of defeasible rules, where

Example 4.2 (adapted from Grosof et al. (2003))

Consider the DL axiom:

It would be expressed as the (mal-formed) defeasible rule:

which is rewritten as the pair of defeasible rules:

Next, we present a mapping from DL axioms to strict rules. We are going to assume that strict terminologies are consistent.

Definition 4.3 mapping from DL sentences to DeLP strict rules)

Let A, C, D be concepts, X, Y variables, P, Q properties. The mapping is defined in Figure 4. Besides, intermediate transformations of the form “(H ₁ ∧ H ₂) ← B” will be rewritten as two rules “H ₁ ← B” and “H ₂ ← B.” Similarly, transformations of the form “H ₁ ← H ₂ ← B” will be rewritten as “H ₁ ← B ∧ H ₂,” and rules of the form “H ← (B ₁∨B ₂)” will be rewritten as two rules “H ← B ₁” and “H ← B ₂.”

FIGURE 4 Mapping from DL ontologies to DeLP strict rules.

As DeLP is based on SLD-derivation of literals, simple translation of DL sentences to DeLP strict rules does not allow to infer negative information by modus tollens. For instance, “C⊑D” (all C's are D's) is translated as “D(X) ← C(X),” DeLP is not able to derive “∼C(a)” from “∼D(a)”. Thus given “C ₁ ⊓ C ₂ ⊓…⊓ C _n−1 ⊓ C _n ⊑D,” instead of only including the strict rule “D(X) ← C ₁(X), C ₂(X),…, C _n−1(X), C _n (X)” in its translation, we propose including all of its transposes.

Definition 4.4 (transposes of a strict rule)

Let r = H ← B ₁, B ₂, B ₃,…, B _n−1, B _n be a DeLP strict rule. The set of transposes of rule r, noted as “Trans(r),” is defined as

Definition 4.5 (𝒯_Π mapping from DL sentences to DeLP strict rules)

We define the mapping from DL ontologies into DeLP strict rules as .

Notice that reasoning with transposed strict rules is not more computationally expensive than reasoning without them. Observe that even though as this seems computationally expensive, it is only as expensive as deriving ∼b from a ← b and ∼a.

Also notice that following trends in nonmonotonic reasoning, we do not consider transposition of defeasible rules (Brewka, Dix, and Konolige, 1997; Caminada, 2008). In this respect, but in the context of default logic, Brewka et al. (1997, p. 45) say that:

Default logic expressive power is due mainly to the representation of defaults as (nonstandard) inference rules. This representation avoids problems with contraposition of defaults. In classical logic, an implication A ⊃ B is equivalent to its contraposition ¬ B ⊃ ¬ A. For defaults, contraposition is sometimes unwanted. For instance, one might believe that computer scientists typically do not know much about nonmonotonic reasoning. From this belief it certainly does not follow that those who know much about nonmonotonic reasoning are typically not computer scientists.

The reader should also notice that the price paid for translating DL ontologies into DeLP programs is the loss of some expressiveness. For instance, as noted by Grosof et al. (2003), DL axioms that generate a rule with a disjunction in its head cannot be represented in logic programming.

DELP-BASED ONTOLOGIES

As previously mentioned, traditional DL reasoners are not capable of inferring information in the presence of inconsistent ontologies. In this section, we present a framework where inconsistent definitions for concepts in an ontology are expressed as a set of defeasible inclusion and equality axioms. These axioms are to be considered as an initial, tentative attempt at exploring the problem. Thus, in the presence of inconsistency, to determine the epistemic status of a sentence about some individual's membership in a concept description, a dialectical analysis will be carried out considering all arguments in favor and against its membership.

Knowledge Representation: δ-Ontologies

An ontology is defined as a set of classes and a set of individuals that belong to such classes. We redefine the notion of DL ontology to make it suitable for our approach.

Definition 5.1 (δ-Ontology)

Let C be an ℒ _b -class, D an ℒ _h -class, A, B ℒ _hb -classes, P, Q properties, a, b individuals. Let T be a set of inclusion and equality sentences in ℒ _DL of the form C⊑D, A ≡ B, ⊤ ⊑ ∀ P.D, ⊤ ⊑ ∀ P ⁻.D, P⊑Q, P ≡ Q, P ≡ Q ⁻, or P ⁺⊑P such that T can be partitioned into two disjoint sets T _S and T _D . Let A be a set of assertions disjoint with T of the form a: D or ⟨a, b⟩: P. A δ-ontology Σ is a tuple (T _S , T _D , A). The set T _S is called the strict terminology (or Sbox), T _D the defeasible terminology (or Dbox) and A the assertional box (or Abox).

In what follows we assume that the knowledge engineer determines how to encode ontologies in terms of defeasible and strict axioms. Establishing such distinction automatically is a well-known open problem and we discuss some approaches to it in a later section.

Example 5.1

Let Σ_5.1 = (T _S , T _D , A) be a δ-ontology, where

and

The Sbox T _S says both that chickens and penguins are birds, and that penguins do not fly. The Dbox T _D expresses that birds usually fly, chickens typically do not fly unless they are scared, and that flying animals normally nest in trees. The Abox A establishes that Tina is a chicken, Tweety is a penguin and Tina is scared. ³

The Sbox will be interpreted as a set of strict rules, the Abox as a set of facts, and the Dbox as a set of defeasible rules.

Semantic Interpretation of δ-Ontologies as DeLP Programs

The traditional approach to reasoning in DLs is based on model-theoretic semantics. As DLs are a subset of first-order logic (FOL), entailment has an explosive effect in the presence of inconsistent ontologies (i.e., inconsistency allows to derive all well-formed formulas in the theory). In this work, we propose an argumentative approach to reasoning with inconsistent ontologies. Thus a δ-ontology will be interpreted as a DeLP program. We are assuming that under a traditional DL interpretation, the set T _S ∪ A has a model; provided that is the case, then, as required by the DeLP framework, the set 𝒯_Π(T _S ) ∪ 𝒯_Π(A) will have a model under a standard logic programming interpretation as well.

Definition 5.2 (interpretation of a δ-Ontology)

Let Σ = (T _S , T _D , A) be a δ-ontology. The interpretation of Σ is a DeLP program 𝒫 = (𝒯_Π(T _S ) ∪ 𝒯_Π(A), 𝒯_Δ(T _D )).

Example 5.2 (continues Ex. 5.1)

Consider again the δ-ontology Σ_5.1. Σ_5.1 is interpreted as the DeLP program 𝒫_5.1 = (Π, Δ), where

and

Inference Tasks in δ-Ontologies

In the DL approach to reasoning with ontologies in the semantic web, once a knowledge engineer has designed the terminology and used the DL reasoning service for checking that all of the terminology's concepts are satisfiable, the Abox can be filled with assertions about individuals. In order to keep consistency within an argument as required by Def. 3.2, we must enforce some internal coherence between the Abox and the Tbox.

Definition 5.3 (internal coherence in Aboxes. Consistency of Aboxes w.r.t. Sboxes)

Let Σ = (T _S , T _D , A) be a δ-ontology. The Abox A is internally coherent iff there are no pair of assertions a: C and a: ¬ C, for any individual a and any class C. The Abox A is consistent w.r.t. the terminology T _S iff it is not possible to derive two literals C(a) and ∼C(a) from 𝒯_Π(T _S ) ∪ 𝒯_Π(A).

Example 5.3

Let Σ_5.3 = (T _S , ∅, A) be a δ-ontology such that T _S  = {(C⊑D), (D⊑ ¬ F)} and A = {(B: C), (B: F)}.

Σ_5.3 is expressed as 𝒫_5.3 = (Π, ∅), where Π = 𝒯_Π(T _S ) ∪ 𝒯_Π(A) = {c(b), c(b), (d(X) ← c(X)), (∼c(X) ← ∼d(X)), (∼f(X) ← d(X)), (∼d(X) ← f(X))}, from which it is possible to strictly derive f(b) and ∼f(b). Therefore A is not consistent w.r.t. T _S .

Instance Checking

In the traditional DL setting, instance checking refers to determining whether the assertions in the Abox entail that a particular individual is an instance of a given concept description (Baader et al., 2003). We propose a set of definitions to capture this notion in the context of δ-ontologies.

Definition 5.4 (potential, justified, and strict membership of an individual to a class)

Let Σ = (T _S , T _D , A) be a δ-ontology. Let C be a class name, a an individual, let 𝒫 = (𝒯_Π(T _S ) ∪ 𝒯_Π(A), 𝒯_Δ(T _D )).

1. The individual a potentially belongs to class C (noted as “”) iff there exists an argument ⟨𝒜, C(a)⟩ w.r.t. 𝒫.

2. The individual a justifiedly belongs to class C (noted as “”) iff there exists a warranted argument ⟨𝒜, C(a)⟩ w.r.t. 𝒫.

3. The individual a strictly belongs to class C (noted as “”) iff there exists an argument ⟨∅, C(a)⟩ w.r.t. 𝒫.

We have the following straightforward result.

Property 5.1

Given a δ-ontology Σ, a concept name C, and an individual a, implies , and implies .

Proof

The former holds because in DeLP empty arguments (i.e., literals derived exclusively from strict rules) have no defeaters and they are thus warranted. The latter trivially holds because warranted arguments are arguments.

The next example remarks the way our proposal is capable of handling instance checking under the Open World Assumption assumed by Semantic Web standards.

Example 5.4

Consider the δ-ontology Σ_5.4 = (∅, ∅, {TWEETY: Bird}), that is interpreted as the DeLP program 𝒫_5.4 = ({bird(tweety)}, ∅). It holds that as the argument ⟨∅, bird(tweety)⟩ is trivially warranted w.r.t. 𝒫_5.4. However it holds neither nor as the answer for bird(opus) is Undecided because no argument for that literal (or its negation) can be built from 𝒫_5.4.

We now extend the notion of membership to arbitrary concept expressions.

Definition 5.5 (potential, justified, and strict membership of an individual to a class (extended version))

Let Σ = (T _S , T _D , A) be a δ-ontology. Let C, D class names in Σ, a, b individuals in Σ, R an atomic property in Σ, 𝒫 = (𝒯_Π(T _S ) ∪ 𝒯_Π(A), 𝒯_Δ(T _D )). Let E be a class name not present in Σ. The potential (resp. justified) membership of a to a complex concept is defined as:

	¬C: (resp. ) iff there exists an argument (resp. warranted argument)⟨𝒜, ∼ C(a)⟩ w.r.t. 𝒫.
	C ⊓ D: Let 𝒫2 = (Π, Δ ∪ 𝒯Δ(C ⊓ D⊑E)). (resp. ) iff there exists an argument (resp. warranted argument) ⟨𝒜, E(a)⟩ w.r.t. 𝒫2.
	C ⊔ D: Let 𝒫2 = (Π, Δ ∪ 𝒯Δ(C ⊔ D⊑E)). (resp. ) iff there exists an argument (resp. warranted argument) ⟨𝒜, E(a)⟩ w.r.t. 𝒫2.
	∃R.C: Let 𝒫2 = (Π, Δ ∪ 𝒯Δ(∃ R.C⊑E)). (resp. ) iff there exists an argument (resp. warranted argument) ⟨𝒜, E(a)⟩ w.r.t. 𝒫2.

The strict membership of a to a complex concept is defined as:

	¬C: iff there exists an argument ⟨∅, ∼ C(a)⟩ w.r.t. 𝒫.
	C ⊓ D: Let 𝒫2 = (Π ∪ 𝒯Π(C ⊓ D⊑E), Δ). iff there exists an argument ⟨∅, E(a)⟩ w.r.t. 𝒫2.
	C ⊔ D: Let 𝒫2 = (Π ∪ 𝒯Π(C ⊔ D⊑E), Δ). iff there exists an argument ⟨∅, E(a)⟩ w.r.t. 𝒫2.
	∃R.C: Let 𝒫2 = (Π ∪ 𝒯Π(∃ R.C⊑E), Δ). iff there exists an argument ⟨∅, E(a)⟩ w.r.t. 𝒫2.

Notice that in the above definition the concept E can be actually larger than the complex concept it represents and it is introduced solely for expressing the initial DeLP query.

Property 5.2

Let Σ = (T _S , T _D , A) be a δ-ontology. It cannot be the case that an individual a belongs justifiedly to concept C and ¬ C simultaneously.

Proof

Suppose that both and . Then it must be the case there exist two warranted arguments ⟨𝒜, C(a)⟩ and ⟨ℬ, ∼ C(a)⟩ w.r.t. (𝒯_Π(T _S ) ∪ 𝒯_Π(A), 𝒯_Δ(T _D )). But this is impossible as DeLP cannot warrant two complementary literals simultaneously (as shown in Property 3.1).

Property 5.3

Let Σ = (T _S , T _D , A) be a δ-ontology. It cannot be the case an individual a belongs strictly to concept C and ¬ C simultaneously.

Proof

Suppose that and , then there must exist two arguments ⟨∅, C(a)⟩ and ⟨∅, ∼ C(a)⟩ w.r.t.\ (𝒯_Π(T _S ) ∪ 𝒯_Π(A), 𝒯_Δ(T _D )). Therefore 𝒯_Π(T _S ) ∪ 𝒯_Π(A) will be inconsistent contradicting Definition 5.3.

Retrieval

When DL knowledge bases are considered, we would want to know all individuals that are instances of a certain concept. In the traditional DL setting, given an ontology (T, A) and a concept C, in the retrieval problem we are interested in knowing all the individuals a such that T ∪ A⊧a: C (Baader et al., 2003). We present naïve solutions to two related problems:

	Open retrieval: Given a δ-ontology Σ = (T S , T D , A) and a class C, find all individuals that are instances of C. We solve this problem by finding all the individuals a such that there exists a warranted argument ⟨𝒜, C(a)⟩ w.r.t. DeLP program (𝒯Π(T S ) ∪ 𝒯Π(A), 𝒯Δ(T D )) (see Figure 5).
	Retrieval of all classes: Given a δ-ontology Σ = (T S , T D , A) and an individual a, find all named classes C such that a is an instance of C. We solve this problem by finding all the classes C such that there exists a warranted argument ⟨𝒜, C(a)⟩ w.r.t. DeLP program (𝒯Π(T S ) ∪ 𝒯Π(A), 𝒯Δ(T D )) (see Figure 6).

FIGURE 5 Open retrieval.

Property 5.4

The running time of the processes for “open retrieval” and “retrieval of all classes” is finite.

Proof

As a δ-ontology has a finite number of both named concepts and individual constants, the DeLP program obtained from it is finite. Cecchi, Fillottrani, and Simari (2006) have shown that determining if there exists an argument for a literal is NP; besides, as the warrant procedure always builds a finite dialectical tree (García and Simari, 2004), then processes for “open retrieval” and for “retrieval of all classes” always terminate.

FIGURE 6 Retrieval of all classes.

DELP-BASED INTEGRATION OF DL ONTOLOGIES

In this section, we introduce an application for ontology integration in the semantic web based on the framework presented above. Ontology integration is the problem of combining ontologies residing in different sources and to provide the user with a unified view of such ontologies (Calvanese et al., 2001). The problem of designing systems for ontology integration in the semantic web is particularly important because ontologies are to be developed independently from each other, and for this reason, they can be mutually inconsistent. One possible architecture for ontology integration systems is based on a global schema and a set of local sources. The local sources contain the actual data while the global schema provides a reconciled, unified view of the underlying sources. A basic service provided by ontology integration systems is that of answering queries posed in terms of the global schema.

Definition 6.1 (ontology integration system)

An ontology integration system ℐ is a triple (𝒢, 𝒮, ℳ) where

	𝒢 is a global ontology expressed as a δ-ontology over an alphabet 𝒜𝒢.
	𝒮 is a set of n source ontologies 𝒮1,…, 𝒮 n expressed as δ-ontologies over alphabets 𝒜𝒮1 ,…, 𝒜𝒮 n , resp. Each alphabet 𝒜𝒮 i includes a symbol for each concept or role name of the source 𝒮 i , i = 1,…, n.
	ℳ is a set of n mappings ℳ1,…, ℳ n between 𝒢 and 𝒮1,…, 𝒮 n , resp. Each mapping ℳ i is constituted by a set of assertions of the form q 𝒮 i ⊑q 𝒢, where q 𝒢 and q 𝒮 i are queries of the same arity defined over the global ontology 𝒢 and 𝒮 i , i = 1,…, n, resp. Queries q 𝒢 are expressed over alphabet 𝒜𝒢 and queries q 𝒮 i are expressed over alphabet 𝒜𝒮 i . The sets ℳ1,…, ℳ n are called bridge ontologies.

Next we show a case study in which several DL source ontologies and a DL global ontology are integrated. These ontologies will be interpreted as DeLP programs. Queries posed w.r.t. the global ontology are going to be interpreted as queries answered on the basis of such DeLP programs.

Example 6.1

Consider the global δ-ontology presented in Figure 7. The Dbox expresses that computer geeks are usually not good in sports; expert swimmers are normally good at sports, and, if somebody is either capable of swimming both a race stroke and a rescue stroke or is a diver, then she is typically considered an expert swimmer.

FIGURE 7 Global ontology .

Notice that the terminology expresses a conflict w.r.t. the concept “Good”. If we find that some individual in the Abox can be proven to be member of both concepts “Swimmer” and “Greek”, then the Abox would be incoherent from a traditional DL point of view because that individual would belong both to “Good” and to “¬ Good, indicating that the concept “Good” should be empty and having one individual at the same time. We will show how this type of situation can be handled naturally in DeLP.

Example 6.2 (continues Ex. 6.1)

In Figure 8, we present two source ontologies: 𝒮₁ about water activities, and 𝒮₂ on computer programming. In local source ontology , Dbox says that both free and scuba divers are divers, saturation divers are a particular class of scuba divers, and somebody capable of swimming some kind of stroke is usually a swimmer. Abox A ^𝒮₁ establishes that John swims both crawl and side strokes, Paul is a saturation diver, and crawl and side are swimming strokes.

FIGURE 8 Source ontologies 𝒮₁ and 𝒮₂.

In local source ontology , Sbox expresses that among programming languages, both logic programming and object-oriented languages can be found. Dbox says that a programmer is usually somebody who can program in some programming language, and that someone who can read and write code in such a language can program unless she has failed the elementary programming course. Abox A ^𝒮₂ establishes that Prolog is a logic programming language and that John can read and write Prolog code; that Java is an object-oriented language and that Mary can read and write Java code, and that Paul is capable of reading and writing Java code although he failed the elementary programming course.

Notice how, in particular, source ontology 𝒮₂ is inconsistent from a traditional point of view because the individual named Paul belongs at the same time to concepts “Programmer” and “¬ Programmer.” Therefore, this ontology cannot be processed by traditional DL reasoners. We will show how can this be achieved in the framework of δ-ontologies.

As mentioned above, our goal is to answer queries about the membership of individuals to a certain concept in a global ontology using the data defined in source ontologies. The relationship of the global ontology with the local ontologies is achieved through bridge ontologies. A bridge ontology allows to map concepts and properties between two ontologies. Thus a concept in one ontology corresponds to a view of one or several concepts in some other ontology. In the examples we present, we consider bridge ontologies as given; for techniques on semi-automatic discovery of such mappings implemented as articulation rules see Mitra (2004)Euzenat and Shvaiko (2007). Moreover, we are going to assume unique name assumption w.r.t. references to individuals in Aboxes through our presentation.

Example 6.3 (continues Ex. 6.2)

Consider again global ontology 𝒢 and source ontologies 𝒮₁ and 𝒮₂. Articulation of definitions in 𝒢 with those in 𝒮₁ and 𝒮₂ is done by bridge ontologies ℳ₁ and ℳ₂, resp. (see Figure 9). For clarity, in bridge ontologies we tag concept and property names with their defining ontology name.

FIGURE 9 Bridge ontologies ℳ₁ and ℳ₂.

Bridge ontology ℳ₁ expresses that role “swims” in 𝒮₁ corresponds to role “can < _1 > swim” in 𝒢; concept “Diver” in 𝒮₁ refers to “Diver” in 𝒢; the concept (anonymously defined by the one-of construct) composed of individual “SIDE” in 𝒮₁ is mapped to the concept “rescue < _1 > stroke” in 𝒢, and, the concept composed by individual “CRAWL” in 𝒮₁ is mapped to “Race < _1 > Stroke” in 𝒢. Bridge ontology ℳ₂ indicates that the concept “Programmer” in 𝒮₂ corresponds to the concept “Greek” defined in 𝒢.

As discussed above, in the global-as-view approach to ontology integration, queries are posed w.r.t. a global ontology which is used as a way to access data found in local source ontologies. Next we show how to extend the task of instance checking for individual membership to concepts defined in a global ontology in the context of an ontology integration system. We will show how an ontology integration system can be regarded as a DeLP program and queries to the ontology integration system can be interpreted as queries w.r.t. such a DeLP program.

Definition 6.2 (interpretation of an ontology integration system)

Let ℐ = (𝒢, 𝒮, ℳ) be an ontology integration system such that 𝒮 = {𝒮₁,…, 𝒮 _n } and ℳ = {ℳ₁,…, ℳ _n }, where

	with i = 1,…, n,
	with i = 1,…, n.

The system ℐ is interpreted as the DeLP program ℐ _DeLP  = (Π, Δ), with

Example 6.4 (continues Ex. 6.3)

The interpretation as DeLP programs of global ontology 𝒢; sources 𝒮₁ and 𝒮₂, and bridges ℳ₁ and ℳ₂ are shown in Figures 10-12, resp. Global ontology 𝒢 is interpreted as the DeLP program 𝒫_𝒢 = (∅, Δ_𝒢); source ontology 𝒮₁, as 𝒫₁ = (Π₁, Δ₁); source ontology 𝒮₂, as 𝒫₂ = (Π₂, Δ₂); bridge ontology ℳ₁, as the set of defeasible rules Δ_ℳ1 , and bridge ontology ℳ₂, as Δ_ℳ2 .

FIGURE 10 DeLP program 𝒫_𝒢 = (∅, Δ_𝒢) obtained from global ontology 𝒢.

FIGURE 11 DeLP programs 𝒫₁ and 𝒫₂ obtained from source ontologies 𝒮₁ and 𝒮₂, resp.

FIGURE 12 Bridge ontologies expressed as defeasible rules.

Thus, the interpretation of ℐ is the DeLP program 𝒫_ℐ = (Π, Δ) where Π = Π₁ ∪ Π₂, and Δ = Δ_𝒢 ∪ Δ₁ ∪ Δ₂ ∪ Δ_ℳ1  ∪ Δ_ℳ2 .

Possible inferences in the integrated ontology ℐ _DeLP are modeled by means of a dialectical analysis in the DeLP program that is obtained when each DL sentence of the ontology is mapped into DeLP clauses. Thus warranted arguments will be the valid consequences that will be obtained from the original ontology, provided the strict information in ℐ _DeLP is consistent.

Definition 6.3 (potential, justified, and strict membership of individuals to concepts in ontology integration systems)

Let ℐ = (𝒢, 𝒮, ℳ) be an ontology integration system. Let a be an individual name, and C a concept name defined in 𝒢.

1. Individual a potentially belongs to concept C iff there exists an argument 𝒜 for the literal C(a) w.r.t. DeLP program ℐ _DeLP .

2. Individual a justifiedly belongs to concept C iff there exists a warranted argument 𝒜 for the literal C(a) w.r.t. DeLP program ℐ _DeLP .

3. Individual a strictly belongs to concept C iff there exists an empty argument for the literal C(a) w.r.t. DeLP program ℐ _DeLP .

Next we will show some of the arguments that can be built from the integrated ontology system. In the rest of the presentation, we are assuming generalized specificity (Simari and Loui, 1992; Stolzenburg et al., 2003) as the criterion for argument comparison. This is just an example as other criteria could be used (e.g., (Ferreti, Errecalde, García, and Simari, 2007)).

Example 6.5 (continues Ex. 6.4)

Consider again the DeLP program ℐ _DeLP . We are interested in determining the justified membership of individuals John, Mary, and Paul to concepts “Good” and/or “¬ Good.” According to Def. 6.3, it is necessary to determine if there exist warranting arguments for literals good(john), good(mary), and good(paul), resp. Notice that answers to queries cannot be ambiguous as it is not possible to warrant complementary literals in DeLP. We will see that as John is both a geek and a swimmer, it will not be possible to determine if he is good at sports or not. In spite of this result, we will also see that as Mary is a Java programmer, she will not be regarded as good at sports. In the case of Paul, as he is a diver, and although he programs in Java but failed the elementary programming course, he will not be considered a programmer and thus, he will be regarded as good at sports.

First, we will consider the dialectical analysis for the query “good(john).” There are reasons to assert that John belongs potentially to the concept “Good.” Formally, there exists an argument ⟨𝒜₁, good(john)⟩ where

However, John belongs potentially to the concept “¬ Good” because he is a computer geek. Formally, there is an argument ⟨𝒜₂, ∼ good(john)⟩ that defeats argument 𝒜₁, where

Thus, in the dialectical tree for the query “good(john),” defeated argument 𝒜₁ appears labeled as a D-node while victorious argument 𝒜₂ appears marked as a U-node. (see Figure 13(a)). On the other hand, when we consider the membership of John to concept “¬ Good,” we discover that argument 𝒜₂ supporting this conclusion is defeated by argument 𝒜₁ (see Figure 13.(b)). Therefore, the answer to query “good(john)” is UNDECIDED.

FIGURE 13 Dialectical trees for queries good(john), good(mary), and good(paul).

Second, we consider the dialectical analysis for determining if Mary belongs to concept “good.” Mary belongs justifiedly to concept “¬ Good” as the answer to query “good(mary)” is No because there is a warranted argument ⟨ℬ, ∼ good(mary)⟩ (see Figure 13.(c)), where

Third, we will see why Paul belongs justifiedly to concept “Good.” Let us consider the dialectical tree for the literal “good(paul).” There is an argument ⟨𝒞₁, good(paul)⟩, based on the defeasible information that expresses that Paul is an expert swimmer (because he is a saturation diver), with

But argument 𝒞₁ is attacked by an argument ⟨𝒞₂, ∼ good(paul)⟩, where

Nevertheless, Paul also belongs potentially to concept “𝒮₂: ¬ Programmer” (because he failed the elementary programming course), as an argument ⟨𝒞₃, 𝒮₂: ∼ programmer(paul)⟩ can be found, where

Thus, the dialectical tree for the query “good(paul)” has three nodes (see Figure 13.(d)). With respect to the query “∼good(paul)” for determining if Paul belongs justifiedly to the concept “¬ Good,” argument 𝒞₂ is defeated by argument 𝒞₁ (see Figure 13.(e)). Therefore, the answer to the query “good(paul)” is YES, and we conclude that Paul belongs justifiedly to the concept “Good.”

EVALUATION OF THE PROPOSAL

In order to evaluate our approach, we propose using the framework presented by Huang et al. (2005) for reasoning with inconsistent ontologies with a nonstandard inference relation. With classical reasoning, a query φ given an ontology Σ can be expressed as an evaluation of the consequence relation Σ⊧φ; there are two answers to a query: either “yes” (Σ⊧φ) or “no” (Σ⊭φ). For reasoning with inconsistent ontologies with a nonstandard inference relation, Huang et al. (2005) propose using an alternative classification to distinguish answers to queries.

Definition 7.1 (epistemic status of an answer (Huang et al., 2005))

Given an ontology Σ and a query φ, the answer to φ will have one of the four epistemic states:

1. Overdetermined: Σ|≈φ and Σ|≈¬ φ;

2. Accepted: Σ|≈φ and Σ∤ ≈¬ φ;

3. Rejected: Σ∤ ≈φ and Σ|≈¬ φ;

4. Undetermined: Σ∤ ≈φ and Σ∤ ≈¬ φ.

If we regard the relation |≈as “justified membership” of instances to concepts (see Def. 5.4), Σ|≈φ corresponds to a YES answer to query φ w.r.t. program 𝒯(Σ).

Property 7.1

Let |≈be the “justified membership” of instances to concepts relationship. Let Σ be a δ-ontology. The answer to a query φ is never overdetermined.

Proof

Suppose, on the contrary that the answer to φ is overdetermined. Then it must be the case that there exist two warranted arguments ⟨𝒜, φ⟩ and ⟨𝒜, ∼ φ⟩ w.r.t. 𝒯(Σ). This cannot be the case as it would contradict Property 3.1.

Notice that as required by traditional DL reasoning, DeLP does not adopt the closed-world assumption. That is, not being able to prove Q in DeLP does not imply that ∼Q will be assumed. On the contrary, such an answer will be the result of a dialectical analysis that will take into account all of the reasons for Q and ∼Q. Notice also that according to Volz (2004), the transformation from DL to logic programming is sound but not complete.

Definition 7.2 (soundness Huang et al., 2005)

An inconsistency reasoner |≈is sound if the formulas that follow from an inconsistent theory Σ follow from a consistent subtheory of Σ using classical reasoning.

Property 7.2

|≈is a sound inconsistency reasoner.

Proof

Let Σ = (T _S , T _D , A) be a δ-ontology. If Σ|≈φ then there exists a warranted argument ⟨𝒜, φ⟩ w.r.t. 𝒯(Σ) = (Π _S  ∪ Π _A , Δ), where Π _S  = 𝒯_Π(T _S ), Π _A  = 𝒯_Π(A), and Δ = 𝒯_Δ(T _D ). The set Π _S  ∪ Π _A  ∪ 𝒜 (see Def. 3.2) is consistent and as 𝒯 is a transformation that preserves semantics Grosof et al. (2003), there must exist a subset Σ′ ⊆ Σ such that 𝒯(Σ′) = Π _S  ∪ Π _A  ∪ 𝒜.

Definition 7.3 (consistency (Huang et al., 2005))

An inconsistency reasoner |≈is consistent iff Σ|≈φ ⇒ Σ∤ ≈¬ φ.

Property 7.3

|≈is a consistent inconsistency reasoner.

Proof

Corollary of Prop. 7.1.

Definition 7.4 (meaningfulness (Huang et al., 2005))

An answer given by an inconsistency reasoner is meaningful iff it is consistent and sound. An inconsistency reasoner is said to be meaningful iff all of its answers are meaningful.

Property 7.4

|≈is a meaningful inconsistency reasoner.

Proof

Trivial from Props. 7.2 and 7.3.

Implementation Issues

We base our translation function from DL to DeLP on the work reported by Grosof et al. (2003). In this respect, Volz (2004) shows that the fragment of DL expressible in logic programming (referred to as DLP) is sufficient to express most available web ontologies. Volz has analyzed the largest currently available collection of web ontologies and checked which fragment of those ontologies can be expressed in DLP; he claims that DLP languages suffice to express 77–87% of the analyzed ontologies and that they can express 93–99% of the individual axioms in the analyzed ontologies.

As performing defeasible argumentation is a computationally complex task, an abstract machine called justification abstract machine (JAM) has been specially developed for an efficient implementation of DeLP (García and Simari, 2004). The JAM provides an argument-based extension of the traditional Warren's abstract machine (WAM) for PROLOG. A full-fledged implementation of DeLP is available online, ⁴ including facilities for visualizing arguments and dialectical trees.

When we map DL equality axioms into DeLP rules, a DL axiom of the form “C ≡ D” generates two rules of the form “C(X) −≺ D(X)” and “D(X) −≺ C(X).” This situation can clearly produce loops during argument construction when solving queries in actual DeLP programs. Nevertheless, the examples considered in this work model an important part of ontologies where this situation does not happen, notice this is an intrinsic problem of DeLP implementations based on a PROLOG meta interpreter. A possible solution involves modifying the DeLP interpreter such that it keeps track of the search space of rule instantiations into ground rules. To avoid such looping situations, every time a new rule is about to be instantiated, the modified DeLP interpreter needs to check if the rule instance was already computed.

COMPUTING THE PARTITION OF TBOXES IN SBOXES AND DBOXES

One of the advantages of ontology representation languages based on DL is that existing reasoners can be used to compute implicit subsumption relations between classes. As a byproduct, this process is useful to identify unsatisfiable (inconsistent) classes. However, standard DL reasoners based on the tableaux algorithm (such as Racer (Haarslev and Möller, 2001), FaCT (Horrocks, 1998), Pellet (Parsia and Sirin, 2004)), only provide a list of unsatisfiable classes. The process of “debugging” the ontology (i.e., to determine why a reasoner has inferred that a class is unsatisfiable is left to the user). When the knowledge engineer is faced with several unsatisfiable classes on moderately large ontology, this process can become rather difficult (Wang et al., 2005). As it was mentioned in the first section, a notable exception is a recent work of Horridge et al. (2008) that is capable of providing justifications (explanations) of how an entailment holds.

In the approach proposed in this work, problematic axioms in the terminology of an ontology are separated in a distinguished set called Dbox while nonproblematic axioms are conserved in a set called Sbox. In the previous sections, such sets have been considered as given—that is, given a certain terminology T, the knowledge engineer decides somehow how to partition it in order to populate the Sbox T _S and the Dbox T _D . In this section, we discuss how to perform such partition automatically.

Two Naïve Approaches

We now present two simple approaches to the problem of partitioning a Tbox in an Sbox and a Dbox: the first consists of considering all the axioms in the Tbox as defeasible (i.e., all the Tbox axioms are regarded as Dbox axioms); the second consists of grouping all the logic programming rules obtained from the Tbox that have heads with complementary literals.

Definition 8.1 (associate δ-ontology)

Let Σ = (T, A) be a DL ontology, we define Σ's associate δ-ontology, noted Asoc(Σ), as the δ-ontology obtained from Σ by applying some partition strategy to T.

Definition 8.2 (associate DeLP program)

Given a DL ontology Σ = (T, A), we define Σ's associate DeLP program, noted Prog(Σ), as the DeLP program obtained when translating Σ to DeLP.

Strategy 8.1

Given a DL ontology Σ = (T, A), Σ's associate δ-ontology is Asoc(Σ) = (∅, T, A); and Σ's associate DeLP program is Prog(Σ) = (𝒯_Π(A), 𝒯_Δ(T)).

Example 8.1

Consider the DL ontology Σ_8.1 = (T, A), where: T = {(C⊑D), (E⊑ ¬ D)} and A = {(a: C), (a: E)}. In this case, Σ's associate δ-ontology is Asoc(Σ_8.1) = (∅, T, A) and Σ's associate DeLP program is Prog(Σ_8.1) = ({(d(X) −≺ c(X)), (∼d(X) −≺ e(X))}, {c(a), e(a)}).

Property 8.5

Given a DL ontology Σ = (T, A), if the Abox A is coherent, then the set of facts 𝒯_Π(A) is consistent.

Strategy 8.2

Let Convert be the function that converts a set of strict rules into a set of defeasible rules. ⁵ Given a DL ontology Σ = (T, A), let 𝒫 an extended logic program where its set of facts is defined as 𝒯_Π(A) and its set of strict rules as . Let Part: ℒ _ELP  → (ℒ _{DeLP Π} , ℒ _{DeLP Δ} ) be a function that partitions such a set of rules into a subset of strict rules and another subset of defeasible rules. Formally, Part(R) = (R _Π, R _Δ), where

Example 8.2

Consider the Tbox T _8.2 with

From this Tbox, the following set R of rules is generated:

By the application of Strategy 8.2, we obtain the following sets R _Π of strict rules and R _Δ of defeasible rules, where

and

Approach Based on Converting Problematic DL Axioms into Dbox Axioms

We now consider another approach to the problem of partitioning a Tbox in an Sbox and a Dbox automatically. In the previous section, given an inconsistent DL ontology, we worked with the DeLP rules generated by the translation function from DL to DeLP, turning some strict rules into defeasible ones. We propose instead to work directly with DL axioms by separating them into strict and defeasible axioms in order to see how to obtain a δ-ontology to reason with the framework previously presented.

Lam et al. (2006) propose an algorithm that extends Meyer, Lee, Booth, and Pan's (2006) tableaux algorithm. The algorithm not only pinpoints the problematic axioms, but also traces which parts of the axioms are responsible for the unsatisfiability of a target concept C. We present next an example of Lam et al. (2006) that explains how this process can be performed.

Example 8.3 (Lam et al., 2006)

Assume that a DL ontology Σ contains the following axioms:

It can be shown that the concept A is unsatisfiable, by using standard DL TBox reasoning. Existing approaches either identify the minimally unsatisfiable sub-ontology Σ _min  = {r ₁, r ₂, r ₃} or calculate the maximally satisfiable sub-ontologies Σ _{max 1}  = {r ₂, r ₃, r ₄}, Σ _{max 2}  = {r ₁, r ₃, r ₄} and Σ _{max 3}  = {r ₁, r ₂, r ₄}. In short, one of the axioms r ₁, r ₂ or r ₃ should be removed from Σ. However, it can be shown that we do not need to remove any of the above ‘whole’ axioms. In fact, we can simply remove any one of the following parts of axioms: (i) A⊑C, (ii) A⊑D, (iii) C⊑E, or (iv) E⊑ ¬ D, and Σ becomes satisfiable.

Thus, using Lam et al.'s (2006) algorithm as a “black box,” we propose the following strategy to partition a DL Tbox into a δ-ontology Sbox and a Dbox.

Definition 8.3 (set of concepts associated to an axiom/terminology)

Let r ₁,…, r _n a set of DL inclusion axioms such that form a terminology T = {r ₁,…, r _n }. We define Concepts(r _i ) as the set of named concepts of axiom r _i . We extend the definition to the set of named concepts in a terminology T as:

Definition 8.4 (Lam et al.'s algorithm)

Let T be a DL terminology and C a named concept in T. We define the function Lam _C (T) as Lam's algorithm that takes as input T and C, and returns as output the set of named concepts in T relevant to the unsatisfiability of C.

Strategy 8.3

Let Σ = (T, A) be a DL ontology and C a concept name such that C ∈ Concepts(Σ). The separation function Sep of a DL Tbox in a δ-ontology Sbox and Dbox, is defined as Sep(T) = (T _S , T _D ) where:

and

Example 8.4

Consider the following DL terminology T _8.1 (taken from Lam et al. (2006)):

Following Lam et al.'s (2006) notation, the concepts labeled with a star are relevant to the unsatisfiability of the concept “Penguin”; therefore,

Thus, instead of just eliminating all the axioms containing at least a concept labeled with an star (i.e., r ₁ and r ₃), which would cause the loss of some inferences, we propose converting them into Dbox axioms. Hence, the T _8.4 is partitioned as an Sbox T _S  = {r ₂} and a Dbox T _D  = {r ₁, r ₃}.

RELATED WORK

Grosof et al. (2003) show how to interoperate, semantically and inferentially, between the leading semantic web approaches to rules (RuleML Logic Programs) and ontologies (OWL DL) by analyzing their expressive intersection. They define a new intermediate knowledge representation called Description Logic Programs (DLPs), and the closely related Description Horn Logic (DHL) which is an expressive fragment of FOL. They show how to perform the translation of premises and inferences from the DLP fragment of DL to logic programming. Part of our approach is based on Grosof's work as the algorithm for translating DL ontologies into DeLP is based on it. However, as Grosof et al. (2003) use standard Prolog rules, they are not able to deal with inconsistent DL knowledge bases as our proposal does.

Heymans and Vermeir (2002) extend the DL 𝒮ℋ𝒪𝒬(D) with a preference order on the axioms. With this strict partial order, certain axioms can be overruled if defeated with more preferred ones. They also impose a preferred model semantics, introducing nonmonotonicity into 𝒮ℋ𝒪𝒬(D). Similarly to Heymans and Vermeir (2002), we allow to perform inferences from inconsistent ontologies by considering subsets (arguments) of the original ontology. Heymans and Vermeir (2002) also impose a hard-coded comparison criterion on DL axioms. In our work, the system, and not the programmer, decides which DL axioms are to be preferred as we use specificity as argument comparison criterion. We think that our approach can be considered more declarative in this respect. In particular, the comparison criterion in DeLP is modular, so that rule comparison could also be adopted (García and Simari, 2004).

Eiter, Lukasiewicz, Schindlauer, and Tompits (2004) propose a combination of logic programming under the answer set semantics with the DLs 𝒮ℋℐℱ(D) and 𝒮ℋ𝒪ℐ𝒩(D). This combination allows for building rules on top of ontologies. In contrast to our approach, they keep separated rules and ontologies and handle exceptions by codifying them explicitly in programs under answer set semantics.

Huang et al. (2005) use paraconsistent logics to reason with inconsistent ontologies. They use a selection function to determine which consistent subsets of an inconsistent ontology should be considered in the reasoning process. In our approach given an inconsistent ontology Σ, we consider the set of warranted arguments from 𝒯(Σ) as the valid consequences.

Williams and Hunter (2007) use argumentation to reason with possibly inconsistent rules on top of DL ontologies. In contrast, we translate possible inconsistent DL ontologies to DeLP to reason with them within DeLP. Laera et al. (2006) propose an approach for supporting the creation and exchange of different arguments, which support or reject possible correspondences between ontologies in the context of a multi-agent system. In our work, we assume correspondences between ontologies as given.

Antoniou and Bikakis (2007) propose a rule-based approach to defeasible reasoning based on a translation to logic programming with declarative semantics that can reason with rules, Resource Description Framework Schema (RDF(S)) and parts of OWL ontologies. RDF data of the form rdf(Subject, Predicate, Object) is translated as Prolog facts of the form Predicate(Subject, Object). They also define Prolog rules for processing RDF Schema information (e.g., C(X): -rdf: type(X, C)) for modeling the type construct). All of the rules are created at compile time before actual querying takes place. To the best of our knowledge, Antoniou and Bikakis's (2007) approach distinguishes between strict and defeasible and possess flexibility for defining different priority relations between arguments. As our approach is based on DeLP, it also distinguishes between strict and defeasible rules, and it also allows to replace the comparison criterion between arguments in a modular way. Antoniou and Bikakis translate the semantics of their argumentation system into Prolog, the semantics of OWL sentences into Prolog, the semantics of RuleML sentences into Prolog and then they perform query processing. We translate OWL into DL and the into DeLP, thus keeping the knowledge representation (in DeLP) separated from the query processing (performed into the JAM).

Horridge et al. (2008) present a justification-based approach to reasoning with ontologies. In that context, a justification for an entailment in an OWL ontology is a minimal subset of the ontology that is sufficient for that entailment to hold. Besides they are able to find laconic justifications that provide minimal axioms supporting an entailment, which can also be used to pinpoint the cause of inconsistencies. The notion of justification for an entailment in Horridge et al. (2008) is similar to the notion of argument for a literal in our work as an argument is made up of a minimal subset of the defeasible information in a DeLP program along with the strict information that allows to derive a defeasible conclusion (see Def. 3.2), thus providing a sort of justification for an entailment to hold. However, in the case of inconsistencies, DeLP is not only able to consider all the arguments for a literal, but also the defeat relation holding among those arguments in order to determine what the valid consequences of a δ-ontology are (characterized as the warranted arguments). Similarly, to axiom minimization in laconic justifications, the DeLP rules interpreting a δ-ontology can be considered as minimal versions of DL axioms (see Definitions 4.2 and 4.3) as they are horn-rules where disjunctions in the body and conjunctions in the head trigger the proliferation of rules. For example, in Horridge et al. (2008), the inclusion axiom A ⊓ B⊑C ⊓ D is expressed as two (smaller) axioms A ⊓ B⊑C and A ⊓ B⊑D; DeLP represents the former axiom as two rules c(X) −≺a(X), b(X) and d(X) −≺a(X), b(X), thus providing a de facto minimization.

Horridge et al. (2008, Sect. 3) consider two cases for motivating fine-grained justifications: internal and external masking. When internal masking occurs, Horridge et al. (2008) present the ontology Σ = {B⊑ ¬ C ⊓ D, B⊑ ¬ C}, where the concept B is unsatisfiable for two distinct reasons. We show next how our approach can detect the pairs of conflicting arguments depicting that situation. In our framework, Σ along with an Abox assertion a: B is interpreted as the DeLP program {(∼c(X) −≺ b(X)), (d(X) −≺ b(X)), (c(X) −≺ b(X)), (∼d(X) −≺ b(X)), b(a)} from where the following arguments can be found:⟨{c(a) −≺b(a)}, c(a)⟩, ⟨{∼c(a) −≺b(a)}, ∼ c(a)⟩, ⟨{d(a) −≺b(a)}, d(a)⟩, and ⟨{∼d(a) −≺b(a)}, ∼ d(a)⟩, indicating the presence of inconsistency and showing that and along with and . In spite of this, our framework will not be able to determine the justified membership of a to neither C nor D as the DeLP answers for the queries c(a) is d(a) undecided. Likewise, in the case of external masking, Horridge et al. (2008) present the ontology Σ′ = {B⊑D ⊓ ¬ D ⊓ C, B⊑ ¬ C}, where the concept B is unsatisfiable but there is no justification for that fact. Our framework interprets Σ′ as the DeLP program {(d(X) −≺ b(X)), (∼d(X) −≺ b(X)), (c(X) −≺ b(X)), (∼c(X) −≺ b(X)), b(a)} from where, as in the former case, there are arguments for the literals c(a), ∼c(a), d(a) and ∼d(a) indicating the source of inconsistency, yet the answer for the justified membership of individual a to the concepts C or D is undecided.

CONCLUSIONS

We have presented a framework for reasoning with inconsistent DL ontologies. Our proposal involves expressing a DL ontology in terms of a DeLP program by means of a translation function 𝒯. This resulted in the characterization of δ-ontologies, encoded using strict and defeasible axioms. We also provided a semantic interpretation of δ-ontologies as DeLP programs, formalizing two major inference tasks associated with a traditional DL setting, namely, instance checking and retrieval. Given a query φ and an inconsistent ontology Σ, these inference tasks rely on a dialectical analysis to be performed on the DeLP program 𝒯(Σ), where all arguments in favor and against φ's acceptance are taken into account. In this setting, the notion of class membership was suitably extended to distinguish among potential, justified, and strict membership of an individual to a class.

We have also presented an application to ontology integration based on the global-as-view approach to ontology integration where queries respect a global ontology are posed while data is extracted from local ontologies that could be inconsistent. Several issues need to be solved and part of our efforts are focused on that matter. For instance, as DeLP does not support disjunctions in the head of rules, our approach is not able to deal with DL axioms that require the construction of such rules. A possible solution to this problem could be taken in that direction using some suitable extension of disjunctive logic programming (Terracina, Francesco, Panetta, and Leone 2008; Ricca and Leone 2007). Part of our current research work is oriented in this direction.

This research was funded by TIN2006-15662-C02-01 (MEC, Spain), PGI 24/ZN10 (SGCyT, UNS, Argentina), by CONICET (Project PIP 112-200801-02798), and by COST Action IC0801 on Agreement Technologies (ESF – European Union). The present article unifies and further develops the content of Gómez et al. (2006)Gómez et al. (2008a).

Notes

http://www.w3c.org/

This example, as well as Example 2.3, are based on García and Simari (2004).

This example appears in García and Simari (2004) in a different context.

See http://lidia.cs.uns.edu.ar/DeLP

For example, Convert({a(X) ← b(X)}) = {a(X) −≺b(X)}.