A CONSTRAINT PROGRAMMING HEURISTIC FOR A HETEROGENEOUS VEHICLE ROUTING PROBLEM WITH SPLIT DELIVERIES

Abstract

This article considers fresh goods distribution of a retail chain store in Turkey. The problem is formulated as a vehicle routing problem with a heterogeneous fleet for which no exact algorithm has ever been designed to solve it. A fast and effective algorithm based on constraint programming is proposed for the solution. The procedure is tested on some of the benchmark problems in literature. The real-life case is first solved assuming that delivery of a customer cannot be split between vehicles. Then it is resolved considering split deliveries. Solutions of both strategies are compared with the current performance of the firm to determine a distribution strategy. Results indicate considerable improvement in the performance of the firm.

INTRODUCTION

Vehicle routing problems (VRPs) have received a lot of attention in the operations research literature for its commercial value. VRP consists of designing m vehicle routes to minimize total cost, each starting and ending at the depot such that each customer is visited exactly once. As the number of demand nodes (customers) and vehicles increase, solution time increases non-polynomially. Thus many researchers have dedicated their studies to develop efficient algorithms for dealing with VRP and its extensions.

In the classical version of VRP, which is called capacitated VRP, all vehicles are assumed to be identical with a uniform capacity Q. However, in real-life problems there exists a fixed fleet of vehicles mostly made up of different types with different capacities. Also, these vehicles may have different fixed and variable traveling costs. When this is the case, the problem is formulated as a heterogeneous VRP (HVRP) for which, due to its high computational complexity, no exact algorithm has ever been designed to solve it.

In this article the fresh goods distribution of a retail chain store in Turkey is handled. The problem is to perform the weekly distribution of fresh goods to the chain stores spread in the west and south regions of Turkey. It is formulated as an HVRP. A fast and effective algorithm based on constraint programming (CP) was designed to solve the problem.

The proposed algorithm begins with the decomposition of HVRP into smaller scale ones and assigning vehicles to each subproblem by integer programming (IP). Then at second phase, each subproblem is solved using a CP model. The problem is not only to design vehicle routes but to determine a distribution strategy at the same time. Thus, in the second phase of the algorithm, the subproblems are first handled assuming that delivery of a customer cannot be split between vehicles. Then they are resolved considering split deliveries. Split delivery VRP (SDVRP) is a relaxation of the classical VRP. In capacitated VRP a customer can only be visited by one vehicle (as long as the demand does not exceed the capacity of the vehicle). On the other hand, in SDVRP the deliveries of a customer can be split between two or more vehicles. However, including this assumption does not make the problem easier to be solved. It is still np-hard. There are very few studies concerning SDVRP in literature, but no exact algorithm exists for SDVRP.

The proposed algorithm is tested on the well-known benchmark instances of Golden et al. (1984). These instances are both solved under nonsplit and split delivery assumptions. In addition, because the proposed algorithm is a cluster first route second type, it is tested on the clustered benchmark problems of Solomon (Cordeau et al., 2002).

Computational results indicate that CP may be a useful tool in routing decisions. Also, the performance of the proposed algorithm is highly competitive, especially for naturally clustered distribution problems. After testing the performance of the proposed algorithm, distribution of fresh goods of a retail chain store in Turkey is handled under both nonsplit and split delivery assumptions. Results revealed that both distribution strategies are dominant over the current operational performance of the firm. In addition, distribution with split deliveries provided better solutions than nonsplit delivery distribution.

The rest of the article is organized as follows. First, a brief literature review on HVRP and SDVRP is given. Next, the proposed algorithm is defined in detail. Then, performance tests of the proposed algorithm are given, and the algorithm is then applied to the distribution problem of the retail chain store. Finally, conclusions are given.

LITERATURE REVIEW

HVRP is studied in two different versions in literature. Some researchers make an assumption that there is an unlimited number of vehicles of each type. They try to find the optimal set of vehicles to be scheduled in the problem. This is called the fleet size and mix VRP (FSMVRP). Other researchers study the case where there is a fixed vehicle fleet. They try to schedule this fleet of vehicles to the customers in an optimal way. This problem is called heterogeneous fixed fleet VRP (HFVRP). Although HFVRP is more realistic than FSMVRP, it has attracted less attention in literature. Some of the earlier studies considering FSMVRP are Golden et al. (1984), Ulusoy (1985), and Desrochers Verhoog (1991). More recently, researchers have applied more sophisticated approaches to FSMVRP. For instance, Salhi and Sari (1997) proposed a multilevel composite heuristic that simultaneously allocates customers to depots and determines the best fleet composition for the delivery routes. Also, Thangiah and Salhi (2001) handled the multidepot vehicle routing problem and developed a clustering heuristic based on genetic algorithms. Ochi et al. (1998) used parallel genetic algorithms together with scatter search to solve the problem. A tabu search heuristic is presented for FSMVRP by Gendreau et al. (1999). Liu and Shen (1999) presented a route construction method for FSMHVRP based on several different insertion heuristics. Lima et al. (2004) proposed a genetic algorithms methodology. Taillard (1999) presented a heuristic column generation method. Choi and Tcha (2007) also used column generation. They built an IP model and solved the linear relaxation by column generation technique.

As stated before, the other version of HVRP is where there is a heterogeneous fixed fleet of vehicles. Fewer studies exist in literature for HFVRP compared with FSMVRP. Tarantilis and Kiranoudis (2001) proposed an adaptive threshold accepting algorithm for HFVRP. In addition, Burchett and Campion (2002) applied tabu search to HFVRP in grocery supply industry. Faulin (2003) also handled the logistics problem of a company in Spain and developed a MIXALG procedure for the case. In addition to these studies, Ferrari et al. (2003) studied the car pooling problem (which tries to make the best use of available vehicles) and developed some heuristic algorithms based on savings functions. In another study in this area, Moghaddam et al. (2006) proposed a linear IP model and solved the model using SA hybridized with nearest neighborhood heuristic. Also, Li et al. (2007) developed a record-to-record travel algorithm for the heterogeneous fleet.

To the best of our knowledge, split deliveries are not considered in any of the HVRP studies listed above. However, some studies in literature did handle split deliveries. These studies consider VRP where all vehicles are identical and allow split delivery assumption. This problem was first introduced by Dror and Trudeau in 1989 (Archetti et al., 2006) who showed the savings that can be achieved by allowing split deliveries. Dror et al. (1994) formulated the problem as an integer linear program. Then, branch and bound algorithm is applied with the relaxation of constraints. Frizzell and Giffin (1995) developed three heuristics for SDVRP and tested these on some benchmark problems. Belenguer et al. (2000) developed an efficient lower bound for SDVRP where the quantities delivered to customers are integer numbers.

SDVRP is formulated as a dynamic program with infinite numbers of states and solution spaces by Lee et al. (2002). Ho and Haugland (2004) considered SDVRP with time windows. They presented a tabu search algorithm to solve the problem and analyzed the performance of the approach on problems with 100 distribution points. More recently, Archetti et al. (2006) proposed a tabu search algorithm for SDVRP. Also, Archetti et al. (2008) studied and identified the distribution environments in which allowing split deliveries are more beneficial. Moghaddam et al. (2007) also studied split deliveries and developed a simulated annealing approach.

In today's world, timeliness is very important to have a competitive edge in distribution. That means fast and effective decision making is as important as efficient distribution. Therefore some researchers studied real-time vehicle routing (Du et al., 2007; Chen et al., 2006).

Similarly, the purpose of this study is to find an efficient solution to the distribution problem of the retail chain store in an effective time. CP-based algorithms have been successfully applied to capacitated VRP (Shaw, 1998; Pisinger and Ropke, 2006); however, to the best of our knowledge, it has not yet been applied to HVRPs. None of the SDVRP studies considers a heterogeneous fleet and none of the HVRP studies allows split deliveries. Therefore this study is the first to

	Consider HVRP with split deliveries
	Apply CP for both nonsplit and split delivery distribution strategies
	Compare nonsplit delivery and split delivery assumptions on the same basis and on the same test problems
	Provide some benchmark values for HVRP with split deliveries.

PROPOSED ALGORITHM

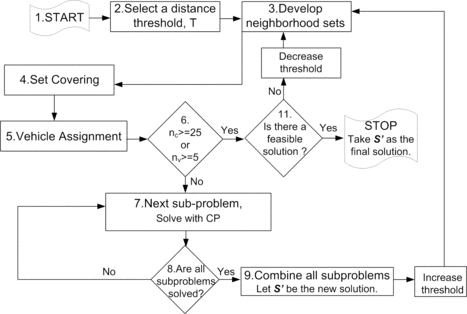
The algorithm proposed in this study is a cluster first route second type of algorithm. These types of algorithms are based on the idea of splitting a large size problem into subproblems and solving them faster. These algorithms have found wide application in the literature (Laporte and Semet, 2002). The success of these algorithms mainly depends on how well the clusters are formed. Therefore an effective procedure to split the problem into clusters followed by solving the clusters to optimality is expected to work well for HVRP.

In the clustering phase of the proposed approach, IP is used to solve a set covering problem. Then, from the sets selected, clusters are formed and vehicles are assigned through another IP model. In the finalization of the proposed approach, subproblems are solved through CP. The flow of algorithm can be seen in Figure 1.

FIGURE 1 Flow diagram of the proposed algorithm.

1. Start

2. Select a threshold T. Let there be n _c customers to be served.

3. Develop the neighborhood sets of each customer within distance T to the customer. This makes up totally n _c sets.

4. Set covering: In this phase among the n _c sets developed in step 3, a number of them are selected to cover all customers in the most centralized way. An IP model, given in Formulation 1, is used in this step. The notation used is given in Table 1.

   TABLE 1 Notation Used in Model SC

   The objective function Eq. (1a) does not only select arbitrarily the minimum number of sets but, rather, it minimizes the distances between the central point and the neighborhood points. Eq. (1b) states that all demand nodes should be covered at least once, and Eq. (1c) are the binary constraints.

5. Vehicle assignment: The sets selected in step 4 may be intersecting. These should be turned into nonintersecting sets, and the necessary vehicles should be assigned to each set to develop subproblems. When assigning the vehicles their fixed costs should be taken into consideration. To do so, an IP model, given in Formulation 2 (notation used is given in Table 2), is built.

   TABLE 2 Notation Used in Model VA

   The objective of the model is to assign vehicles to each subproblem such that total fixed cost of vehicles is minimized (Eq. 2a). At the same time the model assigns each customer to only one of the sets (found in step 4) in which it appears (Eqs. 2b and 2c). In addition, Eqs. (2d) and (2e) ensure that the total capacity of vehicles assigned to a subproblem must be greater than or equal to the total demand of customers in that subproblem. Equation (2f) states that a vehicle can only be allocated to at most one subproblem. The output of the model determines the subproblems as well as the vehicles assigned to each one.

6. When the main problem is decomposed into subproblems, each one is handled on its own. However, every time the threshold is increased, the subproblems get larger in size. Hence, the solution time increases quadratically. After a certain level of T, the optimal solution cannot be found with the existing technology. Therefore the algorithm should be stopped at that level of T. After a number of various experiments, that level is determined to be n _c  ≥ 25 (number of nodes) or n _v  ≥ 5 (number of vehicles). In other words if n _c  ≥ 25 or n _v  ≥ 5 for any one of the subproblems, then go to step 11.

7. Each subproblem is solved by CP. The model is given in Formulation 3 and the necessary notation is given in Table 3.

   TABLE 3 Additional Notation Used in Model CPM

   The objective function (Eq. 3a) minimizes total distance traveled. Eqs. (3b) and (3c) ensure that each customer is visited exactly once (nonsplit deliveries). In addition, each vehicle should visit the depot once because the vehicles assigned to the problem are known in advance (from Vehicle Assignment model, given in Formulation 2). This is included in the model with Eqs. (3d) and (3e). Equation (3f) provides that a vehicle visiting a customer should leave that customer. Finally, it is stated by Eq. (3 g) that capacity of vehicles should not be exceeded.

   If a single vehicle is assigned to the subproblem, then it becomes a traveling salesman problem. In this case, Eq. (3 g) becomes unnecessary. However, if the subproblem requires more than one vehicle, then it is a VRP and all constraints are applicable. The model is written and solved in ILOG OPL Studio 3.7 (ILOG, 2003).

   In Formulation 3, one can easily notice that subtour elimination constraints are missing (A subtour is a route where a vehicle goes back and forth between a number of customers without visiting the depot node.) To decrease computation time, subtour elimination constraints are handled with an OPL Script (ILOG, 2003) algorithm. To understand the script algorithm, one should know that CP displays all in-between solutions until the optimum is achieved.

   OPL Script (ILOG, 2003) Subtour Elimination Algorithm:

   The algorithm written in OPL Script (ILOG, 2003) language handles the first possible solution of the CP model (model CPM). It controls whether the solution consists of a subtour. If it is a full solution (does not contain any subtours), then it is displayed. Then the algorithm goes on by analyzing the next solution of the model CPM and makes subtour controls. The procedure makes complete enumeration through the solutions of model CPM. That is, it looks for the full solutions (solutions which do not contain any subtours) on the track of the model CPM while it minimizes total distance travele.

8. If all subproblems are finished, then go to step 9; otherwise, go to step 7.

9. Combine the solutions of all subproblems to give the solution of the main problem.

10. Increase threshold by s units, T: = T + s. Go to step 3.

11. If there is there a feasible solution achieved (from the previous iteration), then the algorithm STOPS. However, if no solution is achieved yet, then the procedure goes on by lowering the threshold and to step 3.

TESTS ON SAMPLE INSTANCES

To the best of our knowledge, there are no lower bounds for HVRP in literature. The only way to test newly developed algorithms is to try them on benchmark instances given in literature and compare the solutions with other known techniques. In this study, 12 instances are solved, which are taken from Gendreau et al. (1999). They are also solved by Golden et al. (1984), Taillard (1999), Choi and Tcha (2007), and Li et al. (2007). Golden et al. (1984) and Li et al. (2007) only considered total traveling cost, leaving total fixed cost of vehicles out. On the other hand, Taillard (1999), Gendreau et al. (1999), and Choi and Tcha (2007) considered both traveling and fixed costs. Similar to these studies, both cost terms are considered in the proposed algorithm.

The benchmark instances used are 20-node, 50-node, and 75-node instances, respectively. Distance values are all found analytically from the coordinates of customer nodes. The details of problem data are given in Table 4. Numbering schemes of the problems are similar to Gendreau et al. (1999). All problems contain vehicle-dependent fixed costs. However, variable costs are set to be one in all problems. In other words, total solution cost is the sum of fixed costs and total distance traveled.

TABLE 4 Data Belonging to Test Instances

		A		B		C		D		E		F
Test instance	Number of nodes	Capv	Costv	Capv	Costv	Capv	Costv	Capv	Costv	Capv	Costv	Capv	Costv
3	20	20	20	30	35	40	50	70	120	120	225
4	20	60	1000	80	1500	150	3000
5	20	20	20	30	35	40	50	70	120	120	225
6	20	60	1000	80	1500	150	3000
13	50	20	20	30	35	40	50	70	120	120	225	200	400
14	50	120	100	160	1500	300	3500
15	50	50	100	100	250	160	450
16	50	40	100	80	200	140	400
17	75	50	25	120	80	200	150	350	320
18	75	20	10	50	35	100	100	150	180	250	400	400	800
19	100	100	500	200	1200	300	2100
20	100	60	100	140	300	200	500

The test instances listed in Table 4 are solved using the proposed approach. The solutions achieved are compared with the other solutions in literature (Table 5).

TABLE 5 Performance of the Proposed Algorithm in [151984Golden et al.] Test Problems

					Proposed algorithm
Problem no.	Number of nodes	Taillard 1999	Gendreau et al. 1999	Choi and Tcha 2007	Cost	Time	Deviation in cost (%)
3	20	961.03	961.03	961.03	983.1	52	2.24
4	20	6437.3	6437.33	6437.3	6437.33	32	0.00
5	20	1008.59	1007.05	1007.05	1052.15	70	4.29
6	20	6516.5	6516.47	6516.5	6516.47	131	0.00
13	50	2413.78	2408.41	2406.36	2440.78	113	1.41
14	50	9119.03	9119.03	9119.03	9138.25	374	0.21
15	50	2586.37	2586.37	2586.37	2620.54	200	1.30
16	50	2741.5	2741.5	2720.43	2746.3	43	0.94
17	75	1747.24	1749.5	1744.83	1783.33	340	2.16
18	75	2373.63	2381.43	2371.49	2394.16	442	0.95
19	100	8661.81	8675.16	8664.29	8734.35	453	0.83
20	100	4047.55	4086.76	4039.49	4139.8	261	2.42

It can be seen from Table 5 that the threshold algorithm is able to find the same solution costs in literature for some of the instances (Instance 4 and 6). For others the solution cost turned out to be within at reasonable deviations from the best known. On the other hand, when solution times are considered, it is not possible to compare solution times with other approaches. This is because solution times of different approaches are achieved on different computer systems. Also, the times of the studies are very different from each other. The solution times of the proposed approach are achieved on a Pentium 4 3.0 GHZ computer. Though we cannot compare with other approaches, it can be said that all solution times of the proposed approach are reasonable to wait and quite good. It should be noticed that the deviation in solution cost is independent from the number of nodes in the problem. In addition, as the number of nodes increases, the computation time of the threshold algorithm would stay same on the average. This is due to the clustering phase of the algorithm. The number of clusters increases, but the sizes of the clusters are approximately equivalent. Therefore the computation time does not increase noticeably. And, hence, we can assume that for larger scale problems, the threshold algorithm will provide good solutions within much competitive time. For real-life cases where there are several hundreds of demand points to be handled, threshold algorithm may be functional.

Clustered Test Problems

The findings in Golden et al. (1984) test instances are reasonable but not good enough for the performance of the proposed algorithms. To prove the usefulness of the proposed algorithm, another set of test instances are handled and solved.

Because the proposed approach is a cluster first route second type of algorithm, it is expected to work very efficiently for problems where there exist natural clusters. Hence, the clustered test instances of Solomon (Cordeau et al., 2002) are handled with the proposed approach. The solutions achieved can be seen in Table 6.

TABLE 6 Performance of the Proposed Algorithm on Solomon Test Problems

			Proposed algorithm
Problem no.	Number of nodes	Best known in literature	Cost	Deviation in cost (%)	Solution time (sec)
C101	100	828.9	828.9	0.00	< = 1
C102	100	828.9	828.9	0.00	4
C103	100	828.06	828.9	0.10	27
C104	100	824.8	828.9	0.49	89
C105	100	828.9	828.9	0.00	< = 1
C106	100	828.9	828.9	0.00	< = 1
C107	100	828.9	828.9	0.00	< = 1
C108	100	828.9	828.9	0.00	4
C109	100	828.9	828.9	0.00	9
C201	100	591.6	591.6	0.00	81
C202	100	591.6	591.6	0.00	484
C203	100	591.2	591.2	0.00	215
C204	100	590.6	591.6	0.17	1024
C205	100	588.9	591.6	0.46	78
C206	100	588.5	591.6	0.52	96
C207	100	588.3	591.6	0.56	85
C208	100	588.3	591.6	0.56	561

It can be seen from Table 6 that for many of the problems, best-known solutions in the literature are obtained in very promising solution times. Therefore it can be said that the proposed approach works very well for naturally clustered problems. This also shows that the CP approach used in the routing phase provides both effective and efficient solutions.

Employing Split Delivery Strategy

In addition to the previous test sets, we wanted to test the proposed algorithm on split delivery strategy. To the best of our knowledge, no studies exist considering benchmark problems for HVRP with split deliveries. Therefore in this study the benchmark problems of heterogeneous vehicle routing (Golden et al., 1984) are considered under split delivery assumptions and solved by the proposed algorithm.

Because the delivery of a customer can be split among two or more vehicles, another decision variable is necessary:

Model CPM is revised according to split delivery assumptions and given in Formulation 4. The objective function Eq. (4a) and Eqs. (4d), (4e), and (4f) are similar to model CPM. However, instead of Eqs. (3b) and (3c) (nonsplit deliveries), Eqs. (4b) and (4c) are included stating that every customer may be visited by one or more vehicles. (Split deliveries are allowed.). Equation (3 g) is completely removed and, instead, Eqs. (4 g) and (4 h) are added to the model. Equation (4 g) ensures that the capacities of vehicles are not exceeded, and Eq. (4 h) ensures demands of all customers are satisfied. Finally, Eqs. (4i) and (4j) build the relation between decision variables X and A.

The new model is used in the routing phase of the algorithm. The test instances from Golden et al. (1984) are solved under split delivery assumption. The solutions achieved can be seen in Table 7.

TABLE 7 Performance of the Proposed Algorithm on [151984Golden et al.] Test Problems Under Split Delivery Assumption

			Proposed algorithm
Problem no.	Number of nodes	Best known ∗ in literature	Cost	Deviation in cost (%)	Solution time (sec)
3	20	961.03	970.53	0.98	104
4	20	6437.3	6421.88	−0.24	45
5	20	1008.59	998.74	−0.83	84
6	20	6516.5	6514.09	−0.04	137
13	50	2413.78	2440.78	1.41	146
14	50	2406.36	9138.25	0.21	412
15	50	2586.37	2616.11	1.14	298
16	50	2720.43	2719.89	−0.02	302
17	75	1744.83	1783.33	2.16	317
18	75	2371.49	2394.16	0.95	486
19	100	8661.81	8722.49	0.67	506
20	100	4039.49	4130.48	2.20	396

As seen from Table 7, for Instances 4, 5, 6, and 16, allowing split deliveries decreased solution cost compared with the best known solutions in the literature (for HVRP). For others the proposed approach achieved solution costs within 2% to the best known. These test problems have not been considered under split delivery assumptions before. Therefore the proposed algorithm provides benchmark values (for problem numbers 4, 5, 6, and 16) for HVRP studies with split deliveries to be made in the future.

APPLICATION OF THE PROPOSED ALGORITHM TO A~REAL-LIFE CASE

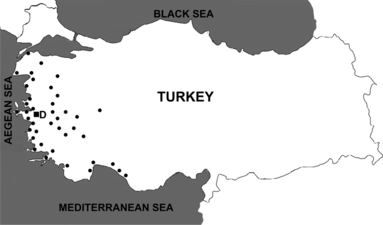
In this study the distribution of fresh goods from a central depot to retail stores is handled. The depot belongs to a retail chain store located in Izmir, Turkey. There are 41 demand points to which the depot should make delivery three times every week (Figure 2). The distances between demand points are in kilometers and measured from main roads. In other words, because physical road and land restrictions exist, some of the distance figures may not satisfy triangle inequality. The firm owns nine vehicles assigned for this distribution. The data belonging to vehicles are given in Table 8. As seen from Figure 2, the demand points are in natural clusters such as the east region, the north region, and so on according to the depot node (D represents the depot in Figure 2.). Therefore it is expected that the proposed algorithm would be beneficial for the case.

FIGURE 2 Demand points of the retail chain store.

TABLE 8 Data Belonging to Vehicles Available

Vehicle	Capacity	Fixed cost
1	11,484	1148.4
2	11,144	1114.4
3	14,314	1431.4
4	10,514	1051.4
5	9980	998
6	11,824	1182.4
7	10,514	1051.4
8	15,724	1572.4
9	12,000	1200

The first threshold level is taken to be 80 km (T = 80). When set covering model is solved, 12 sets are selected. This means that at least 12 vehicles are required. In this case the solution is unfeasible (because there are 9 vehicles). Therefore threshold is increased to 100 km, and after that it is increased by 20 km at each iteration. The algorithm is stopped when T = 240. In the result, four vehicles are assigned (vehicles 1, 2, 4, and 5) with a fixed cost of 4311 TL. Total traveling cost turned out to be 3792 TL, which make up a total cost of 8103 TL.

The distribution problem is resolved by model SDM. The results of nonsplit delivery and split delivery strategies together with the current performance of the retail chain store can be seen in Table 9.

TABLE 9 Comparison of Different Distribution Strategies and the Current Performance of the Firm

	No. of vehicles allocated	Fixed cost (TL)	Traveling cost (TL)	Total cost (TL)	Solution time (sec)	Improvement (%)
	5	5362	3908	9270	–	–
Nonsplit delivery strategy	4	4311	3792	8103	36	12.59
Split delivery strategy	4	4311	3787	8098	73	12.64

CONCLUSION

In this article a two-phase algorithm based on CP is developed for HVRP. The algorithm is a cluster first route second type where it splits the main problem into subproblems based on a distance threshold level and simultaneously assigns vehicles to them. Then each subproblem is solved by CP. The proposed algorithm is able to be applied both under nonsplit delivery and split delivery strategies. It is tested on some of the benchmark problems in the literature. According to the results of test problems, the algorithm is found to be highly competitive in terms of both solution cost and time, especially for naturally clustered distribution problems. This shows that CP may be a useful tool for HVRPs. Also, some new benchmark values are provided for HVRP under split delivery strategy.

The algorithm is then used to solve the distribution problem of a retail chain store in Turkey and to offer a distribution strategy to the decision makers. The results showed that both nonsplit delivery and split delivery strategies decrease the current distribution costs of the firm in a considerable way. That is, the total distribution cost has decreased by about 12%. The routes of both strategies are given in Figure 3.

FIGURE 3 Routes of (a) nonsplit delivery distribution strategy and (b) split delivery distribution strategy.

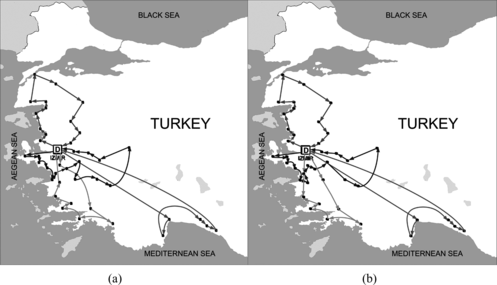
When the two strategies are compared within themselves, split delivery strategy provides a better solution than the nonsplit delivery strategy in terms of solution cost. Because the solution times of both strategies are reasonable, split delivery strategy is advised to the firm.

Notes

These test problems also impose time window constraints (Cordeau et al. 2002).

Best known solutions for HVRP are taken from Table 5.