A HYBRID SIMULATED ANNEALING ALGORITHM FOR SOLVING MULTI-OBJECTIVE CONTAINER-LOADING PROBLEMS

Abstract

In this article, we explored a new approach to solution of multi-objective container-loading problems mostly encountered in transportation and wholesaling industries. Our goal is to load the items (boxes) that would provide the highest total weight to the container in the best possible way. These two objectives (weight maximization and volume utilization) are conflicting because the volume of a box is usually not proportional to its weight. A weighted goal programming model is formulated and presented. A simulated annealing (SA) algorithm accompanied by a heuristic filling procedure is then proposed to solve the model. The proposed algorithm has been first tested on a set of benchmark problems available in the literature and then used for real-world data provided by a distribution company. The computational results have validated significance and usefulness of the proposed approach.

The container-loading problem (CLP) is an active research area and has numerous applications in the real world, particularly in container transportation and distribution industries. Efficient cargo transportation is of high economic value in logistics, and near-optimal cargo loading leads to lower costs all over the distribution system (Huang and He, 2007). Design of efficient loading schemes based on a single objective or multi-objectives (e.g., volume utilization and weight maximization) for saving logistics costs is a key research problem. Development of practical solution approaches for solving multi-objective CLPs in the distribution industry is still needed and a valuable research direction.

A medium-sized distribution company in Gaziantep (a metropolitan area located at the southeast of Turkey) delivers the goods ordered by supermarkets that are located in the southeast part of the country. The logistics department of the company delivers the orders within 24 hours to the channel, organizes the delivery of goods from manufacturers and supplier companies to warehouses, and provides protection, preservation, and allocation. The firm mainly distributes Procter & Gamble's products as well as their own products like paper towels, toilet tissues, paper napkins, etc., which are manufactured at their own plant in Gaziantep, Turkey. The orders are stored in a database and a the decision maker decides which orders/products to load to their own vehicles or to rented carriers. The rented trucks are paid according to the total weight of the shipment regardless of the total volume (e.g., $10 per ton). Thus, the decision maker prefers to load and ship a shipment with high total weight to its own vehicles rather than a shipment with low total weight. On the other hand, shipping the shipment in an on-time manner is an important issue for the company. If the decision maker can utilize the capacity of the owned vehicle in the best possible way, he or she can guarantee the on-time delivery of all of the products in its own vehicle. Another issue that the decision maker should take into account is the relation between the volume of the items and the weight of the items. In particular, the weight of the household, personal care, sanitary paper products, and shaving products per unit volume drastically differ from one product to the other; that is, x cm³ of product A may yield a smaller weight than y cm³ of product B (x ≫ y). Having considered this situation, each day the decision maker should load the items (boxes) that would provide the highest total weight to the vehicles in the best possible way to decrease transportation cost and in turn increase the profitability of the company.

Inspired from the above described situation, two objective functions for the CLP are defined in this study. The first objective is to obtain a total weight as close to the maximum available weight that can be carried by the owned vehicle as possible and the second objective is to obtain a packing pattern in which the utilization of the container is maximized.

The problem that we studied in this article is a single-container-loading problem that was categorized by Wäscher, Haussner, and Schumann (2007) as single large object placement problems. The aim of the CLP is to arrange a set of rectangular packages (boxes) into a rectangular container in such a way that the volume of the packed boxes is maximized or, in other words, unemployed spaces in the container are minimized.

Many approaches have been developed to solve the CLPs along with many practical constraints and different objective functions. There are several reasons for this popularity, as reported in Ertek and Kılıç (2006). First of all, the CLP is a Non-deterministic Polynomial-time hard (NP-hard) problem (Pisinger, 2002) and it has been recognized that it has a wide range of industrial applications. It is also possible to define new variants of the CLPs by using different types of objective functions and the constraints, as well. Therefore, there are many approaches (both heuristic and metaheuristic based) proposed to solve the CLPs that are a subproblem of cutting and packing problems. Because the CLPs are NP-hard and do not have exact solutions in polynomial time (Scheithauer, 1992), heuristics are an often-sought approach (Wang and Li, 2007) to obtain near-optimal solutions in reasonable time (Wang and Li, 2007). The use of artificial intelligence is also frequent for the same reason. Most of the published work on the subject utilizes different types of data structures such as graphs or trees (Morabito and Arenales, 1994; Eley, 2002; Lim, Rodrigues, and Yang, 2005), dynamic programming (Scheithauer, 1992), heuristics algorithms (George and Robinson, 1980; Bischoff, Janetz, and Ratcliff, 1995; Gehring, Menschner, and Meyer, 1990; Haessler and Talbot, 1990; Ngoi, Tay, and Chua, 1994; Pisinger, 2002; Bischoff, 2003; Moura and Oliveira, 2005), and metaheuristic algorithms such as genetic algorithms (GAs; Gehring and Bortfeldt, 1997; Bortfeldt and Gehring, 2001; Yeung and Tang, 2005), simulated annealing (SA; Brusco, Thompson, and Jacobs, 1997; Faina, 2000) and tabu search (TS; Bortfeldt and Gehring, 1998) to solve different variants of the problem. Different variants of above-mentioned heuristics and metaheuristics as well as hybrid approaches enable the researchers to blend and match different concepts and paradigms depending on the application or the problem to be solved. For example, Pimpawat and Chaiyaratana (2004) have used a cooperative coevolutionary genetic algorithm (CCGA) in conjunction with a heuristic rule for solving a 3D container-loading problems. Leung, Wong, and Mok (2008) have focused on the design of optimal carton boxes (considered containers) for distributing various kinds of towel products to a large number of retail outlets. Their objective was to lower the overall future distribution costs by improving the space utilization of carton boxes while reducing the number of carton types. They used a multi-objective genetic algorithm (MOGA) in order to search the optimal design of carton boxes for a one-week sales forecast and a 53-week sales forecast. Finally, it is worth mentioning that a few parallel approaches including (i) parallel GA (Gehring and Bortfeldt, 2002), (ii) parallel TS (Bortfeldt, Gehring, and Mack, 2002), and (iii) parallel hybrid local-search metaheuristic (Mack, Bortfeldt, and Gehring, 2004) are also available in the literature.

Despite this considerable attention, studies on the CLPs with multiple objectives are very limited (Liu et al., 2006). This issue was also pointed out by Dyckhoff (1990), where he stated that for many cutting and packing problems more than one objective has to be considered. The main contribution of this article is to study CLPs with multiple objectives that can be encountered in a usual transportation process. In order to solve the mentioned problem, a weighted goal programming model is proposed. Due to the complexity of the model, an SA algorithm hybridized with a heuristic filling (placement) procedure is designed to solve the model.

The rest of the article is organized as follows. Following the presentation of the problem formulation in the next section, the heuristic filling procedure is outlined. The proposed goal programming model and SA algorithm are then described. The following section presents the computational work. A discussion section is provided in order to discuss some outstanding features of the proposed approaches. The article is finalized with a conclusion section.

PROBLEM FORMULATION

CLPs with multi-objectives can be defined as follows; Given a set of n items with width (w _i ), depth (d _i ), height (h _i ), weight (weight _i ), and a single container with known dimensions (W, D, H) where w _i  ≤ W, h _i  ≤ H, and d _i  ≤ D, as well as weight capacity of the container (t_weight _max), the problem is to pack items into the container without overlapping while maximizing the total weight of the packed items and the utilization rate of the container. The problem is solved under the following assumptions:

	Items are rectangular boxes defined with known dimensions (w i , d i , h i ) Each box can be arranged originally in the container in a maximum of six “rotation variants” if not prohibited.
	Each box can lie on the container floor or can be stacked on top of another.
	Stability of the box arrangements is not considered thus we assumed that spacing material can be used to avoid possible problems.

HEURISTIC FILLING PROCEDURE

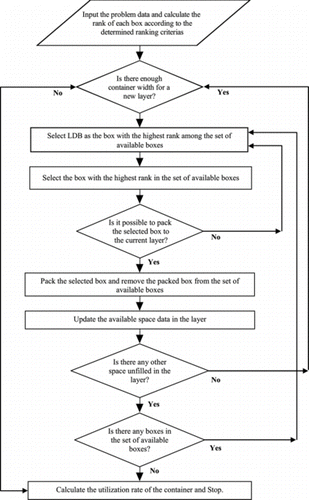
The proposed filling heuristic is designed by taking the neighborhood structure described for the container-loading problem into account. It is clear that it is impractical to run an SA algorithm without a neighborhood search. Although it is possible to adapt some filling heuristics from the literature to work with SA, we prefer to develop our own filling heuristic in this work. The proposed heuristic filling procedure is a kind of wall-building procedure that was proposed in George and Robinson (1980). The proposed procedure loads the container “layer-by-layer.” Before filling each layer, the dimensions of each layer are determined. This is done by choosing the width of the layer. Determination of the layer dimensions is discussed in the next section.

Layers are filled one at a time where each box is allocated to an empty space in the layer in a recursive manner. If it is not possible to fill the empty spaces in the current layer with the boxes in the set of available boxes, the current layer is closed and a new layer is started. The procedure is repeated until it is not possible to locate a new layer to the remaining container width or the set of available boxes is empty. As a result of the packing process, the container is filled with the isolated vertical layers where spanning of the boxes between layers is avoided.

Determination of Layer Dimensions

Before starting the filling process, it is important to determine the dimensions of a layer because the width of a layer must be carefully selected to obtain a good performance (Pisinger, 2002). This means that selecting the first box of the layer that determines the width of the started layer is a vital issue to obtain a good solution.

In George and Robinson's approach (George and Robinson, 1980), the first box is chosen according to the magnitude of the smallest dimension of a box; that is, the larger this dimension is, the higher ranked the box is (Pisinger, 2002). In case of a tie in the first ranking criteria, the boxes are ranked according to the quantity of the boxes in the box type. In case of a tie in this second ranking criterion, the box with the largest length dimension is given a higher rank. In Gehring, Menschner, and Meyer (1990) approach, the first box is chosen as the box with the highest volume. In this article, the width of each layer w_l _j is set equal to the width of the layer-determining box (LDB). In order to determine the LDB, first the boxes among the set of available boxes are sorted by width dimension in nonincreasing order. Thus, the box with the biggest width dimension is given a higher rank. In case of a tie among the boxes with the same width dimension, the box with the smallest depth dimension d _i is given a higher rank. In a case of a tie in both width and depth dimensions of candidate boxes, a third ranking criteria in which the box with the smallest height dimension h _i is given a higher rank. Finally, the box with the higher rank in the set of available boxes is chosen as the LDB. After the determination of the LDB, the layer having width w_l _j equal to the width w _i of the LDB, height h_l _j and depth d_l _j equal to those of the container is filled. As a result, the dimensions of the layer are determined as follows:

Filling the Layers

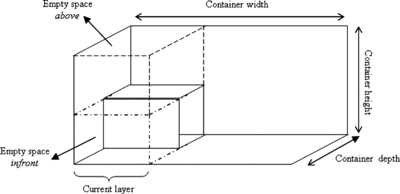
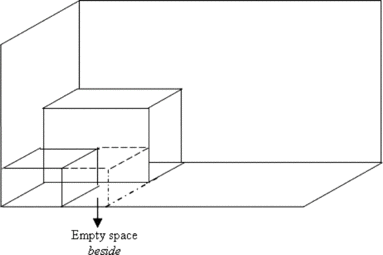
Following the determination of the layer dimensions, it is possible to fill (pack) the layers. When the first box (LDB) is allocated into the layer, three empty new spaces, namely “beside,” “in front,” and “above,” of the packed box are produced. In the given situation (see Figures 1 and 2), only two of these spaces, in front and above, occur as a result of the allocation of the first box into the layer. Thus, only these spaces are shown in Figure 1. However, when a box having the width that is smaller than the LDB is packed into the layer, an empty space besides the packed box occurs as shown in Figure 2. In the proposed filling procedure, the empty spaces are filled in the following order: first the empty space in front of the packed box is filled, then empty spaces above and beside the packed box are filled, respectively.

FIGURE 1 Empty space in front and above of the LDB.

FIGURE 2 Empty space beside a packed box in the layer.

Suppose that there is a packed box in the layer as shown in Figure 1 and it is desired to pack the next higher ranked box in the set of available boxes to the container. First, the space in front of the packed box is checked. If it is possible to allocate this box into this space, the box is packed to this space and the packed box is removed from the set of available boxes. Then the empty space above the packed box is checked. After processing these empty spaces, the empty space beside the packed box in the current layer is checked. If it is possible to allocate this box into this space, the box is packed to this space and the packed box is removed from the set of available boxes. Otherwise, the suitability of the filling the empty spaces in the layer with the next box with the higher rank in the set of available boxes is investigated. The process is repeated in a recursive manner for each box in the set of available boxes and for empty spaces available in current layer until it is not possible to fill empty spaces with a box in the set of available boxes or there is not any empty space available.

As mentioned before, the proposed filling procedure makes use of a wall-building approach in which it is essential to determine the dimensions of a layer because the width of a layer must be carefully selected to obtain a good performance (Pisinger, 2002). It should be noted that the width of the layers is set equal to the width of the boxes that have the highest priority in the set of available boxes in our procedure. Therefore, it is obvious that if the priority of the boxes in the set of available boxes can be altered, alternative widths for the layers can also be considered to reach a good container-loading performance. Because the priorities of the boxes (in the set of available boxes) are changed by enabling or disabling the rotation of the boxes in our algorithm, the alteration of the priorities in the set of available boxes is not considered. The main steps of the heuristic filling procedure are presented in Figure 3.

FIGURE 3 The proposed heuristic filling procedure.

GOAL PROGRAMMING MODEL

Goal programming (GP) was first introduced by Charnes and Cooper (1961) as a tool to resolve infeasible linear programming (LP) problems. It is one of the most commonly used mathematical programming tools to model multiple-objective optimization problems (Baykasogˇlu, 2005). There are two main methods for solving GP models: weighted GP and preemptive GP. In the weighted GP method, the goals are assigned weights and a single-objective function is formulated as the minimization of weighted deviations from the defined goals. In preemptive GP, the goals are grouped according to their importance and more important goals are achieved before less important goals. In this study, the multi-objective container-loading problem is transformed to a single objective problem using weighted GP method.

For the presented goal programming model the following notations are used:

i	=	1, 2,…n; index for the boxes
x i	=
v i	=	Volume of box i, where v i  = w i  × d i  × h i
weight i	=	Weight of box i
V c	=	Volume of the container c, where V c  = W × D × H
u c	=	Volume utilization rate of the container c
t_weight t	=	Total weight of the packed boxes

Goal 1: Obtaining a packing pattern having total weight as close to t_weight _max (weight capacity of the owned vehicle) as possible where is the underachievement and is the overachievement of the weight goal.

Goal 2: Maximizing the volume utilization rate u _c of the container c, where is the underachievement and is the overachievement of the volume utilization goal.

In order to reach these goals, a weighted GP model is formulated. The objective is to minimize the weighted sum of deviations from the defined goals.

Because the defined goals are of different magnitudes, the goals are normalized using the worst and the best possible values of the objectives. In order to solve the proposed weighted GP model, an SA algorithm is designed, which is described in the next section.

SIMULATED ANNEALING ALGORITHM

In order to solve the weighted GP model proposed in the previous section, an SA algorithm is proposed. SA is a method for obtaining good solutions to difficult optimization problems that has received much attention over the last few decades (Eglese, 1990). It was introduced by Kirkpatrick, Gelatt, and Vecchi (1983) as an analogy to the statistical mechanics of annealing in solids.

SA differs from iterative algorithms in that it has a mechanism that helps it to escape from local optimum and rather to reach global optimum. This is because SA not only accepts neighborhood solutions better than the current solution but also accepts neighborhood solutions worse than the current solution with a probability. This probability, which is known as acceptance probability, is related to the temperature, which decreases during the process. As the temperature decreases, the acceptance probability decreases, too. This means that as the temperature decreases, the probability of accepting worse neighborhood solutions decreases. During the annealing process, the temperature decreases gradually. At each temperature, a predetermined number of iterations to search the solution space are conducted. The search terminates when the stopping criteria are met (Dereli and Das, 2007).

Motivated by the work of Baykasogˇlu (2005), the proposed weighted GP model is solved with the SA algorithm, which is the adapted to solve the weighted goal programming problems. The fundamentals of the proposed algorithm are summarized as follows:

FIGURE 4 Neighborhood solution generation using the flip operator (only for base-rotated boxes).

FIGURE 5 Neighborhood solution generation using the flip operator (rotation in any orientation is possible).

	A solution is represented by a bit string representation. For example, bit string representation of a solution composed of seven different types of boxes, for which only the base rotation is permitted, is presented in Figure 4. It should be noted that the length of this string is determined by the number of different types of boxes in the problem. This structure is preferred to the structure in which each bit in the string represents a box in the problem. In a problem where there are 100 boxes of seven different box types, the second structure will yield a bit string of length 100, which will be a very inconvenient and time-consuming structure for the large-sized problems.
	In order to reach neighborhood solutions, an operator working in the same fashion as a mutation operator in genetic algorithms is defined. This operator is called flip and was inspired by the approach described in Kong, Tian, and Kao (2008), who designed a simple random “4-flip” method as the local search. This operator randomly selects four variables from the solution and flips their values from “1 to 0” or “0 to 1.” The defined operator flip is used for reaching the different rotation variants a particular box type through changing the value of the selected bit according to the type of the problem. For example, if a problem in which only the base rotation of the boxes is permitted, the flip operator either enables rotation of the boxes of the same type or disables the rotation of the boxes of the same type. When the flip operator is applied to a randomly selected bit (the fourth bit in this example as shown in Figure 4) of this string as shown in Figure 4, where “1” represents a base-rotated box (it means that width and depth dimensions can be replaced with each other) and “0” vice versa (not rotated), a new solution is found in which only the boxes having box type of 1, 5, and 7 are rotated. For problem types in which box types can be rotated in any box orientation, the flip operator represents the rotation of the box in a determined orientation. For example, if the before mentioned boxes can be rotated in any box rotation, then the flip operator works as shown in Figure 5. That is to say, the boxes having box type of 4 will be rotated in the before mentioned rotation-variant 5 rather than rotation-variant 6.
	Objective function of a solution is presented as the weighted sum of the deviations from the defined goals.
	If a neighborhood solution having the objective value of (0.11) is obtained as a result of the flip operator, this solution should be accepted when the previous solution has an objective value of (0.12) because the sum of the deviations is minimized in the reached neighborhood solution. However, a neighborhood solution having an objective value (0.13) should be accepted with probability.

The pseudo-code of the weighted GP based SA algorithm that is hybridized with the heuristic filling procedure is presented in Table 1.

TABLE 1 A Pseudo-code of the Proposed SA

Step 1. Generate an initial solution and calculate the sum of the weighted goal deviations to form the fitness value fitness0 using the heuristic filling algorithm:

Step 2. Parameter initialization:2.1. Set the annealing parameters: T in., T f , il max , and α.2.2. Read the number of box types N.

Step 3. Annealing schedule:3.1. Inner loop initialization; il = 0.3.2. At every temperature achieve equilibrium. Execute inner loop until the condition in 3.2.4 is met.3.2.1. il = il + 1;3.2.2. Generate a neighborhood solution and calculate the sum of the weighted goal deviations to form the fitness value fitness il using the heuristic filling algorithm;3.2.3. Accept or reject the solution as described by the weighted GP approach;3.2.4. IF (il ≥ il max ) THEN terminate inner loop and GOTO step 3.3 ELSE continue inner loop and GOTO step 3.2.1 3.3. T iter+1 = α*T iter ;3.4. IF (T iter+1 < T f ) THEN terminate inner loop and GOTO step 4 ELSE continue inner loop and GOTO step 3.1

Step 4. Terminate the best solution and stop.

COMPUTATIONAL WORK

Solution of CLPs with Single Objective Function

The proposed algorithm was tested on two sets of test cases from the literature known as Loh and Nee test cases (Loh and Nee, 1992) and Bischoff and Ratcliff (BR1 to BR7) test cases (Bischoff and Ratcliff, 1995). Both test cases were composed of problems defined with a single objective function. In each test problem, the aim was to allocate a set of boxes with varying dimensions into a container to maximize the volume utilization of the container. The proposed SA algorithm was implemented in C+ + language and the problems were run on a computer with 3.06 GHz. Intel Pentium IV. Each test problem was run with three different seed values and average values obtained from these three runs were used to compare the obtained results with other studies. The following choices were made for the solution of the Loh and Nee test cases with the SA algorithm.

	Initial value of the temperature T in was set to 200.
	To change the temperature a proportional temperature function was employed: where α is a constant and lies between 0.8 and 0.99. In this work, the value of α was 0.987.
	The number of iterations il max that should be performed at each temperature was equal to the number of box types N in each order.
	When the value of the final temperature T f fell below 0.05 the algorithm was terminated.

Loh and Nee test cases were also solved by some of the previous works using different heuristic and metaheuristic algorithms. The results obtained by the proposed algorithm for these test cases along with the previously reported results are presented in Tables 2 and 3. When comparing the performance of the proposed algorithms, it should be noted that figures computed by Loh and Nee (called packing density) are not directly comparable to the volume utilization figures in the other columns, because they are quoted only on the basis of the smallest rectangular enclosure of the loaded boxes, rather than the actual container dimensions (Bischoff and Ratcliff, 1995).

TABLE 2 Comparative Results with the Test Cases of Loh and Nee (1992)—Heuristic Approaches

	Packing density (%)	Volume utilization (%)
Problem	(Loh and Nee 1992)	(Ngoi, Tay, and Chua 1994)	(Bischoff, Janetz, and Ratcliff 1995)	(Bischoff and Marriott 1990)	(Eley 2002)	(Bischoff 2003)	(Lim, Rodrigues, and Yang 2005)
LN01	78.1	62.5	62.5	62.5	62.5	NC*	62.5
LN02	76.8	80.7	89.7	90.0	90.8	NC*	80.4
LN03	69.5	53.4	53.4	53.4	53.4	NC*	53.4
LN04	59.2	55.0	55.0	55.0	55.0	NC*	55.0
LN05	85.8	77.2	77.2	77.2	77.2	NC*	76.7
LN06	88.6	88.7	89.5	83.1	87.9	NC*	84.8
LN07	78.2	81.8	83.9	78.7	84.7	NC*	77.0
LN08	67.6	59.4	59.4	59.4	59.4	NC*	59.4
LN09	84.2	61.9	61.9	61.9	61.9	NC*	61.9
LN10	70.1	67.3	67.3	67.3	67.3	NC*	67.3
LN11	63.8	62.2	62.2	62.2	62.2	NC*	62.2
LN12	79.3	78.5	76.5	78.5	78.5	NC*	69.5
LN13	77.0	84.1	82.3	78.1	85.6	NC*	73.3
LN14	69.1	62.8	62.8	62.8	62.8	NC*	62.8
LN15	65.6	59.5	59.5	59.5	59.5	NC*	59.5
Mean	74.19	69.00	69.54	68.64	69.91	—	67.05

TABLE 3 Comparative Results with the Test Cases of Loh and Nee (1992)—Metaheuristic Approaches

	Volume utilization (%)
Problem	(Gehring and Bortfeldt 1997)	(Bortfeldt and Gehring 1998)	(Bortfeldt and Gehring 2001)	(Gehring and Bortfeldt 2002)	(Bortfeldt, Gehring, and Mack 2002)	(Moura and Oliveira 2005)	This work
LN01	62.5	65.5	62.5	NC*	NA**	NA**	62.5
LN02	90.7	96.7	89.8	NC*	NA**	NA**	90.1
LN03	53.4	53.4	53.4	NC*	NA**	NA**	53.4
LN04	55.0	55.0	55.0	NC*	NA**	NA**	55.0
LN05	77.2	77.2	77.2	NC*	NA**	NA**	77.2
LN06	91.1	96.3	92.4	NC*	NA**	NA**	85.8
LN07	82.7	84.7	84.7	NC*	NA**	NA**	84.2
LN08	59.4	59.4	59.4	NC*	NA**	NA**	59.4
LN09	61.9	61.9	61.9	NC*	NA**	NA**	61.9
LN10	67.3	67.3	67.3	NC*	NA**	NA**	67.3
LN11	62.2	62.2	62.2	NC*	NA**	NA**	62.2
LN12	78.5	78.5	78.5	NC*	NA**	NA**	78.1
LN13	85.6	85.6	85.6	NC*	NA**	NA**	83.9
LN14	62.8	62.8	62.8	NC*	NA**	NA**	62.8
LN15	59.5	59.5	59.5	NC*	NA**	NA**	59.5
Mean	69.99	71.07	70.15	—	70.90	70.30	69.55

As can be seen from Table 3, the proposed algorithm finds optimal solutions for all problems except for problems 2, 6, 7, and 13 (138.86 sec; average computation time for all problems). When the performance of the proposed algorithm was compared to the heuristic approaches, it performed quite well after the heuristic proposed in (Eley, 2002). When compared to the metaheuristic approaches, the performance gap between the best performing algorithm and the proposed algorithm was only about 2.14%.

Following the solution of Loh and Nee test cases, the test cases from Bischoff and Ratcliff (BR1 to BR7) were also solved. Each class in BR test bases included 100 problems. For these problems—which were harder compared to Loh and Nee test cases—SA parameters were redetermined experimentally as T _in  = 5000, α = 0.987, il _max = N (equal to the number of box types in each problem), and T _f  = 0.0001. The results obtained by the proposed algorithm for the test cases along with the previously reported results are presented in Tables 4 and 5.

TABLE 4 Comparative Results with the Test Cases of Bischoff and Ratcliff (1995) (BR1 to BR7)—Heuristic Approaches

	Volume utilization (%)
Problem	(Bischoff, Janetz, and Ratcliff 1995)	(Bischoff and Ratcliff 1995)	(Eley 2002)	(Bischoff 2003)	(Lim, Rodrigues, and Yang 2005)
BR1	81.76	83.79	NA**	89.39	87.40
BR2	81.70	84.44	NA**	90.26	88.70
BR3	82.98	83.94	NA**	91.08	89.30
BR4	82.60	83.71	NA**	90.90	89.70
BR5	82.76	83.80	NA**	91.05	89.70
BR6	81.50	82.44	NA**	90.70	89.70
BR7	80.51	82.01	NA**	90.44	89.40
Mean	81.97	83.45	88.75	90.55	89.13

TABLE 5 Comparative Results with the Test Cases of Bischoff and Ratcliff (1995) (BR1 to BR7) —Metaheuristic Approaches

	Volume utilization (%)
Problem	(Gehring and Bortfeldt 1997)	(Bortfeldt and Gehring 1998)	(Bortfeldt and Gehring 2001)	(Gehring and Bortfeldt 2002)	(Bortfeldt, Gehring, and Mack 2002)	(Moura and Oliveira 2005)	This work
BR1	85.80	92.63	87.81	88.10	93.52	89.07	86.38
BR2	87.26	92.70	89.40	89.56	93.77	90.43	87.70
BR3	88.10	92.31	90.48	90.77	93.58	90.86	87.06
BR4	88.04	91.62	90.63	91.03	93.05	90.42	86.61
BR5	87.86	90.86	90.73	91.23	92.34	89.57	86.10
BR6	87.85	90.04	90.72	91.28	91.72	89.71	85.47
BR7	87.68	88.63	90.65	91.04	90.55	88.05	84.49
Mean	87.51	91.26	90.06	90.43	92.65	89.73	86.26

Bischoff and Ratcliff test cases were solved in a reasonable amount of time (195 sec; average computation time for single problem) by using the proposed SA algorithm with a filling performance of 86.26%. When compared to the average value of volume utilization of all previous approaches, which was 88.68%, the performance gap is only 2.73%. We believe that our hybrid algorithm could still be improved through the development and implementation of superior local neighborhood search mechanisms as well as through the improvement of the heuristic-based filling procedure. However, the development and presentation of a best performing algorithm for single-objective CLPs was not the central purpose of this article. Having considered the multi-objective approach as the main feature of this article, we proposed a simple but fairly effective SA-based hybrid algorithm in order to solve multi-objective CLPs.

Solution of CLPs with Multi-Objective Functions (through a Real Example)

In the previous section, the performance of the SA algorithm that was hybridized with the heuristic filling procedure was discussed. This section will focus on the solution of the previously mentioned multi-objective CLP. As discussed in the first section of the article, we have two objectives, namely, weight maximization and volume utilization, where the first objective is to obtain a packing pattern in which the aim is to obtain a packing pattern having a total weight as close to the maximum available weight that can be carried by the owned vehicle and the second objective is to maximize the volume utilization of the vehicle.

The current problem data were collected from the company that distributes Procter & Gamble's products as well as their own products (paper towels, toilet tissues, paper napkins, etc.), which are manufactured at their own plant. The logistics department of the company provided their order lists, which include the products (12 different products in the example) to be shipped in a particular day as well as quantities, dimensions (width × depth × height), and weights of the boxes. An order list including all of the required data for the solution of the multi-objective CLP is given in Table 6. The company uses their own vehicles with a loading capacity of (530 × 220 × 210) cm³ (in width × depth × height) and weight capacity of 7200 kg.

TABLE 6 An Order List Including All of the Required Data for Multi-Objective CLP

Product ID	Product description	Dimensions (cm) width/ depth/height	Number of boxes	Weight of boxes (kg)	Total volume (cm^3)
1	Detergent	40/36/28	325	20	13,104,000
2	Bleaching liquid	54/28/30	25	22	1,134,000
3	Personal care	54/28/30	75	2.35	3,402,000
4	Detergent	39/29/32	75	20	2,714,400
5	Shaving product	15/10/20	10	1.47	30,000
6	Baby care	42/37/25	150	2.8	5,827,500
7	Toothpaste	36/18/18	3	3.72	34,992
8	Shampoo	18/17/22	25	4.97	168,300
9	Shampoo	22/17/22	50	5	411,400
10	Shampoo	12/11/16	5	1.33	10,560
11	Bleaching liquid	30/27/40	20	17.6	648,000
12	Shaving product	19/7/21	3	0.12	8379
Total			766	9905.37	27,493,531

The model is solved with the proposed SA algorithm with the parameters T _in  = 5000, α = 0.987, il _max = N (equal to the number of box types in each problem), and T _f  = 0.0001. The goals are given weights between 0 to 1 by 0.1 increment/decrements. The trade-offs between these two goals can be seen in Table 7.

TABLE 7 Results Obtained for the Multi-Objective Container-Loading Problem

Weights (Goal 1, Goal 2)	(0.1, 0.9)	(0.2, 0.8)	(0.3, 0.7)	(0.4, 0.6)	(0.5, 0.5)	(0.6, 0.4)	(0.7, 0.3)	(0.8, 0.2)	(0.9, 0.1)
	6713.37	6713.37	7157.06	7157.06	7150.41	7150.41	7150.41	7151.37	7151.37
Goal 2— volume util.	87.51	87.51	86.13	86.13	86.09	86.09	86.09	85.96	85.96
Dev. from Goal 1 (kg)	486.63	486.63	42.94	42.94	49.59	49.59	49.59	48.63	48.63
Dev. from Goal 2 (%)	12.49	12.49	13.87	13.87	13.91	13.91	13.91	14.04	14.04
Weighted sum of deviations	0.119169	0.113438	0.098879	0.085606	0.072994	0.059773	0.046551	0.033483	0.020119

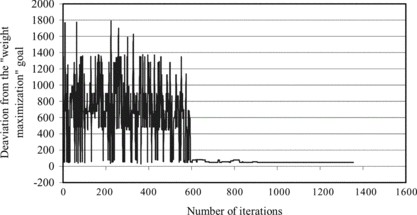
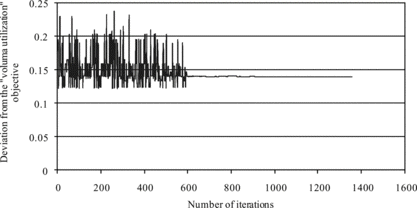
The results offer a set of solutions for the decision maker. In the described situation, the decision maker seeks a solution that provides a good balance between the defined goals. In this case, the decision maker should choose the packing pattern 85.96% of volume utilization and 7151.37 kg, which yields the smallest weighted sum of deviations from the defined goals. The convergence graph for this solution can be seen in Figures 6 and 7. If the decision maker favors this solution, the final view of the packing pattern for this order is shown in Figure 8.

FIGURE 6 Convergence graph for the first goal.

FIGURE 7 Convergence graph for the second goal.

FIGURE 8 Filled container. (A) Side view; (B) top view.

If transporting as many goods as possible to obtain an on-time delivery is an important goal for the decision maker, then the packing pattern with the 87.51% of volume utilization can be a good solution. In spite of this, if a very profitable solution is desired, the decision maker can choose the packing pattern with 86.13% of volume utilization and 7157.06 kg of total weight, because this packing pattern has the highest total weight among the other solutions. At this stage, it is the decision maker's job to select the best alternative by taking into account the company's transportation policy, profitability, and on-time delivery of the shipments.

Finally, the problem is also solved by considering each goal alone. This way the differences between the solution obtained by considering one and more objectives can be figured out. The single-objective problems are also solved with the same set of SA parameters that are used for the multi-objective problem. In case of the consideration of the goal of weight maximization alone, a total weight of 7173.52 kg and a volume utilization of 83.06% is achieved, whereas when only the goal of volume utilization is considered, a total weight of 6713.37 kg and a volume utilization of 87.51% is achieved. As is obvious, the proposed solution with 85.96% of volume utilization and 7151.37 kg is a satisfactory and more desirable solution for the company compared to solutions obtained from the solution of the problem in a single-objective manner. The handling of the defined multi-objective problem in a single-objective manner revealed that by handling the defined problem in a multi-objective manner it is able to consider objectives simultaneously, which results in a compromise between the objectives.

DISCUSSION OF THE RESULTS AND APPROACHES

It is a well-known fact that each method has its own advantages and disadvantages. It has been stated that a multi-objective optimization problem can generally be handled in four different ways depending on when the decision maker articulates his or her preference on the different objectives: never, before, during, or after the actual optimization procedure (Andersson, 2000). Because the decision maker articulates her or his preferences before the process in our case, we utilized a goal programming method, which is a priori articulation of preferences. It has also been employed for the solution of numerous types of multi-objective optimization problems in the literature. Marler and Arora (2004) have also underlined that the most common way of conducting multi-objective optimization is by a priori articulation of the decision maker's preferences. This means that before the actual optimization is conducted, the different objectives are somehow aggregated to one single figure of merit. The aggregation of the different objectives can be done in many ways. Given the variety of methods (conducting multi-objective optimization by a priori articulation of the preferences) available for the question arises as to which method is the best. Unfortunately, there is no absolute answer to this question. Moreover, it is worth pointing out that in terms of CPU time, the methods with a posteriori articulation of preferences are less efficient than methods with a priori articulation of preferences. Because only one solution is selected, the time spent determining other Pareto optimal points is wasted. Regardless of the specific method that is being used, clearly, presenting the Pareto optimal set can be a formidable task, as well (Marler and Arora, 2004). That is actually why we have employed a goal programming method for the solution of the problem described in this work. However, future work could focus on considering limitations of goal programming, as well as other solution approaches like weighted-sum model.

Nonderivative methods are more likely to find a global optimum and not be stuck on local optima as gradient methods might be. Some of these methods are simulated annealing, genetic algorithms, random search, tabu search, and complex/simplex. SA is one of the most powerful and robust nonderivative optimization methods. It is also slightly less computationally expensive compared to genetic algorithms (Andersson, 2000). In this study, the methodology proposed for the solution of multi-objective container-loading problem makes use of SA with the main purpose of having the outstanding and inherent properties of SA described above. Goal programming and a heuristic filling procedure have been also embedded within the SA algorithm.

It should also be noted that the proposed heuristic filling algorithm is a kind of wall-building procedure, as mentioned previously. It loads the container layer-by-layer. Before filling each layer, the dimensions of each layer is determined. This is done by choosing the width of the layer. Determination of the layer dimensions is explained in detail in the relevant section of the article. As a result of the packing process, the container is filled with the isolated vertical layers where spanning of the boxes between layers is avoided. Because the proposed algorithm uses isolated vertical layers and fills the empty spaces in a layer in a recursive manner and the procedure does not produce suitable unused space to fill, the amalgamation of the empty spaces between and/or within a layer is not considered in this study. Unused spaces are treated as isolated spaces that are not fused with the adjacent empty places. It has also been reported that amalgamation can create some stability problems in container loading (Hemminki, 1993). Stability is an important aspect to consider in container-loading problems (Moura and Oliveira, 2005). It prevents cargo from being damaged during transportation. However, stability of packing is in general not considered by wall-building heuristics (Kocjan and Holmström, 2006). The real case study presented in this article focused on a medium-sized company that distributes the goods ordered by supermarkets. It mainly distributes Procter & Gamble's products as well as their own products (paper towels, toilet tissues, paper napkins, etc.) and is rarely faced with the problem of stability. The use of spacing materials is considered, if any problem related to stability will occur. Because our heuristic filling procedure uses no amalgamation of unused spaces in the filling process while exploiting a wall-building approach and it is not strictly required by the company, the stability constraint is not considered in this work. This issue is also considered in the list of assumptions given in the Problem Formulation section.

Performance of the proposed approach is firstly compared for the well-known test cases from the literature with single-objective function. This analysis was only important to recognize the performance of the proposed approach for single-objective CLPs, just before attempting to solve the multi-objective CLP described in this article. The analysis revealed that the proposed approach is relatively useful in solving the single objective CLPs and hence it can also be employed for multi-objective CLPs. The algorithm is then tested on a real case (which is really large compared to the problems in the literature) including 766 items/boxes. The suitability of the algorithm for the multi-objective case is also checked and the results showed that the proposed algorithm can produce a set of feasible solutions offering some trade-offs between the two objectives. Supported with this knowledge, it is the decision maker's job to evaluate the set of solutions and choose a desired solution according to their particular application. At this point, what the decision maker should do is actually to select the best solution by taking into account the company's transportation policy, profitability, and on-time delivery of the shipments. The proposed algorithm can further be extended with the employment of a different set of objectives in case of different situations. The methodology can also be embedded in a decision-making framework as well.

CONCLUSIONS

The container-loading problem has many applications in industry. It is one of the NP-hard optimization problems in the literature. In order to find an alternative solution for these difficult problems, an SA-based algorithm is employed in this study. Hybridized with a heuristic filling procedure to obtain the fitness values of the alternative solutions, the proposed algorithm is capable of solving multi-objective CLPs. The need for the hybridization is explained in detail in the article. The performance of the proposed algorithm against the performances of the other heuristics and metaheuristics approaches is compared based on the volume utilization. The research results reached in this work have shown that the proposed approach is a promising technique capable of solving multi-objective CLPs. To the best of the authors’ knowledge, this is one of the few attempts that focuses on the solution of multi-objective CLPs as well as provides a real-world case study.

Having been inspired from a real-world case, a multi-objective CLP is first described and a solution algorithm for the described problem is then proposed in this article. The newly defined problem aims to load the items (boxes) that would provide the highest total weight into the container in the best possible way. The proposed solution approach to solve the multi-objective CLP is an SA algorithm based on a weighted goal programming model that is hybridized with a heuristic filling procedure.

Consideration of the multi-objectives is the main feature of our work. Goal programming and a heuristic filling procedure have been embedded within the SA algorithm. The proposed filling heuristic is designed by taking the neighborhood structure described for the container-loading problem into account. Reasonable results (for single-objective case) that are comparable with those produced by other algorithms in the literature have been produced. The idea underlying this comparison was to discuss the suitability of our approach for the solution of the multi-objective container-loading problem described in this article.

It should also be noted that the development and presentation of a best performing algorithm was not the main objective of this article. There are already several high-performing algorithms available in the literature. We proposed a simple but fairly effective SA-based hybrid algorithm in order to solve multi-objective CLPs described in this work. However, it is worth pointing out that the work is still ongoing and the authors are trying to improve their algorithms further. This issue is left as future work as well. We believe that there is still much work to be done to realize the full potential of metaheuristics like SA by the development of more improved (i) programming techniques, (ii) local neighborhood search mechanisms, and (iii) hybridization schemes. Future research could also focus on the CLPs with more objectives and multiple containers.

This research is based on a real-world case study, concerning a company that mostly distributes Procter & Gamble's products along with their own products (paper towels, toilet tissues, paper napkins, etc.) that are manufactured at their own plant. The proposed methodology in this study has been also used in the above-mentioned company with positive results. It produced about 10% overall increase in the volume utilization and total weight distributed per year and provided an exceptional flexibility for planning the container-loading problems. It should be noted that the CLP has many applications in industry. Design and development of efficient algorithms for solving multi-objective CLPs is therefore important. The problem described in this article is quite suitable for practical use, particularly in logistics industry. The proposed approach in this article can also be used for other industries as well.

Acknowledgments

The authors are grateful to Mr. Mehmet Tarik Ozdemir (BSc in Industrial Engineering) and ADNAN A.S. (http://www.adnan.com.tr/english/index.html) for providing data for this work. The second author thanks the Scientific and Technological Research Council of Turkey (TUBITAK) for their support under the PhD Fellowship program.

Notes

*These values are not computed and/or presented.

*These values are not computed and/or presented.

**These values are not available separately.

*These values are not available separately.