k-ATTRACTORS: A PARTITIONAL CLUSTERING ALGORITHM FOR NUMERIC DATA ANALYSIS

Abstract

Clustering is a data analysis technique, particularly useful when there are many dimensions and little prior information about the data. Partitional clustering algorithms are efficient but suffer from sensitivity to the initial partition and noise. We propose here k-attractors, a partitional clustering algorithm tailored to numeric data analysis. As a preprocessing (initialization) step, it uses maximal frequent item-set discovery and partitioning to define the number of clusters k and the initial cluster “attractors.” During its main phase the algorithm uses a distance measure, which is adapted with high precision to the way initial attractors are determined. We applied k-attractors as well as k-means, EM, and FarthestFirst clustering algorithms to several datasets and compared results. Comparison favored k-attractors in terms of convergence speed and cluster formation quality in most cases, as it outperforms these three algorithms except from cases of datasets with very small cardinality containing only a few frequent item sets. On the downside, its initialization phase adds an overhead that can be deemed acceptable only when it contributes significantly to the algorithm's accuracy.

INTRODUCTION

Clustering is a descriptive data mining task that aims to identify homogeneous groups of objects, based on the values of their attributes. It is particularly useful in problems where there is little prior information available about the data and a minimum number of assumptions are required. Clustering is appropriate for the exploration of interrelationships among the data points when assessing their structure (Jain, Murty, and Flynn 1999).

Clusters can be broadly created by using either hierarchical or partitional algorithms. The former organize data into a hierarchical structure based on a proximity matrix, whereas the latter identify the partition that optimizes, usually locally, a clustering criterion.

k-Means is a classic partitional clustering algorithm (Hartigan 1975). It represents each cluster with the mean value of its objects. As a result, intercluster similarity is measured based on the distance between the object and the mean value of the input data in a cluster. It is an iterative algorithm in which objects are moved among clusters until a desired set is reached. Its main problems are that the users have to define the number of clusters k and that it is sensitive to the initial partitioning. That is, different initial partitions, indicated by user input, lead to different results (Han and Kamber 2001).

This article presents a further elaborated version of k-attractors, a partitional clustering algorithm introduced in Kanellopoulos et al. (2007) that has the following characteristics:

	It locates the initial attractors of cluster centers with high precision.
	The final number of the derived clusters is defined without user intervention, by using the maximal frequent item-set discovery.
	It measures distance based on a composite metric that combines the Hamming distance and the inner product of transactions and clusters' attractors.

The k-attractors algorithm can be used for numeric data analysis and is based on the assumption that such data demonstrate identifiable patterns. The most prevalent of these patterns, that is, the initial centers and the number of clusters, can form the basis for cluster analysis. For this reason we use the frequent item-sets discovery technique, which has the ability to extract such patterns from large datasets (Agarwal and Srikant 1994).

WEKA's implementations of k-means, EM, and FarthestFirst algorithms (Witten and Frank 2005) were used to compare our algorithm in terms of performance (i.e., convergence speed) and accuracy (i.e., quality clusters formation). The results are promising, because k-attractor in its main phase was faster and formed more accurate (i.e., better quality) clusters than the above mentioned algorithms, in most cases. The algorithm did not perform well in cases where the data did not exhibit a sufficient number of patterns that could be captured. Also, the experiments showed that the initialization phase of k-attractors adds an overhead, which can be acceptable only in the cases that it contributes significantly to algorithm's accuracy.

The article is organized as follows: section 2 presents a review of existing clustering algorithms; section 3 discusses the background on clustering, association rules, and related problems; section 4 introduces our approach; section 5 details k-attractors; section 6 presents experimental results; and section 7 concludes with directions for future work.

CLUSTERING ALGORITHMS REVIEW

Various research has been reported to deal with clustering algorithms. Zhuang and Dai (2004) present a maximal frequent item-set approach for clustering web documents. Based on maximal frequent item-set discovery, they propose an efficient way to precisely locate the initial points for the k-means algorithm (Hartigan 1975). Fung, Wang, and Ester (2003) propose the frequent item-set–based hierarchical clustering for document clustering. The intuition of this algorithm is that there are some frequent item sets for each cluster (topic) in the document set and different clusters share few frequent item sets. Wang, Xu, and Liu (1999) propose a similarity measure for a cluster of transactions based on the notion of large items.

Han et al. (1997) introduced association rules hypergraph partitioning algorithm. It constructs a weighted hypergraph to represent the relationships among discovered frequent item sets. It aims to find k partitions such that the vertices in each partition are highly related. Kosters et al. (1999) propose a method that uses association rules having high confidence to construct a hierarchical sequence of clusters. The work of Li et al. (2007) discusses an efficient method based on spectra analysis to effectively estimate the number of clusters in a given data set.

The work of Jing, Ng, and Zhexue (2007) provides a new clustering algorithm called EWKM which is a k-means type subspace clustering algorithm for high-dimensional sparse data. Patrikainen and Meila (2006) present a framework for comparing subspace clusterings, whereas Lin, Liu, and Chen (2005) introduce a new algorithm called dual clustering on two domains, the optimization, and the constraint domain. This algorithm combines the information in both domains and iteratively uses a clustering algorithm on the optimization domain and also a classification algorithm on the constraint domain to reach the target clustering effectively.

Except for the algorithms described above, three of the most important clustering algorithms are k-means, EM, and FarthestFirst (Jain, Murty, and Flynn 1999; Witten and Frank 2005). They are characteristic, commonly used clustering algorithms. Moreover, they are implemented in WEKA 3 (http://www.cs.waikato.ac.nz/ml/weka/), an open source data mining tool frequently used in the literature, thus facilitating experimental replication. Those algorithms are extensively described in Witten and Frank (2005).

k-Means is a classic iterative-based clustering algorithm. The user first specifies in advance how many clusters are being sought: This is the parameter k. Then k points are chosen at random as clusters centers. All instances are assigned to their closest cluster center according to the ordinary Euclidean distance metric. Next the centroid, or mean, of the instances in each cluster is calculated. These centroids are taken to be new center values for their respective clusters. Finally, the whole process is repeated with the new cluster centers. Iteration continues until no more points change clusters, at which stage the cluster centers are stable (Witten and Frank 2005).

The EM (expectation maximization) clustering algorithm is based on a statistical model called finite mixtures. A mixture is a set of k probability distributions, representing k clusters, that govern the attribute values for members of that cluster. In other words, each distribution gives the probability that a particular instance would have a certain set of attribute values if it was known to be a member of that cluster. Each cluster has a different distribution. Finally, the clusters are not equally likely: Some probability distribution reflects their relative populations. The problem is that we know neither the distribution that each training instance came from nor the parameters of the mixture model. For that reason the EM adopts the same procedure used for the k-means clustering algorithm and iterates. It starts with some initial guesses for the parameters of the mixture model, uses them to calculate the cluster probabilities for each instance, and finally uses these probabilities to reestimate the parameters and repeats (Witten and Frank 2005).

The FarthestFirst algorithm performs a farthest-first traversal over the dataset. Starting with an arbitrary chosen point and adding it to the set, the algorithm picks that point in the dataset that is farthest away from the current centroids and adds to X in each iteration.

At the end of k iterations, each point in X acts as a center for a stratum and the result of the algorithm is a disjoint partitioning, obtained by assigning each point in the dataset to its nearest point in X (Witten and Frank 2005).

In section 6 we base our experiments on comparing k-attractors with the three algorithms described above. This facilitates repeatability of the experiments as WEKA is an open source data mining suite.

PRELIMINARIES

This section presents the main concepts that form the basis for k-attractors. More specifically, we present the concepts of the frequent item-sets discovery and their subsequent graph construction and partitioning. These two techniques help create the initial attractors and define the maximum number k of the derived clusters.

Frequent Item-Sets Discovery: APriori Algorithm

A frequent item set is a set of items that appear together in more than a minimum fraction of the whole dataset. More specifically, let J be a set of quantitative data. Any subset I of J is called an item set. Let T = <t ₁, … ,t _n > be a sequence of item sets called a transaction database. Its elements t ϵ T will be called item sets or transactions.

An item set can be frequent if its support is greater than a minimum support threshold, denoted as min_sup. The support of an item X in T denoted as min_sup T(X) is the number of transactions in T that contain X. The term “frequent item” refers to an item that belongs to a frequent item set. If now an item X is frequent and no superset of X is frequent, then X is a maximally frequent item set and we denote the set of all maximally frequent item sets by Maximally Frequent Itemset (MFI). From these definitions it is easy to see that the following relationship holds MFI ⊆ FI, where FI is the set of the most frequent item sets. APriori, the well-known association rule mining algorithm, was used to discover frequent item sets (Agarwal and Srikant 1994).

According to Bodon (2005) the APriori's moderate traversal of a data search space is the most suitable when mining very large databases. APriori scans the transaction dataset several times. After the first scan the frequent items are found and in general after the lth scan, the frequent item sequences of size l (we call them l-sequences) are extracted. The method does not determine the support of every possible sequence. In an attempt to narrow the domain to be searched, before every pass it generates candidate sequences. A sequence becomes a candidate if every subsequence of it is frequent. Obviously, every frequent sequence is a candidate too; hence, it is enough to calculate the support of candidates. Frequent l-sequences generate the candidate (l + 1)-sequences after the lth scan. Candidates are generated in two steps. First, pairs of l-sequences are found, where the elements of the pairs have the same prefix of size l − 1. Here we denote the elements of such a pair with <i ₁, i ₂, … , il − 1, il> and <i ₁, i ₂, … , il − 1, i'l>.

Depending on items il and i'l we generate one or two potential candidates. If il <> il', then they are <i ₁, i ₂, … , il − 1, il, i‘l> and <i ₁, i ₂, … , il − 1, i‘l, il>; otherwise, it is <i ₁, i ₂, … , il − 1, il, il> (Manilla, Toivonen, and Verkamo 1995). In the second step the l-subsequences of the potential candidate are checked. If all subsequences are frequent, it becomes a candidate. As soon as the candidate (l + 1)-sequences have been generated, a new scan of the transactions is started and the precise support of the candidates is determined. This is done by reading the transactions one-by-one. For each transaction t the algorithm decides which candidates are contained by t. After the last transaction is processed, the candidates with support below the support threshold are thrown away. The algorithm ends when no new candidates are generated.

Frequent Item-Sets Graph Partitioning: KMetis Algorithm

The discovered frequent item sets often reveal hidden relationships and correlations among data items. By constructing and partitioning a weighted hypergraph from those item sets, using similarity (i.e., based on hyperedges' weights) criteria related to the confidence of their association rules, we can reduce their size by eliminating those that are not similar.

A hypergraph H = (V, E) consists of a set of vertices (V) and a set of hyperedges (E). A hypergraph is an extension of a graph in the sense that each hyperedge can connect more than two vertices. In this work, the vertex set corresponds to the distinct items in the database and the hyperedges correspond to the frequent item sets. For example, if {A B C} is a frequent item set, then the hypergraph contains a hyperedge that connects A, B, and C. The weight of a hyperedge is determined by a function of the confidences for all the association rules involving all the items of the hyperedge.

The kMetis algorithm (Karypis and Kumar 1998) has a very simple structure. The graph G = (V, E) is first coarsened down to a small number of vertices, a k-way partitioning of this much smaller graph is computed, and then this partitioning is projected back, toward the original graph (finer graph) by successively refining the partitioning at each intermediate level.

OUR APPROACH

In this research work we propose a partitional algorithm that uses a preprocessing method for its initial partitioning and incorporates a distance measure adapted to the way initial attractors are determined by this method. More specifically, k-attractors uses the maximal frequent item-set discovery and partitioning, similarly to Zhuang and Dai (2004) and Han et al. (1997). However, k-attractors is different because it is not used in the context of document clustering. It is applied to numeric data that are expected to demonstrate patterns that can be identified by the maximal frequent item-sets discovery technique. The discovered frequent item sets often reveal hidden relationships and correlations among data items. By constructing and partitioning a weighted hypergraph from those item sets, using similarity criteria (based on the weights of hyperedges) related to the confidence of their association rules, their size can be reduced by eliminating those that are not interesting (i.e., their support is below a certain threshold). The final set of rules will be used to define the final number of clusters and the initial attractors of their centers. The intuition in k-attractors is that a frequent item set is a set of measurements that occur together in a minimum part of a dataset. Transactions with similar measurements are expected to be in the same cluster. The term “attractor” is used instead of centroid, because it is not determined randomly but is determined by its frequency in the whole population of a given dataset.

An important characteristic of k-attractors is that it proposes a distance measure that is adapted to the way the initial attractors are determined by the preprocessing method. Hence, it is primarily based on the comparison of frequent item sets. More specifically, a composite metric based on the Hamming distance and the dot (inner) product between each transaction and the attractors of each cluster is used.

The Hamming distance is given by the number of positions that a pair of strings differ from each other. Put another way, it measures the number of substitutions required to transform the one string to the other. In this work we consider a string as a set of data items and more specifically as a vector of numeric data. Furthermore, the dot product of two vectors is a measure of the angle and the orthogonality of two vectors. It is used to compensate for the position of both vectors in the Euclidean space (Kosters, Marchiori, and Oerlemans 1999).

ALGORITHM DESCRIPTION

This section details the basic steps of k-attractors along with some examples.

Overview

The two basic phases of k-attractors are as follows:

Initialization phase The first step of this phase generates frequent item sets using the APriori algorithm. The derived frequent item sets are used to construct the item-set graph, and kMetis, a graph partitioning algorithm, is used to find the maximum number of the desired clusters and to assign each frequent item set to the appropriate cluster. As soon as the maximum number of the desired clusters k is determined, we select the maximal frequent item sets from every cluster, forming a set of k frequent item sets as the initial attractors.

Main phase As soon as the attractors are found, we assign each transaction to the cluster that has the minimum distance against its attractor. When all transactions have been assigned to clusters we recalculate the attractors for each cluster, in the same way as in the initialization phase.

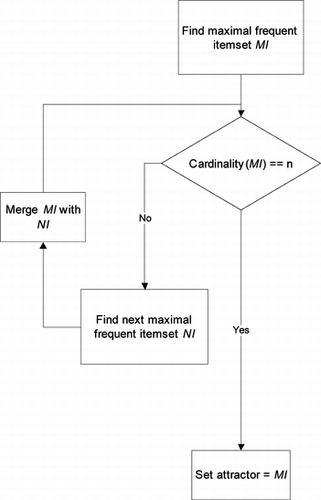
Figure 1 illustrates an overview of k-attractors. We detail its two phases next.

FIGURE 1 k-Attractors overview.

Initialization Phase

There are two goals of the initialization phase: identify the most frequent item sets of the input data and determine the number of clusters. For the most frequent item sets to be discovered, we apply the APriori algorithm against the input data file. The APriori algorithm takes as input the absolute support s of the required item sets and returns all the one-dimensional and multidimensional item sets with support greater than or equal to s. The value of s is defined empirically by an expert user, based on the statistical characteristics of the dataset under consideration.

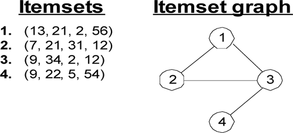
Once the most frequent item sets have been discovered, we form the item-set graph. Given the set of the most frequent item sets FI = {fi ₁, fi ₂, … fi _m }, the item-set graph is a graph G(V, E), where V = {fi _i  ∈ FI} and E = {e _ij |f i _i  ∩ fi _j  ≠ Ø}. The intuition behind this graph is that if two item sets have at least one common item, then they should possibly belong to the same cluster and thus we connect them with an edge in the item-set graph. For more accuracy we could have weighted each edge with the number of common items between the two corresponding item sets/vertices, but to keep the initialization phase as simple and fast as possible, we decided not to weigh the edges. Figure 2 demonstrates an example of the item-set graph's construction.

FIGURE 2 Item-set graph example.

In the next step we apply a graph partitioning algorithm to the item-set graph. In our case we used the kMetis algorithm to partition the item-set graph (Han et al. 1997). kMetis partitions the item-set graph into a number of distinct partitions and assigns each vertex of the graph (i.e., each item set) to a single partition. The final number of the derived partitions is the number of clusters that we use in the main phase of the k-attractors algorithm.

The final step of the initialization phase is the attractors' discovery, which is presented in Figure 3. During this step every previously determined graph partition is examined. In Kanellopoulos et al. (2007) the procedure for discovering the initial attractors is summarized. For each partition we find the maximal frequent item-set MI belonging to this partition and check the cardinality of its dimensions. If the number of dimensions is equal to the input data items' number of dimensions n, then we assign the corresponding item set as the attractor of the corresponding partition. However, in most cases the cardinality of the maximal item set is less than n. In such cases we search for the next maximal frequent item-set NI in the corresponding partition and merge it with the previous item-set MI. Merging occurs only in dimensions that are absent from the first maximal item-set MI. We repeat this procedure until we have formed an item set with cardinality equal to n and assign the formed item set as attractor of the corresponding partition.

FIGURE 3 Attractors discovery.

To provide more flexibility, k-attractors performs a postprocessing step against the previously determined attractors. The algorithm defines a threshold, called attractor similarity ratio, r. This threshold defines the maximum allowed similarity between two different attractors. After several experiments for calibrating k-attractors we use 0.8 as the default value for r. The similarity between two attractors a ₁, a ₂ is defined as follows:

In other words, the similarity between two attractors is the ratio of the number of common items divided by the number of total dimensions. If the similarity of two attractors is more than r, then we randomly discard one of the two attractors; thus the number of total partitions is decreased by one.

It has to be noted that the initialization phase adds a significant overhead to the overall algorithm's performance. The reason for this is the combination of the APriori and kMetis algorithms for the extraction of frequent item sets and their partitioning, respectively. As long as it contributes significantly to the algorithm's accuracy compared with other algorithms, this overhead is not considered a disadvantage.

Main Phase

The goal of k-attractor's main phase is to assign each input data item to a cluster, using a partitional approach. At first, we form a set of k empty clusters, where k is the number of distinct graph partitions discovered during the initialization phase. Every formed cluster is then assigned to the corresponding attractor calculated in the previous phase.

Once the clusters have been formed, the main phase of k-attractors begins. This phase resembles a partitional algorithm, where every data item is assigned to a cluster according to a predefined distance metric and in every step the centers of every cluster are recalculated until the algorithm converges to a stable state where the clusters' centers do not change.

The k-attractors algorithm uses a hybrid distance metric based on vector representation of both the data items and the cluster's attractors. The distance of these vectors is measured by using the following composite distance metric:

In this formula the first term is the Hamming distance between the attractor a _i and the data item t _j . It is given by the number of positions that a pair of strings is different and is defined as follows:

Because our algorithm is primarily based on item set similarity, we want to measure the number of substitutions required to change one item set into another. The second term is the dot (inner) product between this data item and the attractor a _i . It is used to compensate for the position of both vectors in the Euclidean space (Kosters et al. 1999).

The multipliers h, i in Eq. (2) define the metric's sensitivity to Hamming distance and inner product respectively. For example, i = 0 indicates that the composite metric is insensitive to the inner product between the data item and the cluster's centroid. Both h and i are taken as input parameters in our algorithm during its execution. Thus, k-attractors provides the flexibility of changing the sensitivity of the composite distance metric to both Hamming distance and inner product.

Using this distance metric, k-attractors assigns every data item to a single cluster and recalculates the attractors for every cluster. Recalculation includes finding the data item in a cluster that minimizes the total sum of distances between the other data items belonging to that cluster. The above procedure is repeated until the attractors of all clusters do not change any further.

The final step of the k-attractors' main phase involves outlier handling. During this step every cluster is checked for outliers, according to a threshold d. Specifically, a data item t, belonging to cluster i, is considered an outlier if

where av g _i (Score(a _i , t _j )) is the average distance between the data items of cluster i and the attractor a _i .

The discovered outliers of all clusters are grouped into a new cluster, called outliers cluster, and thus the total number of formed clusters is k + 1.

EXPERIMENTAL RESULTS

Datasets Used

The evaluation of the proposed clustering algorithm involved two main experiments that were performed with a Pentium M 2.0 GHz machine with 1 GByte RAM. The scope of those experiments was the comparison of k-attractors with the set of clustering algorithms contained in WEKA 3 (http://www.cs.waikato.ac.nz/ml/weka/), the Java open source data mining tool. In particular, we compared k-attractors with the clustering algorithms described in section 2: k-means, EM and FarthestFirst.

The datasets used in our experiments were the Iris dataset (Orange, http://www.ailab.si/orange/datasets.asp), the Wisconsin breast cancer dataset (Orange, http://www.ailab.si/orange/datasets.asp), the vehicle dataset (Orange, http://www.ailab.si/orange/datasets.asp), the Haberman surgery dataset (Machine Learning Datasets, http://mlearn.ics.uci.edu/), and an industrial software measurement dataset derived from parsing a fragment of System2, a large logistics system implemented in Java (6782 classes). This last dataset consisted of a set of 10 calculated software metrics for 50 java classes of the parsed system. The main characteristics of the datasets used are summarized in Table 1.

TABLE 1 Characteristics of the Employed Datasets

Dataset	No. of items	No. of classes
Iris	150	3
Wisconsin breast cancer	699	2
Vehicle	946	4
Haberman surgery	306	2
Software measurement data	50	4

k-Attractors Evaluation

The purpose of our experiments was to evaluate k-attractors against the clustering algorithms contained in WEKA 3: k-means, EM, and FarthestFirst. For that reason we used five datasets for which there is previous knowledge of data item classification.

For our experiments we used the recall, precision, and F-measure external metrics to evaluate the accuracy (quality) of the clusters formed by k-attractors, k-means, EM, and FarthestFirst for every dataset. Precision, recall and F-measure are external cluster quality metrics based on the comparison of the formed clusters to previously known external classes (e.g., different domains). Given a class Z _j of data items with a number n _j of items and a cluster C _i , formed by a clustering algorithm, with n _i items, let be the number of items in C _i belonging to Z _j . Then, the precision, recall, and F-measure are defined as follows:

To properly measure the total quality of the formed clusters by every clustering algorithm, we calculated the weighted F-measure for the clusters formed by every clustering algorithm in each dataset and compared the resulted weighted F-measures. The weighted F-measure of a clustering algorithm in a dataset is defined as follows:

where F _i denotes the F-measure for the ith cluster and n _i denotes the number of items in the ith cluster.

Additionally, for every dataset used, we measure the number of iterations required by k-attractors's main phase and k-means for the clusters to converge into a stable state. Because every iteration in k-attractors' main phase and k-means has a complexity of O(n), we can compare the performance of the two algorithms by comparing the number of iterations performed. The more the required iterations, the longer the clustering process lasts. However, because EM and FarthestFirst are not partitional clustering algorithms, we did not compare k-attractors with them in terms of performance (i.e., converge speed).

Tables 2 and 3 present the experimental results for the breast cancer dataset. As is easily seen, k-attractors in its main phase performs slightly better than k-means and FarthestFirst (weighted F-measure 0.97 regarding the weighted F-measure 0.95 of k-means and FarthestFirst) and much better than EM. Additionally, it requires one less iteration (four iterations regarding the five iterations of k-means). Thus, regarding the breast cancer dataset, k-attractors is better compared with the other three clustering algorithms in terms of both accuracy and performance.

TABLE 2 Breast Cancer Experimental Results (k-Attractors and k-Means)

		k-Attractors			k-Means
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	458	0.98	0.97	0.98	0.96	0.92	0.94
2	241	0.95	0.97	0.96	0.96	0.98	0.97
		Weighted F-measure		0.97	Weighted F-measure		0.95
		Iterations		4	Iterations		5

TABLE 3 Breast Cancer Experimental (EM and FarthestFirst)

		EM			FarthestFirst
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	458	1.00	0.92	0.96	0.96	0.93	0.94
2	241	0.87	1.00	0.93	0.96	0.98	0.97
		Weighted F-measure		0.92	Weighted F-measure		0.95

Tables 4 and 5 present the experimental results for the iris dataset. It can be seen that k-attractors in its main phase performs slightly worse than k-means and EM (weighted F-measure 0.87 regarding the weighted F-measure 0.89 of k-means and 0.90 of EM) and slightly better than FarthestFirst. In addition, the main phase of k-attractors requires 20 iterations regarding the 4 iterations required by k-means until it converges. This is because the iris dataset contains only a few frequent item sets, with very small cardinality. Hence, k-attractors cannot use those frequent item sets to form the initial attractors for the clustering process. k-Attractors uses the statistical mean to approximate the value of each attribute in the initial attractors instead. This approach leads to the fact that the initial attractors are very similar to each other, because most of their attributes have the same value and as a result the performance of k-attractors is relatively poor.

TABLE 4 Iris Experimental Results (k-Attractors and k-Means)

		k-Attractors			k-Means
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	50	0.98	1.00	0.99	0.77	0.94	0.85
2	50	0.92	0.68	0.78	1.00	1.00	1.00
3	50	0.76	0.94	0.84	0.92	0.72	0.81
		Average F-measure		0.87	Average F-measure		0.89
		Iterations		20	Iterations		4

TABLE 5 Iris Experimental Results (EM and FarthestFirst)

		EM			FarthestFirst
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	50	0.78	0.90	0.88	0.85	0.70	0.77
2	50	1.0	1.0	1.0	1.0	1.0	1.0
3	50	1.0	0.72	0.84	0.75	0.88	0.81
		Weighted F-measure		0.90	Weighted F-measure		0.86

Tables 6 and 7 present the experimental results for the vehicle dataset. As is easily seen, k-attractors in its main phase performs better than the other clustering algorithms (weighted F-measure 0.43 regarding the weighted F-measure 0.37 of k-means, 0.37 of EM, and 0.24 of FarthestFirst). Additionally, k-attractors requires only two iterations compared with the eight iterations required by k-means. This is because the vehicle dataset contains enough frequent item sets for the initial attractors to be calculated right; thus, k-attractors in its main phase performs better than the other clustering algorithms both in accuracy and time performance.

TABLE 6 Vehicle Experimental Results (k-Attractors and k-Means)

		k-Attractors			k-Means
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	240	0.43	0.35	0.38	0.41	0.47	0.44
2	240	0.59	0.52	0.55	0.42	0.33	0.37
3	240	0.37	0.38	0.38	0.23	0.21	0.22
4	226	0.36	0.45	0.40	0.42	0.49	0.45
		Weighted F-measure		0.43	Weighted F-measure		0.37
		Iterations		2	Iterations		8

TABLE 7 Vehicle Experimental Results (EM and FarthestFirst)

		EM			FarthestFirst
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	240	0.41	0.47	0.44	0.27	0.77	0.39
2	240	0.42	0.33	0.33	0.49	0.21	0.29
3	240	0.23	0.21	0.21	0.33	0.01	0.02
4	226	0.42	0.49	0.49	0.35	0.21	0.26
		Weighted F-measure		0.37	Weighted F-measure		0.24

Tables 8 and 9 present the experimental results for the Haberman surgery dataset. As is seen, k-attractors in its main phase performs better than the other three algorithms and requires only two iterations whereas k-means requires six iterations. This performance boost comes from the fact that the range of attribute values in this dataset is relatively small (varies between one and five) and thus there is a lot of frequent item to efficiently calculate the initial attractors for the k-attractors algorithm.

TABLE 8 Haberman Surgery Experimental Results (k-Attractors and k-Means)

		k-Attractors			k-Means
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	225	0.56	0.77	0.65	0.28	0.57	0.37
2	81	0.91	0.78	0.84	0.75	0.47	0.58
		Weighted F-measure		0.69	Weighted F-measure		0.43
		Iterations		2	Iterations		6

TABLE 9 Haberman Surgery Experimental Results (EM and FarthestFirst)

		EM			FarthestFirst
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	225	0.42	0.67	0.51	0.74	0.98	0.84
2	81	0.85	0.67	0.75	0.33	0.02	0.05
		Weighted F-measure		0.57	Weighted F-measure		0.63

Table 10 shows that k-attractors' clusters are closer to the domain expert's clusters. k-Attractors achieves a weighted 0.85 F-measure, whereas k-means achieves a weighted 0.60 F-measure. Especially, regarding the two largest clusters (cluster 1 and cluster 2), the corresponding calculated F-measure is very high and better than the two corresponding k-means clusters. Considering now the smallest cluster in k-attractors (cluster 4) and k-means (cluster 4), these clusters correspond to the domain expert's outlier cluster. It is obvious that k-attractors approximates the domain expert's cluster because of the application of the outlier handling phase. k-Means lacks such a phase; thus, the recall, precision, and f-measure of the corresponding cluster are both 0.

TABLE 10 Software Measurement Data Experimental Results

		k-Attractors			k-Means
Cluster	Population	Precision	Recall	F-measure	Precision	Recall	F-measure
1	35	0.88	0.97	0.92	0.80	0.65	0.72
2	9	0.88	0.80	0.84	0.15	0.50	0.23
3	4	0.66	0.66	0.66	1.00	0.70	0.82
4	2	0.50	0.25	0.33	0.00	0.00	0.00
		Weighted F-measure		0.85	Average F-measure		0.60

Hence, the experimental results show that k-attractors forms more accurate (better quality) clusters, in terms of higher F-measure, than k-means, approximating the domain expert's manually created clusters. This can be explained by the fact that software measurement data are expected to demonstrate specific behavior and not random patterns or trends as in software development projects programmers follow certain specifications, design guidelines, and code styles. Thus, this type of data usually contains frequent common item sets that can be captured during k-attractors' initial phase leading to more accurate results (Kanellopoulos et al. 2007).

Discussion

We conducted a series of experiments to compare k-attractors with k-means, EM, and FarthestFirst clustering algorithms. The results are promising because in most cases k-attractors, in its main phase, performs better than the other clustering algorithms both in performance (converge speed) and in accuracy (quality of the formed clusters). This efficiency of k-attractors is a result of the calculation of the approximate initial attractors for each formed cluster during the initialization phase. However, this phase adds a significant overhead to the overall algorithm's performance, but as long as it contributes significantly to its accuracy this overhead is considered justifiable.

k-Attractors performed worse on the iris dataset compared with k-means, EM, and FarthestFirst in terms of performance and accuracy. This was because the iris dataset contains only a few frequent item sets with very small cardinality. Hence, k-attractors could not use those frequent item sets to form the initial attractors for the clustering process and was outperformed by the other clustering algorithms. As mentioned in section 5.2, in case of few discovered frequent item sets, k-attractors uses the statistical mean of every dimension to calculate the attractors. Thus, the formed attractors are very similar to each other, resulting in poor performance. It would be interesting to use a more sophisticated statistical measurement to approximate the missing dimensions and test whether this improves the performance of k-attractors.

CONCLUSIONS AND FUTURE WORK

The aim of this work was the development of a new partitional clustering algorithm, k-attractors, tailored to numeric data analysis, overcoming the weaknesses of other partitional algorithms.

The initialization phase of the proposed algorithm involves a preprocessing step that calculates the initial partitions for k-attractors. During this phase the exact number of k-attractors clusters was calculated in addition with the initial attractors of each cluster. Thus, the problems of defining the number of clusters and initializing the centroids of each cluster are resolved. In addition, the constructed initial attractors approximate the real clusters' attractors, improving that way the convergence speed of the proposed algorithm.

The main phase of k-attractors forms clusters using a composite distance metric that uses the Hamming distance and the inner product of data item vector representations. Thus, the employed metric is adapted to the way the initial attractors are determined by the preprocessing step.

The last step deals with outliers and is based on the distance between a data item and its cluster's attractor. The discovered outliers are grouped into a separate cluster.

The results from the conducted experiments are promising, as k-attractors' main phase outperformed in performance and accuracy the other algorithms in most of the cases. This is attributed to its initialization phase, which, however, adds an overhead that is deemed acceptable when it contributes significantly to algorithm's accuracy.

For this reason we plan on improving the way the initial attractors are derived to minimize the cost of the initialization phase. We could also attempt to customize the proposed distance metric to adapt it to categorical semantics, thus making it applicable to categorical datasets.

This research was partially supported by the Greek General Secretariat for Research and Technology (GSRT) and Dynacomp S.A. within the program “P.E.P. of Western Greece Act 3.4.” We thank Rob van der Leek, Patrick Duin, and Harro Stokman from the Software Improvement Group for their valuable comments and feedback concerning our clustering results.