PARTICLE SWARM OPTIMIZATION-BASED ALGORITHM FOR BILEVEL JOINT PRICING AND LOT-SIZING DECISIONS IN A SUPPLY CHAIN

Abstract

This study considers joint pricing and lot-sizing policies in a single-manufacturer–single-retailer system. Because a supply chain is a hierarchical system, we adopt a bilevel programming technique to establish a bilevel joint pricing and lot-sizing model guided by the manufacturer. The objective of the problem here is to respectively maximize the manufacturer's and the retailer's net profits by determining the manufacturer's and retailer's lot size, the wholesale price and the retail price simultaneously. Following the properties of the bilevel programming problem (BLPP), we design a novel bilevel particle swarm optimization algorithm (BPSO), and it can solve BLPP without any assumed conditions of the problem. BPSO shows a good performance on eight benchmark bilevel problems. Then BPSO is employed to solve the proposed bilevel model, and the experimental data are used to analyze the features of the proposed bilevel model, and the results support the finding that BPSO is effective in optimizing BLPP.

INTRODUCTION AND LITERATURE REVIEW

Supply chain members gain interest by selling products, and the market demand is sensitive to the selling price of the product. At the same time, lot-sizing ordering can effectively reduce some operation costs such as the retailer's ordering costs and the manufacturer's production costs, so that the decision of pricing and lot-sizing play important roles in optimizing profits in a supply chain. In reality, the retail price should not be too low or too high. On the one hand, if the retail price is too low, the retailer will suffer from low profit or even deficit; on the other hand, the customer will have a lower purchasing intention when the product is too expensive, and this will lead to excess inventory and extra inventory costs for the retailer. Moreover, because of excess inventory, the retailer will reduce ordering times or order quantities from the manufacturer; thus, there will be a serious financial loss for the manufacturer. Therefore, it is very important and necessary to make reasonable pricing and lot-sizing policies. Based on these reasons, there has been substantial research on the optimal pricing problem. Lee and Rosenblatt (1986) develop a quantity discount pricing model for a joint problem of ordering and offering a price discount by a supplier to his sole/major buyer. However, they consider this problem only from the perspective of the supplier, without considering the retail pricing problem from the perspective of the retailer. Yang, Wee, and Yu (2007) consider the collaborative pricing and replenishment addressing an NP-hard network pricing problem. Marcotte, Savard, and Zhu (2009) consider the policy for hi-tech industry. Brotcorne et al. (2011) focus on an improved exact algorithm for characterization of optimal strategies for a service firm acting in an oligopolistic environment, and the decision problem is formulated as a leader–follower game played on a transportation network. In addition, Dewez et al. (2008) and Gao et al. (2011) also establish bilevel models for pricing problems.

As one of the most important problems in supply chain management, the lot-sizing problem has also been extensively studied by many researchers. Guan and Liu (2010) study the stochastic version of lot-sizing problems with inventory bounds and order capacities, and then develop two models in stochastic programming. Lu and Qi (2011) study a new multiproduct, dynamic lot-sizing problem, in which the inventories of all products are replenished jointly with the same quantity whenever a production occurs. Li and Meissner (2011) look into the dynamic lot-sizing and resource competition problem of an industry consisting of multiple firms, and they develop a capacity competition model that combines the complexity of time-varying demand with cost functions and economies of scale arising from dynamic lot-sizing costs.

Although pricing and lot-sizing problems have been extensively studied for the last three decades, the literature on the joint pricing and lot-sizing policies is very sparse. Kunreuther and Richard (1971) are the first to incorporate pricing decisions into the lot-sizing problem, and they derive optimal pricing and lot-sizing decisions for a retailer. Abad (1994) considers the pricing and lot-sizing problem when demand is price sensitive and formulates the problem of coordination between a vendor and a buyer as a two-person, fixed bargaining game. Subsequently, Abad (2003) considers the pricing and lot-sizing problem for a perishable good under finite production, exponential decay, and partial back ordering and lost sale. Then, Teng, Ouyang, and Chen (2007) extend Abad's (2003) model by adding not only the backlogging cost but also the cost of lost goodwill. Dye and Ouyang (2011) establish a deterministic economic order quantity model for a retailer to use to determine optimal selling price, replenishment number, and replenishment schedule with fluctuating demand under two levels of trade credit policy.

In most of the above studies, the pricing and lot-sizing problems are based on traditional modeling methods, and some mature results also have been obtained. However, these traditional modeling methods often neglect the supply chain's characteristic of hierarchy. In fact, supply chain is a complex hierarchical system, and it contains many different interested participants, such as supplier, manufacturer, distributor, retailer, and end customer. These members compose a very long and hierarchical chain. Each of the members in the chain independently controls a set of decision variables, disjoint from the others, and they need to make decisions based on their own interests, while still considering the choice of the others, as the other's decisions will have an influence on their own interests. Therefore, it is very suitable to adopt a bilevel programming problem (BLPP) to model the pricing and lot-sizing problems in a supply chain.

Bilevel programming techniques aim to deal with decision problems involving two decision makers with a hierarchical structure. The leader at the upper level of the hierarchy aims to optimize his own objective function but incorporate within the optimization scheme the reaction of the follower to his course of action Calvete and Galé (2011). Bilevel programming techniques have been remarkably successful when applied to many different areas (Gao et al. 2011), such as mechanics, decentralized resource planning, electric power markets, logistics, civil engineering, and road network management.

Generally speaking, it is very difficult to solve a bilevel programming problem; one reason is that a bilevel programming problem is an NP-hard problem (Jeroslow 1985), and the other reason is the concavity of a bilevel programming problem. Thus far, there are many different methods for solving this problem. The main methods for solving linear bilevel programming problems can be divided into the following four categories (Hejazia et al. 2002): (a) methods based on vertex enumeration, (b) methods based on Kuhn–Tucker conditions, (c) fuzzy approach, and (d) methods based on metaheuristics, such as genetic algorithm-based approaches, simulated annealing-based approaches, and so on. It needs to be pointed out that methods based on vertex enumeration and Kuhn–Tucker conditions have some limitations on solving bilevel programming problems, such as they rely on differentiability of objective function or convexity of search space, and the like, whereas methods based on metaheuristics are independent of these limiting conditions, and they are suitable for solving highly complex nonlinear problems, which traditional search algorithms cannot solve. The metaheuristic optimization algorithms are most widely used in management applications (Sadegheih and Drake 2011). In reality, most of bilevel problems are not merely linear problems; there are many much more complex bilevel programming problems, such as nonlinear bilevel decision problems, multileader bilevel decision problems, multifollower decision bilevel problems, multiobjective bilevel decision problems, and fuzzy bilevel decision problems. Thus, it is very important and necessary to develop effective and efficient methods to solve these problems.

Because of their inherent merits, metaheuristics have won wide attention from many researchers, and they have also been applied to solving bilevel programming problems. Genetic algorithms (GA) have been developed in Hejazia and colleagues (2002), Calvete, Galé, and Mateo (2008), and Li, Lin, and Wang (2010); tabu search is applied in Wen and Huang (1996), Rajesh and coauthors (2003), and Lukač, Šorić, and Rosenzweig (2008); simulated annealing (SA) is applied in Sahin and Ciric (1998); and a neural network approach (NN) is proposed in Shih and colleagues (2004) and Lan and colleagues (2007). A particle swarm optimization (PSO) algorithm is developed for solving the bilevel programming problem in Gao and colleagues (2011), Kuo and Huang (2009), and Li, Tian, and Min (2006).

In this article, we consider the joint pricing and lot-sizing policies by using bilevel programming techniques in a two-echelon system with finite planning horizon. We designate the manufacturer as the leader of the supply chain, and the objective of the problem here is to determine the number of replenishments, the wholesale price, and the retail price simultaneously. Following the properties of the bilevel model derived from this study, we propose a bilevel PSO-based algorithm (BPSO) to find the optimal solutions. Several numerical experiments are used to illustrate the performance of the proposed BPSO algorithm, and then the proposed BPSO algorithm is used to deal with the proposed bilevel model in this article; finally, we analyze the features of the proposed bilevel model by using several examples.

MATHEMATICAL MODEL OF BLPP

BLPP is a special case of multilevel programming problems. In the context of BLPP, the decision maker at the upper level first specifies a strategy, and then the decision maker at the lower level specifies a strategy so as to optimize the objective with full knowledge of the action of the decision maker at the upper level. According to the common notations in bilevel programming, general bilevel problems can be formulated as follows:

where , x is the vector of variables controlled by the leader (upper level variables), and y is the vector of variables controlled by the follower (lower level variables); f ₁(x, y) and f ₂(x, y) are the leader's and the follower's objective functions, respectively; and G (x, y) ≤ 0 and g (x, y) ≤ 0 are corresponding constraints of the upper- and lower-level problems.

In formal terms, bilevel programming problems are mathematical programs in which the subset of variables y is required to be an optimal solution of another mathematical program parameterized by the remaining variables x.

The hierarchical process means that the leader sets the value of his variables first, and then the follower reacts, bearing in mind the selection of the leader.

MODEL FORMULATION

Figure 1 represents a two-echelon hierarchical system, and in this section, a decentralized two-echelon supply chain such as seen in Figure 1 is considered. The manufacturer purchases raw materials from the supplier first, then, after the manufacturer's production and processing, the end products are sold to the retailer. In our model, we suppose that one unit product is produced by one unit raw material, and the product's joint pricing and lot-sizing decisions are also considered. Let the manufacturer be a leader who makes a decision first, and, as a follower, the retailer makes a decision after the manufacturer. The manufacturer may influence but cannot control the retailer's decisions. The manufacturer sets the wholesale price of the products first and then the retailer reacts, bearing in mind the selection of the manufacturer, determining the retail price. In addition, the lot-size decisions of the manufacturer and the retailer are considered, combined with their pricing decisions.

FIGURE 1 A two-echelon hierarchical system.

The first-level objective function defines the manufacturer's number of orders ordered from the supplier and the wholesale price determined by the manufacturer in order to maximize the manufacturer's net profit. The manufacturer's net profit is obtained by deducting the purchasing cost, production cost, transportation cost, holding cost, and ordering cost from the sales revenue. The second-level objective function defines the retailer's number of orders ordering from the manufacturer and the retail price determined by the retailer. The goal is to maximize the retailer's net profit, and the net profit is obtained by deducting the purchasing cost, holding cost, and ordering cost from the sales revenue.

Assumptions and Notations

Some assumptions are given to formulate the mathematical bilevel model.

1.	Both manufacturer and retailer aim to maximize their own profit, and both of them have the right to make decisions.
2.	The market demand is a monotone decreasing function of the retail price.
3.	Manufacturer's and retailer's replenishment rates are instantaneous.
4.	Each replenishment time interval is the same, and no shortage is allowed.
5.	Finite planning horizon is considered.
6.	The component purchase cost and the product price to an end customer do not vary with time in the planning horizon.

The notations used in the article are as follows:

Table

The manufacturer's decision variables
β:	manufacturer's number of orders in the planning horizon
p m :	unit wholesale price of the product
The retailer's decision variables
α:	number of retailer's lot size per manufacturer's lot size
Q :	retailer's lot size
p r :	unit retail price of the product
Other related parameters are as follows
T:	weekly length of the planning horizon
D:	weekly demand rate D = b − a * p r
h m :	manufacturer's weekly holding cost rate
h r :	retailer's weekly holding cost rate
O m :	manufacturer's ordering cost per order
O r :	retailer's ordering cost per order
p s :	manufacturer's unit purchase cost
T c :	unit transportation cost
M c :	unit manufacturing or procurement cost for the manufacturer
∏ m :	manufacturer's net profit in the planning horizon
∏ r :	retailer's net profit in the planning horizon

Model Construction

The net incomes of the manufacturer and the retailer in the planning horizon are, respectively, denoted by I _m and I _r as follows:

Because the manufacturer–retailer-combined average inventory level is α Q/2, and the retailer's average inventory level is Q/2, so the manufacturer's inventory level is Q (α − 1)/2.

The holding costs of the manufacturer and the retailer in the planning horizon are, respectively, denoted by H _m and H _r as follows:

The ordering costs of the manufacturer and the retailer in the planning horizon are, respectively, denoted by C _m and C _r as follows:

The net profits of the manufacturer and the retailer in the planning horizon are, respectively, denoted by ⊓ _m and ⊓ _r as follows:

By combining Equations (1) and (2), we establish a bilevel joint pricing and lot-sizing model in a supply chain as follows:

The relationship between the lot size and the number of deliveries is

We suppose that the retail price is a multiple of the wholesale price, that is,

where k denotes the ratio of the retail price to the wholesale price, and k ≥ 1.

In reality, the wholesale price and retail price should not be too high, and they should have upper limits. Based on Equations (4) and (5), we can transform problem (3) to problem (6) as follows:

where and represent the upper bounds of p _m and k respectively.

The above bilevel model describes a nonlinear bilevel decision problem, for which there is no solution in the classical method. We will develop a PSO-based algorithm to solve the bilevel decision model in the next section.

A BILEVEL PSO-BASED ALGORITHM FOR BLPP

Basic Particle Swarm Optimization

A PSO algorithm is proposed in Kennedy and Eberhart (1995). PSO is a stochastic, population-based evolutionary algorithm (Kumar and Kumar 2010), and PSO has been used effectively in solving complicated optimization problems with simple coding and fewer parameters. PSO takes every single individual as a particle without quality or volume. Each particle flies in the search area with a certain velocity, and it is shown by its geometric position and velocity vector. During each iteration, the particle will track two extreme values: one is the best solution of each particle gained so far, which represents the cognition level of each particle; the other is the overall best solution gained so far by any particle in the population, which represents society cognition level. We suppose that the dimension of the search area is D, and the number of the colony is N. The particle's position and velocity are represented, respectively, by x _i  = (x _i1, x _i2, … , x _iD ) and v _i  = (v _i1, v _i2, … , v _iD ); p _i  = (p _i1, p _i2, … , p _iD ) denotes the best position that the particle has visited, and p _g  = (p _g1, p _g2, … , p _gD ) denotes the best position that the swarm has visited. The particles are manipulated according to the equations below:

and

where 1 ≤ d ≤ D, 1 ≤ i ≤ N, and c ₁ and c ₂ are nonnegative constants, which are called the cognitive and social parameter, respectively; r ₁ and r ₂ are random numbers, which are uniformly distributed in the range (0,1). The pre-set maximum speed is v _id  ∈ [−v _max, v _max], v _max. When j, we set t. Inertia weight is represented by w, which determines the degree of influence that the particle's previous speed has on the current speed.

Inertia weight w plays a very important role in balancing global search ability and local search ability. When w is higher, the global search ability becomes stronger while the local search ability becomes weaker; on the contrary, there is a converse situation.

Shi and Eberhart (1999) propose the linearly decreasing strategy as follows:

where the superscript t denotes the tth iteration, and t _max denotes the iteration's maximum number. The minimum and maximum of original inertia weight are denoted by w _min and w _max, respectively.

Bilevel PSO Algorithm

Constraint Handling Mechanism

For BLPP (1), both the upper-level and the lower-level programming problems are standard constraint optimization problems without considering the information interaction between the leader and the follower, and the constraint handling mechanism is very important for the constraint optimization problem. In this section, we use a penalty function-based technique to deal with the constraints.

First, considering the constraint optimization problem below:

where S is the search space, x ∈ S, and S ⊆ R ⁿ .

By using a penalty factor, Equation (10) can be transformed to the following problem:

where M is a pre-set and very large positive constant called a penalty factor.

Without loss of generality, we take the lower-level programming problem as a single independent constraint optimization problem to describe the constraint handling technique (which is similar to the upper-level programming problem).We suppose that there are p inequality constraints and q equality constraints in the lower-level programming problem, and we also suppose that the decision variable of the upper-level programming problem, x, is given. In the search space, a particle that satisfies the constraints is called a feasible particle, otherwise it is called an infeasible particle. In this condition, we can calculate all particles’ fitnesses (including feasible and infeasible particles) according to the following equations:

and

where S denotes the search space, and Ω(x) is the feasible set of the lower level programming problem.

The Framework of BPSO for Solving BLPP

The following section will present the steps of BPSO for solving BLPP. It contains a main programming algorithm and a subprogramming algorithm, and both of them are based on a basic PSO algorithm. According to the interactive iterations of two basic PSO algorithms, BPSO can solve BLPP without any assumed conditions of BLPP, such as the gradient information of the objective functions, the convexity of constraint regions, and so on. The details are explained as follows.

Algorithm 1

Main programming

	Step 1: Parameters initialization: Initiate the population size N 1, maximum iteration T max1, learning factors c 1 and c 2, maximum inertia weight w max and minimum inertia weight w min, maximum speed v max, and penalty factor M.
	Step 2: Population initialization: Initiate each particle's position x i and velocity v xi according to upper decision variables’ range in the upper level. Initiate each particle's position y i and velocity v yi according to the decision variables’ range in the lower level.
	Step 3: Initiate the leader's loop counter t 1 = 0.
	Step 4: If the algorithm meets the convergence criteria or a maximum number of iterations is attained, go to the final step, if not, execute the following steps (Step 4.1–Step 4.5). Step 4.1: For each given x i , adopt Algorithm 2 to solve the lower-level programming problem to obtain the optimal solution of the lower-level problem y *. Output y * as the response from the follower. Step 4.2: Calculate the fitness value of each particle according to Equations (11) and (12). Step 4.3: Record the ith particle's own best position p xi and the population's best position p xg : if the fitness value (p xi ) is better than the best fitness value in history, set the current value as the new p xi ; choose the particle with the best fitness value of all the particles as the p xg . Step 4.4: Update each particle's position according to Equations (7)–(9). Step 4.5: t 1 = t 1 + 1.
	Step 5: If the algorithm meets the convergence criteria or the maximum number of iterations is attained, go to Step 5; if not, go to Step 3.
	Step 6: Output the final optimal results.

Algorithm 2

Subprogramming PSO-F

	Step 1: Initialize the population size N 2, and the maximum iteration T max2.
	Step 2: Initiate the follower's loop counter t 2 = 0.
	Step 3: Calculate the fitness value of each particle according to Equations (11) and (12).
	Step 4: Record the ith particle's own best position p yi and the population's best position p yg.
	Step 5: Update follower's velocities and positions according to Equations (7)–(9).
	Step 6: t 2 = t 2 + 1.
	Step 7: If the algorithm meets the convergence criteria or the maximum number of iterations is attained, go to Step 8, if not, go to Step 5.
	Step 8: Output the optimal solution of the lower-level problem y *.

NUMERICAL EXPERIMENTS AND MODEL EVALUATION

This section contains two parts: numerical experiments and model evaluation. We test BPSO by using eight bilevel programming problems to illustrate the performance of BPSO; and then, we use BPSO to solve the proposed bilevel joint pricing and lot-sizing model.

Numerical Experiments

To illustrate BPSO's performance, we adopt four linear bilevel programming problems (Kuo and Huang 2009) and four nonlinear bilevel programming problems (Li, Tian, and Min 2006) to test the proposed algorithm BPSO, and then we compare the results solved by BPSO with the results solved by algorithms in the literature.

Parameters setting: Iterations T _max1 = T _max2 = 100; population size N ₁ = N ₂ = 20; learning factors c ₁ = c ₂ = 2.0; maximum inertia weight w _max = 0.9 and minimum inertia weight w _min = 0.4; maximum speed v _max = 10; penalty factor M = 100,000.

For each bilevel problem, we execute BPSO 20 times independently. GA and PSO are two different algorithms given in Kuo and Huang (2009). Hierarchical PSOBLP (HPSOBLP), trust region method(TRM), and original are three different algorithms shown in Li, Tian, and Min (2006).

The best and average results of the four linear bilevel programming problems solved by BPSO are given in Table 1, and the comparisons are given in Table 2 and Table 3. The best results of the four nonlinear bilevel programming problems solved by BPSO and the comparisons are given in Table 4.

TABLE 1 Best and Average Results Based on BPSO

Test problems	Best results		Average results
	f 1	f 2	f 1	f 2
Problem 1	97.7092	−47.8544	88.0164	−45.8822
Problem 2	10.9967	−10.9967	10.9471	−10.9471
Problem 3	15.7157	−3.9211	15.6553	−3.9343
Problem 4	29.7327	−3.0834	29.0413	−3.2731

TABLE 2 Comparisons of the Best Results Based on Different Algorithms

Test problems		BPSO		GA		PSO
		Best solutions	Best values	Best solutions	Best values	Best solutions	Best values
Problem 1	f 1	x = (13.7128,11.3775)	97.7092	x = (17.4582,10.9055)	85.0551	x = (17.4535,10.9070)	85.0700
	f 2		−47.8544		−50.16937		−50.1745
Problem 2	f 1	x = (15.7590,10.9967)	10.9967	x = (15.9984,10.9968)	10.9968	x = (15.9999,10.9998)	10.9998
	f 2		−10.9967		−10.9968		−10.9998
Problem 3	f 1	x = (3.9524,3.9211)	15.7157	x = (3.9994,3.9974)	15.9917	x = (4,4)	16
	f 2		−3.9211		−3.94636		−4
Problem 4	f 1	x = (0.1932,0.3920) y = (0.5424,0.6753,0.4443)	29.7327	x = (0.000,0.898) y = (0.000,0.599,0.399)	29.1480	x = (0.0004,0.8996) y = (0,0.5995,0.3993)	29.1788
	f 2		−3.0834		−3.1930		−3.1977

TABLE 3 Comparisons of the Average Results Based on Different Algorithms

Test problems		Average values
		BPSO	GA	PSO
Problem 1	f 1	88.0164	84.657812	84.85119
	f 2	−45.8822	−50.03023	−50.0781
Problem 2	f 1	10.9471	10.8082	10.9961
	f 2	−10.9471	−10.8082	−10.9961
Problem 3	f 1	15.6553	15.82567	15.98811
	f 2	−3.9343	−3.946363	−3.996343
Problem 4	f 1	29.0413	21.52948	24.81256
	f 2	−3.2731	−3.39072	−3.1977

TABLE 4 Comparisons of the Best Results Based on Different Algorithms

Test problems		Best results
		BPSO	HPSOBLP	TRM	Original
Problem 5	f 1	−15.2023	−14.7578	−12.68	−12.68
	f 2	1.0346	0.2067	−1.016	−1.016
Problem 6	f 1	66.9516	88.7757	88.79	88.79
	f 2	−15.8347	−0.7698	−0.77	−0.77
Problem 7	f 1	2.0191	2.0000	2	2
	f 2	23.9841	24.0190	24.02	24.02
Problem 8	f 1	1.0376	2.7039	2.75	2.75
	f 2	−0.5164	0.5602	0.57	0.57

It can be seen in Table 1 that for the four linear test functions, BPSO can find their solutions. From Table 2 and Table 3, we derive that the best results and average results of the four linear bilevel programming problems solved by BPSO are all better than the results solved by GA and PSO. That is to say, BPSO exhibits a better performance than GA and PSO.

Based on BPSO, we get the best solutions of the four nonlinear bilevel problems as follows: the best solution of Problem 5 is (0.0412, 1.9329, 2.8684, 1.4393), the best solution of Problem 6 is (0.7884, 1.8557), the best solution of Problem 7 is (3.9960, 0.0004), and the best solution of Problem 8 is (0.5014, 0.2026, 0.8275).

From Table 4, we can see that both the best results of the upper-level objective function and lower-level objective function of Problem 6 and Problem 8 solved by BPSO are much better than the results solved by the three algorithms in Li, Tian, and Min (2006). For the best result of the upper-level objective function of Problem 5, BPSO shows a higher accuracy than the other three algorithms. Although for the best result of the lower-level objective function of Problem 5, BPSO is not as good as the other three algorithms, the differences between them are very slight. For the best result of the upper-level objective function of Problem 7, there is only a marginal difference between BPSO and the other three algorithms, and for the best result of the lower-level objective function, BPSO is better than the other three algorithms. In a word, BPSO also shows a good performance on the above four bilevel nonlinear programming problems.

Model Evaluation

In this section, we will adopt BPSO for solving the proposed bilevel joint pricing and lot-sizing model (6). The parameters in model (6) are set as follows: T = 52; h _m  = 0.001; O _m  = 2000; p _s  = 4; h _r  = 0.001; O _r  = 200; T _c  = 0.5; M _c  = 1.

To analyze our model better, we first give the wholesale price an upper bound, . Then we separately consider two upper bounds of the ratio of the retail price to the wholesale price, k ^* = 2 and k ^* = 5. The parameters’ settings of BPSO are the same as the last section, and the results are shown in Table 5 and Table 6.

TABLE 5 Different Results Based on Different Groups of Coefficients (k ^* = 2)

Coefficients of demand function	α	β	p m	k	p r	Q	∏ m	∏ r
a = 2, b = 600	4	4	9.8824	1.9686	19.4545	1824	119290	276100
a = 4, b = 600	4	2	9.4028	1.9422	18.2612	3425	101800	240750
a = 6, b = 600	3	4	9.7944	1.9334	18.9365	2108	100180	228820
a = 8, b = 600	3	3	9.6816	1.9353	18.7368	2601	91331	210130

TABLE 6 Different Results Based on Different Groups of Coefficients (k ^* = 5)

Coefficients of demand function	α	β	p m	k	p r	Q	∏ m	∏ r
a = 2, b = 600	3	4	9.3223	4.6885	43.7076	2221	95188	914110
a = 4, b = 600	5	2	9.8255	4.4534	43.7569	2210	90668	747830
a = 6, b = 600	5	3	9.5964	4.7733	45.8065	1127	62795	609250
a = 8, b = 600	2	2	9.8184	4.3010	42.2289	3408	54517	441050

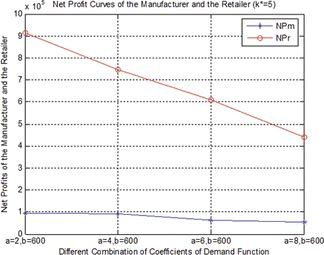
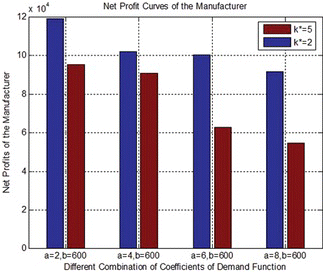
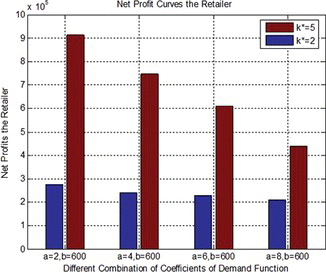
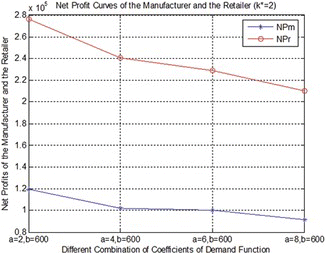
From Table 5 and Table 6, we can see that the higher demand's sensitivity to the price, the lower net profits owned by the manufacturer and the retailer. That is to say, the demand's sensitivity to the price and the manufacturer's and the retailer's net profits are negatively correlated, and this situation abides by the market's rule. The following four figures are given based on Table 5 and Table 6 to illustrate this phenomenon more intuitively.

Figures 2 and 3 show that both the manufacturer's and the retailer's net profits will decrease when the demand's sensitivity to the price is higher, and in these two figures, NP _m and NP _r , respectively, denote the manufacture's and the retailer's net profits. Figures 4 and 5, respectively, show the variations of manufacturer's and the retailer's net profits under different demands. The blue bars and red bars, respectively, denote the conditions of k ^* = 2 and k ^* = 5. From Figures 4 and 5, we can see that for the same demand function, the manufacturer's net profit under the condition of k ^* = 5 is less than under the condition of k ^* = 2, while the retailer's net profit under the condition of k ^* = 5 is much more than under the condition of k ^* = 2, and this is because, compared with k ^* = 2, when k ^* = 5, the retail price increases, but the wholesale price has not changed much. If the manufacturer's interest is violated because of the higher retail price, the manufacturer would raise the wholesale price, and this may lead to increasing retail prices, and eventually the products’ sales volume may reduce because of the higher selling price; and obviously, the manufacturer's and the retailer's profits will reduce too, and this will finally lead to a lower efficiency of the whole supply chain. Therefore, if the manufacturer and the retailer want to maximize their own profits simultaneously, and want to avoid becoming trapped in a vicious circle when the market demand is a monotone decreasing function of the retail price, they should not always raise the price of the product.

FIGURE 2 Net profit curves of the manufacturer and the retailer under the condition of k* = 2. (Color figure available online.)

FIGURE 3 Net profit curves of the manufacturer and the retailer under the condition of k* = 5. (Color figure available online.)

FIGURE 4 Comparison of the manufacturer's net profits. (Color figure available online.)

FIGURE 5 Comparison of the retailer's net profits. (Color figure available online.)

CONCLUSION

In this article, we consider the joint pricing and lot-sizing decisions in a single-manufacturer–single-retailer system with a finite planning horizon. Because the traditional modeling methods often neglect the consideration that a supply chain is a complex hierarchical system, we adopt a bilevel programming technique to establish a bilevel joint pricing and lot-sizing model guided by the manufacturer, and the objective of the problem here is to maximize the manufacturer's and the retailer's net profits, respectively, by determining the manufacturer's and the retailer's number of orders, the retailer's lot size, the wholesale price, and the retail price simultaneously. Following the properties of the bilevel programming problem and the bilevel model derived from this article, we propose a bilevel particle swarm optimization algorithm (BPSO) to find the optimal solutions. To illustrate the performance of BPSO, we first use eight bilevel programming problems including four linear problems and four nonlinear problems to test BPSO. Comparing with other algorithms, BPSO shows a better performance on the eight bilevel programming problems. Then we use BPSO to deal with the bilevel model proposed in this article, and we get the optimal manufacturer's and retailer's number of orders, the optimal retailer's lot size, the optimal wholesale price, and the optimal retail price simultaneously under given conditions. Based on the data, we obtain some results that abide by the market's rule, and one of them is that the demand's sensitivity to the price and the manufacturer's and the retailer's net profits are negatively correlated. We also find that, when the market demand is sensitive to the selling price, if the manufacturer and the retailer want to maximize their own profits simultaneously, they should not always raise the wholesale price and the retail price, because this may lead to the adverse results and a lower efficiency of the whole supply chain. The results of this work also support that BPSO is effective in dealing with BLPP.

Acknowledgments

This work was partly supported by the National Natural Science Foundation of China (71071113), a Ph. D. Programs Foundation of Ministry of Education of China (20100072110011), a Foundation for the Author of National Excellent Doctoral Dissertation of PR China (200782), Shanghai Pujiang Program, and Shanghai Philosophical and Social Science Program (2010BZH003), the Fundamental Research Funds for the Central Universities.

APPENDICES

APPENDIX 1 Linear Bilevel Programming Problems

Problem 1	Problem 2
Problem 3	Problem 4

APPENDIX 2 Nonlinear Bilevel Programming Problems

Problem 5	Problem 6
Problem 7	Problem 8