Immigrant Population Search Algorithm for Solving Constrained Optimization Problems

Abstract

This article introduces the Immigrant Population Search Algorithm (IPSA) inspired by the pattern of human population migration to find better habitats. The algorithm is viewed as a new optimization method for solving constrained optimization problems, and it belongs to the set of population-based algorithms that are proposed for combinatorial optimization. In this algorithm, the life environment is the solution space of the problem. Every point of this space is a solution for the problem, which may be feasible or infeasible, and the quality of life at that point is the value of fitness function for that solution. Each population group tries to investigate feasible and better habitats. In other words, it tries to optimize the problem. After the algorithm steps are described, the efficiency of the algorithm is compared to that of three other metaheuristic algorithms that are used to optimize some mathematic problems. The results show that the proposed algorithm performs better than the other three methods.

INTRODUCTION

Constrained optimization issues are used in several applications such as structural optimization, engineering designs, economy, allocation, and location matters. Usually, optimization should be done on complex or hard functions that are mostly multivariable and nonlinear with some constraints. Most of the time, an analytic solution does not exist, or an access to it is very difficult and time consuming. For example, NP-complete or NP-hard problems cannot be solved within a reasonable time when they are large. Using metaheuristic algorithms (Gogna and Tayal 2013) is a good way to find an optimal or a near-optimal solution to those problems. Some metaheuristic methods are based on a population of solutions. These methods, which are mostly inspired by natural phenomena, suggest solutions to problems by using swarm intelligence. They can be adjusted to solve constrained problems. Some metaheuristic algorithms that are based on the population of solutions are mentioned below as examples.

Genetic algorithm (GA) is based on the theory of Darwinian evolution and is inspired by genetic and natural evolution (D’Ambrosio et al. 2013). In this algorithm, solutions are shown as chromosomes, and the fitness function of the solution represents the quality of the chromosomes. The population of a solution evolves through genetic operators, and a new population is made. There are some methods designed to solve constrained problems by GA (Yeniay 2005).

Particle swarm optimization (PSO) is inspired by the social behavior of animals such as schools of fish or flocks of birds that live in groups and search for food together (Lazinica 2009; Neri, Mininno, and Iacca 2013). In this method, each animal (particle) tries to move in a direction toward where the best individual and group experiences have occurred. For this reason, the velocity of each particle is calculated based on its current position, its best position, and the best position of all the particles. Then, the new position of the particle is calculated. Some surveys were done to adjust PSO to solve constrained problems (Parsopoulos and Vrahatis 2002).

Differential evolution (DE) is a stochastic search that uses the distance and direction information of the current population for a search operation. This characteristic makes it different from other methods (Wang et al. 2013). Also, DE can solve constrained problems (Mezura-Montes, Velázquez-Reyes, and Coello Coello 2006).

Artificial bee colony (ABC) is inspired by the intelligent behavior of honey bees that search for flower nectar (Xiang and An 2013). In this method, each solution is a nectar source, and the amount of nectar in each source is the value of the fitness function for that solution. The honey bees search the problem space to find sources with more nectar (better solutions). Also, ABC is capable of adjusting to solve constrained problems (Karaboga and Basturk 2007; Stanarevic, Tuba, and Bacanin 2011).

Ant colony optimization (ACO) is inspired by the natural behavior of ants that search for food (Dorigo and Stützle 2010). In this method, the path of each ant is a solution to the problem. The method uses a factor that is named a pheromone after the natural chemical substances secreted by ants to communicate with each other. The amount of pheromone represents the abundance of selecting a path in previous solutions. This factor and the quality of a partial solution affect the selection of the partial solution. Constrained optimization problems can be solved by ACO, too (Afshar 2007).

Imperialist competitive algorithm (ICA) is inspired by the social behavior of imperialist countries that benefit from colony countries (Atashpaz-Gargari and Lucas 2007; Abdechiri, Faez, and Bahrami 2010). In this algorithm, every solution is a country, and the power of each country is related to its fitness function value. Powerful countries are imperialists, and weak ones are colonies. Each imperialist has some colonies, and the colonies move toward their imperialists and evolve. Also, imperialists compete to capture each other’s colonies, and the algorithm continues until only one imperialist remains. This method can be used for constrained optimization (Zhang, Wang, and Peng 2009).

Electromagnetism-like algorithm (EM) is inspired by the physical process of attraction and repulsion between charged particles (Jouzdani, Barzinpour, and Fathian 2012). In this algorithm, each solution is a particle, and its fitness function value relates to the amount of its charge. All the particles push one another, and the result of the pushing forces moves the particles. This process usually leads the particles to find better solutions. Also, EM is adjustable to solve constrained problems (Rocha and Fernandes 2008).

In this article, a new optimization algorithm inspired by the social behavior of human population groups that migrate to find better habitats is introduced, and the way of using it for constrained optimization is explained. The algorithm, which is based on the population of solutions, is referred to as an Immigrant Population Search Algorithm (IPSA). The structure of this article is as follows. The next section describes “Constrained Optimization” and is followed by an explanation of the “Conceptual Idea of the Proposed Algorithm.” In “Immigrant Population Search Algorithm,” the steps of the algorithm are described, and “Computational Results” compares the performance of the algorithm with three other algorithms. Finally, “Conclusions” presents the results.

CONSTRAINED OPTIMIZATION

A constrained optimization problem is usually written as an optimization problem in the form of Equation (1):

(1)

where vector is a solution that has m elements (dimensions) and is the objective function. The feasible region is defined by a+b constraints that include a inequality constraints (g) and b equality constraints (h). Equality constraints are difficult to satisfy because they define a very small search space. Therefore, it is a common practice to rewrite equality constraints as inequality constraints, as seen in Equation (2) (Rocha and Fernandes 2008):

(2)

To solve constrained optimization problems, two functions are used: an objective function and a constraint violation function (CV). The value of the constraint violation function is calculated by Equations (3)–(5) (Rocha and Fernandes 2008). Considering Equation (1), Equation (3) calculates the constraint violation value for the inequality constraints. Its violation value is equal to zero if the constraint value is less than or equal to zero (i.e., it satisfies the condition), and it is equal to the constraint value (the violation value) if it is more than zero (i.e., it does not satisfy the condition). Also, considering Equation (2), Equation (4) calculates the constraint violation values for the equality constraints. Its violation value is equal to zero if the constraint value is near zero (i.e., it satisfies the condition), and it is equal to the constraint absolute value (the violation value) if its value is far enough from zero (i.e., it does not satisfy the condition). Finally, the sum of the violation values is calculated by Equation (3):

(3)

(4)

(5)

CONCEPTUAL IDEA OF THE PROPOSED ALGORITHM

The geographical area of a land has regions with different living conditions such as availability of water and food, temperature, wind intensity, amount of rainfall, sunshine intensity, fertility of the ground, availability of natural defense, and so forth. As observed in different land areas, some regions have a higher human population density than others. The higher the quality of the habitat is, the higher the human population density. The quality of a habitat is the result of all the living conditions in that place. But some conditions have more effect and some have less.

The focus of population groups in high-quality habitats is the result of settling, eliminating, and searching processes. When a new land is discovered, there is no information about the quality of its regions. So, when the first population groups want to settle in that land, they are randomly distributed on the land and inhabit there. But later, when a new population group wants to settle and inhabit the land, it observes the habitats of the current population groups and, after comparing their qualities, it chooses a place to inhabit in the neighborhood. The higher the relative quality of a habitat is, the higher the chance of selection by a new population group. This process is repeated for all newly arriving population groups.

Another factor that affects human population density is death. Some population groups are eliminated by the death process, and the quality of their habitats has an effect on it. The lower the relative quality of a habitat is, the higher the probability the population group will be eliminated. So, population groups that inhabit in higher quality habitats have a better chance of remaining.

Also, neighborhood searching affects human population density. Current population groups that have survived a death process search the neighborhood of their habitats to find better ones to inhabit. Neighborhood searching process promotes habitats to higher quality regions.

New coming populations are repeated, settled, and eliminated, and searching processes are done regularly. With an increase in the number of repetitions of this cycle, population groups concentrate around the best-quality residential areas of a given land.

IMMIGRANT POPULATION SEARCH ALGORITHM (IPSA)

In this algorithm, the land is the problem’s solution space, and the different living conditions (e.g., availability of water and food, temperature, etc.) are the dimensions of the land. The number of living conditions (dimensions) is represented by m, and the lower and upper limits of the kth dimension are shown as and , respectively. Each population group lives in a habitat, and each habitat is a solution that has dimensions. If the solution is shown as , its elements (dimensions) are shown as . Also, the life quality of each habitat is the value of the fitness function in that solution and is shown as .

In each repetition of the algorithm, there are some population groups that currently live on the land and some other groups that come newly to settle there. The ith current population group lives in a habitat (solution) that is shown by , and its life quality (fitness function) is shown as . Also, the ith new coming population group settles in a habitat (solution), which is shown by , and its life quality (fitness function) is represented as .

Overview

The proposed algorithm has the following parameters. The size of the current population, represented by nc, and the size of the new coming population, represented by cc. The total number of iterations is represented by MI, and MR is the modification rate. The number of local search iterations is LI; is equal to the final ratio of the local search domain; and Δ is a value for converting equality constraints to inequality constraints. In the algorithm stages, C is the loop counter, RN is the ratio of the neighborhood domain, RL is the ratio of the local search domain, XRL is the ratio coefficient of the local search domain, is the current population, is the new coming population, is the fitness function of the current population, and is the fitness function of the new coming population. The main stages of the proposed algorithm are shown in Algorithm 1. According to this algorithm, after initializing, the steps of migrating, eliminating, local searching, and updating are repeated MI times.

Table

Algorithm 1.

1- Initializing

2-

3- C = C + 1

4- Migrate New Population Group

5- Eliminate Weak Groups

6- Local Search to Find Better Habitats

7- Updating Ratios

8- if , then go to 3

9- End

In the progress of the proposed algorithm, it is necessary to compare two different solutions to determine the better one. Because the solutions can be feasible or infeasible, direct comparing of objective functions is not correct. So, Deb’s rules (Mezura-Montes, Velázquez-Reyes, and Coello Coello 2006) are used instead of that comparison. According to these rules,

1. any feasible solution is better than any infeasible solution;

2. among two feasible solutions, the one having a better objective function value is better;

3. among two infeasible solutions, the one having smaller constraint violation is better.

Initializing

In this stage, the first population groups are established on the vacant land. Thus, according to the lower and upper limits of the problem dimensions, the primary population is randomly created and distributed in the problem space and then RN, RL, and XRL ratios are initialized by Algorithm 2. In this algorithm, U(0,1) is a random real number between 0 and 1. According to the algorithm, XRL ratio is initialized such that, after MI times multiplying, the value of RL reaches the value of .

Table

Algorithm 2.
1- for = 1 to do
1-1- for = 1 to do
1-1-1-
1-1-2-
1-1-3- End for
1-2-
1-3- End for
2-

Migrating

Each newly arriving population group () that decides to settle on the land chooses one of the current population groups by the roulette wheel selection rule and then migrates to its neighborhood. If FXⁱ is the fitness function and CVⁱ is the constraint violation for solution , then the value of Kⁱ is calculated by Equation (6) for feasible solutions in minimizing problems, the value of Kⁱ is calculated by Equation (7) for feasible solutions in maximizing problems, and the value of Kⁱ is calculated by Equation (8) when the solution is infeasible (Stanarevic, Tuba, and Bacanin 2011). Then, using the value of Kⁱ, the selection probability for the ith neighborhood (Pⁱ) is calculated by Equation (9) and, according to this probability, the roulette wheel randomly selects a solution () within the population of current solution ().

(6)

(7)

(8)

(9)

Algorithm 3 is used to establish a new population in the neighborhood of the current population. In this algorithm, after selecting a current solution () by the roulette wheel (line 1-1), the new solution () is equated to it, and then one of the dimensions (gth dimension) is selected randomly. The gth dimension of the new solution () is modified (lines 1-4 to 1-6) considering the neighborhood radius value (R) that is calculated according to the ratio of the neighborhood domain (RN). After this modification, if the value of is out of the upper or lower limits of the problem dimensions, it will be equated to the limit (lines 1-7 and 1-8). The value of fitness function (FYⁱ) is calculated then. This cycle is repeated for times to create a new population.

Table

Algorithm 3.
1- for = 1 to do
1-1- Select from by roulette wheel
1-2-
1-3-
1-4-
1-5-
1-6-
1-7- if then
1-8- if then
1-9-
1-10- End for

Eliminating

To prevent enlargement of the problem, the size of the population must be kept constant; some of the weak solutions, thus, must be eliminated. Accordingly, population is defined as the union of the two populations (current population) and (new coming population). So, population has members, and is the fitness function of its ith member. To eliminate weak solutions, members from population are selected, and the remaining members are eliminated. The best solution of population is always selected, but other nc-1 solutions whose selection probability is proportional to their quality (objective function value) are selected randomly.

In this part, the best solution in population is selected according to Deb’s rules and, after eliminating it from this population, it is added to empty population . Then, for nc-1 times, by using the roulette wheel selection rule (as what is done in “Migrating”), a solution is selected from population and, after eliminating it from this population, it is added to population . Finally, the members of population are replaced by the members of population , and then population is removed.

Local Searching

Local search can improve the solutions. In this part, the algorithm can take two policies. The first policy is that the local search be done in each iteration for all the current population solutions. The second policy is that the local search be done in each iteration only for the best solution of the current population. By the first policy, rather than the second one, better solutions are obtained, but more computing time is taken.

Local searching is the repetition of a process that includes finding a neighbor for the solution, comparing the neighbor with the solution, and replacing the solution with the neighbor if it is better. The steps of the local search are shown in Algorithm 4. In this algorithm, is the current solution that the local search is searching. At first, the neighbor solution () is equated to the current solution (). Then, all of its dimensions are surveyed, and each dimension is selected with the probability MR to modify. The modification (lines 1-2-2-1 to 1-2-2-3) considers the neighborhood radius value (R) that is calculated according to the ratio of the local search domain (RL). The surveyed dimension of the neighbor solution () is then checked not to be out of the upper limit (U_k) or the lower limit (L_k) of that dimension. If it is, then it will be equated to that limit. After surveying all the dimensions, the fitness function is calculated for the neighbor solution. If the neighbor solution () is better (Deb’s rules) than the current solution (), it will be replaced. Otherwise, it will be ignored. These steps are repeated LI times.

Table

Algorithm 4.

1- for = 1 to do

1-1-

1-2- for = 1 to do

1-2-1-

1-2-2- if then

1-2-2-1-

1-2-2-2-

1-2-2-3-

1-2-2-4- if then

1-2-2-5- if then

1-2-2-6- End if

1-2-3- End for

1-3- If is better than then

1-3-1- ,

1-3-2- End if

1-4- End for

Updating

To reach a convergence in the population of the solutions, the ratio of the neighborhood domain must be decreased. Also, the ratio of the local search domain must be decreased by the algorithm progress in order to focus on a solution region and to find a more accurate solution. The experimental computations show that when the ratio of the neighborhood domain decreases linearly and the ratio of the local search domain decreases geometrically, better solutions are obtained. So, according to Equations (10)–(11), the ratios are decreased. In the equation, C is the number of the algorithm iterations.

(10)

(11)

Convergence of the Algorithm

The proposed algorithm structure has three factors that create a scatter in the solution’s population, but the effects of these factors decrease with the algorithm’s progress, as described below.

1. Primary population: the primary population is scattered randomly in the solution space, but, with the progress of the algorithm, the new solutions are created nearby the better previous solutions, and they are finally pulled toward the best solution.

2. Finding neighbors: because the radius of the neighborhood is descending, it is expected that, with the algorithm’s progress, the neighbors will not scatter far from the solutions but rather focus around them.

3. Local search: the radius of finding neighbors in the local search is also descending. So, with the progress of the algorithm, the local search does not find the solutions far from their previous locations.

So, with the algorithm’s progress, it seems that the solutions are converged nearby the best solution of the population.

COMPUTATIONAL RESULTS

To show the performance of the proposed algorithm (IPSA) in solving constrained optimization problems, thirteen sample problems that have been surveyed by other researchers are given from Runarsson and Yao (2000) and used. Each of these problems is a nonlinear programming problem that has some equality and inequality constraints with an objective function that should be maximized or minimized. These problems have been solved 30 times by the IPSA method. Table 1 presents the results including the mean, best, worst, and standard deviation of the objective function’s values. In this table, the bold numbers are the values that reach the problem’s optimal value. As can be seen, the mean, best, and worst values reach the problem’s optimal value for five, six, and five times, respectively. Also, the solutions converge for problems g03, g04, g06, g08, g11, and g12 (the value of their standard deviation is near zero).

TABLE 1 Results of Solving Sample Problems by IPSA

Problem	Goal	Optimal	Mean	Best	Worst	S.D.
g01	Min	−15.000	−14.799998	−14.999999	−12.999998	0.610257
g02	Max	0.803619	0.759755	0.803562	0.706772	0.020177
g03	Max	1.000	1.004634	1.004866	1.004206	0.000192
g04	Min	−30665.539	−30665.538639	−30665.538660	−30665.538599	0.000014
g05	Min	5126.498	5914.861264	5127.526282	6112.198192	360.711661
g06	Min	−6961.814	−6961.809276	−6961.813026	−6961.802327	0.002391
g07	Min	24.306	25.139169	24.498111	26.764343	0.581283
g08	Max	0.095825	0.095825	0.095825	0.095825	0.000000
g09	Min	680.63	680.793875	680.658206	681.069672	0.093441
g10	Min	7049.25	7704.834277	7362.194521	8355.855430	222.668683
g11	Min	0.75	0.749005	0.749000	0.749034	0.000008
g12	Max	1.000	1.000000	1.000000	1.000000	0.000000
g13	Min	0.053950	1.477502	0.135751	10.560852	1.865055

The results are compared with the results of solving those problems 30 times by PSO (Muñoz Zavala, Aguirre, and Villa Diharce 2005), DE (Rocha and Fernandes 2008), and EM (Rocha and Fernandes 2008) methods shown in Tables 2 to 4. In each row of these tables, the bold numbers are the best values in that row.

TABLE 2 Mean Solutions Obtained by IPSA and Three Other Methods

Problem	Goal	Optimal	PSO (Muñoz Zavala, Aguirre, and Villa Diharce 2005)	DE (Rocha and Fernandes 2008)	EM (Rocha and Fernandes 2008)	IPSA
g01	Min	−15.000	−14.710	−14.555	−14.590470	−14.799998
g02	Max	0.803619	0.419960	0.665	0.427705	0.759755
g03	Max	1.000	0.764813	1.000	0.999661	1.000000
g04	Min	−30665.539	−30665.539	−30665.539	−30591.897	−30665.539000
g05	Min	5126.498	5135.973	5264.270	5338.583	5914.861264
g06	Min	−6961.814	−6961.814	—	−6942.915	−6961.809276
g07	Min	24.306	32.407	24.310	53.08965	25.139169
g08	Max	0.095825	0.095825	0.095825	0.095825	0.095825
g09	Min	680.63	680.630	680.630	689.896	680.793875
g10	Min	7049.25	7205.5	7147.334	9492.735	7704.834277
g11	Min	0.75	0.749	0.901	0.749079	0.749005
g12	Max	1.000	0.998875	1.000	1.000000	1.000000
g13	Min	0.053950	0.569358	0.872	2.083421	1.477502

As Tables 1 to 4 suggest, some of the results are better than the problem’s optimal value. This difference is because of the error that results when equality constraints are converted to inequality constraints. In the IPSA, the local search is done for all the current population, and the parameters are determined by a trial-and-error method as follows: , , , , , , and the total iteration value emerges in such a way that the total number of objective function evaluations (240,000) is equal to that for other methods (350,000 times for PSO and 240,000 times for DE and EM). This is also in order for the methods to compete with one another in equal conditions.

Table 2 shows the mean values of the solutions obtained by the IPSA method and compares them with those obtained by the three other methods. As can be seen, these values that are the results of PSO, DE, EM, and IPSA are the best values for eight, seven, four, and six times, respectively, whereas DE solutions are infeasible at least one time during 30 times of solving the g06 problem.

Table 3 shows the best solutions obtained by PSO, DE, EM, and IPSA methods in 30 times of problem solving. As can be seen, these values are the best for seven, nine, six, and eight times, respectively.

TABLE 3 Best Solutions Obtained by IPSA and Three Other Methods

Problem	Goal	Optimal	PSO (Muñoz Zavala, Aguirre, and Villa Diharce 2005)	DE (Rocha and Fernandes 2008)	EM (Rocha and Fernandes 2008)	IPSA
g01	Min	−15.000	−15.000	−15.000	−14.999805	−14.999999
g02	Max	0.803619	0.669158	0.472	0.444939	0.803562
g03	Max	1.000	0.993930	1.000	1.002983	1.004866
g04	Min	−30665.539	−30665.539	−30665.539	−30642.600	−30665.538660
g05	Min	5126.498	5126.484	5126.484	5135.818	5127.526282
g06	Min	−6961.814	−6161.814	−6954.434	−6953.411	−6961.813026
g07	Min	24.306	24.370153	24.306	27.46692	24.498111
g08	Max	0.095825	0.095825	0.095825	0.095825	0.095825
g09	Min	680.63	680.630	680.630	681.777	680.658206
g10	Min	7049.25	7049.381	7049.248	7187.181	7362.194521
g11	Min	0.75	0.749	0.752	0.749001	0.749000
g12	Max	1.000	1.000	1.00	1.000000	1.000000
g13	Min	0.053950	0.085655	0.385	0.063196	0.135751

The worst solutions obtained by PSO, DE, EM, and IPSA methods in 30 times of problem solving are shown in Table 4. As can be seen, these values are the best for eight, seven, three, and seven times, respectively.

TABLE 4 Worst Solutions Obtained by IPSA and Three Other Methods

Problem	Goal	Optimal	PSO (Muñoz Zavala, Aguirre, and Villa Diharce 2005)	DE (Rocha and Fernandes 2008)	EM (Rocha and Fernandes 2008)	IPSA
g01	Min	−15.000	−13.000	−11.828	−12.500515	−12.999998
g02	Max	0.803619	0.299426	0.472	0.377406	0.706772
g03	Max	1.000	0.464	1.000	0.996438	1.004206
g04	Min	−30665.539	−30665.539	−30665.539	−30521.434	−30665.538599
g05	Min	5126.498	5249.825	5534.610	6117.660	6112.198192
g06	Min	−6961.814	−6961.814	−6954.434	−6933.264	−6961.802327
g07	Min	24.306	56.055	24.330	103.5507	26.764343
g08	Max	0.095825	0.095825	0.095825	0.095825	0.095825
g09	Min	680.63	680.631	680.631	701.344	681.069672
g10	Min	7049.25	7894.812	9264.886	16395.51	8355.855430
g11	Min	0.75	0.749	1	0.749346	0.749034
g12	Max	1.000	0.994	1.000	1.000000	1.000000
g13	Min	0.053950	1.793361	0.990	20.784428	10.560852

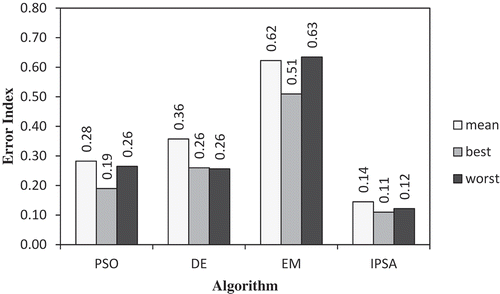
To compare the performance of IPSA with that of the three other mentioned methods, an error index is defined as Equation (12). In this equation, Y is the value of the solution that is obtained by a method, Y_B is the best value, and Y_W is the worst value among the values that result from the methods for the problem.

(12)

For example, for problem g01 in Table 2, the best value and the worst values are −14.800 and −14.555, respectively. So the value of the error index for the PSO method (the solution value of which is −14.710) is 0.3673.

Table 5 shows the values of the error index for the mean of the solutions obtained by IPSA and the other three methods. This table results from Table 2. Because the DE algorithm could not obtain a feasible solution for problem g06, a penalty value 2 is assigned to its error index in Table 5.

TABLE 5 Error Index of the Mean Solutions Obtained by IPSA and the Other Three Methods

Problem	PSO	DE	EM	IPSA
g1	0.3673	1.0000	0.8552	0.0000
g2	1.0000	0.2789	0.9772	0.0000
g3	1.0000	0.0000	0.0014	0.0000
g4	0.0000	0.0000	1.0000	0.0000
g5	0.0000	0.1647	0.2601	1.0000
g6	0.0000	2.0000	1.0000	0.0002
g7	0.2813	0.0000	1.0000	0.0288
g8	0.0000	0.0000	0.0000	0.0000
g9	0.0000	0.0000	1.0000	0.0177
g10	0.0248	0.0000	1.0000	0.2377
g11	0.0000	1.0000	0.0005	0.0000
g12	1.0000	0.0000	0.0000	0.0000
g13	0.0000	0.1999	1.0000	0.5998

Calculating the error index is done also for the best of solutions (resulting from Table 3) and the worst of solutions (resulting from Table 4) as what is done for the mean of solutions. The average of the mean, best, and worst of the calculated error index values are shown and compared in Figure 1. As shown, the IPSA method results in the lowest error index for all the three mean solutions, best solution, and worst solution.

FIGURE 1 Comparing the average of the error index values of IPSA and those of three other methods.

CONCLUSION

In this article, inspired by the migration model of human population groups, the use of an Immigrant Population Search Algorithm for constrained optimization problems is introduced for the first time. The steps of the algorithm include initializing, finding a neighborhood to establish a new population, eliminating weak solutions, replacing the remaining solutions as a current population, and a local search for improving the current solutions. In order to show the performance of this algorithm, thirteen sample problems were solved by the algorithm, and the results—including the mean, best, and worst of the solutions—are compared with the results obtained by solving those problems using PSO, DE, and EM optimization methods through defining an error index. The results show that the proposed method (IPSA) has the lowest error index for all the three means of the solutions, the best solution, and the worst solution.