A Solution to the Combined Economic and Emission Dispatch Using Hybrid PSOGSA Algorithm

ABSTRACT

This article presents a new hybrid algorithm based on particle swarm optimization (PSO) and the gravitational search algorithm (GSA) for solving the combined economic and emission dispatch (CEED) problem in power systems. Performance of this approach for the CEED problem is studied and evaluated on three test systems with 3, 6, and 40 generating units, with various cost curve nature and different constraints. The results obtained are compared to those reported in the recent literature. Those results show that the proposed algorithm provides an effective and robust high-quality solution of the CEED problem.

Introduction

The economic dispatch (ED) problem has a significant importance in the power system’s operation, planning, economic scheduling, and security. The ED problem solution aims to minimize the cost generating electric power through optimal adjustment of the committed generating unit outputs, while satisfying all unit and system constraints. It is a large-scale nonlinear constrained optimization problem. With increased public awareness of environmental pollution, the traditional ED, which ignores the pollutant emissions of fossil fuels used by thermal plants, no longer satisfies the environmental need (Aydin et al. 2014). When the environmental concerns are combined with the ED, then the problem becomes a combined economic and emission dispatch (CEED) problem. This problem considers two objectives: minimization of the fuel cost, and emission from the thermal power plants with both equality and inequality constraints. So, the CEED problem is a multiobjective mathematical problem in which conflicting objectives are optimized simultaneously (Aydin et al. 2014; Güvenç et al. 2012).

The environmental aspect adds complexity to the solution of the economic dispatch problem due to the nonlinear characteristics of the mathematical models used to represent emissions. In addition, the CEED problem can be complicated even further if nonsmooth and nonconvex fuel cost functions are used to model generators, such as valve point loading effects. All these considerations make the CEED problem a highly nonlinear and a multimodal optimization problem (Benasla, Belmadani, and Rahli 2014).

Generally, three approaches to handle the CEED problem have been reported in the literature (Abido 2009). In the first approach, the emission is treated as a constraint with a permissible limit. However, this formulation has severe difficulty in getting the trade-off relations between cost and emission. The second approach treats the emission as another objective in addition to the cost objective. In this case, the CEED problem is converted into a single objective optimization problem either by linear combination of both objectives or by considering one objective at a time for optimization. In the third approach, simultaneously conflicting objectives are evaluated together in the solution of the CEED problem. Both the fuel cost and the emission are minimized together.

In practice, the economic dispatch problem has been solved by using deterministic (classical) and population-based optimization methods. In the past few decades, many classical optimization methods such as gradient method, Newton’s method, linear programming, nonlinear programming, dynamic programming, goal programming technique, and Lagrangian relaxation algorithm have been applied to various ED problems. However, most of them have difficulties in solving ED problems due to nonlinearity and nonconvexity fuel cost and emission characteristics. The conventional optimization methods are highly sensitive to the starting point and frequently converge to local optimum solution. Moreover, these methods are not able to find a solution with a significant computational time for a medium or large-scale CEED problem (Benasla, Belmadani, and Rahli 2014; Niu et al. 2014). It becomes essential to develop optimization methods able to overcome these drawbacks and handle such difficulties.

Recently, many population-based methods have been used to solve complex constrained optimization problems. Generally, achieving an optimal or near-optimal solution for a specific problem will require multiple trials as well as appropriate tuning of associated parameters (Ghasemi et al. 2014). A wide variety of population-based techniques such as the artificial bee colony algorithm (ABC) (Aydin et al. 2014), gravitational search algorithm (GSA) (Güvenç et al. 2012), spiral optimization algorithm (SOA) (Benasla, Belmadani, and Rahli 2014), genetic algorithm (GA) (Gjorgiev and Cepin 2012), nondominated sorting genetic algorithm (NSGA), niched Pareto genetic algorithm (NPGA) (Abido 2006), nondominated sorting genetic algorithm (NSGA II) (Ah King and Rughooputh 2003; Ah King, Rughooputh, and Deb 2005; Alawode, Jubril, and Komolafe 2010), tabu search (Roa-Sepulveda et al. 1996), multiobjective evolutionary programming (MOEP) (Jeyakumar, Venkatesh, and Kwang 2007), DE (Abou El Ela, Abido, and Spea 2010; Perez-Guerrero and Cedeno-Maldonado 2005), multiobjective differential evolution (MODE) (Basu 2011; Sharma et al. 2011; Wu et al. 2010), particle swarm optimization (PSO) (Hazra and Sinha 2011), multiobjective particle swarm optimization (MOPSO) (Abido 2009), and modified bacterial foraging algorithm (MBFA) (Hota, Barisal and Chakrabarti 2010) have been applied in solving the nonlinear CEED problems with different objective functions.

Today, some hybrid algorithms have been proposed to solve the CEED problem. A combination of several population-based algorithms in a hybrid algorithm allows them to exploit the strength of each algorithm. In Niu et al. (2014), the authors proposed a hybrid harmony search (HS) with arithmetic crossover operation, ACHS, for solving five different types of ED problems. Bhattacharya and Chattopadhyay proposed a hybrid DE and biogeography-based optimization (BBO) algorithm, DE/BBO, for solving the economic emission load dispatch problem (Bhattacharya and Chattopadhyay 2011). To solve the highly constrained environmental/economic dispatch problem involving conflicting objectives, the authors in Gong, Zhang, and Qi (2010) proposed a hybrid multiobjective optimization algorithm based on PSO and DE (MODE/PSO). In Sayah, Hamouda, and Bekrar (2014), a hybrid differential evolution algorithm with harmony search (DE-HS) has been proposed to solve the multiobjective environmental/economic dispatch problems that feature nonsmooth cost curves.

This study proposes a hybrid PSO and GSA (hybrid PSOGSA) algorithm to solve the CEED problem. This algorithm profits from the abilities of both PSO and GSA algorithms. The performance of the proposed algorithm is tested on three standard test systems, with different constraints and various cost curve natures. Numerical results obtained by the proposed approach were compared with other optimization results reported in the literature recently.

The rest of the article is organized as follows. In “Problem Formulation,”

the bi-objective CEED problem has been formulated and converted into a single objective optimization problem by the weighted sum method (the second approach was used to handle the CEED problem). In “Hybrid PSOGSA Algorithm,”

the proposed algorithm is presented. “Simulation Results” presents the results of simulation. The conclusion is given in the final section.

Problem Formulation

The solution of the combined economic and emission dispatch problem is achieved by minimizing the objective function (OF) combined with the weighted sum method under the system constraints (Aydin et al. 2014).

(1)

In Equation (1), the fuel cost rate ($/h) is shown with and emission rate (ton/h) with . Scaling factor, weight factor, and the set of all the thermal generation units are denoted as , , and N_G, respectively; corresponds to the minimization of total fuel cost only, likewise, corresponds to the minimization of total emission only.

Fuel Cost Function

Fuel cost function of each generator in the system may be represented as a quadratic function of real power generation:

(2)

where a_n, b_n, and c_n are the cost coefficients.

Large steam turbine generators will have a number of steam admission valves that are opened in sequence to control the power output of the unit. As the unit loading increases, the input to the unit increases, and the incremental heat rate decreases between the opening points for any two valves. However, when a valve is first opened, the throttling losses increase rapidly and the incremental heat rate rises suddenly. This is called valve point effect that leads to nonsmooth, nonconvex input–output characteristics (Benasla, Belmadani, and Rahli 2014). Usually, valve point effect is modeled by adding a recurring rectified sinusoid to the basic quadratic cost function:

(3)

where d_n and e_n are fuel cost coefficients for valve point effects.

Emission Function

Fossil-fueled thermal units cause atmospheric waste emission composed of gases and particles such as carbon dioxide (CO₂), sulfur dioxide (SO₂), nitrogen oxide (NO_x). Different mathematical models were proposed to represent the emission function of thermal generating units (Bhattacharya and Chattopadhyay 2011). In this work, the emission function of each thermal unit is defined as the sum of a quadratic function and an exponential function (Aydin et al. 2014; Güvenç et al. 2012):

(4)

where , , , , and are coefficients of the nth generator emission characteristics. In Equations (2)–(4), the is in MW.

Constraints

During the minimization process, some equality and inequality constraints must be satisfied. In this process, an equality constraint is called a power balance and an inequality constraint is called a generation capacity constraint.

Power Balance Constraint

The total power generation must cover the total load demand P_load and the real power loss in transmission lines P_loss. Accordingly, the power balance constraint can be represented as follows:

(5)

The transmission losses of the system are represented by loss coefficients (B_nj), normally referred to as B-loss matrices. The B-loss matrices approximate the system losses as a quadratic function of the generator real powers:

(6)

where B_nj, B_0n, and B₀₀ are the coefficients of the B-loss matrices.

Generation Capacity Constraint

For stable operation, real power output of each generator is restricted by minimum and maximum power limits as follows:

(7)

Slack Generator Calculation

To enforce the active power balance constraint given in Equation (5), a dependent generator (slack generator) should be selected. As the slack generator, the generator indexed with N_G is adopted. The value of generation power, , is calculated by using Equation (8) where the initial value of power loss is set to zero (Aydin et al. 2014; Gjorgiev and Cepin 2012).

(8)

After obtaining , new power loss, , is determined from Equation (6). According to this, is calculated using the following equation:

(9)

The result of this equation is controlled in Equation (10) and if the error value (ε) is below error tolerance value, TOL_ε (e.g., TOL_ε = 10^–6), the equation satisfies the power balance constraint.

(10)

The obtained is checked to learn whether it satisfies the constraint defined in Equation (7). Consequently, the variable is defined as:

(11)

Inequality constraint of the dependent variable, that is is added to the objective function as a quadratic penalty term. The new expanded objective function to be minimized becomes:

(12)

where λ_p is the penalty factor.

Hybrid PSOGSA Algorithm

Overview of PSO Algorithm

PSO is basically developed through simulation of bird flocking in two-dimensional space. It uses a number of particles (candidate solutions), which fly around in the search space to find the best solution. Meanwhile, the particles all look at the best particle (best solution) in their paths. In other words, particles consider their own best solutions as well as the best solution found thus far. Each particle tries to modify its position using the following information: the current position, the current velocity, the distance between the current position and Pbest, and the distance between the current position and Gbest (Mirjalili and Hashim 2010; Mirjalli, Hashim, and Sardroudi 2012).

The basic elements of the PSO technique are briefly stated and defined as follows (Abido 2002):

Particle, X(t): a candidate solution represented by an n-dimensional vector, where n is the number of control variables. At time (iteration) t, the ith particle X_i(t) can be described as , where xs are the optimized parameters and is the position of the ith particle with respect to the kth dimension, i.e., the value of the kth control variable in the ith candidate solution.

Population, pop(t): a set of N particles at time (iteration) t, i.e.,

Swarm: an apparently disorganized population of moving particles that tend to cluster together although each particle seems to be moving in a random direction.

Particle velocity, V(t): the velocity of the moving particles represented by an n-dimensional vector. At time (iteration) t, the ith particle velocity V_i(t) can be described as , where is the velocity component of the ith particle with respect to the kth dimension.

Individual best, Pbest(t): As a particle moves through the search space, it compares its fitness value at the current position to the best fitness value it has ever attained at any time up to the current time. The best position that is associated with the best fitness encountered so far is called the individual best, Pbest(t). For the ith particle, individual best can be expressed as .

Global best, Gbest(t): the best position among all individual best positions achieved thus far. Hence, global best can be expressed as .

Stopping criteria: the conditions under which the search process will terminate. In this study, the search will terminate if the number of iterations (t) reaches the maximum allowable number.

The PSO can be mathematically expressed as follows:

(13)

(14)

Where w(t) is a weighting factor, C₁ and C₂ are positive constants, r₁ and r₂ are uniformly distributed random numbers in [0, 1].

The first term of Equation (13) provides exploration ability for PSO. For initial stages of the search process, large w to enhance the global exploration is recommended whereas, for the last stages, the weight factor is reduced for better local exploration. The second term of Equation (13) represents the cognitive part of PSO where the particle changes its velocity based on its own thinking and memory. The third term represents the social part of PSO where the particle changes its velocity based on the social-psychological adaptation of knowledge.

The PSO starts by randomly placing the particles in a problem space. In each iteration, the velocities of particles are calculated using Equation (13). After defining the velocities, the positions of particles can be calculated as Equation (14). The process of changing particles’ positions will continue until an end criterion is met.

Overview of GSA Algorithm

The GSA is a newly stochastic search algorithm developed by Rashedi, Nezamabadi-pour, and Saryazdi (2009). In GSA, the search agents are a collection of masses that interact with each other based on the Newtonian gravity and the laws of motion. In this algorithm, agents are considered as objects and their performances are measured by their masses. All these objects attract each other by the gravity force, and this force causes a global movement of all objects toward the objects with heavier masses. The position of the mass corresponds to the solution of the problem, and its gravitational and inertial masses are determined using a fitness function. In other words, each mass presents a solution. The algorithm is navigated by properly adjusting the gravitational and inertial masses. By lapse of time, the masses will be attracted by the heaviest mass, which it represents as an optimum solution in the search space.

The GSA could be considered as an isolated system of masses. It is like a small artificial world of masses obeying the Newtonian laws of gravitation and motion. In a system with N agents (masses), the position of the ith agent is defined by:

(15)

where n is the search space dimension of the problem, i.e., the number of control variables, and defines the position of the ith agent in the kth dimension.

After evaluating the current population fitness, the mass of each agent is calculated as follows (Rashedi, Nezamabadi-pour, Saryazdi, 2009):

(16)

where

(17)

where fit_i(t) represents the fitness value of the agent i at time (iteration) t; best(t) and worst(t) is the best and worst fitness of all agents, respectively, and defined as follows (for a minimization problem):

(18)

(19)

According to Newton’s gravitation theory, the total force that acts on the ith agent in the kth dimension at t time is specified as follows:

(20)

where r_j is a random number in the interval [0, 1], G(t) is gravitational constant at time t, M_i(t) and M_j(t) are masses of agents i and j, ɛ is a small constant, and R_ij(t) is the Euclidian distance between the two agents i and j, given by the following equation:

(21)

Kbest is the set of first K agents with the best fitness value and biggest mass, which is a function of time, initialized to K₀ at the beginning and decreased with time. In such a way, at the beginning, all agents apply the force, and as time passes, Kbest is decreased linearly and at the end there will be just one agent applying force to the others. By the laws of motion, the acceleration of the ith agent, at t time in the kth dimension is given by following equation:

(22)

The searching strategy on this notion can be defined to find the next velocity and next position of an agent. Next velocity of an agent is defined as a function of its current velocity added to its current acceleration. Hence, the next position and next velocity of an agent can be computed as follows:

(23)

(24)

where r_i is a uniform random variable in the interval [0, 1]. This random number is utilized to give a randomized characteristic to the search. The position of agent i in dimension k is represented by , is the velocity, and is the acceleration.

It must be pointed out that the gravitational constant G(t) is important in determining the performance of GSA. It is initialized at the beginning and will be reduced with time to control the search accuracy. In other words, the gravitational constant is a function of the initial value G₀ and time t:

(25)

where α is a user-specified constant, t the current iteration, and T is the maximum iteration number. The parameters of maximum iteration T, population size N, initial gravitational constant G₀ and constant α control the performance of GSA.

Hybrid PSOGSA Algorithm

The basic idea of PSOGSA is to combine the ability for social thinking (gbest) in PSO with the local search capability of GSA (Mirjalili and Hashim 2010; Mirjalli, Hashim, and Sardroudi 2012). In order to combine these algorithms, Equation (26) is proposed as follows (Radosavljević, Arsić, and Jevtić 2014):

(26)

where is the velocity component of the ith agent with respect to the kth dimension at iteration t, C₁ and C₂ are positive constants, r₁, r₂, and r₃ are uniformly distributed random numbers in [0, 1], is the acceleration component of the ith agent with respect to the kth dimension at iteration t, and is the kth dimension of the best solution thus far at iteration t, N is the size of the population (the number of agents), n is the search space dimension of the problem, i.e., the number of control variables.

In each iteration, the positions of agents are updated as follows:

(27)

In PSOGSA, at first, all agents are randomly initialized. Each agent is considered as a candidate solution. After initialization, the gravitational constant and resultant forces among agents are calculated using Equation (25) and Equation (20), respectively. After that, the accelerations of agents are defined as Equation (22). In each iteration, the best solution thus far should be updated. After calculating the accelerations and updating the best solution thus far, the velocities of all agents can be calculated using Equation (26). Finally, the positions of agents are updated by Equation (27). The process of updating velocities and positions will be stopped by meeting an end criterion.

PSOGSA Implementation

The proposed hybrid PSOGSA approach has been applied to solve the CEED problem. The control variables of the CEED problem constitute the individual position of several agents that represent a complete solution set. In a system with N agents, the position of the ith agent is defined by

(28)

The elements of agent X_i are real power outputs of all generation units, except the slack generator. Different steps to solve the CEED problem using PSOGSA are listed in Table 1.

Table 1. Steps of PSOGSA-based approach to solve CEED problem.

Step 1	Search space identification. Initialize PSOGSA parameters such as: N, T, G0, α, C1, and C2.
Step 2	Initialization: generate random population of N agents. The initial positions of each agent are randomly selected between minimum and maximum values of the control variables (i.e., real power outputs of the generation units).
Step 3	Calculate the real power output of slack generator for each agent in current population.
Step 4	Calculate the fitness value for each agent, using Equations (1) and (12).
Step 5	Update the G(t) Equation (25), best(t) Equation (18), worst(t) Equation (19) and Mi(t) Equation (16) for i = 1,2,…,N.
Step 6	Calculation of the total force in different directions, using Equation (20).
Step 7	Calculation of acceleration of each agent using, Equation (22).
Step 8	Calculation of velocity of all agents, using Equation (26).
Step 9	Update each agent’s position, using Equation (27).
Step 10	Repeat Steps 3–9 until the stop criteria is reached. That is a predefined number of iterations, T.
Step 11	Return best solution. Stop.

Simulation Results

The proposed hybrid PSOGSA algorithm is tested on three test systems with 3, 6, and 40 generating units. These test systems are widely used as benchmarks in the power system field for solving the CEED problem (Benasla, Belmadani, and Rahli 2014).

The algorithms have been implemented in MATLAB 2011b computing environment and run on a 2.20 GHz PC with 3.0 GB RAM. Twenty consecutive test runs have been performed for each case examined. The results shown are the best values obtained over these 20 runs. The different algorithms’ parameters used for the simulation are summarized in Table 2. These values of algorithms’ parameters have been adopted after a number of careful experimentations.

Table 2. Simulation parameters used for different algorithms for different test systems.

Methods	Test system 1						Test system 2						Test system 3
	N	T	G0	α	C1	C2	N	T	G0	α	C1	C2	N	T	G0	α	C1	C2
PSO	30	50	-	-	2	2	30	50	-	-	0.5	1.5	100	500	-	-	2	2
GSA	30	50	100	10	-	-	30	50	1	20	-	-	100	500	100	1	-	-
Hybrid PSOGSA	30	50	100	10	2	2	30	50	1	20	0.5	1.5	100	500	100	10	2	2

Test System 1

A system with three units considering NO_x and SO_x emission is used to examine the applicability of the proposed algorithm with a total demand of 850 MW. The operating limits, fuel cost coefficients, and emission coefficients for this system are taken from Benasla, Belmadani, and Rahli (2014) and illustrated in Table 3. The error tolerance value in Equation (10) is taken as MW. The expression for transmission line losses is given by

(29)

Table 3. Generation limits, fuel cost, and emission coefficients of test system 1 (Benasla, Belmadani, and Rahli 2014).

Unit
1	150	600	561	7.9200	0.001562	0.043732540	−9.4868099e-5	1.4721848e-7	0.5783298	0.00816466	1.6103e-6
2	100	400	310	7.8500	0.001940	0.055821713	−9.7252878e-5	3.0207577e-7	0.3515338	0.00891174	2.1999e-6
3	50	200	78	7.9700	0.004820	0.027731524	−3.5373734e-4	1.9338531e-6	0.0884504	0.00903782	5.4658e-6

For this system, the fuel cost and the NO_x and SO_x emission are individually optimized and these individual results are reported in Tables 4–6, respectively. It can be seen that the fuel cost and emission are conflicting objectives. Emission has maximum value when cost is minimized. Table 7 shows the best compromise solution between fuel cost, NO_x emission, and SO_x emission for the test system 1 obtained from proposed approach. In this case, the scaling factor for NO_x emission is taken as 147582.78814 ($/ton) and the scaling factor for SO_x emission is taken as ($/ton). These values are taken from Bhattacharya and Chattopadhyay (2011). The results obtained by the proposed hybrid PSOGSA algorithm were compared to those obtained using other algorithms reported in the literature as shown in Tables 4–7.

Table 4. Minimum fuel cost for test system 1 (P_load</i> = 850 MW).

Method	SOA (Benasla, Belmadani, and Rahli 2014)	NSGA-II (Ah King and Rughooputh 2003)	TS (Roa-Sepulveda et al. 1996)	MOEP (Jeyakumar, Venkatesh, and Kwang 2007)	BBO (Bhattacharya and Chattopadhyay 2011)	DE/BBO (Bhattacharya and Chattopadhyay 2011)	PSOGSA
PG,1 (MW)	445.404	435.885	435.69	437.87	435.1966	435.1978	435.19729
PG,2 (MW)	289.445	299.989	298.828	299.45	299.9723	299.9696	299.96973
PG,3 (MW)	130.427	129.951	131.28	128.49	130.6600	130.6604	130.66195
Total generation (MW)	865.27	865.825	865.798	865.81	865.8289	865.8289	865.82897
Ploss (MW)	15.277	15.826	15.798	15.81	15.8289	15.8289	15.82897
Fuel cost ($/h)	8342.658	8344.598	8344.598	8344.69	8344.5927	8344.58319	8344.59272
NOx emission ton/h)	0.09816	0.09860	0.09863	0.0987	0.098686	0.098686	0.098686
SOx emission (ton/h)	9.00988	9.02129	9.02146	9.01951	9.02195	9.02194	9.021955
ΔP (MW)	−0.25694	−7.4950e-4	−0.00174	0.00661	−1.3096e-4	−0.00113	−1.3605e-6

Table 5. Minimum NO_x emission for test system 1 (P_load</i> = 850 MW).

Method	SOA (Benasla, Belmadani, and Rahli 2014)	NSGA-II (Ah King and Rughooputh 2003)	TS (Roa-Sepulveda et al. 1996)	MOEP (Jeyakumar, Venkatesh, and Kwang 2007)	BBO (Bhattacharya and Chattopadhyay 2011)	DE/BBO (Bhattacharya and Chattopadhyay 2011)	PSOGSA
PG,1 (MW)	511.223	505.810	502.914	507.26	508.5813	508.5813	508.58037
PG,2 (MW)	246.439	252.951	254.294	253.13	250.4433	250.4433	250.44249
PG,3 (MW)	105.751	106.023	108.592	104.41	105.7212	105.7212	105.72297
Total gen. (MW)	863.413	864.784	865.8	864.80	864.7459	864.7459	864.74583
Ploss (MW)	13.414	14.784	15.8	14.8	14.7459	14.7459	14.74583
Fuel cost ($/h)	8355.227	8363.627	8371.143	8364.7	8365.11464	8365.11464	8365.11410
NOx emission (ton/h)	0.09586	0.09593	0.0958	0.09593	0.095923	0.095923	0.095924
SOx emission (ton/h)	8.95982	8.97472	8.9860	8.97428	8.973667	8.973667	8.973668
ΔP (MW)	−1.23536	0.00120	0.97736	0.00571	−5.1003e-5	−5.1003e-5	−1.0205e-6

Table 6. Minimum SO_x emission for test system 1 (P_load</i> = 850 MW).

Method	SOA (Benasla, Belmadani, and Rahli 2014)	NSGA-II (Ah King and Rughooputh 2003)	TS (Roa-Sepulveda et al. 1996)	BBO (Bhattacharya and Chattopadhyay 2011)	DE/BBO (Bhattacharya and Chattopadhyay 2011)	PSOGSA
PG,1 (MW)	599.251	541.308	549.247	552.1111	552.11106	552.11139
PG,2 (MW)	177.771	223.249	234.582	219.4441	219.44402	219.44465
PG,3 (MW)	83.629	99.919	81.893	92.96053	92.95969	92.95979
Total gen. (MW)	860.651	864.476	865.722	864.5158	864.51579	864.51583
Ploss (MW)	10.651	14.476	15.722	14.5158	14.51579	14.51583
Fuel cost ($/h)	8413.031	8387.518	8403.485	8396.4665	8396.4573	8396.46666
NOx emission (ton/h)	0.09950	0.09638	0.0974	0.096817	0.096817	0.096817
SOx emission (ton/h)	8.9371	8.96655	8.974	8.965937	8.965927	8.965937
ΔP (MW)	−3.80554	0.0019	0.91447	−8.3391e-5	−0.00102	1.7869e-6

Table 7. Best compromise solution of fuel cost and NO_x, SO_x emission for test system 1 (P_load</i> = 850 MW).

Method	SOA (Benasla, Belmadani, and Rahli 2014)	NSGA-II (Ah King and Rughooputh 2003)	BBO (Bhattacharya and Chattopadhyay 2011)	DE/BBO (Bhattacharya and Chattopadhyay 2011)	PSOGSA
PG,1 (MW)	513.82835	496.328	507.11954	507.11941	507.12164
PG,2 (MW)	238.96754	260.426	251.64262	251.64185	251.64046
PG,3 (MW)	110.40421	108.144	106.00042	106.00028	106.00047
Total gen. (MW)	863.200	864.898	864.76258	864.76255	864.76257
Ploss (MW)	13.32001	14.898	14.76258	14.76255	14.76257
Fuel cost ($/h)	8356.27194	8358.896	8364.31126	8364.3019	8364.31239
NOx emission (ton/h)	0.09594	0.09599	0.0959248	0.095924	0.095925
Equivalent cost of NOx emission ($/h)	14158.52277	14166.47183	14156.84943	14156.84686	14156.854959
SOx emission (ton/h)	8.95838	8.97870	8.974201	8.974190	8.974200
Equivalent cost of SOx emission ($/h)	8689.90946	8709.62245	8705.25828	8705.24820	8705.257558
Total cost ($/h)	31204.70417	31234.99029	31226.41898	31226.39702	31226.42491
ΔP (MW)	−1.322672	3.8739e-4	−1.8258e-5	−0.001016	4.4107e-6

Tables 4–7 show that the results obtained using hybrid PSOGSA are either better or comparable to those obtained using other techniques. It is quite obvious that the minimum fuel cost, minimum NO_x emission, and minimum SO_x emission obtained from the proposed approach more than the SOA algorithm did(Benasla, Belmadani, and Rahli 2014). However, after the real power losses computation by Equation (29) with control variables reported in Benasla, Belmadani, and Rahli (2014), the obtained results are different from the corresponding values reported in Benasla, Belmadani, and Rahli (2014). So, power generation is not matching load plus losses, and this approach did not meet the power balance constraint. Consequently, the results obtained from the SOA algorithm (Benasla, Belmadani, and Rahli 2014) must be declared as infeasible solutions. In this regard, in order to assess the relevance of the results presented in Tables 4–7, a power balance indicator was introduced as follows:

.

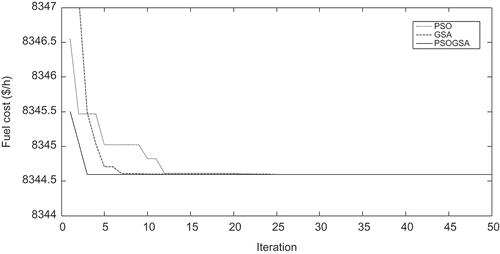
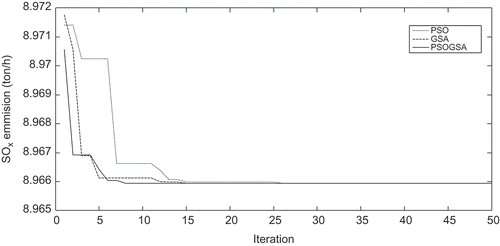
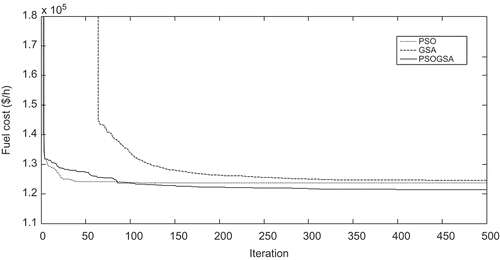
The comparison min, max, and standard deviation of the results obtained by PSO, GSA, and hybrid PSOGSA, over 20 runs, are presented in Table 8. It is obvious that the proposed hybrid PSOGSA approach provides better solutions compared to the original PSO and GSA. Figures 1–3 illustrate convergence characteristics of the algorithms for the fuel cost, SO_x emission and combined fuel cost, and NO_x and SO_x emission minimization, respectively. As can been seen, the proposed hybrid PSOGSA algorithm can converge to its global optimal solution in fewer iterations compared with the original PSO and GSA algorithms.

Table 8. Min, max, and standard dev. of the results obtained over 20 runs with PSO, GSA, and hybrid PSOGSA for test system 1.

Methods	Fuel cost minimization			NOx emission minimization			SOx emission minimization
	Min	Max	Std dev	Min	Max	Std dev	Min	Max	Std dev
PSO	8344.59272	8344.59282	2.04e-5	0.095924	0.095924	1.40e-9	8.965937	8.965937	1.94e-8
GSA	8344.59272	8344.81452	0.05178	0.095924	0.095924	1.69e-8	8.965937	8.966495	1.24e-4
PSOGSA	8344.59272	8344.59272	3.47e-8	0.095924	0.095924	2.59e-12	8.965937	8.965937	1.49e-11

Figure 1. Convergence of algorithms for test system 1 in the case of fuel cost minimization.

Figure 2. Convergence of algorithms for test system 1 in the case of SO_x emission minimization.

Figure 3. Convergence of algorithms for test system 1 in the case of combined fuel cost, NO_x, and SO_x emission minimization.

Test System 2

The standard IEEE 30-bus six-generator system for P_load = 283.4 MW is considered as test system 2. The fuel cost coefficients and the NO_x emission coefficients, including the limits of generation for the generators are listed in Table 9. In this study, the scaling factor in Equation (1) is taken as ($/ton) and the error tolerance value in Equation (10) is MW. The B-loss matrix values are shown as follows:

Table 9. Generation limits, fuel cost, and emission coefficients of test system 2 (Aydin et al. 2014).

Unit
1	5	150	10	200	100	4.091e-2	−5.554e-2	6.940e-2	2.0e-4	2.857
2	5	150	10	150	120	2.543e-2	−6.047e-2	5.638e-2	5.0e-4	3.333
3	5	150	20	180	40	4.258e-2	−5.094e-2	4.586e-2	1.0e-6	8.0
4	5	150	10	100	60	5.326e-2	−3.550e-2	3.380e-2	2.0e-3	2.0
5	5	150	20	180	40	4.258e-2	−5.094e-2	4.586e-2	1.0e-6	8.0
6	5	150	10	150	100	6.131e-2	−5.555e-2	5.151e-2	1.0e-5	6.667

For the purpose of comparison with the reported results, the test system 2 is considered for two cases as follows, Case A: considering P_loss and Case B: neglecting P_loss.

Table 10 shows the optimum solution values of PSOGSA for the weight factor: w = 1 (fuel cost minimization), w = 0 (NO_x emission minimization), and w = 0.5 (combined fuel cost and NO_x emission minimization—CEED minimization).

Table 10. The best solution for fuel cost and NO_x emission for test system 2.

	w	Generation (MW)						Fuel cost ($/h)	NOx emission (ton/h)	Ploss (MW)
		PG,1	PG,2	PG,3	PG,4	PG,5	PG,6
Case A	1	12.09740	28.63094	58.35308	99.28439	52.39978	35.19063	605.99837	0.220728	2.55623
	0	41.09414	46.36880	54.44345	39.03819	54.44012	51.54843	646.20838	0.194179	3.53313
	0.5	22.55343	35.45531	57.00411	74.54079	54.82271	41.55636	612.25222	0.203571	2.53271
Case B	1	10.97109	29.97677	52.42842	101.61927	52.43249	35.97196	600.11141	0.222145	-
	0	40.60721	45.90711	53.79299	38.29620	53.79338	51.00310	638.27284	0.194203	-
	0.5	23.22992	36.03249	53.88335	74.57626	53.88213	41.79586	606.79829	0.203289	-

Under the same system data, control variable limits and constraints, the results for Cases A and B obtained using the hybrid PSOGSA approach are compared to some other algorithms reported in the literature as shown in Tables 11 and 12, respectively. From these tables, it can be seen that the proposed approach outperforms many techniques used to solve CEED problems because the results obtained using hybrid PSOGSA are either better or comparable to those obtained using other techniques. This highlights its ability to find a better-quality solution.

Table 11. Comparison of best solution of test system 2 for Case A.

Methods	Fuel cost minimization (w = 1)		NOx emission minimization (w = 0)		CEED minimization (w = 0.5)
	Fuel cost ($/h)	NOx emission (ton/h)	Fuel cost ($/h)	NOx emission (ton/h)	Fuel cost ($/h)	NOx emission (ton/h)
ABC (Aydin et al. 2014)	605.4258	0.2210	646.0455	0.1942	612.195	0.2035
MOPSO (Abido 2009)	607.7900	0.2193	644.7400	0.1942	615.000	0.2021
PSO (Hazra and Sinha 2011)	607.8400	0.2192	642.9000	0.1942	-	-
GA (Abido 2006)	607.7800	0.2199	645.2200	0.1942	-	-
NSGA (Abido 2006)	607.9800	0.2191	638.9800	0.1947	617.8000	0.2002
NPGA (Abido 2006)	608.0600	0.2207	644.2300	0.1943	617.7900	0.2004
NSGA II (Ah King, Rughooputh, and Deb 2005)	607.8010	0.2189	644.1330	0.1942	-	-
NSGA II (Alawode, Jubril, and Komolafe 2010)	613.6759	0.2223	648.7090	0.1942	-	-
DE (Abou El Ela, Abido, and Spea 2010)	608.0658	0.2193	645.0850	0.1942	-	-
DE (Perez-Guerrero and Cedeno-Maldonado 2005)	606.0000	0.2217	645.5900	0.1942	-	-
MODE (Wu et al. 2010)	606.4160	0.2221	643.5190	0.1942	614.170	0.2043
MODE/PSO (Gong, Zhang, and Qi 2010)	606.0073	0.2209	646.0243	0.1942	-	-
MBFA (Hota, Barisal, and Chakrabarti 2010)	607.6700	0.2198	644.4300	0.1942	616.496	0.2002
MA θ-PSO (Niknam and Doagou-Mojarrad 2012)	605.9984	0.2206	649.2070	0.1942	-	-
PSOGSA	605.99837	0.220728	646.20838	0.194179	612.25222	0.203571

Table 12. Comparison of best solution of test system 2 for Case B.

Methods	Fuel cost minimization (w = 1)		NOx emission minimization (w = 0)		CEED minimization (w = 0.5)
	Fuel cost ($/h)	NOx emission (ton/h)	Fuel cost ($/h)	NOx emission (ton/h)	Fuel cost ($/h)	NOx emission (ton/h)
SOA (Benasla, Belmadani, and Rahli 2014)	600.986	0.20889	640.749	0.18729	624.604	0.18708
MOPSO (Abido 2009)	600.12	0.2216	637.42	0.1942	608.65	0.2017
PSO (Hazra and Sinha 2011)	600.13	0.2199	636.62	0.1943	-	-
GA (Abido 2006)	600.11	0.2221	638.26	0.1942	-	-
NSGA (Abido 2006)	600.34	0.2241	633.83	0.1946	606.03	0.2041
NPGA (Abido 2006)	600.31	0.2238	636.04	0.1943	608.90	0.2015
NSGA II (Ah King, Rughooputh, and Deb 2005)	600.155	0.22188	638.269	0.19420	-	-
NSGA II (Alawode, Jubril, and Komolafe 2010)	600.7422	0.2204	636.7316	0.1942	-	-
DE (Abou El Ela, Abido, and Spea 2010)	600.1114	0.2221	638.2907	0.1942	-	-
DE (Perez-Guerrero and Cedeno-Maldonado 2005)	600.11	0.2231	638.860	0.1952	-	-
MODE/PSO (Gong, Zhang, and Qi 2010)	600.115	0.22201	638.270	0.194203	-	-
MBFA (Hota, Barisal, and Chakrabarti 2010)	600.17	0.2200	636.73	0.1942	610.906	0.2000
MA θ-PSO (Niknam and Doagou-Mojarrad 2012)	600.1114	0.2221	638.2734	0.1942	-	-
PSOGSA	600.11141	0.222145	638.27284	0.194203	606.79829	0.203289

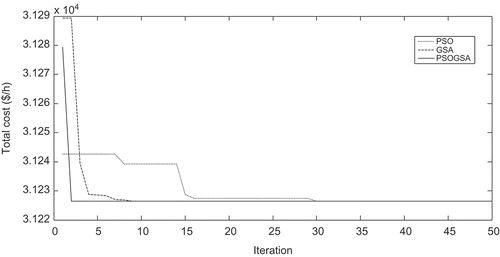
Figure 4 illustrates the convergence characteristics of PSO, GSA, and proposed hybrid PSOGSA for the fuel cost minimization (w = 1) in Case A for the test system 2.

Figure 4. Convergence of algorithms for the fuel cost minimization in Case A for test system 2.

Test System 3

This test system consists of 40 generating units with valve point loading effects and NO_x emission. The total load demand is set to 10,500 MW and no transmission losses are considered. The input data for this test system are taken from (Aydin et al. 2014) and presented in Table 13.

Table 13. Generation limits, fuel cost, and emission coefficients of test system 3 (Aydin et al. 2014).

Unit	(MW)	(MW)	($/h)	($/MWh)	($/(MW)^2h)	($/h)	(rad/MW)	(ton/h)	(ton/MWh)	(ton/(MW)^2h)	(ton/h)	(1/MW)
1	36	114	94.705	6.73	0.0069	100	0.084	60	−2.22	0.048	1.31	0.0569
2	36	114	94.705	6.73	0.0069	100	0.084	60	−2.22	0.048	1.31	0.0569
3	60	120	309.54	7.07	0.02028	100	0.084	100	−2.36	0.0762	1.31	0.0569
4	80	190	369.03	8.18	0.00942	150	0.063	120	−3.14	0.054	0.9142	0.0454
5	47	97	148.89	5.35	0.0114	120	0.077	50	−1.89	0.085	0.9936	0.0406
6	68	140	222.33	8.05	0.01142	100	0.084	80	−3.08	0.0854	1.31	0.0569
7	110	300	278.71	8.03	0.00357	200	0.042	100	−3.06	0.0242	0.655	0.02846
8	135	300	391.98	6.99	0.00492	200	0.042	130	−2.32	0.031	0.655	0.02846
9	135	300	455.76	6.6	0.00573	200	0.042	150	−2.11	0.0335	0.655	0.02846
10	130	300	722.82	12.9	0.00605	200	0.042	280	−4.34	0.425	0.655	0.02846
11	94	375	635.2	12.9	0.00515	200	0.042	220	−4.34	0.0322	0.655	0.02846
12	94	375	654.69	12.8	0.00569	200	0.042	225	−4.28	0.0338	0.655	0.02846
13	125	500	913.4	12.5	0.00421	300	0.035	300	−4.18	0.0296	0.5035	0.02075
14	125	500	1760.4	8.84	0.00752	300	0.035	520	−3.34	0.0512	0.5035	0.02075
15	125	500	1728.3	9.15	0.00708	300	0.035	510	−3.55	0.0496	0.5035	0.02075
16	125	500	1728.3	9.15	0.00708	300	0.035	510	−3.55	0.0496	0.5035	0.02075
17	220	500	647.85	7.97	0.00313	300	0.035	220	−2.68	0.0151	0.5035	0.02075
18	220	500	649.69	7.95	0.00313	300	0.035	222	−2.66	0.0151	0.5035	0.02075
19	242	550	647.83	7.97	0.00313	300	0.035	220	−2.68	0.0151	0.5035	0.02075
20	242	550	647.81	7.97	0.00313	300	0.035	220	−2.68	0.0151	0.5035	0.02075
21	254	550	785.96	6.63	0.00298	300	0.035	285	−2.22	0.0145	0.5035	0.02075
22	254	550	785.96	6.63	0.00298	300	0.035	285	−2.22	0.0145	0.5035	0.02075
23	254	550	794.53	6.66	0.00284	300	0.035	295	−2.26	0.0138	0.5035	0.02075
24	254	550	794.53	6.66	0.00284	300	0.035	295	−2.26	0.0138	0.5035	0.02075
25	254	550	801.32	7.1	0.00277	300	0.035	310	−2.42	0.0132	0.5035	0.02075
26	254	550	801.32	7.1	0.00277	300	0.035	310	−2.42	0.0132	0.5035	0.02075
27	10	150	1055.1	3.33	0.52124	120	0.077	360	−1.11	1.842	0.9936	0.0406
28	10	150	1055.1	3.33	0.52124	120	0.077	360	−1.11	1.842	0.9936	0.0406
29	10	150	1055.1	3.33	0.52124	120	0.077	360	−1.11	1.842	0.9936	0.0406
30	47	97	148.89	5.35	0.0114	120	0.077	50	−1.89	0.085	0.9936	0.0406
31	60	190	222.92	6.43	0.0016	150	0.063	80	−2.08	0.0121	0.9142	0.0454
32	60	190	222.92	6.43	0.0016	150	0.063	80	−2.08	0.0121	0.9142	0.0454
33	60	190	222.92	6.43	0.0016	150	0.063	80	−2.08	0.0121	0.9142	0.0454
34	90	200	107.87	8.95	0.0001	200	0.042	65	−3.48	0.0012	0.655	0.02846
35	90	200	116.58	8.62	0.0001	200	0.042	70	−3.24	0.0012	0.655	0.02846
36	90	200	116.58	8.62	0.0001	200	0.042	70	−3.24	0.0012	0.655	0.02846
37	25	110	307.45	5.88	0.0161	80	0.098	100	−1.98	0.095	1.42	0.0677
38	25	110	307.45	5.88	0.0161	80	0.098	100	−1.98	0.095	1.42	0.0677
39	25	110	307.45	5.88	0.0161	80	0.098	100	−1.98	0.095	1.42	0.0677
40	242	550	647.83	7.97	0.00313	300	0.035	220	−2.68	0.0151	0.5035	0.02075

Table 14 shows the optimum results obtained from the PSOGSA for test system 3. For the purpose of comparison with the reported results, four different cases have been considered, as follows.

• Fuel cost minimization (w = 1).

• NO_x emission minimization (w = 0).

• CEED minimization, with the weight factor and the scaling factor in Equation (1) taken as w = 0.92 and ($/ton).

• CEED minimization, with the weight factor and the scaling factor in Equation (1) taken as w = 0.5 and ($/ton).

Table 14. Best dispatch results of the proposed PSOGSA algorithm for test system 3.

Unit	Fuel cost minimization (w = 1)	NOx emission minimization (w = 0)	CEED minimization (γNOx = 1, w = 0.92)	CEED minimization (γNOx = 0.35198, w = 0.5)
PG,1	113.1715	114.00018	113.99288	114.00008
PG,2	112.8790	114.00000	113.99463	114.00000
PG,3	97.4091	120.00000	120.00000	120.00000
PG,4	179.7441	169.39980	179.73392	178.22399
PG,5	96.9970	97.00000	97.00000	97.00000
PG,6	140.0000	124.37399	139.99861	129.45096
PG,7	259.9108	299.61829	300.00000	300.00000
PG,8	284.6112	297.76836	300.00000	299.88151
PG,9	284.6168	297.24768	299.43437	299.13243
PG,10	130.0000	130.00000	130.00051	130.00000
PG,11	94.0000	298.73754	318.39126	307.47843
PG,12	94.0000	297.98429	318.40027	307.07323
PG,13	214.7602	433.64298	394.29678	433.24767
PG,14	394.2856	421.86130	394.27868	408.80268
PG,15	394.2773	422.33780	394.27977	411.45448
PG,16	394.2807	423.22892	394.27753	410.53116
PG,17	489.2805	439.30460	489.28134	452.30768
PG,18	489.2813	439.36318	489.26948	452.16100
PG,19	511.2746	439.32862	424.05038	437.23697
PG,20	511.2790	439.32231	426.23089	437.48707
PG,21	523.2826	439.34045	433.56936	437.61601
PG,22	523.2804	439.34068	434.43738	437.56132
PG,23	523.3031	439.72475	435.06994	438.12224
PG,24	523.2796	439.66590	434.30689	438.04826
PG,25	523.2825	440.03222	438.95774	437.84051
PG,26	523.2828	440.05940	433.81587	437.88104
PG,27	10.0000	29.13564	10.87493	19.57977
PG,28	10.0000	29.04292	11.47228	19.57858
PG,29	10.0016	29.03909	10.64229	19.55932
PG,30	88.3025	97.00000	96.99793	97.00000
PG,31	190.0000	172.37274	189.99659	175.83358
PG,32	189.9976	172.37803	189.99144	175.79553
PG,33	190.0000	172.35819	189.99684	175.79774
PG,34	199.9994	200.00000	200.00000	200.00000
PG,35	199.9987	200.00000	200.00000	200.00000
PG,36	164.9176	200.00000	200.00000	200.00000
PG,37	110.0000	100.85525	109.99744	104.26519
PG,38	89.7335	101.00509	110.00000	104.27832
PG,39	110.0000	100.79025	109.99126	104.26062
PG,40	511.2794	439.33953	422.97053	437.51262
Fuel cost ($/h)	121461.42914	129986.50060	125710.73492	128710.90485
NOx emission (ton/h)	358155.359339	176678.019377	195418.786862	178591.659226

In Table 15, the optimization results are compared to other optimization algorithms in the literature. Except in the case of the fuel cost minimization, the minimum values of fuel cost and NO_x emission obtained from the proposed PSOGSA are lesser in comparison to reported best results in the literature. The best fuel cost in the case of the fuel cost minimization obtained by PSOGSA is very close to that found with ABC (Aydin et al. 2014), MBFA (Hota, Barisal, and Chakrabarti 2010) and modified adaptive θ-particle swarm optimization (MA θ-PSO) (Niknam and Doagou-Mojarrad 2012) (0.04% difference).

Table 15. Comparison of the results for test system 3.

Methods	Fuel cost minimization (w = 1)		NOx emission minimization (w = 0)		CEED minimization (γNOx = 1, w = 0.92)		CEED minimization (γNOx = 0.35198, w = 0.5)
	Fuel cost ($/h)	NOx emiss. (ton/h)	Fuel cost ($/h)	NOx emiss. (ton/h)	Fuel cost ($/h)	NOx emiss. (ton/h)	Fuel cost ($/h)	NOx emiss. (ton/h)
ABC (Aydin et al. 2014)	121414.80	356421.70	129995.47	176682.25	-	-	-	-
GSA (Güvenç et al. 2012)	-	-	-	-	1.2578e5	2.1093e5	-	-
SOA (Benasla, Belmadani, and Rahli 2014)	125248.114	334880.054	152262.549	120590.839	-	-	140044.658	154291.141
MODE (Basu 2011)	1.2184e5	3.7479e5	1.2996e5	1.7668e5	1.2579e5	2.1119e5	-	-
NSGA II (Basu 2011)	-	-	-	-	1.2583e5	2.1095e5	-	-
MODE (Sharma et al. 2011)	121836.98	374790.56	129956.09	176683.27	-	-	-	-
NSGA II (Sharma et al. 2011)	124963.50	262489.27	129965.89	176691.96	-	-	-	-
MBFA (Hota, Barisal, and Chakrabarti 2010)	121415.653	356424.497	1299950.00	176682.27	-	-	-	-
DE-HS (Sayah, Hamouda, and Bekrar 2014)	121414.937	356432.902	129994.249	176679.684	-	-	128713.887	178634.097
MA θ-PSO (Niknam and Doagou-Mojarrad 2012)	121412.570	359902.189	129995.271	176682.265	-	-	-	-
NPSO-LRS (Selvakumar, Thanushkodi, 2007)	121664.431	-	-	-	-	-	-	-
DEC-SQP (Coelho, Mariani, 2006)	121741.979	-	-	-	-	-	-	-
PSOGSA	121461.429	358155.359	129986.501	176678.019	125710.735	195418.787	128710.905	178591.659

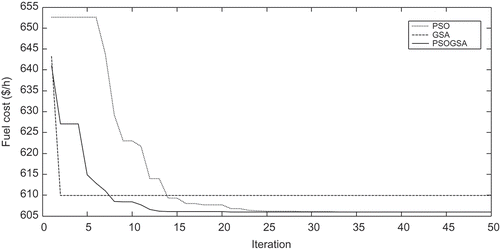
The convergence characteristics of the PSO, GSA, and hybrid PSOGSA for the fuel cost minimization of the 40-generator system are shown in Figure 5. It is clear that the proposed hybrid PSOGSA algorithm can converge to its global best in fewer iterations compared with PSO and GSA algorithms.

Figure 5. Convergence of algorithms for test system 3 in the case of fuel cost minimization.

Conclusion

In this article, a novel hybrid PSOGSA optimization algorithm has been proposed and successfully applied to solve the CEED problem. The proposed approach has been tested and investigated with three different test systems. Simulation results show that the hybrid PSOGSA algorithm provides an effective and robust high-quality solution. Moreover, the results obtained using hybrid PSOGSA are either better or comparable to those obtained using other techniques reported in the literature.

The proposed hybrid PSOGSA algorithm is suitable for solving the complex CEED problem because it benefits from the advantages of both PSO and GSA algorithms.

Funding

This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia under research grant TR 33046.

Additional information

Funding

This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia under research grant TR 33046.