ABSTRACT
This paper presents a trajectory tracking approach based on terminal sliding mode control (TSMC) technique for wheeled mobile robot where the wheel-soil friction can be measured and the estimated errors will converge to their stable values within finite-time, by which the control system is able to be designed in accordance with the prescribed performance. Three kinds of friction effects and their acting mechanisms, at the first place, are argued by exploring the disturbance-like friction behaviors, and then two updated laws, i.e., taking uncertain friction as an entire term or as a parametric form for varied effects, are proposed. In addition, the adoption of TSMC enables the tracking error estimation being faster and more reliable, and the stability and reliability of closed-loop control system are guaranteed by means of Lyapunov stability theorem. Subsequently, the numerical simulation validates the feasibility and effectiveness of the proposed controllers by which the terrain adaptability, movement precision, and maneuvering capability will be improved significantly.
Introduction
Wheeled mobile robots (WMRs) as classic ground vehicle have been paid much more attention for their widespread application value for the past few decades, especially in the sophisticated unstructured environment, see (de Jes´us Rubio, Aquino, and Figueroa Citation2013; Ghaffari, Shariati, and Shamekhi Citation2016; Jiang, Lefeber, and Nijmeijer Citation2001; Li, Zhang, and Yang Citation2010; Samson Citation1995; Sun and Li Citation2015) and the reference herein. For instance, they can be executed independently or with the aid of manipulator to perform dexterous manipulation in varied situation, such as planet exploration, military detecting, opening field exploration, disaster rescue, and so on. However, most of these exploration fields are full of unknown disturbance, and the assignments are dynamic and changeable, which will seriously deteriorate the motion performance, greatly reduce the operating precision, and even directly cause the failure of the detection. Therefore, provided that the mobile platform is under various and dynamic circumstances, determining how to realize flexible operations, strong adaptability, and high reliability is still one of the major problems to be faced with for control community.
The complicated wheel-soil interaction, among the varied unknown disturbance acting on WMRs, is a main source of the perturbation because the contact points of the wheel and ground are the unique place of contact. This wheel-soil interactive force must be considered as designing the control system because it greatly impacts robot performance. The force is different from other tiny forces, e.g. aerodynamic resistance, that can be often neglected especially when the robot undergoes a low speed. After a comprehensive investigation, it reveals that it is similar to the friction that are closely related to the robot velocity, which can also be considered as an uncertain disturbance for the mobile robot, and then in this regards it is named after a wheel-soil friction disturbance in this study. As far as this kind of friction disturbance is concerned, considerable research devotes to establish formulation to compute the values in prior according to the soil parameters and obtain satisfactory application effect when the soil condition is homogeneous (Ding et al. Citation2011; Iagnemma et al. Citation2004; Li, Ding, and Liu Citation2016). However, when the mobile robot suffers from the sophisticated geological conditions, for instance, the hybrid ground mixed by ice or snow and muddy road, it is difficult to accurately calculate this friction disturbance by formulae in advance. In this regard, numerous investigations consider adopting adaptive algorithms to construct update laws for estimating the true values of the friction disturbance instead, which is proven to be much more feasible and effective, especially for the complex and varied geologic conditions. Some researchers were likely to consider the wheel-soil friction as an entire term including both matched and unmatched entries to estimated (see e.g., (Yang et al. Citation2014; Zhang et al. 2015a)), while other studies were concerned with the friction as a parametric form comprised by various friction effects, referred to the reference (De Wit et al. Citation1995; Fang et al. Citation2003; Yue, Wei, and Li Citation2015). Roughly speaking, it is hard to judge which one of the estimated methods have definite advantages since the former is simple and practical, while the latter is detailed and flexible. Hence, for practical implementation, appropriate estimation approach should be chosen according to the special properties and control objective of the control system synthesis.
Furthermore, the closed-loop control system of WMR should guarantee the rapid tracking performance for any arbitrary desired trajectory during the mobile robot performing exploration, which is a significant index to measure the superiority of the robot. Extensive research suggests to apply various schemes to assure the fast convergence of the control system, such as backstepping algorithm (Cui, Guo, and Mao Citation2014; Niu, Liu, and Liu Citation2016), recursive technique (Jiang and Nijmeijer Citation1999; Liu and Jiang Citation2014), fuzzy logic (Li et al. Citation2014b, Citation2016b), neural network Li et al. (Citation2009), Citation2015), model predictive procedure (Yan and Wang Citation2014; Zhang, Zhuang, and Braatz Citation2016), variable structure control (Li et al. Citation2016a; Zhang and Xiang Citation2016), and so on. Among these methods, the common sliding mode control (SMC) exhibits distinguished advantages, e.g., parametric insensitivity and disturbance rejection; however, the control performance cannot be guaranteed strictly because the terminal convergent time of the closed-loop system can merely regulated by trial-and-error method. To overcome this drawback, the developed terminal sliding mode control (TSMC) in recent years abstracts much more attention due to its finite-time convergent property, by which the controller can be designed in accordance with the prescribed desired performances (Hu, Jiang, and Friswell Citation2014; Hu, Zhang, and Friswell Citation2015; Zhang et al. Citation2015b). This unique merit is well suited to the trajectory tracking control for WMR because the desired control performance usually requires the finite time convergence property for friction estimation. A few references were explored by TSMC for WMR where the longitudinal and rotational movements were separately governed, and the results validate the particular effectiveness of TSMC, see (Ding, Li, and Li Citation2010; Hu, Jiang, and Zhang Citation2016; Niu et al. Citation2013) for example.
This study, motivated by the previous works, intends to utilize TSMC to estimate the wheel-soil friction disturbance so as to realize the high tracking performance of the mobile platform. The controllable estimated convergence time makes the closed-loop control system have numerous excellent properties; for instance, the system controller is able to obtain the true values of uncertain friction information with a desired estimated speed, and accordingly, the feed-forward compensation will be more targeted rather than arbitrary, thereby leading to the possibility to design robot controller with prescribed performance. In addition, two main adaptive approaches are employed to estimate friction and comparison studies will develop to illustrate their advantages and disadvantages. The study hereunder is expected to provide a feasible and effective methodology to enhance the mobile robot performance under the sophisticated environment being full of uncertain dynamics and wheel-soil friction disturbance.
Formulation and problem statement
Nonholonomic WMRs system
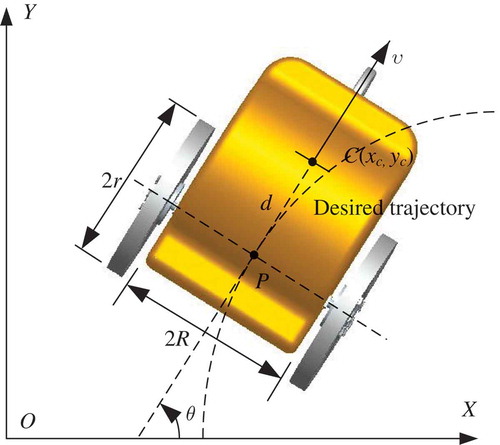
Consider a wheeled mobile robot (as seen in ), and from numerous references, see e.g. (Dixon, Jiang, and Dawson Citation2000), a general dynamic model described such WMRs system can be governed by
where represents system states with
, indicating the coordinates of the center of mass of the vehicle, and θ being the orientation of the vehicle platform with respect to the earth-fixed frame. The control input vector is
where
denote the drive torques for the left and right wheels.
is a symmetric positive definite inertia matrix;
is a centripetal and Coriolis matrix, and it should be noted that
if the mass center is coincident with the centroid;
denotes gravity matrix, and in this case, it equals to zero since the robot operates on the plane;
represents input transformation matrix; and
,
are the entries related to the system nonholonomic constraints.
Meanwhile, the nonholonomic constraints, i.e., pure rolling and nonslipping, need to be satisfied under the condition that enough friction can be provided by the wheel-soil interaction; the vehicle velocities, in this case, should be described as
where and
represent the velocity transformation matrix and velocity vector, respectively, where
denotes the linear velocity of the mass center and
indicates the angular velocity of the mobile robot. In addition,
is the perpendicular distance from the mass center to the wheel axis. It is straightforward that system (2) is a typical nonholonomic constraint because it cannot be integrated to be a linear form.
Provided that is the null space of the matrix
, it holds that
. Differentiating Equation (2) with respect to time and substituting the results in Equation (1), and then multiplying by
on both sides of the equation, the constraint matrix
can be ultimately eliminated from the entire system. Then, an improved dynamic model of the vehicle can be achieved by
Furthermore, for simplification, the system (3) can be rewritten as follows:
where is a symmetric positive definite inertia matrix,
is the centripetal and Coriolis matrix, and
is an input transformation matrix.
With the aid of Lagrange method, with deeply theoretical analyses and calculation, the specific entries of model (1) and (4) can be computed as follows
where is the mass of the vehicle,
is the wheel radius,
is the half wheel base of the mobile platform, and
is the moment of inertia of vehicle with respect to the midpoint of two wheel axles.
Wheel-soil friction disturbance
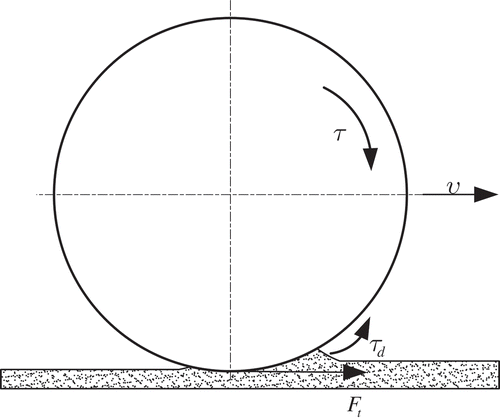
Friction exists extensively in various mechanical motion system, which need to be considered if high performances are required. As for a mobile platform, the friction arises from not only the internal mechanical transmission but also the wheel-soil interaction. The wheel-soil friction plays a much more vital role to determine motion performance since the ground will dissipate larger amounts of drive energy, especially in sophisticated outdoor environment. In general, this kind of wheel-soil friction can be deemed as disturbances for the drive torque of wheel motor because it always takes place as a force or torque form, as illustrated in . Consequently, the disturbance signal can be introduced for the terrain friction on robot wheels, where
denote disturbances for the left and right wheels, respectively, and then the dynamic model (4) can be further formulated as
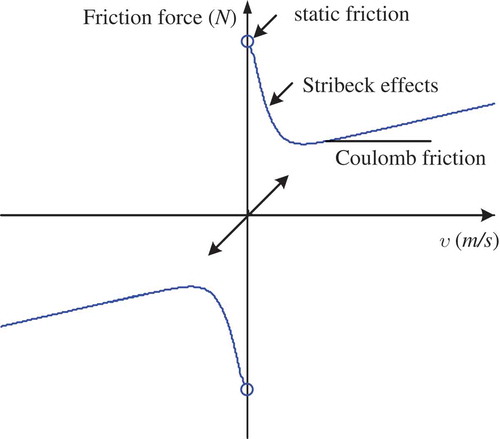
Furthermore, on the basis of preliminary studies and the relative literature bodies about the friction model, it is revealed that most of the friction can be partitioned into three categories: Static, Coulomb, and Stribeck effects, and numerous friction is able to be considered as a combination of these three effects. There exists several models, such as Dahl and Lumped LuGre friction, to address these effects, which are all closely related to the vehicle velocity as shown in , such as Dahl and Lumped LuGre friction. Motivated by the reference (Fang et al. Citation2012; Li et al. Citation2014c; Liu and Tong Citation2016), this study attempts to utilize Stribeck dynamic friction model to describe the sophisticated friction effects of wheel-soil interaction due to its simplicity to facilitate parametric compensation.
In addition, it is well-known that the vehicle friction can be treated as two parts, which is related to the longitudinal and rotational motions respectively. Moreover, the control matrix related to the vehicle geometry parameters can also be considered as a kind of disturbance gain without loss of generality in most cases. Therefore, the wheel-soil friction disturbance can be equivalently augmented as . Then, based on the longitudinal and rotational velocities, the wheel-soil friction disturbances can be governed by
where and
represent unknown positive constants, which denote different friction coefficients of disturbance. With the above definition and assumption, the system (5) can be further rewritten as
Remark 2 The wheel-soil friction model (6) is introduced under the assumption that the pure rolling constraint is hold, that is, it is supposed that there exists sufficient friction to prevent the slipping and skidding of vehicle wheels.
Consequently, the control objective of this study, from system (7), is to find a control input such that the actual velocity
can track the desired velocity generated by the reference trajectory, all signals of the closed-loop tracking system need to converge to a compact set in finite time, and the wheel-soil friction disturbance should be rejected adaptively.
Finite-time SMC
SMC, as a kind of variable structure control technique, has numerous advantages, such as parameter insensitivity, fast convergent rate, and disturbance rejection. Besides, compared with other traditional design methods, TSMC is widely used recently since the convergence time can be effectively controlled, which will enable the close-loop systems to reach the desired prescribed performance (see e.g. (Li et al. Citation2013, Citation2014a; Hu, Xiao, and Shi Citation2015)); thus, the TSMC with finite-time property is utilized here to construct the controllers for the WMRs.
On the other hand, it needs to be emphasized that systems (5) and (7) are based on the vehicle velocities, but for practical implementation, the WMRs must fulfill position tracking. In this regard, the sliding mode surface must include vehicle position messages; taking into account this point, the system (7) needs to be rewritten as
where with
representing the longitudinal displacement and
denoting the orientational angle of the mobile platform;
, with
,
, represents the new control input for simplicity along the vehicle longitudinal and rotational directions, respectively;
is a symmetric positive definite inertia matrix;
is the disturbance term including system uncertainty. Define the desired reference trajectory as
, then it holds that
. Consequently, a series of tracking errors and their differentiation can be calculated as follows:
,
,
in the following.
Lemma 3 The system can be globally stabilized in finite time under the feedback control law:
where satisfying
and
with
representing the signum function.
With the above Lemma 3, a sliding mode surface with fractional order can be defined as
where is a positive definite symmetric matrix,
, and
satisfying
.
Based on the above analysis, a theorem can be given as follows:
Theorem 3.1. Consider the WMRs system (5) related to the vehicle velocities and its another form [Equation (8)] based on the posture with the wheel-soil friction as Equation (6), and if the terminal sliding mode surface is defined as Equation (10), then the closed-loop mobile robot tracking system is uniformly ultimately bounded (UUB) and the tracking errors will converge to any arbitrary reference trajectory in finite time with the system controller as
Where and
are positive definite symmetric matrices;
, and
are positive design parameters.
Proof: Consider a positive Lyapunov function candidate as
Differentiating Equation (12) with respect to time along the trajectory [Equation (8)] yields
By substituting the proposed controller (11) into (13), it results in
According to Lyapunov Stability Theorem and LaSalle Invariance Principle, it is straightforward to conclude that Theorem 3.1 holds.
Adaptive laws for estimation
As seen from controller (11), it cannot be directly applied in practice because the friction disturbance term is unavailable in prior; therefore, the adaptive laws need to be utilized to enhance the feasibility of control system, regarding the slow time-varying behaviors of the disturbance-like wheel-soil friction. The estimated value of disturbance term, in order to adopt adaptive laws, should be defined in the first place as follows:
where represents the introduced parameters to describe the different friction effects.
Considering the diverse mechanism of longitudinal and rotational movements, different are employed for these two categories in this scenario. Besides, the estimated errors, in the following, can be defined as
where represents the parameters related to the estimated errors.
Entire friction estimation
From the above analysis, the wheel-soil friction disturbance can be treated as a global uncertain term or parameterized form to be estimated in real time. In the first place, the friction disturbance, for simplicity, can be deemed as a global entry when the inner friction effect mechanisms are ignored; in this regard, an updated law can be introduced to approach the true value of the uncertain disturbance. Notice that due to the slow time-varying characteristic of the wheel-soil friction feature, i.e.
. Therefore, a theorem can be given as
Theorem 4.1. Consider the WMRs system (5) where the uncertain wheel-soil friction is considered as a global term, and if the terminal sliding mode surface is defined as Equation (10), then the closed-loop mobile robot tracking system is uniformly ultimately bounded (UUB) and the tracking errors will converge to any arbitrary reference trajectory in finite time with the system controller as
where the estimated friction term can be governed by the updated law as
where is the design parameter by which the convergence time can be regulated according to the required control performance.
Proof Consider the following positive Lyapunov function candidate as
Differentiating Equation (17) with respect to time yields
By substituting Equations (15) and (16) into Equation (18), it holds that
According to Lyapunov stability theorem and LaSalle invariance principle, the system under the action of the adaptive controller (15) and updated law (16) is asymptotically stable.
Parametric friction estimation
The wheel-soil friction disturbance, as previous analysis, can be partitioned into three entries with varied coefficients according to the different friction effect mechanisms for a practical WMR; likewise, the updated law can also be designed to estimate the parameter in real time to enhance the adaptability of closed-loop system. In the same way, define
as the estimated value of friction coefficients of disturbance, and then let
be the estimated error for the parametric wheel-soil friction. Hence, according to the slow time-varying characteristic of physical parameter, it indicates that the friction disturbance with parametric form can be estimated by constructing adaptive laws. Then, a theorem based on this standpoint can be given as
Theorem 4.2 Consider the WMRs system (5) where the uncertain wheel-soil friction is considered as a parametric form, and if the terminal sliding mode surface is defined as Equation (10), then the closed-loop mobile robot tracking system is uniformly ultimately bounded (UUB) and the tracking errors will converge to any arbitrary reference trajectory in finite time with the system controller as
and the parametric coefficients can be updated by
where , which is the design parameter determining the convergence time of estimated process.
Proof Consider the following positive Lyapunov function candidates as follows:
As far as the longitudinal movement is concerned, in the first place, differentiating with respect to time yields
Likewise, with the rotational movement, differentiating with respect to time results in
By substituting the previous controllers (19), and the updated laws (21) into , it holds that
Similarly, by substituting the previous controller (20), and the updated laws (21) into , it follows that
It implies that . According to Lyapunov stability theorem and LaSalle Invariance Principle, the theorem can be readily proven.
Last but not least, it should be pointed out that the sign function, , in the previous controllers, such as Equations (11), (15), (19), and (20) can be replaced by hyperbolic tangent function, i.e.,
, where the design parameter
is a positive design parameter. In addition, the design parameters are selected with a trial-and-error process, which is essentially a trade-off between various control performances.
Numerical study
This section is concerned with the numerical simulation to validate the effectiveness and feasibility of the proposed controllers for a practical WMR suffered from the uncertain wheel-soil friction disturbance. Let us assume the mechanical parameters of the simulated WMR as follows: ; after that, by trial-and-error approach, according to the required control performance, the design parameters in controllers (19)–(21) can be chosen as follows:
and
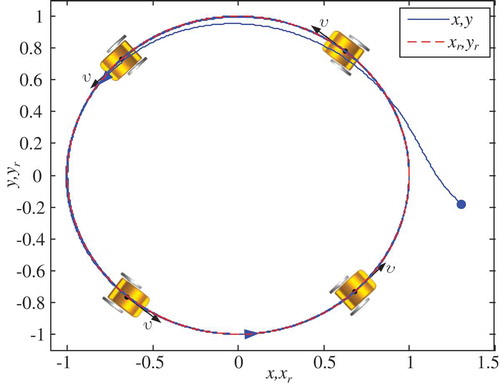
. Meanwhile, a wheel-soil friction disturbance with abrupt forms is introduced to verify the disturbance adaptability of the closed-loop control system. Besides, in order to demonstrate the steering and tracking performances of the mobile robot much better, a circular reference trajectory is hypothesized with
and
, and afterward, the reference trajectory can be computed by
where
in this case denotes the circle radius, and
. In addition, the initial posture errors in earth-fixed frame are taken as
.
The reference and practical trajectories are illustrated in , which reveal that the WMR can track the arbitrary reference trajectory well after a period of adjusting time, although the robot is suffering with uncertain wheel-soil friction disturbances. It should be mentioned that the adjusting time will become shorter by increasing the design parameters, such as and
, while the other tracking performance, like maximum overshoot, will become severe afterwards. Therefore, the tracking performances are a trade-off between various excellent but incompatible performances; in this regard, the design parameters can be determined by trial-and-error approach according to the required control objective.
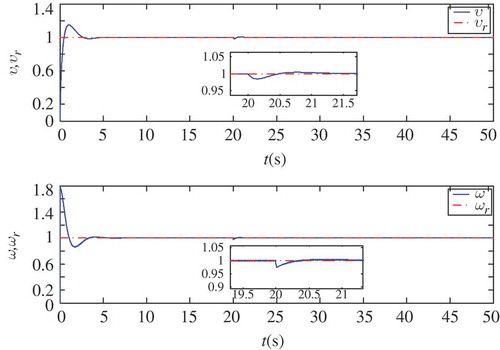
illustrates the responses of velocity tracking process of WMR, where it is clearly shown that the velocities of the mobile platform, i.e., and
, can approach the desired velocities i.e.,
and
, that are calculated by the coordinates of earth-fixed frame. Also, it is noted that the tracking process is closely related to the sign or hyperbolic tangent functions used in the controllers, and the simulation results imply that if the continuous and differentiable hyperbolic tangent functions are applied to replace the sign function, then the tracking process becomes gentle suddenly, thereby leading to the implementation of the control input to the WMR system.
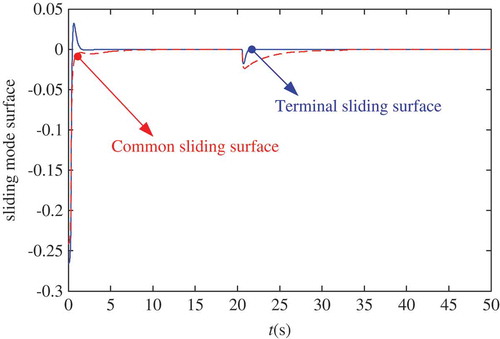
Furthermore, another contribution lies in that the TSMC is adopted to achieve excellent control performance; thus, the comparison is carried out here to highlight the special advantages with respect to the common sliding mode algorithm. The time responses of sliding mode surfaces, including both common SMC and TSMC, are depicted in , which implies that both SMC and TSMC are able to make the sliding manifold converge to zero, despite the sudden change in the uncertain wheel-soil friction disturbance. For example, at the start time, the convergent time of common sliding mode surface is about 5 seconds, while that of the terminal sliding mode surface only undergoes 1 second. Similar faster convergent phenomena also takes place on 20s where a sudden changed friction occurs. Meanwhile, the convergent time for terminal sliding mode surface can be controlled by selecting appropriate design parameters, such as and
, of course, at the expense of increasing the overshoot.
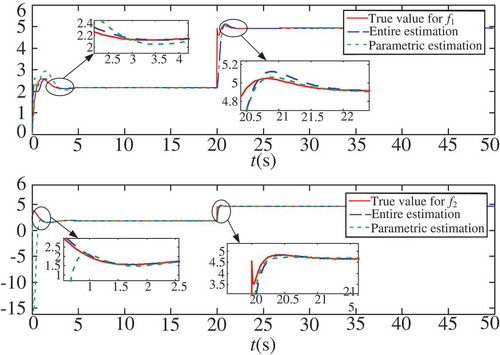
Moreover, the special merit of this proposed controller is the adaptivity with respect to the uncertain friction disturbance, and in order to highlight this point, the estimation for a hypothesized friction is depicted in , where the true disturbance with sudden changed form is plotted by a solid line, and the estimated value is given by the broken line: one for entire estimation and the other for parametric estimation. The simulation results demonstrate that, with the selected control parameters, both of the regulation times are fast enough to be acceptable for the required estimated performance; therefore, it also reveals that TSMC shows significantly convergence properties. From the drawings of partial enlargement, it suggests that the estimation process for parametric friction seems to be little worse compared with the entire friction one. This is because that the parametric friction has much more parameters to be estimated, thereby leading to the worse performance.
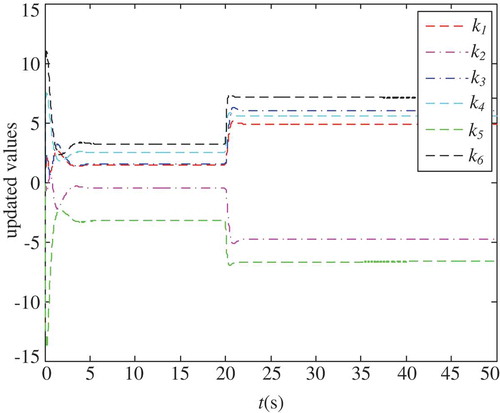
Considering that the friction disturbances acting on the left and right wheels are quite complicated, the proposed approach employs six independent coefficients to describe the longitudinal and rotational movements related to the mobile robot separately. It is supposed that the initial wheel-soil friction with the coefficients as , change to be another series at 20 seconds, and the system initial friction coefficients are redefined as
. As shown in , each friction coefficient quickly reaches its new steady value in 4 seconds under the action of TSMC at the initial scenario, while as for the abrupt scenario, it merely takes about 2 seconds that each friction coefficient rapidly makes the adaptive adjustment and eventually reaches other new stable values. This result clearly demonstrates that by the proposed updated laws, each friction coefficient can converge to a steady value at a fast enough speed, which further indicates the excellent self-adapting feature and embodies the contributors of varied friction effects.
Conclusion
In this study, an adaptive TSMC approach is proposed for the trajectory tracking of wheeled mobile robot, in which the wheel-soil friction acting on the robot wheel is taken into account as an uncertain disturbance. This friction disturbance can be estimated by a whole item or by three parametric entries in real time, and then, it will be compensated by feed-forward compensation in the following. The research results reveal that TSMC enables the friction estimation with finite-time convergence characteristic, thereby making the friction compensation fast and accurate; therefore, compared with the common SMC, TSMC is more suitable for the practical tracking control system. Admittedly, in terms of the friction estimation, two methods, including taking friction as a whole item or as three parametric entries, are adopted, and the investigation verifies their respective advantages: the former is simple and practicable, but the latter can clearly exhibit various friction effects, which will provide the possibility of purposeful control for the wheel-soil friction.
Funding
This research is supported by grants from the National Natural Science Foundation of China (Nos. 61573078 and 51475115), the International S&T Cooperation Program of China (No. 2014DFB70120) and the State Key Laboratory of Robotics and System (Nos. SKLRS2015ZD06 and SKLRS2009MS07).
Additional information
Funding
References
- Cui, R. X., J. Guo, and Z. Y. Mao. 2014. Adaptive backstepping control of wheeled inverted pendulums models. Nonlinear Dynamics 79:501–11. doi:10.1007/s11071-014-1682-9.
- De Jes´Us Rubio, J., V. Aquino, and M. Figueroa. 2013. Inverse kinematics of a mobile robot. Neural Computing and Applications 23:187–94. doi:10.1007/s00521-012-0854-0.
- De Wit, C. C., H. Olsson, K. J. Astrom, and P. Lischinsky. 1995. A new model for control of systems with friction. IEEE Transactions on Automatic Control 40:419–25. doi:10.1109/9.376053.
- Ding, L., H. B. Gao, Z. Q. Deng, K. Nagatani, and K. Yoshida. 2011. Experimental study and analysis on driving wheels performance for planetary exploration rovers moving in deformable soil. Journal of Terramechanics 48:27–45. doi:10.1016/j.jterra.2010.08.001.
- Ding, S. H., S. H. Li, and Q. Li. 2010. Global uniform asymptotical stability of a class of nonlinear cascaded systems with application to a nonholonomic wheeled mobile robot. International Journal of Systems Science 41:1301–12. doi:10.1080/00207720902974579.
- Dixon, W. E., Z. P. Jiang, and D. M. Dawson. 2000. Global exponential setpoint control of wheeled mobile robots: A Lyapunov approach. Automatica 36:1741–6. doi:10.1016/S0005-1098(00)00099-6.
- Fang, Y. C., W. E. Dixion, D. M. Dawson, and E. Zergeroglu. 2003. Nonlinear coupling control laws for an underactuated overhead crane system. IEEE/ASME Transactions on Mechatronics 8:418–23. doi:10.1109/TMECH.2003.816822.
- Fang, Y. C., B. J. Ma, P. C. Wang, and X. B. Zhang. 2012. A motion planning-based adaptive control method for an underactuated crane system. IEEE Transactions on Control Systems Technology 20:241–8.
- Ghaffari, A., A. Shariati, and A. H. Shamekhi. 2016. A modified dynamical formulation for two-wheeled self-balancing robots. Nonlinear Dynamics 83:217–30. doi:10.1007/s11071-015-2321-9.
- Hu, Q. L., B. Y. Jiang, and M. I. Friswell. 2014. Robust saturated finite time output feedback attitude stabilization for rigid spacecraft. Journal of Guidance, Control, and Dynamics 37:1914–29. doi:10.2514/1.G000153.
- Hu, Q. L., B. Y. Jiang, and Y. M. Zhang. 2016. Output feedback attitude tracking for spacecraft under control saturation and disturbance. Journal of Dynamic Systems, Measurement, and Control, Transactions of the ASME 138:011006. doi:10.1115/1.4031855.
- Hu, Q. L., B. Xiao, and P. Shi. 2015. Tracking control of uncertain Euler-Lagrange systems with finite-time convergence. International Journal of Robust and Nonlinear Control 25:3299–315. doi:10.1002/rnc.v25.17.
- Hu, Q. L., J. Zhang, and M. I. Friswell. 2015. Finite-time coordinated attitude control for spacecraft formation flying under input saturation. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME 137:061012. doi:10.1115/1.4029467.
- Iagnemma, K., S. Kang, H. Shibly, and S. Dubowsky. 2004. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers. IEEE Transactions on Robotics 20:921–7. doi:10.1109/TRO.2004.829462.
- Jiang, Z. P., E. Lefeber, and H. Nijmeijer. 2001. Saturated stabilization and tracking of a nonholonomic mobile robot. Systems and Control Letters 42:327–32. doi:10.1016/S0167-6911(00)00104-3.
- Jiang, Z. P., and H. Nijmeijer. 1999. A recursive technique for tracking control of nonholonomic systems in chained form. IEEE Transactions on Automatic Control 44:265–79. doi:10.1109/9.746253.
- Li, Z. J., Z. T. Chen, J. Fu, and C. Y. Sun. 2016b. Direct adaptive controller for uncertain MIMO dynamic systems with time-varying delay and dead-zone inputs. Automatica 63:287–91. doi:10.1016/j.automatica.2015.10.036.
- Li, H. Y., B. Chen, C. Lin, and Q. Zhou. 2009. Mean square exponential stability of stochastic fuzzy Hopfield neural networks with discrete and distributed time-varying delays. Neurocomputing 72:2017–23. doi:10.1016/j.neucom.2008.12.006.
- Li, Y. K., L. Ding, and G. J. Liu. 2016. Attitude-based dynamic and kinematic models for wheels of mobile robot on deformable slope. Robotics and Autonomous Systems 75:161–75. doi:10.1016/j.robot.2015.10.006.
- Li, H. Y., H. J. Gao, P. Shi, and X. D. Zhao. 2014a. Fault-tolerant control of Markovian jump stochastic systems via the augmented sliding mode observer approach. Automatica 50:1825–34. doi:10.1016/j.automatica.2014.04.006.
- Li, H. Y., X. J. Jing, H. K. Lam, and P. Shi. 2014b. Fuzzy sampled-data control for uncertain vehicle suspension systems. IEEE Transactions on Cybernetics 44:1111–26. doi:10.1109/TCYB.2013.2279534.
- Li, H. Y., P. Shi, D. Y. Yao, and L. G. Wu. 2016a. Observer-based adaptive sliding mode control for nonlinear Markovian jump systems. Automatica 64:133–42. doi:10.1016/j.automatica.2015.11.007.
- Li, Y. M., S. C. Tong, Y. J. Liu, and T. S. Li. 2014c. Adaptive fuzzy robust output feedback control of nonlinear systems with unknown dead zones based on a small-gain approach. IEEE Transactions on Fuzzy Systems 22:164–76. doi:10.1109/TFUZZ.2013.2249585.
- Li, H. Y., J. Y. Yu, C. Hilton, and H. H. Liu. 2013. Adaptive sliding-mode control for nonlinear active suspension vehicle systems using T–S fuzzy approach. IEEE Transactions on Industrial Electronics 60:3328–38. doi:10.1109/TIE.2012.2202354.
- Li, Z. J., H. Z. Xiao, C. G. Yang, and Y. W. Zhao. 2015. Model predictive control of nonholonomic chained systems using general projection neural networks optimization. IEEE Transactions on Systems, Man, and Cybernetics: Systems 45:1313–21.
- Li, Z. J., Y. N. Zhang, and Y. P. Yang. 2010. Support vector machine optimal control for mobile wheeled inverted pendulums with unmodelled dynamics. Neurocomputing 73:2773–82. doi:10.1016/j.neucom.2010.04.009.
- Liu, T. F., and Z. P. Jiang. 2014. Distributed nonlinear control of mobile autonomous multiagents. Automatica 50:1075–86. doi:10.1016/j.automatica.2014.02.023.
- Liu, Y. J., and S. C. Tong. 2016. Barrier Lyapunov Functions-based adaptive control for a class of nonlinear pure-feedback systems with full state constraints. Automatica 64:70–5. doi:10.1016/j.automatica.2015.10.034.
- Niu, B., L. N. Liu, and Y. Y. Liu. 2016. Adaptive backstepping-based fuzzy tracking control scheme for output-constrained nonlinear switched lower triangular systems with time-delays. Neurocomputing 175:759–67. doi:10.1016/j.neucom.2015.11.006.
- Niu, B., J. Zhu, Y. K. Su, H. Y. Li, and L. Li. 2013. Tracking control of uncertain switched nonlinear cascade systems: A nonlinear H∞ sliding mode control method. Nonlinear Dynamics 73:1803–12. doi:10.1007/s11071-013-0905-9.
- Samson, C. 1995. Control of chained systems application to path following and time-varying point-stabilization of mobile robots. IEEE Transactions on Automatic Control 40:64–77. doi:10.1109/9.362899.
- Sun, J. J., and Z. J. Li. 2015. Development and implementation of a wheeled inverted pendulum vehicle using adaptive neural control with extreme learning machines. Cognitive Computation 7:740–52. doi:10.1007/s12559-015-9363-7.
- Yan, Z., and J. Wang. 2014. Robust model predictive control of nonlinear systems with unmodeled dynamics and bounded uncertainties based on neural networks. IEEE Transactions on Neural Networks and Learning Systems 25:457–69. doi:10.1109/TNNLS.2013.2275948.
- Yang, C. G., Z. J. Li, R. X. Cui, and B. G. Xu. 2014. Neural network-based motion control of an underactuated wheeled inverted pendulum model. IEEE Transactions on Neural Networks and Learning Systems 25:2004–16. doi:10.1109/TNNLS.2014.2302475.
- Yue, M., X. Wei, and Z. J. Li. 2015. Zero-dynamics-based adaptive sliding mode control for a wheeled inverted pendulum with parametric friction and uncertain dynamics compensation. Transactions of the Institute of Measurement and Control 37:91–9. doi:10.1177/0142331214532999.
- Zhang, X. B., Y. C. Fang, and N. Sun. 2015. Visual servoing of mobile robots for posture stabilization: From theory to experiments. International Journal of Robust and Nonlinear Control 25:1–15.
- Zhang, L. X., S. Wang, H. R. Karimi, and A. Jasra. 2015. Robust finite-time control of switched linear systems and application to a class of servomechanism systems. IEEE/ASME Transactions on Mechatronics 20:2476–85. doi:10.1109/TMECH.2014.2385796.
- Zhang, L. X., and W. M. Xiang. 2016. Mode-identifying time estimation and switching-delay tolerant control for switched systems: An elementary time unit approach. Automatica 64:174–81. doi:10.1016/j.automatica.2015.11.010.
- Zhang, L. X., S. L. Zhuang, and R. D. Braatz. 2016. Switched model predictive control of switched linear systems: Feasibility, Stability and Robustness. Automatica 67:8–21. doi:10.1016/j.automatica.2016.01.010.