Malignant Mesothelioma Disease Diagnosis using Data Mining Techniques

ABSTRACT

Malignant mesothelioma (MM) is very aggressive progress tumors of the pleura. MM in humans results from exposure to asbestos and asbestiform fibers. The incidence of MM is extremely high in some Turkish villages. Under computationally efficient data mining (DM) techniques, classification procedures were performed for MM disease diagnosis. The support vector machine (SVM) achieved promising results, outperforming the multilayer perceptron ensembles (MLPE) neural network method. It was observed that SVM is the best classification with 99.87% accuracy obtained via 10-fold crossvalidation in 5 runs when compare to MLPE neural network, which gives 99.56% classification accuracy. Sensitivity analysis is performed to find the important inputs for MM disease diagnosis under SVM model. Alkaline phosphatase (ALP) ranging from 300 to 500 gives the maximum possibility of having the MM disease. The MM disease dataset was prepared from a faculty of medicine’s database using new patient’s hospital reports from the south east region of Turkey.

Introduction

It is well known that any type of Malignant mesotheliomas (MMs) is very rare and aggressive type tumor and it has an high association with asbestos exposure. (Wagner, Sleggs, and Marchand 1960). However, it may also be related to previous simian virus 40 (SV40) infection and quite possible for genetic predisposition. The incidence of MM is extremely high in some Turkish villages where there is a low-level environmental exposure to erionite, which is a naturally occurring fibrous mineral that belongs to a group of minerals called zeolites. Environmental asbestos exposure and MM are among the major public health problems of Turkey. Molecular mechanisms can also be implicated in the development of mesothelioma (Zervos, Bizekis, and Pass 2008). Rural living is associated with the development of mesothelioma (Constantopoulos et al. 1991; McConnochie et al. 1987; Yazicioglu et al. 1980). Soil mixtures containing asbestos, known as “white-soil” or “corak,” can be found in Anatolia, Turkey, and “Luto” in Greece (Constantopoulos et al. 1991; Metintas et al. 2008, 2002, 1999; Nishimura and Broaddus 1998). MM is a fatal cancer of increasing incidence associated with asbestos exposure (Peto et al. 1999). MM is a malignancy that is resistant to the common tumor-directed therapies, but again individual patients might respond to chemotherapy, radiotherapy, or immunotherapy, and selected patients might benefit from radical surgery and multimodality treatment (Burgers and Damhuis 2004). MM is a rare disease with an incidence rate of 1–2 per million/year (McDonald and McDonald 1996) in the general population. In industrialized countries, the rate ranges from 1 to 5 per million/year for women and 10–30 per million/year for men (Leigh et al. 1991; Peto et al. 1995; Spirtas et al. 1986). The higher incidence rates in industrialized countries may be due to asbestos exposure (Metintas et al. 2008). It was recently observed that MMs are responsible for approximately 15,000–20,000 deaths annually worldwide (Zervos, Bizekis, and Pass 2008). An estimated 1000 patients have MM in Turkey per year. The annual incidence of pleural mesothelioma was 22.4/1,000,000 in Anatolia (National Mesothelioma Committee 2014) (accessed November 10, 2014).

Diagnosis usually appears when a patient visits the doctor to have symptoms checked out. Patients may be met with shortness of breath, pain in the chest or back, painful, persistent coughing, or any number of other symptoms, none of which immediately alert the doctor to a diagnosis of mesothelioma (Mesothelioma News (accepted: June 29, 2011)). Clinically many studies were done regarding MM disease in south east of Turkey (Tanrikulu et al. 2006; Senyiğit et al. 2000(a); Senyiğit et al. 2000(b)). There are many studies on MM disease diagnosis using artificial intelligence techniques also, such as probability neural networks (PNNs), learning vector quantization (LVQ) (Orhan et al. 2011), artificial immune system (AIS) and multilayer neural network (MLNN) (Orhan, Tanrikulu, and Abakay 2015) with prognostic data. MM disease diagnosis is an important classification issue. Classification is often a very important part of process in many different fields like medicine. The use of artificial intelligence methods in medical diagnosis has been increasing gradually. There is no doubt that evaluations of data taken from patients and decisions of experts are the most important factors in diagnosis. However, sometimes different artificial intelligence techniques need for classification disease (Kadoz et al. 2008).

In health care, data mining (DM) plays a vital role in the medical applications including diagnosis, prognosis, and therapy. Applying DM in healthcare applications is usually referred to as clinical data mining (CDM) (Shomona and Ramani 2012). CDM involves the conceptualization, extraction, analysis, and interpretation of the available clinical data for practical knowledge-building, clinical decision-making, and partition reflection (Shomona and Ramani 2012).

Among the various medical applications, DM mainly targets the diagnosis ones (Al-Khasawneh and Hijazi 2014). To diagnose a disease is to decide whether a patient suffers from a specific disorder depending on the medical signs, symptoms, and tests. Computer programs used to help in this aid are called clinical decision support systems (CDSSs), or more specifically diagnosing decision support systems (DDSSs).

A medical diagnosis is a classification problem (Saidi, Chikh, and Settouti 2011). Hence, the majority of the CDSS employs predictive DM to diagnose a disease (Al-Khasawneh and Hijazi 2014). Predictive DM is a supervised model-building algorithm (Williams 2011) which tries to predict trends and future behaviors depending on historical variables (Omari 2013) and values wherein the probable values of the outcome are specified previously. The goal of predictive DM in the diagnosis process is to build models from old observations or historical data (i.e., usually patients’ records) to predict the outcome of new patients or observations to help in the clinical decision-making process. In the predictive DM, the dataset consists of instances; each instance is characterized by attributes or features and another special attribute represents the outcome variable or the class (Bellazzi and Zupan 2008).

Often, the goal of any DM project is to build a model from the available data. Thus, DM models are objective models rather than subjective, since it is driven by the available data. Predictive DM builds both classification and regression modeling using several algorithms, such as decision trees, random forests, boosting, support vector machines (SVMs), linear regression, and neural networks (NNs) (Williams 2011) & (Al-Khasawneh and Hijazi 2014). Descriptive DM uses cluster analysis and association rules’ modeling techniques (Williams 2011).

DM techniques (Witten and Frank 2005) aim at extracting high-level knowledge from raw data. There are several DM algorithms, each one with its own advantages. DM techniques perform regression and classification tasks. When modeling continuous data, the linear/multiple regression (MR) is the classic approach and for binary data classification discriminant analysis (DA), decision tree (DT), and k-nearest neighborhood are used. In case of NNs, the backpropagation algorithm was first introduced in 1974 (Werbos 1974) and later popularized in 1986 (Rumelhart, Hinton, and Williams 1986). Since then, NNs have become increasingly used. More recently, SVMs have also been proposed (Boser, Guyon, and Vapnik 1992; Smola and Schölkopf 2004). Due to their higher exibility and nonlinear learning capabilities, both NNs and SVMs are gaining an attention within the DM field, often attaining high predictive performances (Hastie, Tibshirani, and Friedman 2008; Huang et al. 2004). SVMs present theoretical advantages over NNs, such as the absence of local minima in the learning phase. In effect, the SVM was recently considered one of the most influential DM algorithms (Wu et al. 2008). Therefore, in this article, a study of SVM on MM disease diagnosis was realized. The MM disease dataset was prepared from a faculty of medicine’s database using patient’s hospital reports. Also, the SVM results were compared with the results of the MLPE focusing on MM disease diagnosis and using the same database.

The major objective of this study is to find a best classifier which gives a good performance evolution measures and also to try to find the important input variables for MM disease diagnosis using strong DM techniques. Many authors had used various classification techniques to this dataset for MM disease diagnosis (Orhan, Tanrikulu, and Abakay 2015; Orhan et al. 2011), but probably, SVM and MPLE are not been used under proper modeling scheme. This study shows highest classification accuracy rate (as per previous records) and presented a significant variable input importance chart for MM disease diagnosis.

Methods

Data source

In order to perform the research reported, the patient’s hospital reports from Dicle University, Faculty of Medicine, were used in this work. One of the special characteristics of this diagnosis study is to use the real dataset taking from patient reports from this hospital. Three hundred and twenty-four MM patient data were diagnosed and treated. These data were investigated retrospectively and the files were analyzed. In the dataset, all samples have 34 features because it is more effective than other factor subsets by doctor’s guidance. These features are age, gender, city, asbestos exposure, type of MM, duration of asbestos exposure, diagnosis method, keep side, cytology, duration of symptoms, dyspnea, ache on chest, weakness, habit of cigarette, performance status, white blood cell count, hemoglobin, platelet count, sedimentation, blood lactic dehydrogenases (LDHs), alkaline phosphatase (ALP), total protein, albumin, glucose, pleural LDHs, pleural protein, pleural albumin, pleural glucose, dead or not, pleural effusion, pleural thickness on tomography, pleural level of acidity (pH), C-reactive protein (CRP), and class of diagnosis. Diagnostic tests of each patient were recorded. For this study, the dataset was collected from UCI Machine Learning Repository (https://archive.ics.uci.edu/ml/datasets/Mesothelioma).

MM disease diagnosis using DM techniques

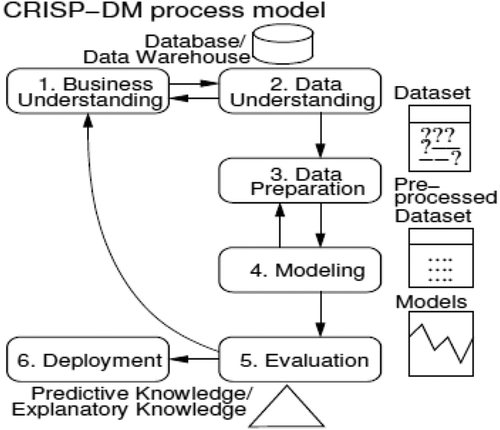
DM is an iterative process that consists of several steps. The CRISP-DM (Chapman et al. 2000), a tool-neutral methodology supported by the industry (e.g., SPSS, DaimlerChryslyer), partitions a DM project into six phases (Figure 1): (1) business understanding; (2) data understanding; (3) data preparation; (4) modeling; (5) evaluation; and (6) deployment.

Figure 1. The CRISP-DM tool.

This work addresses steps 4 and 5, with an emphasis on the use of NNs and SVMs to solve classification and regression goals. Both tasks require a supervised learning, where a model is adjusted to a dataset of examples that map I inputs into a given target. In case of classification, models output a probability p(c) for each possible class c, such that = 1. For assigning a target class c, one option is to set a decision threshold D ϵ [0, 1] and then output c if p(c) > D, otherwise return c. This method is used to build the receiver operating characteristic (ROC) curves. Another option is to output the class with the highest probability, and this method allows the definition of a multiclass confusion matrix. For more details, see Cortez (2015).

To evaluate a model for classification, common metrics are (Witten and Frank 2005) as follows: ROC area (AUC), confusion matrix, accuracy (ACC) and true positive/negative rates (TPR/TNR). A classifier should present high values of ACC, TPR, TNR, and AUC. The model’s generalization performance is often estimated by the holdout validation (i.e., train/test split) or the more robust k-fold crossvalidation (Hastie, Tibshirani, and Friedman 2008). The latter is more robust but requires around k times more computation, since k models are fitted.

MLP and MLPE neural network model

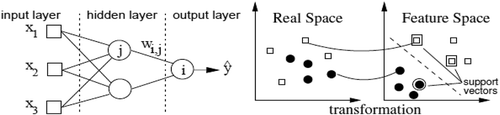
In DM techniques, NN means the popular multilayer perceptron (MLP). MLPs have proven to be an effective way to solve classification tasks. A major concern in their use is the difficulty to define the proper network for a specific application, due to the sensitivity to the initial conditions and overfitting and underfitting problems which limit their generalization capability. Moreover, time and hardware constraints may seriously reduce the degrees of freedom in the search for a single optimal network. A very promising way to partially overcome such drawbacks is the use of MLP ensembles (MLPE); averaging and voting techniques are largely used in classical statistical pattern recognition and can be fruitfully applied to MLP classifiers. For classification problem, MLPEs are used, which are combinations of MLP models, and it is observed in many situations that MPLEs give better results than any of its single MLP. In this study, MLPEs show better results than MLP (Orhan et al. 2011).This network includes one hidden layer of H neurons with logistic functions (Figure 2 (left)). The overall model is given in the form:

(1)

Figure 2. MLP neural network (left) and SVM (right).

where is the output of the network for node i, is the weight of the connection from node to I, and is the activation function for node j. For a binary classification ( = 2), there is one output neuron with a logistic function. Under multiclass tasks ( > 2), there are linear output neurons and the softmax function is used to transform these outputs into class probabilities:

(2)

where is the predicted probability and is the NN output for class i. The training (BFGS algorithm) is stopped when the error slope approaches zero or after a maximum of epochs. For classification, it maximizes the likelihood (Hastie, Tibshirani, and Friedman 2008). Since NN training is not optimal, the final solution is dependent on the choice of starting weights. To solve this issue, the solution adopted is to train different networks and then select the NN with the lowest error or use an ensemble of all NNs and output the average of the individual predictions (Hastie, Tibshirani, and Friedman 2008). In DM technique, the former option of NN is MLP model, while the latter option of NN is called multilayer perceptron ensemble (MLPE) model. In general, ensembles are better than individual learners (Rocha, Cortez, and Neves 2007). The final NN performance depends crucially on the number of hidden nodes. The simplest NN has H = 0, while more complex NNs use a high H value.

SVM model

When compared with NNs, SVMs present theoretical advantages, such as the absence of local minima in the learning phase (Hastie, Tibshirani, and Friedman 2008). The basic idea is to transform the input x ϵ into a high m-dimensional feature space using a nonlinear mapping. Then, the SVM finds the best linear separating hyperplane, related to a set of support vector points, in the feature space (Figure 2 (right)). The transformation (φ(x)) depends on a kernel function.

Here, SVM uses the sequential minimal optimization (SMO) learning algorithm adopting the popular Gaussian kernel, which presents less parameters than other kernels (e.g., polynomial):

The classification performance is affected by two hyperparameters:, the parameter of the kernel, and C, a penalty parameter. The probabilistic SVM output is given by (Wu, Lin, and Weng 2004):

where m is the number of support vectors, ϵ is the output for a binary classification, and are coefficients of the model, and A and B are determined by solving a regularized maximum likelihood problem. When >2, the one-against-one approach is used, which trains binary classifiers and the output is given by a pairwise coupling (Wu, Lin, and Weng 2004).

In the proposed DM technique, the NN and SVM hyperparameters (e.g., H,) are optimized using a grid search. To avoid overfitting, the training data are further divided into training and validation sets (holdout) or an internal k-fold is used. After selecting the best parameter, the model is retrained with all training data. For more details, see Cortez (2015).

Sensitivity analysis

The sensitivity analysis is a simple procedure that is applied after the training procedure and analyzes the model responses when a given input is changed. Let denote the output obtained by holding all input variables at their average values except, which varies through its entire range (). Variance () of is used as a measure of input relevance (Kewley, Embrechts, and Breneman 2000). If >2 (multiclass), it sets as the sum of the variances for each output class probability (). A high variance () suggests a high relevance; thus, the input relative importance () is given by:

(4)

For a more detailed analysis, the variable effect characteristic (VEC) curve (Cortez et al. 2009) has been proposed, which plots the values (x axis) versus the predictions (y axis).

Performance evolution measures

Classification accuracy (ACC)

Classification accuracy refers to the ability of the model to correctly predict the class level of new or previous unseen data. Classification accuracy is the percentage (%) of testing set examples correctly classified by the classifier. The quality of classification can be assessed through overall accuracy. That is

(5)

(6)

where is the set data items to be classified (the test set in this case), is the class of item and returns the classification of by the used classifier (here, SVM and MLPE). For more details, see Watkins (2001).

In this present article, measurement for performance evolution is basically based on classification accuracy described in Equations (5) and (6). Except this, some other performance measures are also observed. Some brief descriptions of other measures are given below.

AUC and ROC curve

AUC is a common evaluation metric for binary classification problems. Consider a plot of the true positive rate (TPR) versus the false-positive rate as the threshold value for classifying an item as 0 or is increased from 0 to 1 and if the classifier is very good, the TPR will increase quickly and the AUC will be close to 1. One characteristic of the AUC is that it is independent of the fraction of the test population which is class 0 or class 1; this makes the AUC useful for evaluating the performance of classifiers on unbalanced datasets.

In an ROC curve, the TPR (sensitivity) is plotted in function of the false-positive rate (100-specificity) for different cutoff points. Each point on the ROC curve represents a sensitivity/specificity pair, i.e., TPR/TNR corresponding to a particular decision threshold. For more details, see Witten and Frank (2005).

TPR, true negative rate (TNR), and F1 score

To know about TPR, TNR, and F1 score correctly, we need to introduce a 2 × 2 contingency table described below.

Table

Total population	Predicted condition positive	Predicted condition negative
Condition positive	True positive (TP)	False negative (FN)
Condition negative	False positive (FP)	True negative (TN)

True positive rate (or sensitivity): TPR = TP/(TP+FN), with TPR value closer to 100% indicating good classifier.

True negative rate (or specificity): TNR = TN/(FP+TN), with TNR value closer to 100% also indicating good classifier.

F1 score: F1 = 2TP/(2TP+FP+FN); F1 score reaches its value at 1 or 100% indicates good classifier. For more details, see Witten and Frank (2005).

k-fold crossvalidation

k-Fold crossvalidation is a common technique for estimating the performance of a classifier. Given a set of m training examples, a single run of k-fold crossvalidation proceeds as follows:

1. Arrange the training examples in a random order.

2. Divide the training examples into k-folds (k chunks of approximately m/k examples each).

3. For

   1. Train the classifier using all the examples that do not belong to fold.

   2. Test the classifier on all the examples in fold.

   3. Compute, the number of examples in fold that were wrongly classified.

4. Return the following estimate to the classifier error:

(7)

To obtain an accurate estimate to the accuracy of a classifier, k-fold crossvalidation is run several times, each with a different random arrangement in Step 1. After performing these steps several numbers of times, take an average of each run result to produced the final classification accuracy. For more details, see Hastie, Tibshirani, and Friedman (2008).

These mentioned DM techniques and performance evolution measures are used for MM disease diagnosis. For this study, classification models are developed under SVM and MLPE models using 5 runs of the more robust 10-fold crossvalidation, in a total 5 × 10 = 50 experiments for tested configuration. All statistical and DM works are performed in R statistical software (http://www3.dsi.uminho.pt/pcortez/rminer.html; Cortez 2015).

Results

An application of DM techniques (SVM and MLPE methods) along with 10-fold crossvalidation method for MM disease diagnosis is presented in this work. Two classifiers SVM and MLPE have been used for this classification task. The SVM results were compared with the results of the MLPE NNs focusing on MM disease diagnosis and using the same database. The performance evolution measures, namely classification accuracy (ACC), AUC, TPRs, TNRs, and F1 score obtained by SVM and MLPE NNs for MM disease, are presented in Table 1. The classification accuracies obtained by SVM and MLPE NNs in 5 runs, where in each run a 10-fold crossvalidation was performed, are presented in Table 2. A comparative study in terms of average classification accuracy obtained by various classifiers used for MM disease diagnosis is presented in Table 3.

Table 1. Comparison between SVM and MLPE methods for MM disease diagnosis in terms of average performance evolutions by 10-fold crossvalidation in 5-run test methods.

Performance evolution
Methods	ACC (%)	AUC (0–1)	TPR (%)	TNR (%)	F1(%)
SVM	99.87	0.9999	99.8245	100	99.9560
MLPE	99.56	0.9998	99.5614	98.5416	99.6485

SVM: Support vector machine, MLPE: Multilayer perceptron ensembles, ACC: Classification accuracy rate, AUC: Area under curve, TPR: True positive rate, TNR: True negative rate, F1: F1 score.

Table 2. Average of classification accuracies for MM disease dataset by 10-fold crossvalidation in 5 runs.

Results (%) per run (average of 10-fold crossvalidation outputs in each run)
Methods	1^s	2^nd	3^rd	4^th	5^th	Average
SVM	100	100	99.69	100	99.69	99.87
MLPE	99.38	99.35	99.69	99.69	99.69	99.56

SVM: Support vector machine, MLPE: Multilayer perceptron ensembles

Table 3. Comparison of different methods used to measure the performance evolution for MM disease diagnosis in terms of average classification accuracy.

Methods	Number of fold crossvalidation	Number of runs	ACC (%)
SVM*	10	5	99.87
MLPE*	10	5	99.56
AIS	10	—-	97.70
NN	10	—-	91.30
PNN	3	—-	96.30
MLNN	3	—-	94.41
LVQ	3	—-	91.14

‘*’: Proposed methods in this study, AIS: Artificial immune systems, NN: Neural network, PNN: Probabilistic neural network, MLNN: Multilayer neural network, LVQ: Learning vector quantization.

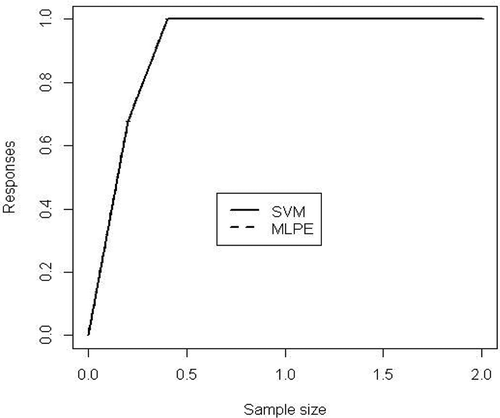
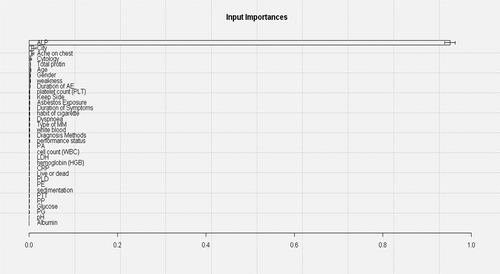
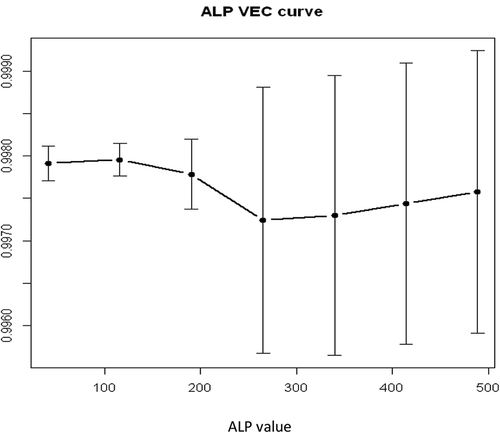
LIFT plot for MM disease diagnosis using SVM and MLPE NN are shown in Figure 3. Figure 4 and Figure 5 present the input importance bar chart and variable effective chart (VEC), respectively, for MM disease dataset. Input importance bar chart shows, how much importance (in terms of a score 0-1) a particular input variable consumes for the response variable. For a more detailed analysis, a VEC plot is used, which plots the most important input variable against the response variable according to x axis and y axis.

Figure 3. LIFT plot for MM disease diagnosis using SVM and MLPE neural network.

Figure 4. Input importance bar charts for MM disease diagnosis using 34 input variables.

Figure 5. Variable effect curve for the input variable ALP.

Discussion

The objective of this article was to find a best classifier and important input variable identification for this MM disease diagnosis. After performing DM techniques, the results are presented in Tables 1–3 and in Figures 3–5. From Table 1, it is observed that in all cases of performance evolution measures, SVM and MLPE produced almost the same result. After taking the average of 5 runs and 10-fold crossvalidation, classification accuracy for SVM is 99.87%, whereas for MLPE NN, it is 99.56%. In case of AUC measure, SVM gives 0.9999 and MLPE shows 0.9998, which is almost the same with the SVM output. The same trend of results is repeated in the rest of the performance measures. In case of true positive and true negative rates, SVM produced 99.8245% and 100%, whereas MLPE gives 99.5614% and 99.5416%. Finally, in the case of F1 score, SVM score is 99.9560% and MLPE score is 99.6485%. After discussing the results of Table 1, it is concluded that SVM is the better classifier than MLPE NN considering all the performance measures. From Table 2, run-wise results of SVM and MLPE can be checked in terms of classification accuracy. The best result for the average classification accuracy was obtained by using SVM (with 10-fold crossvalidation and 5-run structure) with a value of 99.87% as seen in the Table 3. This result is quite good for MM disease diagnosis problem. The second best result for the classification accuracy was obtained using MLPE NN (with 10-fold crossvalidation and 5 runs, two hidden layers) with a value of 99.56%. These two are the proposed methods in this article. The third best result for the classification accuracy was obtained using AIS with only 10-fold crossvalidation but no repetitions in experiment. It gives 97.70% classification accuracy. The PNN and MLNN also give good results for MM disease diagnosis problem (Orhan, Tanrikulu, and Abakay 2015; Orhan et al. 2011). In Figure 3, the LIFT plot shows a comparison between SVM and MLPE NN. Both these two methods take almost the same area from baseline and that is why the two lines coincide. Input importance bar charts of 34 input variables for MM disease dataset are presented in Figure 4.

It shows very interesting results for this MM disease diagnosis problem. ALP is the most important input variable for MM disease diagnosis. It is also observed from Figure 4 that the variable City is also an important factor for diagnosis. Actually the location of the particular patient is playing very important role here. Information of patient's location stores in the variable "City". It is well established that asbestos exposures is one of the major causes for MM disease. So it may be important that from where the patient belongs, if he/she may has the experience of asbestos exposure. Finally, for the most important variable ALP, VEC plot is presented in Figure 5. Value of ALP from 300 to 500 gives the maximum chance to present MM disease in patients.

Conclusion

Two different DM methods to the MM disease diagnosis problem using the same dataset have been applied in this study. As it can be seen from this study, a patient can be classified as having an MM disease or not. According to the overall results, it is seen that the most reliable and stable DM methods are SVM and MLPE NN structure for classifying MM data. It was seen that all others ANN structures could also be successfully used to help the diagnosis of MM disease. This classification accuracy is highly reliable for such a problem because only a few samples were misclassified by the system. Ten-fold crossvalidation technique with repeated experimental setup is more suitable than any other conventional validation algorithm for ANN structures for the diagnosis of MM disease. Finally, ANN structures can be helpful as learning-based DSS to contribute to the doctors in their diagnosis decisions. Besides this, it is also known from this study that the important input factors or variables are very influential for any type of disease diagnosis problem. This article highlighted that ALP is the most important input variable for MM disease diagnosis. ALP is generally a good biomarker in case of liver disease and a very excessive amount of ALP in human body causes cancer as well. Sensitivity analysis and input importance bar chart find other factors like city, pain in chest, age, and gender of patient, which are also very important for MM disease reorganization. This portion of the study can be a major contribution to the doctors in their diagnosis process.