A Novel Approach to Efficient Resource Allocation in NOMA Heterogeneous Networks: Multi-Criteria Green Resource Management

ABSTRACT

Nowadays, Green Communications has been introduced as an appealing approach to achieve the maximum degree of energy efficiency in new generation heterogeneous networks. To achieve the effective resource management, this paper suggests a novel approach to joint optimal power allocation and user association techniques in which cells are powered via a common grid network and alternative energy resources. This research focuses on resource assignment in energy-cooperated heterogeneous systems with non-orthogonal multiple access so that the quality of experience indexes are assumed to be bounded during multicell multicast sessions. The solution to the introduced problem has been developed to a mixed-integer programming framework in which the goal function is solved based on a Lagrangian convex optimization method by considering user association constraints. The effectiveness of the suggested approach has been confirmed by the numerical results and we compared the complexity of the proposed model to those of the conventional schemes. Also, the results reveal that non-orthogonal multiple access can provide greater energy efficiency than orthogonal multiple access in heterogeneous wireless networks.

1. Introduction

In order to increase the energy efficiency in the next generation heterogeneous networks, the context of green resource management is a promising approach in which the physical resources of one network provider, for example, spectrum, power, and infrastructure, are shared among different service providers, also called slices. Generally, each slice comprises of a set of users, and has its own quality-of-service (QoS) requirements. To harvest the potential advantages of the network, effective resource allocation is a major concern, which has been drawing a lot of attention in recent years [1]. Also, because of the increase in fast speed services such as the Internet of Things and mobile data services, a large percentage of user equipment (UE) will be connected to next-generation cellular networks [2]. This will cause an unprecedented increase in general energy consumption by adding a huge number of subscribers [3]. The latest researches about global energy consumption patterns indicate that one-tenth of all energy consumed is for data transfer and telecommunications. Furthermore, global environmental issues such as uncontrolled use of carbon fuel are a significant concern and greener approaches must be considered to increase network performance based on efficient energy consumption patterns. Among the novel approaches, the use of renewable energy as an alternative resource is a viable approach [4].

The current grid energy consumption of next-generation cellular networks can be significantly reduced by permitting each evolved node-B (eNB) to change the energy consumption model and pick up energy from alternative energy sources (for example, wind or solar power). Furthermore, promoting energy-based cooperation among eNBs using a smart grid infrastructure can increase the efficiency of an alternative energy distribution scheme [5].

Most of the current schemes have focused on analyzing the resource allocation problem in a single-cell scenario. However, in practice, the coverage of a specific region may require a set of BSs, in a multicell scenario. The key question in such a multicell scenario is how to allocate the resources to maintain the QoS of each slice, while improving the total performance of the network over a specific region. In this paper, we consider a multicell OFDMA-based heterogeneous network where the coverage of the region is provided by a set of BSs serving different groups of users belonging to different slices.

1.1 Related Works and Motivation

We can claim that the presented approach lies along joint of two major concepts in green resource management. In the aforementioned works, the BS assignment algorithm is separated from the subcarrier allocation, while joint subcarrier and power allocation is applied for multicell scenario. Compared to this approach, we consider multilayer energy control which jointly assigns the BS and subcarrier for each user and then allocates power allocation to network entities. Furthermore, we consider the implementation limitations of multicell OFDMA networks by proposing new constraints. Although using new energy resources appears to be an alternative to the current grid energy in next-generation mobile networks, some critical issues exist such as how to become used new energies in eNBs and radio resource management circumstances [6]. With the ability to harvest alternative (renewal) energy in the network, base stations will pick up variable levels of the alternative resource because of the fluctuating nature of such alternative power resources. But when the alternative energy dedicated to the eNB fails to be consistent with the traffic load, the harvested energy will not be sufficient to meet user requirements. Under these conditions, some subscribers should be handed over to more distant eNBs having sufficient energy, although service will be affected by signal-level degradation. Also, some eNBs may have more accessible energy, based on weather and environmental conditions, in which the unusable power will be wasted. However, integrating eNBs with massive power storage systems will impose additional costs on the network [7] and the deployment of storage devices cannot resolve energy fluctuations in the architecture of the distributed cell layer in multicarrier mobile networks. So, power-sharing and energy cooperation among the eNBs through power management strategies may be the only viable solution [8]. Power-sharing in a point-to-multipoint transmission scenario has previously been investigated [5,8,9].

Ulukus studied one-way resource sharing and power transfer through a multi-direction Gaussian channel using multiple access techniques [9]. This was extended to a cooperative energy model based on two-way energy transfer pattern by Hussein Al Haj [5]. A valuable energy-cooperated approaches by Liu [10] implemented based on multiple access techniques CDMA/OFDMA and relay-based multiple access channels in the networks. Deng in [11] presented a novel resource cooperation method in cognitive radio wireless networks in which the performance of the scheme was evaluated from spectrum efficiency and energy management perspectives. The potential of renewable energy management and alternative power cooperation in next-generation cellular networks is now being taken into consideration and a significant number of researchers have formulated energy cooperation frameworks and the related optimization problems. One valuable work that combines energy efficiency and spectrum assignment has been presented by Xu [7], who introduced an energy-aware spectrum sharing scheme among neighbor cellular networks. The authors also tried to solve the convex optimization problem to minimize the cost of energy distribution and spectrum sharing. Mohajer in [12] formulated a new power control scheme in a distributed eNB layer in which energy demand of eNBs and the picked-up energy is assumed to be deterministic.

The aim of Huang in [13] was to minimize the cost of an energy exchange framework through a categorized-prices smart grid. The target of Zhang [14] was to maximize the total transmission rate by solving convex optimization problems in which eNBs are distributed in a coordinated cluster. Bingyu [15] formulated the goal functions to achieve the optimal value for the mean cost of the resources exchanged by eNBs. The Lyapunov dynamic optimization model was applied here instead of statistical analysis of the transmission channels.

Not only the most reviewed studies were static, based on a solid foundation, but also, previous studies had only considered energy cooperation and power-sharing in new-generation mobile networks with orthogonal multiple access (OMA) technology and had ignored non-orthogonal multiple access (NOMA) for energy cooperation in multicarrier mobile networks. Multiple access techniques in cellular mobile networks enable the system to share accessible resources such as bandwidth, power, and time between subscribers within a distinct resource control algorithm [16]. Multiple access techniques can be divided in terms of orthogonality into twofold OMA and NOMA schemes. In the OMA approach, power, time, and frequency resources are assigned orthogonally in order to decrease the intercell/intra-cell interference. Resource allocation in NOMA is based on exploiting domains such as code and power and the most effective specification of this approach is related to saving bandwidth and time resources [17]. One major difference between NOMA and OMA is spectral efficiency; thus in NOMA, eNBs are permitted to serve multiple subscribers at a same time at a distinct frequency.

The main topic of the current research is improvement of network performance with NOMA technology with a focus on resource management. In a scenario with multiple users and one serving base station, the system approaches the ideal level of downlink energy efficiency by achieving optimal value for goal function [18]. This work has been extended to increase the network capacity using MIMO to multiply the downlink throughput. This research has shown that the quality of experience (QoE) in NOMA systems is one of the most critical indexes. Tabassum [19] suggested an adaptive downlink/uplink resource allocation framework and a dynamic power control formulated for dual stream wireless networks in which the average downlink throughput and outage timing constraints were bounded. Wu [20] has proposed a novel approach in distributed resource control by solving iterative convex optimization problems with the goal of minimizing transmission power and providing acceptable rate fairness.

In addition to investigating schemes for optimized resource allocation, other studies [21–23] have focused on joint resource control and power allocation in NOMA systems as a new concept beyond current resource management. Di [21] applied a combination of subcarrier allocation and resource assignment to achieve the optimal point of the overall network consuming energy. Jiang [22] solved the resource/subchannel assignment problem to minimize the total dedicated power. Lei [23] introduced a suboptimal framework as a centralized multicarrier scheme for maximizing total capacity in NOMA systems under a single eNB scenario. Despite the valuable researches conducted on the architecture and configuration of non-orthogonal systems, cooperative resource management in this kind of networks has not been discussed. User association (UA) is relevant to user grouping and specification of base stations to each user group for transmission management [24] and the number of users assigned to each base station has a significant effect on system performance and energy-efficiency in NOMA systems. Resource control techniques also have a significant role in intra-cell/intercell interference coordination and using resource control techniques the QoE for users located at the cell edges will improve and subscriber satisfaction will increase accordingly.

1.2 Challenges and Contributions

Generally, most of the current works have focused on analyzing the resource allocation problem in a single-cell VWN scenario, but in the proposed model, to achieve the effective resource management, we suggested a novel approach to joint optimal power allocation and UA techniques in which cells are powered via a common grid network and alternative energy resources. This research focuses on resource assignment in energy-cooperated heterogeneous systems with NOMA so that the QoE indexes are assumed to be bounded during multicell multicast sessions. The solution to the introduced problem has been developed to a mixed-integer programming framework in which the goal function is solved based on a Lagrangian convex optimization method by considering UA constraints. Although some studies have examined resource management and power control in conventional OMA systems, cooperative resource management in NOMA systems remains an open problem, particularly from the UA perspective. Most current non-orthogonal systems are based on single site scenarios [18-23] and the effect of intercell and external interference in practical multicarrier mobile networks has not been discussed, while intercell interference has a major effect on network functionality.

Scenarios such as those for Parsaeefard [25] have used joint resource allocation and UA in current OMA mobile networks and single site NOMA networks [26]. Previous schemes have not considered radio frequency characteristics of multicell non-orthogonal networks and do not seem to be effective. Also, current studies on UA-based alternative energy harvesting scenarios [27] merely consider the design of UAs in OMA systems without power-sharing and resource cooperation. It can be concluded joint UA and resource control in an energy-cooperative multicell network with NOMA has not been thoroughly addressed so far. While considering these concepts, the current article addresses energy-cooperative resource allocation and UA problems in two-layered heterogeneous mobile networks with NOMA. The main contributions of this article are:

In target scenario in a multi layered NOMA heterogeneous network in which a high-power macro eNB is the serving base station for distributed small cells and pico cells, each eNB will be powered by both the usual grid energy and alternative energy (solar energy or wind power) and cells can share the renewable energy among themselves. This novel approach goes beyond conventional resource allocation and power control concepts to optimize the UA, downlink transmission power, energy exchanged among eNBs, and consumption of the grid resource with the goal of achieving energy efficiency for the overall network in addition to satisfying user QoE constraints. This research focuses on resource assignment in energy-cooperated heterogeneous systems with NOMA so that the QoE indexes are assumed to be bounded during multicell multicast sessions. The solution to the introduced problem has been developed to a mixed-integer programming framework in which the goal function is solved based on a Lagrangian convex optimization method by considering UA constraints. Next, a hybrid cooperative power control and UA algorithm is suggested to further maximize energy efficiency. The functionality of the proposed algorithms is compared with previous schemes for samples without alternative energy management and cooperative energy schemes such as fractional transmission power allocation (FTPA). The experimental results prove that although the complexity of our algorithm is restricted, this model can provide significant improvement in energy efficiency. The proposed resource management and power control framework comprehensively considers the effect of intercell/intra-cell interference in contrast to current schemes. Furthermore, by applying the proposed algorithm, more diversity gain and eNB densification gain will be achievable.

The rest of this paper is organized as follows. In Section 2, the system model and problem formulations are introduced. Section 3 presents the framework of the proposed resource management with fixed downlink transmission power. Section 4 demonstrates the cooperative energy resource allocation scheme with dynamic UA and the proposed combined adaptive resource control and UA approaches. Simulation results and their detailed analysis will be presented in Section 5 and finally, conclusion and future works will be mentioned in Section 6.

2. System Architecture and Problem Formulation

This section presents the system model for resource allocation, energy harvesting, cooperative resource management, and UA in heterogeneous NOMA networks.

2.1 Downlink Transmission Model

Figure 1 shows the two-layered cooperative energy heterogeneous network with a macro base station (MBS) and distributed pico base stations (PBSs). The number of MBSs is denoted by M and the frequency bandwidth shared by all base stations is assumed to be the same. In this scenario, the “eNB” as a component of LTE Radio Access Network in the new-generation mobile networks is called “base station” in order to simply understanding the scenario. Each base station is powered by both the usual grid and alternative energy resources (solar energy or wind power) and the base stations can share the renewal energy among themselves through a smart grid.

Figure 1. Structure of cooperative energy multilayered heterogeneous systems powered via current grid and alternative resources

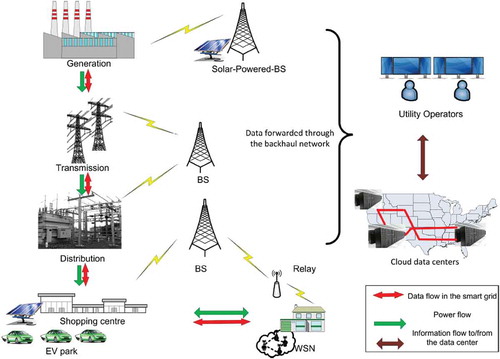
Assume that is the m^th base station, where in this notation, the macro cell is indicated with m = 1 (we have only one MBS in each region) and the other values denote the PBSs. Assume that N is the randomly distributed UE in the area covered by the network. Each UE is associated with just one base station. All base stations and UE are represented by single omnidirectional antenna nodes. Also, the general perfect channel state information (CSI) is assumed to be accessible. The index denotes the j^th UE. In accordance with the NOMA schemes, the signal transmitted by base station m is where in which is the binary index and indicates the UA. if the j^th UE will be assigned to base station m and else, . denotes the assigned downlink transmission power and denotes the data flow of the j^th user. If UE j is served by base station m, the signal received by UE will be:

(1)

where and represent intra-cell and intercell interference, respectively. Also, in this formulation parameter is the coefficient of the downlink channel belonging to the m^th base station and includes the propagation path loss, Rayleigh fading factor, and constant gains of the antennas, is the coefficient of the interference-limited channel from base station and denotes the Gaussian noise which is calculated as an additive variable. Index has a specified density of power denoted as . In NOMA, it is assumed that the successive interference cancelation (SIC) ability has been implemented for all UE to eliminate intra-cell interference from the signals of powerful network elements. In the same vein, assuming that UE exist to organize an association covered by base station m at a specified time-slot in a same bandwidth, the formulation of the corresponding transmission channel to the interference + noise ratio (CINR) can be expressed as:

(2)

where intercell interference is denoted as power indicator of UE j and the power of white noise is denoted as . In multicellular NOMA during resource allocation to user signals, the power allocation algorithm of cell m should meet constraint of Equation (3).

(3)

In this constraint, denotes the total transmission power of the m^th base station and demonstrates K number of users associated with base station m. This seems optimal when the requirements of user QoE are satisfied in which, in order to obtain favorable user experience, more power should be assigned to the weaker signals and downlink traffic channels under severe interference. In an exceptional case when considering only one cell, Equation (3) reduces the order in accordance with the power gain of the channel. Accordingly, based on Equation (1), by SIC at the j^th UE, the throughput can be expressed as:

(4)

In Equation (4), W denotes the system frequency bandwidth and represents the formulation of the signal to interference + noise ratio (SINR) as:

(5)

where , .

By implementation of SIC, the remaining intra-cell interference can be denoted as index and illustrates that the total transmission power belongs to the mʹ^th base station. It should be noted that while this paper considers a system with a single-carrier frequency domain, it is easily possible to deploy it in HetNets with multi-carrier air interfaces by assuming W as the bandwidth of each subcarrier in which the throughput of the subcarrier can be obtained by multiplying by the subcarrier indicator. The optimal solution over all subcarriers in the multicell networks can be achieved iteratively by following the proposed primal-dual decomposition approach.

2.2 Distributed Activation Energy Model

The power of each base station is provided by both the usual grid energy and alternative energy (solar energy or wind power) and the cells can share the renewal energy among themselves. The grid energy received by base station m is denoted as . The alternative energy received by base station m is denoted as . The energy transmitted from base station m to base station is expressed as and the efficiency factor of the transferred power between the base stations is denoted as . In this regard, denotes the loss of energy during the power sharing process.

It is assumed that there is no possibility of using a battery because this is time-consuming and waste of power is inevitable with using such static storage devices. The energy cooperation and power sharing problems also are assumed to be independent for each time slot. The length of the time slots is normalized in order to simplify the framework of correspondence between power and energy. When power utilization in base station m is determined, Equation (6) should be satisfied as:

(6)

where expresses the total transmission power by the m^th base station. In Equation (6), using the cooperative energy resource allocation approach, the level of grid energy consumption will be affected by three items:

• The amount of alternative energy harvested

• The density of the energy transferred

• The power level of transmission

As shown in the equations, the grid energy consumption as the dependent variable is a function of the alternative energy harvested and the density of transferred energy, which are not constant values. The functionality of this model is significantly different from current systems without the feature of cooperative energy.

2.3 Problem Formulation

Achieving maximum energy efficiency in the overall HetNet is the target of this study. In bit/Joule units, this can be defined as:

The utilization function of the network is defined as:

(7)

In order to minimize the usage of the grid energy, the amount of alternative energy harvested should be maximally utilized [4]. The main problem can be formulated as follows:

(8)

s.t. C1:

C2:

C5:

C6:

C7:

In this multi-constraint formulation, , , , . denotes the lower bound of the data rate required for UE and denotes the maximum transmission power of base station m. Constraint C1 guarantees the desired user QoS. Constraints C2 and C5 prevent the UE from being served by more than one base station. Constraint C3 relates to the power utilization model. Constraint C4 defines the limits of resource assignment with NOMA through a specific base station. Inequality C6 demonstrates that the grid power used and shared power are positive and constraint C7 defines the upper bound of the transmission power.

From problem P1 and relevant constraint (C3), it is evident that when a larger amount of the alternative resource is harvested and transferred between base stations, the total usage of grid energy in both network layers will decrease subsequently, which increases the energy efficiency.

3. Fixed-Power Efficient Resource Management

Nonlinear problem P1 is shown as a mixed integer programming framework. The problem now needs to be formulated so that the transmission power is assumed to be fixed; hence, the primal problem P1 will be simplified to problem P2.

(9)

s.t. C1, C2, C3, C4, C5, C6

The simplified primary problem P2 has discrete modality and is a combination of several subproblems. To find an efficient solution for P2, an iterative decomposition approach was applied. Using indicators G and , P2 can be modified as:

(10)

s.t. C1,C2,C4,C5

3.1 Lagrangian Dual Decomposition

Using the goal function, the Lagrangian equation has been formulated to take the problem constraints (P2.1) into account as:

(11)

in which and are the Lagrange coefficients with positive values. The dual function can be defined as:

(12)

Using the primal-dual principles, the dual problem can be used to simply produce the solution. Using P2.1, the dual problem can be defined as shown in Equation (13) as:

(13)

Using the dual Lagrangian coefficients and , the optimum value of parameter x for the Lagrange formula can be calculated as:

(14)

where, in Equation (14), with:

(15)

The optimal solution in Equation (14) means that subscribers choose base stations (which supply the maximum achievable throughput) according to the grid power consumption. Because the goal of the dual function is not differentiable, the sub-gradient method was applied to achieve the solution with maximum optimality of the dual problem. This can be expressed as:

(16)

(17)

In Equations (16) and (17), , t is the indicator of iteration and denotes the step size. Of the various step size patterns available, such as fixed and decreasing step sizes, in this study decreasing step size was applied as introduced by Zhang [29].

After achieving the optimal values using Equations (16) and (17), the optimal value of index x will be the response to main problem P2:1. Using the iterative decomposition method, UA can be designed in both centralized and decentralized modes, which this is a specific capability of the proposed approach. The centralized UA system needs an intensive controller which has access to global CSI and is aware that the subscriber is served by which specific base station. Based on Algorithm 1, this article suggests a decentralized UA approach in which there is no requirement for gathered control data. Also, because the convergence requirements (described in [29]) are satisfied through the proposed algorithm, convergence is definite. For each iteration, the proposed algorithm has complexity order . Convergence of the resource management algorithm appears to be fast because convergence occurs usually in less than 40 repetitions. This is significantly less than the Brute Force approach with complexity order . The broadcast operations applied in the proposed model have little effect on the order of time complexity.

Algorithm 1:

Efficient UA Algorithm

3.2 Genetic-based UA Algorithm

Next, a genetic algorithm (GA)-based UA is implemented to solve main problem P2.1. The aim is to compare the results of proposed Algorithm 1 with genetic-based approaches. As stated by Abdelaziz [30], a genetic-based algorithm has good functionality if the number of potential solutions is adequate. In particular, each chromosome represents a feasible solution which meets the requirements of problem P2.1 and is formulated as:

(18)

In Equation (18), denotes the gene for the base station to which UE j is connected, with a variable amount between interval [1 M+1]. K denotes the density indicator of the population. In any production process, all chromosomes will be assessed based on compatibility to allow selection of the most compatible chromosomes and generates the most compatible children. In the goal of primal problem P2.1, the compatibility of chromosome is computed as:

(19)

In this evaluation, all chromosomes having rank r are ranked according to their fitness and compatibility. For a chromosome, the possibility of producing child is equal to with predefined value q that has been defined in [30]. During all production stages, a monotonous crossover action with possibility is applied for generation of a child by exchanging or merging genes using the generator chromosomes. A monotonous mutation action with probability has been applied and the generation method is repeated until the highest amount of production is achieved as shown in Algorithm 2. Considering the highest amount of production and a constant population density equal to K, the computational complexity order of the proposed framework is equal to . The performance of the UA based on genetic-based algorithm depends upon the number of generations and the size of the population [30]. The simulation results confirm that the effectiveness of Algorithm 1 is greater than genetic-based Algorithm 2. Also, it is revealed that when the density of the population in the GA is not sufficient, it has lower computational complexity.

Algorithm 2:

Genetic-based UA

The aforesaid approach obtains an optimal UA framework for P2.1. By achieving the optimal value of UA ], parameters are achievable according to linear-based programming (LP) method in Equation (20):

(20)

s.t. C3.C6.

P2:2 is effectively solvable by applying software tools, such as CVX tool.

If power sharing is not permitted, as for the optimal amount of grid requested power (G) is for P2.2 based on UA solution ]. This can be calculated using Equation (21) as:

(21)

where .

Using the solutions obtained for subproblems P2.1 and P2.2, Algorithm 3 is introduced as an optimal framework for solving P2 iteratively.

Algorithm 3:

Fixed-Power Efficient Resource Management

4. Efficient Resource Management with Dynamic Power Control

The goal of this subsection is providing a formal framework for resource-allocation optimization problem with the perspective of dynamic power control mechanism. We tried to apply an efficient resource management algorithm to joint optimal power allocation and UA techniques to achieve the maximum degree of energy efficiency for the whole system in which the QoE parameters are assumed to be bounded during multicell multicast sessions. The solution of the introduced problem in a scenario with dynamic transmission power is an improved decentralized algorithm that supplies effective UA. The model then modified to develop joint multilayered resource control and UA that can distinguish the service pattern in cooperative energy heterogeneous systems with NOMA to obtain more resource optimality. We have formulized the problem as the following:

(22)

C1:

C2:

C3:

C4:

C5:

C6:

C7:

In this formulation, and demonstrate UA and resource allocation matrix, respectively.

(23)

The decomposition method used for the indicated goal function is based on Lagrangian formulation.

(24)

where, in this formulation the Lagrangian coefficients are defined as: , , , and . Also, we define the dual problem as the following:

(25)

So, the Lagrangian formula can be changed to Equation (26)

(26)

3.1 Dual Decomposition

For problem simplicity and decreasing the complexity of the scheme, the goal problem has been divided to two subproblems. The main problem will be solved if we can find the optimal solutions for these two independent subproblems. In this regard, the problem (22) can be considered as the following.

(27)

Note that the mentioned condition (C1) is used to find the solution for both separated subproblems. So, the dual decomposition approach is introduced as

(28)

where

(29)

(30)

By considering (X, P) and , the main problem indicated in Equation (22) with condition (23) will be modified to (29) and (30). Thus, the original problem in (22) under condition (23) is transformed into subproblems (29) and (30). In order to solve this modified form of the problem we used sub-gradient approach which is shown as Equation (31)

(31)

The optimal value of Equation (27) is achievable by considering of the formulation (19) which can be expressed as

(32)

Where

(33)

This algorithm is iterative and we can claim that the decision relevant to user service level and base station utility will be made in K’th iteration which the value of K is achievable by sub-gradient solving Equation (30) as indicated in (34)

(34)

In this formulation, will be used by base stations for UA. Also, for updating the Lagrangian coefficients we used sub-gradient methods as expressed in the following formulations.

(35)

(36)

(37)

(38)

The step sizes are defined as and . The optimal value of mentioned dual Lagrangian problem will be achievable via obtaining the updated values of the Lagrangian coefficients and by formulations (35)–(38).

3.2 Energy Efficiency and Power Allocation

We applied the Newton–Raphson method for obtaining the optimal solution of the mentioned efficient power allocation problem. In this regard, the main problem (Equation 24) can be adjusted as:

(39)

In this formulation if subscriber i be associated with base station j, is assumed to be equal to 1. Also, the first and second derivation order of the power formulation (39) can be exhibited as Equations (40) and (41).

(40)

(41)

It should be noted that the parameter will be updated in each iteration as Equation (42).

(42)

where in this formulation, denotes the step size. Also, is defined as:

(43)

Considering the QoS constraint indicated in previous formulations, the minimum transmission power is achievable via the following relation.

(44)

The control of the total consumable power and its impact on UA is done by adjustment on transmit power variable. Actually, with adjusting the value of the power variable, the total consuming power will be modified correspondingly. In this framework, as soon as convergence of the power control algorithm, the model will obtain a suboptimal load-balanced condition which in this condition UA is done intelligently right based on the network load distribution. So, system can handover the traffic from congested microcell to the neighbors low-load femtocells. Using this approach, the possibility of occurring the congestion will be reduced and the UA is stablished with better level of SINR.

3.3 Iterative Gradient Algorithm

In the following, an efficient distributed gradient method, which is shown as Algorithm 4, is suggested to obtain the targeted UA. The targeted UA is done under constraints of (23). It should be noted that in order to decrease the computational complexity and quick convergence, Newton’s method is applied for updating the parameter .

Algorithm 4:

Optimal Gradient Algorithm

3.4 Complexity Analysis

The computational complexity of the suggested approach has been investigated in this part. It is obvious, there is needed mathematical operations for UA relations among base stations and subscribers during each iteration. Also, degree of complexity is imposed on the network by implementation of power assignment algorithm and it is assumed that finding optimal solution of the formulation (22) needs to I iteration. In this model, each subscriber selects a base station which be able to satisfy its QoS constraints, for example, throughput level. So, each subscriber should be in communication with all neighbor base stations. Also, from the base station side, each base station should update the list based on the network load reports and the achievable requested data rate. In this regard, the Lagrangian coefficients and need to mathematical operations, and needs order of complexity. So, the overall degree of computational complexity of Algorithm 4 is equal to .

5. Simulation Results

This section presents the simulation results for different scenarios to illustrate the effectiveness and complexity of the suggested approach in comparison with previous schemes. The entry rate of the alternative energy (solar energy or wind power) will be modified gradually in real systems while it is fixed in a time slot. The power level harvested by a MBS and PBS is assumed to be constant and the same level of alternative energy is allocated to each pico cell in each time slot.

For simplicity, analysis of the simulation, the proposed algorithms are assumed to be independent of the distribution of alternative energy. Time-slotted Rayleigh/Rician fading in a slight mobility environment is applied because UA is usually done in large-scale timing mode and slow fading can be neglected [27]. Furthermore, pico cells and UE are identically distributed for the coverage of each macro cell. Table 1 shows the major simulation parameters.

Table 1. Effective Simulation parameters

Parameters	Values
Network bandwidth	4*5 MHz
Noise power	-250 dBm/Hz
Cell radius	200-3000 m
Path loss level of macro cells
Path loss level of pico cells
Maximum transmission power - macro cells	42 dBm
Maximum transmission power - pico cells	30 dBm

5.1 Fixed-Power Optimal UA

This section presents the various UA algorithms with constant transmission power. This system does not use power control at the base stations. Using the power allocation formulation of NOMA systems in Equation (3), the total transmission power at each base station is . A progressive resource allocation pattern is used for simplicity. For example, the transmission power of subscriber signaling is when subscribers have been added to the independent power domain of sector m. The target is to analyze the performance of various UA approaches based on coverage level and signal quality using an identical power allocation state. The functionality of the proposed algorithm is compared with conventional UA using reference signal received power (RSRP).

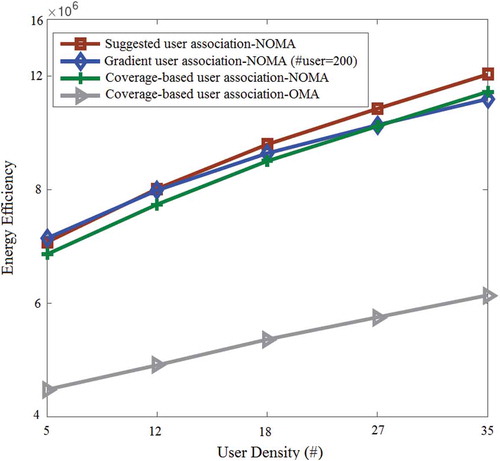
Figure 2 shows the power efficiency versus UE density assuming the number of pico cells is 8 (M = 8) and given power transfer efficiency index . The minimum acceptable QoS constraint is assumed to be bits/s/Hz. The amount of energy picked up by the MBSs and PBSs is 36 and 26 dBm, respectively. The highest production by the genetic-based UA is 10, q = 0.1 and . According to the results, it is obvious that the proposed UA approach with NOMA is more energy-efficient than previous schemes.

Figure 2. Comparison of user association schemes from energy efficiency viewpoint

Energy efficiency improved with an increase in the amount of UE due to gains in multiuser diversity. Each subscriber experiences a certain amount of path loss and fading and more UE with less path loss increased the total energy efficiency. The results indicate that NOMA outperformed orthogonal cases. With the use of the genetic-based UA, power efficiency slowly increased corresponding with the growth of the amount of UE because the efficiency of the genetic-based algorithm depends on user density [30]. However, assuming high user density (i.e. K = 200 in the network coverage area) any acceptable solution for a GA is not achievable because with a high density of UE more potential solutions are required [30].

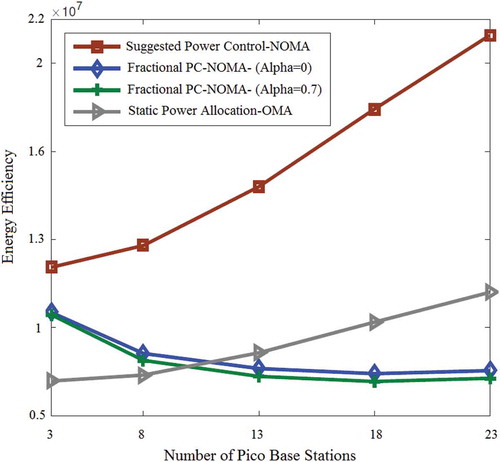
Figure 3 shows the power efficiency versus the density of PBSs for UE at N = 50 and power transfer efficiency index . The minimum acceptable QoS constraint was determined to be bits/s/Hz and the power accrued by the MBSs and pico cells was 36 and 26 dBm, respectively. The highest production of the GA is 10, q = 0.1 and . The results illustrate the proposed UA approach using NOMA obtained a higher spectral efficiency than the conventional cases. The proposed UA algorithm outperformed the RSRP-based UA and this gap in efficiency was larger after deploying more PBSs because the proposed UA obtained more base station density gain [28]. For the genetic-based algorithm UA approach with a density of K = 600 distributed users in the network coverage area, the number of solutions was lower with high pico cell density [30].

Figure 3. Comparison of user association schemes from energy efficiency viewpoint VS #Pico base stations

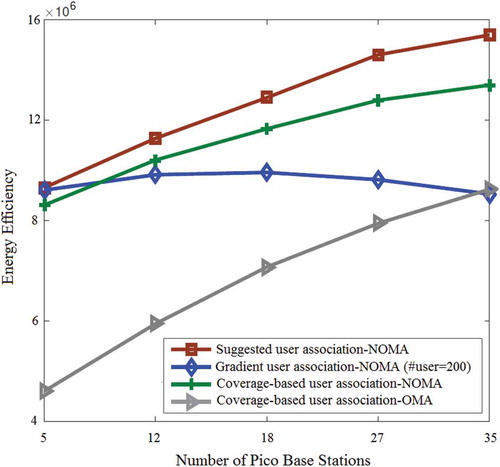
Figure 4 denotes the power efficiency versus density of base stations assuming the amount of UE to be N = 60. The power transfer efficiency index was set at . The minimum acceptable QoS constraint was determined to be bits/s/Hz. The level of energy picked up by the macro cells and pico cells is 36 and 26 dBm, respectively. It is evident that energy efficiency increased quickly as the number of PBSs increased using the proposed power control algorithm in NOMA mode. The proposed algorithm outperformed the conventional schemes but also, this gap of efficiency will be larger by deploying more pico cells. This improvement shows that the proposed resource control approach can gain more base station densification and effectively eliminate intercell interference. When the density of pico cells is lower than normal, NOMA with FTPA can achieve better performance than the conventional orthogonal case, because NOMA offers superior spectral efficiency. With FTPA, NOMA cannot increase power efficiency simply by adding more PBSs. This occurs because more UE will be handed over to the pico cells according to effect of the stronger intercell interference. Under these conditions, more transmission power should be allocated to each user-stream to overcome intercell interference. As shown in subsection 4.1, the FTPA at increases energy efficiency than at because user streams with weaker channel quality (degraded CINR) would be assigned more resources in the FTPA scheme at , which decreases the overall data rate with a similar power consumption pattern.

Figure 4. Comparison of resource allocation strategies from energy efficiency viewpoint VS #Pico base stations

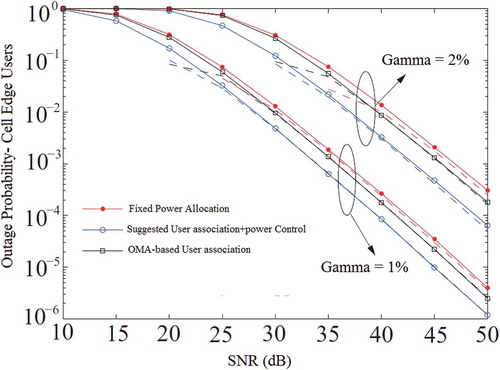
5.2 Outage Probability

We have evaluated our approach in comparison with other schemes from the view point of outage probability in various conditions with different signal-to-noise ratio. In this regard, we divided all area to some sections with distinct SNR level in which SNR interval is from 10 to 50 dB. For more explanation of the achieved result, we can mention that the evaluation has been done in two modes so that Gamma denotes congestion level. Based on this scenario, we will face to lower outage level when the network congestion is lower.

As it is obvious in this assessment (Figure 5), our suggested UA with power control has the best result. Also, orthogonal-based UA scheme gives better result than Fixed power allocation scheme which is introduced as a static approach.

Figure 5. Comparison of outage probability of cell edge users VS SNR (dB)

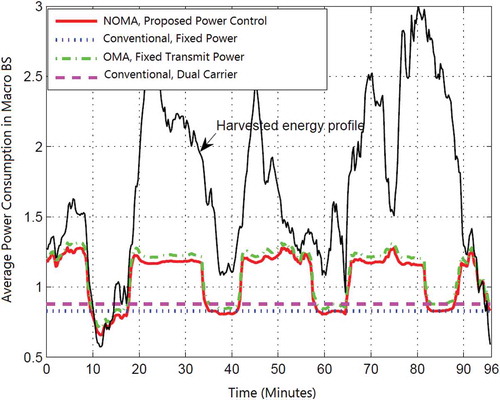
5.3 Interference Coordination through NOMA HetNets

In comparison with the single-cell orthogonal system, the effect of intercell interference on resource allocation in the double-layer NOMA HetNets is considerable. In this regard, we have evaluated the algorithm efficiency in interference-limited condition. Figure 6 shows that the level of harvested energy is very different based on changes in alternative energy resources. Also, conventional fixed power schemes cannot use any kind of energy except grid resources so we expect that the pattern of energy consumption of these schemes remains constant as conditions change. But as it is obvious, the achieved energy efficiency of the NOMA controlled power is better than OMA fixed power mode. It should be noted that Figure 6 is relevant to the functionality of only one base station and this difference will be completely considerable when we consider total consumed energy of network.

Figure 6. Comparison of power consumption in the simulation time interval

5.4 Complexity Analysis

The computational complexity of the suggested approach has been investigated in this part. It is obvious, there is needed mathematical operations for UA relations among base stations and subscribers during each iteration. Also, degree of complexity is imposed on the network by implementation of power assignment algorithm and it is assumed that finding optimal solution of the formulation (22) needs to I iteration. In this model, each subscriber selects a base station which be able to satisfy its QoS constraints, for example, throughput level. So, each subscriber should be in communication with all neighbor base stations. Also, from the base station side, each base station should update the list based on the network load reports and the achievable requested data rate. In this regard, the Lagrangian coefficients and need to mathematical operations, and needs order of complexity. So, the overall degree of computational complexity of Algorithm 4 is equal to .

In comparison with other schemes, we can conclude that the complexity of our scheme is somehow more than the degree of complexity in Fixed Power OMA/NOMA algorithms but these little changes are not considerable. Also, GA introduced in part 3 has the highest degree of computational complexity because of so many high-order logical operations. Also, further investigation about the comparison among the degree of computational complexity of various algorithms is introduced as future work of this research.

6. Conclusion and Future Research Directions

In order to achieve the effective resource management, we suggested a novel approach to joint optimal power allocation and UA techniques in which cells are powered via a common grid network and alternative energy resources. This research focuses on resource assignment in energy-cooperated heterogeneous systems with NOMA so that the QoE indexes are assumed to be bounded during multicell multicast sessions. The solution to the introduced problem has been developed to a mixed-integer programming framework in which the goal function is solved based on a Lagrangian convex optimization method by considering UA constraints. The effectiveness of the suggested approach has been confirmed by the numerical results and we compared the complexity of the proposed model to those of the conventional schemes. Also, the results reveal that NOMA can provide greater energy efficiency than OMA in heterogeneous wireless networks.

For future works, researcher can consider other UA optimization schemes in multicell NOMA systems such as symmetric, proportional, and max/min fairness are recommended. Furthermore, imperfect global CSI has a considerable effect on the likelihood of outages and the average throughput in NOMA. Interference coordination is other main issue which has severe impaction on radio performance which should be eliminated in two-sided communications through uplink/downlink transmissions. For decreasing the fading effect, smart selection of transmission mode and the kind of using MIMO technology with non-orthogonal networks is recommended for future important research to enhance energy efficiency in which MIMO-based non-orthogonal systems, inter-UE interference decreases effectiveness. So, finding ways of decreasing inter-user interference appears to be necessary. Finally, joint resource control and UA solutions in multicell non-orthogonal systems have not been deployed, especially in MIMO-based system and more research effort should be devoted to this subject.

Additional information

Notes on contributors

Faramarz Nikjoo

Faramarz Nikjoo received his B.Sc. degree in Computer Software Engineering from Shahid Bahonar Technical Faculty of Shiraz, Iran, in 2005, and the M.S. degree in Computer Software Engineering from Islamic Azad University Science and Research, Ardebil Branch, in 2018. He currently works in ISC (Faradis Alborz), Iran. His research interests include artificial intelligence, mobile computing, and big data. E-mail: [email protected]

Abbas Mirzaei

Abbas Mirzaei received his Master degree in Telecommunication Engineering from Tabriz University, Tabriz, Iran, in 2007, and the PhD degree in Computer and Communications from Malek Ashtar University of Technology. He currently works as an assistant professor at the Faculty of Computer Engineering, Islamic Azad University, Ardabil Branch. His research interests include computer security and reliability, artificial intelligence, computer communications (networks), cellular network optimization, heterogeneous networks, data mining, and wireless resource allocation. E-mail: [email protected]

Amin Mohajer

Amin Mohajer received the BE degree in bioelectric engineering from Shahed University, Tehran, Iran, in 2008, and the MS degree in Telecommunications engineering from the Malek-Ashtar University of Technology, Tehran, Iran, in 2011. In August 2012, he joined Iran Telecom Industries where he is currently working in the field of radio frequency planning and network optimization. His research interests include wireless networks, optimization, next generation mobile networks, and data analysis. E-mail: [email protected]