Approximate Q-Learning for Stacking Problems with Continuous Production and Retrieval

ABSTRACT

This paper presents for the first time a reinforcement learning algorithm with function approximation for stacking problems with continuous production and retrieval. The stacking problem is a hard combinatorial optimization problem. It deals with the arrangement of items in a localized area, where they are organized into stacks to allow a delivery in a required order. Due to the characteristics of stacking problems, for example, the high number of states, reinforcement learning is an appropriate method since it allows learning in an unknown environment. We apply a Sarsa$(\lambda )$ algorithm to real-world problem instances arising in steel industry. We use linear function approximation and elaborate promising characteristics of instances for this method. Further, we propose features that do not require specific knowledge about the environment and hence are applicable to any stacking problem with similar characteristics. In our experiments we show fast learning of the applied method and it’s suitability for real-world instances.

Introduction

This paper is about the application of an online reinforcement learning (RL) algorithm to stacking problems with continuous production and retrieval. The considered stacking problem is motivated by a real-world problem instance arising in steel industry. There steel slabs are continuously produced and need to be delivered in a certain order or in predefined transport loads, that consist out of up to four slabs. Since the slabs are not produced in the required delivery sequence, they need to be rearranged. For that purpose a certain number of buffer stacks exist. The goal of the optimization is to deliver all slabs in the required order while minimizing the number of shuffling movements. Figure 1 shows the stacking problem exemplarily. Here the continuous production and retrieval are represented by frequently increasing/decreasing production/delivery stacks.

Figure 1. Example of a stacking problem with continuous production and retrieval of steel slabs having a required delivery order.

The considered problem has been proposed by (Rei, Kubo, and Pedroso 2008) as the steel stacking problem. It has been formalized and first heuristic methods have been developed. In (Rei and Pedroso 2012) further semigreedy heuristics are proposed and computationally compared regarding the number of constructed solutions and the best solution obtained using each heuristic. (Boysen and Emde 2016) proposed the considered problem as parallel stack loading problem (PSLP) and developed exact and heuristic solution procedures. A dynamic programming approach is presented for small instances, for large instances heuristic rules are presented.

Stacking problems in their general form deal with the stockpiling of items on top of each other. Such items can be containers in storage yards (Gharehgozli et al. 2014; Kefi et al. 2009; Salido, Sapena, and Barber 2009; Shin and Kim 2015), pallets in warehouses (Nishi and Konishi 2010) or slabs in the steel industry (Boysen and Emde 2016; Kim, Koo, and Sambhajirao 2011; Rei and Pedroso 2012; Tang, Zhao, and Liu 2012; Zäpfel and Wasner 2006). (Caserta et al. 2011a), (Caserta et al. 2011b) and (Lehnfeld and Knust 2014) provide a comprehensive survey on stacking problems regarding loading, unloading or premarshalling of items. However, most of the summarized research work address the Blocks Relocation Problem (BRP) (Caserta et al. 2011a, Kim and Hong 2006) or the Pre-Marshalling Problem (Bortfeldt and Forster 2012). Both problem types consider an initial configuration of stacks of items. The BRP deals with the rearrangement of items in order to allow a continuous retrieval in a certain order. The Pre-Marshalling Problem is about rearranging the initial configuration in order to obtain a new layout, which allows a later retrieval without further relocations. In contrast to the proposed stacking problem, neither the BRP nor the Pre-Marshalling Problem takes a continuous production of items into account. The considered stacking problem deals with a continuous input of items (here: slabs) while also having an ongoing retrieval (see Section 3). Further, as well for the BRP as for the Pre-Marshalling Problem many solution approaches have been researched and developed, but none of those instances are solved by using RL, as the surveys by (Caserta et al. 2011a) and (Lehnfeld and Knust 2014) show.

Stacking problems seem to be reasonably solvable by RL, since it is known to be very efficient in learning in an unknown environment. It is a machine learning framework for solving sequential decision problems that can be modeled as a Markov Decision Process (MDP). An agent interacts with an initially unknown environment, modifies its actions through trial and error in order to develop a policy that maximizes a numerical cumulative reward.

Especially, the Q-Learning algorithm can be used to find an optimal policy without requiring a model of the environment (Sutton and Barto 1998). In (Hirashima 2008) a marshaling plan for container yard terminals is proposed obtained by using Q-Learning. The marshaling process is divided into two stages: In the first stage, the container to be rearranged is selected. In the second stage, containers to be removed, above the target container from stage one, and their destination stacks are selected. The Q-values are then updated iteratively per episode until the destination layout is reached. However, Q-Learning is a so called offline algorithm, which means that the optimal policy is learned and updated, no matter which actions the agent actually carries out; whereas an online algorithm also takes exploratory and random moves into account (Sutton and Barto 1998). Further, in Q-Learning all Q-values of each episode are stored in a look-up table, which requires a lot of memory. In order to reduce the needed memory size, (Hirashima 2009) present an update rule that limits the length of an episode and corresponding Q-values in order to avoid ineffective stacking moves due to preventable long episodes.

Nevertheless, the high number of states, the concomitant required memory size and the offline/online aspect is a crucial point that makes Q-Learning in real-world problems impractical. Further, the data needed to fill the look-up tables accurately is often not available. One approach to solve this is the so-called approximate RL that combines RL with function approximation. Currently, there are three methodologies within the focus of the research community differing in which part of the solution shall be approximated (Van Hasselt 2012, Xu, Zuo, and Huang 2014): model approximation, value approximation or policy approximation. Those methodologies have received more interests by the research community in recent years (Busoniu et al. 2010; Melo, Meyn, and Ribeiro 2008; Tsitsiklis and Roy 1997; Uther and Veloso 1998; Wang, Cheng, and Yi 2007). Further, (Baird 1995) present a class of residual algorithms with function approximation. The paper proposes RL combined with general function approximation systems and prove analytically and in experimental tests fast learning with guaranteed convergence. (Bertsekas and Tsitsiklis 1995) give an overview of methods that combine ideas from the fields of neural networks, artificial intelligence, cognitive science, simulation, and approximation theory. Further, the paper describes the use of features for function approximation with neural networks. (Melo, Meyn, and Ribeiro 2008) analyze the combination of RL with linear function approximation of the Q-function with infinite state spaces. The paper investigates the convergence of linear function approximation and of using the Sarsa algorithm (Sutton and Barto 1998). However, they conclude that the target function must be close to a linear function to obtain results of practical value. In (Xu, Zuo, and Huang 2014) a comprehensive survey on recent developments in RL with function approximation is presented, convergence and feature-based representations of various methods are analyzed. For general introductions to RL and derived methods we refer to the literature in (Bertsekas and Tsitsiklis 1996; Busoniu et al. 2010; Sutton and Barto 1998; Szepesvári 2010).

Applications of approximate RL can be found in computer games or practical applications. RL has been applied to how to play games for many years. The first application of RL was the game Backgammon (Tesauro 1994). Another popular game for applying approximate RL is Tetris (Bertsekas and Ioffe 1996; Bertsekas and Tsitsiklis 1996; Gabillon, Ghavamzadeh, and Scherrer 2013; Tsitsiklis and van Roy 1996). Further, approximate RL can be applied to packet routing (Boyan and Littman 1994), job-shop scheduling (Zhang and Dietterich 1995) or elevator dispatching (Crites and Barto 1996). Also traffic signal control can be solved with various RL algorithms (Abdulhai, Pringle, and Karakoulas 2003; Balaji, German, and Srinivasan 2010; Prashanth and Bhatnagar 2011). For further information on applications, see (Xu, Zuo, and Huang 2014), where a comprehensive overview of several applied RL algorithms is presented.

Applications of Sarsa($\lambda$) can be found in (McPartland and Gallagher 2011; Stone, Sutton, and Kuhlmann 2005). In the paper of (McPartland and Gallagher 2011) a tabular version of Sarsa($\lambda$) applied to First Person Shooter Games is proposed. The state and action spaces are discrete. The paper presents several results using Sarsa($\lambda$) for training the behaviors of the acting agents. Although the algorithm was not able to meet the industry standard, the paper shows successful use of approximate RL. (Stone, Sutton, and Kuhlmann 2005) propose a SMDP Sarsa($\lambda$) with linear tile-coding function approximation and variable $\lambda$ for learning a higher-level decision sequence in RoboCup soccer. The paper deals with a continuous state space, but discrete action space. The results show that multiple agents are learning simultaneously very fast and empirical results prove the efficiency of approximate RL.

The focus of our work is on the methodology of policy approximation in the sense of storing a policy directly and updating its values in order to obtain the optimal policy. The Q-values must be learned by the agent to approximate the optimal Q-function. It is about online learning, whereas the error between the actions and states that actually occur and the approximated values is minimized (Sutton and Barto 1998). States are represented by so-called features. They contain information about relevant parts of the environment and are updated each time an action has been applied (Sutton and Barto 1998). Currently, the research community focus on developing features for which no specific knowledge is needed (Prashanth and Bhatnagar 2011).

Our contribution is the development of a feature-based RL-algorithm, namely Sarsa($\lambda$), applied to a real-world stacking problem. The features do not need specific knowledge about the environment and hence are applicable to any stacking problem having similar properties, like continuous production and retrieval or a certain (un)loading order. In experimental studies, we show fast learning of the proposed method and good results for real-world problem instances. Further, we work out for which characteristics of instances the considered algorithm is best suitable. The paper is organized as follows. Section 2 provides a short overview of the theory of RL. Section 3 describes the considered problem. In Section 4, the application of the method, for example, approximated Q-Learning, to the considered stacking problem is presented, for which the results are presented in Section 5.

The RL Framework

Reinforcement learning (RL) (Sutton and Barto 1998) is a method of machine learning designed to allow an autonomous agent to maximize the accumulated rewards received while interacting with its environment. By observing the obtained rewards and the feedback of the environment, the agent learns to optimally execute actions until a predefined target is reached. In any problem environment there exists a set of states, defining the state space $S$, which can be finite or infinite and discrete or continuous. A state represents the actual environment conditions as well as possible follow-up actions. Actions are activities, which an agent is able to apply in certain states. The action space $A$ can be finite or infinite. Beside that, there can be identified four elements of RL (Sutton and Barto 1998): policy, value function, reward function, and optionally a model of the environment.

The model of the environment represents the behavior of the agents environment. Being in a certain state and applying an action, the model may predict the resultant state and reward. A model can be considered for planning, in the sense of deciding which actions to take for experiencing future situations before actually undergoing them. However, those models are often not known or to complex in case of high dimensions of state and action spaces.

A policy $\pi$ defines the sequence of actions. Roughly speaking, a deterministic policy is a mapping from states to actions, determining which action needs to be taken while being in a certain state.

$\pi :S\times A\to [0,1],\sum _a\pi (s,a)=1$

$\pi (s,a)$ defines the probability of selecting action $a$ while being in state $s$. The goal of RL is to find the optimal policy that maximizes the sum of received rewards in the long run. Due to the fact that a model of the environment is only optional, this is usually done by estimating the expected accumulated reward using a value function. The value function gives the sum of rewards an agent can expect when being in that state assuming that the agent acts optimally from here on until the target is reached. Regarding the value function, we distinguish between the state-value function and the action-value function. The state-value function can be seen as a mapping from states to the sum of rewards.

$V^{\pi }(s):S\to R,V^{\pi }(s)={\mathbb{E}}_{\pi }\left[R_t|s=s_t\right]$

Similarly, the action-value function is defined as a mapping from state-action pairs to the sum of rewards.

$Q^{\pi }(s,a):S\times A\to R,Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[R_t|s=s_t,a=a_t\right]$

$Q^{\pi }(s,a)$ determines the expected return when starting in state $s$ and performing action $a$ and following from here on an optimal policy. From the definition, it can be seen that each policy has a different value function.

Whereas the value function represents which behavior is good in the long run, the reward function returns an immediate feedback. A reward is a numerical value for each state after performing an action.

$R_{s{s}^{\prime }}^a=\mathbb{E}\left\{r_t|s_t=s,s_{t+1}=s^{\prime },a_t=a\right\}$

where $r_t$ is the actual reward returned in state $s$ after performing $a$. The reward function helps the agent to learn the optimal behavior, in the sense of when obtaining a low reward the agent learns to not choose that action in that state anymore and vice versa.

The Stacking Problem

This work considers a stacking problem arising in steel industry at the production stage. $N$ slabs are continuously cast and come with a production and delivery date. Slabs belonging to a certain transport load have the same delivery date. After being cast, slabs are lifted either to the so-called hot storage area to allow for an arranging process or directly to the delivery stack. The hot storage area consists of $M$ buffer stacks, one delivery stack and one crane for moving slabs. Each stack has a maximum height $H$. It is important that the slabs are moved to the delivery stack in assorted loads, for example same delivery dates must be delivered in common, whereas the order of the loads plays a minor role as long as the loads are completely produced, given by the delivery date. The challenge is that the order of the production dates is not identical with the order of the delivery dates. The optimization goal is to deliver all slabs, respectively transport loads, to the delivery stack in an assorted order while minimizing shuffling movements.

Due to the fact that there are as many possibilities to place a single slab as stacks exist, a high number of possible states accrues when considering all slabs; whereas a state describes the position of each slab and the height of each stack at a certain time (see Section 4.1).

RL in the Stacking Problem

In our work, we developed an online method for finding the optimal stacking policy. The state-action value function, for example, Q-function, shall be approximated by a linear function using a gradient-descent Sarsa$(\lambda )$ algorithm (Sutton 1988). We use a linear approximation since the convergence can be guaranteed for a suitable step size (Tsitsiklis and Roy 1997). An advantage of the Sarsa$(\lambda )$ algorithm is that no model of the environment is required. We focus on approximating the state-action value function $Q_t\approx Q^{\pi }$ that shall be represented as a parameterized functional form with parameter vector ${\theta }_t$. The gradient-descent update for the state-action value prediction is then

(1) ${\theta }_{t+1}={\theta }_t+\alpha {\delta }_t{e}_t$(1)

with a prediction error

${\delta }_t=r_{t+1}+\gamma Q_t(s_{t+1},a_{t+1})-Q_t(s,a),$

eligibility traces

(2) $e_t=\gamma \lambda e_{t-1}+{\mathrm{\nabla }}_{{\theta }_t}{Q}_t(s_t,a_t),$(2)

with $e_0=0$ and a step size $\alpha$. $\gamma$ is a discount factor, representing the weighting of states in the past or future. $\lambda$ influences the learning rate, in the sense that it determines how many past states shall be recorded as visited by the eligibility traces (see Section 4.4). The step size $\alpha$ plays an important role for the convergence of the algorithm. In order to achieve convergence in stochastic approximation we need to assure (Sutton and Barto 1998):

(3) $\sum _{k=1}^{\mathrm{\infty }}{\alpha }_k=\mathrm{\infty }\wedge \sum _{k=1}^{\mathrm{\infty }}{\alpha }_k^2<\mathrm{\infty },$(3)

which means that the step size must be large enough to not get caught by random behavior, but decrease enough to ensure convergence.

For updating the state-action value function, we use a feature representation in order to reduce the high dimensionality which is due to the high number of possible states.

$Q_t=\sum _{i\in {\mathbb{F}}_a}{\theta }_t(i)$

where ${\mathbb{F}}_a$ is the set of used features. Features describe the current state and are weighted by the parameter vector $\theta$ (see Section 4.3).

In the following section, the stacking problem and the developed algorithm are described in detail as well as all components of it.

State Space

The state space $S$ is represented by all possible states $s_t$. A state $s_t$ indicates

• the location of each slab being placed on a buffer or delivery stack within the hot storage area at time $t$,

• properties of each slab, like length, width, temperature, delivery date, and transport load number and

Regarding $M+1$ stacks, for example, $M$ buffer stacks and one delivery stack, $N$ slabs and all possibilities of placing and relocating them we obtain a dimension of $\left(\begin{array}{c}M+N\\ M\end{array}\right)$ at a fixed time $t$ without considering any retrieval until $t$, for example having 6 stacks and 35 slabs we get 4.496.388 possibilities of placing them. Due to the high number of states, we consider an approximate algorithm where each state is represented by a feature vector (see Section 4.3).

Action Space

The action space $A$ is represented by six possible actions.

Put Action: one slab is moved from the production to a buffer stack.

Put Direct Action: one slab is moved from the production to the delivery stack.

Relocate Action: one slab is moved from one buffer stack to another buffer stack.

Remove Action: one slab is moved from a buffer stack to the delivery stack.

Delivery Action: one transport load, consisting of up to four slabs, is moved away from the delivery stack by a transport vehicle.

NOP Action: nothing happens.

Only slabs being placed on top of a stack can be moved. Hence, whether an action for a certain slab can be performed depends on the current location of that slab.

Features

Features represent the state space in the sense that they give information about the locations of slabs or transport loads. On the one hand, we consider action features independent of the current state, on the other hand we use state-action features indicating a value for performing a certain action and getting to a certain state. All used features are binary features.

• State-independent features

  • Each type of action

• State-action features

  • Relocate action frees/does not occupy slabs of the same load as the delivery stack contains at the source/target stack

  • Relocate action when source stack is unsorted regarding to delivery dates, for example, earlier dates are beneath later dates

  • Relocate action implies that source and target stack are sorted

  • Relocate action reduces/does not increase shuffles for the next or any completely produced load at the source/target stack

  • Put action places slabs of the same load at the same stack

  • Put action could place the current slab better, for example, slabs of the same load as the current slab are placed on other stacks than the chosen target stack

  • NOP action in case no improvement can be reached

Features are weighted by the parameter vector $\theta$, that is updated at each time step, as can be seen in equation (1). Due to the decreasing step size $\alpha$, the parameter vector converges as the algorithm proceeds. $\theta$ represents the approximated Q-function. We use binary features in order to keep the weights in a bounded range.

Eligibility Traces

Eligibility traces support learning by recording which states have recently been visited. They define how likely each state is eligible for undergoing learning changes (Sutton and Barto 1998). What “recently” means, that is, how many states in the past may be remembered, is determined by $\lambda$. In case $\lambda =0$, only the current state is changed by the prediction error. The larger $\lambda$, still $\lambda <1$, the more preceding states are undergoing learning changes. Still, due to the definition of the traces (equation (2)), the more recent a state is, the more it is changed. In case $\lambda =1$, only the discount rate $\gamma$ has an impact on the effects of preceding states.

Reward Function

The reward function shall support the agent in learning an optimal behavior. As the goal of our agent is to deliver all transport loads to the delivery stack with minimal movements, the reward function $R_{s{s}^{\prime }}^a$ remunerates actions that support the delivery of slabs and penalizes additional movements: $-10$ for each relocate action, $+10$ for each put-direct or remove action, and $+100$ for each delivery action.

Learning-Algorithm

In our work, a gradient-descent Sarsa$(\lambda )$ algorithm with linear function approximation of the state-action value function is applied. It is an online algorithm that learns in interaction with a simulation framework calculating current representations of states and rewards. The state-action values are represented by features, which must be weighted by the algorithm. The learned weights represent the optimal policy. The simulation runs $T$ episodes, whereas the agent learns from episode to episode but also within one episode. In each episode the agent chooses an action for each time step following an $ϵ$-greedy policy, that is, with the probability of $ϵ$ a random action is chosen, with probability $1-ϵ$ the agent performs the action with the highest Q-value. The exploration rate $ϵ$ is defined as

${ϵ}_t=\frac{1}{t+2},t=0,\dots ,T,$

ensuring that exploration decreases with proceeding episodes. In case of random moves, the eligibility traces are set to $0$, since no learning can be extracted. The step size $\alpha$ is set to

${\alpha }_t=\frac{1}{t+2},t=0,\dots ,T.$

Algorithm 1 presents the applied gradient-descent Sarsa$(\lambda )$ algorithm with linear function approximation and binary features.

Experimental Studies

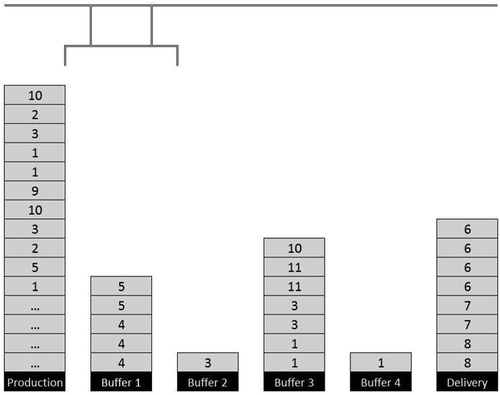
The model is implemented in HeuristicLab (Wagner et al. 2014) using the framework SimSharp (Beham et al. 2014). Since for the stacking problem no benchmark instances exist, we have defined nine test instances, available at the HeuristicLab website [HEAL, 2015]. There are three instances of varying time horizons and number of slabs, each of them having three varying complexities. The complexities differ in the time slots between production and delivery of slabs or transport loads. Figure 2 shows the schema of the test instances. The abscissa represents the past time from the beginning of the production. Each column represents a test instance, having production slots colored in dark gray and delivery slots colored in light gray. The written number within the column stands for the number of slabs being produced/delivered within that slot. The number at the end of each column represents the total number of processed slabs per instance. Test instances of number 1 have a wide time horizon of around 14 hours while processing 20 slabs. Instances of number 2 have a time horizon of around 4 hours, but processing 27 slabs. Instances of number 3 have a relatively short horizon of 2 hours, while processing 12 slabs. The second number describes the complexity of the production/delivery order. Instances marked with .1 have a slight mix of production and delivery. .2 instances show a strictly separated order. Instances of complexity .3 have a strong mix of productions and deliveries. Each test instance has five buffer stacks, one delivery stack and one crane.

Figure 2. Schema of production and delivery order per test instance.

All tests were calculated on a laptop with an Intel(R) Core(TM) i7-4600U CPU $@$2.10 GHz 2.70 GHz processor.

Model Parameters

Based on the content of Section 4.3, we have defined 19 binary features for representing the states. The discount factor $\gamma$ is set to 0.8 ($\gamma =1$ means no discount over time). $\lambda$ is set to 0.7, referring to (Sutton and Barto 1998) concluding that the peak of performance is reached for $\lambda$ within the interval $\left[0.7;0.8\right]$.

Exploration and Learning Rate

The exploration rate $ϵ$ is set to 0,5 at the beginning and is gradually decreasing over time (see Section 4.6). The relatively high rate during the first episodes ensures that the agent is exploring many actions and consequent rewards, whereas the gradual decrease effects that more promising actions are taken the more the time proceeds. Beside that, starting with a relatively high exploration rate guarantees that an acceptable performance is reached during early episodes. This fact is reflected in the exponential behavior of the learning curves, discussed in Section 5.3.

Likewise, the learning rate, or step size, $\alpha$ is set to 0,5 at the beginning and is gradually decreasing over time. In order to achieve convergence, $\alpha$ must satisfy equation (3). The decreasing step size effects that the weighting of features is less updated the more the time proceeds, as equation (1) shows.

Performance Results

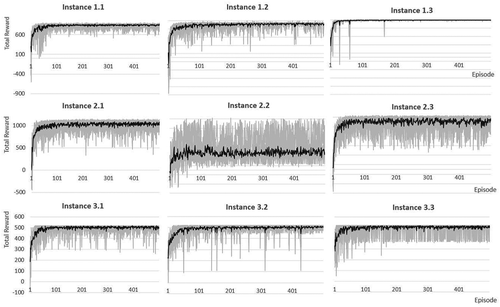
Each test instance performed 10 runs, each with 500 episodes. The figures below show the averaged results over all runs per instance. As the main objective of RL is to maximize the cumulated reward over time, and the goal of the considered stacking problem is to minimize shuffling movements, we present performance results regarding the total reward and the number of shuffling movements. Further, we discuss results regarding the weighting of features since this represents the final approximation of the Q-function. Worth to mention is that each run converged. Divergence only occurs in case of nondecreasing exploration and learning rates.

Figure 3 shows the learning behavior regarding the total reward obtained during a run. The light-colored area represents the results of each run. The dark-colored curve shows the averaged result of 10 runs. The results show that all runs have an exponential-like shape indicating a fast convergence rate of the model. This is also due to the high exploration and learning rate during early episodes, as described in Section 5.2. Further, instances of type 2, for example, having many processed slabs in a relatively short time horizon, show a wide variance regarding the behavior of the single runs. Especially instance 2.2 seems hard to solve referring to the variance of the results. In general, it can be seen that instances of complexity .2, for example, having strictly separated production/delivery order, perform widely spread regarding the total reward. As expected, instances of type 3, for example, having a short time horizon and a little number of processed slabs, performs best regarding constant results over all runs. Summarized it can be said that the more mixed the production/delivery order is, the easier is the instance to solve. This fact is due to the occupancy rate of the buffer stacks. Since a continuous delivery effects a lower occupancy rate which makes it easier to deliver the required slabs or transport loads which again effects a high reward.

Figure 3. Total reward obtained per instance over 500 episodes.

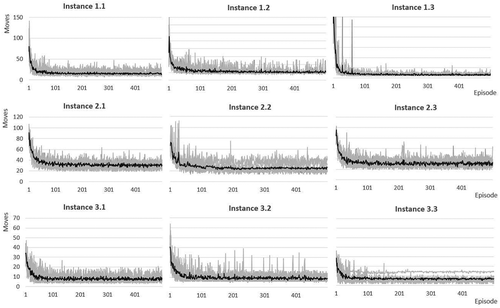
Figure 4 shows the learning behavior regarding the shuffling movements. Again, the light-colored area shows the results of all runs, whereas the dark-colored curve represents the averaged result. Similarly, we can see the exponential-like shape showing good results for minimizing the number of movements.

Figure 4. Shuffling movements needed per instance over 500 episodes.

However, when looking at the number of shuffling movements, we need to take the percentage of reaching the goal, for example, the number of delivered slabs or transport loads, into account. Since it is intelligible that less movements were needed in case not all required slabs could be delivered. Table 1 shows the percentage of successfully delivered transport loads in average over 10 runs.

Table 1. Averaged percentage of delivered slabs over 10 runs per instance.

	Complexity
Instance	.1	.2	.3
1	99.6%	99.1%	99.9%
2	48%	19.6%	51.4%
3	78.4%	99.9%	49.6%

Taking only instances with a high percentage of achieving the goal into account, we see that instances of type 1 perform best regarding goal achievement, shuffling movements and total reward, especially 1.1 and 1.3. As well when looking at instances of type 2: 2.1 and 2.3 perform better than 2.2 regarding the total reward and the percentage of goal achievement. Only test instance 3.2 could be solved better than 3.1 and 3.3. This is due to the little number of processed slabs. The results shown in Table 1 coincide with the results regarding the total reward. A wide variance of obtained cumulated rewards goes along with a low percentage of goal achievement.

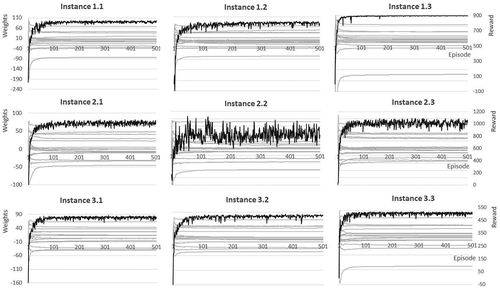
Another important result is the behavior of the weights of each feature, as the weights represent the final approximation of the Q-function. In Figure 5, we can see the behavior of the averaged weighting of each feature (light gray) in comparison to the curve of the total reward (dark gray). What we can derive from here is the correlation between single features and the total reward. As an example in terms of the features content, the action-features type of action is delivery action or type of action is remove action are positive correlated to the total reward; whereas the feature type of action is relocate action shows a negative correlation.

Figure 5. Behavior of the weights per feature averaged over 10 runs compared to the total reward.

Further, it can be seen that the weights of each feature converge. This is an important result in order to obtain a reliable approximation of the Q-function. The weighting of each feature depends on the impact on the total reward. Features get higher weights in case they contribute to a high reward, for example, that a relocate action reduces shuffling movements needed for the next or any completely produced transport load.

Taken all results together we can derive that the denser the production and delivery events are the harder is the problem to solve. Further, instances of complexity .2, for example, having production only followed by delivery only, seem to be hard to solve with our model. The reason for that could be that a linear approximation of the Q-function is not good enough in that case, since the production process calls for other features than the delivery process. However, even though the developed features do not require specific knowledge about the environment, the weighting plays an important role. Due to that fact, the linear approximation may not be suitable for each problem type. Instances that show a strictly separated character of production and delivery events may require a nonlinear approximation of the Q-function; whereas the linear approximation works well for instances having a mixed character of events.

Conclusion

We have applied a linear, gradient-descent Sarsa$(\lambda )$-algorithm to complex real-world problem instances. Even though the model did not perform well at all test instances, we elaborated the characteristics of promising instances. For those, the agent achieves good results with remarkably few episodes. Even though no theoretical results guarantee a successful performance of Sarsa$(\lambda )$, it performs quite well in practice. This paper provides another method for solving complex stacking instances that often arise in real world. Since stacking problems are very hard to solve, especially for real-world applications, this paper is a remarkable contribution to the research community.

Future work will include a nonlinear approximation of the Q-function in order to be able to solve also instances of other characteristics, for example, in case another order of production and delivery events is required. Our future work will also focus on a comprehensive comparison study, including exact approaches as well as heuristic methods.

List of Algorithms

1 Linear, gradient-descent Sarsa(λ) with binary features and replacing traces (Sutton and Barto 1998), 28.

Algorithm 1 Linear, gradient-descent Sarsa(λ) with binary features and replacing traces (Sutton and Barto 1998)

Require: Let $\theta$ and e be vectors having a component for each feature.

Let ${\mathbb{F}}_a$ be a set of features for each action.

Initialize $\theta$= 0, ${\mathbb{F}}_a=\mathrm{\varnothing }$.

repeat

 $e=0$

$S,A\leftarrow$ initial state and action of episode ($ϵ$-greedy)

${\mathbb{F}}_A\leftarrow$ set of features, when choosing $A$ in $S$

repeat

for all $i\in {\mathbb{F}}_a$ do

$e_i\leftarrow 1$

end for

Take action $A$, observe reward $R$ and next state $S^{\prime }$

$\delta \leftarrow R-{\sum }_{i\in {\mathbb{F}}_a}{\theta }_i$

if $S^{\prime }$ is terminal state then

$\theta \leftarrow \theta +\alpha \delta \mathbf{e}$

Go to next episode

else

for all $a\in \mathbb{A}(S^{\prime })$ do

${\mathbb{F}}_a\leftarrow$ set of features, when choosing $a$ in $S^{\prime }$

$Q_a\leftarrow {\sum }_{i\in {\mathbb{F}}_a}{\theta }_i$

end for

$A^{\prime }\leftarrow$ new action in $S^{\prime }$ ($ϵ$-greedy)

$\delta \leftarrow \delta +\gamma Q_{A^{\prime }}$

$\theta \leftarrow \theta +\alpha \delta \mathbf{e}$

$\mathbf{e}\leftarrow \gamma \lambda \mathbf{e}$

$S\leftarrow S^{\prime }$

$A\leftarrow A^{\prime }$

end if

until $S^{\prime }$ is terminal state

until Terminal episode is reached

Acknowledgments

The work described in this paper was done within the COMET Project #843532 Heuristic Optimization in Production and Logistics (HOPL) funded by the Austrian Research Promotion Agency (FFG) and the Government of Upper Austria.