Accurate Computation of Vocal Tract Filter Parameters Using a Hybrid Genetic Algorithm

ABSTRACT

This paper reports an original technique for accurately estimating the parameters of human vocal tract filters for vowels in English for speech processing applications such as voice recognition. In this paper, the vocal tract filter design problem is reformulated as a general nonlinear optimization problem and solved using a hybrid Genetic Algorithm (GA). The hybrid GA computes a rough estimate of the global minimum using GA and refines using computationally cheap local search. Issues that are of concern in digital filtering such as achieving stability and overcoming finite precision effects are addressed. The objective function for optimization used in this paper is formulated in terms of poles and zeros of the filters to avoid ill-conditioning and to take advantage of symmetries in the location of poles and zeros. Simulation results indicate that the approach presented in this paper provides a close fit in terms of mean square error between the experimental and designed filters.

Introduction

Extraction of vocal tract filter parameters is a problem of long-standing interest in speech signal processing, automatic voice recognition and bandwidth reduction in speech transmission systems (Rabiner and Schafer 1993). The human vocal tract has a complex frequency response with numerous local maxima and minima. In this paper, a technique for designing digital filters that closely approximate vocal tract filters using a novel hybrid GA is presented. Vocal tract filters corresponding to vowels in American English are considered.

The production of speech is a complicated process involving a variety of organs. For vowels, in particular, this process can be viewed as an excitation starting from the larynx of lungs and shaped by the vocal tract (Chiba and Kajiyama 1941). Thus, the vocal tract acts as a filter with a definite frequency response which can be experimentally measured. The excitation (also referred to as phonation) and filtering (also referred to as articulation) can be performed independently by humans while generating vowel sounds. Independent action allows the entire process of vowel sound production to be viewed as a source excitation $x[n]$ (larynx) driving a linear time-invariant system $h[n]$ (vocal tract) to produce vowels $y[n]$ (Chiba and Kajiyama 1941).

Figure 1 summarizes the model for vowel sound production. The analog source excitation is sampled to obtain the discrete time signal $x[n]$. A Digital Signal Processor (DSP) is used to filter $x[n]$ to obtain the output signal $y[n]$. Finally, the analog speech sound is synthesized by reconstructing $y(t)$ from $y[n]$ using a digital-to-analog converter.

Figure 1. Block diagram of the digital filter.

The relationship between input and output sequences can be written as:

(1) $y[n]=x[n]\ast h[n]$(1)

where ‘$\ast$’ refers to discrete convolution. Each vowel is generated by a corresponding periodic waveform exciting the vocal tract. Equation (1) can be simplified by taking the Discrete Time Fourier Transform (DTFT) which reduces the complicated operation of convolution in time domain to multiplication in the frequency domain.

In the frequency domain, the spectrum of the vowel sound $Y(e^{j\mathrm{\Omega }})$ is the product of source $X(e^{j\mathrm{\Omega }})$ and filter $H(e^{j\mathrm{\Omega }})$ frequency response functions.

(2) $Y(e^{j\mathrm{\Omega }})=X(e^{j\mathrm{\Omega }})H(e^{j\mathrm{\Omega }})$(2)

The main advantage of the approach given in this paper is that it is possible to design the vocal tract filters without delving into the mechanics of speech production. This approach is useful for vowels but cannot be generalized for every speech sound. For example, the phonemes in American English are classified as vowels, affricates, diphthongs, plosives, fricatives, and whispers (Quatieri 2002). It is known that for certain phonemes the vocal tract cannot be considered as a linear time-invariant system limiting the application of the approach presented here (Chiba and Kajiyama 1941).

The frequency response of the vocal tract is complex with multiple local minima and maxima. This complex and nonstandard vocal tract frequency response cannot be well approximated by standard filter design literature methods used to design low-pass, high-pass, and band-pass filters. In this paper, this nonstandard filter design problem is formulated as an optimization problem and solved using a hybrid Genetic Algorithm (GA). Alternate formulations of the filter design optimization problem are considered, and the choice between alternatives is explained.

Though significant work in the area of design of standard digital filters using optimization techniques has been explored by (Antoniou 1993, Nambiar, Tank, and Mars 1992, Slowik and Bialko 2007, Suckley 1991, Thamvichai, Bose, and Haupt 2002, Tsai, Chou., and Liu 2006, Xu and Daley 1995, Yang and Xinjie 2007), the design of vocal tract filters using global optimization techniques has not been addressed to the best of the knowledge of the authors.

An interesting work of (Slowik and Bialko 2008) addresses non-standard filters but is not suitable for vocal tract filter design for the following reasons. In (Slowik and Bialko 2008), the magnitude response is confined between an arbitrary upper bound and lower bound for the passband. Another set of upper bound and lower bound is fixed for the stopbands. Thus, the design approach presented in (Slowik and Bialko 2008) can only be applied to the design of filters with piecewise constant amplitude response. In addition, the approach presented in (Slowik and Bialko 2008) is susceptible to numerical ill-conditioning effects.

The approach presented in this paper can be used to design stable and minimum phase filters with an arbitrary frequency response from experimentally obtained samples of the amplitude response. The fundamental issue in the design of digital filters with complex frequency responses such as instability and finite precision effects are discussed.

The paper is organized as follows: first the filter design problem is formulated as a constrained global optimization problem; secondly an efficient algorithm for the accurate solution of the filter design optimization problem is presented; finally, results comparing the performance of the designed filters and discussion of results is presented.

Problem Formulation

The problem of vowel sound production can ultimately be viewed as the problem of designing a digital filter to approximate the experimentally obtained frequency response function of the vocal tract. The complete frequency response consists of the amplitude and phase response. However, only the amplitude response is available due to experimental limitations. The only restriction imposed on the phase response is the minimum phase constraint. The minimum phase constraint is imposed on the filter to avoid distortions due to delays as noted in (Gruber 1981) and (Karam and Tobagi 2001).

In this paper, the amplitude response curves experimentally obtained by (Russell 2016) is used as input information for vocal tract filter design. Let $H(\mathrm{\Omega })$ be the experimentally obtained frequency response that we desire to approximate. $H(\mathrm{\Omega })$ can be approximated with a general IIR frequency response function $H_d(\mathrm{\Omega })$ given by Equations (3) and (4). Thus, the goal of filter design is to choose the parameters in (4) such that the difference between $H(\mathrm{\Omega })$ and $H_d(\mathrm{\Omega })$ is minimized. The choice of parameters in Equation (4) cannot be performed analytically since $H(\mathrm{\Omega })$ does not resemble the piecewise continuous standard frequency responses considered in literature. In addition to ensuring that the designed filter $H_d(\mathrm{\Omega })$ is close to $H(\mathrm{\Omega })$, stability and round of error implementation constraints have to be addressed. Thus, the filter design problem can be viewed as a constrained optimization problem.

(3) $H_d(\mathrm{\Omega })=k\prod _{i=1}^M\frac{(z-z_{zi})}{(z-z_{pi})}$(3)

(4) $=k\prod _{i=1}^M\frac{(e^{j\mathrm{\Omega }}-r_{zi}{e}^{j{\theta }_{zi}})}{(e^{j\mathrm{\Omega }}-r_{pi}{e}^{j{\theta }_{pi}})}$(4)

where $k$ is the gain, $z_{zi}=r_{zi}{e}^{j{\theta }_{zi}}$ and $z_{pi}=r_{pi}{e}^{j{\theta }_{pi}}$ are the zeros and poles of the transfer function, respectively. Equation (3) represents the filter in rectangular form and Equation (4) is the representation in polar form. $M$ is the order of the system which is to be chosen as small as possible in view of system realization and cost. However, large values of $M$ provide a better fit with the experimental curve.

The poles represent the roots of the denominator polynomial, and the zeros represent the roots of the numerator polynomial of the transfer function. Mathematically poles are isolated singularities of the complex function $H(z)$ or locations in the complex plane at which $H(z)$ fails to be analytic. Physically the poles can be interpreted as values of $z$ at which $H(z)$ becomes infinite. Thus $H(z)$ becomes large in absolute value near the poles and small near the zeros. Thus, the frequencies near pole locations are amplified and frequencies near zero locations are attenuated. Thus, poles and zeros roughly correspond to maxima and minima in the frequency response. Hence, by choosing appropriate pole and zero locations, one can approximate an arbitrary frequency response with many maxima and minima.

Equation (4) indicates that the unknowns are gain $k$, magnitudes of zeros $r_{zi}$, phase of zeros ${\theta }_{zi}$, magnitudes of poles $r_{pi}$ and phase of the poles ${\theta }_{pi}$. To recast the design problem as an optimization problem the unknown values are considered as elements of the vector $\mathbf{x}$ given by

(5) $\mathbf{x}=[k,r_{z1},r_{z2},\dots ,r_{zM},{\theta }_{z1},{\theta }_{z2},\dots ,{\theta }_{zM},r_{p1},r_{p2},\dots ,r_{pM},{\theta }_{p1},{\theta }_{p2},\dots ,{\theta }_{pM}{]}^T$(5)

Since the dimension of $\mathbf{x}$ is $4M+1$ the search space is a subset of ${\mathcal{R}}^{4M+1}$. Noting that the numerator and denominator of the frequency reponse $H_d(\mathrm{\Omega })$ are polynomials with real coefficients it can be reasoned that the poles and zeros having complex roots appear in conjugate pairs. This fact can be advantageously used to reduce the dimension of search space by half.

$H_d(\mathrm{\Omega })$ can be expressed as a ratio of polynomials Equation (6) or in factored form Equation (4). If Equation (6) is considered as the form for $H_d(\mathrm{\Omega })$, the optimization variables are the polynomial coefficients. If Equation (4) is chosen the optimization variables are roots of the numerator and denominator polynomials. Although both Equations (4) and (6) are mathematically equivalent, form Equation (4) is less sensitive to numerical round-off effects.

(6) $H_d(z)=\frac{\sum _{i=0}^{N_z}{b}_i{z}^{-i}}{\sum _{i=0}^{N_p}{a}_i{z}^{-i}}$(6)

where $N_z$ and $N_p$ are the number of zeros and poles, respectively. $b_i$ and $a_i$ are the respective coefficients. In (Lee et al. 1998) and (Karaboga and Cetinkaya 2004) the filter design problem is formulated in terms of polynomial coefficients in Equation (6). This approach is not desirable since roots of a polynomial are sensitive to small changes in the value of the coefficients.

It is known that the roots (solutions) of a polynomial are extremely sensitive to small changes (perturbations) in the values of the coefficients (Atkinson 2004). Thus, to avoid numerical ill-conditioning the frequency response of the filters are directly formulated in terms of its poles and zeros (which are roots of the denominator and numerator polynomial of the transfer function, respectively). In other words, factored forms of all polynomials are used to avoid numerical stability problems. Another reason for this approach is that complex roots of real polynomials occur as complex conjugate pairs reducing the number of variables in the optimization problem (making the optimization more efficient). An experimental comparison of the two approaches is provided in Section 3.1. The zeros and poles finally obtained can be substituted in Equation (4) to yield the polynomial form for hardware realization. Figure 2 summarizes the entire design process.

Figure 2. Summary of design steps.

Stability and Finite-Precision Effects

In addition to optimizing parameters in Equation (4) to make $H_d(\mathrm{\Omega })$ close to $H(\mathrm{\Omega })$, stability must be ensured and effect of round-off errors must be minimized. It is well known that the poles of a stable and causal LTI (linear-time-invariant) system must lie within the unit circle, so magnitude constraints on poles must be imposed. The location of zeros is in general not constrained. However, to achieve the desirable property of minimum phase, zeros are also constrained to lie within the unit circle. Thus, the filter design problem is a constrained optimization problem. In this paper, the penalty function approach (Chong and Zak 2005) is taken to formulate the constrained optimization problem to an unconstrained optimization problem to enable solution using a global optimization algorithm.

When vocal tract filters are realized on digital hardware, the signal samples and transfer function are represented in finite precision because of bit size limitation. This manifests into two potential problems, namely (Proakis and Manolakis 2003)

1. round-off errors due to multiplication and

2. overflow due to addition.

In particular, if the pole values are close to unity the system can have limit cycles, adversely affecting the settling time. These problems are alleviated to some extent by doing saturation arithmetic in which the added value reaches a maximum or minimum and does not overflow or underflow as the case may be (Proakis and Manolakis 2003). Saturation arithmetic, however, makes the system non-linear because of the clipping. The remedy for this problem is to scale the signal or system parameters so that the chances of entry into the non-linear region is avoided (Proakis and Manolakis 2003). Since downscaling signal size will be detrimental to the SNR (signal-to-noise ratio), the usual practice is to minimize the size of the poles. In this work, the penalty forces the poles to be bounded above by a magnitude of 0.9. Thus, the problems of finite precision are dealt with automatically.

The parameters of the designed filter $H(\mathrm{\Omega })$ have to be chosen such that $H(\mathrm{\Omega })$ is close to $H_d(\mathrm{\Omega })$. Thus, a suitable metric for quantifying the closeness between the functions $H(\mathrm{\Omega })$ and $H_d(\mathrm{\Omega })$ must be chosen. In the past metrics like Mean Squared Error (MSE), Mean Absolute Error (MAE) and maximum absolute error have been used to design standard filters (Karaboga and Cetinkaya 2004). All metrics compute the error using uniformly spaced samples of $H(\mathrm{\Omega })$ and $H_d(\mathrm{\Omega })$. The MSE has the advantage of being differentiable and hence results in a smoother objective function. The absolute value function is not differentiable (and hence metrics using absolute deviations are not smooth), so the objective function is formulated in terms of the MSE in this paper. Using the MSE metric the objective function for optimization can be formulated as in Equation (7).

(7) $C(\mathbf{x})=\left(\sqrt{\sum _i{(\left|H({\mathrm{\Omega }}_i)\left|-\right|H_d({\mathrm{\Omega }}_i;\mathbf{x})\right|)}^2}\right)+\gamma P(\mathbf{x})$(7)

The first term in Equation (7) measures the closeness between $H(\mathrm{\Omega })$ and $H_d(\mathrm{\Omega })$ and the second term is a penalty term that penalizes violation of minimum phase and stability constraints. The second term is chosen to be zero if all constraints are met and strictly positive otherwise. The penalty function approach transforms a constrained optimization problem into an unconstrained optimization problem (Chong and Zak 2005).

(8) $P(\mathbf{x})=\sum _{i=1}^M{g}_i^{+}(r_{zi})+\sum _{i=1}^M{g}_i^{+}(r_{pi}),$(8)

Equation (8) defines the penalty function. The value of $\gamma$ is chosen to be large in order to ensure that solutions violating constraints are assigned a large cost. Thus the choice of parameters $\mathbf{x}$ that violate design constraints are eliminated in the optimization process.

Equations (9) and (10) are used to restrict pole and zero magnitudes to be less than 0.9 to robustly achieve stability and minimum phase constraints.

(9) $g_i^{+}(r_{zi})=max(0,r_{zi}-0.9)$(9)

(10) $g_i^{+}(r_{pi})=max(0,r_{pi}-0.9)$(10)

The NMGA Algorithm

In the following, an optimization algorithm that takes advantage of the global search ability of the Genetic Algorithm (GA) and efficient local search ability of the Nelder-Mead (NM) algorithm is proposed. GA is a population-based stochastic optimization algorithm based on a heuristic inspired by natural evolution (Goldberg 1989, Tang et al. 1996). The members of the population also called as chromosomes are randomly initialized. GA runs a sequence of three major steps, namely, crossover, mutation, and reproduction. This sequence is iterated until a satisfactory solution is obtained.

In crossover, a pair of chromosomes (called parents) are selected to undergo an averaging operation. To the resulting vector, two different random weight vectors are added to generate two different offsprings in place of the parents. Crossover is followed by mutation.

The probability of occurrence of mutation is typically one to two orders less than crossover. Mutation is accomplished by adding a random vector with zero mean to the chromosome. In order to keep the results of crossover and mutation steps within the bounds of the feasible set projection operation is necessary.

Reproduction or copy operation is then performed by a arranging the chromosomes according to the fitness value. The fitness value is the objective function evaluated for the corresponding chromosome. For minimization problems, smaller the objective function value fitter the individual. A tournament-based scheme (Chong and Zak 2005) permits the fittest chromosomes to pass on to the next generation. The repeated operation of crossover, mutation and copy operations improve the chances of the chromosomes to progress towards global minimum.

The NM algorithm is based on defining a simplex (Nelder and Mead 1965) of $n$ variables. Simplex is a polytope of $n+1$ vertices in $n$ dimensions. The operations of reflection, contraction, and expansion are performed (Nelder and Mead 1965) within an iterative loop. ${\mathbf{x}}_{\mathbf{e}}$, ${\mathbf{x}}_{\mathbf{c}}$, ${\mathbf{x}}_{\mathbf{r}}$ represent vectors about which operations of expansion, contraction, and reflection are performed. The search of NM is more intensive than GA, as the step size is smaller and it follows a deterministic rule.

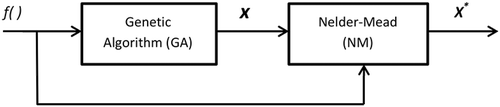
In the NMGA algorithm, a rough solution in the vicinity of the global minimum is computed using the GA and then refined using the computationally efficient NM local search technique. This avoids locating the exact solution using computationally costly random global search with the GA. The complete procedure is outlined in Algorithm 1.

Algorithm 1: NMGA (f)

Step 1. GA: N = 0, Form Initial Population: $P_N$

Compute $f\left({\mathbf{x}}_i\right)$ for each ${\mathbf{x}}_iϵP_N$

repeat

$\left\{\begin{array}{c}\mathrm{C}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}N+1\\ \mathrm{C}\mathrm{o}\mathrm{p}\mathrm{y}:\mathrm{F}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}{P}_{N+1}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\left(1-\chi \right)K\mathrm{o}\mathrm{f}{P}_N\\ \mathrm{C}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}:\mathrm{F}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{f}{P}_{N+1}\\ \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{o}\mathrm{b}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d}\mathrm{b}\mathrm{y}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g}\chi \times K\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}{P}_N\\ \mathrm{a}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{z}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\\ \mathrm{M}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:\mathrm{A}\mathrm{d}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{z}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{o}K\mathrm{o}\mathrm{f}{P}_{N+1}\\ \mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{e}f\left({\mathbf{x}}_i\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}{\mathbf{x}}_iϵP_N\end{array}\right.$

until Stopping criterion met

Step 2. NM: Initialize Simplex: ${\mathbf{x}}_{\mathbf{1}},{\mathbf{x}}_{\mathbf{2}},...,{\mathbf{x}}_{\mathbf{n}+\mathbf{1}}$

while Stopping criterion not met

$\mathbf{d}\mathbf{o}\left\{\begin{array}{c}\mathrm{S}\mathrm{o}\mathrm{r}\mathrm{t}:f\left({\mathbf{x}}_{\mathbf{1}}\right)<f\left({\mathbf{x}}_{\mathbf{2}}\right)<\cdots <f\left({\mathbf{x}}_{\mathbf{n}+\mathbf{1}}\right)\\ {\mathbf{x}}_{\mathbf{c}}=\frac{{\sum }_{i=1}^n{\mathbf{x}}_{\mathbf{i}}}{n}\\ {\mathbf{x}}_{\mathbf{r}}=2{\mathbf{x}}_{\mathbf{c}}-{\mathbf{x}}_{\mathbf{n}+\mathbf{1}}\\ \mathbf{i}\mathbf{f}f\left({\mathbf{x}}_{\mathbf{r}}\right)<f\left({\mathbf{x}}_{\mathbf{1}}\right)\\ \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}{\mathbf{x}}_{\mathbf{e}}\leftarrow {\mathbf{x}}_{\mathbf{r}}-{\mathbf{x}}_{\mathbf{c}}\\ \mathbf{i}\mathbf{f}f\left({\mathbf{x}}_{\mathbf{e}}\right)<f\left({\mathbf{x}}_{\mathbf{r}}\right)\\ \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}{\mathbf{x}}_{\mathbf{n}\mathbf{e}\mathbf{w}}\leftarrow {\mathbf{x}}_{\mathbf{r}}\\ \mathbf{i}\mathbf{f}f\left({\mathbf{x}}_{\mathbf{1}}\right)\le f\left({\mathbf{x}}_{\mathbf{r}}\right)<f\left({\mathbf{x}}_{\mathbf{n}}\right)\\ \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}{\mathbf{x}}_{\mathbf{n}\mathbf{e}\mathbf{w}}\leftarrow {\mathbf{x}}_{\mathbf{r}}\\ \mathbf{i}\mathbf{f}f\left({\mathbf{x}}_{\mathbf{n}+\mathbf{1}}\right)<f\left({\mathbf{x}}_{\mathbf{r}}\right)\\ \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}{\mathbf{x}}_{\mathbf{n}\mathbf{e}\mathbf{w}}\leftarrow \frac{{\mathbf{x}}_{\mathbf{n}+\mathbf{1}}+{\mathbf{x}}_{\mathbf{c}}}{2}\\ \mathbf{e}\mathbf{l}\mathbf{s}\mathbf{e}{\mathbf{x}}_{\mathbf{n}\mathbf{e}\mathbf{w}}\leftarrow \frac{{\mathbf{x}}_{\mathbf{r}}+{\mathbf{x}}_{\mathbf{c}}}{2}\\ \mathrm{F}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{e}\mathrm{w}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{x}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\mathbf{x}}_{\mathbf{n}+\mathbf{1}}\leftarrow {\mathbf{x}}_{\mathbf{n}\mathbf{e}\mathbf{w}}\\ \mathbf{i}\mathbf{f}f\left({\mathbf{x}}_{\mathbf{n}\mathbf{e}\mathbf{w}}\right)\ge f\left({\mathbf{x}}_{\mathbf{n}+\mathbf{1}}\right)\\ \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}\mathrm{F}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{e}\mathrm{w}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{x}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\\ x^i=\frac{x^i+x_1}{2};i=1,2,\cdots ,n\end{array}\right.$

GA is computationally expensive since it performs a random search over many local minima of the cost function. The deterministic NM algorithm, on the other hand, converges accurately and efficiently to the nearest local minimum. By obtaining only an approximate solution using the computationally expensive GA and refining it using the efficient NM local search algorithm the advantages of the GA and NM method are synergistically combined. In summary, the overall algorithm can be illustrated by the block diagram shown in Figure 3. $\mathbf{x}$ is the result of GA which is fed as input to NM to yield ${\mathbf{x}}^{\ast }$.

Figure 3. Proposed NMGA optimization method for the problem.

Results and Discussion

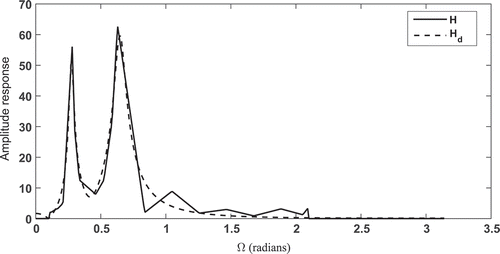
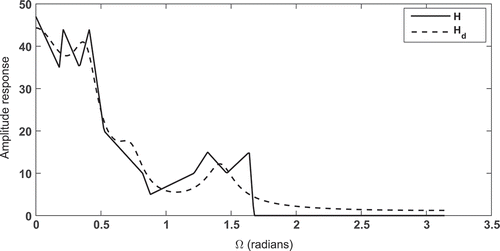
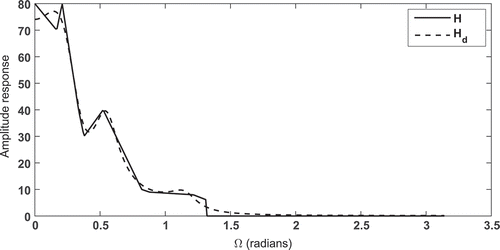
In this paper, the experimentally measured vocal tract frequency response presented in (Russell 2016) was used. The desired frequency response $H(\mathrm{\Omega })$ was determined over the entire frequency range by linear interpolation of the data presented in (Russell 2016). In Figures 4–6 the solid curve is the experimentally determined vocal tract frequency response for different vowel sounds. The dashed curve in Figures 4–6 is the frequency response $H_d(\mathrm{\Omega })$ of the filter designed by optimizing Equation (7) using the NMGA algorithm. By minimizing Equation (7) the best value of the parameters (gain, poles, and zeros) defined in Equation (5) are obtained.

Figure 4. Frequency response of the vocal tract and filter designed with NMGA for vowel sound $a$.

Figure 5. Frequency response of the vocal tract and filter designed with NMGA for vowel sound $o$.

Figure 6. Frequency response of the vocal tract and filter designed with NMGA for vowel sound $u$.

In this paper, the parameter $\gamma$ in Equation (7) was set to 100. A large value of $\gamma$ assigns a high penalty cost to solutions that violate stability and minimum phase constraints relative to function approximation error. If a small value of $\gamma$ is chosen solutions that lead to a smaller difference between $H(\mathrm{\Omega })$ and $H_d(\mathrm{\Omega })$ are preferred even if they violate constraints. Thus, a small value of $\gamma$ results in a filter that has a frequency response close to the experimental frequency response but not necessarily stable or minimum phase. Similarly, a large value of $\gamma$ results in a stable and minimum phase filter but the frequency response of the designed filter might differ substantially from the experimental vocal tract frequency response $H(\mathrm{\Omega })$. Empirical observations in line with (Slowik and Bialko 2008) indicate that a value of 100 provides a good trade-off between function approximation and constraint satisfaction.

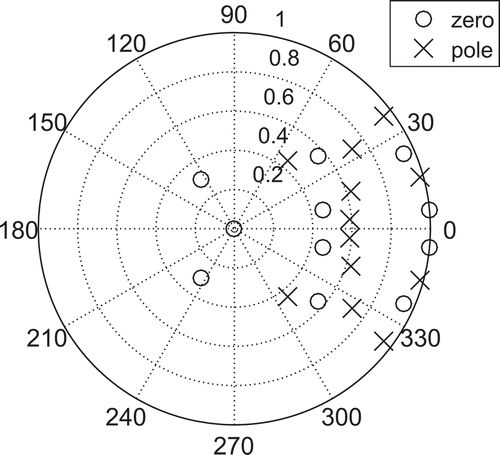
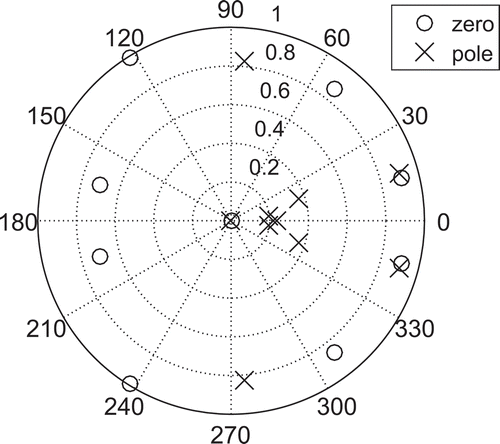
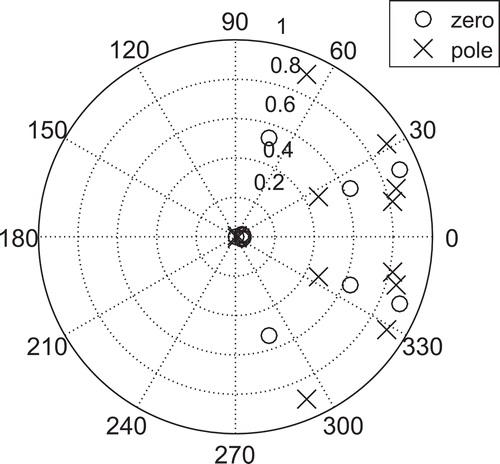
Figures 4–6 indicate that the designed filters have poles and zeros inside the unit circle, thus the designed filter is both stable and minimum phase.

In Table 1 the parameter settings for different algorithms used in generating the results in this paper is presented. The GA was stopped after 2400 iterations. A population size of 24 was used. Running GA more than 2400 iterations did not show significant improvement in solution quality. The same stopping criterion is used for the NM algorithm. The values of different parameters used to generate the results are summarized in Table 2 for convenience.

Table 1. Optimal values of the filter parameters computed by NMGA for different vowel sounds.

	$k$	$z$	$p$
$a$	−1.1114	0.5660$\mathrm{\angle }\pm$0.7197; 0.3033$\mathrm{\angle }\pm$2.1651;	0.9807$\mathrm{\angle }\pm$0.2739; 0.5880$\mathrm{\angle }\pm$0.7995;
		0.4627$\mathrm{\angle }\pm$0.2018; 0.9446$\mathrm{\angle }\pm$0.4146;	0.9533$\mathrm{\angle }\pm$0.6470; 0.6254$\mathrm{\angle }\pm$0.3129;
		0.9999$\mathrm{\angle }\pm$0.0964; 0.0049$\mathrm{\angle }\pm$2.7575.	0.4393$\mathrm{\angle }\pm$0.9047; 0.7276$\mathrm{\angle }\pm$0.5954.
$o$	1.1394	0.4566$\mathrm{\angle }\pm$0.7275; 0.6060$\mathrm{\angle }\pm$0.6804;	0.2691$\mathrm{\angle }\pm$0.7095; 0.7901$\mathrm{\angle }\pm$0.0717
		2.1563$\mathrm{\angle }\pm$0.6670; 0.4828$\mathrm{\angle }\pm$2.7773;	0.9000$\mathrm{\angle }\pm$0.7402; 0.3133$\mathrm{\angle }\pm$0.0254;
		0.0785$\mathrm{\angle }\pm$1.1057; 0.5579$\mathrm{\angle }\pm$0.6855.	0.9000$\mathrm{\angle }\pm$0.3950; 0.9010$\mathrm{\angle }\pm$1.4192.
$u$	2.0036	0.8977$\mathrm{\angle }\pm$0.3822; 0.4137$\mathrm{\angle }\pm$0.0947;	0.8186$\mathrm{\angle }\pm$0.2173; 0.4654$\mathrm{\angle }\pm$0.4503;
		0.0352$\mathrm{\angle }\pm$0.4254; 0.6317$\mathrm{\angle }\pm$0.3989;	0.9044$\mathrm{\angle }\pm$0.5517; 0.0013$\mathrm{\angle }\pm$0.5998;
		0.53142$\mathrm{\angle }\pm$1.2459; 0.0006$\mathrm{\angle }\pm$1.2090.	0.9000$\mathrm{\angle }\pm$1.1595; 0.8509$\mathrm{\angle }\pm$0.2886.

Table 2. Summary of parameter values used.

Parameter	Value
Crossover probability	0.80
Mutation probability	0.01
$\gamma$	100
Filter order ($M$)	12

Figures 4–6 clearly indicate the complex and highly multimodal nature of the vocal tract frequency response. It is observed that the frequency response of the designed filter $H_d(\mathrm{\Omega })$ provides a good approximation to the experimentally obtained vocal tract frequency response. In this paper, the mean squared error computed on uniformly spaced sampled of the function $H(\mathrm{\Omega })$ and $H_d(\mathrm{\Omega })$ was considered as the metric for comparison of the performance of different algorithms. Table 3 indicates that the performance of NMGA is superior to the pure GA on all three benchmark filter design problems.

Table 3. Comparison of vocal tract filters designed with GA and NMGA.

	Vowel sounds
Mean Squared Error (MSE)	$a$	$o$	$u$
GA	84.489	100.014	77.088
NMGA	39.766	38.9578	28.441

Comparison with an Alternate Approach

An experimental comparison with the work by (Slowik and Bialko 2008) was performed. In (Slowik and Bialko 2008) the optimization problem is formulated in terms of polynomial coefficients instead of polynomial roots. The same cost used in (Slowik and Bialko 2008) was optimized using the NMGA algorithm proposed in this paper. Simulation results show that the best solution had a MSE of 214.902, 230.716 and 258.803 for the vowels $a$, $o$ and $u$, respectively. Thus, the formulation provided by Slowik et al. results in more than five times the MSE in the final solution compared to the approach suggested in this paper. The high MSE in Slowik et al.’s approach can be attributed to the sensitivity of the polynomial roots to small changes in the values of the coefficients (numerical ill-conditioning).

The pole-zero plots of the optimal filter designed using the NMGA approach are shown in Figures 7–9. Since all the poles are inside the unit circle, the filters designed are stable in the bounded input-bounded output sense. The zeros can also be observed to lie within the unit circle indicating that the designed filters are of minimum phase as desired.

Figure 7. Pole-Zero plot of the filter designed with NMGA for vowel $a$.

Figure 8. Pole-Zero plot of the filter designed with NMGA for vowel $o$.

Figure 9. Pole-Zero plot of the filter designed with NMGA for vowel $u$.

Conclusion

Vocal tract filters have complex nonstandard frequency responses with numerous minima and maxima. Hence, the design of vocal tract filters is not amenable to standard filter design techniques. Stability and round off error constraints in practical implementations further complicate the design.

In this paper, the vocal tract filter design problem is effectively reformulated as a nonlinear optimization problem and solved using a hybrid GA. In the NMGA algorithm, a rough solution in the vicinity of the global minimum is first computed using a GA and then refined using the computationally efficient NM local search technique. This approach avoids the need for extensive computationally costly random search to exactly calculate the filter parameters. Filter designs obtained using the NMGA algorithm proposed in this paper are stable, minimum phase and fit experimentally observed vocal tract frequency response well. Future work can address the problem of design of vocal tract filters for other sounds.