An Innovative Genetic Algorithm for a Multi-Objective Optimization of Two-Dimensional Cutting-Stock Problem

ABSTRACT

This paper addressed an important variant of two-dimensional cutting stock problem. The objective was not only to minimize trim loss, as in traditional cutting stock problems, but rather to minimize the number of machine setups. This additional objective is crucial for the life of the machines and affects both the time and the cost of cutting operations. Since cutting stock problems are well known to be NP-hard, we proposed an approximate method to solve this problem in a reasonable time. This approach differs from the previous works by generating a front with many interesting solutions. By this way, the decision maker or production manager can choose the best one from the set based on other additional constraints. This approach combined a genetic algorithm with a linear programming model to estimate the optimal Pareto front of these two objectives. The effectiveness of this approach was evaluated through a set of instances collected from the literature. The experimental results for different-size problems show that this algorithm provides Pareto fronts very near to the optimal ones.

Introduction

The primary objective in cutting stock problem is to minimize material waste. In real applications, it is often necessary to consider auxiliary objectives, one of which is to reduce the number of different cutting patterns (setups). In many wood, paper and steel industries, the cutting process imposes a new setup every time a different pattern is cut (Enrico, Rosa, and Paolo 2014), (Kallrath et al. 2014), (Yaodong, Cheng, and Yi 2015), (Mahdi and Khalil 2016). This additional objective is crucial for the life of the machines and is important in determining the cutting operations cost. It is desirable to have a cutting plan with a reduced number of patterns, on the one hand, and to keep the waste of material as low as possible, on the other. Unfortunately, this deals with two conflicting objectives.

In this work, we addressed a bi-criteria decision for an important variant of the two-dimensional cutting-stock problem. The objectives were to minimize both the number of machine setups and the waste of material.

Before providing the details of this problem and the details of the elaborated algorithm, we briefly reviewed the resolution techniques available in the literature.

The large number of columns in practical cutting problems is one of the difficulties that was to be taken into account. In Haessler (1975), a pattern is selected, if it satisfies the aspiration levels of waste and frequency.

Farley and Richardson (1984) modeled a pattern minimization cutting stock problem as a single objective, the sum of patterns and setup costs.

Vanderbeck (2000) proposed a quadratic integer programming formulation to minimize the number of setups in the one-dimensional case. He proposed a decomposition-based method and a branch-and-bound procedure to solve their problem.

Umetami, Yagiura and Ibaraki (2003) proposed a heuristic that searches a solution which minimizes the quadratic deviation of item cuts from the requirements after the number of different patterns is fixed to a predefined value. They reviewed some other works that combined two patterns into one.

Horacio and Marcelo (2006) proposed a hybrid procedure to obtain a reduced number of different patterns. Initially, patterns with limited waste that fulfill the demands of at least two items are generated. The problem is reduced and the residual problem is solved. Then, pattern reduction techniques based on local search are applied starting with the generated solution. The scheme is simple and can be used in cutting stock problems of any dimension. Variations of the procedure are also indicated.

Mellouli et al. (2010) proposed a mixed integer linear formulation to reduce the total cost, the sum of patterns and setups costs. This formulation is used for small and medium size problems, for large size, an approximate approach was presented and evaluated.

Mobasher and Ekici (2013) developed a mixed integer linear program model and proposed two local search algorithms and a column generation-based heuristic algorithm in order to minimize total production cost including both material and setup costs.

Kallrath et al. (2014) developed new column generation approaches integrated into an Enterprise Resource Planning system to solve a variety of cutting stock problems occurring in real-world problems. Among them is the simultaneous minimization of the number of rolls and the number of patterns while not allowing any overproduction.

Cui, Cui and Zhao (2015) presented a pattern-set generation algorithm. It also generates a set of patterns in the first stage and solves an Integer Linear Problem model over the generated patterns in the second stage. The pattern-set generation algorithm uses a residual heuristic to produce the patterns.

Yaodong, Cheng and Yi (2015) presented an integer linear programming model to minimize the sum of material and setup costs over a given pattern set, and described a sequential grouping procedure to generate the patterns in the set.

The fact that, most, heuristics have been proposed in the literature to solve this kind of problem can be explained. Indeed, the bi-objective problem version is more difficult from solving each objective alone. Moreover, the cutting stock problem which considers only one of these two objectives is already NP-hard (Fekete, Schepers, and Veen 2007), (Enrico, Rosa, and Paolo 2014), (Mahdi and Khalil 2016), (Ayadi et al. 2017).

From these heuristics, the genetic algorithm is the most commonly used. With a long history of development, it was widely used for single-objective cutting stock problems (Godfrey and Michael 2003), (Leo and Wallace 2004), (Wong, Mok, and Kwong 2007), (Jose 2015) and for multi-objective cutting stock problems (Leung, Wong, and Mok 2008), (Ramiro et al. 2007), (Yanira, Gara, and Coromoto 2016).

Genetic algorithm has gained an increasing attention among researchers in recent years for the multi-objective problems. Once it is algorithmically efficient because the discovery of one solution close to the Pareto-optimal front pulls a number of other population members towards the Pareto-optimal front, thereby making a parallel and simultaneous discovery. On the other hand, it is able to find multiple Pareto-optimal solutions in one single simulation run. It has two distinct goals: convergences to the true Pareto-optimal front and maintains diversity in the non-dominated solutions. It differs from the standard genetic algorithm for single objective problems in the way that fitness is assigned to each solution in the population (Geetha and Muthukumaran 2013), (Radhia, Slim, and Lamjed 2016).

For these reasons, we propose to use this powerful tool to solve an important variant of a bi-criteria decision of the two-dimensional cutting-stock problem.

In this work, we proposed an innovative genetic algorithm to estimate the optimal Pareto front for the following two conflicting objectives: minimize material waste and the number of setups machine. This approach is interesting because it differs from the previous works by the generation of a front with many solutions. Therefore, the decision maker or production manager can choose the better one from the set of the non-dominated solutions based on other additional constraints such as the number of available operators to prepare setups machine, for instance, if a set of operators are absent, the production manager selects the solution with a low number of setups machine to answer the due date of the customer demands. The remaining of this paper was organized as follows: Section 2 described the problem and the mathematical formulation proposed. Section 3 introduced the details of the genetic algorithm elaborated. Section 4 revealed and discussed the experimental results. Finally, the concluding remarks were forwarded in Section 5.

Problem Formulation

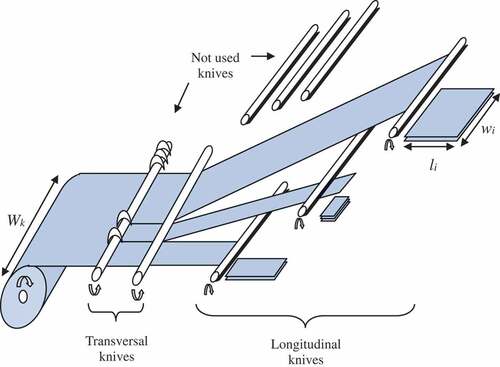
The machine presented in Figure 1 is used to cut rolls of material with standard widths W_k (k =1,…, K), into small rectangles with dimensions w_i×l_i (i =1,…, N) and quantities d_i (i =1,…, N). The cutting patterns must satisfy the following constraints related to this machine. First, the number of available levels allows cutting at most six rectangle types in the same patterns. Second, small rectangles are obtained by guillotine and oriented cuts.

Figure 1. Cutting process schematic representation.

For this problem, it is required to estimate the set of non dominated solutions for two objectives. The first is to minimize the amount of material needed to satisfy customer orders. The second is to minimize the number of machine setups by reducing the number of used patterns.

In order to formulate the mathematical model of this problem the following notations related to cutting orders, roll sizes and cutting patterns were introduced.

Sets and parameters

Table

$⌊x⌋$	: Greatest integer lower than x
$⌈x⌉$	: Lowest integer greater than x
N	: Number of pieces orders to be fulfilled
K	: Number of available rolls widths in stock
wi	: Width of the i ^th pieces order (i =1,…, N), arranged in a decreasing width (w1 ≥ w2 ≥…≥wN)
li	: Length of the i ^th pieces order (i =1,…, N)
di	: Demand of the i ^th pieces order (i =1,…, N)
Wk	: Width of the k ^th width roll (k =1,…, K), arranged in a decreasing width (W1 > W2 >…>WK)
Vkji	: Number of units of width wi to be cut according to the j ^th pattern from the k ^th width roll
Vkj	: j ^th cutting pattern of the k ^th roll width (with independence of the length)
Lkj	: Length produced with the pattern Vkj.
Ykj	: Equal to 1, if the pattern Vkj is used (Lkj>0) and 0 otherwise (Lkj =0)
Xkji	: denotes the integer value$⌊L_{kj}/l_i⌋$ if Vkji >0 (hence, XkjiVkji is the number of pieces of width wi contained in pattern Vkj through the length Lkj.
Jk	: Number of patterns of Wk roll width
M	: Huge positive constant, which can be calculated as $M=\sum _{i=1}^N{l}_i{d}_i$

Before providing the mathematical formulation, it is necessary to determine the set of feasible patterns V_kj that satisfy the following constraints:

(1) $\sum _{i=1}^N{V}_{kji}\le 6\left(k=1,2\dots ,K,j=1,2\dots ,J_k\right)$(1)

(2) $W_{k+1}<\sum _{i=1}^N{V}_{kji}{w}_i\le W_k\left(k=1,2\dots ,K-1,j=1,2\dots ,J_k\right)$(2)

(3) $\sum _{i=1}^N{V}_{Kji}{w}_i\le W_K\left(j=1,2\dots ,J_K\right)$(3)

Constraints (1) are technological constraints related to the number of levels in the machine. Constraints (2) and (3) are used to select for each pattern V_kj the nearest greater width roll.

Objective functions:

Area of the material needed:

(4) $F_1=\left(\sum _{k=1}^K{W}_k\sum _{j=1}^{J_k}{L}_{kj}\right)$(4)

Number of used patterns (setups):

(5) $F_2=\left(\sum _{k=1}^K\sum _{j=1}^{J_k}{Y}_{kj}\right)$(5)

Under these notifications, we can formulate a multi-objective Mixed Integer Linear Problem (MILP) for the two-dimensional cutting-stock problem described above, in the following form:

(6) $\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}[F_1,F_2]$(6)

Subject to

(7) $\sum _{k=1}^K\sum _{j=1}^{J_k}{X}_{kji}{V}_{kji}\ge d_i(i=1,2\dots ,N)$(7)

(8) $l_i{X}_{kji}\le L_{kj}\left(k=1,2\dots ,K,j=1,2\dots ,J_k,i=1,2\dots ,N\right)$(8)

(9) $L_{kj}\le M{Y}_{kj}\left(k=1,2\dots ,K,j=1,2\dots ,J_k\right)$(9)

(10) $L_{kj}\ge 0X_{kji}\in {\mathrm{Z}}_{+}{Y}_{kj}\in \{0,1\}$(10)

Equations (4), (5) and (6) represent the objectives to minimize. Constraints (7) guaranty the demand orders satisfaction. Constraints (8) link the lengths to produce L_kj with the number of pieces X_kji. Constraints (9) impose for each used pattern V_kj (L_kj>0) to have Y_kj equal to one. Constraints (10) introduce non-negativity and integrality conditions.

Illustrative Example

Four rectangular pieces with the specifications shown in Table 1 are to be cut from rolls with two widths: W₁ =2.5 m; W₂ =2 m.

Table 1. Data example.

Item Number (It N)	Width wi	Length li	Demand di
1	1.3	2.2	650
2	1.2	2.3	600
3	1.2	2	200
4	0.5	1.4	380

The set of feasible patterns V_kj that responds to constraints (1), (2) and (3) with the associated roll widths were presented in Table 2 (Mellouli and Dammak 2008).

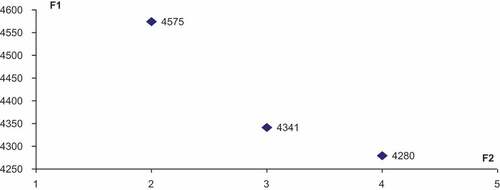
The optimal Pareto Front is displayed in Figure 2

Figure 2. Optimal Pareto front.

To obtain the non dominated solutions we could proceed by considering single objective version F₁ in which the number of setups is given as a hard constraint.

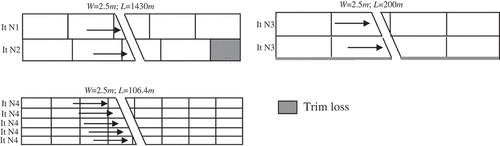
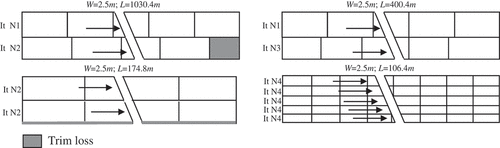
- Solution with two setups: F₂= 2 (see Figure 3):

$L_{11}=1430Y_{11}=1X_{111}=⌊L_{11}/l_1⌋=650X_{112}=⌊L_{11}/l_2⌋=621$

$L_{18}=400Y_{18}=1X_{183}=⌊L_{18}/l_3⌋=200X_{184}=⌊L_{18}/l_4⌋=285$

$F_1=\left(2.5x\left(1430+400\right)\right)=4575$

- Solution with three setups: F₂= 3 (Figure 4):

$L_{11}=1430Y_{11}=1X_{111}=⌊L_{11}/l_1⌋=650X_{112}=⌊L_{11}/l_2⌋=621$

$L_{17}=200Y_{17}=1X_{173}=⌊L_{17}/l_3⌋=100$

$L_{19}=106.4Y_{19}=1X_{194}=⌊L_{19}/l_4⌋=76$

$F_1=\left(2.5x\left(1430+200+106.4\right)\right)=4341$

- Solution with four setups: F₂= 4 (Figure 5):

$L_{11}=1030.4Y_{11}=1X_{111}=⌊L_{11}/l_1⌋=468X_{112}=⌊L_{11}/l_2⌋=448$

$L_{12}=400.4Y_{12}=1X_{121}=⌊L_{12}/l_1⌋=182X_{123}=⌊L_{12}/l_3⌋=200$

$L_{14}=174.8Y_{14}=1X_{142}=⌊L_{142}/l_2⌋=76$

$L_{19}=106.4Y_{19}=1X_{194}=⌊L_{19}/l_4⌋=76$

$F_1=\left(2.5x\left(1030.4+400.4+174.4+106.4\right)\right)=4280$

The determination of the optimal Pareto Front is restricted for low size problems. For problems of medium or large sizes, it is necessary to use heuristics and meta-heuristics such as genetic algorithm to estimate the optimal Pareto Front.

Figure 3. Optimal solution with two setups.

Figure 4. Optimal solution with three setups.

Figure 5. Optimal solution with four setups.

Genetic Algorithm

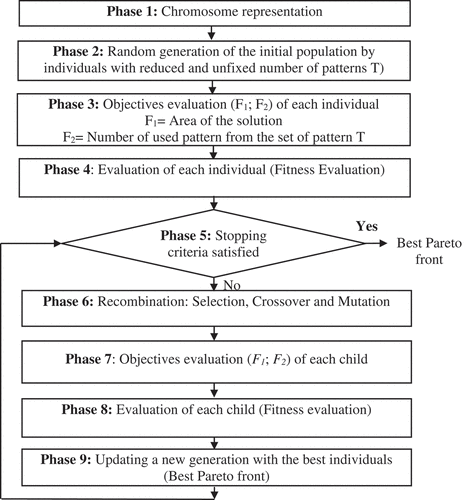
The main idea of this algorithm is to solve many problems with good and small number of patterns than to solve the basic problem with very high number of patterns. Genetic tools are used to improve the front quality through the successive generations until the stopping criterion is reached.

The flow chart presented in Figure 6 summarizes these steps.

Figure 6. Flowchart of the proposed genetic algorithm.

This section presents the different phases of this genetic algorithm: chromosome representation, initial generation, feasibility and correction, evaluation of the objectives, fitness evaluation, crossover, mutation and Stopping criteria.

Chromosome Representation

An individual with T patterns is represented by a non-negative integer value matrix where the number of rows is the number of customer orders N. And the number of columns is the number of cutting patterns T.

Initial Generation

The initial generation is randomly generated by a set of individuals respecting the following conditions:

- The number of pattern T must be between T_min and N. T_min represents an estimation of the lowest number of patterns that allows the generation of feasible solutions (Alves and Carvalhoa 2007).

- The width of each pattern has to be smaller than the biggest roll width.

- Each type of customer order appears at least once in one of the cutting patterns.

Feasibility and Correction

In our algorithm the recombination operators applied cannot guarantee the feasibility of the solutions, the number of unfeasible solutions in a population may easily grow as the algorithm progresses. Thus, we proposed that unfeasible solutions be repaired instead of being rejected. To ensure a feasible solution, it is enough, considering the chromosome representation adopted in our algorithm, that each type of customer order appears at least once on a cutting pattern. Once a missing type is found in a given solution, a correction procedure is called upon to repair it.

Evaluation of the Objectives F₁, F₂

This phase consists in calculating for each individual the lengths $L_{kj}$ relative to its patterns T. The objective is to satisfy the customers’ orders with the minimal area of material F₁. At the end, F₂ is updated by computing the number of used patterns.

Fitness Evaluation

The fitness of each individual was evaluated through the Pareto Fitness Genetic Algorithm (PFGA) introduced by Elaoud, Loukil, and Teghem (2007). This algorithm has shown high efficiency in solving multiple objective optimization problems.

Crossover and Mutation

Crossover is a genetic operator used to vary chromosomes from one generation to the next. It represents the process of taking more than one parent solution and producing a child solution from them. Many crossover techniques were presented in the literature such as One-point crossover, Two-point crossover, Cut and splice, partially matched crossover (PMX), cycle crossover (CX), order crossover operator (OX1)… (Aimin et al. 2011), (Geetha and Muthukumaran 2013).

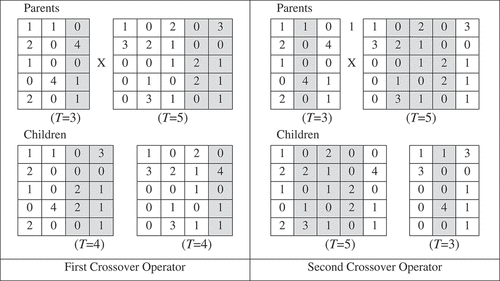
For this problem the “Cut and splice” crossover was chosen. This is justified by the fact that it changes the length of the children strings. The reason for this difference is that each parent string has a separate choice of crossover points which perform diversification for the two-objective problems.

Two variants of “Cut and splice” crossover are proposed: the First Crossover Operator (FCO) with one point and the Second Crossover Operator (SCO) with two points.

These crossovers work as follows (Figure 7):

• First, parents are chosen through the roulette wheel selection (RWS) (Rennera and Ekart 2003).

• Second, each parent is divided randomly into two and three portions for the FCO and the SCO, respectively.

• Third, the second portion is exchanged between the two parents in order to generate two children for the FCO, respectively; the middle portion is exchanged for the SCO.

• Fourth, a procedure is called to check the feasibility and to repair the unfeasible children.

Figure 7. First and second crossover operator.

In order to introduce genetic diversity, mutation is designed with one of the two following possibilities:

• Replace a cutting pattern by another which is randomly generated.

• If the number of cutting patterns is greater than T_min, eliminate one from the matrix.

After mutation, the correction procedure is called to check the feasibility of the solutions and repair the unfeasible ones.

Stopping Criteria

The algorithm is stopped after 2000N evaluations of the fitness function, then for a population of 20N individuals, the algorithm is stopped after 100 generations and returns the best solution. Otherwise, the algorithm is stopped autonomously after 10 successive generations if there is no amelioration.

It is worth noting that an external set is created to maintain better solutions in the whole evolution process. This set is updated at each generation by introducing new non-dominated solutions and removing the dominated ones. The final Pareto front will derive from this set.

Implementation and Experimental Results

The objectives of this study were to determine the better parameters of the elaborated algorithm and evaluate its effectiveness.

Selection of the Genetic Algorithm Parameter Values

The objective of this part was to find the better genetic algorithm parameter values.

To this end, extensive testing was performed. The parameters that were assessed in this series of experiments were:

• Size of the population (SP): Two population sizes were used (10N and 20N).

• Crossover Operator (CO): Two crossover operator types were used. The FCO with one point for each parent, and the SCO with two points for each parent.

• Probability of mutation (Pmut): values between 0 and 1 indicate the probability that a newly generated solution string is generated through one of the mutation possibilities. Two probabilities of mutation are performed 0.1 and 0.15.

An experimental study was elaborated to perform the genetic algorithm parameters. The better results were obtained with the following configuration (SP = 20N, SCO, Pmut = 0.15).

This means that this genetic algorithm works better with the higher population size, the higher crossover points and the higher mutation probability, which is in agreement with the basically known concepts of genetic algorithms. The following experiments would be achieved with these parameters.

Evaluation of the Genetic Algorithm Effectiveness

Quality of the Fronts

The objective of this study was to evaluate the effectiveness of this genetic algorithm. A number of experiments have been carried out by the means of 18 problems collected from the literature (Benati 1997).

Problem 1 (N = 17), Problem 2 (N = 12), Problem 3 (N = 22). For the first and the second problems, the test was carried out with the following sets of roll widths: A1 = (1.33), A2 = (1.33;1.25), A3 = (1.33;1.25;0.77), B1 = (1.15), B2 = (1.15;1.05), B3 = (1.15;1.05;1.01).

For the third problem, the test was carried out with the following sets of roll widths: C1 = (1.33), C2 = (1.33;1.12), C3 = (1.33;1.12;1.05) and B1, B2, B3.

The quality of this genetic algorithm was evaluated through the value of the relative error between the optimal front Pareto and the front Pareto generated through the genetic algorithm.

$VRE=\frac{1}{(N-T_{min}+1)}\sum _{T=T_{min}}^N\frac{F_1(T)-{F_1}^{\ast }(T)}{{F_1}^{\ast }(T)}$

where VRE, F₁(T) and F₁*(T) denote respectively, the value of the relative error, the value of the better solution generated for the first objective with T cutting patterns and the value of the optimal solution generated by CEPLEX solver for the first objective with T cutting patterns.

The proposed genetic algorithm was implemented with MATLAB 7.6. All experiments were run in the Windows 8 environment on a desktop PC with Intel (R) Core (TM) i3-3120M, CPU 2.5 GHz Processor. Note that this algorithm was executed for three runs for each instance of problem.

The experimental results are presented in Table 3.

Table 2. Feasible patterns with the associated roll widths.

Vkj	V11	V12	V13	V21	V14	V15	V16	V22	V17	V18	V23	V19	V24
	1(V111)	1	1	1	0	0	0	0	0	0	0	0	0
	1(V112)	0	0	0	2	1	1	1	0	0	0	0	0
	0(V113)	1	0	0	0	1	0	0	2	1	1	0	0
	0(V114)	0	2	1	0	0	2	1	0	2	1	5	4
Wk	2.5	2.5	2.5	2	2.5	2.5	2.5	2	2.5	2.5	2	2.5	2

Table 3. Experimental results.

Code	VRE (%)
	First run	Second run	Third run	Average
P1-A1	1.42	1.37	1.54	1.44
P1-A2	1.11	1.28	1.28	1.22
P1-A3	1.07	0.98	1.14	1.06
P1-B1	1.37	1.56	1.64	1.52
P1-B2	1.33	1.24	1.24	1.27
P1-B3	1.22	1.19	1.19	1.20
P2-A1	1.08	1.19	1.32	1.20
P2-A2	0.78	0.74	0.95	0.82
P2-A3	0.72	0.74	0.83	0.76
P2-B1	0.94	1.12	0.98	1.01
P2-B2	0.7	0.86	0.92	0.83
P2-B3	0.76	0.68	0.76	0.73
P3-B1	1.96	1.82	1.39	1.72
P3-B2	1.14	1.25	1.31	1.23
P3-B3	1.24	1.11	1.03	1.13
P3-C1	1.82	1.89	1.97	1.89
P3-C2	1.62	1.53	1.53	1.56
P3-C3	1.22	1.13	1.04	1.13

The comparison of the results given by this genetic algorithm with the optimal fronts Pareto shows the great success of this algorithm to generate very close fronts Pareto to the optimal ones because the value of the relative error (VRE) in % does not exceed a rate of 2% with an average of 1.2%.

Considering only the first objective, this approach suggests competitive solutions to those proposed by Rinaldi and Franz (2007) with 2% VRE average.

The results obtained for each example through the three runs show the stability of this algorithm because the difference between the highest and the lowest values of the relative error (VRE) in % for each example does not exceed a rate of 1%.

The average value of the relative error (VRE) in % for the first problem decreases from A1 to A3. This can be explained by the number of available rolls for A1, A2 and A3 which is equal to 1, 2 and 3, respectively. The increase of the number of available rolls from A1 to A3 increases the number of patterns and reduces the trim loss which influences positively the quality of the fronts. This remark was confirmed by the results obtained with (P1-B1, P1-B2, P1-B3), (P2-A1, P2-A2, P2-A3), (P2-B1, P2-B2, P2-B3), (P3-B1, P3-B2, P3-B3) and (P3-C1, P3-C2, P3-C3).

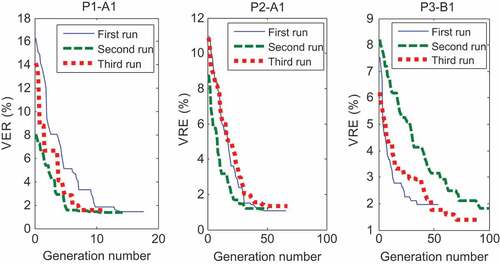
Figure 8 presents the evolution of the value of the relative error (VRE) in % through the generations of the following problems P1-A1, P2-A2 and P3-B1. The common fact between these figures is the high and continuous decrease of the VRE for the first generations and the stagnation with a low decrease for the last generations. This is explained by the fact that the initial population is generated randomly then we have more chances to develop the quality of the fronts for the first generations. With the progress of the algorithm the generated fronts will be closer and close to the optimal one, then the chance to perform the solutions and the fronts will be very small. As a result, we see a low decrease and a stagnation of the VRE for the last generations. This justifies the additional stopping criteria: the algorithm stops after a set of generations without any amelioration.

Figure 8. Evolution of VRE (%) for P1-A1, P2-A1 and P3-B1.

Computing Time

In order to evaluate the computing time (CT) of this approach compared to the computing time of the exact method with a CPLEX solver, a set of experiments were elaborated with different size problems. The results are presented in Table 4.

Table 4. Computing time with the elaborated genetic algorithm and CPLEX solver.

Problem Number	N	K	Average CT
			Genetic algorithm	CPLEX solver
1-2-3	10	1-2-3	2 min 11 sec	9min 1 sec
4-5-6	15	1-2-3	4 min 6 sec	307 min 10 sec
7-8-9	20	1-2-3	5 min 3 sec	1836 min 16 sec
10-11-12	30	1-2-3	15 min 12 sec	OM
13-14-15	40	1-2-3	31 min 19 sec	OM

OM: out of memory

Table 4 shows that the proposed genetic algorithm solves problems of different sizes in reasonable time. However, the exact approach with CPLEX solver is limited for low-sized problems. This study proves the effectiveness of the proposed genetic algorithm.

Conclusion

In this paper, we introduced a general version of the cutting stock problem, called Cutting Stock Problem with Setups. Our goal was to minimize both the material waste and the setup number for industrial applications with two-dimensional guillotine oriented cutting-stock problem. This goal is suitable for a wide range of problems appearing in production and manufacturing companies. A front with many solutions helps the decision maker to select the best one based on his needs. When the raw material is cheap or when the number of operators to prepare the setups is low, a solution with a low setup number is highly recommended. When the raw material is expensive, a solution with low material waste is preferred.

We initially developed a mixed integer linear model with two objectives. The first goal was to reduce the material waste while the second was to minimize the setup number. Then, we proposed an innovative algorithm meant to generate good front solutions in a reasonable time for this NP-hard problem. This algorithm combines a genetic algorithm with a linear programming model. Its main idea was to use genetic algorithm tools to ensure diversification and intensification for better populations and better solutions. To enhance our quest, a crossover with unequal-length segments exchange and a fitness function penalizing crowded and dominated regions were used.

Full experiment design was elaborated to identify better combination parameters. The numerical results show that this algorithm generates, in a reasonable time, a good front which is very close to the optimal one (the VRE does not exceed 2%).