A Hybrid Greedy Sine Cosine Algorithm with Differential Evolution for Global Optimization and Cylindricity Error Evaluation

ABSTRACT

Sine-cosine algorithm (SCA) has found a widespread application in various engineering optimization problems. However, SCA suffers from premature convergence and insufficient exploitation. Cylindricity error evaluation is a typical engineering optimization problem related to the quality of cylindrical parts. A hybrid greedy sine-cosine algorithm with differential evolution (HGSCADE) is developed in this paper to solve optimization problems and evaluate cylindricity error. HGSCADE integrates the SCA with the opposition-based population initialization, the greedy search, the differential evolution (DE), the success history-based parameter adaptation, and the Levy flight-based local search. HGSCADE is tested on the CEC2014 benchmark functions and is employed in cylindricity error evaluation. The results show the superiority of HGSCADE to other state-of-the-art algorithms for the benchmark functions and cylindricity error evaluation.

Introduction

Optimization refers to reaching the optimal objective value of a certain problem under-related constraints. Optimization problems exist in different areas of engineering or science. Meta-heuristic algorithms (MAs) have been developed to solve complex optimization problems that possess the properties of discontinuity, nondifferentiability, nonconvexity, nonlinearity, and multimodality (Yang 2008). Generally, MAs take the optimization problem as a black box and search for the solution based on stochastic rules. By transferring and exchanging information among search agents, the positions of the search agents are constantly updated to a promising region with the optimal solution.

No Free Lunch (NFL) theorem (Wolpert and Macready 1997) states that it is impossible to solve all optimization problems by a specific algorithm, i.e., an algorithm is applicable to a given optimization problem that may not be applicable to another one with distinct characteristics. Therefore, MAs need to be further studied to deal with different optimization problems. The research directions of MAs can be categorized as initiating new algorithms, improving existing algorithms and combining different algorithms. Some of the well-known MAs are genetic algorithms (GAs) (Srinivas and Patnaik 1994), particle swarm optimization (PSO) (Kennedy and Eberhart 1995), differential evolution (DE) (Storn and Price 1997), ant colony optimization (ACO) (Dorigo and Di Caro 1999), harmony search (HS) (Geem, Kim, and Loganathan 2001), bacterial foraging optimization (BFO) (Passino 2002), artificial bee colony (ABC) (Karaboga and Basturk 2007), biogeography-based optimization (BBO) (Simon 2008), gravitational search algorithm (GSA) (Rashedi, Nezamabadi-pour, and Saryazdi 2009), gray wolf optimizer (GWO) (Mirjalili, Mirjalili, and Lewis 2014), ant lion optimizer (ALO) (Mirjalili 2015), whale optimization algorithm (WOA) (Mirjalili and Lewis 2016), sine-cosine algorithm (SCA) (Mirjalili 2016), salp swarm algorithm (SSA) (Mirjalili et al. 2017).

As a crucial index to evaluate the machining accuracy and form error of cylindrical parts, cylindricity error is closely related to the product quality and performance. The minimum zone cylindricity (MZC) error evaluation method is consistent with the international standards, but a general algorithm that corresponds to MZC has not been developed. Essentially, cylindricity error evaluation can be regarded as a single objective real-parameter numerical optimization problem. Therefore, MAs has been applied for cylindricity error evaluation under the MZC principle, such as GA (Lai et al. 2000), PSO (Wen et al. 2010), HS (Yang et al. 2018), etc. It is very important to improve the convergence speed and accuracy of MAs in cylindricity error evaluation.

SCA, proposed by Mirjalili (2016), is a population-based optimization algorithm for solving optimization problems. SCA presents a good performance in some cases (Das, Bhattacharya, and Chakraborty 2018; Li, Fang, and Liu 2018; Mirjalili 2016), but it suffers from premature convergence and insufficient exploitation. Therefore, SCA variants were developed and applied for different optimization problems like feature selection (Sindhu et al. 2017), object tracking (Nenavath and Jatoth 2018; Nenavath, Kumar Jatoth, and Das 2018), pairwise local sequence alignment (Issa et al. 2018), optimal power flow (Attia, El Sehiemy, and Hasanien 2018), engineering design (Abd Elaziz, Oliva, and Xiong 2017; Chegini, Bagheri, and Najafi 2018; Gupta and Deep 2019; Rizk-Allah 2018), etc.

In this study, a novel algorithm called hybrid greedy sine-cosine algorithm with differential evolution (HGSCADE) is proposed for solving benchmark problems and evaluating cylindricity error. In HGSCADE, the opposition-based learning (OBL) is applied in population initialization, and the greedy search is employed to prevent excluding good solutions. Meanwhile, the DE is incorporated into SCA to improve the exploitation ability and maintain the population diversity, and a success history-based parameter adaptation is introduced to overcome invalid search. Then, a Levy flight-based local search is used to escape from local optima. HGSCADE is compared with standard SCA, other state-of-the-art MAs, and SCA variants over the CEC2014 benchmark functions. Finally, the proposed HGSCADE algorithm is used for cylindricity error evaluation as a real engineering case. The test and experiment results testify to the superiority and effectiveness of the proposed algorithm.

The remainder of this paper is organized as follows: the brief introduction of SCA is present in Section 2. The proposed HGSCADE algorithm is described in Section 3. The test results and comparisons are presented in Section 4. The application of HGSCADE for cylindricity error evaluation is introduced in Section 5. Eventually, conclusions are drawn in Section 6.

Sine-Cosine Algorithm

Similar to other MAs, the standard SCA starts with random candidate agents. Then, the agents are updated by sine and cosine functions to create new ones.

(1) $X_{i,j}^{t+1}=\left\{\begin{array}{c}{X}_{i,j}^t+r_1\times sin(r_2)\times \left|r_3{X}_{gb,j}^t-X_{i,j}^t\right|,r_4<0.5\\ X_{i,j}^t+r_1\times cos(r_2)\times \left|r_3{X}_{gb,j}^t-X_{i,j}^t\right|,r_4\ge 0.5\end{array}\right.$(1)

where $X_{i,j}^t$ is the position of the i-th agent in j-th dimension at t-th iteration, r₁/r₂/r₃ are random numbers, $X_{gb,j}^t$ is the best position obtained so far in j-th dimension, r₄ is a random number in [0, 1], and || denotes the absolute value.

The variable r₁ is adjusted with the number of iterations by Equation (2)(2) $r_1=a-(a\times t)/T$(2) :

(2) $r_1=a-(a\times t)/T$(2)

where a is a constant, t is the t-th iteration and T represents the upper limit of iterations.

The Proposed Algorithm

In this section, the proposed HGSCADE algorithm is introduced in detail. Although the standard SCA has found a widespread application in various engineering optimization problems, it suffers from premature convergence and insufficient exploitation. To overcome the drawbacks of SCA, we integrate five strategies into SCA as follows:

Opposition-based Population Initialization

Random population initialization generates some useless agents due to the absence of systemic knowledge. Therefore, the OBL is employed to form the initial population. The opposite value of a real number x ∈ [l, u] (l, u ∈ R) is specified as (Tizhoosh 2005):

(3) $\bar{x}=l+u-x$(3)

where l and u are the lower limit and upper limit of x, respectively.

Firstly, a population ${\mathit{X}}^0=\{{\mathit{X}}_i^0=[x_{i,1}^0,x_{i,2}^0,\dots ,x_{i,d}^0{]\}}_{i=1}^N$ is generated from the uniform distribution. Secondly, the opposite vector ${\bar{\mathit{X}}}_i^0(i=1,2,\dots ,N)$ for each agent is calculated by Equation (3)(3) $\bar{x}=l+u-x$(3) . Thirdly, the objective values of the populations ${\mathit{X}}^0$ and ${\bar{\mathit{X}}}^0$ are computed, and the best N agents are selected from ${\mathit{X}}^0\cup {\bar{\mathit{X}}}^0$, as the initial population.

Greedy Search

In the earlier search stage of SCA (r₁ > 1), the optimal position might be skipped over. Therefore, the greedy search is employed to update the position of each agent, i.e.

(4) ${\mathit{X}}_i^{t+1}=\left\{\begin{array}{c}{\mathit{X}}_i^{t+1},fit({\mathit{X}}_i^{t+1})<fit({\mathit{X}}_i^t)\\ {\mathit{X}}_i^t,otherwise\end{array}\right.,i=1,2,\dots ,N$(4)

where ${\mathbf{X}}_i^t$ and ${\mathbf{X}}_i^{t+1}$ are the parent position and new position of i-th agent, respectively.

Combined with Differential Evolution

The standard SCA uses the knowledge of a best-so-far agents to produce new members, which may result in insufficient population diversity and premature convergence. Hence, DE is incorporated into SCA in a parallel way. The component of position oversteps the boundary is set to be the mean of the overstepped boundary and the corresponding component of the parent position. For each iteration, the agent i will be updated by the SCA method if rand_i < pu_i, where rand_i is a random number in [0, 1] and pu_i ∈ [0, 1] is the updating rate. Otherwise, the agent i will be updated by the DE method as follows:

Firstly, a donor/mutant vector ${\mathit{V}}_i^t$ is produced by the parent vectors$\{{\mathit{X}}_i{\}}_{i=1}^N$.

(5) ${\mathit{V}}_i^t=\left\{\begin{array}{c}{\mathit{X}}_{R_1}^t+F_i\cdot ({\mathit{X}}_{R_2}^t-{\mathit{X}}_{R_3}^t),\hspace{0.17em}ran{d}_m<p_m\\ {\mathit{X}}_i^t+F_i\cdot ({\mathit{X}}_{pt}^t-{\mathit{X}}_i^t)+F_i\cdot ({\mathit{X}}_{R_2}^t-{\mathit{X}}_{R_3}^t),ran{d}_m\ge p_m\end{array}\right.$(5)

where indexes R₁, R₂, and R₃ represent integers stochastically generated from [1, N], and $R_1\ne R_2\ne R_3\ne i$. F_i is the scaling factor uniformly distributed in [0, 1]. ${\mathit{X}}_{pt}^t$is the position of the one picked out from the top N × pt (pt ∈ (0, 1)) agents in the population at t-th iteration stochastically (the agents in the population are sorted according to their fitness values), rand_m represents a random number in [0, 1], $p_m=1-t/T$.

Secondly, a trial vector ${\mathit{U}}_i^t$ is generated by crossing ${\mathit{V}}_i^t$ with ${\mathit{X}}_i^t$.

(6) $U_{i,j}^t=\left\{\begin{array}{c}{V}_{i,j}^t,r_{ij}<cr\mathrm{o}\mathrm{r}j=j_0\\ X_{i,j}^t,otherwise\end{array}\right.,j=1,2,\dots ,d$(6)

where r_ij is a random number uniformly distributed in [0, 1], j₀ is a random integer generated from [1, d], cr ∈ [0, 1] denotes the crossover rate.

Finally, the survivor is selected from the better one between ${\mathit{U}}_i^t$ and ${\mathit{X}}_i^t$.

(7) ${\mathit{X}}_i^{t+1}=\left\{\begin{array}{c}{\mathit{U}}_i^t,fit({\mathit{U}}_i^t)<fit({\mathit{X}}_i^t)\\ {\mathit{X}}_i^t,otherwise\end{array}\right.,i=1,2,\dots ,N$(7)

Success History-Based Parameter Adaptation

To reduce invalid search, HGSCADE regulates the critical parameters adaptively by the mechanism developed in (Tanabe and Fukunaga 2013). As shown in Table 1, the historical information for three memory parameters M_pu, M_F , and M_cr is stored with H entries. At each iteration, pu_i, F_i , and cr_i for each agent i are generated as follows:

(8) $\left[\begin{array}{c}p{u}_i\\ F_i\\ c{r}_i\end{array}\right]=\left[\begin{array}{c}rand{n}_i(M_{pu,r_i},0.1)\\ rand{c}_i(M_{F,r_i},0.1)\\ rand{n}_i(M_{cr,r_i},0.1)\end{array}\right]$(8)

Table 1. The historical memory

Index	1	2	…	H–1	H
Mpu	Mpu,1	Mpu,2	…	Mpu,H−1	Mpu,H
MF	MF,1	MF,2	…	MF,H−1	MF,H
Mcr	Mcr,1	Mcr,2	…	Mcr,H−1	Mcr,H

where index r_i is randomly selected from [1, H], randn_i(μ, σ) and randc_i(μ, σ) denote two values generated from Gaussian distribution and Cauchy distribution, respectively. In the case that the generated value of pu_i or cr_i is out of [0, 1], set it to the closest limit value. For F_i, truncate it to be 1 if F_i ≥ 1 or regenerate it if F_i < 1.

At each iteration, the values of pu_i, F_i , and cr_i that successfully generate a superior offspring are recorded as S_pu, S_F , and S_cr. If and only if superior offspring are generated, the values of M_pu, M_F , and M_cr are updated as follows:

(9) $\left[\begin{array}{c}{M}_{pu,k}\\ M_{F,k}\\ M_{cr,k}\end{array}\right]=\left[\begin{array}{c}mea{n}_{WA}(S_{pu})\\ mea{n}_{WL}(S_F)\\ mea{n}_{WA}(S_{cr})\end{array}\right]$(9)

where index k (1 ≤ k ≤ H) indicates the entry to be updated. k is initialized to 1 at the first iteration and is incremental with iteration. When k > H, reset k = 1. mean_WA(S_pu) and mean_WA(S_cr) are the weighted mean. mean_WL(S_F) is the weighted Lehmer mean.

(10) $\left[\begin{array}{c}mea{n}_{WA}(S_{pu})\\ mea{n}_{WA}(S_{cr})\\ mea{n}_{WL}(S_F)\end{array}\right]=\left[\begin{array}{c}{\sum }_{i=1}^{\left|S_{pu}\right|}{\omega }_i\cdot S_{pu,i}\\ {\sum }_{j=1}^{\left|S_{cr}\right|}{\omega }_j\cdot S_{cr,j}\\ \left({\sum }_{j=1}^{\left|S_{cr}\right|}{\omega }_j\cdot {(S_{F,j})}^2\right)/\left({\sum }_{j=1}^{\left|S_{cr}\right|}{\omega }_j\cdot S_{F,j}\right)\end{array}\right]$(10)

where ${\omega }_i=\mathrm{\Delta }{f}_i/{\sum }_{i=1}^{\left|S_{pu}\right|}\mathrm{\Delta }{f}_i$, ${\omega }_j=\mathrm{\Delta }{f}_j/{\sum }_{j=1}^{\left|S_{cr}\right|}\mathrm{\Delta }{f}_j$, $\mathrm{\Delta }{f}_i=\left|f_i^{t+1}({\mathit{X}}_i)-f_i^t({\mathit{X}}_i)\right|$, $\mathrm{\Delta }{f}_j=\text{break}\left|f_j^t({\mathit{U}}_j)-f_j^t({\mathit{X}}_j)\right|$.

Local Search Based on Levy Flight

SCA may stagnate if the best agent is caught in local optima. Therefore, a Levy flight disturbance (Jensi and Jiji 2016) is applied to the best agent in the current population:

(11) ${\mathit{X}}_{cbLevy}={\mathit{X}}_{cb}+step\oplus \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}(\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}({\mathit{X}}_{cb}))$(11)

where step = Levy(β) ⊕ X_cb, the symbol ⊕ denotes entry-wise multiplication. Levy(β) is derived from Equation (12)(12) $Levy(\beta )=scale\times \left(u/{\left|v\right|}^{1/\beta }\right)$(12) :

(12) $Levy(\beta )=scale\times \left(u/{\left|v\right|}^{1/\beta }\right)$(12)

where scale is a factor to control the step size of Levy flight, β ∈ [0, 2] is Levy index, u and v are derived from Gaussian distributions, i.e.

(13) $u\sim N(0,{\sigma }_u^2),v\sim N(0,{\sigma }_v^2)$(13)

(14) ${\sigma }_u={\left\{\frac{\mathrm{\Gamma }(1+\beta )sin(\pi \beta /2)}{\mathrm{\Gamma }\left[(1+\beta )/2\right]\beta 2^{(\beta -1)/2}}\right\}}^{1/\beta },{\sigma }_v=1$(14)

where Γ is the standard gamma function.

Then, compute the opposite vector ${\bar{\mathit{X}}}_{\ast }$ for X_cbLevy, and substitute X_cb with the best one chosen from $\left\{{\mathit{X}}_{cb},{\mathbf{X}}_{cbLevy},{\bar{\mathit{X}}}_{\ast }\right\}$.

Overall Implementation

The overall implementation steps of HGSCADE are described in Algorithm 1. HGSCADE involves three stages: Firstly, the OBL is employed to form the initial population, and the initial values of parameters are given. Secondly, each agent in the population is updated by the greedy search SCA method or DE method according to the updating rate, and the success history-based mechanism is used for critical parameter adaptation. Thirdly, the Levy flight-based local search is applied to the current best agent, and the search continues until the termination condition is reached.

Algorithm 1 The HGSCADE

1. Randomly generate a population X of N agents.

2. Compute the opposite population $\bar{\mathit{X}}$ by Equation (3)(3) $\bar{x}=l+u-x$(3) .

3. Evaluate the fitness of $\mathit{X}$ and $\bar{\mathit{X}}$ by calculating the corresponding objective function values.

4. Select the best N agents from $\mathit{X}\cup \bar{\mathit{X}}$

5. Initialize the values of parameters a, M_pu, M_F, M_cr, pt, H, β, scale

6. k = 1, t = 0

7. While (t < T) do

8. Update the global best position X_gb

9. Randomly select an index r_i from [1, H]

10. Generate pu, F and cr by Equation (8)(8) $\left[\begin{array}{c}p{u}_i\\ F_i\\ c{r}_i\end{array}\right]=\left[\begin{array}{c}rand{n}_i(M_{pu,r_i},0.1)\\ rand{c}_i(M_{F,r_i},0.1)\\ rand{n}_i(M_{cr,r_i},0.1)\end{array}\right]$(8)

11.For (i = 1: N) do

12. Generate a random number rand_i in [0, 1]

13. If (rand_i < pu_i) then

14. Update the position of the i-th agent by Equations (1)(1) $X_{i,j}^{t+1}=\left\{\begin{array}{c}{X}_{i,j}^t+r_1\times sin(r_2)\times \left|r_3{X}_{gb,j}^t-X_{i,j}^t\right|,r_4<0.5\\ X_{i,j}^t+r_1\times cos(r_2)\times \left|r_3{X}_{gb,j}^t-X_{i,j}^t\right|,r_4\ge 0.5\end{array}\right.$(1) and (4(4) ${\mathit{X}}_i^{t+1}=\left\{\begin{array}{c}{\mathit{X}}_i^{t+1},fit({\mathit{X}}_i^{t+1})<fit({\mathit{X}}_i^t)\\ {\mathit{X}}_i^t,otherwise\end{array}\right.,i=1,2,\dots ,N$(4) )

15. Else

16. Randomly select an agent X_pt from the top N × pt (pt ∈ (0, 1)) members in the population.

17. Update the position of the i-th agent by Equations (5)(5) ${\mathit{V}}_i^t=\left\{\begin{array}{c}{\mathit{X}}_{R_1}^t+F_i\cdot ({\mathit{X}}_{R_2}^t-{\mathit{X}}_{R_3}^t),\hspace{0.17em}ran{d}_m<p_m\\ {\mathit{X}}_i^t+F_i\cdot ({\mathit{X}}_{pt}^t-{\mathit{X}}_i^t)+F_i\cdot ({\mathit{X}}_{R_2}^t-{\mathit{X}}_{R_3}^t),ran{d}_m\ge p_m\end{array}\right.$(5) , (6(6) $U_{i,j}^t=\left\{\begin{array}{c}{V}_{i,j}^t,r_{ij}<cr\mathrm{o}\mathrm{r}j=j_0\\ X_{i,j}^t,otherwise\end{array}\right.,j=1,2,\dots ,d$(6) ) and (7(7) ${\mathit{X}}_i^{t+1}=\left\{\begin{array}{c}{\mathit{U}}_i^t,fit({\mathit{U}}_i^t)<fit({\mathit{X}}_i^t)\\ {\mathit{X}}_i^t,otherwise\end{array}\right.,i=1,2,\dots ,N$(7) )

18. End if

19.End for

20. Evaluate the fitness of each agent by calculating the corresponding objective function value.

21. Update M_pu, M_F, M_cr using Equation (9)(9) $\left[\begin{array}{c}{M}_{pu,k}\\ M_{F,k}\\ M_{cr,k}\end{array}\right]=\left[\begin{array}{c}mea{n}_{WA}(S_{pu})\\ mea{n}_{WL}(S_F)\\ mea{n}_{WA}(S_{cr})\end{array}\right]$(9)

22. k = k + 1

23. If (k > H) then

24. k = 1

25. End if

26. Perform Levy flight disturbance for the current best position X_cb by Equation (11)(11) ${\mathit{X}}_{cbLevy}={\mathit{X}}_{cb}+step\oplus \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}(\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}({\mathit{X}}_{cb}))$(11)

27. Compute the opposite position ${\bar{\mathit{X}}}_{\ast }$ for X_cbLevy

28. Update the current best position X_cb

29. Update r₁, r₂, r₃ , r₄

30. t = t + 1

31. End While

32. Return The global best position X_gb

Results and Discussion

In this section, the performance of HGSCADE is evaluated on the CEC2014 benchmark functions. This test series contains 30 functions that can be categorized as unimodal functions (H1–H3), simple multimodal functions (H4–H16), hybrid functions (H17–H22), and composition functions (H23–H30) (Liang, Qu, and Suganthan 2013). The population size N is set as 50 and the maximum number of function evaluations is fixed as 10⁴ × D (D denotes the dimension of problem) for all the given problems. Fifty-one independent algorithm runs are executed for each problem. Moreover, the best value (the difference between the obtained best solution and the true optimal solution) for each run will be truncated to 0 if it is smaller than 10^–8. The statistical measures as mean and standard deviation (Std.) are reported, and the best is highlighted in bold.

Compared Algorithms

To verify the effectiveness and competitiveness of the proposed algorithm, it is compared with the standard SCA, other state-of-the-art MAs, and the variants of SCA:

• SCA: a population-based optimization algorithm which updates the population by sine and cosine functions (Mirjalili 2016b).

• DE: a powerful and straightforward evolutionary algorithm which was primarily designed for real-parameter optimization problems (Storn and Price 1997).

• ABC: a swarm-based optimization algorithm which simulates the intelligent foraging behavior of a honeybee swarm (Karaboga and Basturk 2007).

• GWO: a swarm intelligence algorithm which mimics the social behavior of gray wolves in chasing and hunting the prey (Mirjalili, Mirjalili, and Lewis 2014).

• WOA: a meta-heuristic algorithm which is inspired by the bubble-net hunting strategy of humpback whales (Mirjalili and Lewis 2016).

• SSA: a bio-heuristic algorithm which is inspired by the swarming behavior of salps when navigating and foraging in oceans (Mirjalili et al. 2017).

• HSCAPSO: a hybrid algorithm which adds memory-enabled behavior of PSO to SCA approach, and hybridizes SCA with PSO in iteration level (Nenavath, Kumar Jatoth, and Das 2018).

• HSCADE: a hybrid algorithm which incorporates DE operators into SCA in iteration level, and performs a greedy search (Nenavath and Jatoth 2018).

• PSOSCALF: a hybrid algorithm which combines PSO with the position updating equations of SCA and Levy flight (Rizk-Allah 2018).

• m-SCA: a hybrid algorithm which adds a self-adaptive component to SCA, and incorporates opposite perturbation into SCA (Gupta and Deep 2019).

The parameters settings for existing algorithms are extracted from the original reference. The parameter settings for the proposed HGSCADE algorithm are the combination of suggested parameter settings from SCA (a, r₂, r₃, r₄) (Mirjalili 2016), SHADE (M_pu, M_F, M_cr, pt, H) (Tanabe and Fukunaga 2013), and PSOLF (β, scale) (Jensi and Jiji 2016). The parameter values for all algorithms are set in Table 2.

Table 2. The parameters of algorithms and their values

Algorithms	Parameters	Values
SCA	r2, r3, a, r4	2π*rand, 2*rand, 2, rand
DE	F, cr	[0.2, 0.8], 0.2
ABC	φ, limit	[−1,1], 20
GWO	r1, r2, a	rand, rand, 2 − 2*t/T
WOA	a, a2, l, b, p	2 − 2* t/T, −1 − t/T, (a2 − 1)*rand + 1, 1, rand
SSA	c2, c3	rand, rand
HSCAPSO	r2, r3, a, r4, ω, c1, c2, vmax	2π*rand, 2*rand, 2, rand, 0.9 to 0.4, 2, 2, 4
HSCADE	r2, r3, a, r4, F, cr	2π*rand, 2*rand, 2, rand, [0.2, 0.8], 0.2
PSOSCALF	r2, r3, a, r4, ωmax, ωmin	2π*rand, 2*rand, 2, rand, 0.9, 0.4
	c1max, c1min, c2max, c2min,	0.5, 2.5, 0.5, 2.5
	K, limit, β, scale	10,10, 1.5, 0.01
m-SCA	r2, r3, a, r4, SR, JR	2π*rand, 2*rand, 2, rand, rand, 0.1
HGSCADE	r2, r3, a, r4	2π*rand, 2*rand, 2, rand,
	Mpu, MF, Mcr, pt, H, β, scale	0.5, 0.5, 0.5, 20, 10, 1.5, 0.01

Test Results

The CEC2014 benchmark functions are considered with the dimension of D = 30 and D = 50. Due to space constraints, only the test results for D = 30 are reported in Table 3.

Table 3. Wilcoxon signed rank test between HGSCADE and other algorithms for the CEC2014 functions with D = 30 at a 5% level of significance

Methods	Cylindricity error (mm)
	Data set 1	Data set 2	Data set 3	Data set 4	Data set 5
SCA	0.2032	0.5754	0.0330	0.0168	0.8600
DE	0.0083	0.0196	0.0320	0.0164	0.0158
ABC	0.0239	0.1385	0.1376	0.1570	0.1432
GWO	0.0032	0.1252	0.0321	0.0164	0.2288
WOA	0.1847	0.4239	0.0350	0.0179	1.8552
SSA	0.002788	0.0195	0.03184	0.0164	0.0154
HSCAPSO	10.5857	9.4527	21.9388	15.1798	21.0804
HSCADE	0.0968	0.4573	0.0325	0.0166	0.6378
PSOSCALF	0.002788	0.0196	0.0320	0.0164	0.0146
m-SCA	0.0671	0.1167	0.0321	0.0165	0.3051
HGSCADE	0.002788	0.0194	0.03183	0.0164	0.0143
LSM	0.037162	0.0234	0.0366	0.0195	0.0168
Published results	0.002788	0.01938	0.0319	0.0167	0.0143

As seen in Table 3, HGSCADE provides the best results in terms of the mean for all unimodal functions (H1–H3). By introducing a greedy search, DE, and Levy flight-based local search, the population can exploit the nearby area of every individual best position. Therefore, the exploitation ability of HGSCADE is enhanced.

For simple multimodal functions, HGSCADE provides the best results in terms of mean on functions H4–H6, H8–H12, H15, and H16, ABC on functions H8, H13, and H14, and DE on functions H7 and H8. By inheriting the randomness of SCA and Levy flight disturbance, the population can explore the whole search space. Therefore, the exploration ability of HGSCADE is enhanced.

HGSCADE provides the best results in terms of the mean for all hybrid functions (H17–H22). For composition functions, HGSCADE provides the best results in terms of mean on functions H23, H25, H26, H29, and H30, DE on functions H23, H26–28, ABC on functions H23 and H26, and SSA on function H26. For function H24, SCA, GWO, and m-SCA give the same best results in terms of the mean. By the success history-based adaptation of parameter pu_i, each agent is automatically updated by the SCA method or DE method to balance the trade-off between exploration and exploitation.

In addition, it can be observed that HGSCADE is the best algorithm in terms of overall standard deviation, i.e., HGSCADE has the highest stability. The opposition-based population initialization, greedy search, and success history-based parameter adaptation improve the stability of HGSCADE.

Statistical Analysis

Considering the effect of each run, a non-parametric statistical test called Wilcoxon signed rank test is implemented at a significance level of 5%. The calculated p-value determines to accept or reject the null hypothesis. The grade symbols +, ≈ and – signify that HGSCADE is superior, similar, and inferior to a compared algorithm, respectively. The character string N/A signifies that the two samples are identical and the Wilcoxon signed rank test is invalid. Accordingly, the Wilcoxon signed rank test results are presented in Table 4. The grades are summarized in the last row of the table.

Table 4. The cylindricity error evaluation results of different algorithms

No.	Criterion	SCA	DE	ABC	GWO	WOA	SSA	HSCAPSO	HSCADE	PSOSCALF	m-SCA	HGSCADE
H1	Mean	2.62E+08	1.77E+07	1.12E+07	7.57E+07	3.15E+07	1.62E+06	3.84E+07	3.89E+08	1.99E+07	2.04E+07	8.63E+03
	Std.	7.37E+07	3.91E+06	3.17E+06	5.26E+07	1.42E+07	7.29E+05	2.95E+07	6.96E+07	2.19E+07	6.87E+06	7.17E+03
H2	Mean	1.81E+10	3.36E-01	2.19E+02	4.23E+09	4.69E+06	8.71E+03	1.06E+07	2.72E+10	1.84E+05	2.71E+08	0.00E+00
	Std.	3.39E+09	2.29E+00	2.25E+02	3.14E+09	8.04E+06	7.61E+03	3.53E+06	3.70E+09	1.06E+06	5.34E+07	0.00E+00
H3	Mean	4.15E+04	1.89E+02	6.50E+02	2.93E+04	4.06E+04	2.11E+03	5.33E+04	7.57E+04	1.76E+04	2.50E+04	0.00E+00
	Std.	8.35E+03	1.89E+02	4.83E+02	9.80E+03	2.78E+04	1.07E+03	1.29E+04	1.22E+04	1.29E+04	5.64E+03	0.00E+00
H4	Mean	1.16E+03	1.14E+02	1.60E+01	2.90E+02	1.86E+02	7.97E+01	2.72E+02	2.87E+03	1.51E+02	1.72E+02	9.03E+00
	Std.	2.43E+02	1.68E+01	2.11E+01	1.42E+02	6.06E+01	2.96E+01	1.23E+02	4.84E+02	4.96E+01	1.54E+01	2.39E+01
H5	Mean	2.09E+01	2.06E+01	2.04E+01	2.09E+01	2.03E+01	2.01E+01	2.11E+01	2.09E+01	2.09E+01	2.09E+01	2.01E+01
	Std.	5.70E-02	4.51E-02	4.35E-02	4.49E-02	2.00E-01	1.04E-01	9.05E-02	5.85E-02	4.99E-02	5.80E-02	3.03E-02
H6	Mean	3.48E+01	1.84E+01	1.51E+01	1.39E+01	3.53E+01	2.02E+01	2.48E+01	3.65E+01	2.52E+01	1.86E+01	1.13E+01
	Std.	2.85E+00	1.28E+00	1.53E+00	3.40E+00	3.83E+00	3.77E+00	3.91E+00	1.44E+00	2.93E+00	2.34E+00	2.25E+00
H7	Mean	1.48E+02	6.05E-09	4.80E-06	4.11E+01	1.01E+00	1.12E-02	1.10E+00	2.49E+02	5.55E-01	4.06E+00	1.35E-03
	Std.	2.73E+01	4.18E-08	1.02E-05	3.59E+01	5.22E-02	9.37E-03	3.50E-02	3.26E+01	1.52E+00	7.34E-01	4.33E-03
H8	Mean	2.45E+02	0.00E+00	0.00E+00	8.10E+01	1.81E+02	1.23E+02	7.99E+01	2.75E+02	9.12E+01	9.85E+01	0.00E+00
	Std.	1.53E+01	0.00E+00	0.00E+00	1.98E+01	3.44E+01	2.98E+01	1.63E+01	1.41E+01	2.09E+01	1.29E+01	0.00E+00
H9	Mean	2.77E+02	1.14E+02	8.41E+01	1.04E+02	2.44E+02	1.31E+02	1.03E+02	3.19E+02	1.33E+02	1.23E+02	3.55E+01
	Std.	2.12E+01	1.02E+01	1.04E+01	2.24E+01	6.53E+01	3.15E+01	2.81E+01	1.34E+01	3.15E+01	1.38E+01	6.75E+00
H10	Mean	6.17E+03	5.91E+01	1.34E+00	2.12E+03	3.97E+03	3.41E+03	3.55E+03	6.48E+03	3.19E+03	4.03E+03	1.35E-02
	Std.	4.86E+02	2.74E+01	8.02E-01	5.22E+02	5.88E+02	5.82E+02	7.19E+02	2.56E+02	9.51E+02	4.87E+02	1.81E-02
H11	Mean	7.02E+03	4.76E+03	2.17E+03	2.63E+03	4.66E+03	3.49E+03	5.77E+03	6.99E+03	6.59E+03	4.96E+03	1.56E+03
	Std.	2.97E+02	2.36E+02	2.64E+02	4.85E+02	9.02E+02	7.33E+02	1.31E+03	2.96E+02	7.64E+02	5.64E+02	3.71E+02
H12	Mean	2.41E+00	1.01E+00	4.24E-01	1.55E+00	1.62E+00	4.54E-01	2.93E+00	2.40E+00	2.54E+00	1.85E+00	1.71E-01
	Std.	2.99E-01	1.35E-01	5.60E-02	1.13E+00	5.14E-01	2.17E-01	7.54E-01	2.65E-01	2.97E-01	2.72E-01	2.95E-02
H13	Mean	3.10E+00	3.50E-01	2.47E-01	5.13E-01	4.97E-01	4.73E-01	5.25E-01	4.06E+00	7.25E-01	4.62E-01	2.55E-01
	Std.	3.25E-01	3.55E-02	2.50E-02	3.78E-01	1.05E-01	9.95E-02	1.05E-01	2.97E-01	1.70E-01	6.28E-02	5.87E-02
H14	Mean	4.85E+01	2.78E-01	1.96E-01	7.95E+00	2.77E-01	2.76E-01	3.25E-01	7.99E+01	7.62E-01	3.16E-01	2.68E-01
	Std.	9.40E+00	2.93E-02	1.60E-02	9.71E+00	8.98E-02	4.25E-02	6.23E-02	9.06E+00	3.55E-01	4.35E-02	4.33E-02
H15	Mean	4.23E+03	1.26E+01	1.09E+01	2.74E+02	7.13E+01	7.89E+00	2.34E+01	1.03E+05	4.42E+01	1.90E+01	3.55E+00
	Std.	4.53E+03	7.89E-01	1.27E+00	5.13E+02	2.34E+01	3.22E+00	2.54E+00	5.01E+04	1.68E+01	1.61E+00	9.77E-01
H16	Mean	1.29E+01	1.13E+01	1.07E+01	1.08E+01	1.26E+01	1.17E+01	1.27E+01	1.30E+01	1.28E+01	1.22E+01	9.60E+00
	Std.	2.80E-01	3.70E-01	2.59E-01	7.39E-01	4.74E-01	6.41E-01	4.69E-01	1.59E-01	3.88E-01	2.21E-01	6.60E-01
H17	Mean	6.40E+06	1.21E+06	2.83E+06	1.63E+06	3.44E+06	1.14E+05	1.61E+06	9.37E+06	2.57E+06	5.08E+05	1.11E+03
	Std.	2.68E+06	4.48E+05	1.33E+06	1.58E+06	2.29E+06	9.11E+04	9.68E+05	3.05E+06	2.11E+06	2.52E+05	4.76E+02
H18	Mean	1.93E+08	7.06E+03	6.98E+03	8.49E+06	4.80E+03	2.01E+03	5.35E+03	2.61E+08	6.82E+04	6.44E+05	6.89E+01
	Std.	1.01E+08	4.55E+03	4.10E+03	1.95E+07	4.86E+03	2.21E+03	5.39E+03	8.68E+07	2.50E+05	3.80E+05	3.25E+01
H19	Mean	8.90E+01	7.92E+00	7.39E+00	4.10E+01	4.04E+01	1.53E+01	6.06E+01	1.32E+02	2.77E+01	1.51E+01	4.23E+00
	Std.	2.26E+01	6.36E-01	6.56E-01	2.44E+01	3.07E+01	9.89E+00	3.25E+01	2.37E+01	2.21E+01	1.64E+00	1.19E+00
H20	Mean	1.62E+04	2.49E+03	4.87E+03	1.63E+04	2.25E+04	3.86E+02	2.52E+04	2.52E+04	1.55E+04	6.91E+03	9.80E+01
	Std.	5.39E+03	1.10E+03	1.92E+03	9.54E+03	1.48E+04	1.17E+02	1.37E+04	9.19E+03	7.45E+03	2.82E+03	5.27E+02
H21	Mean	1.74E+06	1.91E+05	4.37E+05	6.05E+05	1.03E+06	6.66E+04	4.58E+05	2.08E+06	7.84E+05	9.11E+04	3.51E+02
	Std.	9.87E+05	9.69E+04	1.56E+05	1.00E+06	8.70E+05	4.66E+04	2.90E+05	1.01E+06	7.57E+05	4.47E+04	1.85E+02
H22	Mean	8.45E+02	1.48E+02	3.03E+02	3.75E+02	8.02E+02	3.87E+02	5.40E+02	8.31E+02	5.10E+02	1.79E+02	1.43E+02
	Std.	1.65E+02	6.84E+01	8.43E+01	1.57E+02	2.29E+02	1.44E+02	1.92E+02	1.25E+02	1.95E+02	6.30E+01	8.24E+01
H23	Mean	3.75E+02	3.15E+02	3.15E+02	3.38E+02	3.31E+02	3.15E+02	3.34E+02	4.49E+02	3.16E+02	3.22E+02	3.15E+02
	Std.	1.45E+01	4.02E-13	1.42E-01	1.34E+01	7.52E+00	5.07E-02	1.53E+01	2.65E+01	2.33E+00	9.43E-01	8.10E-13
H24	Mean	2.00E+02	2.24E+02	2.27E+02	2.00E+02	2.06E+02	2.33E+02	2.37E+02	3.25E+02	2.50E+02	2.00E+02	2.27E+02
	Std.	3.11E-01	8.74E-01	2.58E+00	8.64E-04	3.93E+00	9.02E+00	1.12E+01	1.09E+01	1.01E+01	5.46E-03	3.61E+00
H25	Mean	2.30E+02	2.08E+02	2.09E+02	2.10E+02	2.19E+02	2.13E+02	2.21E+02	2.44E+02	2.16E+02	2.11E+02	2.06E+02
	Std.	6.25E+00	1.01E+00	9.05E-01	5.19E+00	1.59E+01	2.70E+00	5.99E+00	6.40E+00	4.80E+00	1.71E+00	2.73E+00
H26	Mean	1.03E+02	1.00E+02	1.00E+02	1.43E+02	1.08E+02	1.00E+02	1.01E+02	1.04E+02	1.01E+02	1.01E+02	1.00E+02
	Std.	6.32E-01	3.72E-02	6.09E-02	4.97E+01	4.38E+01	1.07E-01	1.37E-01	2.81E-01	1.62E-01	5.31E-02	5.83E-02
H27	Mean	7.84E+02	3.77E+02	4.04E+02	6.67E+02	1.03E+03	7.04E+02	7.20E+02	7.63E+02	7.68E+02	4.20E+02	4.23E+02
	Std.	3.23E+02	6.36E+01	5.55E+01	1.34E+02	3.82E+02	1.80E+02	2.47E+02	1.47E+02	3.04E+02	5.97E+00	5.96E+01
H28	Mean	1.92E+03	8.41E+02	9.64E+02	1.23E+03	2.10E+03	1.10E+03	3.11E+03	2.51E+03	1.57E+03	1.09E+03	8.48E+02
	Std.	3.27E+02	2.80E+01	4.86E+01	3.01E+02	5.05E+02	2.93E+02	9.10E+02	3.70E+02	4.12E+02	4.13E+01	3.46E+01
H29	Mean	1.04E+07	1.76E+03	1.14E+03	1.62E+06	6.27E+06	3.15E+06	3.83E+07	1.71E+07	4.91E+06	3.59E+04	9.68E+02
	Std.	6.27E+06	1.90E+02	1.14E+02	3.68E+06	4.73E+06	5.86E+06	6.97E+07	5.59E+06	7.37E+06	1.56E+04	2.96E+02
H30	Mean	2.45E+05	2.74E+03	3.96E+03	5.81E+04	9.00E+04	9.62E+03	7.05E+04	3.27E+05	3.67E+04	2.06E+04	1.86E+03
	Std.	8.35E+04	7.18E+02	9.68E+02	4.93E+04	6.94E+04	1.03E+04	8.23E+04	7.94E+04	3.42E+04	6.36E+03	8.94E+02

From Table 4, HGSCADE performs better than HSCAPSO, HSCADE, and PSOSCALF in all the CEC2014 benchmark functions for D = 30. In 29, 22, 26, 29, 28, 26, and 28 out of 30 CEC2014 benchmark functions for D = 30, HGSCADE performs better than SCA, DE, ABC, GWO, WOA, SSA, and m-SCA, respectively. It verifies the test results that HGSCADE is the best algorithm in comparison with other algorithms.

Convergence Analysis

Considering that there are too many functions, four functions (H3, H13, H20, and H30) from different categories are selected to exemplify the convergence behavior. The median of the obtained best values is displayed on the vertical axis in logarithmic scale, while the number of function evaluations is displayed on the horizontal axis. The convergence curves for the selected functions are shown in Figures 1–2.

Figure 1. The convergence curves of all algorithms for certain CEC2014 functions (H3, H13, H20, and H30) with D = 30

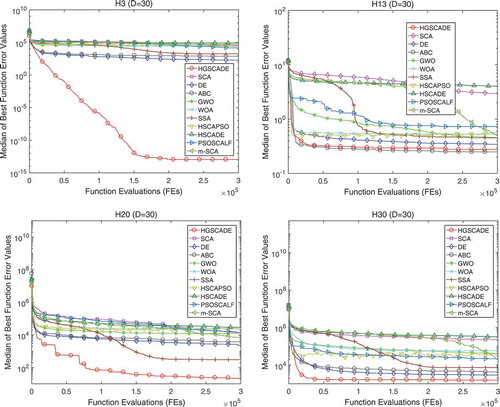
Figure 2. The convergence curves of all algorithms for certain CEC2014 functions (H3, H13, H20, and H30) with D = 50

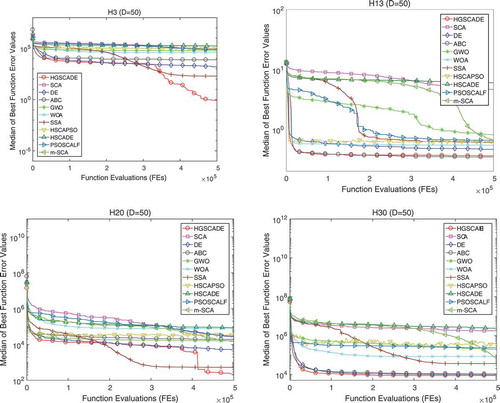
It can be observed that HGSCADE has a faster convergence speed to produce an accurate solution than that of compared algorithms except for H13. It indicates that HGSCADE has the ability to create a balance between exploration and exploitation. The opposition-based population initialization provides initial solutions with favorable distribution, and the greedy search prevents excluding good solutions; thus, the convergence speed is accelerated. The DE enhances the exploitation ability and maintains the population diversity, the Levy flight-based local search avoids local optima, and the success history-based parameter adaptation strengthens the stability; thus, the solution accuracy is improved.

Complexity Analysis

The complexity of HGSCADE (represented by notation O) can be calculated as O (HGSCADE) = O (positions initializing by OBL) + O (positions updating by greedy SCA) + O (positions updating by DE) + O (global best position updating) + O (current best position updating by local search), i.e.

(15) $O(\mathrm{H}\mathrm{G}\mathrm{S}\mathrm{C}\mathrm{A}\mathrm{D}\mathrm{E})=O[N+T\times (N\times D+2N+2)]$(15)

where N is the population size, D is the dimension of the problem and T is the maximum number of iterations. Similarly, the complexity of SCA is $O(\mathrm{S}\mathrm{C}\mathrm{A})=O[T\times (N\times D+N)]$. The opposition-based population initialization, the greedy search, and the Levy flight-based local search increase the computational complexity of the proposed algorithm.

HGSCADE for Cylindricity Error Evaluation

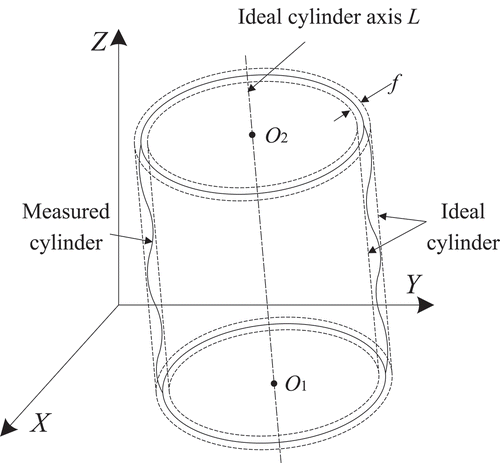
Mathematical Model of Cylindricity Error

As shown in Figure 3, the cylindricity error f is defined as the minimum radius difference between two coaxial theoretical cylinders which envelop the actual contour of a cylindrical part. It is assumed that the measured points in the Cartesian coordinate system are p_i(x_i, y_i, z_i) (i = 1, 2, … , n), where x_i, y_i, z_i are coordinate values, and n is the number of measured points. Supposing that the fixed point of L is (x₀, y₀, z₀) and the directional vector of L is [a, b, c]. Then, the parametric equation of L can be defined as:

(16) $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$(16)

Figure 3. Schematic of cylindricity error

The distance from point p_i to axis L can be calculated by:

(17) $r=\sqrt{(A^2+B^2+C^2)/(a^2+b^2+c^2)}$(17)

where A = (y_i – y₀) × c – (z_i – z₀) × b, B = (z_i – z₀) × a – (x_i–x₀) × c, C = (x_i–x₀) × b – (y_i – y₀) × a.

Finally, the cylindricity error is defined as:

(18) $f(x_0,y_0,z_0,a,b,c)=min(max(r)-min(r))$(18)

Data Sets

Five original-measured data sets from corresponding literature are used to experiment. These data sets are named as Data set 1 (24 samples cited from Lai et al. 2000), Data set 2 (32 samples cited from Yang et al. 2018), Data set 3 (80 samples cited from Lei et al. 2011), Data set 4 (24 samples cited from; Li et al. 2009), and Data set 5 (60 samples cited from Zhao, Wen, and Xu 2015), respectively.

Experiments and Analysis

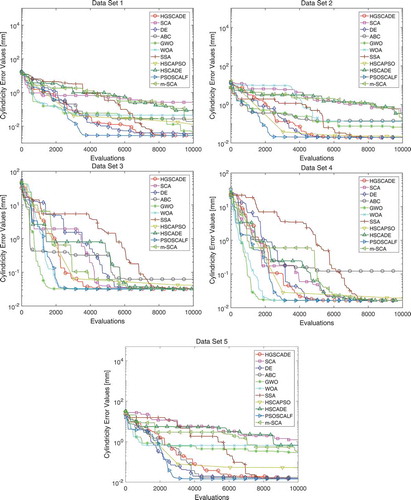
HGSCADE is used for cylindricity error evaluation and compared with other algorithms. For all algorithms, the population size is fixed to 30, the search space of variables (x₀, y₀, z₀) is set as the data range, and the search space of variables (a, b, c) is set from – 1 to 1. The search will be terminated when the number of evaluations reaches 10000. The evaluation results (the mean of 30 independent evaluation values for each data set) of HGSCADE and other comparison algorithms are listed in Table 5. The convergence curves of HGSCADE and other comparison algorithms are shown in Figure 4.

Table 5. Mean and standard deviation of 51 independent runs for all algorithms on the CEC2014 functions with D = 30

No.		HGSCADE versus
		SCA	DE		ABC	GWO	WOA	SSA	HSCAPSO	HSCADE	PSOSCALF
H1	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H2	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H3	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H4	p-Values	0.000000	0.000000		0.000512	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H5	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000026	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	-	+	+	+
H6	p-Values	0.000000	0.000000		0.000000	0.000389	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H7	p-Values	0.000000	0.078125		0.000140	0.000000	0.000000	0.000026	0.000000	0.000000	0.000000
	Grades	+	≈		+	+	+	-	+	+	+
H8	p-Values	0.000000	N/A		N/A	0.000000	0.000000	0.000026	0.000000	0.000000	0.000000
	Grades	+	≈		≈	+	+	-	+	+	+
H9	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H10	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H11	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H12	p-Values	0.000000	0.000000		0.000000	0.000001	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H13	p-Values	0.000000	0.000000		0.404705	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		≈	+	+	+	+	+	+
H14	p-Values	0.000000	0.277409		0.000000	0.000000	0.679119	0.349193	0.000009	0.000000	0.000000
	Grades	+	≈		-	+	≈	≈	+	+	+
H15	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H16	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H17	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H18	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H19	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H20	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H21	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H22	p-Values	0.000000	0.856213		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	≈		+	+	+	+	+	+	+
H23	p-Values	0.000000	0.003906		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	-		+	+	+	+	+	+	+
H24	p-Values	0.000000	0.000000		0.012990	0.000000	0.000000	0.000018	0.000000	0.000000	0.000000
	Grades	-	-		+	-	≈	+	+	+	+
H25	p-Values	0.000000	0.000027		0.000001	0.000001	0.000002	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H26	p-Values	0.000000	0.000000		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H27	p-Values	0.000000	0.000645		0.363840	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	-		≈	+	+	+	+	+	+
H28	p-Values	0.000000	0.415328		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	≈		+	+	+	+	+	+	+
H29	p-Values	0.000000	0.000000		0.001009	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
H30	p-Values	0.000000	0.000006		0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
	Grades	+	+		+	+	+	+	+	+	+
Grades + / ≈ / -		29/0/1	22/5/3		26/3/1	29/0/1	28/1/1	26/1/3	30/0/0	30/0/0	30/0/0

Figure 4. The convergence curves of all algorithms for cylindricity error evaluation

As can be observed from Table 5, the cylindricity error evaluation results of HGSCADE are much better than that of SCA, ABC, WOA, HSCAPSO, HSCADE, and LSC for all the data sets. Although SSA and PSOSCALF provide the same results as HGSCADE for Data set 1 and Data set 4, DE and GWO provide the same results as HGSCADE for Data set 4, they cannot give the best results for all the data sets. Moreover, the results of HGSCADE are well in agreement with the published results (equally for Data set 1, Data set 4 and Data set 5, slightly worse for Data set 2, slightly better for Data set 3). It can be observed from Figure 4 that the evaluation speed of HGSCADE is not the fastest, but HGSCADE can give the best evaluation results with relative efficiency. HGSCADE keeps a very good balance between exploration and exploitation in cylindricity error evaluation, so satisfactory results are obtained. The availability of HGSCADE for cylindricity error evaluation is verified by the experiment.

Conclusions

In this study, a novel HGSCADE algorithm is proposed for solving optimization problems and evaluating cylindricity error. The proposed algorithm combines SCA with five strategies: (1) Opposition-based learning (2) Greedy search (3) Differential evolution (4) Success history-based parameter adaptation (5) Local search based on Levy flight. HGSCADE is compared with the standard SCA, other state-of-the-art MAs, and the variants of SCA on the CEC2014 benchmark functions. The comparison and analysis of the test results prove that the performance of HGSCADE is better than that of other compared algorithms. In addition, the proposed algorithm is applied for cylindricity error evaluation of five measured cylindrical parts and is verified to be an effective mean to evaluate cylindricity error.

However, the test results of HGSCADE for several CEC2014 functions are worse than that of certain-compared algorithms (SSA for H5, H7, and H8; DE for H23, H24, and H27; ABC for H14; SCA, GWO, WOA, and m-SCA for H24). This suggests that HGSCADE accords with the NFL theorem. The future work will be concentrated in two directions: (1) Attempting to apply HGSCADE in solving other engineering optimization problems (2) Extending the study of SCA for solving more complex problems.

Disclosure Statement

The authors declare that they have no conflict of interest.

Additional information

Funding

This work was supported by the National Natural Science Foundation of China under Grant [51565033]; and the Natural Science Foundation of Gansu Province under Grant [18JR3RA142].