Comparative Evaluation of the Fast Marching Method and the Fast Evacuation Method for Heterogeneous Media

ABSTRACT

The evacuation problem is usually addressed by assuming homogeneous media where pedestrians move freely in the presence of several exits and obstacles. From a more general perspective, this work considers heterogeneous media in which the velocity of pedestrians depends on their location. We use cellular automata with a floor field that indicates promising movements to pedestrians and, in this context, we extend two competitive evacuation methods in order for them to be applied to heterogeneous media: the Fast Marching Method and the Fast Evacuation Method. Furthermore, we evaluate the performance that these two methods exhibit over different simulated scenarios characterized by the presence of heterogeneous media. The resulting winning method in terms of evacuation effectiveness is greatly influenced by the particular problem being simulated.

Introduction

Pedestrian evacuation (Corrêa, Bicho, and Adamatti 2019; Martínez-Gil et al. 2017; Schadschneider, Chowdhury, and Nishinari 2011) constitutes a relevant problem that has been extensively studied in the past. In emergency situations taking place in buildings or means of transport, to mention two of many other potential evacuation scenarios, it arises the important task of how to safely and efficiently move crowds. Specifically, the present work deals with the type of evacuation in which a group of pedestrians move in a two-dimensional environment with known obstacles and exits. Due to the fact that real-world evacuations are difficult to carry out in practice, computer simulations are normally used to analyze evacuation methods.

In order to simulate and study human behavior during evacuation processes, several models have been designed. Depending on the detail level, such models can be classified into microscopic, mesoscopic, or macroscopic (Duives, Daamen, and Hoogendoorn 2013; Shiwakoti, Sarvi, and Rose 2008). The main microscopic approaches to modeling pedestrian evacuation are social forces (Helbing, Farkas, and Vicsek 2000; Helbing and Molnár 1995), lattice gas (Helbing et al. 2003; Isobe, Helbing, and Nagatani 2004; Tajima and Nagatani 2001; Tajima, Takimoto, and Nagatani 2001), and cellular automata (CA) (Burstedde et al. 2001; Kirchner et al. 2003; Kirchner and Schadschneider 2002; Schadschneider 2002; Varas et al. 2007). While the social force model considers pedestrians as particles interacting with the environment under continuous space and time, the CA model employs discrete floor fields in order to establish how pedestrians move in discrete time. Precisely, the present work deals with CA evacuation models that make use of floor fields to indicate promising movements to pedestrians.

In a discrete floor field, space is partitioned into rectangular cells and a weight is assigned to each cell at every time step. The movement of pedestrians is determined by the cell weights and the rules of pedestrian interaction. Generally, a pedestrian moves to the neighboring empty cell with the lowest weight. In the literature, the floor fields for the evacuation problem are based on minimizing the evacuation time for each pedestrian. Specifically, for each CA cell, either the shortest path to an exit (Burstedde et al. 2002; Schadschneider 2002) (typically combined with dynamic measures of pedestrian density or distribution) or the quickest path to an exit (Kretz 2009a, 2009b) are calculated. While the shortest path is static and only depends on the room structure, exit location, and obstacle distribution, the quickest path is dynamic since the distribution of pedestrians is also taken into account. Due to the typical appearance of congestions in evacuation processes, considering the quickest path normally leads to more realistic and efficient simulations. The most competitive method among those based on quickest paths consists in applying the Fast Marching Method (Sethian 1999) to calculate the cell weights. Alternatively, the Fast Evacuation Method (Galán 2019) was recently introduced in order to tackle the evacuation problem from a different perspective than minimizing the estimated remaining travel time (or travel distance) for each pedestrian. The new perspective is based on minimizing the estimated duration of the remaining global evacuation process by distributing the workload of pedestrian evacuation in an equitable way among the available exits. The Fast Evacuation Method has two important advantages: first, the effectiveness of the evacuation process is improved since a lower number of time steps is necessary in general and, second, the efficiency is also improved since the running time employed for each time step is reduced.

The evacuation problem has been typically tackled in the past by considering homogeneous media in which pedestrians move freely in the presence of several exits and obstacles. By adopting a more general perspective, the present work considers heterogeneous media where the velocity of pedestrians depends on their location. We use CA with a floor field that indicates promising movements to pedestrians and, in this context, the contributions of this work are twofold:

• On the one hand, we extend two competitive evacuation methods in order for them to be applied to heterogeneous media: the Fast Marching Method and the Fast Evacuation Method.

• On the other hand, we conduct an experimental evaluation in order to compare the performances of the two extended methods over different simulated scenarios containing heterogeneous media. The experimental results show that the particular problem being simulated has a great influence in determining the winning method in terms of evacuation effectiveness.

The rest of the paper is organized as follows. Section 2 reviews several widely used methods for solving the evacuation problem. Section 3 explains the extension of the Fast Marching Method and the Fast Evacuation Method to heterogeneous media. Section 4 describes a series of experiments for comparatively evaluating the new extended methods. Finally, Section 5 summarizes the main results obtained in this work and enumerates future research directions.

Related Work

The main component of a CA (Galán 2020; Hassan and Tazaki 2010; Ioannidis, Sirakoulis, and Andreadis 2011; Toffoli and Margolus 1987; von Neumann 1966; Wolfram 2002) is a regular grid of cells, denoted as $C$, where each cell $c\in C$ adopts one of the set of states. Three characteristics of CA are that they consist of many identical simple processing cells, interactions between cells take place in a small neighborhood compared to the grid size, and discrete time is used. In a two-dimensional square grid, the von Neumann neighborhood is formed by a cell and its vertical and horizontal neighbors, whereas the Moore neighborhood incorporates the diagonal neighbors.

CA for pedestrian dynamics were introduced in the 1990s (Fukui and Ishibashi 1996, 1999a, 1999b). Typically, navigation in the CA employs a floor field representing a scalar function that increases with growing distance from the exits. Thus, pedestrians move by minimizing the floor field values in a local way.

Schadschneider introduced a sophisticated CA model of evacuation (Burstedde et al. 2002; Schadschneider 2002) that represented a breakthrough in the field of pedestrian dynamics. This model probabilistically combines a static floor field based on shortest paths and long-range pedestrian interactions inspired by the process of chemotaxis. The static floor field reflects the distribution of exits and obstacles, while the interactions among pedestrians are implemented through chemotaxis. Other relevant probabilistic models (Dias and Lovreglio 2018; Lovreglio et al. 2018, 2017) use a multinomial logit formulation in order to specify the probabilities to select a cell.

Posterior to the appearance of Schadschneider’s model, the introduction of models incorporating a dynamic floor field based on quickest paths (Kretz 2009a, 2009b) became the standard method for modeling evacuation processes. The values of this dynamic floor field highly depend on the distribution of pedestrians. Due to their close relationship with the present work, quickest-path floor fields are reviewed in the next section.

Fast Marching Method

Congestions or jams around exits are usual in evacuations of large crowds. In a congested environment, following the quickest rather than the shortest path to an exit is more realistic for pedestrian dynamics simulation. The quickest path from each location to an exit depends on the spatial distribution of pedestrians.

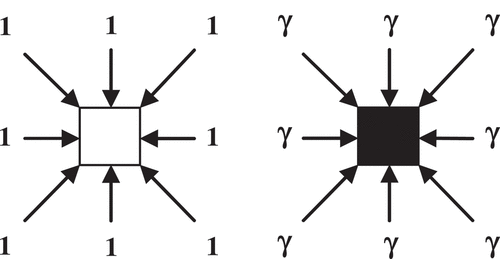
The Flood Fill method (FF) (Kretz 2009a,b) employs a floor field that associates a cost to each CA cell, representing the estimated time spent to move to the cell from any of its neighboring cells. Specifically, a cost equal to unity is associated to empty cells, whereas occupied cells are assigned a cost $\gamma >1$. This method uses the neighborhood relationships among cells and the Dijkstra algorithm in the induced graph to calculate the quickest path from each CA cell to an exit. The Dijkstra algorithm is an efficient algorithm whose time complexity is $\mathcal{O}(|C|\cdot log|C|)$, where $C$ is the set of cells. This is due to the fact that the list containing the visited cells to be expanded can be implemented through a heap data structure. The operations of extracting the best cell from the heap and inserting its neighboring unvisited cells can be efficiently implemented in $\mathcal{O}(log|C|)$ time. An advantage of FF is that the first weight calculated by the Dijkstra algorithm for a cell does not need to be reconsidered. This is a consequence of the way FF assigns costs to cells (see Figure 1). However, FF produces somewhat unrealistic movement by pedestrians, which tend to form square jams around the exits instead of circular ones. This drawback was partially solved in (Kretz, Bönisch, and Vortisch 2010), where the costs associated to the diagonal links in Figure 1 are multiplied by $\sqrt{2}$. This correction to the diagonal costs provokes that the weights calculated by the Dijkstra algorithm for a cell may need to be reconsidered over the course of the execution.

Figure 1. Costs associated to moving to an empty cell (white cell in the left-hand figure) and to an occupied cell (black cell in the right-hand figure) in the FF method. The parameter $\gamma$ is chosen such that $\gamma >1$

An approach similar to FF that produces more realistic pedestrian dynamics consists in applying the Fast Marching Method (FMM) (Sethian 1999) to obtain the cell weights. The underlying idea, rather than calculating minimum distances in a graph of costs, is to expand a wavefront from each exit in the two-dimensional domain of interest. Thus, the cell weights are established as the travel time of the wavefront, which coincides with the shortest distance to an exit when the wavefront propagates across empty cells with a velocity equal to unity. The arrival time of the wavefront to point $x$, $T(x)$, is determined by the eikonal equation:

(1) $\begin{array}{cc}\left|\mathrm{\nabla }T(x)\right|=\frac{1}{F(x)}& \mathrm{f}\mathrm{o}\mathrm{r}x\in \mathrm{\Omega }(\mathrm{a}\mathrm{t}\mathrm{w}\mathrm{o}-\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t})\\ T(x)=0& \mathrm{f}\mathrm{o}\mathrm{r}x\in \delta \mathrm{\Omega }(\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{o}\mathrm{f}\mathrm{\Omega }\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s})\end{array},$(1)

where $F(x)$ is the velocity of the wavefront such that $F(x)=0$ in obstacle cells, $F(x)=1$ in empty cells, and $F(x)=1/\gamma$ (with $\gamma >1$) in occupied cells. FMM efficiently solves the eikonal equation on a discretized grid (see Chiang et al. (2007) for a comparison with A* search) through a finite difference approximation of Equation 1(1) $\begin{array}{cc}\left|\mathrm{\nabla }T(x)\right|=\frac{1}{F(x)}& \mathrm{f}\mathrm{o}\mathrm{r}x\in \mathrm{\Omega }(\mathrm{a}\mathrm{t}\mathrm{w}\mathrm{o}-\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t})\\ T(x)=0& \mathrm{f}\mathrm{o}\mathrm{r}x\in \delta \mathrm{\Omega }(\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{o}\mathrm{f}\mathrm{\Omega }\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s})\end{array},$(1) resulting in the following formula:

(2) ${\left\{max\left(0,T_{ij}-T_{i-1,j},T_{ij}-T_{i+1,j}\right)\right\}}^2+{\left\{max\left(0,T_{ij}-T_{i,j-1},T_{ij}-T_{i,j+1}\right)\right\}}^2=\frac{1}{F_{ij}^2},$(2)

where $T_{ij}$ and $F_{ij}$ stand for the value at cell $(i,j)$ of $T$ and $F$, respectively. FMM considers the von Neumann neighborhood rather than the Moore neighborhood, for example when applying Equation 2(2) ${\left\{max\left(0,T_{ij}-T_{i-1,j},T_{ij}-T_{i+1,j}\right)\right\}}^2+{\left\{max\left(0,T_{ij}-T_{i,j-1},T_{ij}-T_{i,j+1}\right)\right\}}^2=\frac{1}{F_{ij}^2},$(2) to calculate a candidate weight $T_{ij}$ for cell $(i,j)$. ($T_{ij}$ is obtained by solving the quadratic equation defined by Equation 2(2) ${\left\{max\left(0,T_{ij}-T_{i-1,j},T_{ij}-T_{i+1,j}\right)\right\}}^2+{\left\{max\left(0,T_{ij}-T_{i,j-1},T_{ij}-T_{i,j+1}\right)\right\}}^2=\frac{1}{F_{ij}^2},$(2) .) Like FF, the order of cell updating in FMM is carried out by using a heap data structure, which gives rise to $\mathcal{O}(|C|\cdot log|C|)$ time complexity. Nonetheless, unlike FF under the costs depicted in Figure 1, FMM needs to reconsider some of the weight updates over the course of its execution. FMM is widely used in evacuation modeling due to its realistic results.

Fast Evacuation Method

The Fast Evacuation Method (FEM) (Galán 2019) constitutes a CA model of pedestrian evacuation that aims at minimizing the duration of the whole evacuation process by employing a dynamic floor field that distributes the evacuation workload among the exits in an equitable way. The floor field defined by FEM at each time step can be calculated in an efficient manner in time proportional to the number of CA cells and gives rise to a fast and effective evacuation process.

As in typical CA, discrete time and space are assumed. Space is divided into square cells of equal size.¹ Each CA cell can be empty, occupied by a pedestrian (only one at a time), represent an exit, or represent an obstacle. In each time step, the pedestrians are updated asynchronously in a random order, according to the values contained in a dynamic floor field. Every pedestrian moves by occupying the neighboring empty cell with a minimum floor field value. Pedestrians are assumed to know their environment or, equivalently, be in contact with an external agent that provides them with the floor field information.

In each time step, FEM calculates a complete floor field $\varphi$ previously to moving each pedestrian to a neighboring cell.² The floor field $\varphi$ is calculated in an iterative way such that a wavefront is initiated from every exit cell at the first iteration. The arbitrary neighborhood relationship established for wavefront propagation determines the wavefront shape. (The Moore and von Neumann neighborhoods give rise to square wavefronts; however, the probabilistic neighborhood ${\mathcal{N}}_{\sigma =0.2}$ (Galán 2019) produces wavefronts more similar to circles.) A wavefront propagates freely across empty cells and, when occupied cells are reached, the wavefront stops for a number of iterations equal to the number of pedestrians reached at the current iteration. Thus, it is possible that some wavefronts keep propagating while others remain stopped. The value of $\varphi$ for a cell is determined by the iteration in which the first wavefront arrives in the cell.

Extending Evacuation Methods to Heterogeneous Media

When a homogeneous medium is considered, the CA approach to evacuation modeling assumes that pedestrians move freely across empty cells at a velocity equal to unity. This velocity is the maximum possible for pedestrians. In this way, at the next time step, every pedestrian is allowed to move to one of the empty neighboring cells of its current cell or location.

The CA approach to evacuation modeling can be generalized to heterogeneous media by assuming that pedestrians move at a velocity that depends on the current cell where they are located. For example, pedestrians would move at different velocities (all of them less than unity) across media containing water, sand, stones, or debris. As a result, getting across one cell would take a pedestrian more than one time step in general.

In this work, we model heterogeneous media by assigning each cell $(i,j)$ a real number representing the velocity $v_{ij}$ at which a pedestrian (or a wavefront) moves across the cell. Alternatively, it can be specified the time $t_{ij}$ that takes a pedestrian (or a wavefront) to get across the cell horizontally or vertically. If the cell’s size is assumed to be 1 × 1, then $t_{ij}=1/v_{ij}$.

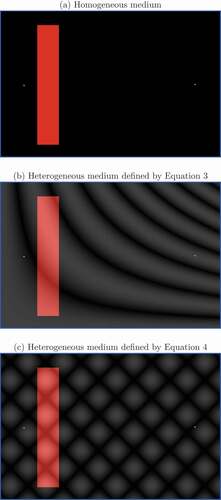
Figure 2 illustrates how an example of evacuation problem in a homogeneous medium (see Figure 2a) can be transformed into two evacuation problems in heterogeneous media (see Figure 2b and 2c). In Figure 2a, a 225 × 150 grid is depicted consisting of the following elements: 746 blue cells representing border obstacles, 2684 red cells representing pedestrians forming a rectangular group, and 2 yellow cells representing exits. The rest of cells are depicted in black and constitute empty cells where pedestrians can move at velocity 1. In Figure 2b and 2c, for each cell $(i,j)$ which is not an obstacle, its $t_{ij}$ values are depicted for two different heterogeneous media such that

Figure 2. Evacuation problems for a rectangular group of pedestrians in three different media

• Cell $(i,j)$ is depicted in black if $t_{ij}=1$, the minimum value in the grid.

• Cell $(i,j)$ is depicted in white if $t_{ij}=t_{ij}^{max}$, the maximum value in the grid.

• The rest of cells are depicted in shades of gray color proportionally to their $t_{ij}$ values in the range $(1,t_{ij}^{max})$.

Specifically, Figure 2b employs

(3) $t_{ij}=1+2\cdot \left|cos\left(\frac{\pi }{180}\cdot \frac{x}{3}\cdot \frac{y}{9}\right)\right|,$(3)

where $x$ and $y$ are the coordinates of cell $(i,j)$’s center, and $x=y=0$ for the bottom-left cell in the grid. Likewise, in the case of Figure 2c:

(4) $t_{ij}=1+2\cdot \left|cos\left(\frac{\pi }{180}\cdot (10x-100)\right)+sin\left(\frac{\pi }{180}\cdot (10y-50)\right)\right|.$(4)

These functions are selected due to two main reasons: (1) They exhibit a high spatial variability for $t_{ij}$, which helps illustrate the importance of the medium heterogeneity in the evacuation process, and (2) Since they have the property that $t_{ij}\in [1,3]$ and $t_{ij}\in [1,5]$ respectively, evacuation times are kept within fair margins.

FMM for Heterogeneous Media

FMM can be extended to be applied to heterogeneous media in a straightforward manner. Since each particular cell $(i,j)\in C$ is assigned a specific arbitrary value $v_{ij}=F_{ij}\ge 1$ representing the velocity of a wavefront when traveling in that cell, such a value can be directly substituted in Equation 2(2) ${\left\{max\left(0,T_{ij}-T_{i-1,j},T_{ij}-T_{i+1,j}\right)\right\}}^2+{\left\{max\left(0,T_{ij}-T_{i,j-1},T_{ij}-T_{i,j+1}\right)\right\}}^2=\frac{1}{F_{ij}^2},$(2) provided that cell $(i,j)$ is empty; otherwise, if cell $(i,j)$ is occupied by a pedestrian and $F_{ij}>1/\gamma$ then $F_{ij}$ is decreased such that $F_{ij}=1/\gamma$ in Equation 2(2) ${\left\{max\left(0,T_{ij}-T_{i-1,j},T_{ij}-T_{i+1,j}\right)\right\}}^2+{\left\{max\left(0,T_{ij}-T_{i,j-1},T_{ij}-T_{i,j+1}\right)\right\}}^2=\frac{1}{F_{ij}^2},$(2) , where $\gamma >1$ 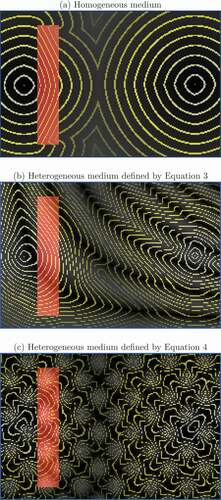is defined in Section 2.1. Figure 3 illustrates the resulting FMM floor fields for the evacuation problems defined in Figure 2. A value of $\gamma =2$ is arbitrarily assigned to occupied cells in Figure 3. Note that this figure illustrates the initial configuration of pedestrians, in which nobody has started moving yet.

Figure 3. FMM floor fields for $\gamma =2$ and the three evacuation problems in Figure 2

FEM for Heterogeneous Media

FEM is extended to heterogeneous media by assigning the variable $t_{ij}$ to each cell $c_{ij}\in C$ (see Section 3). When a pedestrian enters cell $c_{ij}$, $t_{ij}$ is initialized with the user-defined time period that such an individual will remain moving in that cell before leaving to a neighboring cell. As time goes by, $t_{ij}$ is reduced by one at every time step. As long as $t_{ij}>0$, the pedestrian is not allowed to leave cell $c_{ij}$; otherwise, if $t_{ij}\le 0$, the pedestrian moves to an empty neighboring cell $c{{ }^{\mathrm{\prime }}}_{ij}$. In the latter case, cell $c{{ }^{\mathrm{\prime }}}_{ij}$ is initialized with $t{{ }^{\mathrm{\prime }}}_{ij}+t_{ij}$ rather than with only $t{{ }^{\mathrm{\prime }}}_{ij}$, where $t{{ }^{\mathrm{\prime }}}_{ij}$ is defined by the user for $c{{ }^{\mathrm{\prime }}}_{ij}$ and $t_{ij}$ is a negative value at this time step.

Figure 4 contains the pseudocode of the FF${ }_{\mathrm{F}\mathrm{E}\mathrm{M}}$ (Floor Field for FEM) algorithm, which calculates the floor field $\varphi$ used by FEM for a heterogeneous medium at each time step. First, lines 1–8 in Figure 4 initialize the exit cells. Likewise, the rest of non-obstacle cells in the grid are initialized in lines 9–11. Then, an iterative process takes place in lines 12–38. This iterative process corresponds to the propagation of wavefronts across the grid.

Figure 4. Pseudocode for the FF${ }_{\mathrm{F}\mathrm{E}\mathrm{M}}$ algorithm that generates the floor field used by FEM in each time step of the evacuation process taking place in a heterogeneous medium

The following variables and functions are used by FF${ }_{\mathrm{F}\mathrm{E}\mathrm{M}}$:

• c.assignedExit: Variable that contains the exit assigned to a cell $c$. This exit is the origin of the wavefront that first arrived in the cell.

• c.isUpdated?: Variable that stores whether or not the floor field value of a cell $c$ has already been calculated.

• delayOfExit[]: Array indexed by an exit that specifies the number of remaining iterations that the wavefront originated at the given exit will be stopped.

• wavefront[]: Array indexed by an exit that stores the cells that are part of the current wavefront originated at the given exit.

• goOn?: Variable used for the termination condition. The algorithm ends after the current iteration (see line 35 in Figure 4) if no wavefront is delayed and no wavefront has propagated at the current iteration.

• activeCells: Variable that contains those cells in wavefront[] whose assigned exit is not delayed.

• updateExitDelays1: Function that carries out the normal updating of delays for the exits after one iteration (see line 17 in Figure 4). For example, if there are five exits whose delays are stored in the array [0 5 0 4 1], the new delays for the exits will be [0 4 0 3 0]. Therefore, the delays equal to 0 are not changed, while the rest of delays are decremented by 1.

• ${\mathcal{N}}_{\mathbf{F}\mathbf{E}\mathbf{M}}$: Function that assigns the new $t_{ij}$ values to all $c_{ij}\in \mathbf{a}\mathbf{c}\mathbf{t}\mathbf{i}\mathbf{v}\mathbf{e}\mathbf{C}\mathbf{e}\mathbf{l}\mathbf{l}\mathbf{s}$ according to the explanation in the first paragraph of Section 3.2. Next, this function returns the neighboring cells of those cells $c_{ij}\in \mathbf{a}\mathbf{c}\mathbf{t}\mathbf{i}\mathbf{v}\mathbf{e}\mathbf{C}\mathbf{e}\mathbf{l}\mathbf{l}\mathbf{s}$ whose new $t_{ij}$ value becomes negative or equal to zero, and these latter cells are removed from the wavefronts. In this work, we employ the probabilistic neighborhood ${\mathcal{N}}_{\sigma =0.2}$ (Galán 2019), which gives rise to wavefronts similar to circles in an efficient way.

• newCells: Variable that stores the cells generated after activeCells expansion through ${\mathcal{N}}_{\mathbf{F}\mathbf{E}\mathbf{M}}$ that have not been updated yet (see line 15 in Figure 4). Note that each of these cells is assigned an exit in line 21. If the cell belongs to the Moore neighborhoods of wavefront cells with different assigned exits, it is finally assigned the exit of its nearest wavefront cell. (The Euclidean distance ${\delta }_{\mathrm{E}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}}$ from the cell to a neighboring wavefront cell can only be 1 or $\sqrt{2}$.)

• c.isOccupied?: Variable that determines whether or not a cell $c$ is occupied by a pedestrian.

• updateExitDelays2: Function that develops the updating of delays when none of them is equal to zero (see line 29 in Figure 4). For example, if there are five exits whose delays are stored in the array [2 5 6 4 2], the new delays for the exits will be [0 3 4 2 0]. Thus, the delays are decremented by the minimum of them. This operation improves the efficiency of the algorithm, since it makes no sense that all the wavefronts are stopped at the same time.

• updateExitDelays3: Function that carries out the updating of delays when newCells is empty and at least one exit delay is greater than zero (see line 33 in Figure 4). For example, under the mentioned conditions, if there are five exits whose delays are stored in the array [0 0 0 4 2], the new delays for the exits will be [0 0 0 2 0]. Therefore, the delays greater than zero are decremented by the minimum of them, which makes it possible that a wavefront assigned to a new exit is checked for expansion at the next iteration.

In line 15 of algorithm FF${ }_{\mathrm{F}\mathrm{E}\mathrm{M}}$ (see Figure 4), ${\mathcal{N}}_{\mathrm{F}\mathrm{E}\mathrm{M}}$ calculates the neighborhoods of the propagating wavefronts. The most immediate option is to use either the von Neumann neighborhood or the Moore neighborhood; however, these two options tend to produce wavefronts and jams of square shape in homogeneous media, which is not realistic. In order to produce nearly circular wavefronts in the specific case of homogeneous media, a probabilistic neighborhood ${\mathcal{N}}_{\sigma =2}$ (Galán 2019) is employed for wavefront propagation in FF${ }_{\mathrm{F}\mathrm{E}\mathrm{M}}$.

The time complexity of FF${ }_{\mathrm{F}\mathrm{E}\mathrm{M}}$ is $\mathcal{O}(k\cdot |C|)$, where $C$ is the set of CA cells and the constant $k\in [1,{max}_{ij}\{t_{ij}\}]$ depends on the specific medium where the evacuation takes place. For $k\stackrel{>}{\sim \phantom{{ }_x}}1$, this constitutes an improvement of efficiency in comparison with the algorithms calculating floor fields based on quickest paths (see Section 2.1), whose time complexity is $\mathcal{O}(|C|\cdot log|C|)$. The additional $log|C|$ factor is a consequence of applying the Dijkstra algorithm.

Figure 5 contains the resulting FEM floor fields for the evacuation problems defined in Figure 2. In Figure 5, the initial configuration of pedestrians is depicted (no movement has taken place yet). Note that FEM produces in Figure 5 a more equitable distribution of pedestrians among the two exits in comparison to FMM in Figure 3. Specifically, while all the pedestrians would head to the left exit in the case of FMM, some of them would head to the right exit in the case of FEM. As a result, FEM ultimately produces a faster evacuation of the pedestrians. In order for FMM to be comparable to FEM in these evacuation problems, the value of $\gamma$ should be increased.

Figure 5. FEM floor fields for the three evacuation problems in Figure 2

Application Example of FMM and FEM for Heterogeneous Media

Consider a 225 × 150 grid with the distribution of pedestrians, exits, and obstacles illustrated in Figure 6 for $t=0$. There are 584 pedestrians distributed in nine groups. Two exits are located at coordinates $(20,75)$ and $(205,77)$ respectively, where $(0,0)$ corresponds to the coordinates of the bottom left cell. While the border of the grid is occupied by obstacles, the black cells correspond to the heterogeneous medium defined by Equation 3(3) $t_{ij}=1+2\cdot \left|cos\left(\frac{\pi }{180}\cdot \frac{x}{3}\cdot \frac{y}{9}\right)\right|,$(3) .

Figure 6. Example of evacuation simulation in a heterogeneous medium for 584 pedestrians, distributed in 9groups, through two exits (top figure). FMM (with fine-tuned cost $\gamma =60$ for each occupied cell) and FEM are compared for time steps $t\in \{10,50,250,400\}$

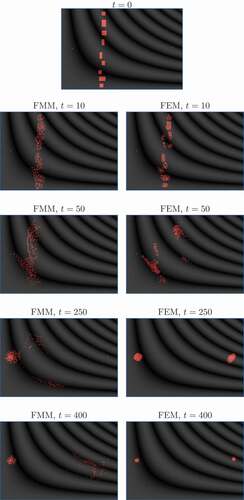
In Figure 6, the extended FMM and FEM methods explained in Section 3 are compared for time steps $t\in \{10,50,250,400\}$. Note that FMM is sensitive to parameter $\gamma$ (the cost for each occupied cell), and establishing a satisfactory $\gamma$ value is problem-dependent and time-consuming for the user. This is an important advantage for FEM, which requires no parameter fine-tuning. In the problem presented in Figure 6, $\gamma =60$ constitutes an appropriate value for FMM.

It can be observed in Figure 6 that all the pedestrians head to the left exit at $t=10$ in the case of FMM. This is due to the fact that, at the first 10 time steps, the quickest path for each pedestrian ends at the left exit. At $t=50$, the pedestrians are near the left exit, where a congestion is starting to form. At $t=250$, the jam around the left exit provokes that some peripheral pedestrians head to the right exit, which is now more promising in terms of evacuation time. Finally, at $t=400$, the right exit is at last about to receive pedestrians, and 276 pedestrians remain to be evacuated.

In the case of FEM, Figure 6 shows that a subset of the pedestrians head to the right exit at $t=10$. This is because, even at the first 10 time steps, both exits have been assigned pedestrians. At $t=50$, some pedestrians are on their way to the right exit, much earlier than under FMM. At $t=250$, a jam around the right exit appears, again much earlier than under FMM. Finally, at $t=400$, only 90 pedestrians remain to be evacuated (276 under FMM at this time step) and are equally distributed between both exits.

In summary, for the evacuation problem illustrated in Figure 6, FEM develops a more effective evacuation process compared to FMM with optimized $\gamma$. At $t=400$, 186 out of the 584 initial pedestrians have been evacuated under FEM, but remain on the grid under FMM. In the next section, a comparative evaluation is carried out of the extended FMM and FEM methods. Evacuation effectiveness and simulation runtime are analyzed over a set of evacuation problems in heterogeneous media.

Experimental Evaluation

This section comparatively evaluates the extended versions of FMM and FEM to heterogeneous media. The two evaluated algorithms are implemented within NetLogo (Wilensky 1999), an agent-based modeling and programming environment well suited for modeling and inspecting complex systems developing over time. The experiments are carried out on an Intel Core i5 processor (2.67 GHz) with 8 Gb of memory.

Ten different evacuation problems are used for the comparative evaluation and combined with the two heterogeneous media defined in Section 3: (1) the problem illustrated in Figure 3 and in Figure 5, (2) the problem depicted in Figure 6, (3) a problem consisting of four groups of pedestrians around a central exit and eight lateral exits, (4) three problems widely used in the literature for evacuations in a lecture hall, a corner, and a U-turn (Burstedde et al. 2002; Kretz et al. 2011), (5) two problems with initial randomly distributed pedestrians, and (6) two additional problems with a high presence of obstacles near the exits. Figure 7 illustrates the homogeneous versions of these 10 evacuation problems, and Table 1 shows their main structural characteristics. These problems cover a wide range of crowd motion features as classified in (Chen et al. 2018; Duives, Daamen, and Hoogendoorn 2016, 2013; Helbing 2001; Helbing et al. 2005; Shi et al. 2018; Shiwakoti, Shi, and Ye 2019), with the peculiarity that the present work deals with evacuation processes. For example, some of the motion cases covered in this work are: entering, exiting, rounding a corner, and straight flow.

Table 1. Structural characteristics of the 10 evacuation problems illustrated in Figure 7

Evacuation problem	Grid	Pedestrians	Exits	Obstacles
1group	225 × 150	2684	2	746
9groups	225 × 150	584	2	746
4groups	225 × 150	1205	9	746
lecture-hall	225 × 150	8760	33	9473
corner	225 × 150	8436	109	9182
U-turn	225 × 150	7210	77	849
random500	225 × 150	500	4	746
random500bottlenecks	225 × 150	500	4	1210
obstacles1	225 × 150	510	4	812
obstacles2	225 × 150	621	4	3188

Figure 7. The 10 homogeneous versions of the evacuation problems used in the experimental evaluation

The best values for parameter $\gamma$ in FMM are selected via manual fine-tuning. This constitutes a costly and problem-dependent task for the user and is an important disadvantage of this algorithm with respect to FEM, which requires no parameter fine-tuning. The selected $\gamma$ values (see Table 2) are those leading to the best results regarding the average number of time steps necessary to evacuate a pedestrian in a simulation, which is called “mean evacuation time steps” later in Section 4.1.

Table 2. Manually fine-tuned best $\gamma$ values for each evacuation problem in Figure 7 under FMM

Evacuation problem	$\gamma \left(\mathrm{F}\mathrm{M}\mathrm{M}\right)$
1group_Eq3	18
1group_Eq4	17
9groups_Eq3	60
9groups_Eq4	60
4groups_Eq3	25
4groups_Eq4	33
lecture-hall_Eq3	4
lecture-hall_Eq4	5
corner_Eq3	5
corner_Eq4	4
U-turn_Eq3	7
U-turn_Eq4	8
random500_Eq3	45
random500_Eq4	50
random500bottlenecks_Eq3	66
random500bottlenecks_Eq4	15
obstacles1_Eq3	4
obstacles1_Eq4	4
obstacles2_Eq3	6
obstacles2_Eq4	3

There are two main aspects to be considered when the performance of an evacuation method is evaluated: on the one hand, the effectiveness of the evacuation process and, on the other hand, the efficiency of the simulation. These two aspects are explored in the following two sections, in which every single considered measure is averaged over 10 evacuation simulations.

Evacuation Effectiveness

In this section, the mean evacuation time steps (mets) is the measure used to evaluate evacuation effectiveness. It is defined as the average number of time steps that it takes a pedestrian to exit the grid of cells in an evacuation simulation. In each time step, the floor field is calculated for the whole grid and, subsequently, each pedestrian moves to one of the empty neighboring cells according to the floor field values calculated for that time step. Table 3 contains the mets obtained for FMM and FEM when applied to the evacuation problems defined in Table 1. In order to clearly show the degree of improvement obtained by the best of the two methods for a particular problem, Table 3 includes $\mathrm{\Delta }(mets(\mathrm{F}\mathrm{M}\mathrm{M}),mets(\mathrm{F}\mathrm{E}\mathrm{M}))$, where $\mathrm{\Delta }(a,b)$ is defined as follows for two positive real numbers $a$ and $b$:

$\mathrm{\Delta }(a,b)=\frac{\left|a-b\right|}{max(a,b)}\cdot 100\mathrm{\%}.$

Table 3. Mean evacuation time steps obtained for the evaluated methods over the evacuation problems defined in Table 1

Evacuation problem	mets(FMM)	mets(FEM)	$\mathrm{\Delta }(mets(\mathrm{F}\mathrm{M}\mathrm{M}),mets(\mathrm{F}\mathrm{E}\mathrm{M}))$
1group_Eq3	854.13	862.06	0.92%
1group_Eq4	844.56	855.40	1.27%
9groups_Eq3	353.50	285.08	19.35%
9groups_Eq4	337.73	275.90	18.31%
4groups_Eq3	236.37	202.78	14.21%
4groups_Eq4	194.33	175.46	9.71%
lecture-hall_Eq3	409.63	422.01	2.93%
lecture-hall_Eq4	440.54	471.28	6.52%
corner_Eq3	480.37	487.01	1.36%
corner_Eq4	457.90	492.89	7.10%
U-turn_Eq3	661.98	653.39	1.30%
U-turn_Eq4	673.93	725.51	7.11%
random500_Eq3	116.25	105.46	9.28%
random500_Eq4	100.89	95.37	5.47%
random500bottlenecks_Eq3	156.50	141.38	9.66%
random500bottlenecks_Eq4	152.98	145.87	4.65%
obstacles1_Eq3	181.63	190.50	4.66%
obstacles1_Eq4	183.79	192.36	4.45%
obstacles2_Eq3	515.3	475.54	7.72%
obstacles2_Eq4	487.86	455.07	6.72%

The best result in each row appears highlighted in bold.

As a complementary measure, the global evacuation time steps (gets) are included in Table 4. This measure represents the number of time steps that it takes the grid to become empty in a simulation.

Table 4. Global evacuation time steps obtained for the evaluated methods over the evacuation problems defined in Table 1

Evacuation problem	gets(FMM)	gets(FEM)	$\mathrm{\Delta }(gets(\mathrm{F}\mathrm{M}\mathrm{M}),gets(\mathrm{F}\mathrm{E}\mathrm{M}))$
1group_Eq3	1643	1680	2.20%
1group_Eq4	1628	1670	2.51%
9groups_Eq3	576	459	20.31%
9groups_Eq4	588	450	23.47%
4groups_Eq3	375	316	15.73%
4groups_Eq4	302	296	1.99%
lecture-hall_Eq3	691	865	20.11%
lecture-hall_Eq4	753	886	15.01%
corner_Eq3	718	824	12.86%
corner_Eq4	745	850	12.35%
U-turn_Eq3	985	991	0.60%
U-turn_Eq4	988	1236	20.06%
random500_Eq3	281	232	17.44%
random500_Eq4	217	202	6.91%
random500bottlenecks_Eq3	364	265	27.20%
random500bottlenecks_Eq4	302	275	8.94%
obstacles1_Eq3	260	269	3.35%
obstacles1_Eq4	263	290	9.31%
obstacles2_Eq3	692	641	7.37%
obstacles2_Eq4	667	578	13.34%

The best result in each row appears highlighted in bold.

The example described in Section 3.3 shows that, for the 9groups evacuation problem, FEM develops a more effective evacuation process compared to FMM. This preliminary result is now confirmed by the measures reported in Tables 3 and 4 for the 9groups problem.

The following conclusions can be derived from the results shown in Tables 3 and 4:

1. Both methods win in a similar number of evacuation problems. In Table 3, whereas FMM wins in 9 cases, FEM wins in 11. Likewise, in Table 4 the two methods win in 10 cases. Therefore, deciding which method is better regarding evacuation effectiveness seems to be problem dependent.

2. The performance difference is greater when FEM wins: (1) In Table 3, an average $\mathrm{\Delta }=4.04\mathrm{\%}$ is obtained when FMM wins compared to an average $\mathrm{\Delta }=9.67\mathrm{\%}$ when FEM wins, and (2) In Table 4, an average $\mathrm{\Delta }=9.84\mathrm{\%}$ results when FMM wins compared to an average $\mathrm{\Delta }=14.27\mathrm{\%}$ when FEM wins. Consequently, FEM clearly exhibits a more robust behavior.

3. In this section, we obtain the optimized results for FMM after a careful and costly fine-tuning of $\gamma$, which is not necessary in the case of FEM.

Simulation Efficiency

This section employs the simulation runtime to evaluate the efficiency of the evaluated evacuation methods. Table 5 includes the running times obtained for FMM and FEM when applied to the evacuation problems defined in Table 1.

Table 5. Runtimes in seconds obtained for the evaluated methods over the evacuation problems defined in Table 1

Evacuation problem	runtime(FMM)	runtime(FEM)	$\mathrm{\Delta }(runtime(\mathrm{F}\mathrm{M}\mathrm{M}),runtime(\mathrm{F}\mathrm{E}\mathrm{M}))$
1group_Eq3	1870.73	457.18	75.56%
1group_Eq4	1982.17	485.11	75.53%
9groups_Eq3	640.11	129.96	79.70%
9groups_Eq4	688.19	135.83	80.26%
4groups_Eq3	442.49	77.08	82.58%
4groups_Eq4	371.05	78.30	78.90%
lecture-hall_Eq3	534.29	220.26	58.77%
lecture-hall_Eq4	609.96	235.42	61.40%
corner_Eq3	578.81	273.02	52.83%
corner_Eq4	602.89	305.27	49.37%
U-turn_Eq3	1021.37	386.74	62.13%
U-turn_Eq4	1101.34	483.21	56.12%
random500_Eq3	331.82	63.84	80.76%
random500_Eq4	266.87	60.22	77.43%
random500bottlenecks_Eq3	410.92	74.63	81.84%
random500bottlenecks_Eq4	343.86	83.45	75.73%
obstacles1_Eq3	296.16	71.14	86.11%
obstacles1_Eq4	322.14	82.86	74.28%
obstacles2_Eq3	707.92	163.84	76.86%
obstacles2_Eq4	705.11	154.88	78.03%

The best result in each row appears highlighted in bold.

Additionally, it is interesting to calculate the runtime (see Table 5) divided by the evacuation time steps (see Table 4). Table 6 shows these results for each problem simulation, which give an idea of the efficiency of the methods to carry out the tasks included in one time step.

Table 6. Running times in Table 5 divided by the global evacuation time steps in Table 4

Evacuation problem	$\frac{runtime}{gets}$(FMM)	$\frac{runtime}{gets}$(FEM)	$\mathrm{\Delta }\left(\frac{runtime}{gets}(\mathrm{F}\mathrm{M}\mathrm{M}),\frac{runtime}{gets}(\mathrm{F}\mathrm{E}\mathrm{M})\right)$
1group_Eq3	1.14	0.27	76.31%
1group_Eq4	1.22	0.29	76.23%
9groups_Eq3	1.11	0.28	74.77%
9groups_Eq4	1.17	0.30	74.36%
4groups_Eq3	1.18	0.24	79.66%
4groups_Eq4	1.23	0.26	78.86%
lecture-hall_Eq3	0.77	0.25	67.53%
lecture-hall_Eq4	0.81	0.27	66.67%
corner_Eq3	0.81	0.33	59.26%
corner_Eq4	0.81	0.36	55.56%
U-turn_Eq3	1.04	0.39	62.50%
U-turn_Eq4	1.11	0.39	64.86%
random500_Eq3	1.18	0.27	77.12%
random500_Eq4	1.23	0.30	75.61%
random500bottlenecks_Eq3	1.13	0.28	75.22%
random500bottlenecks_Eq4	1.14	0.30	73.68%
obstacles1_Eq3	1.14	0.26	77.19%
obstacles1_Eq4	1.22	0.29	76.23%
obstacles2_Eq3	1.02	0.26	74.51%
obstacles2_Eq4	1.06	0.27	74.53%

The best result in each row appears highlighted in bold.

Table 5 shows that, for the global evacuation process, FEM is the most efficient method. Exclusively in terms of one time step, these same conclusions can be obtained from Table 6 as well.

Conclusion and Future Research

Evacuation problems are usually tackled by considering homogeneous media where pedestrians move freely in the presence of exits and obstacles. From a more general viewpoint, heterogeneous media are characterized by the fact that the velocity of pedestrians depends on their location. The specific structure of the heterogeneous medium has a great influence on how pedestrians can be evacuated in a more effective way, even if both exits and obstacles remain unchanged.

FMM and FEM are two competitive methods for evacuation problems in homogeneous media. The present paper extends FMM and FEM to heterogeneous media and evaluates them over a set of simulated scenarios. Even though deciding which method outperforms the other is problem dependent, FEM has a more robust behavior over the whole set of simulated heterogeneous scenarios. Besides, contrarily to FMM, FEM has the important advantage of not requiring any kind of fine-tuning previously to its execution.

The present work opens up the following research directions:

• It would be interesting to investigate whether the extended versions of FMM and FEM to heterogeneous media can be adapted to the context of the Social Force Model for pedestrian dynamics.

• The extended versions of FMM and FEM can be easily applied to dynamic environments where exits, obstacles, and the medium change over time. This could produce important applications with a high impact on society.

• The viability and benefits of the static version of FEM (Galán 2019) could be investigated for evacuation problems in heterogeneous media. Static FEM uses the floor field created in the initial time step as the floor field for the whole evacuation process. This static version would be much faster than FEM, although it would be subject to some inaccuracies.

• In order to perform a thorough evaluation of the new versions of FMM and FEM, their simulation results should be compared with existing empirical data (Shi et al. 2018; Wijermans et al. 2016) and extended to other different media (see Equations 3(3) $t_{ij}=1+2\cdot \left|cos\left(\frac{\pi }{180}\cdot \frac{x}{3}\cdot \frac{y}{9}\right)\right|,$(3) and 4(4) $t_{ij}=1+2\cdot \left|cos\left(\frac{\pi }{180}\cdot (10x-100)\right)+sin\left(\frac{\pi }{180}\cdot (10y-50)\right)\right|.$(4) ) and evacuation problems (see Figure 7) from those used in this work.

• Regarding the practical application of the extended versions of FMM and FEM, it remains to study how these new methods can be achieved in real-life evacuation scenarios (Wijermans et al. 2016).

Notes

1. Specifically (see for example (Schadschneider 2002)), it is usual to consider in the literature that every cell is 40 cm × 40 cm (typical space occupied by a pedestrian in a dense crowd) and a single pedestrian (not interacting with others) moves at a velocity of one cell per time step. Since the empirical average velocity of a pedestrian is about 1.3 m/s, this gives an estimated time step of 0.3 s.

2. In this work, the Moore neighborhood is considered for the movement of pedestrians.