The Vehicle Routing Problem with Fuzzy Payloads considering Fuel Consumption

ABSTRACT

This paper considers the Vehicle Routing Problem (VRP) with fuzzy payloads with the aim to minimize two criteria: the travel distance and the fuel consumption. VRP with fuzzy payloads is an NP-hard problem, in which a fleet of vehicles with finite capacity leaves from a central depot empty of goods and has to serve a set of geographically dispersed customers associated with fuzzy payloads. Thus, an optimization approach based on a bi-objective Genetic Algorithm is developed that is integrated with fuzziness. This problem differentiates from the classic VRP, since it also considers the fuel consumption to reduce the energy consumption. The efficiency of the developed method is investigated and discussed through a set of test instances. The experimental results highlight the impact of both criteria on the resulted optimum solution and prove that increasing the uncertainty in customers’ collection quantities results in more costly solutions.

Introduction

The Vehicle Routing Problem (VRP) is a combinatorial optimization problem introduced by Dantzig and Ramser (1959) and has many practical applications, especially in transportation and distribution logistics. VRP involves the problem of determining the optimal routes of minimum cost for a fleet of vehicles starting and ending to a central depot that is assigned to serve a set of geographically dispersed customers of minimum total cost satisfying certain constraints. The cost is usually expressed as a function of the total distance traveled.

Apparently, the operating cost of a vehicle traveling along a route depends on several factors. The minimization of energy consumption is a great challenge for logistics and thus, the minimization of fuel consumption offers a great potential to reduce the cost as well as environmental pollution that poses major threats to human health. Fuel consumption is a factor that is strongly related to the travel distance and mainly depends on distance and load.

The Energy Minimizing Vehicle Routing Problem (EMVRP) was firstly introduced in (Kara, Kara, and Yetis 2007, 2008) as an extension of the classical VRP, where the optimization objective is the minimization of the energy consumption along the tour through a distance-weighted load function instead of minimizing the traditional total distance. In other words, fuel consumption per unit distance is proportional to the total weight of the vehicle.

In (Xiao et al. 2012), the Fuel Consumption Rate (FCR) is added to the Capacitated Vehicle Routing Problem (CVRP). FCR is taken as a load dependent function, where FCR is linearly associated with the vehicle’s load. The formulation of the FCR is based on statistical data, proposed by the Ministry of Land, Infrastructure, Transport and Tourism of Japan. In this context, a mathematical optimization model is proposed and a Simulated Annealing algorithm with a hybrid exchange rule is developed.

Gaur, Mudgal, and Singh (2013) study the cumulative Vehicle Routing Problem that is a generalization of the Capacitated Vehicle Routing Problem with objective of minimizing the fuel consumption. They examined four versions of the problem and gave constant factor approximation algorithms. For all examined versions, they considered that the vehicles have infinite capacity and an arbitrary number of depot offloads are allowed.

In (Fukasawa, He, and Song 2016), a variant of the Capacitated Vehicle Routing Problem is studied in the context of energy minimization. The authors define cost of traversing an arc as the product of the arc length and the total vehicle weight when it traverses that arc. Two mixed-integer linear programming formulations are presented: an arc-load formulation and a set partitioning. A branch-and-cut algorithm is proposed for the arc-load formulation and a branch-cut-and-price algorithm is proposed for the set partitioning formulation strengthened by additional constraints.

Wang et al. (2019) solve an extension of the VRP with the aim to minimize the fuel consumption considering fuzzy travel times between the customers due to the traffic load condition. They transform the fuzzy chance constrained programming model into an equivalent deterministic model and then they revise the original hybrid intelligent algorithm by replacing the embedded fuzzy simulation with analytical function calculation in order to improve the effectiveness of the algorithm.

Wang, Liu, and Chu (2020) study the Energy Minimization Traveling Salesman Problem with the aim to find the minimum energy cost tour. The objective is to minimize the sum of the product of load (including curb weight of the vehicle) and distance for each arc. The basic model is based on one commodity flow model presented in (Fukasawa, He, and Song 2016). An approximation algorithm has been developed and a fast lower bound based on the well known 1-tree bound has been proposed.

There exist a wide literature focusing on the deterministic VRP and its variants. Recently, the research community has focused on the variants of VRP considering stochasticity and energy costs (Altabeeb, Mohsen, and Ghallab 2019; Asgharia and Mirzapour Al-e-hashem 2021; Barma, Dutta, and Mukherjee 2019; Basso et al. 2019; Elshaer and Awad 2020; Huang et al. 2019; Jianyu et al. 2019; Keskin, Laporte, and Çatay 2019; Li, Soleimani, and Zohal 2019; Marković et al. 2020; Moghdani et al. 2021; Oyola, Arntzen, and Woodruff 2017; Pelletier, Jabali, and Laporte 2019; Queiroga, Sadykov, and Uchoa 2021; Wang et al. 2020; Xidias and Azariadis 2019; Zacharia and Xidias 2020). In most cases, it is difficult to describe the parameters of the VRP as deterministic, because real-world systems are usually afflicted with uncertainty resulting in uncertain, subjective, ambiguous and vague data. Fuzzy concepts express this uncertainty and thus the fuzzy models are closer to realistic situations that take place in real-world systems. The VRP with fuzzy parameters differs from the deterministic VRP in several fundamental aspects. Thus, the solution of VRP considering fuzzy parameters becomes even more intricate.

In the relevant literature (Bruglieri et al. 2019; Majumdar and Bhunia 2011; Pamucar 2020; Pamucar and Janković 2020), imprecision in data in realistic environments is treated using different approaches for the variables: stochastic variables that follow a probability distribution, interval arithmetic, gray numbers and rough numbers. In this work, a fuzzy variable approach has been chosen due to the fact that in recent years fuzzy concepts have become a powerful tool for decision-makers to deal with impreciseness embedded in real-world application problems. It should also be noticed that mixing fuzzy logic with genetic algorithms is a promising resolution approach for complex routing and scheduling problems.

Last years, fuzziness in the context of a VRP version has attracted researchers’ interest. There are some works that consider fuzziness in some parameter: fuzzy travel times (Zarandi, Hemmati, and Davari 2011; Zheng and Liu 2006), fuzzy time windows (Ghannadpour et al. 2014), fuzzy demands (Erbao and Mingyong 2009; Ghaffari-Nasab, Ahari, and Ghazanfari 2013; Kuo and Zulvia 2017). The proposed fuzzy models are based on the credibility theory introduced in (Liu 2004) in order to rank fuzzy numbers. The credibility theory is a modification to possibility theory based on the concepts of possibility, necessity and credibility of a fuzzy event.

The deterministic VRP and its variants are regarded as NP-hard optimization problems and therefore, they are computationally intractable. Due to the combinatorial explosion, exact algorithms can hardly be used to yield exact optimal solutions. Thus, researchers resort to metaheuristics, Evolutionary Algorithms, Tabu Search, Simulating Annealing etc. Following this trend, the optimization approach presented in this work is based on a Genetic Algorithm that belongs to robust metaheuristics and has been proved a very promising tool for solving a wide variety of real-world combinatorial optimization problems. Our choice of using a GA to solve the problem is based on the success of GAs to solve various variants of the VRP. Several authors have also highlighted the benefits of using GAs to solve VRP (López-Castro and Montoya-Torres).

This paper considers the significantly challenging aspect of energy consumption in the context of the Vehicle Routing Problem. This study considers concurrently two optimization criteria: the travel distance and the fuel consumption. Fuel consumption is inextricably linked to the total vehicle’s weight while serving the customers. In order to be close to real-life situations, the customers’ quantities are not deterministic; instead, they are considered as fuzzy and are represented by triangular fuzzy numbers. Fuzzy consideration is based on the concept of the total integral value. A bi-objective Genetic Algorithm (GA) is developed that incorporates the fuzzy concepts considering the collection quantities associated with the customers. The experimental tests examine the solution efficiency and effectiveness of the GA and investigate the impact of each criterion as well as the impact of the uncertainty of the loads on the final solution.

The literature review reveals that no research has been conducted on the solution of VRP considering two optimization criteria and incorporating fuzziness in the collection quantities. In this regard, this work is an extension to the classical CVRP with an additional optimization criterion (energy consumption) and fuzziness in the collection quantities in an attempt to show the potential of the proposed model to be integrated in a real-life environment. To this end, the main innovations and contribution of this work are summarized in the following:

• The traditional vehicle routing problem focuses on the travel distance. In this work, it is extended to take into consideration the energy consumption in terms of fuel consumption, which is a key issue in transportation and distribution logistics. Two competitive objectives are optimized with the aim to find the best compromise and reach a trade-off.

• Unlike the classic VRP, payloads are considered as fuzzy instead of fixed deterministic in order to reflect the uncertainty embedded in real-world situations. The fuzzy concepts based on the total integral value are incorporated in the optimization solution method. The research studies the effect of the uncertainty in customers’ collection quantities on the optimum route.

• The problem at hand is an NP-hard optimization problem that becomes even more complex due to the integration of fuzziness as well as the concurrent optimization of two objectives. A heuristic approach for the solution of the fuzzy bi-objective VRP is developed to handle the NP-hard nature of the problem.

The rest of the paper is organized as follows. In Section 2, the problem is formulated, the fuzzy concepts are presented and the model formulation is delineated. Section 3 analyses and discusses the main characteristics of the proposed bi-objective Genetic Algorithm. In Section 4, computational analysis is conducted and experimental instances are employed to test the performance of the proposed approach. Finally, Section 5 presents the conclusions and directions for future work.

Problem Formulation

Problem Statement

Consider a fleet of m vehicles with a maximum capacity located at a depot in a graph G(V, E), where $V=\left\{0,1,2,\dots ,n\right\}$ is the vertex set and E is the edge set. Vertex 0 corresponds to the depot and n is the number of vertices (customers) associated with uncertain collection quantities. All vehicles start their tours from the same depot and must return to the depot after serving all customers. The goal is to devise a travel schedule for the vehicle so that all the quantities are collected. Depending on the fuzzy collection quantity of the next customer, it should be decided whether the vehicle will return to the depot or whether it will continue to the next customer. The conditions to be satisfied are the following:

• Each customer is served exactly by one vehicle.

• Each route starts and ends at the depot.

• For each collection tour, the payload cumulates as much as preceding customer’s collection quantities.

• The payload on any edge of each tour doesn’t exceed the available capacity of the vehicles.

Under these conditions, the problem can be stated as:

The problem concerns a number of Autonomous Guided Vehicles (AGVs) starting from a depot to serve a number of customers with fuzzy collection quantities. The aim is to determine the number of vehicles starting and ending at the depot so that all customers are served exactly once. The objectives to be minimized are the total travel distance of the vehicles as well as the fuel consumption regarding that the capacity of each vehicle is finite.

Fuzzy Numbers

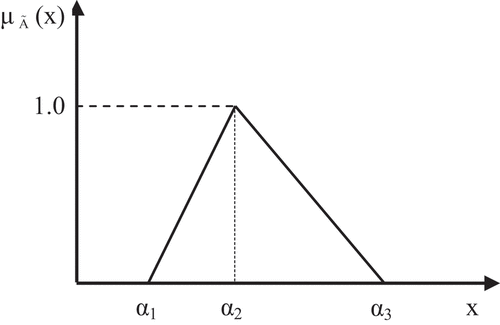
The concept of fuzzy set was firstly introduced by Zadeh (1965). The use of fuzzy numbers to represent the uncertainty in payloads is very plausible and more realistic. In this study, the fuzziness of data is represented by Triangular Fuzzy Numbers (TFNs). A TFN $\tilde{A}$ (see Figure 1) is denoted as a triplet $\left(a_1,a_2,a_3\right)$, where is the most plausible value, $a_1$ is the most optimistic value (less than $a_2$) and is the most pessimistic value (greater than $a_2$). In other words, the actual demand may be equal to $a_2$ (most plausible value), smaller (up to the optimistic value $a_1$) or greater (up to pessimistic value) than $a_2$. Thus, the value of α₂ corresponds to a grade of membership of 1. In practice, a dispatcher or analyst studying the problem can subjectively estimate the boundaries (α₁, α₃) of the variable data as well as the most plausible value (α₂) based on experience and/or intuition.

Figure 1. A typical triangular fuzzy number A.

Since collection quantities are modeled as triangular fuzzy numbers, fuzzy operations are needed for the calculations. In particular, the sum of the TFNs $\tilde{A}\left({\alpha }_1,{\alpha }_2,{\alpha }_3\right)$ and $\tilde{B}\left({\beta }_1,{\beta }_2,{\beta }_3\right)$ is calculated as follows:

(1) $\tilde{A}+\tilde{B}=\left({\alpha }_1+{\beta }_1,{\alpha }_2+{\beta }_2,{\alpha }_3+{\beta }_3\right)$(1)

To compare fuzzy numbers, a method for ranking fuzzy numbers is necessary. In this paper, a flexible method based on the integral value concept has been developed in (Liou and Wang 1992). According to this method, the total integral value for a TFN $\tilde{A}=\left(a_1,a_2,a_3\right)$ is a convex combination of the left and right integral values through an index of optimism $\lambda \in \left[0,1\right]$. The left integral is used to reflect the optimistic viewpoint and the right integral is used to reflect the pessimistic viewpoint of the manager. The total integral value is

(2) $E^{\lambda }\left(\tilde{A}\right)=\frac{1}{2}\left(\lambda a_3+a_2+\left(1-\lambda \right)a_1\right)$(2)

and is used as the ranking function. Therefore, for any two fuzzy numbers $\tilde{\mathrm{A}}$ and $\tilde{\mathrm{B}}$, if $E^{\lambda }\left(\tilde{\mathrm{A}}\right)<E^{\lambda }\left(\tilde{\mathrm{B}}\right)$ then $\tilde{\mathrm{A}}<\tilde{\mathrm{B}}$, if then $\tilde{\mathrm{A}}=\tilde{\mathrm{B}}$ and if $E^{\lambda }\left(\tilde{\mathrm{A}}\right)>E^{\lambda }\left(\tilde{\mathrm{B}}\right)$ then $\mathrm{A}>\mathrm{B}$. The index of $\lambda$ represents the degree of optimism of a decision maker. A larger $\lambda$ indicates a higher degree of optimism and a smaller $\lambda$ indicates a pessimistic decision maker’s viewpoint. For a moderate decision maker, $\lambda$ is equal to $0.5$.

Model Description

In this paper, we consider the VRP considering two optimization criteria: the travel distance and fuel consumption. Based on the model presented in (Gaur, Mudgal, and Singh 2013), the energy consumption is proportional to the friction force of the vehicle on the road and the travel distance. Since the payload of a vehicle affects the friction force, the energy consumption is strongly affected by the payload and the travel distance. As a result, the payload is dynamic and depends on the sequence with which the vehicle visits the customers.

Assume that the vehicles are initially empty of goods when they depart from the depot. Each vehicle should collect the fuzzy quantity ${\tilde{q}}_i$ from each customer before it returns to the depot. For the sake of simplicity, all vehicles are identical, i.e. the maximum available capacity $Q_0$ is the same for all vehicles. The available fuzzy capacity of each vehicle after serving $k$ customers will be:

(3) ${\tilde{Q}}_k=Q_0-\sum _{i=1}^k{\tilde{q}}_i$(3)

If the available fuzzy capacity is greater than the fuzzy collection quantity at the next node, then the vehicle is sent to the next node; otherwise, the vehicle should return to the depot. In other words, the capacity constraint imposes that the fuzzy collection quantity corresponding to each customer should not exceed the available fuzzy capacity of the vehicle.

(4) ${\tilde{q}}_{k+1}\le {\tilde{Q}}_k$(4)

Εq.(4) is modeled as based on Eq.(2)(2) $E^{\lambda }\left(\tilde{A}\right)=\frac{1}{2}\left(\lambda a_3+a_2+\left(1-\lambda \right)a_1\right)$(2) .

Since ${\tilde{q}}_{k+1}$ and ${\tilde{Q}}_k$ are triangular fuzzy numbers in the form of ${\tilde{q}}_{k+1}=\left(q_{k+1,1},q_{k+1,2},q_{k+1,3}\right)$ and ${\tilde{Q}}_k=\left(Q_{k,1},Q_{k,2},Q_{k,3}\right)$, Εq.(4) is transformed to

(5) $E^{\lambda }\left({\tilde{q}}_{k+1}\right)\le E^{\lambda }\left(Q_k\right)$(5)

(6) $\lambda q_{k+1,3}+q_{k+1,2}+\left(1-\lambda \right)q_{k+1,1}\le \lambda Q_{k,3}+Q_{k,2}+\left(1-\lambda \right)Q_{k,1}$(6)

The capacity constraint is checked for each customer to establish a decision about sending the vehicle to the next customer or sending it back to the depot. If the capacity constraint is satisfied, the vehicle should be sent to the next customer. If the capacity constraint is violated, the vehicle returns to the depot and the route ends. Another vehicle is sent from the depot to the next customer starting a new route and this process is repeated until all customers are served.

The first optimization criterion is the minimization of the total travel distance $T{D}_{total}$ considering all vehicles and is computed as:

(7)

and $T{D}_i$ is given by:

(8) $T{D}_i=d_{01}^i+\sum _{j=1}^{k-1}\left(d_{j,j+1}^i\right)+d_{10}^i$(8)

where $d_{01}^i$ is the distance from depot to the first customer of the route i, $d_{j,j+1}^i$ is the distance from customer j to customer j + 1, $d_{10}^i$ is the distance from the first customer of the route $i$ to the depot and $r$ is the total number of routes resulting from the capacity constraint.

The second optimization criterion is the minimization of the fuel consumption for all vehicles according to the following formula based on (Gaur, Mudgal, and Singh 2013):

(9) $F{C}_{total}=\mathrm{a}\sum _{i=1}^{r}T{D}_i+b\sum _{j=1}^n{q}_j{D}_j$(9)

where ${\mathrm{D}}_{\mathrm{j}}$ is the distance traveled by a vehicle between picking up the quantity from j-customer and dropping it at the depot according to the travel route. The constants are defined as

(10) $\mathrm{a}=\mu W_0$(10)

and

(11) $b=\mu$(11)

where $W_0$ is the weight of the empty vehicle and μ is the coefficient of friction.

The fuel consumption expressed by Εq.(7) consists of two parts. The first part concerns the fuel consumption due to the weight of the empty vehicle and the second part concerns the fuel consumption due to the weight of the quantities collected along the tour.

It should be noted that the computation of fuel consumption is different for the cases of collection and delivery. For the collection case (i.e. the case discussed in this work), the payload is increased as the vehicle visits the customers resulting in increased fuel consumption rate.

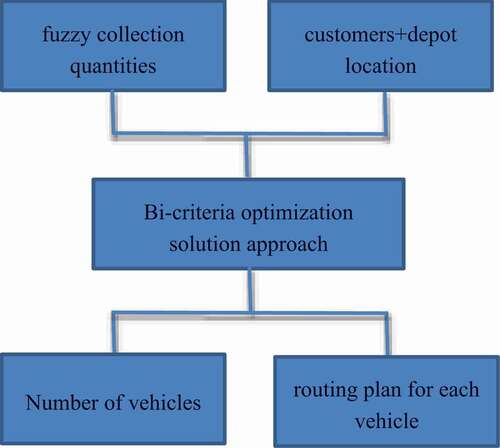
In Figure 2, a schematic overview of the developed model is presented including the general mechanism and its main stages. Given the fuzzy collection quantity for each customer as well as the location for the customers and the depot, the optimization solution method is applied to produce the number of necessary vehicles as well as the routes for each one vehicle starting and ending at the depot. In the following Section, the proposed optimization solution approach is presented in detail.

Figure 2. A schematic overview of the developed model.

The Proposed Bi-objective Genetic Algorithm

The vehicle routing problem is a very challenging NP-hard problem that can hardly be solved using traditional methods. Thus, researchers often resort to intelligent algorithms, such as Genetic Algorithms (Goldberg 1989). Genetic Algorithms are adaptive search techniques based on the principles and mechanisms of natural selection and the ‘survival of the fittest.’ GAs are a very promising tool for solving a wide variety of real-world combinatorial optimization problems. They are well suited to large and complex combinatorial optimization problems and are proved to be robust to local optima. In this study, a GA is developed integrated with fuzzy considerations based on the total integral value concept, and its main characteristics described analytically in the following:

Solution representation: Each solution is represented as an n-dimensional vector, which is a permutation of integer numbers. Each integer number represents a customer and the sequence of the integer numbers represents the order with which the customers will be served. A possible chromosome is in the form of

$10825641379$

representing a possible path for the vehicle starting and ending to the depot. However, the final tours (and therefore, the total number of vehicles) are defined by the capacity constraint.

The evaluation mechanism: The fitness function expresses the possibility that the chromosome will survive and reproduce in the next generation and is strongly associated to the objective function. The fitness function of the problem at hand is expressed by:

(12) $fitness=\frac{1}{w_{1}T{C}_{total}+w_{2}F{C}_{total}}$(12)

where $w_1$ and are the weight factors.

Genetic operators: In the proposed GA, reproduction is based on the roulette wheel selection scheme, where the parent chromosomes are selected with rates proportional to their fitness. In general, chromosomes with higher fitness value have more chances to be selected for reproduction. For the implementation of the roulette wheel scheme, the following steps should be followed:

• Calculate the sum of all chromosomes’ fitness (S).

• Generate a random number (r) between 0 and S.

• Starting from the top of the population, keep adding the finesses to the partial sum P, till P < S. The individual for which P exceeds S is the chosen individual.

Crossover is a recombination operator that combines the genetic information of the parents to produce new offspring. The Order Crossover (OX) (Michalewitz 1996) is applied according to a randomly chosen crossover rate according to the following steps:

• Create two random cut-points in the parent and copy the segment between them from the first parent to the first offspring.

• Starting from the second crossover point in the second parent, copy the remaining unused numbers from the second parent to the first offspring, omitting numbers that are already present. The sequence is placed in the first offspring, starting from the second cut-point.

• Repeat for the second offspring with the parent’s role reversed.

  Table

  Parent#1

  3

  10

  9

  1

  6

  5

  8

  2

  4

  7

  7 9 3 4 10

  Table

  Parent#2

  9

  3

  6

  4

  10

  1

  2

  5

  7

  8

  7 3 9 6 8

  Table

  Offspring#1

  3

  4

  10

  1

  6

  5

  8

  2

  7

  9

  Table

  Offspring#2

  9

  6

  8

  4

  10

  1

  2

  5

  7

  3

Mutation is applied in order to inject new genetic material into the population and thereby maintain genetic diversity. The inversion (Michalewitz 1996) is used for mutation according to a randomly chosen mutation rate and works for a single parent with two random cut-points as follows:

Table

Parent#1

3

10

1

6

2

9

7

8

4

5

Table

Offspring#1

3

10

7

9

2

6

1

8

4

5

Computational Experiments

The simulation tests were implemented in Matlab R2015b and the machine used is an intel core i5-8265 U CPU @ 1.60 GHz PC. The control settings for the GA parameters are as follows: population size = 100, maximum generation number = 300, a random crossover rate taken values in the range [0.7–0.85], a random mutation rate taken values in the range [0.06–0.1]. In addition, a and b are assigned to be equal to 1.7 and 0.5, respectively. Concerning the index of $\lambda$, for a moderate decision maker, λ is set to 0.5. For all the test instances examined in this section, the collection quantities are fuzzified by setting the two extreme (least likely) values of the triplet ${\alpha }_1={\alpha }_2\cdot {\delta }_1$ and ${\alpha }_3={\alpha }_2\cdot {\delta }_2$, where and .

Firstly, the performance of the algorithm is evaluated considering both optimization criteria (travel distance and fuel consumption) considering 10 customers and one depot. These tests are performed in order to gather all the solutions and find the best one. Note that for all test cases the algorithm runs for 20 times and the best solution is presented. Table 1 presents the resulted solutions for the two criteria as well as the best found solution and the average results for 20 runs of the proposed algorithm, the median, the standard deviation and the variance. The last column of Table 1 presents the iteration number where the best solution was found for the first time as well as the average iteration number.

Table 1. The resulted solutions for 20 different runs

# of runs	optimum $T{D}_{total}$	optimum $F{C}_{total}$	Iteration
1	426.4	2829.7	84
2	399.4	2579.7	121
3	408.8	2662.5	163
4	399.4	2579.7	71
5	407.8	2551.0	111
6	399.4	2579.7	333
7	410.3	2769.9	10
8	395.6	2720.1	214
9	395.6	2720.1	76
10	407.8	2551.0	250
11	407.8	2551.0	176
12	426.0	2789.0	468
13	394.7	2652.4	26
14	393.8	2697.4	114
15	396.5	2675.2	226
16	445.7	2779.9	77
17	399.4	2579.7	300
18	408.8	2662.5	188
19	417.7	2661.8	305
20	393.8	2697.4	116
Average	406.7	2664.5	171.5
Best	393.8	2551.0
Median	403.6	2662.5
Standard deviation	13.5	86.8
Variance	182.3	7537.4

We conduct the experiment for the collection of fuzzy quantities from 10 customers and maximum available capacity $Q_0=30$. The fuzzy collection quantity for each customer is shown in Table 2. To compare the experimental results, we generate two scenarios: one with the objective of minimizing travel distance and one with the objective of minimizing the total expenditure (travel distance and fuel consumption).

Table 2. The fuzzy collection quantity for each customer

Customer #	Fuzzy collection quantities
1	(3.40, 4.00, 5.20)
2	(4.25, 5.00, 6.50)
3	(4.25, 5.00, 6.50)
4	(3.40, 4.00, 5.20)
5	(2.55, 3.00, 3.90)
6	(4.25, 5.00, 6.50)
7	(3.40, 4.00, 5.20)
8	(5.10, 6.00, 7.80)
9	(2.55, 3.00, 3.90)
10	(4.25, 5.00, 6.50)

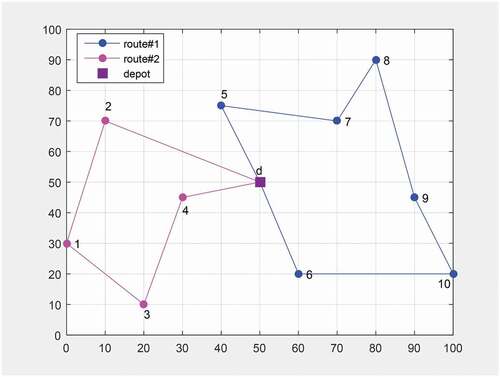
The best solution for the 1^st scenario includes 2 tours, as shown in Figure 3; vehicle#1 serves 6 customers and vehicle#2 serves 4 customers:

Figure 3. The resulted optimal solution for the 1^st instance.

Vehicle#1: depot → 6 → 10 → 9 →8 → 7 → 5 → depot

Vehicle#2: depot → 4 → 3 → 1 → 2 → depot

and the total carrying payload corresponding to each tour is (22.10, 26.00, 33.80) and (15.3, 18.00, 23.40).

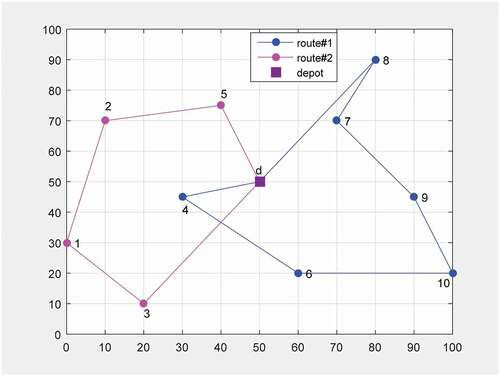
The best solution for the 2^nd scenario includes 2 tours as shown in Figure 4, where the customers are distributed to the two vehicles as follows:

Figure 4. The resulted optimal solution for the 2^nd instance.

Vehicle#1: depot → 8 → 7 → 9→ 10 → 6 →4 → depot

Vehicle#2: depot → 3 → 1 → 2 → 5 → depot

and the total carrying payload corresponding to each tour is (21.25, 25.00, 32.50) and (15.30, 18.00, 23.40).

In order to study the effect of the objective function on the optimal solution, we investigate the two scenarios when increasing the number of customers. Table 3 summarizes the results for the different numbers of customers. The % deviation of each value from the best possible is also calculated. As shown in Table 3, the travel distance for all test cases is smaller for the 1^st scenario compared to those yielded form the 2^nd scenario. On the other hand, for the 2^nd scenario where both objectives are optimized, the increase of the travel distance varies in the range from 0.5 to 37.4%, but the fuel consumption is decreased compared to the 1^st scenario and this reduction varies from 1.9 to 55.1%. It can be concluded from Table 3 that the minimization of travel distance leads to routes with more fuel consumption, but the minimization of both travel distance and fuel consumption leads to tours with a slight increase in the travel distance and a considerable decrease in fuel consumption. As a conclusion remark, the two objectives are competitive, since minimizing one will be on the cost of the other.

Table 3. The optimal results for the two scenarios

# of customers	Minimizing travel distance		Minimizing both criteria		% deviation for travel distance	% deviation for fuel consumption
	Travel distance	Fuel consumption	Travel distance	Fuel consumption
10	296.7	3956.0	407.8	2551.0	37.4	55.1
12	410.9	3039.2	483.1	2967.0	17.5	2.4
14	581.4	5426.6	598.5	4400.1	2.9	23.3
16	616.5	5124.4	619.5	4755.2	0.5	7.8
18	651.9	5346.1	685.8	5.2447	5.2	1.9
20	786.3	8777.3	806.4	7383.6	2.6	18.8

As already mentioned, no other research considers the bi-objective problem with fuzzy collection quantities as defined in this paper; thus, no benchmarks are available in the open literature for comparison. However, in order to show the validity of the proposed approach, the benchmark instances proposed by (Christofides and Eilon 1969) that were initially generated for the Capacitated Vehicle Routing Problem are transformed and applied to this problem. To this end, the newly generated test instances have been modified so that crisp collection quantities are transformed to triangular fuzzy payloads. For each crisp payload, a TFN is built by setting equal to this crisp quantity (representing the most likely value). The collection quantities are fuzzified by setting the two extreme (least likely) values of the triplet equal to ${\alpha }_1={\alpha }_2\cdot {\delta }_1$ and ${\alpha }_3={\alpha }_2\cdot {\delta }_2$; where ${\delta }_1=0.85$ and ${\delta }_2=1.3$, as in the previous test cases.

The proposed optimization algorithm was tested on 11 different benchmark instances with varying customers, collection quantities and maximum available capacity. The proposed algorithm is tested again for the two scenarios: one with the objective of minimizing travel distance and one with the objective of minimizing both travel distance and fuel consumption. The algorithm runs 20 times for each test instance and the best solution is written down. Table 4 summarizes the results of the benchmark instances obtained by (Christofides and Eilon 1969) and the results using the proposed GA integrated with fuzziness for a single criterion and for two criteria. One should keep in mind that the optimal solutions are not known for the bi-objective problem with fuzzy collection quantities, since the benchmarks solutions are provided for the CVRP that has only one optimization criterion (traveled distance) and all variables are crisp values. In addition, the idea behind assigning the customers to the vehicles is rather different.

Table 4. Comparison results for benchmark instances

		Benchmark results		GA results with one criterion		GA results with two criteria
Instance	number of customers	number of routes	Travel cost	number of routes	Travel cost	number of routes	Travel cost	Fuel consumption
E-n22-k4	22	4	375	5	422.4	5	523.15	493960
E-n23-k3	23	3	569	3	631.72	4	1207.08	561200
E-n30-k3	30	3	534	3	794.82	4	913.07	492910
E-n33-k4	33	4	835	4	1051.2	5	1484.85	1940600
E-n51-k5	51	5	521	6	1067.4	6	1280.1	43554
E-n76-k7	76	7	682	7	1718.5	7	1940.6	94523
E-n76-k8	76	8	735	9	1672.2	9	1977.9	8849.9
E-n76-k10	76	10	830	11	1730.9	12	21819	80138
E-n76-k14	76	14	1021	16	1919.7	16	2218.0	74561
E-n101-k8	101	8	815	8	2396.7	8	3031.8	153990
E-n101-k14	101	14	1067	16	2013.7	15	3167.7	123230

Even though no direct comparison is possible, some conclusions can still be drawn. It can be seen from Table 4 that for most instances, the proposed GA can achieve results relatively close to the results of the benchmarks concerning the number of routes. It is also clear from the results that the integration of fuzziness results in some cases in a small increase in the number of the routes. In other words, fuzziness in the collection quantities causes an increase in the number of routes, which in turn causes an increase in the travel cost. In regard of the optimization criteria, the integration of the 2^nd criterion (fuel consumption) leads to an increase in the number of routes as well as an increase in the travel cost, as expected.

In order to investigate the effect of the uncertainty in customers’ collection quantities on the optimum solution, we change the width of the supports of the fuzzy collection quantities. We consider the following cases: $\left({\delta }_1,{\delta }_2\right)=\left(0.7,1.6\right)$, $\left({\delta }_1,{\delta }_2\right)=\left(0.9,1.2\right)$ in order to compare the results with the already examined test case where $\left({\delta }_1,{\delta }_2\right)=\left(0.85,1.3\right)$. Apparently, a wider support (e.g. $\left({\delta }_1,{\delta }_2\right)=\left(0.7,1.6\right)$) implies more uncertainty in the customers’ collection quantities and a narrower support (e.g. $\left({\delta }_1,{\delta }_2\right)=\left(0.9,1.2\right)$) decreases the uncertainty and leads toward the most plausible collection quantities.

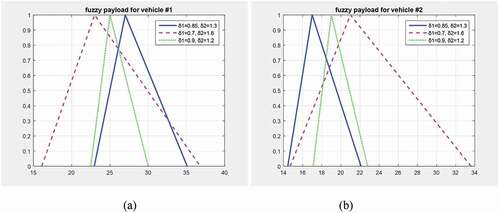
The effect of the change in uncertainty is tested for the test case of 10 customers and the results considering the total fuzzy payloads for vehicle#1 and vehicle#2 are shown in Figure 5(a) and (b), respectively. As one can see from Figure 5(a) and (b), more uncertainty in customers’ collection quantities results in a wider support (i.e. more uncertainty) of the total fuzzy payload. On the contrary, less uncertainty in customers’ collection quantities (i.e., when ${\delta }_1=0.9$ and ${\delta }_2=1.2$) results in a narrower support (i.e. closer to the most plausible value) of the total fuzzy payload.

Figure 5. The total fuzzy payload for (a) vehicle#1 (b) vehicle#2 for the test case of 10 customers.

This test is repeated for the test case of 15 customers and the results for the three vehicles used are depicted in Figure 6(a-c). The results for the test case of 20 customers are omitted since they present similar performance. However, it should be noticed that for the combinations (0.85, 1.3) and (0.7, 1.6), four vehicles are used to serve all the customers, but for the combination (0.9, 1.2) expressing less uncertainty, the number of vehicles needed is three.

Figure 6. The total fuzzy payload for (a) vehicle#1 (b) vehicle#2 and (c) vehicle#3 for the test case of 15 customers.

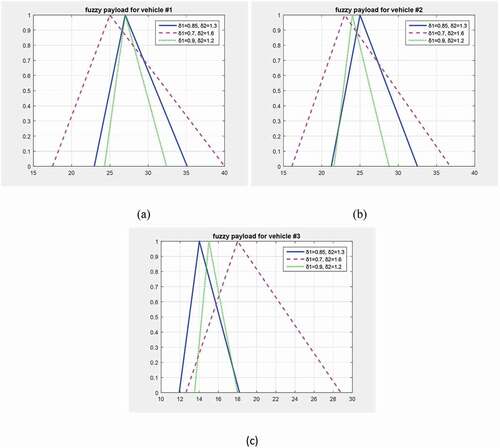
Without loss of generality, we conclude that the increase in the uncertainty of collection quantities results in the expansion of the supports concerning the fuzzy payloads of the vehicles. On the contrary, the decrease in the uncertainty of collection quantities leads to narrower supports of the fuzzy payloads and it is also likely to lead to the decrease of the number of the vehicles necessary to serve the customers. The latter is reasonable since improvement on the certainty leads to solutions that are closer to the real situations. On the contrary, the increase in ambiguity leads to solutions that diverge from real situations as much as uncertainty is increased. This, in turn, leads to more costly solutions (by increasing the number of vehicles) that express a risk averse attitude as the intention is to act in a way least likely to take risks.

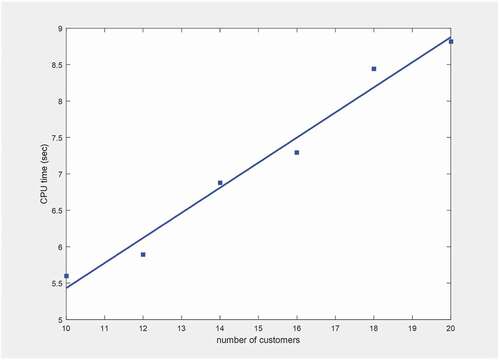
Lastly, a study concerning the computational time required by the proposed approach to design the vehicle’s route has been conducted. In Figure 7, the average computational time (in seconds) is plotted versus the number of customers. As depicted, the computational time is nearly proportional to the number of the customers despite the fact that the problem’s complexity is NP-hard.

Figure 7. The CPU time versus the number of customers.

Conclusions

The classic vehicle routing problem concerns the minimization of travel distance considering specific constraints. However, energy consumption is a challenging issue, since fuel consumption has negative environmental impacts and increases the operational costs. This paper studies the vehicle routing problem considering two objectives: the minimization of travel distance and the minimization of fuel consumption. Fuel consumption mainly depends on the vehicle’s load while following a route. In an attempt to approach more realistic solutions, the proposed model considers fuzzy customers’ collection quantities that are formulated by triangular fuzzy numbers. In order to encounter the computational complexity of the problem, an optimization approach based on a bi-objective Genetic Algorithm is developed that is integrated with fuzziness.

The effectiveness of the proposed approach is firstly validated through a numerical example of 10 geographically dispersed customers linked with fuzzy collection quantities. In order to study the effect of the objective function on the optimal solution, we investigate the two instances: one for the minimization of the travel distance and the other for the minimization of both travel distance and fuel consumption. The experimental results proved that the minimization of both travel distance and fuel consumption leads to tours with a slight increase in the travel distance and a considerable decrease in fuel consumption. Next, the efficiency of the proposed algorithm is evaluated through existing benchmarks that have been transformed to conform with the integrated problem. Although no direct comparison is possible, the result are close to the existing ones that amplifies the validity of the proposed algorithm. Lastly, the effect of the uncertainty in customers’ collection quantities on the optimum solution is studied, we conclude that more uncertainty in customers’ collection quantities results in more costly solutions as expectation diverges more from reality.

The main contribution of this work is three-fold. First, the developed model considers the minimization of both travel time and fuel consumption that reflects better the real needs encountered in real-life situations compared to the classic VRP. Second, the integration of fuzzy collection quantities to the model to express better the real-world situations and the analysis of their effect on the vehicles’ payload. Third, the developed optimization algorithm easily integrates the fuzzy concepts with two criteria and succeeds to handle the NP-hard nature of the problem.

Since energy saving is a great challenge in transportation and logistics, there is much ground for further research with respect to both new problem variants and solution approaches. The developed solution model is limited to situations where the vehicles serve the customers ignoring collision problems. The next step is to study the problem considering the motion planning while the vehicles move concurrently with different velocity profiles. Concerning fuel consumption, the model of this work focused on the correlation with distance and payload, since they both considerably affects energy consumption. In this regard, it is quite interesting to study the real-life route factors affecting fuel consumption (weather conditions, terrain, roads’ slope, driver’s behavior etc.)

Future work will also be devoted to the consideration of traffic conditions in order to simulate more realistic situations. Traffic conditions, such as congestion, will be considered, since they significantly affect the vehicle speed. Since traffic congestion is time-varying and non-uniformly distributed, a prediction schedule based on historical data is essential.

Disclosure Statement

No potential conflict of interest was reported by the author(s).