Explainable Analytics to Predict the Quality of Life in Patients with Prostate Cancer from Longitudinal Data

ABSTRACT

Prostate cancer (PCa) is a complicated cancer with high level of unexplained variability that might affect the patient’s health-related quality of life (HRQoL). Using 2670 patients’ information with 433 measures per patient, our objective is to identify the minimal set of important variables which can predict 1-year follow-up HRQoL for PCa patients while adding interpretability to the proposed model. We address three problems of dimension reduction, prediction, and interpretability by first developing deep neural networks on top of a clustering algorithm to extract minimal set of important variables of baseline visit. Second, we build a model to predict a 1-year follow-up of HRQoL for PCa patients using the extracted important baseline variables. Third, we utilize Bayesian networks method to provide insights into the proposed model results to discover the relationship between patients’ baseline variables and their 1-year follow-up satisfaction. The results support the use of the proposed machine-learning technique as an essential tool in identifying potential baseline variables for predicting 1-year HRQoL. Furthermore, our approach to interpret the findings will help to establish guidelines for a better shared decision-making platform for PCa patients.

KEYWORDS:

• deep neural networks
• Bayesian network
• prostate cancer
• health-related quality of life
• clustering

Introduction

According to the World Health Organization (WHO), prostate cancer (PCa) is the second most prevalent cancer in men, with 1.3 million cases per year worldwide (Wild et al. 2020). There are a variety of modalities for treating PCa, including surgery, radiotherapy, chemotherapy, hormone therapy, and active surveillance. All of these treatments are associated with risks of potential side effects (Luszczak et al. 2020) that can have negative consequences on patients’ health-related quality of life (HRQoL). HRQoL outcomes have emerged as a major consideration when making treatment decisions for PCa given that the 5-year survival rate for most men with local or regional PCa is nearly 100% (McLean*, Cunningham, and Ricke 2019). Thus, being able to predict (we use both predict and estimate terms interchangeably, although predict is often equated only with classification prediction not regression) patients’ HRQoL prior to treatment would presumably help patients make an informed decision. For example, problems with urinary function that occur in men with localized PCa are likely the result of treatment. This is supported by evidence from comparison group and cross-sectional studies (Eton and Lepore 2002) across different groups in which men treated with radical prostatectomy (RP) had almost twice as often as men treated with external beam radiotherapy (EBR). However, RP is generally associated with decreased risk of overall and cancer-specific mortality in high-risk patients (Chen et al. 2017). Given said that, we need accurate prognostic information about patients’ future HRQoL prior to treatment. To achieve this goal, we either need clinician judges or predictive models. According to several studies (Kattan et al. 2013; Walz et al. 2007), clinicians are often poor judges of future patient outcomes while predictive models perform significantly better.

Developing predictive models for post-PCa treatment (henceforth post-treatment) HRQoL poses several challenges. For one, the causes of HRQoL dysfunction (e.g. UI (UI) and erectile dysfunction) are multifactorial (Eastham, Scardino, and Kattan 2008; Michl et al. 2006), which complicates the development of predictive models. Being multifactorial typically includes four broad categories: physical, functional, social, and emotional well-being. Therefore, HRQoL refers to when a medical condition or its treatment affects one’s usual or expected physical, social, and emotional well-being (Cella 1995). As a result, an appropriate measurement of HRQoL should incorporate the patient’s perspective while capturing physical, social, and mental well-being. Besides being multifactorial, modeling HRQoL outcomes is also challenging because of the longitudinal data sets. While cross-sectional data can provide a snapshot of a patient’s behavior and perceptions, longitudinal studies help to clarify the trajectory of HRQoL in men treated for PCa. The key problems are long-term patient engagement/recruitment and attrition rate. High occurrence of attrition rates across longitudinal data is the concern as it can rapidly deplete the longitudinal data validity. From prediction point of view, the analysis is complicated by complex correlation structures, irregularly spaced visits of the patients and missing data. Confusion on these points can lead to non-comprehensive and inaccurate analysis. Among the numerous techniques that are used to create predictive (O’Callaghan et al. 2017), regression-based methods are the most popular because of their commonality in many statistical software packages and being relatively fast to perform. However, when it comes to big data analysis, the regression-based methods may not have enough appropriate validation in terms of accuracy and speed. Therefore, having a variable extraction/selection method that can identify the influential variables out of big data set is necessary. Furthermore, most of the research studies, to-date, predicting HRQoL do so at the population level (Delobel et al. 2017; Kim et al. 2020; Schaake et al. 2018), and present results based on the entire observation group. However, patients require individual-level prediction models in order to make treatment decisions. In other words, variables marked with high global importance may not be relevant to predict an individual’s risk of negative side effects.

Despite the fact that such complex (black-box) prediction models are able to achieve high validation results (R-squared in our study), they lack an explanation of the prediction outcome. In May 2018, General Data Protection Regulation requested industries to have a meaningful way to explain any automated decision and after that the interpretability of machine-learning models has been receiving huge attention. Noteworthy is that when using predictive analytics in critical domains such as predicting HRQoL outcomes in PCa patients, the explanation power is noticeably more important than the model predictive power.

Despite a variety of clinical interpretation approaches having been explored (Wheat et al. 2009), no work has yet explored the potential of Bayesian Networks (BNs) as an explanation framework to be used on top of Black-box prediction. BNs (Pearl 1988), which typically reflect the problem structure, can be used to generate explanations of the predictions we already have.

To the best of our knowledge, this is the first study to use variable extraction on cluster-based population that can predict the 1-year HRQoL outcomes prior to treatment as a regression prediction not only classification prediction and the first to create the insight into prediction method using BNs for PCa patients.

Related Work

Complex predictive models were used intensively in different areas including health care sector. Despite the fact that such complex (black-box) models are able to achieve high accuracy, they lack an explanation of the predicted outcome. Thus, there is still an enormous potential to discover new patterns from massive amount of data and transform those new black-box models into human-understandable knowledge.

The following literature successfully applied machine-learning techniques to make predictions on HRQoL, in the context of PCa, from various domains ranging from UI (Grivas et al. 2018; Rossi et al. 2018; Sadahira et al. 2019; Schaake et al. 2018; Tienza et al. 2018), sexual (Kim et al. 2020), fecal incontinence (Carrara et al. 2018; Delobel et al. 2017; Rossi et al. 2018), rectal bleeding (Delobel et al. 2017; Rossi et al. 2018), etc., and methodologies from different regression-based models (Multivariate logistic regression (Rossi et al. 2018; Sadahira et al. 2019), Binary logistic regression (Grivas et al. 2018; Kim et al. 2020)), artificial neural network (ANN) (Carrara et al. 2018), etc. Summary of papers describing predicting tools relating to patient-reported outcomes (PROs) (September 2016 – July 2019) is shown in Table 1. Table 2 lists the models for predictive tools in PROs and their explanations. The literature explained here is the extension of two main surveys that introduce the existing approaches in the literature in more detail. The first one (O’Callaghan et al. 2017) covers July 2007 to September 2016 and the second one (Shariat et al. 2008) explores papers prior to July 2007. Most of the existing research have had three main limitations: 1) Using population-level data set for training the model and presenting the results based on the entire observation group. However, the model should consider patients in minority group as well. Otherwise, it might underestimate the variables that affect similar patients which are in a relatively small group but with similar output. 2) Developing black-box machine-learning models which are not interpretable that contribute negatively toward establishing trust and confidence in their predictions for stakeholders. 3) They usually only consider two domains of HRQoL, mostly UI and sexual dysfunction. To the best of our knowledge, there are no previous studies that address the problem of estimating a more comprehensive set of side effects, such as bowel and hormonal domains. Therefore, the objective of this study is to present a computational mechanism that fills the gap in research on predicting post-treatment HRQoL for patients with PCa while maintaining the interpretability of the model so that patients and physicians can understand the decisions made by the proposed prediction model.

Table 1. Summary of papers describing predicting tools relating to pros (September 2016 – July 2019). ng (not given), pros (patient-reported outcomes).

Author/year	Recruited	Country	Population	Outcome	Study Type	Setting	Tool Developed
Wouter Schaake et al. 2018 (Schaake et al. 2018)	2005–2009	Netherlands	243 patients with PCa confined to the prostatic capsule (stage T1-3). All patients were treated with radiotherapy	UI, hematuria, pain and increased voiding frequency;	Prospective	Multicenter	No
Tienza et al. 2018(Tienza et al. 2018)	2002–2012	Spain	787 consecutive patients that underwent RP	UI	Retrospective	Single center	Nomogram
Jean-Bernard Delobel et al. 2017 (Delobel et al. 2017)	2000–2012	France	972 patients undergoing definitive radiotherapy for localized prostate adenocarcinoma	Rectal bleeding, urgency/tenesmus, diarrhea, and fecal incontinence	Retrospective (487 patients) Prospective (485 patients)	Multicenter	Nomogram
Nikolaos Grivas et al. 2018 (Grivas et al. 2018)	January 2012-March 2016	NG	439	Postoperative incontinence, defined as any involuntary urine loss irrespective of inlay use or amount of urine loss, according to ICIQ‐SF	Retrospective	NG	Calculator
Mauro Carrara et al. 2018 (Carrara et al. 2018)	2002–2004 and 2010–2014	Italy Switzerland	598	Late Fecal Incontinence (LFI)	Prospective	Multicenter	graphical classification tools (GCTs)
Linda Rossi et al. 2018 (Rossi et al. 2018)	NG	NG	820	Rectal bleeding, fecal and UI, and nocturia	NG	Multicenter	No
Takuya Sadahira et al. 2019 (Sadahira et al. 2019)	2010–2017	Japan	571	UI	Retrospective	Single center	NG
Mylona et al. 2019 (Mylona et al. 2019)	May 2008 and July 2018	France	272	Incontinence, retention, dysuria, hematuria, and frequency	Prospective	Multicentric	No
Lawrence H.C. Kim et al. 2020 (Kim et al. 2020)	2015–2016	NG	190	UI	Retrospective	Single center	No
Robert T. Dess et al. 2018 (Dess et al. 2018)	2008–2013	NG	373	Functional erections	Prospective	Single center	No

Table 2. Explanations of the models for predictive tools in pros. ng (not given), pros (patient-reported outcomes).

Author	Model Type	Variables	Validation (I/E)	Accuracy	N(events)
Wouter Schaake et al. (Schaake et al. 2018)	Multivariable NTCP (Normal Tissue Complication Probability); R	Dosimetric predictors of all bladder structures, pre-treatment variables diabetes, age, cardiovascular disease, abdominal surgery, adjuvant hormonal treatment and TURP.	InternaL	AUC = 0.66, R-square = 0.10	243
Antonio Tienza et al. (Tienza et al. 2018)	Multivariable logistic regression; SPSS and Orange 2.7	Age, urethral wall thickness, history of transurethral resection of the prostate, and membranous urethral length	No	AUC = 71.7	746
Jean-Bernard Delobel et al. (Delobel et al. 2017)	Regression logistic; SPSS V18 and R	Total dose, dose per fraction, RT technique	Internal	C-index = 60%	972
Nikolaos Grivas et al. (Grivas et al. 2018)	Cox multivariate analysis and multivariate binary logistic regression; SPSS V22.0	FP score, ILD and MUL	Internal; bootstrap	AUC = 0.779	439
Mauro Carrara et al. (Carrara et al. 2018)	ANN;	Mean dose, previous abdominal surgery, use of anticoagulants, use of antihypertensive drugs, use of neoadjuvant and adjuvant hormone therapy	Internal; 4-fold cross validation	AUC = 0.78	664
Linda Rossi et al. (Rossi et al. 2018)	Multivariate logistic regression; MATLAB, SPSS V21 and R (R 3.3.2)	Age, Baseline, Turp, GI Comorbidity, LRHGE, ContrastNGTDM	Internal; bootstrap	AUC = 0.73	820
Takuya Sadahira et al. (Sadahira et al. 2019)	Multivariate logistic regression	MUL and LAM	Internal	NG	571
Eugenia Mylona (Mylona et al. 2019)	Multivariate logistic; Python and R	Whole bladder region and SRS	Internal	AUC = 0.73	272
Lawrence H.C. Kim et al. (Kim et al. 2020)	Binary logistic regression SPSS version V22.0	MRI variables: age and coronal MUL	Internal	AUC = 0.78	190
Robert T. Dess et al. (Dess et al. 2018)	Logistic regression	Baseline sexual HRQoL Age	NG	AUC = 0.81	373

Given our objective, in this paper, we present a framework to predict and interpret post-treatment (1-year follow-up) HRQoL outcomes for PCa patients out of high dimensional data set. We utilized the k-means algorithm (Jain 2010; MacQueen et al. 1967) to put similar patients in the same clusters and avoid fitting the model on the entire training data. In the next step, we used deep neural networks (DNNs) (Rosenblatt 1961) to fit each cluster separately and identify the most influential variables in each cluster. This will prevent underestimation of any small group of similar patients, which might have same influential variables. Furthermore, we develop a combined BN method to provide interpretation of prediction model for a variety of HRQoL domains. After aggregating the top results for the patient groups, our results provide insightful recommendations for improving patient experiences. The rest of the work is organized as follows. We present the data set and Expanded Prostate Cancer Index Composite-26 (EPIC-26) measurement method first. Then the proposed methods for prediction and explanation are demonstrated. After that we show the results and insights. Finally, we present remarks and discussions, conclusions, and an outlook for future research.

Quality of Life in PCa Patients and Data

To demonstrate our approach to predicting post-treatment HRQoL for patients with PCa based on their pre-treatment prognostic factors, we are using data collected as part of the Alberta PCa Research Initiative (APCaRI). The APCaRI is enrolling the population of men undergoing diagnosis for PCa in Calgary and Edmonton, Canada. These men were referred for a diagnostic biopsy based on conventional clinical guidelines (e.g., elevated PSA and/or abnormal digital rectal examination) with average age 64.75 years at baseline visit. We filtered the data to include only those patients without a prior PCa diagnosis (i.e. excluding recurrence), which resulted in 2,670 patients and involving 433 unique variables collected prior to treatment (i.e. a study “baseline”). The variables include demographic characteristics were collected during the in-person interview prior to biopsy, clinical data from laboratory, pathology, or pre-treatment reports. Given that we want to predict 1-year HRQoL, we further excluded those patients who did not have 1-year data completed. This process resulted in a data set of 1,214 patients.

Desired output,

We used the EPIC-26 to measure HRQoL. The EPIC-26 is a common and valid PRO measure of HRQoL for men with PCa (Szymanski et al. 2010). The items of EPIC-26 are responded to using either a 4- or 5-item Likert scale. Responses are transformed to a 0–100 scale, higher scores measured represent better HRQoL (Szymanski et al. 2010). Items are grouped into one of five domains by using the available scoring instructions: urinary incontinence (UI) (4 items), urinary irritative/obstructive (UIO) (4 items), bowel (B) (6 items), sexual (S) (6 items), and hormonal (H) (5 items) (Wei et al. 2000). As Table 1 in (Sharifi et al. 2019) presented, there are 26 items in which one item (i.e. “Overall, how big a problem has your urinary function been for you during the last 4 weeks?”) is not included in any domain. For each domain, item scores are averaged to calculate the domain summary score (Szymanski et al. 2010). In this study, independent variables are the unique 433 variables, and dependent variables or desired outcomes are EPIC-26 variables which are UI, UIO, bowel (B), sexual (S), and hormonal (H).

Cluster-based DNN (CB-DNN) Prediction Model

Patients’ severity for each of the EPIC-26 domains is a temporal continuous score between 0 and 100, with 0 indicating the highest severity and 100 indicating the least. All of the dependent variables and most of the independent variables are temporal whose states change with time (i.e. the variable values are different in baseline and 1-year follow-up). CB-DNN aims at predicting the EPIC-26 values for next year (1-year follow-up) for the patients at their baseline visit in which the independent variables at baseline visit should be used. Considering that the dimension of the data set is large, the CB-DNN algorithm starts by finding the most important variables which can have adequate description of the data by having an acceptable prediction of the quality of life for 1-year follow-up. The method’s steps are detailed below.

Firstly, a K-means (Jain 2010; MacQueen et al. 1967) is used to group the data points into K clusters according to the distance measure. The Euclidean distance is calculated as $\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{d}}{({\mathrm{x}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}})}^2}$ where $d$ is the number of dimensions (433 in our study), $x_i$ and $y_i$ are two patients in a d-dimensional Euclidean space. The main idea is to define $K$ centroids, one for each cluster. These centroids should be placed as much as possible far away from each other. The Elbow method (Ng 2012) is used to find the best number of the clusters, $K$. It is a visual method to determine approximately the best number of clusters. The EPIC-26 values in 1-year follow-up is a highly imbalanced data. Table 3 demonstrates that there are 7.4%, 12.19%, 3.62%, 37.56%, and 3.79% in first three quartiles (i.e. less than 75) in 1-year follow-up for UI, UIO, B, S, and H, respectively. Therefore, we prevent the classification model to overlook these more severe responses which are minority by using clustering. Patients which are similar (i.e. less satisfied patients) would probably end up in the same cluster. Then considering these clusters separately for variable extraction will help to find the influential variables on minority responses as well as on majority responses in which include the patients in the less severe quartile (i.e. there EPIC-26 values are more than 75).

Table 3. Statistical characteristics of patients for all the epic-26 domains score quartiles in 1-year follow-up. epic-26 domains are UI, UIO, b (bowel), s (sexual) and h (hormonal).

	No. of Patients for each EPIC-26 Domain
Range of Score	UI (%)	UIO (%)	B (%)	S (%)	H (%)
[0–25)	2 (0.16)	1 (0.08)	0 (0)	204 (16.80)	2 (0.17)
[25–50)	10 (0.82)	13 (1.07)	9 (0.74)	132 (10.87)	6 (0.49)
[50–75)	78 (6.42)	134 (11.04)	35 (2.88)	120 (9.89)	38 (3.13)
[75–100]	768 (63.26)	893 (73.56)	1033 (85.09)	238 (19.61)	1006 (82.87)
Missing Values	356 (29.32)	173 (14.25)	137 (11.29)	520 (42.83)	162 (13.34)

Second, for each resulting cluster from the previous step, a DNN is trained to extract the important variables per cluster. Deep learning aims at learning variable hierarchies with variables from higher levels formed by the composition of lower level variables. In this paper, we use the DNN as a conventional multi-layer perceptron (MLP) (Rosenblatt 1961). Variable importance in DNN is calculated using the Gedeon (Gedeon 1997) method. It is a modification of Garson method (David Garson 1991) which the hidden layer weights are partitioned into components associated with each input node. After that, the percentage of all hidden node weights assigned to a particular input node is used to measure the importance of that input variable. Mainly it is based on using the weight matrix of the trained neural network itself to determine which inputs are significant. In our study, the top important variables which are considered are those with importance more than 0.85 (it is selected by try and error to get the most efficient threshold which the extracted variables does not exceed 10 variables) in at least one of the clusters.

DNN is well suited for APCaRI data set of this study. There are two main reasons for this. In the first place, DNN can help to provide abstract representations which are generally invariant to most local changes of the input which is helpful if other hospitals want to reproduce our results based on their data set. Moreover, In the context of categorical concepts, given that most of the independent variables in this study are either binary or ordinal, DNN is helpful as it can detect categories that cover different kinds of concepts. In DNN, the tanh (hyperbolic tangent) activation function, ADADELTA optimizer (Zeiler 2012), and five hidden layers with 100 neurons each were used. For improving generalization I specify the input layer dropout ratio as 0.2.

Thirdly, The important variables extracted from previous step which is for patients in baseline visit are fed as input to an ANNs for each domain separately. The 1-year follow-up EPIC-26 variables are considered as the output of the ANN. The data were divided into 70%, 15%, and 15% for training, validation, and testing, respectively. The ANN used for prediction is a simple MLP with 3 layers containing 10 neurons in the hidden layer. The network has 10 inputs which are the minimal set of important variables extracted by each of the methods, and one output is a continuous number for EPIC-26 domain value. We used the logistic function as the activation function inside the neurons with backpropagation as the learning mechanism. The ANN model is used as nonlinear prediction model in the last step of the proposed model. That is because unlike traditional machine-learning models such as linear or logistic regression which has been used widely in the literature for predicting quality of life (Delobel et al. 2017; Dess et al. 2018; Kim et al. 2020), ANN models can learn more complex nonlinear data representation.

Note that, as we are facing a big data problem, in order to use all processing power of the system, fast and distributed, both clustering and DNN implementation are on H2O 2018c. H2O is a framework in the machine learning for predictive and descriptive analytic that can be stand alone or executed on top of the Hadoop (Borthakur 2007) or spark (Zaharia et al. 2010) frameworks. H2O handles billions of data rows in-memory by using in-memory compression (Landry and Angela 2018), it also enables the connection between R, an open source statistical programming environment, with a big data infrastructure which is Hadoop Distributed file System.

A. Evaluation Metric

As we are predicting a continuous value for each of the 5 domains in EPIC-26, the performance of the proposed techniques is evaluated using the coefficient of determination ($R^2$). It gives a quantitative assessment of the ability of the model to explain the variance in unseen data by measuring how well the model is compared to the average model. This is a well-established measure of the strength of the relationship between the predicted outcome and actual outcome in regression problem. This coefficient is defined as:

$R^2=1-\frac{\sum _{i=1}^n{\left({\hat{Y}}_i-Y_i\right)}^2}{\sum _{i=1}^n{\left(Y_i-\bar{Y}\right)}^2}.$

where ${\hat{Y}}_i$ denotes the value of the outcome variable predicted by the proposed method for the $i^{th}$ data point. $Y_i$ and $\bar{Y}$ are the actual value of the outcome variable and its mean respectively. The coefficient of determination can have the value from 0 to 100%, higher coefficient values suggest that the predicted values and the actual values are more the same. In this study, the minimally important differences (MID) reported in (Skolarus et al. 2015) is applied before calculating the $R^2$ values. MID provides a measure of the smallest change in the EPIC-26 values that patients perceive as important. All errors less than the MID value of the EPIC-26 domain are considered as zero for calculating coefficient of determination.

BN-based Explanation Model

A BN (Pearl 1988) represents a class of graphical models as a Directed Acyclic Graph (DAG) over $\mathbf{X}$ (a set of random variables). Such that random variables are associated with the nodes in DAG. In this section, we develop our method for learning the structure of a BN. It is important to note that we adhere to the standard assumption behind the Naïve Bayes rule which mentions that there is no interaction between the input variables given the outcome (Barik and Honorio 2019; Kocaoglu, Shanmugam, and Bareinboim 2017; Spirtes et al. 2000; Yang-Bo and Geng 2008).

EPIC-26 may be modeled using one BN for each of the five domains. The structure of the BN prediction model is for two time slices: baseline visit and 1-year follow-up visit. All the nodes included in the model are temporal except in_002 (How would you classify your race?) whose state does not change with time. It is also noteworthy to mention that some of the temporal nodes such as UI, UIO, bowel, sexual and hormonal variables are included with their 1-year follow-up values, while others extracted from CB-DNN are considered with their baseline values. The reason behind utilizing the BN as the base for the proposed explanation model is to find the relationship between the baseline variables proposed by CB-DNN as important variables that can predict the 1-year EPIC-26 values, and 1-year EPIC-26 output values. Therefore, time lags in each BN model include a 1-year lag in the effect of variables extracted by CB-DNN on 1-year EPIC-26 output values. Baseline variables extracted by CB-DNN are reported in Tables 4, 5, 6, 7, and 8, for UI, UIO, B, S, and H, respectively. As we only need the arcs which end up to 1-year EPIC-26 value, we do not need the latent variables to reduce the conditional probability tables for the BN. However, we applied some minor changes on BN learning process to get the best explanation results for our model.

Algorithm 1: Greedy BN Algorithm

Input: a data set $\mathcal{D}$ from $\mathbf{X}$, an initial DAG $\mathcal{G}$ (usually the empty DAG),

Schwarz Information Criterion as score function $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(\mathcal{G},\mathcal{D})$

Output: the DAG ${\mathcal{G}}_{max}$ that maximizes $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(\mathcal{G},\mathcal{D})$

1. Compute the score of $\mathcal{G}$, $S_{\mathcal{G}}=\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(\mathcal{G},\mathcal{D})$.

2. Set $S_{max}=S_{\mathcal{G}}$ and ${\mathcal{G}}_{max}=\mathcal{G}$

3. Hill climbing: repeat while $S_{max}$ increases:

   • for every possible arc addition, deletion, or reversal in ${\mathcal{G}}_{max}$ that the arc ends up to the 1-year follow-up EPIC-26 domain value, resulting in a DAG:

   • compute the score of the modified DAG ${\mathcal{G}}^{\ast }$, $S_{{\mathcal{G}}^{\ast }}=\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}({\mathcal{G}}^{\ast },\mathcal{D})$:

   • if $S_{{\mathcal{G}}^{\ast }}>S_{max}$ and $S_{{\mathcal{G}}^{\ast }}>S_{\mathcal{G}}$, set $\mathcal{G}={\mathcal{G}}^{\ast }$ and $S_{\mathcal{G}}=S_{{\mathcal{G}}^{\ast }}$.

   • if $S_{\mathcal{G}}>S_{max}$, set $S_{max}=S_{\mathcal{G}}$ and ${\mathcal{G}}_{max}=\mathcal{G}$.

4. Tabu search: for up to Tabu list size:

   • repeat step 3 but choose the DAG $S_{\mathcal{G}}$ with the highest $\mathcal{G}$ that has not been visited in the last Tabu list size steps regardless of $S_{max}$;

   • if $S_{\mathcal{G}}>S_{max}$, set $S_{max}=S_{\mathcal{G}}$, and ${\mathcal{G}}_{max}=\mathcal{G}$ and restart the search from step 3.

5. Max-min hill climbing (MMHC): First add an arc from the most important variable extracted by CB-DNN to its correspondence EPIC-26 domain to the DAG $\mathcal{G}$ with the highest $S_{\mathcal{G}}$ from step 4, then for every arc ${\mathbf{X}}_t$ in it:

   • $P{C}_{{\mathbf{X}}_t}=MMPC({\mathbf{X}}_t,\mathcal{D})$ (Tsamardinos, Brown, and Aliferis 2006)

   • repeat step 3 but for arc addition only add $Y\to {\mathbf{X}}_t$ if ${\mathbf{X}}_t$ is in $P{C}_{{\mathbf{X}}_t}$

Table 4. Top 10 important variables from baseline visit selected by CB-DNN for predicting 1-year follow-up UI along with their definitions. .

Variable	Definition	Type
eq_004	Usual activities	Ordinal
ep_012	How big the problem of Increased frequency of bowel movements, if any, has been for you?	Ordinal
ip_008	During the past month, how many times did you most typically get up to urinate from the time you went to bed at night until the time you got up in the morning?	Ordinal
ib_035	Number of positive cores biopsied from LA	Ordinal
in_029	Relation of the family member diagnosed (If anyone in your family has been diagnosed with PCa)	Nominal
ep_020	How would you describe the FREQUENCY of your erections during the last 4 weeks?	Ordinal
ip_007	In the past month, how often have you had to push or strain to urinate?	Ordinal
rx_008	Which type of medications, vitamins or herbal supplements are you taking now?	Nominal
im_001	Bone scan?	Binary
in_002	How would you classify your race?	Nominal

Table 5. Top 10 important variables from baseline visit selected by CB-DNN for predicting 1-year follow-up UIO along with their definitions. .

Variable	Definition	Type
ib_064	%of first RMZ core involved	Numerical
ib_056	Number of positive cores biopsied from RA	Ordinal
ep_015	How big the problem of Abdominal/Pelvic/Rectal pain, if any, has been for you?	Ordinal
ep_020	How would you describe the FREQUENCY of your erections during the last 4 weeks?	Ordinal
in_016	Have you ever been diagnosed with chronic liver disease?	Binary
ep_021	Overall, how would you rate your ability to function sexually during the last 4 weeks?	Ordinal
ib_011	Gleason secondary grade	Ordinal
in_012	Have you ever been diagnosed with cerebrovascular disease?	Binary
ep_019	How would you describe the usual QUALITY of your erections during the last 4 weeks?	Ordinal
in_009	Have you ever been diagnosed with congestive heart failure?	Binary

Table 6. Top 10 important variables from baseline visit selected by CB-DNN for predicting 1-year follow-up bowel along with their definitions.

Variable	Definition	Type
ib_042	Number of positive cores biopsied from LMZ	Ordinal
ib_029	Intraductal carcinoma	Binary
ib_020	High Grade PIN	Binary
ib_071	%of first RB core involved	Numerical
in_018	Have you ever been diagnosed with Hemiplegia?	Binary
ep_018	How would you describe your ability to reach orgasm (climax) during the last 4 weeks?	Ordinal
ib_013b	Total cores collected	Numerical
ep_012	How big the problem of Increased frequency of bowel movements, if any, has been for you?	Ordinal
in_029	Relation of the family member diagnosed (If anyone in your family has been diagnosed with PCa)	Nominal
ib_006	DRE findings (part of biopsy-diagnostic variables)	Binary

Table 7. Top 10 important variables from baseline visit selected by CB-DNN for predicting 1-year follow-up sexual along with their definitions.

Variable	Definition	Type
ep_018	How would you describe your ability to reach orgasm (climax) during the last 4 weeks?	Ordinal
ib_008	Gland volume	Numerical
in_011	Have you ever been diagnosed with Dementia?	Binary
in_009	Have you ever been diagnosed with congestive heart failure?	Binary
ep_017	How would you describe your ability to have an erection during the last 4 weeks?	Ordinal
in_017	Have you ever been diagnosed with Diabetes?	Binary
ep_013	How big problem of Losing control of your stools, if any, has been for you?	Ordinal
ep_024	How big the problem of Breast tenderness/enlargement, if any, has been for you during the last 4 weeks?	Ordinal
ib_064	%of first RMZ core involved	Numerical
ep_023	How big the problem of Hot flashes, if any, has been for you during the last 4 weeks?	Ordinal

Table 8. Top 10 important variables from baseline visit selected by CB-DNN for predicting 1-year follow-up hormonal along with their definitions.

Variable	Definition	Type
ib_008	Gland volume	Numerical
in_027	Have you ever been diagnosed with HIV infection?	Binary
eq_002	Mobility	Ordinal
ip_006	In the past month how often have you had a weak urinary stream?	Ordinal
ep_014	How big the problem of Bloody stools, if any, has been for you?	Ordinal
ep_003	Which of the following best describes your urinary control during the last 4 weeks?	Ordinal
ep_011	How big the problem of Urgency to have a bowel movement, if any, has been for you?	Ordinal
ip_007	In the past month how often have you had to push or strain to urinate?	Ordinal
ib_051	%of second LB core involved	Numerical
in_008	Have you ever been diagnosed with Myocardial infarction?	Binary

The implementation of BN learning which is proposed in this study for explaining the results of the CB-DNN is shown in Algorithm 1. Steps 1 and 2 are initialization phases followed by a hill-climbing search (step 3), which is then refined with Tabu search (Glover 1997; Russell Stuart and Norvig 2009) in step 4 and MMHC (Tsamardinos, Brown, and Aliferis 2006) in step 5. The variations of each algorithm have been used in large parts of the literature on score-based BN structure learning (Friedman 1997; Tsamardinos, Brown, and Aliferis 2006). Arc additions and deletions is being used in hill climbing to explore the neighborhood of the current candidate to find if there is any DAG that increases the score over ${\mathcal{G}}_{max}$. Being an optimization heuristic, hill climbing cannot guarantee theoretically that ${\mathcal{G}}_{max}$ is a global maximum. In order to escape from local maximum, tabu search is applied. This greedy search tries to move away from ${\mathcal{G}}_{max}$ by allowing additional local moves (up to tabu list size). If a new DAG with a score larger than ${\mathcal{G}}_{max}$ is found in the process, that DAG is taken as the new ${\mathcal{G}}_{max}$ and it reverts to hill climbing in step 3. There is a possibility that no such DAG is found by tabu search. MMHC then tries again to escape the local maximum by first adding a mandatory arc from the most important variable extracted in CB-DNN part to the outcome of interest and then updating as follows. MMHC algorithm can be categorized as a hybrid method (Tsamardinos, Brown, and Aliferis 2006). It combines two main approaches that exist for learning BNs, search-and-score approach (Cooper and Herskovits 1992) and constraint-based approach (Spirtes et al. 2000). It first uses a local discovery algorithm to learn the skeleton of BNs and then a greedy Bayesian-scoring hill-climbing search. If the DAG that was resulted with tabu search, if any, was indeed the global maximum, the assumption is that MMHC will also identify it as the optimal DAG, in which case the algorithm terminates. For sake of complexity and considering the objective of this study, we treat the proposed model in a way that keeps only arc for $x_i\to E$ in which $x_i$ is any of the baseline variables extracted from CB-DNN and $E$ is the EPIC-26 domain which the current BN is trained for. In some cases, those that end up in the final structure might have dependency between themselves.

Results

CB-DNN determines important variables at the global level (i.e. per patient group), while BN can provide reasons at individual patient level. By combining the global and local method, we achieve the objective of the research: to make good HRQoL prediction for 1-year follow-up with high $R^2$ score while maintaining decent degree of interpretability. In the following sections, we show a comparative analysis of the proposed methods, which helps both physicians and patients to understand the results and get the right insights toward better treatment options and outcomes. In this section, we first show the variable importance results and model fitting obtained from CB-DNN; then, we evaluate the performance of BN method by presenting individual explanations for the patients by extracting the relationship between variables; finally, we summarize the top explanations/reasons for both approaches.

A. CB-DNN Results

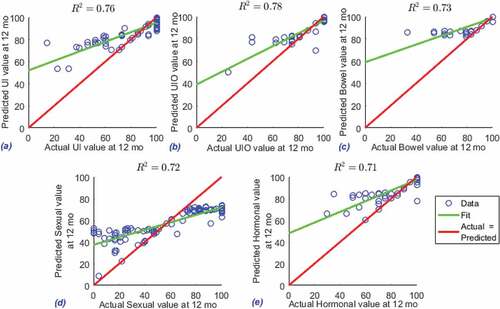
Initially, we have 2,670 patients which have a prior PCa diagnosis data in the data set, after filtering pre-treatment factors with other required pre-processing, as explained in section 3 the data set becomes 1214 patients with 433 variables. The final neural network model includes a total of 1214 patients who have both baseline visit data and 1-year follow-up data. The predictive model, in which we use baseline visit data extracted by CB-DNN to predict 1-year follow-up data, has good performance which the average R-squared ($R^2$) value of 0.74 on the test data. The performance metrics of predictive model (i.e. R-squared value) on the testing data are shown in Figure 1. Given the proposed solution which is regression prediction (i.e. predicting the continuous value of the output variable) not only classification prediction, and given that only pre-treatment variables are used to predict post-treatment HRQoL values, and furthermore managing to improve data reduction (in the variable extraction step), maintaining the accuracy level with average $R^2$ value of 0.74 would be acceptable.

Figure 1. R-squared between predicted and actual values in EPIC-26 domains. EPIC-26 Domains are a) UI b) UIO c) Bowel d) sexual and e) Hormonal.

The top 10 important variables selected by CB-DNN for EPIC-26 domains are reported in Tables 4, 5, 6, 7, and 8, for UI, UIO, B, S, and H, respectively. The top variables from baseline which are predictable for 1-year follow-up for each of the EPIC-26 domains are the following questions: a) UI: Usual activities? (Answer is one of the following options: 1, I have no problems doing my usual activities | 2, I have slight problems doing my usual activities | 3, I have moderate problems doing my usual activities | 4, I have severe problems doing my usual activities | 5, I am unable to do my usual activities); b) UIO: %of first RMZ core involved? (Answer is a numerical value); c) Bowel: Number of positive cores biopsied from LMZ? (Answer is one of the following options: 1, 1 | 2, 2 | 3, Fragmented core tissue); d) Sexual: How would you describe your ability to reach orgasm (climax)? (Answer is one of the following options: 1, Very poor to none | 2, Poor | 3, Fair | 4, Good | 5, Very good; e) Hormonal: How much is your Gland volume (cc)? (Answer is a numerical value).

These variables reflected by these questions point to the most important variable extracted by CB-DNN out of 400 variables which is predictable for each of the EPIC-26 domain. For example, the model discovered that the ability to reach orgasm in baseline visit is the most predictable variable for 1-year follow-up in terms of Sexual quality of life. The results which are presented may vary in a different hospital and with different variables saved in patients databases. Hospital administrators may use their own database to obtain insights from the proposed method.

The following sections are presenting the evaluation of a) the reliability of the CB-DNN model, b) the result in prediction section.

1. Evaluation Results for CB-DNN, extracting important variables: As per expert guide, there is no list of variables in baseline pre-treatment visit that are confirmed to be influential in 1-year follow-up EPIC-26 values. However, we do have the non-temporal influential variables for calculating EPIC-26 domain. Such that, for each EPIC-26 domain in current (baseline or follow-up) visit, the scores of variables listed in Table 9 (Sharifi et al. 2019) are averaged to calculate the domain summary score. Thus, we evaluate the performance of the CB-DNN in following two experiments:

   1. Extracting important variables from baseline data which are influential in baseline EPIC-26 domain values;

   2. Extracting important variables from 1-year follow-up data which are influential in 1-year follow-up EPIC-26 domain values.

   Table 9. The items related to each EPIC-26 domain. EPIC-26 Domains are UI, UIO, B (Bowel) and S (sexual).

   EPIC-26 domain	The items related to EPIC-26 domain	Number of items in the domain
   UI	ep-002, ep-003, ep-004, ep-005	4
   UIO	ep-006, ep-007, ep-008, ep-009	4
   B	ep-011, ep-012, ep-013, ep-014 ep-015, ep-016	6
   S	ep-017, ep-018, ep-019, ep-020 ep-021, ep-022	6
   H	ep-023, ep-024, ep-025, ep-026 ep-027	5

2. Evaluation Results for CB-DNN, 1-year follow-up prediction:

B. BN-based Explanation Model Results

In personalized healthcare, keeping track of patient medical history or even extracting important variables which can predict the outcome of interest is not the only objective for medical practitioners to maintain, but also they need to know the interaction between the important variables and the outcome of interest. Using the idea behind BN, practitioners can analyze the results from previous step and record patient’s important variable for enhancing patient’s quality of life. In addition, through necessary corrective actions, practitioners can get insights from the interaction between the variables in the past and provide better service for future patients. We applied the proposed hybrid BN model to all the patients but now only considering the top 10 variables from baseline visit extracted by CB-DNN and the 1-year follow-up EPIC-26 outcome variables to provide causal explanations for the relationship between the extracted variables and outcome of interest. Given that EPIC-26 outcome is a continuous value between 0 and 100, we need to quantify it before applying the BN model. So we have divided the patients into happy and unhappy groups based on their EPIC-26 outcome values. We call them unhappy because they are the ones with EPIC-26 value less than the mean value of the patients EPIC-26 values excluding those with the value of 100. Looking at test data in Figure 1, which the distribution of the data is the same as whole data set, we see that the data set is imbalanced in terms of the number of patients with their EPIC-26 value is 100. Therefore, to calculate the mean value for each of the domains in EPIC-26, we have excluded those whose number of their EPIC-26 is 100. The happy group is defined as the ones whose EPIC-26 value is more than mean of the patients EPIC-26 values excluding those with the value of 100. For each of the 5 domains in EPIC-26, we build a BN to capture the relationship of most important variables which impact patients’ quality of life/EPIC-26 value after 1 year. The BN models produce two outcomes which impact the patient’s EPIC-26 value. The results are shown in Figures (2,3,4,5,6), for UI, UIO, B, S, and H, respectively. The BNs in these figures only show the interaction between two extracted variables and the outcome of interest, the rest of the interactions that do not affect the EPIC-26 analysis are excluded. The BN results help both medical practitioners and patients to understand the relationship between the predicted outcome in baseline visit and quality of the life for the patients after 1 year. It is worth mentioning that when the BN model is ready, we can start inferring to have answers in terms of probability for our questions or concerns. Now we are taking hormonal domain as an example. From the CB-DNN model, the R-squared value that 10 extracted variables from baseline visit can predict the patients hormonal severity value after 1 year is 0.71. In Figure 6, the BN identified 2 locally important variables which can explain how these variables in baseline visit can affect their 1-year follow-up severity.

Figure 2. BNs explanation for UI. eq_004 (Usual activities?) has the following options:1, I have no problems doing my usual activities | 2, I have slight problems doing my usual activities | 3, I have moderate problems doing my usual activities | 4, I have severe problems doing my usual activities | 5, I am unable to doing my usual activities. im_001 (Bone scan?) has the following options: 1, yes | 2, No.

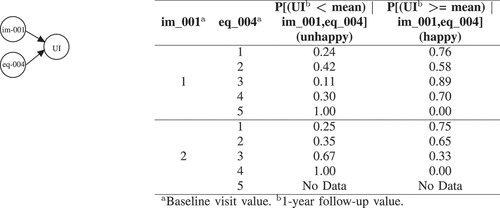
Figure 3. BNs explanation for UIO. ep_015 (Abdominal/Pelvic/Rectal pain?) has the following options: 1, No problem | 2, Very small problem | 3, Small problem | 4, Moderate problem | 5, Big problem. ib_064 (% of first RMZ core involved?) is a numerical variable which those less than the mean and greater than the mean are labeled with 0 and 1 respectively.

Figure 4. BNs explanation for Bowel (B). ib_042 (Number of positive cores biopsied from LMZ?) has the following options: 1, 1 | 2, 2 | 3, Fragmented core tissue. ep_012 (Increased frequency of bowel movements?) has the following options: 1, No problem | 2, Very small problem | 3, Small problem | 4, Moderate problem | 5, Big problem.

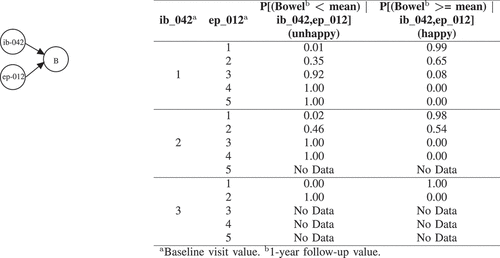
Figure 5. BNs explanation for Sexual (S). ep_017 (How would you describe your ability to have an erection during the last 4 weeks?) has the following options: 1, Very poor to none | 2, Poor | 3, Fair | 4, Good | 5, Very good. ep_018 (How would you describe your ability to reach orgasm (climax) during the last 4 weeks?) has the following options: 1, Very poor to none | 2, Poor | 3, Fair | 4, Good | 5, Very good.

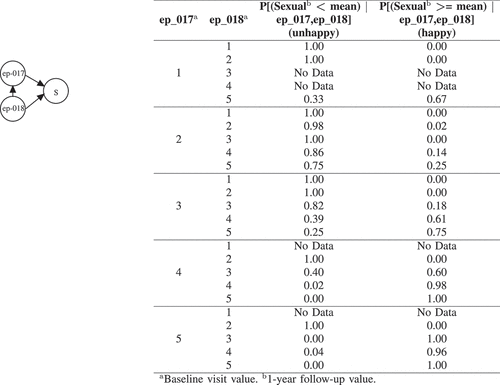
Figure 6. BNs explanation for Hormonal (H). eq_002 (Mobility?) has the following options: 1, I have no problems in walking about | 2, I have slight problems in walking about | 3, I have moderate problems in walking about | 4, I have severe problems in walking about | 5, I am unable to walk about. ib_008 (Gland volume?) is a numerical variable which those less than the mean and greater than the mean are labeled with 0 and 1 respectively.

After inferring the BN learned for Hormonal, of these 2 variables (i.e. eq_002 (Mobility?) and ib_008 (Gland volume?)), we can see that those whose mobility (eq_002) is better have less probability to be unhappy for their hormonal dysfunction after one year. As such, if they have no problems in walking about (option 1 for eq_002) the probability to be unhappy after 1 year is only 0.1, while the probability for those who have moderate problems in walking about (option 3 for eq_002) is 0.38.

Note that although the Hormonal variable is conditioned on 2 variables, we perform the query based on the evidence which is available on only one variable (eq_002). It is straightforward to make our evidence richer by asking more specific question about individual patients. Table 10 depicts the results for what-if analysis to build scenarios on 5 randomly selected patients which are unhappy after 1 year in UI, UIO, B, S, and Hormonal. For example, considering patient V (the fifth patient), the proposed BN method identified two locally important variables in baseline visit which can explain why patient V is unhappy in terms of hormonal quality of life after 1 year. After inspecting the current values of these 2 variables, we can see that this patient has a gland volume greater than mean (option 1 for ib_008) and have moderate problems in walking about (option 3 for eq_002). After performing What-If analysis, the BN shows that if patient V answered 1 (i.e. I have no problems in walking about) instead of 3 for question eq_002, the chances that he would be happy after 1 year for his hormonal quality of life would increase by 30%. We can better explain the impact of the extracted baseline visit variables with CB-DNN on patient’s unhappiness by using this scenario-based what-if analysis that BN provides. As mentioned earlier, in this study, we are using baseline variables which are pre-treatment. However, the use of such a tool is not only useful for pre-treatment suggestion but can also be directly transferred to explain treatment-related variables in a way to predict which treatment might help to improve HRQoL outcomes. The practitioners and patients can use these guidelines for future corrective measures and actions.

Table 10. What-If Analysis Scenarios for Five Patients.

EPIC-26 Variable	State Name	Influential Variable	Current Value	What-if	Changes in EPIC-26 Variable
UI (Patient I)	A	eq_004	2	2 – > 1	+ 12%
	B	im_001	2	2 – > 1	+ 3%
	A and B	eq_004	2	2 – > 1	+ 24%
		im_001	2	2 – > 1
Urinary Irritative /Obstructive (Patient II)	C	ib_064	3	3 – > 1	+ 45%
	D	ep_015	1	1 – > 0	+ 4%
	C and D	ib_064	3	3 – > 1	+ 56%
		ep_015	1	1 – > 0
Bowel (Patient III)	E	ib_042	3	3 – > 1	+ 3%
	F	ep_012	2	2 – > 1	+ 55%
	E and F	ib_042	3	3 – > 1	+ 99%
		ep_012	2	2 – > 1
Sexual (Patient IV)	G	ep_017	2	2 – > 3	+ 21%
	H	ep_018	2	2 – > 3	+ 33%
	G and H	ep_017	2	2 – > 1	+ 16%
		ep_018	2	2 – > 1
Hormonal (Patient V)	I	eq_002	3	3 – > 1	+ 30%
	J	ib_008	1	1 – > 0	0%
	I and J	eq_002	3	3 – > 1	+ 39%
		ib_008	1	1 – > 0

By comparing the top variables between two methods in Table 11, we figured that BN has changed the ranking among those 10 variables extracted by CB-DNN. This suggests us that although some variables might be important in terms of predictability power they have, it cannot be guaranteed that they will have the same rank in terms of explainability power which is suggested by BN. Our finding provides solutions to peek inside the proposed black box and not only extracting the variable importance in a novel way for longitudinal data but also making the results interpretable.

Table 11. Variable importance ranking comparisons between global algorithm CB-DNN and local BNs.

EPIC-26 Variable	Variable Importance Ranking from BNs Results. Rank 1 is:	Variable Importance Ranking by Deep Neural Network
Urinary Incontinence	im_001	Rank 9
UIO	ep_015	Rank 3
Bowel	ep_012	Rank 8
Sexual	ep_017	Rank 5
Hormonal	eq_002	Rank 3

Remarks, Limitations, and Ongoing Work

Longitudinal data provides an excellent opportunity to study PCa patient’s treatment satisfaction and HRQoL-related outcomes over time. However, the analysis of such data (i.e. pre-processing and designing of predictive and interpretable models) is a challenging task due to the complex and hidden data structures, unevenly spread out visits (i.e. not all patients are evaluated at exactly the same time), missing data, and mixtures of time-varying and static measures that may affect the outcome in a nonlinear complex relationships. Most of the literature focused on increasing the predictive power of the prediction models without investigating the ability of the model to explain the prediction. The contribution of this study is designing a model to predict the 1-year follow-up outcomes for the PCa patients with the highest degree of predictive power and with a decent ability to describe the predicted outcomes in terms of the most important influential input collected in the data set. This description will help practitioners and patients to share decisions about patient treatments that might affect certain aspects of their daily life routine and eventually their quality of life. Popular predictive models interpretation methods such as local interpretable model-agnostic explanations (LIME) technique, do not provide explanations of the predicted outcome based on nonlinear relationship. For example, LIME explains the predictions of a given classifier by learning a linear model locally around the prediction. The output of LIME is a list of explanations, describing the effect of each variable on the prediction of a data sample. This provides linear local interpretability, and it also allows to determine which variable changes will have the most impact on the prediction. The LIME is trained on small perturbations of the original instance and should only provide a local approximation. This presents a severe limitation of this method as it holds itself to the quality of the very nearby data points form a linear relationship.

However, in reality, the linear relationship is seldom found especially in the case of longitudinal data with such a complex structure of the data set under test (APCaRI data set). In this paper, we adopt the BN algorithm to learn the hierarchical prediction explanation based on the most influential factors extracted by the CB-DNN algorithm. The CB-DNN algorithm provides a better classification per group as it performs stratified prediction that focuses on each group of the patients and thus reduces the problem of highly imbalanced data.

The limitation of this study is that we adhere to the assumption behind the Naïve Bayes rule which is there is no interaction between the input variables given the outcome. We assume that to be able to interpret the prediction results in the variable domains. This limitation is the special focus of our future work as we believe that the nature of the interaction between the input variables toward the outcome is not linear and also may not be independent given the output. To address this limitation, we may adapt several orthonormal transformations of the variables and study the effect of these transformations on the predictive and interpretability power of the model.

Conclusion

In this paper, we construct a framework to extract important influential variables for PCa EPIC-26 prediction, learn, and interpret PCa patient data in a novel way. We demonstrated how to fit the patient data with the proposed CB-DNN algorithm and make accurate predictions of patients’ HRQoL outcomes. Furthermore, our framework uses a hybrid BN to provide explanations for CB-DNN, which is a black-box algorithm, resulting to represent the probability that the patient will feel a particular outcome in 1-year follow-up based on the baseline visit variables. To the best of our knowledge, this work is the first one to combine machine-learning model and explanation method for analyzing PCa data regarding their HRQoL measure and considering all of the EPIC-26 domains outcomes. The CB-DNN allows stakeholders to extract important variables out of the big data set that might affect the outcome of interest in longitudinal data. The implementation of our methods helps identify the key drivers of patient 1-year follow-up severity, in baseline visit, which the patient is newly diagnosed with PCa. Besides that, the proposed method is also the first that is predicting the continuous value for 1-year follow-up EPIC-26 outcomes, not only general classifications. Therefore, the framework generally can provide guidance for medical practitioners to navigate through the baseline variables to complex future outcomes. Despite the aforementioned strengths of this study and the successful implementation with real-world data, it has its own limitations which can be improved as new directions of future work. To start with, the proposed method is validated in a real-world big data set, but it can be externally validated as well to improve the trust of the end users. Second, the choice of the proposed hybrid model for the BN needs theoretical evidences and needs more investigation. Third, we want to use this framework for improvement in the feedback for their HRQoL outcome even considering their treatment choice. With considering the treatment-related variables, we can advice the future patients on which treatment they should select regarding their HRQoL preferences, this part is still under investigation. Overall, Despite these limitations, this work can contribute to ongoing effort to adopt good predictability and interpretability practices when considering HRQoL outcomes in patients with PCa.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Conjoint Health Research Ethics Board at the University of Calgary [00009687].