CFD Validation for Assessing the Repercussions of Filter Cake Breakers; EDTA and SiO₂ on Filter Cake Return Permeability

ABSTRACT

Drill-in-fluids create what are known as filter cakes. Filter cakes, in some cases, lead to well abandonment because they prevent hydrocarbons from flowing freely from the formation into the wellbore. Cake removal is essential to avoid formation damage. A previous study on filter cake breakers was considered for computational fluid dynamic (CFD) validation. Matlab-CFD and Navier-Stokes equations aimed at predicting and validating visual, multiphase flow under finite element analysis (FEA). The interactions of separate chemical breakers and drill-in-fluid such as ethylenediaminetetraacetic acid (EDTA), silica-nanoparticle (SiO₂), and biodegradable synthetic-based mud drill-in-fluid (BSBMDIF) were monitored under a particle size distribution, viscosity, density, and pressure. Predicting return permeability of filter cake was considered under a simple filtration process. The particles’ deposition created pore spaces between them; barite 74 μm, nano-silica 150 nm, and EDTA 10 μm generally closed up the pores of the filtration medium. Under extreme drilling conditions, barite formed thicker regions, and EDTA chemical properties easily disjointed these particles, while SiO₂ entirely did not. The experimented results of (EDTA) and SiO₂ for return permeability were in full force agreeable with the 2D simulation. A hybrid computational analysis considering CFD under discrete element analysis and neural network can be employed for further research validations.

Introduction

Filter cakes are the medium or seals to prevent the influx of formation fluids into the wellbore. Multiphase fluids are often separated using filtration, which is most common in industries. A medium like a ceramic disc is notable for the laboratory separation of solids and liquids (Picabea et al. 2022; Puhan et al. 2021). In most cases, filter cakes are formed (Fink 2021). During this process, pressure and temperature are influencers of the separation processes. The reduction of pressure determines the energy the process of filtration consumes over time. The resistance of the transition pressure is a result of the physical interactions of the filter cakes to the breakers or the interactions of the solid particles (Jahari et al. 2021) with liquids. Hence, the interactions of ethylenediaminetetraacetic acid (EDTA) and silica nanoparticles (SiO₂) with filter cakes are essential for defining the energy parameters associated and visually explaining the micromechanics involved. The process of validating the fluid micro-processes can be aided by 2D computational fluid dynamics using the Navier Stokes equations for multiphase flow (Ramadanet al. 2021; Sören and Jürgen 2012) as it explains why some chemical breakers (Al-Ibrahim et al. 2015) enhance return permeability. In literal terms, return permeability is the ability of the porous media to recover its damaged pore throats. However, it is worth noting that the interfacial reactions, whose solid-liquid particle flow separation effects are aggregated rather than by their sizes, impact the general fluid flow principle. Electrostatic force and Van-der- Waals forces influence these particles’ repellences.

The data obtained (Wayo 2022) in Figure 1 are from a carefully designed filter cake that was formulated using a biodegradable synthetic (Candler et al. 1993) based mud drill-in-fluid (BSBMDIF) which consists of barite (Siddig, Mahmoud, and Elkatatny 2020; Tariq et al. 2021), synthetic base oil, guar gum, sodium tridecyl ether sulfate, bentonite, caustic soda, calcium chloride, graphene powder, and freshwater. This filter cake interacted with chemical breakers or washers (Irawan et al. 2022) composed of main constituents of EDTA and SiO₂ to ensure a higher yield of return permeability.

Figure 1. Filter cake from BSBMDIF (a), Chemical Breakers; EDTA (b), SiO₂ (c) (Wayo 2022).

According to Al-Ibrahim, the removal process of filter cakes by EDTA had an incredible 93% efficiency (Al-Ibrahim et al. 2015). However, mixing this chelating agent with filter cakes from oil-based mud (Khodja et al. 2022; Ofei, Lund, and Saasen 2021) was free from emulsions, and the process over time took a maximum of 90 hours for such efficiency. Apart from barite (Bageri et al. 2017), calcium carbonate also poses a considerable threat (Bageri et al. 2019; Mahmoud et al. 2020) to the formation. Shaughnessy expresses a scientific view of reducing formation damage with EDTA; it effectively dissolves the metal ions in the cakes (Shaughnessy and Kline 1983). A previous study (Mcelfresh, Olguin, and Ector 2012) also examined the dispersion of nanofluids (Mohammadpour et al. 2022) for paraffin removal. The authors’ findings demonstrated how skin damage could be minimized by an aqueous (Yao et al. 2014) dispersion of nanofluids (Amanullah and Al-Tahini 2009; Chengara et al. 2004). The formulated additive was noted to have disjoined or dissolved forces that had caused the flow of formation fluid into the wellbore.

A further numerical and experimental analysis from a previous experiment (Shojaei and Ghazanfari 2022) demonstrated an elastic investigation of nanoparticle hydrophobicity in reducing formation damage. A weight per cent of 0.2 hydrophobic nano-silica had been observed to increase return permeability at 68.4%.

Nonetheless, sticking particles are assumed to have close contact with the starchy cakes as a result of the adhesive nature of the cakes. This mechanism of particle deformation is not further examined in this study. However, it is possible to consider particles under a gaseous state and their contact with strands because there is a high certainty of particles detaching (Puderbach, Schmidt, and Antonyuk 2021) themselves from the polymeric strands, as indicated in Figure 2.

Figure 2. Detachment of particles from strands (Puderbach, Schmidt, and Antonyuk 2021).

The dispersivity of particles in the filter cake medium is of greater interest, and EDTA and SiO₂ are intended to saturate the surface of the cakes to continually deform and separate particles from their original state and position. Though particle movement (Cundall and Strack 1979) and restructuring are best for the formation of cakes (Wakeman 2007), to increase the said permeability return (Tran, Abousleiman, and Nguyen 2010) using the chemical breakers, it is necessary to focus on particle dispersivity. Particle suspension, deformation, and dispersion under fluid flow concepts can be predicted and validated by the available data.

More so, the dynamics of particles and their kinematics can be validated using a computational fluid dynamic approach from MATLAB FEA Tool Multiphysics software under Navier Stokes equations to define the behavioral trends of particles interacting with chemical fluids to enhance permeability. In this context, numerical simulation (Guo and Curtis 2015) and the computer manipulation of data (Hussain and Sharif 2000) are capable of simulating particle motions under the effect of pressure.

Methods

Experimental Data

The dispersivity of chemical breakers on the surfaces of the filter cakes was crucial for the experiment conducted to attain the efficacy for return permeability. In Table 1, EDTA and SiO₂ were independently formulated (Wayo 2022) using additives such as NaCl, Deionized Water, Surfactant (Dioctyl Sulf. Sodium Salt), and Mutual solvent (1-Butanol), according to the author’s laboratory assessment. Table 2 provides a detailed chemical breakdown of the biodegradable synthetic-based mud drill-in fluid utilized to make the polymeric strand slurry necessary for determining the return permeability with interactions from formation pores and chemical breakers.

Table 1. Influence of EDTA and SiO₂ on return permeability (Wayo 2022).

		24 HR		42 HR
Cake breakers	Filter cakes	Removal efficiency, weight %	Return permeability, %	Removal efficiency, weight %	Return permeability, %
EDTA	#1	65.64	56.48
	#5			80.98	74.89
SiO2	#2	54.21	49.79
	#6			69.13	53.13

Table 2. Composition of filter cake buildup (Biodegradable Synthetic-Based Mud DIF) (Wayo 2022).

	ppg
Base Oil (Synthetic)	4.46
Sodium Tridecyl Ether Sulfate (emulsifier)	0.07
Bentonite (viscosifier)	0.02
Caustic Soda	0.014
Calcium Chloride	0.014
Water	1.43
Graphene Powder (Fluid Loss Control Agent)	0.02
Barite (weighting material)	3.54
Guar Gum (Biopolymer)	0.01
	10.0245

Filter cake buildup (Sauki et al. 2020) in Figure 3 was obtained by using the filtration medium (ceramic disc), high-pressure high-temperature (HPHT) filter press, nitrogen gas, and temperature. The cakes were subject to rigorous serial tests, including a soaking test, where chemical breakers get into close contact with the filter cake for different periods.

Figure 3. Experimental flow procedure to attaining data (Wayo 2022).

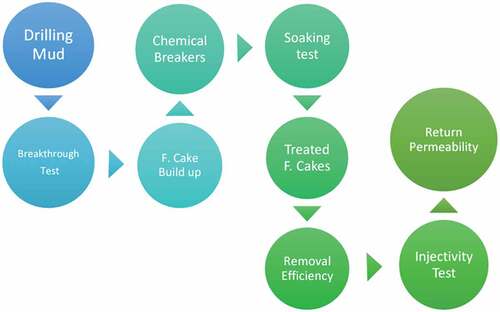
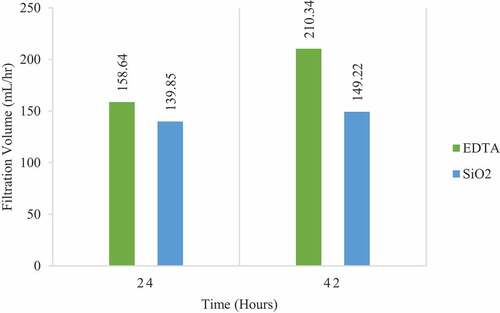
As per the record in Table 1, at 24 and 42 hours, the return permeability of the treated cakes numbered 1,2,5, and 6 gave a promising result indicating the effectiveness of chemical breakers. Even though the study’s concern is to identify and validate the reactions of these chemical breakers and filter cakes, the data will be reprocessed and presented in a mathematical formula under finite element analysis for validation.

Governing Equations for Fluid Flow

This approach filters the flow patterns of solid-liquid particles with the nanopore ceramic disc (Liu et al. 2019). The escape of the liquid phase (fluid base) of the drilling mud (Chilingar and Vorabutr 1981) invading the formation is termed filtration (Parn-anurak and Engler 2005). However, chemical breakers that made contact with the mud cakes underwent a rigorous process of filtration to break polymer strands of the buildup cakes. Under the fluid dynamic validation approach, a general Navier Stokes equation was used to govern the filtration process.

More so, fluids under porous media considered for this simulation process employed Darcy’s Law (Fisher et al. 2000).

(1) $u_i=-\frac{k_{ij}}{\mu }\partial \varphi \partial {\chi }_j$(1)

(2) $\varphi =\mathbf{p}-\rho \mathbf{g}\mathbf{z}$(2)

The volume flow rate $u_i$ is directly proportional to the effective permeability tensor $k_{ij}$ but inversely proportional to the viscosity $\mu$; however, the fluid potential $\mathrm{\Phi }$ is calculated by the differences between the pressure, $p$, and the product of fluid density, $\rho$, gravity, g and height, z. A further mathematical probe was made to define the relationship between fluid saturation, $\mathrm{S}$ and the porosity of the medium $\mathrm{\varnothing }$;

(3) $\varphi \frac{\partial S}{\partial t}\text{=-}\frac{\partial u_i}{\partial {\chi }_i}$(3)

(4) ${\mathit{S}}_{\mathit{w}}={\left(\frac{{\mathit{P}}_{\mathit{b}}}{{\mathit{P}}_{\mathit{c}}}\right)}^{\mathit{\lambda }}\left(\mathbf{1}\mathbf{-}{\mathit{S}}_{\mathrm{\infty }}\right)+\hspace{0.17em}{\mathit{S}}_{\mathrm{\infty }}$(4)

Eq. (4)(4) ${\mathit{S}}_{\mathit{w}}={\left(\frac{{\mathit{P}}_{\mathit{b}}}{{\mathit{P}}_{\mathit{c}}}\right)}^{\mathit{\lambda }}\left(\mathbf{1}\mathbf{-}{\mathit{S}}_{\mathrm{\infty }}\right)+\hspace{0.17em}{\mathit{S}}_{\mathrm{\infty }}$(4) describes the wetting fluid saturation, where $P_c$ is the capillary pressure and $S_{\mathrm{\infty }}$ is the irreducible wetting saturation. The difference between the non-wetting and wetting fluid pressures is known as capillary pressure (Fisher et al. 2000), and $\lambda$ is denoted as pore size distribution.

The modeling of relative permeability and Darcy’s law dived considering the equations relating to wetting $k_{rw}$ and non-wetting $k_{rn}$ fluids as presented in Eq. (5)(5) ${\mathbf{k}}_{\mathbf{r}\mathbf{w}}={\left(\frac{{\mathbf{P}}_{\mathbf{b}}}{{\mathbf{P}}_{\mathbf{c}}}\right)}^{\mathbf{2}\mathbf{+}\mathbf{3}\lambda }$(5) and (6(6) $k_{rn}={\left(1-{\left(\frac{P_b}{P_c}\right)}^{\lambda }\right)}^2\left(1-{\left(\frac{P_b}{P_c}\right)}^{2+\lambda }\right)$(6) ).

(5) ${\mathbf{k}}_{\mathbf{r}\mathbf{w}}={\left(\frac{{\mathbf{P}}_{\mathbf{b}}}{{\mathbf{P}}_{\mathbf{c}}}\right)}^{\mathbf{2}\mathbf{+}\mathbf{3}\lambda }$(5)

(6) $k_{rn}={\left(1-{\left(\frac{P_b}{P_c}\right)}^{\lambda }\right)}^2\left(1-{\left(\frac{P_b}{P_c}\right)}^{2+\lambda }\right)$(6)

Modeling Filtration

The resistivity of the free passage of liquid particles into the formation is characterized by the effects of the filtration medium and the filter cakes. A mathematical probe into finding the resistance or the pressure drop across this simulation is written as (Puderbach, Schmidt, and Antonyuk 2021);

(7) ${\mathbf{v}}_{\mathbf{f}}\left(\mathbf{t}\right)=\frac{\mathbf{\Delta }\mathbf{p}}{\mu .\left({\mathbf{R}}_{\mathbf{C}}\left(\mathbf{t}\right)+{\mathbf{R}}_{\mathbf{M}}\right)}$(7)

(8) ${\mathbf{R}}_{\mathbf{M}}={\mathbf{R}}_{\mathbf{M}0}+{\mathbf{R}}_{\mathbf{M}\mathbf{I}}$(8)

Whiles in Eq. (7(7) ${\mathbf{v}}_{\mathbf{f}}\left(\mathbf{t}\right)=\frac{\mathbf{\Delta }\mathbf{p}}{\mu .\left({\mathbf{R}}_{\mathbf{C}}\left(\mathbf{t}\right)+{\mathbf{R}}_{\mathbf{M}}\right)}$(7) ), $\mathrm{\Delta }p$ denotes the pressure drops, $R_C\left(t\right)$ and $R_M$ are the respective resistance of the filter cake and the filter medium. Where is the velocity of flow (Ozofor et al. 2021), and $\mu$ is the viscosity of the liquid. Eq. (8)(8) ${\mathbf{R}}_{\mathbf{M}}={\mathbf{R}}_{\mathbf{M}0}+{\mathbf{R}}_{\mathbf{M}\mathbf{I}}$(8) further explains the resistivity of the layered cakes; the sectioned equation has $R_{M0}$ as the pure filter medium resistance and $R_{MI}$ as the interference resistance.

For the purposes of flow dynamics, numerical simulations considered from experimental data (Wayo 2022) would be limited to calculations involving the filtrate’s velocity (Puderbach, Schmidt, and Antonyuk 2021) under the influence of the filter cake and medium. However, to understand the flow geometry and pattern, the flow equations must be considered linear (Hund et al. 2020), as shown in Eq. (9(9) $\frac{\mathbf{t}}{{\mathbf{V}}_{\mathbf{F}}}=\frac{\mu \cdot {\mathbf{r}}_{\mathbf{K}}\cdot {\mathbf{K}}_{\mathbf{s}}}{\mathbf{2}\cdot {\mathbf{A}}^{\mathbf{2}}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{V}}_{\mathbf{F}}+\frac{\mu }{\mathbf{A}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{R}}_{\mathbf{M}}$(9) ), where ${\mathrm{V}}_F$ is the filtration volume, t is the filtration time, $K_s$, filtration constant, $r_K$, filter cake resistance and A is the filtration area.

(9) $\frac{\mathbf{t}}{{\mathbf{V}}_{\mathbf{F}}}=\frac{\mu \cdot {\mathbf{r}}_{\mathbf{K}}\cdot {\mathbf{K}}_{\mathbf{s}}}{\mathbf{2}\cdot {\mathbf{A}}^{\mathbf{2}}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{V}}_{\mathbf{F}}+\frac{\mu }{\mathbf{A}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{R}}_{\mathbf{M}}$(9)

CFD Simulation

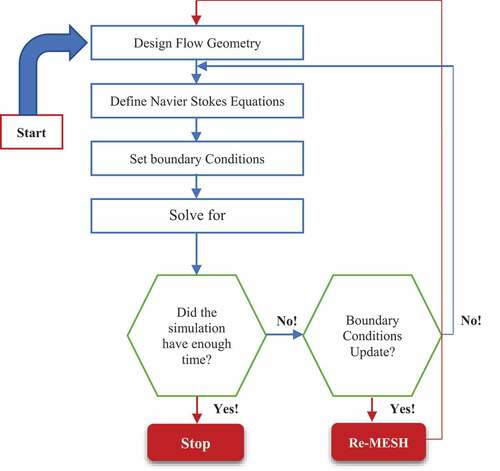
The deposition of chemical particles on the filter cakes and the flow of nitrogen gas across the carrier cell of the filter press are simulated under a finite element analysis tool in MATLAB. This Model supports the interpretation of non-Newtonian properties, yet, the Model’s premise explains that the particle trajectory flow follows the same pattern whether the particles are solid or liquid. This porous medium analysis from a laboratory experiment would represent the actual conditions in the reservoir. Also, the filter cake is a replica of the entire residual slurry (Zhang et al. 2019) circulated in the wellbore, while the base of the ceramic disc represents the walls of the formation. Filter cake or chemical breakers also represent large volumes that would be used for wellbore circulation. Simulation for the fluid dynamic procedures is simplified under the illustration in Figure 4.

Figure 4. CFD algorithm.

The algorithm for the simulation states that, after an identified equation is proposed to solve the flow validation, the first to begin with is to set the geometry of the filter press or the formation, then verify the mathematical representation of the fluid flow as in the case of Navier Stokes equation. In the third step, a boundary condition is set before the final computational analysis is drawn. Suppose the simulations are impeded by the thickness of the medium or by the pore spaces. In that case, the geometry can be readjusted to start the process again since the initial calculations would not be relevant to the results.

Assumptions

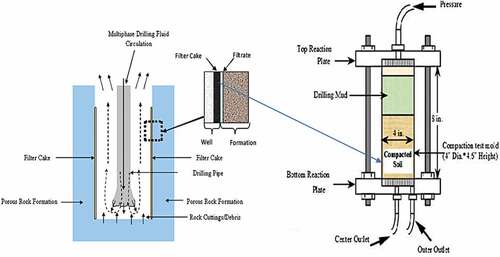
The effect of chemical breakers on the filter cakes was assumed to have similar physiochemical properties. Solid-liquid particles, at best, were considered to have flown and interacted axially in a vertical order of magnitude (Kabir and Gamwo 2011). The filter cake thickness of all samples was considered the same, and the porous medium from the same manufacturer was used as the benchmark for filtration. For an effective degradation of synthetic-based filter cake, the flow rate was determined using a constant pressure of 20 psi from nitrogen gas, as demonstrated in Figure 5. There might be a tolerance level for inaccuracy since the pressure regulators could have been screwed more or less at their initial experimental stages.

Figure 5. Field and Laboratory illustration of slurry invasion/filter cakes (Shehadeh et al. 2021).

Particle Sizes

This study solely focuses on the presence of mud samples in Table 3 and chemical breakers in Table 4 that were formulated from earlier literature (Wayo 2022). The biodegradable mud contained some ingredients pertinent to its suitability for protecting the formation from damage. Barite was used as the main constituent of the formulation in conjunction with guar gum. Other particles (Fred Fu and Dempsey 1998) from chemical breakers were considered to be silica nanoparticles (Medhi et al. 2021) and EDTA; as each of these made contact with the sample mud after a period of treatment, oil was applied, and under pressure, the size of the solid particles under a ceramic disc was made to define recovery (Khan et al. 2021). Barite, Silica nanoparticles (Ahmadabadi, Haghshenasfard, and Esfahany 2020) and EDTA are considered the main spherical-solid (Deshpande, Antonyuk, and Iliev 2020) particles for the CFD simulation. Researchers (Rabbani and Salehi 2017) in their study further explain the rheological (Baba Hamed & Belhadri, 2009) and particle distribution (Feng et al. 2020) of barite and calcium carbonate in Table 5 and Table 6.

Table 3. Sampled drilling fluid’s rheology for cake buildup (Wayo 2022).

		BSBMDIF1	BSBMDIF2	BSBMDIF3
Property	Unit	Range
Density	Ib/ft^3	120.02	120.02	120.02
PV	cP	97.0	93.8	95.9
YP	Ib/100 ft^2	136.4	133.4	135.3
10s gel	Ib/100 ft^2	2.8	2.5	2.7
10 min gel	Ib/100 ft^2	3.2	3.1	3.1
Fluid Loss (Fisher et al. 2000)	mL/30 min	<6
Filter cake thickness	1/32 inch	<2

Table 4. Chemical breakers (Wayo 2022).

Material	Quantity
EDTA/ SiO2	45 g (each)
NaCl	25 g
Deionized Water	40 mL/g
Surfactant (Disodium Salt)	2.38 g
Mutual Solvent(1-Butanol)	10 g

Table 5. Barite rheology (Rabbani and Salehi 2017).

Speed	Unit	Readings
PV	cP	34
YP	100 Ib/sq ft	3
10 Sec Gel	100 Ib/sq ft	2
10 Min Gel	100 Ib/sq ft	4
30 Min Gel	100 Ib/sq ft	5
Mud weight	ppg	11.5

Table 6. Rabbani’s fluid particle size distribution (Rabbani and Salehi 2017).

Drilling fluids	d	d 5 $0\left(\text{mum}\right)$	d 9 $0\left(\text{mum}\right)$
Barite	1.936	33.05	112.188
Fine Calcium Carbonate	0.983	10.092	37.548
Medium Calcium Carbonate	1.002	12.409	55.035
Coarse Calcium Carbonate	1.626	16.421	86.861

The physical distribution of these particles to increase the chances of return permeability is of more significant concern. Table 7 examines the size of particles for the simulation.

Table 7. Mud and breaker particle sizes.

Particle	Size	Quantity	Volume (%)
Barite	$74\left(\text{mum}\right)$	3.54 ppg	35.3
EDTA	$10\left(\text{mum}\right)$	45 g	54.2
Silica	$150\left(\mathrm{n}\mathrm{m}\right)$	45 g	54.2

Geometry

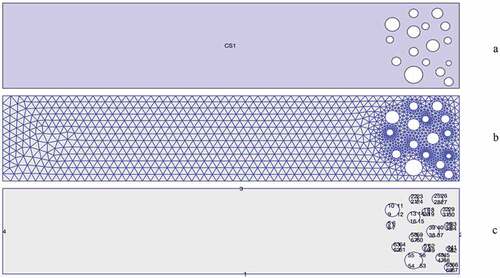
Simulating the above-experimented test results, an HPHT filter press carrier cell (Aging Cell, OFITE Style, 500 ML – OFI Testing Equipment, Inc., n.d.) and a ceramic disc, as illustrated in Figure 6a, were the laboratory materials used for creating the geometry. The pressure flow goes through the carrier cell’s inlet to the outlet. A further probe into Salehi’s Model of filtration experiment in Figure 6b indicates the exact measurement was considered suitable for the current computation. The current geometric models demonstrate a cylindrical pipe with excess vacuum denoted as white and a multicolored dot as the multiphase phase fluid (6.35 mm filter cake) with a porous base medium; ceramic disc with a mean pore throat of about 12 $\text{mum}$ and permeability of 850mD using the new API standard (Filters ; Salehi, Madani, and Kiran 2016).

Figure 6. Laboratory materials for return permeability (a) Salehi’s geometry model (b) Current geometry and flow navigation (c).

Mesh and Boundary

Multiphysics FEATool from MATLAB was used to draw out the 2-D geometry, mesh, and boundaries. A pressure of 20 psi injected into the cylinder had nitrogen gas circulated in a limited boundary. The mesh created had four outer boundaries and sixty-four interior boundaries. However, the flow was further restricted by the spherical solids-liquid particles (Hund et al. 2020) in the cylinder and the thickness of the filter cakes (Falahati, Chellappah, and Routh 2021) chemical breakers and oil. In Figure 7c, the inlet pressure was set at boundary four and the outlet pressure at boundary two. More so, for a smooth flow simulation, the velocity was assumed as superficial velocity, pressure and fluid density were made the main module for defining Navier-Stokes (Elman, Silvester, and Wathen 2014) fluid model.

Figure 7. Geometry (a), Mesh (b), Boundary (c).

Equations Summary

Mirroring the effects of flow results from cake formation and slurry invasion (Zhang et al. 2019) using the HPHT filter press were applied using theories from Navier-Stokes and other related equations. Equation 6(6) $k_{rn}={\left(1-{\left(\frac{P_b}{P_c}\right)}^{\lambda }\right)}^2\left(1-{\left(\frac{P_b}{P_c}\right)}^{2+\lambda }\right)$(6) simply refers to permeability and the probability of particles to nanoparticles colliding under specific force, the very means to determine the mechanical deposition (Rabbani and Salehi 2017) of particles under pressure, as illustrated in Figure 8. Also, Eq. 9(9) $\frac{\mathbf{t}}{{\mathbf{V}}_{\mathbf{F}}}=\frac{\mu \cdot {\mathbf{r}}_{\mathbf{K}}\cdot {\mathbf{K}}_{\mathbf{s}}}{\mathbf{2}\cdot {\mathbf{A}}^{\mathbf{2}}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{V}}_{\mathbf{F}}+\frac{\mu }{\mathbf{A}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{R}}_{\mathbf{M}}$(9) also defines the resistivity of the porous media and the filter cake thickness. The initial conditions of velocity and pressure were set to zero for the mathematical Model in Eq. 10. However, in the analysis of finite elements for this Model, fluid density, viscosity, and pressure were measured at 120 kg/m³, 97 cP, and 20 psi, respectively.

(10) $\mathit{\rho }\left({\mathit{U}}^{\mathit{I}}+\left(\mathit{U}\cdot \mathrm{\nabla }\right)\mathit{U}\right)=-\mathrm{\nabla }\mathit{P}+\mathrm{\nabla }\cdot \left(\mathit{U}\left(\mathrm{\nabla }\mathit{U}\cdot \mathrm{\nabla }{\mathit{U}}^{\mathit{T}}\right)\right)+\mathbf{F},\mathrm{\nabla }\cdot \mathit{U}=0$(10)

Figure 8. Probable mechanical dispersion of particles considered for simulation (Rabbani and Salehi 2017).

Results and Discussions

Filtration

The primary objective of defining return permeability under experimental analysis was subjected to HPHT filter press, treated filter cakes, treatments from chemical breakers; silica (Shafian et al. 2020) and EDTA and base oil. The experiment conducted in the previous work explains that oil under exerted force or pressure must tend to flow through the treated cakes without any impediment; indeed, there is resistance to flow, and pressure drops for this analysis (Liu et al. 2019) were further calculated in records of volume over time in Figure 9. However, the oil filtration or oil recovery under this simulation is calculated using Eq. 6(6) $k_{rn}={\left(1-{\left(\frac{P_b}{P_c}\right)}^{\lambda }\right)}^2\left(1-{\left(\frac{P_b}{P_c}\right)}^{2+\lambda }\right)$(6) .

Figure 9. Filtration volume over time.

Filtration impedance (Elkatatny, Mahmoud, and Nasr-El-Din 2011; Fakhreldin and Sharji 2010; Farahani et al. 2014; Salehi et al. 2015) was noted to be under the influence of particle size; barite, nanoparticles, pore sizes of the ceramic disc, and thickness of cakes. The current Model’s consideration in Eq. 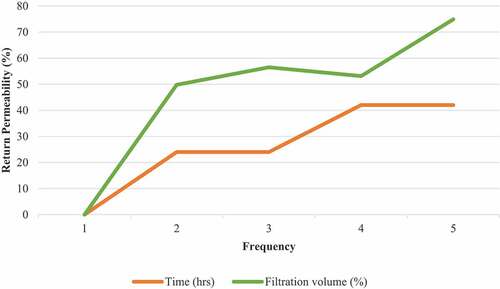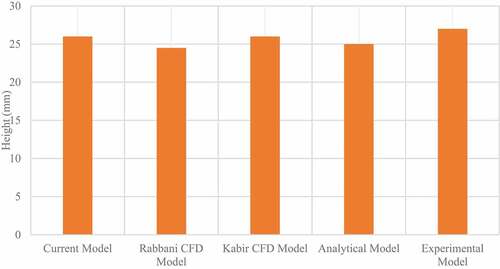9(9) $\frac{\mathbf{t}}{{\mathbf{V}}_{\mathbf{F}}}=\frac{\mu \cdot {\mathbf{r}}_{\mathbf{K}}\cdot {\mathbf{K}}_{\mathbf{s}}}{\mathbf{2}\cdot {\mathbf{A}}^{\mathbf{2}}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{V}}_{\mathbf{F}}+\frac{\mu }{\mathbf{A}\cdot \mathbf{\Delta }\mathbf{p}}\cdot {\mathbf{R}}_{\mathbf{M}}$(9) supports the understanding of permeability. The four treated cakes in Table 1 under the experiment had undergone a filtration process for 24 hours and 42 hours of surveillance. To this effect, the filtration volume over time is shown in Figure 10 in percentages depicting the permeability return. More so, the experimental and analytical results were compared with Rabbani and Kabir’s Model of filtration volume; the current CFD and empirical models are for filter cakes after treatments. The correlation between the present CFD and experimental models is slight variations, whereas the present CFD is significantly below the experimental Model. This is mainly due to the uneven distribution of particles which were seen heavily packed near the surface of the ceramic disc and loosely packed on the surface of the treated filter cake. However, the analytical analysis assumes particle distribution was relatively dispersed (Kabir and Gamwo 2011).

Figure 10. Quantum of filtration predicting rate of permeability.

In the Model from these authors (Rabbani and Salehi 2017), as measured in Figure 11, the CFD model concentrated on an aspect relating to mud cake deposition using filtration; this Model considered four different rock samples (Rabbani et al. 2016) and made use of filter press and ceramic disc. Figure 12a demonstrates barite particle distribution, and their results further explain why using barite for formulating drilling mud is more suitable than any other weighting material; barite under CFD analysis explains the large particle size and the loose compact nature of the weighting material. Hence, an increase in permeability (Acharya, van der Zee, and Leijnse 2004) is more visible in this essence. This research explains the efficacy of the present CFD simulation of barite particle simulation.

Figure 11. Filter cake thickness under comparative models.

Figure 12. Barite particle distribution (a) (Rabbani and Salehi 2017). Filtration of barite particles in shallow and deep wells (b) (Kabir and Gamwo 2011).

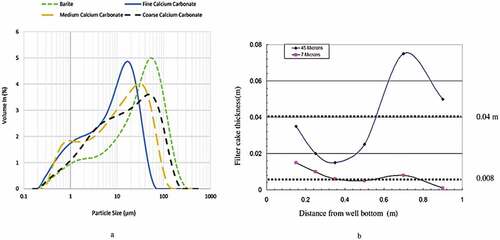
Nonetheless, Kabir’s CFD model in Figure 12b also expounds on the importance of understanding how filter cakes are formed in deep and shallow vertical wells. The researcher’s computer-aided design predicts a non-uniform particle dispersion in the wells; for a better description, the results show that in deep wells, the filter cake (Elkatatny, Mahmoud, and Nasr-El-Din 2011) thickness is greater than that of the shallow wells, high pressure and temperatures are denoted as the influencers. However, Kabir’s CFD model forcefully agrees with Rabbani’s Model, which describes that the effects of an increased thickness of filter cakes in deep wells are a result of larger particle sizes. However, barite was experimented with larger particle sizes and considered suitable for drilling fluid formulation.

Particles in Simulation

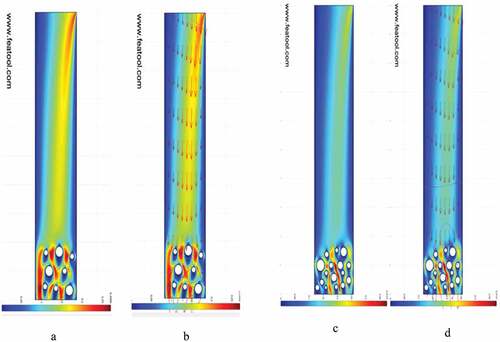
Filter cakes that were treated with EDTA chemical breakers had fewer cakes on the ceramic disc as compared to those that were treated with nano-silica (Khalil et al. 2020). The flow of oil under the colliding forces of particles was simulated using CFD. The dispersion of EDTA particles on the surface of the filter cake efficiently dissolved the interlocking bonds that had increased the velocity of fluids in Figure 13a. The pressure and velocity fields (Zitoun, Sastry, and Guezennec 2001) of the oil recovery in Figure 13b illustrate the direction of flow of nitrogen gas from the inlet valve to the bottom; the red and light green deviations foretell the maneuvering of fluids through particles and their density. The hydrodynamic effects of nanoparticles in a collision (Shafian et al. 2021) with weighting materials, as demonstrated in Figure 13c, were heavily dense, and the reaction of the flow of oil in this system was impeded by its thickness; hence a significant pressure drop is seen; this demonstration represents the effects of nano-silica treated filter cake. Moreover, from its experimented results, the average degradation of the weighting material was significantly appreciable but had more compact particles. Simulating these results in Figure 13d, the pressure and velocity profile indicate that the density of the particles restricted flow optimum.

Figure 13. Particle sizes in simulation to determine permeability return.

To further understand the simulation results, a fairer comparison is made with researchers who, to a greater extent, explain simulated particle migration relative to their size and behavior in porous media. Feng (Feng et al. 2020), on the other hand, placed granular particles in a rectangular box under free gravity fall. These particles were simulated using a discrete element method, and the suspension of these particles was observed to have migrated through a media by fluid flow whose initial velocity was set to zero in Figure 14. However, what this explains in this study is that the pore throats of the ceramic disc and the migration of the particle’s advances are heavily dependent on the particle-to-particle bridging and the existence of pressure from the inlet.

Figure 14. Particle sizes and dispersion (Feng et al. 2020).

Discussions and Conclusions

This current study elaborates on the effects of pressure, liquid viscosity, and density to discretize particles for the enhancement of return permeability under filtration; this study was further modeled by using the Navier-Stokes equation from Multiphysics FEATool in MATLAB to validate experimental results from previous work which was used as the basis for the simulation.

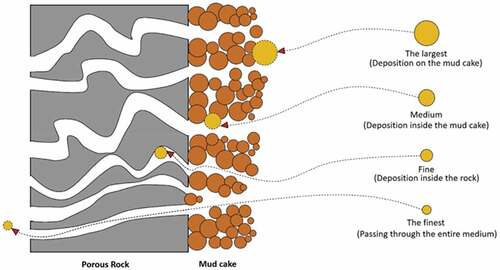
• Particle size distribution from barite, EDTA, and silica in Table 7 showcases the nature of the particles in metric form. Nanoparticles (SiO₂) are considered smaller than microparticles. Yet, the particles from EDTA (micro) containing an organic acid revealed their more significant potential for degrading the synthetic-based mud drill-in-fluid.

• The larger the particles under surveillance, the greater the pore throats it creates in between particles, while the smaller the particles, the smaller the pore throats. Simulating Figure 13a, the composition of the particles were barites and EDTA, which defines the experimental results from the previous studies, and explains why the EDTA was seen to have the highest return permeability value.

• Silica, on the other hand, had closed up the gaps (pore throats in between particles and the ceramic disc), allowing fluid passage difficult to penetrate. This under simulation in Figure 13c shows how compacted particles are distributed, and return permeability for this simulation is not remarkably achieved, validating the previous experimental work.

• It is empirical to note that the density and viscosity of the treated filter cakes under an established constant pressure showed a high-volume flow rate under EDTA treated filter cakes and a low-volume flow rate under nano-silica treated filter cakes over a predetermined period. It also explains that, at the same pressure, the solid particle lose-packed of the treated filter cakes started to expand, leading to particle-to-particle collisions.

• At a longer duration, the excretion of fluid through the tiny pores axially flowed through the ceramic disc into the graduated cylinder. Filtration under EDTA was better off than nano-silica; by this analysis, the return permeability from this perspective validates the experimental results from the previous work (Wayo 2022).

• The Matlab-CFD analysis validates the experimental work done in the previous study. Pressure, viscosity, density, and particle distributions are in force agreeable to the simulation analysis conducted.

• Chemical breakers’ interactions with the BSBMDIF reveal the industry’s propensity to use EDTA and SiO₂ in environmentally acceptable ways.

Acronyms and Nomenclature

Latin letters

CFD	=	Computational Fluid Dynamic
EDTA	=	Ethylenediaminetetraacetic Acid
BSBMDIF	=	Biodegradable Synthetic-Based Mud Drill-in-Fluid
FEA	=	Finite Element Analysis
SiO2	=	Silica Nanoparticles
HPHT	=	High-pressure High-temperature
$u_i$	=	Volume flow rate, m/s
$k_{ij}$	=	Effective permeability tensor, m2
$\rho$	=	Pressure, Pa
g	=	Gravity, ms−2
z	=	Height, mm
S	=	Fluid saturation
$p_c$	=	Capillary pressure, Pa
$S_{\mathrm{\infty }}$	=	Irreducible wetting saturation
$k_{rw}$	=	Relative permeability of the wetting fluid
$k_{rn}$	=	Relative permeability of the non-wetting fluid
${\mathrm{\Delta }}_p$	=	Pressure drops, Pa
$R_c(t)$	=	Resistance of the filter cake
$R_M$	=	Filter medium
$V_f(t)$	=	Velocity of flow, m/s
$R_{M0}$	=	Filter medium resistance
$R_{MI}$	=	Interference resistance
$V_F$	=	Filtration volume
t	=	Time of filtration, s
$K_S$	=	Filtration constant
$r_K$	=	Filter cake resistance
A	=	Filtration area, mm2

Greek letters

$\mu$	=	Viscosity of the liquid, Pa s
$\varphi$	=	Porosity of the medium
$\rho$	=	Fluid density, kgm−3
$\mathrm{\Phi }$	=	Fluid potential, Pa
$\lambda$	=	Distribution of pore size

Authorship Contribution

Dennis Delali Kwesi Wayo and Sonny Irawan designed the experimental work and generated the data. Dennis Delali Kwesi Wayo computed the simulation flow and wrote the manuscript. The methods and results of the manuscripts were reviewed by Sonny Irawan, Javed Akbar Khan and Fitrianti.

Data Availability

The primary data that supports the findings of this study are openly available in [Nazarbayev University Repository] at [http://nur.nu.edu.kz/handle/123456789/6132], and others are duly referenced.

Acknowledgments

We are thankful to Nazarbayev University for the opportunity given us to further share our piece of work under the competitive grant in the School of Mining and Geosciences. Notwithstanding, we passionately acknowledge all authors cited in this piece of work; we are most grateful for their extensive research work that supports knowledge transfer.

Disclosure Statement

We hereby state that no known competing financial interests or personal ties could have influenced the research presented in this study.

Additional information

Funding

The authors declare that the source of funding for this study was from; The Faculty Development Competitive Research Grants for 2020-2022 at Nazarbayev University. Project No. 080420FD1911.