An Enhanced GWO Algorithm with Improved Explorative Search Capability for Global Optimization and Data Clustering

ABSTRACT

In this paper, we have introduced a differential perturbation operator into the gray wolf optimization (GWO) algorithm using three randomly selected omega wolves which assist the three leader wolves of the original GWO algorithm for diversifying the solution quality among the feasible omega wolves. Additionally, we have introduced the use of similar values for the control parameters (A and C) of GWO for each leader wolf while updating the position of a single omega wolf. This diversification among the omega wolves introduces an element of exploration in the exploitation phase and hence further improves the optimization capability of the GWO algorithm. For comparative performance analysis, the results obtained from the proposed algorithm are compared with ten promising recently proposed meta-heuristic algorithms such as IAOA, RSA, mGWOA, VWGWO, mGWO, GWO, SCA, JAYA, ALO and WOA in optimizing 23 mathematical benchmark unimodal, multimodal and fixed dimension functions. Additionally, the performance of the proposed algorithm is tested in 12 promising data clustering problems using four performance measures such as accuracy, precision, F-score and MCC. Superiority of the proposed algorithm in optimizing benchmark functions and data clustering is statistically verified using pairwise Wilcoxon signed-rank test and Friedman and Nemenyi hypothesis test.

Introduction

Global optimization is a challenging task in the field of mathematics and computer science due to its substantial number of interdependent applications. In the essence of global optimization without the loss of generality, an optimization problem can be represented as given in eq. (1)(1) $\underset{x\epsilon R^n}{min}f\left(x\right)$(1) :

(1) $\underset{x\epsilon R^n}{min}f\left(x\right)$(1)

Here, $f\left(x\right)$ is an objective function defined over search space $R^n$, where the search space $R$ covers an n-dimensional space. To be specific, an optimization algorithm can be presented as given in eq. (2)(2) $x\left(t+1\right)=x\left(t\right)+m.d\left(t\right)$(2) :

(2) $x\left(t+1\right)=x\left(t\right)+m.d\left(t\right)$(2)

Where, $m$ is a scalar quantity and $d\left(t\right)$ is a vector. Here, the eq. (2)(2) $x\left(t+1\right)=x\left(t\right)+m.d\left(t\right)$(2) reveals that the optimization algorithms always search from the current position $x\left(t\right)$ to destination $x\left(t+1\right)$ by moving along the direction $d\left(t\right)$ with a step-size given by $m$.

Considering the above properties of optimization algorithm, different algorithms use different procedure to select $m$ and $d\left(t\right).$ Correspondingly, the performance of each algorithm depends on these two parameters. For example, Newton Raphson’s algorithm uses Newton’s steps to select$m$ and $d\left(t\right)$, the gradient descent algorithm uses negative gradients to select these above values with a hope to find optimal solutions. Moreover, these conventional algorithms show difficulties in solving the problems such as stagnation, dependence of initial solutions and converging to local optimal solutions. To tackle such issues, the real-world problems need to be simplified to be inclined toward specific mathematical properties such as continuity, differentiability and convexity. However, inclining such real-world problems toward certain mathematical properties is itself a hard problem as the real-world problems are non-differentiable, discontinuous, multimodal and multidimensional (Jamil and Yang 2013). Considering the above difficulties, the traditional algorithms are not suitable for obtaining satisfactory results.

The above situations expedite to search for new optimization algorithms such as meta-heuristic algorithms that intelligently and adaptively integrate various procedures for solving complex problems. Despite the fact most of the time it is not possible to obtain optimal solutions it is possible to obtain near-optimal solutions within a satisfactory amount of time. These meta-heuristic algorithms no longer require the convexity of the objective function and hence easier to apply in a wide range of optimization problems.

After several years of research in the field of optimization, many meta-heuristic based optimization algorithms have been developed such as Genetic Algorithm (GA) (Abualigah and Alkhrabsheh 2022; Alba and Dorronsoro 2005; Holland 1992; Lamos-Sweeney 2012; Liu, Xindong, and Shen 2011; Maulik and Bandyopadhyay 2000; Saida, Nadjet, and Omar 2014; Xiao et al. 2010; Zeebaree et al. 2017; Zhou, Miao, and Hongjiang 2018), Particle Swarm Optimization (PSO) (Aydilek 2018; Bratton and Kennedy 2007; Das, Abraham, and Konar 2008; X. Hung and Purnawan 2008; Kennedy and Eberhart 1995; der Merwe and Engelbrecht 2003, 2003; Mirjalili, Zaiton Mohd Hashim, and Moradian Sardroudi 2012; Olorunda and Engelbrecht 2008; Rana, Jasola, and Kumar 2010; Van Der Wang, Geng, and Qiao 2014; Zhang et al. 2021), Grey Wolf Optimization (GWO) (Akbari, Rahimnejad, and Andrew Gadsden 2021; Al-Tashi et al. 2019; Al-Tashi, Rais, and Jadid 2018; S. Faris et al. 2018; Gupta and Deep 2019; Kamboj, Bath, and Dhillon 2016; Kapoor et al. 2017; X. Katarya and Prakash Verma 2018; X. Khairuzzaman and Chaudhury 2017; Kumar, Kumar Chhabra, and Kumar 2017; Mirjalili 2015b; Mirjalili, Mohammad Mirjalili, and Lewis 2014a; Singh and Chand Bansal 2022; Teng, Jin-Ling, and Guo 2019; Zhang and Zhou 2015; Zhang et al. 2018, 2021), Sine Cosine Algorithm (SCA) (Mirjalili 2016b), Jaya Algorithm (JAYA) (Rao 2016), Teaching Learning based Optimization (TLBO) (R. V. Rao, Savsani, and Vakharia 2011), Cuckoo Search (CS) (Yang and Deb 2010), Ant Lion Optimization (ALO) (Azizi et al. 2020; Mirjalili 2015a), Whale Optimization Algorithm (WOA) (Chen et al. 2019; Mirjalili and Lewis 2016; Obadina et al. 2022), Bat Algorithm (BA) (Yang 2013; Yang and Hossein Gandomi 2012), Ant Colony Optimization (ACO) (Dorigo 2007), Artificial Bee Colony Optimization (ABC) (Karaboga 2010), Differential Evolution (DE) (Draa, Bouzoubia, and Boukhalfa 2015; Nadimi-Shahraki, Taghian, and Mirjalili 2021; Qin, Ling Huang, and Suganthan 2008), Gravitational Search Algorithm (GSA) (Bansal, Kumar Joshi, and Nagar 2018; Hooda and Prakash Verma 2022; Rashedi, Nezamabadi-Pour, and Saryazdi 2009; Venkateswaran et al. 2022), Moth Flame Optimization (MFO) (Mirjalili 2015c), Multi-Verse Optimizer (MVO) (Seyedali Mirjalili, Mirjalili, and Hatamlou 2016; Abualigah and Alkhrabsheh 2022), Dragonfly Algorithm (DA) (Elkorany et al. 2022; Mirjalili 2016a), Black-hole based Optimization (BBO) (Hatamlou 2013), Grasshopper Optimization algorithm (GOA) (S. Z. Abualigah and Diabat 2020; Mirjalili et al. 2018), Tabu search (TS) (Al-Sultan 1995; Alotaibi 2022; Ghany et al. 2022), Arithmetic Optimization Algorithm (AOA) (Abualigah et al. 2021), Improved Arithmetic Optimization Algorithm (IAOA) (Kaveh and Biabani Hamedani 2022), Reptile Search Algorithm (RSA) (Abualigah et al. 2022), Sand Cat Swarm Optimization (SCSO) (Seyyedabbasi and Kiani 2022), Modified Grey Wolf Optimization Algorithm (mGWOA) (Kar et al. 2022), Modified Grey Wolf Optimization (mGWO) (Mittal, Singh, and Singh Sohi 2016), Variable Weight Grey Wolf Optimization (VWGWO) (Gao and Zhao 2019), Incremental GWO (I-GWO) and Expanded GWO (Ex-GWO) (Seyyedabbasi and Kiani 2021), Improved GWO (Hou et al. 2022), I-GWO (Nadimi-Shahraki, Taghian, and Mirjalili 2021), Multi-Verse Optimizer (MVO) (Mirjalili et al., 2016) and Simulated Annealing (SA) (Kirkpatrick, Daniel Gelatt, and Vecchi 1983; Lee and Perkins 2021; Rutenbar 1989; Selim and Alsultan 1991). These meta-heuristic-based optimization algorithms are now becoming popular among the researchers because: (i) no requirement of gradient information, (ii) easy to implement and simple concept, (iii) has high potentiality to overcome local convergence issue and (iv) independent of problem domains. Additionally, these meta-heuristic algorithms are one of the most effective optimization algorithms which can easily find near-optimal solutions for any complex problem. Therefore, most of the complex optimization problems are solved using meta-heuristic based algorithms. In addition, due to flexibilities in algorithmic steps, the researcher are able to improve the performance with some minor or major modifications.

These nature inspired meta-heuristic algorithms can be categorized into (i) Swarm intelligence based (Parpinelli and Lopes 2011), (ii) evolutionary-based (Thiele et al. 2009), (iii) physics-based (Biswas et al. 2013), (iv) human-based algorithms (R. V. Rao, Savsani, and Vakharia 2011). Among these, many evolutionary algorithms are quite popular that are inspired by natural phenomena such as theory of evolution. These algorithms mainly generate random population in the initial phase and evolve through number of generation to improve the quality of solutions. The key strength of such algorithms is that the most fit chromosomes in the population are allowed to combine together to form chromosome for the next generation that helps the population to optimize the candidate solutions over the course of iterations. However, due to ignorance of search space information over the subsequent iterations these algorithms are unable to perform well to avoid local convergence. These problems have been easily tackled by swarm intelligence-based approaches. The technique of swarm intelligence approach mimics the social behavior of animals. For the last two decades, the swarm intelligence-based optimization algorithms have become more common among researchers than the evolutionary approaches due to the innovation of more numbers of competitive nature-inspired algorithms that use population information for evolving through new generations. The most advantageous features of this swarm-based optimization algorithm is the preservation of population information over the subsequent iterations and requirement of less operators in comparison to evolutionary algorithms. Therefore, these class of meta-heuristics are comparatively easier to implement. Due to such advantageous features, most of the real-life optimization problems are solved using swarm intelligence algorithms such as robot path planning (Kiani et al. 2022), FOPID controller design for power system stability (Kar et al. 2022), medical data analysis (Shial, Sahoo, and Panigrahi 2022a, 2022b), Time Series Forecasting (Panigrahi and Sekhar Behera 2019) and Internet of Things (Kiani and Seyyedabbasi 2022).

Regardless of the nature of each meta-heuristic based optimization algorithm, all these optimization algorithms share a common way of searching process, i.e. the whole search process is divided into two phases, i.e. exploration and exploitation (Alba and Dorronsoro 2005; Bansal and Singh 2021; Lin and Gen 2009; Olorunda and Engelbrecht 2008). In the exploration phase the degree of randomness among the search agents should be as most as possible to select feasible solutions from the most diversified solutions in the search space. Similarly, in the exploitation phase comparatively small degree of randomness should be adapted to search from the local region of the previously selected feasible solutions. Therefore, for an optimization algorithm to find better solutions, in the early stage of search process more exploration is maintained whereas in the later stage more exploitation is maintained. Moreover, maintaining a proper balance between exploitation and exploration is a crucial as well as a challenging task due to the stochastic nature of most nature-inspired meta-heuristic-based optimization algorithms. The research on stochastic optimization algorithms show that the idea of gradual change from exploration to exploitation toward the convergence gives most efficient results for an optimization problem (Mirjalili, Mohammad Mirjalili, and Lewis 2014a).

GWO is a recently developed efficient meta-heuristic algorithm proposed by Mirjalili et al. (Mirjalili, Mohammad Mirjalili, and Lewis 2014b) in the year 2014. The algorithm is mostly inspired by the leader wolf strategy (alpha, beta and delta wolf) of GWO which helps to find the search direction throughout the iterations and ensures fast convergence. In literature, this algorithm has been used for feature selection (Al-Tashi et al. 2019), economic dispatch problem (Pradhan, Kumar Roy, and Pal 2016), control system (Obadina et al. 2022), power dispatch problem (Jayakumar et al. 2016), data clustering (Ahmadi, Ekbatanifard, and Bayat 2021), classifications (Al-Tashi, Rais, and Jadid 2018), etc. Although the performance of GWO algorithm is very promising compared to other well-known algorithms, still for some complex optimization problems this algorithm traps at local optimal solutions and experiences ineffective balance between exploitation and exploration. The striking mechanism of GWO is with its leader wolves and multiple solution-based guided search scheme that provides a balance between exploration and exploitation. Therefore, in the literature several attempts have been made to improve the performance of GWO by modifying its search mechanism. For example, Gao and Zhao (Zhao and Ming Gao 2020) proposed a variable weight GWO and their governing equations which signifies unequal weight to each leading wolves with higher weight to alpha wolf (α) in comparison to beta wolf (β). Similarly, it applies for β and delta wolf (δ) with higher weight to beta in comparison to δ wolf while calculating the positions of each omega wolf during its explorative search. This paper also suggests to make a gradual decline in weight with the change in iterations for giving equal weight to each leader wolf toward the phase of exploitation which generally happens to arise toward the end of all iterations. Mittal et al. (Singh and Chand Bansal 2022) proposed a nonlinear control parameter to improve performance of GWO. It allows to control and balance the exploration and exploitation nature of algorithm. The results from experimental work suggest that the algorithm has achieved better performance but still unable to perform well on multimodal problems. Further, to improve the explorative skill of GWO, Long et al. (Long et al. 2018) proposed enhanced GWO (EEGWO). This algorithm uses a modified equation for position updation in order to improve the exploration capability of the algorithm. This EEGWO also uses a non-linear control parameter for balancing the diversity and the speed of convergence. Similarly, Bansal and Singh (Bansal and Singh 2021) proposed IGWO to enhance the exploration capability and to improve convergence speed using opposition-based learning. However, the mentioned algorithm is beneficial if the optimal result is far from the current solutions. Similarly, Yu, Xu and Li (Xiaobing, WangYing, and ChenLiang 2021) combined opposition-based learning (OBL) with GWO and proposed OGWO and also proposed a non-linear control parameter for enhancing the performance of original GWO. The algorithm improves its search capability in most benchmark problems while skipping true aspect of search process in most of the multimodal problems. Fan et al. (Fan et al. 2021) proposed a modified GWO algorithm by integrating beetle antenna strategy with the existing GWO algorithm for reducing unnecessary searches and to improve the exploration capability. This variant enhances exploration skill of the algorithm but unable to perform well for unimodal benchmark functions which shows poor capability in exploitation. Similarly, focusing on the improvement of exploration skill. Bansal and Singh (Bansal and Singh 2021) incorporated OBL with the explorative equation of GWO. Considering the classical GWO algorithm, it is observed that the algorithm suffers from trapping to local optima and less explorative capability.

The key contributions of the paper are summarized as follows:

• Developed an enhanced GWO algorithm by incorporating a differential perturbation operator along with the use of randomly chosen omega wolves to obtain modified representation of α, β and δ wolves that maintains a better trade between exploration and exploitation.

• Introduced similar values for parameters $A$ and $C$ for each leader wolf while updating the position of a single omega wolf to incorporate an element of exploration in the exploitation phase.

• Applied the proposed GWO algorithm for optimizing 23 mathematical benchmark unimodal, multimodal and fixed dimensional multimodal functions.

• In addition, to test the superiority of our proposed algorithm, we have applied it in 12 promising data clustering problems from UCI machine learning repository.

• Applied Wilcoxon signed-rank test on the results to pairwise compare the algorithms on benchmark problems and 12 data clustering problems.

• Applied Friedman and Nymenyi hypothesis non-parametric test on the obtained results to statistically rank the meta-heuristic algorithms (1 proposed +10 from the recent literature) in optimizing benchmark functions and clustering data.

The rest of the paper is organized as follows: Section 2 briefly introduces the background of GWO algorithm and its related literature. Section 3 describes the proposed enhanced GWO algorithm. Section 4 describes the application of proposed algorithm to data clustering problem. Section 5 describes the performance evaluation of our proposed algorithm using benchmark functions. Section 6 describes the performance evaluations of our proposed algorithm on benchmark clustering datasets. Finally, section 6 concludes the paper with academic implications and future research directions.

Grey Wolf Optimization

Grey wolf optimization (GWO) is a well-known meta-heuristic-based optimization algorithm introduced by Mirjalili et al. (Mirjalili, Mohammad Mirjalili, and Lewis 2014a) by mimicking the process of prey search and attacking procedure of gray wolves. The GWO is used in different fields of optimization such as software testing, medical diagnosis and engineering applications. The most advantageous features of this algorithm are simple concept, high-speed convergence, few adjustable parameters, better exploitation ability and being most appropriate for both linear and complex optimization problems. This algorithm uses a 4-layer pyramid structure to maintain the hierarchical structure of gray wolves for hunting and encircling processes. The hierarchy comprises alpha, beta, delta and omega group of wolves in first, second, third and fourth layers respectively with a decreasing order of dominance behavior among themselfs. Here, most importantly the top three leader wolves help a number of omega wolves to lead the hunting process in order to achieve near-optimal solutions. Again due to such collaborative activities among the wolves in the hierarchy, the chances of falling into local optimal decreases for the omega wolves. The hunting process of gray wolf is simulated in three steps such as (a) encircling, (b) hunting and (c) attacking the prey.

The mathematical illustration for encircling process of gray wolf for the prey is as given in eq. (3)(3) $D=\left|C.X_p\left(t\right)-x\left(t\right)\right|$(3) and eq. (4)(4) $Y=X_p\left(t\right)-A\times D$(4) :

(3) $D=\left|C.X_p\left(t\right)-x\left(t\right)\right|$(3)

(4) $Y=X_p\left(t\right)-A\times D$(4)

where t denotes the current iteration, $X_p\left(t\right)$ represents the location of prey at $t^{th}$ iteration, $x\left(t\right)$ is the current position of a gray wolf at $t^{th}$ iteration and $Y$ is the updated position of gray wolf $x\left(t\right)$. The coefficients of the algorithm such as $C$ and $A$ are calculated as given in eq. (5)(5) $C=2.r1$(5) and eq. (7)(7) $A=2\ast a\ast r2-a$(7) :

(5) $C=2.r1$(5)

(6) $a=2-\frac{2\ast t}{MaxIter}$(6)

(7) $A=2\ast a\ast r2-a$(7)

where r1 and r2 are two random values which range in the interval [0-1] and $a$ is an acceleration coefficient that decreases linearly from 2 to 0 with the course of iteration. The linear change in the value of $a$ can be mathematically represented as given in eq. (6)(6) $a=2-\frac{2\ast t}{MaxIter}$(6) that helps to make a transition from exploration to exploitation.

Hunting: With the assumption that the leader wolves have better knowledge about the location of prey, and therefore, these three leader wolves guide the other wolves in the overall hunting process.

In order to mathematically represent the hunting process of gray wolf, it is assumed that the best three wolves have better knowledge about the location of the prey. Therefore, considering the above assumption with the leadership hierarchy of gray wolf, hunting behavior of each omega group of wolf is mathematically modeled as given in eq. (8)(8) $Y_1=\alpha -A_1\times \left|C_1.\alpha -x\left(t\right)\right|$(8) , eq. (9)(9) $Y_2=\beta -A_2\times \left|C_2.\beta -x\left(t\right)\right|$(9) and eq. (10)(10) $Y_3=\delta -A_3\times \left|C_3.\delta -x\left(t\right)\right|$(10) :

(8) $Y_1=\alpha -A_1\times \left|C_1.\alpha -x\left(t\right)\right|$(8)

(9) $Y_2=\beta -A_2\times \left|C_2.\beta -x\left(t\right)\right|$(9)

(10) $Y_3=\delta -A_3\times \left|C_3.\delta -x\left(t\right)\right|$(10)

where $Y_1,Y_{2}and{Y}_3$ are three different suggestions by the leader wolves, i.e. alpha (α), beta (β) and delta (δ) respectively to help update the position of a single omega wolf (ω) at iteration$t$. The$C_1$,$C_2$ and $C_3$ are three random numbers generated within range [0–2] as given in eq. (5)(5) $C=2.r1$(5) . Similarly, $A_1$,$A_2$ and $A_3$ are three random parameters that helps in making a linear transition from exploration to exploitation. Mathematically, the linearity and randomness are incorporated into the search strategy using eq. (5)(5) $C=2.r1$(5) and eq. (7)(7) $A=2\ast a\ast r2-a$(7) . Most importantly, the value of the control parameters $A$ and $C$ controls the global and local search behavior of the algorithm. Finally, the combined effort of the above three wolves helps to update the position of omega group of wolves using the given eq. (11)(11) $x\left(t+1\right)=\frac{Y_1+Y_2+Y_3}{3}$(11) :

(11) $x\left(t+1\right)=\frac{Y_1+Y_2+Y_3}{3}$(11)

Considering a few control parameters, ease of implementation and simplicity, it has been applied for solving wide variety of problems such as economic despatch problem (Jayabarathi et al. 2016; Pradhan, Kumar Roy, and Pal 2016), parameter estimation (X. Song et al. 2015), Recommender System (Katarya and Prakash Verma 2018), Unit Commitment Problem (Kamboj 2016), Wind Speed Forecasting (Song, Wang, and Haiyan 2018), Optimal Power Flow (Sulaiman et al. 2015) and Feature Selection (Qiang, Chen, and Liu 2019).

Moreover, a lot of research has been carried out to improve the performance of GWO by modifying its search mechanism to come up with some new variant of GWO for avoiding local convergence and improving the speed of the algorithm. Recently, Zhao and Ming Gao (2020) (Zhao and Ming Gao 2020) proposed a variable weight updation strategy to update the positions of omega wolves instead of combining the efforts of each leader wolf by giving equal importance. Additionally, they also proposed a weight updation strategy that helps to give more importance to the $\alpha$ in comparison to $\beta$ and $\delta$. Later, with the change in iteration the weights are updated linearly to give equal importance to each leader wolves to convert the hunting phase into attacking phase. To achieve this three weight factors (w1, w2 and w3) are multiplied with α, β and δ wolves respectively as given in eq. (12)(12) $x\left(t+1\right)=w1.Y_1+w2.Y_2+w3.Y_3$(12) :

(12) $x\left(t+1\right)=w1.Y_1+w2.Y_2+w3.Y_3$(12)

Mathematically, the weight of α would be reduced from $1.0$ to $1/3$ at the same time weight of β and δ would be enhanced from 0 to 1/3 with the change in iterations. Subsequently, thetheta (ϕ) and thephi (φ) are obtained in each iteration to update the above-mentioned weight factors to achieve the goal as given in eq. (13)(13) $\phi =\frac{1}{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(it\right)$(13) and eq. (14)(14) $\varphi =\frac{2}{\pi }arccos\frac{1}{3}.arctan\left(it\right)$(14) . Finally, the weight factors, w1, w2 and w3 are obtained using eq. (15)(15) $w1=cos\varphi$(15) , eq. (16)(16) $w2=\frac{1}{2}sin\varphi .cos\phi$(16) and eq. (17)(17) $w3=1-w1-w2$(17) .

(13) $\phi =\frac{1}{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(it\right)$(13)

(14) $\varphi =\frac{2}{\pi }arccos\frac{1}{3}.arctan\left(it\right)$(14)

(15) $w1=cos\varphi$(15)

(16) $w2=\frac{1}{2}sin\varphi .cos\phi$(16)

(17) $w3=1-w1-w2$(17)

Yu et al. (Xiaobing, WangYing, and ChenLiang 2021) proposed an opposition-based learning strategy to improve the population diversity and to save the algorithm from early convergence and avoid local optimal solutions. According to this algorithm, a group of opposition solutions are selected using opposition-based learning (OBL) following the upper bound and lower bound of each solution in all phase of the search process. Here, the best search agent among the two groups, i.e. original solutions and oppositions, helps to minimize the computational overhead and maximizes the convergence speed.

Additionally, Nadimi-Shaharaki et al. (Nadimi-Shahraki, Taghian, and Mirjalili 2021) proposed an improved GWO by constructing a neighborhood of radius R for solving engineering problems. The algorithm uses a dimension learning-based hunting (DLH) strategy that uses an approach to construct a neighborhood of each wolf for sharing the neighboring information between wolves. It also helps the wolves pack to maintain diversity among themselves and maintains a proper balance between exploration and exploitation.

In most cases, the GWO algorithm suffers from trapping at local optimal solutions and avoiding such local optima may not work well as wolves hunt in regions that is close to each other. Hence, an expanded GWO algorithm (Ex-GWO) (Seyyedabbasi and Kiani 2021) and an incremental GWO algorithm (I-GWO) are proposed to address the global optimization problems. The Ex-GWO method suggest that α, β and δ have better knowledge about the position of prey and hence, each omega wolf update its positions with the help of the newly updated positions of best three leader wolves (as given in eq. (8)(8) $Y_1=\alpha -A_1\times \left|C_1.\alpha -x\left(t\right)\right|$(8) , eq. (9)(9) $Y_2=\beta -A_2\times \left|C_2.\beta -x\left(t\right)\right|$(9) and eq. (10))(10) $Y_3=\delta -A_3\times \left|C_3.\delta -x\left(t\right)\right|$(10) and its previous wolves as given in eq. (18)(18) $x_m\left(t+1\right)=\frac{1}{n-1}\left(Y_1+Y_2+Y_3\right)+{\sum }_{i=4}^{m-1}{x}_i\left(t\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{m}=4,5,6\dots \dots n$(18) :

(18) $x_m\left(t+1\right)=\frac{1}{n-1}\left(Y_1+Y_2+Y_3\right)+{\sum }_{i=4}^{m-1}{x}_i\left(t\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{m}=4,5,6\dots \dots n$(18)

where $n$ denotes the population size, $i$ parameter denotes wolf number in the pack and $t$ denotes the generation counter. $Y_1$, $Y_2$ and $Y_3$ are the updated positions of α, β and δ wolves respectively at the beginning of every iterations.

Similarly the I-GWO algorithm suggests that each wolf updates its position with the help of all previously selected wolves. The authors claim that I-GWO has more changes to find solutions in fewer iterations, but it may not always guarantee to find good solutions. According to the algorithm, the parameter $a$ has major role to select the position of best wolf (α) that only directs the search process. If $\alpha$ is nearer to the prey then algorithm convergences faster and if it is far away from the prey, then the algorithm needs more iterations to reach at the solutions. Hence, the authors suggest an additional improvement of parameters $a$ (as given in eq. (19))(19) $a=2\ast \left(1-\frac{t^j}{T_{max}^j}\right)$(19) to make the algorithm more efficient. Mathematically, the position updation of each wolves is as given in eq. (20)(20) $x_m\left(t+1\right)=\frac{1}{n-1}{\sum }_{i=1}^{m-1}{x}_i\left(t\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{m}=2,3,4\dots \dots \mathrm{n}$(20) :

(19) $a=2\ast \left(1-\frac{t^j}{T_{max}^j}\right)$(19)

(20) $x_m\left(t+1\right)=\frac{1}{n-1}{\sum }_{i=1}^{m-1}{x}_i\left(t\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{m}=2,3,4\dots \dots \mathrm{n}$(20)

where parameters $A$ and $C$ decide the directions for each wolves and parameter $A$ decides the range of motion for the promising regions. The parameter $j$ is used to increase the number of iteration for controlling the explorative capability of the algorithm. $n$ is the population size and $i$ parameter denotes wolf number in the pack. $t$ denotes the generation counter.

GWO algorithm has been applied to analyze and design the FOPID-based damping controllers to enhance the power system stability (Kar et al. 2022). This paper proposes a modified GWO algorithm (mGWOA) to tune the control parameters of fractional-order PID. This paper concludes with superior performance of mGWOA in optimizing the benchmark functions and for damping low-frequency oscillations. To improve the performance of MGWOA, the authors have used a modified update equation for parameter $a$ (as in eq. 21(21) $a=2\ast \left(1-\frac{t^{1.5}}{T_{max}^{1.5}}\right)$(21) ).

(21) $a=2\ast \left(1-\frac{t^{1.5}}{T_{max}^{1.5}}\right)$(21)

where $t$ is the current iteration number and $T_{max}$ is the maximum number iteration for the simulation work.

In this approach, to give more importance to leader wolves and the leadership hierarchy, the weight of α, β and δ are considered as 50%, 33.33% and 16.66% respectively. Mathematically, eq. (11)(11) $x\left(t+1\right)=\frac{Y_1+Y_2+Y_3}{3}$(11) is modified as given in eq. (22)(22) $x_i\left(t+1\right)=\frac{3\ast \alpha +2\ast \beta +\delta }{6}$(22) :

(22) $x_i\left(t+1\right)=\frac{3\ast \alpha +2\ast \beta +\delta }{6}$(22)

where $x_i\left(t+1\right)$ is the $i^{th}$ omega wolf at $\left(t+1\right)$ iteration.

According to eq. (6)(6) $a=2-\frac{2\ast t}{MaxIter}$(6) of GWO algorithm, due to linear operators, half of the iterations are dedicated for exploration and the other half of the iterations are devoted for exploitation. To incorporate such searching technique into the classical GWO algorithm, Mittal et al. (Mittal, Singh, and Singh Sohi 2016) proposed mGWO which decreases value of parameter $a$ from $2$ to $0$ exponentially. The proposed exponential function as given in eq. (23)(23) $a=2\ast \left(1-\frac{t^2}{T_{max}^2}\right)$(23) helps to decrease the value of $a$ exponentially over the course of iterations.

(23) $a=2\ast \left(1-\frac{t^2}{T_{max}^2}\right)$(23)

The above exponential decay equation helps in transitioning from exploration to exploitation from initial iteration to final iteration with a ratio of 70% and 30% respectively. It shows that the mGWO enjoys high exploration in comparisons to classical GWO. This paper suggests that the algorithm is very effective because of high exploration in the initial phase, and hence, it has sufficient capability to avoid trapping to local optima. The paper also discusses the faster convergence behavior and superior performance of mGWO due to the above exponential decay function.

Furthermore, for most of the multimodal optimization problems, the GWO algorithm experiences a small degree of exploration as the algorithm does not hold any separate equation for exploration. Moreover, the control parameters ($A,C$) allow to make a slow transition from exploration to exploitation toward the convergence. This algorithm benefits from the combined effort of leader wolves in the hierarchy which helps for faster convergence with better exploitation. However, due to fast convergence sometimes it traps at local optimal solutions. Therefore, to improve the search capability and to maintain a proper balance between exploration and exploitation here we introduced a differential perturbation equation in the search mechanism of GWO which enables the algorithm to improve its explorative search. To improve the quality of solutions and to achieve better the explorative search capability of existing GWO algorithm, here we have introduced a novel differential perturbation equation into its search process with the help of three randomly chosen search agents. It modifies the algorithmic steps which enables it to achieve better exploration. Most commonly, the real-life problems are multimodal in nature and with the hope to solve such multimodal problems efficiently, we have proposed an enhanced GWO algorithm with improved explorative search capability which still maintains a better trade between exploration and exploitation.

Proposed Enhanced GWO Algorithm

In GWO, it is assumed that the leader wolves have better knowledge about the potential location of prey and hence the position of all omega wolves are updated using eq. (3)(3) $D=\left|C.X_p\left(t\right)-x\left(t\right)\right|$(3) and eq. (4)(4) $Y=X_p\left(t\right)-A\times D$(4) . It is also observed that the searching behavior of GWO is controlled by parameter $C$ and $A$ where the algorithm tries to escape from local optimal solutions using the stochastic parameter $C$. Similarly, the value of $A$ helps in transitioning the algorithm from exploration to exploitation. When $A>1$ it improves diversification among the possible solutions and similarly it minimizes diversification when $A<1$. Therefore, the algorithm performs better by balancing the exploration and exploitation. However, due to most dependencies on leader wolves every generated new solution is stuck at local optimal positions surrounded by leader wolves. Therefore, there is an improper balance between exploration and exploitation. To overcome this issue and improve the performance, we introduced a differential perturbation equation to maintain a trade between both the parameters by minimizing and balancing the biasness of leader wolves during its search process. Additionally, this equation is applied for each leader wolf separately that helps each omega wolf to find its better position with help of leader wolves and with an additional effort of three randomly selected omega wolves. Furthermore, the exploration capability of the existing algorithm has been enhanced by incorporating eq. (24)(24) $Z_1=x_i+f\ast \left(Y_1-x_{rand1}\right)$(24) , eq. (25)(25) $Z_2=x_i+f\ast \left(Y_2-x_{rand2}\right)$(25) and eq. (26)(26) $Z_3=x_i+f\ast \left(Y_3-x_{rand3}\right)$(26) into the traditional GWO algorithm which results in enhancing the robustness of the algorithm by maintaining a good balance between exploration and exploitation. Therefore, we have combined a differential perturbation equation into the classical GWO algorithm which enjoys a high degree of diversification among the population members in the explorative phase. Mathematically, the proposed modifications are given in eq. (24)(24) $Z_1=x_i+f\ast \left(Y_1-x_{rand1}\right)$(24) , eq. (25)(25) $Z_2=x_i+f\ast \left(Y_2-x_{rand2}\right)$(25) , eq. (26)(26) $Z_3=x_i+f\ast \left(Y_3-x_{rand3}\right)$(26) and eq. (27)(27) $X_i\left(t+1\right)=\frac{Z_1+Z_2+Z_3}{3}\hspace{0.17em}$(27) :

(24) $Z_1=x_i+f\ast \left(Y_1-x_{rand1}\right)$(24)

(25) $Z_2=x_i+f\ast \left(Y_2-x_{rand2}\right)$(25)

(26) $Z_3=x_i+f\ast \left(Y_3-x_{rand3}\right)$(26)

where $Z_1,Z_{2}and{Z}_3$ are the corresponding modified representation of the alpha, beta and delta wolf for the $i^{th}$ omega wolf which is represented as $x_i$. The three randomly selected omega wolves ($x_{rand1},x_{rand2}and{x}_{rand3}$) are used to assist the leader wolves to search for more diversified solution around the most promising region of the search space. This improves the explorative skill of the algorithm. Here the original step mentioned in eq. (11)(11) $x\left(t+1\right)=\frac{Y_1+Y_2+Y_3}{3}$(11) of classical GWO algorithm is replaced by eq. (27)(27) $X_i\left(t+1\right)=\frac{Z_1+Z_2+Z_3}{3}\hspace{0.17em}$(27) in our proposed algorithm. Additionally, the three numerator terms of eq. (27)(27) $X_i\left(t+1\right)=\frac{Z_1+Z_2+Z_3}{3}\hspace{0.17em}$(27) i.e. $Z_1,Z_{2}and{Z}_3$ are obtained using eq. (24)(24) $Z_1=x_i+f\ast \left(Y_1-x_{rand1}\right)$(24) , eq. (25)(25) $Z_2=x_i+f\ast \left(Y_2-x_{rand2}\right)$(25) and eq. (26)(26) $Z_3=x_i+f\ast \left(Y_3-x_{rand3}\right)$(26) respectively. The parameters such as $Y_1$, $Y_2$ and $Y_3$ are obtained from eq. (8)(8) $Y_1=\alpha -A_1\times \left|C_1.\alpha -x\left(t\right)\right|$(8) , eq. (9)(9) $Y_2=\beta -A_2\times \left|C_2.\beta -x\left(t\right)\right|$(9) and eq. (10)(10) $Y_3=\delta -A_3\times \left|C_3.\delta -x\left(t\right)\right|$(10) respectively. To incorporate an element of exploration in the exploitation phase, we have used similar values for parameters $A$ and $C$ for each leader wolves while calculating the values of $Y_1$, $Y_2$ and $Y_3$ for a single omega wolf and it keeps on changing with the change in omega wolf in the population.

Additionally, the strategy helps to add a self-adaptive behavior to the population members to enhance the population diversity with the help of the leader wolves and randomly selected population members. Hence, this perturbation strategy improves population diversity that enables to enhance the strength of exploration capability of the GWO algorithm. The coefficient $f$ in the proposed strategy is a scaling factor to improve the exploration capability of the searching agents. The second part of eq. (24)(24) $Z_1=x_i+f\ast \left(Y_1-x_{rand1}\right)$(24) , eq. (25)(25) $Z_2=x_i+f\ast \left(Y_2-x_{rand2}\right)$(25) and eq. (26)(26) $Z_3=x_i+f\ast \left(Y_3-x_{rand3}\right)$(26) are the difference vectors that are calculated by considering the updated position by each of the leader wolves ($\alpha ,\beta \mathrm{a}\mathrm{n}\mathrm{d}\delta$) and one among the three randomly selected omega wolves ($x_{rand1},x_{rand2},x_{rand3}$). If the difference is high, then the perturbation equation with high scaling factor will enjoy more exploration and therefore it maintains more diversity among population members. This allows to incorporate the global search ability of the GWO in its search process. Simultaneously, this diversification helps in avoiding local convergence issue of GWO in most of the multimodal problems.

Additionally, the parameters such as $Y_1$, $Y_2$ and $Y_3$ from in eq. (24)(24) $Z_1=x_i+f\ast \left(Y_1-x_{rand1}\right)$(24) , eq. (25)(25) $Z_2=x_i+f\ast \left(Y_2-x_{rand2}\right)$(25) and eq. (26)(26) $Z_3=x_i+f\ast \left(Y_3-x_{rand3}\right)$(26) respectively are obtained from eq. (8)(8) $Y_1=\alpha -A_1\times \left|C_1.\alpha -x\left(t\right)\right|$(8) , eq. (9)(9) $Y_2=\beta -A_2\times \left|C_2.\beta -x\left(t\right)\right|$(9) and eq. (10)(10) $Y_3=\delta -A_3\times \left|C_3.\delta -x\left(t\right)\right|$(10) respectively.

Finally, the equation eq. (27)(27) $X_i\left(t+1\right)=\frac{Z_1+Z_2+Z_3}{3}\hspace{0.17em}$(27) adds exploitation to the three leader wolf strategy. In comparison to eq. (11)(11) $x\left(t+1\right)=\frac{Y_1+Y_2+Y_3}{3}$(11) , the updated equation holds three diversified operands in its numerator that enables the proposed algorithm to overcome local convergence and to achieve near-optimal result.

(27) $X_i\left(t+1\right)=\frac{Z_1+Z_2+Z_3}{3}\hspace{0.17em}$(27)

The stability of the algorithm is tested with varying range (0 to 1 with an interval 0.1) of parameter $f$ to select its optimum value that gives better result. Experiments suggest that the algorithm provides the best result when $f$ = 0.7.

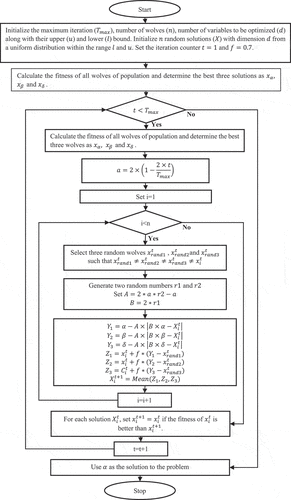
The primary steps of our proposed algorithm is illustrated as shown in Figure 1. Additionally, a boundary checking condition is also inserted in each iteration of the algorithm. The remaining steps of the proposed algorithm are similar to the classical GWO algorithm that selects leader wolves with better fitness at the beginning of each iteration.

Figure 1. Flowchart of Proposed Enhanced GWO Algorithm.

Figure 1 presents the flowchart of our proposed enhanced GWO algorithm that operates in three steps such as Initialization steps, Iteration step and Final step. In the initialization step, the algorithm parameters are initialized such as max Iteration ($T_{max}$), algorithmic specific control parameter such as $f$ (0.7) and number of variables ($d$), population size ($n$), lower bound ($l$), upper bound ($u$) of search space and initial population. In the iterative steps, each omega wolf is updated with the combined effort of the help of leader wolves and three randomly selected omega wolves using differential perturbation equation. Then the omega wolves are allowed to update their positions with greedy selection approach. The iterative step is repeated until the termination criterion is satisfied. In the final step, the $\alpha$ wolf is chosen as the best solution for the optimization problem.

Application of Our Proposed Enhanced GWO Algorithm for Data Clustering

To evaluate the performance of our proposed GWO algorithm, we applied it on 12 clustering problems. The main objective here is to select optimal cluster centers among given $n$ data points in a search space that minimizes intra-cluster distance in order to form compact clusters. To maximize the compactness and minimize the clustering error most similar data points need to belong to a same cluster. Therefore, we have used Euclidean distance measure (as given in eq. (28))(28) $Distance\left(p_m-C_n\right)=\hspace{0.17em}\sqrt{\sum _{r=1}^d{\left(p_m^r-C_n^r\right)}^2}$(28) to evaluate the compactness of each clusters.

(28) $Distance\left(p_m-C_n\right)=\hspace{0.17em}\sqrt{\sum _{r=1}^d{\left(p_m^r-C_n^r\right)}^2}$(28)

where, $p_m=\{p_m^1,\hspace{0.17em}{p}_m^2,\hspace{0.17em}{p}_m^3\dots ..\hspace{0.17em}{p}_m^d\}$ and $C_n=\{C_n^1,\hspace{0.17em}{C}_n^2,\hspace{0.17em}{C}_n^3\dots ..\hspace{0.17em}{C}_n^d\}$ are the cluster members and cluster centers respectively with dimension $d$.

Given a dataset $D$ of $n$ instances with dimension $D$ which can be represented as $D=\left\{x_1^1,x_1^2\dots x_1^d\dots x_n^1\dots x_n^d\right\}$. The aim of clustering task is to form $K$ non-overlapping compact clusters among these data points.

To address the above problem and to assign membership value to each data instance, we have considered the minimization equation of partitional clustering algorithm (Shial, Sahoo, and Panigrahi 2022a; Ikotun et al. 2022Shial, Sahoo, and Panigrahi 2022b). To calculate the exactness of each cluster, we have accessed sum of square error (SSE) within each cluster. To achieve this, the primary focus is to minimize the objective function (as given in eq. (29)(29) $Minimize\sum _{j=1}^K\sum _{i=1}^n{M}_i^j\ast \sqrt{\sum _{r=1}^d{\left(p_i^r-C_j^r\right)}^2}\hspace{0.17em}$(29) ).

(29) $Minimize\sum _{j=1}^K\sum _{i=1}^n{M}_i^j\ast \sqrt{\sum _{r=1}^d{\left(p_i^r-C_j^r\right)}^2}\hspace{0.17em}$(29)

such that

${\sum }_{i=1}^K{\sum }_{j=1}^K{C}_i\cap C_j=\mathrm{\varnothing }$ where, $i\ne j$

AND $\left|{\hspace{0.17em}}_{j=1}^K\cup C_j|\right.=n$

where $p_i$ denotes the $i^{th}$ data instance and $C_j$ denotes the $j^{th}$ cluster center, $M_i^j$ is the membership value of $p_i$ instance to $j^{th}$ cluster, $d$ denotes the dimension of data. $M_i^j$ is 0 for non-membership and 1 for membership of a data instance $p_i$ to a cluster $j$.

Algorithm 1 presents the steps followed to perform data clustering using our proposed enhanced GWO algorithm. The steps of our proposed algorithm operate in three steps such as Initialization step, Iterative step and Final Step. In the initialization step, the algorithm initializes the parameters such as $K$ (number of clusters), number of generations gen, $Ma{x}_{gen}=100$, $f=0.7$, maximum number of iterative steps = 1000. In this step, the population members (the wolf pack) i.e. each solution is having $K\ast d$ number of features where $d$ denotes the number of features of a single data instance. $K$ is the number of clusters (assuming $K$ is known a priori). In the iterative step, all clustering solutions (except the leader wolves) are modified with the combined effort of leader wolves and three randomly selected omega wolves with the classical searching and encircling approach of GWO and using our novel differential perturbation equation. In this step, the greedy selection approach is followed to replace weak wolves from the population and to escape the weak wolves from trapping at local optimal solutions. In the final step, the best fit solution (α) is selected as the near-optimal solution for the clustering problem.

Table

Algorithm 1: Proposed Enhanced GWO Algorithm for Data Clustering

Input: Number of Clusters ($K$), Input Dataset ($D$) Output: Set of $\left(K\right)$ clusters Step1 Initialization Step Initialize the number of clusters ($K$), generation counter $gen=0,Max\mathrm{\_}gen=30,f=0.7,iter=0,Max\mathrm{\_}iter=1000$. Randomly select data points from large dataset $D$ and initialize the initial population ($P^{gen}$) with size n {where, $P^{gen}=\{C_1^{gen},\dots ,C_n^{gen}$} and $C_m^{gen}=\{P_m^{gen,1},\dots ,P_m^{gen,d}\}$ is a single wolf with $D$ dimensional features and $P_m^{gen,l}$ is the $l^{th}$ feature of $m^{th}$ wolf} Calculate the fitness of each wolf of $P^{gen}$ Select top three wolves as $\alpha$, $\beta$ and $\delta$ in decreasing order of dominance Step 2 Iteration Step While (termination criteria is not satisfied) do begin Sort the wolves pack with respect to fitness Select top three wolves as $\alpha$, $\beta$ and $\delta$ in decreasing order of dominance Compute $a=2-\frac{2\ast iter}{Max\mathrm{\_}iter}$ $Fori=4ton$ Generate two distinct random numbers $r1$ and r2 $ComputeA=2\ast a\ast r2-a$ Compute $B=2r1$ Calculate $Y_1=\alpha -A\times \left|B.\alpha -C_i^{gen}\right|$ Calculate $Y_2=\beta -A\times \left|B.\beta -C_i^{gen}\right|$ Calculate $Y_2=\delta -A\times \left|B.\delta -C_i^{gen}\right|$ Calculate $Z_1=C_i^{gen}+f\ast \left(Y_1-C_{rand1}^{gen}\right)$ Calculate $Z_2=C_i^{gen}+f\ast \left(Y_2-C_{rand2}^{gen}\right)$ Calculate $Z_3=C_i^{gen}+f\ast \left(Y_3-C_{rand3}^{gen}\right)$ Calculate $C_i^{gen+1}=\frac{Z_1+Z_2+Z_3}{3}$ Calculate the fitness of $C_i^{gen+1}$. if (fitness($C_i^{gen+1}$) >$fitness\left(C_i^{gen}\right)$)//minimization Set $C_i^{gen+1}=C_i^{gen}$ $Endfor$ gen=gen+1 End while Step 3 Final Step Select the $\alpha -\mathrm{w}\mathrm{o}\mathrm{l}\mathrm{f}$ from the final iteration as the near-optimal cluster centers.

Performance Evaluation of Proposed Enhanced GWO Algorithm Using Benchmark Functions

To measure the performance of our proposed enhanced GWO algorithm, we considered 23 well known mathematical benchmark functions. The functions used for the analysis are denoted by f1, f2, f3 … f23. These group of benchmark functions are unimodal (as given in Table 1), flexible dimension multimodal (as given in Table 2) and fixed-dimension multimodal (as given in Table 3). In each table, the dim represents the dimension of the functions, range represents the higher and lower bound of decision variables. The optimal fitness value of the function is presented in column $f_{min}$. Most commonly researchers from various fields used these benchmark functions for measuring the performance of their proposed algorithms (Bansal, Kumar Joshi, and Nagar 2018; Heidari et al. 2019; Mirjalili 2015a, 2015b). In order to evaluate the performance of the proposed enhanced GWO algorithm, statistical analysis has been made with ten recently proposed promising meta-heuristic algorithms such as Improved Arithmetic Optimization Algorithm (IAOA) (Kaveh and Biabani Hamedani 2022), Reptile Search Algorithm (RSA) (Abualigah et al. 2022), Modified Grey Wolf Optimization Algorithm (mGWOA) (Kar et al. 2022), Variable Weight Grey Wolf Optimization (VWGWO) (Gao and Zhao 2019), Modified Grey Wolf Optimization (mGWO) (Mittal, Singh, and Singh Sohi 2016), Grey Wolf Optimization (GWO) Teng, Jin-Ling, and Guo (2019), Sine Cosine Algorithm (SCA) (Mirjalili 2016b), Jaya Algorithm (JAYA) (Rao 2016), Ant Lion Optimization (ALO) (Azizi et al. 2020; Mirjalili 2015a) and Whale Optimization Algorithm (WOA) (Chen et al. 2019; Mirjalili and Lewis 2016; Obadina et al. 2022). For a fair comparison among the considered algorithms, the swarm size and maximum number of iteration are fixed in all algorithms. Additionally, Table 4 presents the values of different parameters such as number of search agents, maximum number of iterations, number of independent executions and parameter $f$.

Table 1. Unimodal Benchmark Functions.

Problems	Function name	${\mathit{f}}_{\mathit{m}\mathit{i}\mathit{n}}$	Dimension(η)	Range
$f1\left(x\right)=\sum _{i=1}^n{x}_i^2$	Sphere	0	30	[−100, 100]
$f2\left(x\right)=\sum _{i=1}^n{x}_i+\prod _{i=1}^n\left|x_i\right|$	Schwefel 2.22	0	10	[−10,10]
$f3\left(x\right)=\sum _{i=1}^n{\left(\sum _{j=1}^i{x}_j\right)}^2$	Schwefel 1.2	0	10	[−100,100]
$f4\left(x\right)=max\left\{\left|x_i\right|,1\le i\le n\right\}$	Schwefel 2.21	0	10	[−100,100]
$f5\left(x\right)=\sum _{n=1}^{n-1}\left[100{\left(x_{i+1}-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right]$	Rosenbrock	0	10	[−30,30]
$f6\left(x\right)=\sum _{i=1}^n{\left(\left[x_i+0.5\right]\right)}^2$	Step	0	10	[−100,100]
$f7\left(x\right)=\sum _{i=1}^{n}i{x}_i^4+random\left(0,1\right)$	Quartic with noise	0	10	[−1.28,1.28]

Table 2. Flexible Multimodal Benchmark Functions.

Problems	Function name	$f_{\mathit{m}\mathit{i}\mathit{n}}$	Dimension(η)	Range
$f8\left(x\right)=\sum _{i=1}^n-x_{i}sin\left(\sqrt{\left|x_i\right|}\right)+\propto .D$ $\propto$=418.982887272433799807913601398	Schwefel 2.26	−418.9829×D	10	[−500, 500]
$f9\left(x\right)=\sum _{i=1}^n\left[x_i^2-10cos\left(2\pi x_i\right)+10\right]$	Rastrigin	0	10	[−5.12, 5.12]
$f10\left(x\right)=-20exp\left(-0.2\sqrt{\frac{1}{n}\sum _{i=1}^n{x}_i^2}\right)-exp\left(\frac{1}{n}cos\left(2\pi x_i\right)\right)+20+e$	Ackley	0	10	[−32, 32]
$f11\left(x\right)=\frac{1}{4000}\sum _{i=1}^n{x}_i^2-\prod _{i=1}^{n}cos\left(\frac{x_i}{\sqrt{i}}\right)+1$	Griewank	0	10	[−600, 600]
$f12\left(x\right)=\frac{\pi }{n}\left\{10sin\left(\pi y_i\right)+\sum _{i=1}^{n-1}{\left(y_i-1\right)}^2\left[1+10si{n}^2\left(3\pi y_{i+1}\right)\right]+{\left(y_n-1\right)}^2\right\}+\sum _{i=1}^{n}u\left(x_i,10,100,4\right)$ $y_i=1+\frac{x_i+1}{4}$ $\mathrm{u}\left(x_i,a,k,m\right)=\left\{\begin{array}{c}k{\left(x_i-a\right)}^m{x}_i>a\\ 0-a<x_i<a\\ k{\left(-x_i-a\right)}^m{x}_i<-a\end{array}\right.$	Penalized 1	0	10	[−50, 50]
$f13\left(x\right)=0.1\left\{si{n}^2\left(3\pi x_i\right)+\sum _{i=1}^n{\left(x_i-1\right)}^2\left[1+si{n}^2\left(3\pi x_i+1\right)\right]+{\left(x_n-1\right)}^2\left[1+si{n}^2\left(2\pi x_n\right)\right]\right\}+\sum _{i=1}^{n}u\left(x_n,5,100,4\right)$	Penalized 2	0	10	[−50, 50]

Table 3. Fixed-Dimension Benchmark Functions.

Problems	Function name	$f_{min}$	Dimension(η)	Range
$f14\left(x\right)={\left(\frac{1}{500}+\sum _{j=1}^{25}\frac{1}{j+{\sum }_{i=1}^2{\left(x_i-a_{ij}\right)}^6}\right)}^{-1}$	Shekel’s Foxholes	0.998	2	[−65.536 , 65.536]
$f15\left(x\right)=\sum _{i=1}^{11}{\left[a_i-\frac{x_i\left(b_i^2+b_i{x}_2\right)}{b_i^2+b_i{x}_i+x_4}\right]}^2$	Kowalik	0.00030	4	[−5, 5]
$f16\left(x\right)=4x_1^2-2.1x_1^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^4$	Six-hump camel back	−1.0316	2	[−5, 5]
$f17\left(x\right)={\left(x_2-\frac{5.1}{4{\pi }^2}{x}_1^2+\frac{5}{\pi }{x}_1-6\right)}^2\text{break}+10\left(1-\frac{1}{8\pi }\right)cos{x}_1+10$	Branin	0.398	2	LB=[−5, 0] UB=[10, 15]
$f18\left(x\right)=[1+{\left(x_1+x_2+1\right)}^2\left(19-14x_1\text{break}+3x_1^2-14x_2+6x_1{x}_2+3x_2^2\right)]\text{break}[30+{\left(2x_1-3x_2\right)}^2\left(18+32x_1+12x_1^2\text{break}+48x_2-36x_1{x}_2+27x_2^2\right)]$	Goldstein-Price	3	2	[−2, 2]
$f19\left(x\right)=-\sum _{i=1}^4{c}_{i}exp\left(-\sum _{j=1}^2{a}_{ij}{\left(x_j-p_{ij}\right)}^2\right)$	Hartman’s family	−3.86	3	[0, 1]
$f20\left(x\right)=-\sum _{i=1}^4{c}_{i}exp\left(-\sum _{j=1}^6{a}_{ij}{\left(x_j-p_{ij}\right)}^2\right)$	Hartman’s family	−3.32	6	[0, 1]
$f21\left(x\right)=-\sum _{i=1}^5{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	Shekel’s family	−10.1532	4	[0, 10]
$f22\left(x\right)=-\sum _{i=1}^7{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	Shekel’s family	−10.4028	4	[0, 10]
$f23\left(x\right)=-\sum _{i=1}^{10}{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	Shekel’s family	−10.5363	4	[0, 10]

Table 4. Parameter Settings of Meta-heuristic Algorithms.

Number of Search Agents	50
Maximum number of Iterations	1000
Number of independent executions	30
$f$ for proposed GWO algorithm	0.7

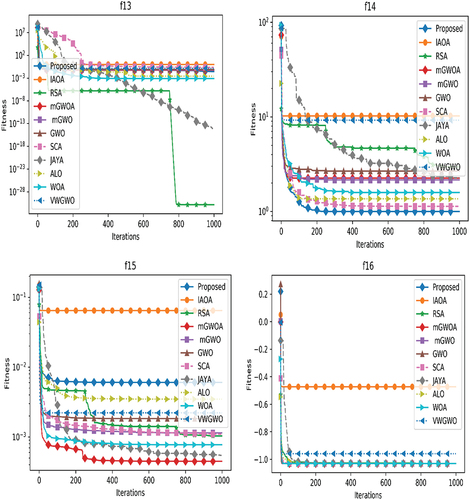
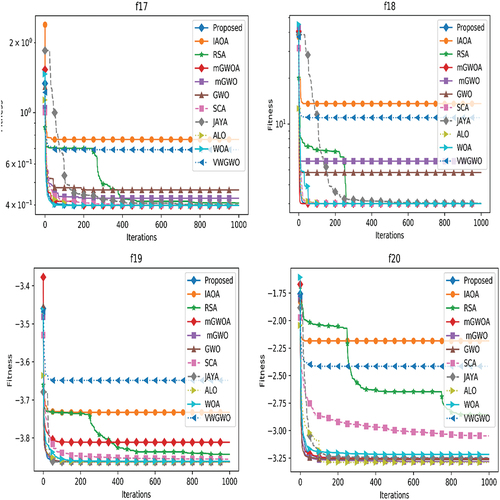
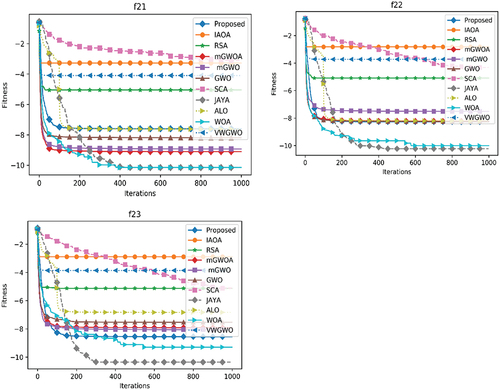
To access the performance of all the considered meta-heuristic algorithms, each algorithm is executed 30 times independently. The mean results for all algorithms are recorded and are statistically verified using Wilcoxon signed-rank test with the proposed algorithm. The mean and standard deviation results are tabulated in Tables 5, Tables 6 and Table 7 for unimodal, multimodal and fixed dimensional functions respectively. In each table the mean denotes average of the fitness functions obtained in 30 independent executions and std. dev. denotes the standard deviation. In each table, the best result among the considered algorithms for each function is highlighted in boldface. One can see that our proposed algorithm achieves best mean results in f9, f10, f11, f12, f14, f16, f17, f18, f19 and f22 functions.

Table 5. Mean and standard deviation of fitness values obtained in 30 independent simulations by meta-heuristic algorithms on unimodal functions.

	Proposed Mean ± Std. Dev.	IAOA (Kaveh and Biabani Hamedani 2022) Mean ± Std. Dev.	RSA (Abualigah et al. 2022) Mean ± Std. Dev.	mGWOA (Kar et al. 2022) Mean ± Std. Dev.	VWGWO (Gao and Zhao 2019)	mGWO (Mittal, Singh, and Singh Sohi 2016) Mean ± Std. Dev.	GWO (Mirjalili, Mohammad Mirjalili, and Lewis 2014b) Mean ± Std. Dev.	SCA (Mirjalili 2016b) Mean ± Std. Dev.	JAYA (Rao 2016) Mean ± Std. Dev.	ALO (Mirjalili 2015a) Mean ± Std. Dev.	WOA (Mirjalili and Lewis 2016) Mean ± Std. Dev.
f1	4.67E-124 ±2.22E-123	0.00E+00 ±0.00E+00	7.92E-237 ±0.00E+00	3.78E-04 ±6.21E-04	0.00E+00 ± 0.00E+00	6.05E-07 ±4.71E-07	4.67E-124 ±0.00E+00	0.00E+00 ±0.00E+00	7.92E-237 ±0.00E+00	3.78E-04 ±0.00E+00	2.49E-32 ±2.99E-32
f2	1.15E-62 ± 2.09E-62	0.00E+00 ± 0.00E+00	8.36E-145 ± 2.03E-144	2.37E-21 ± 6.65E-21	0.00E+00 0.00E+00	1.93E-01 ± 5.45E-01	1.15E-62 ± 0.00E+00	0.00E+00 ± 0.00E+00	8.36E-145 ± 0.00E+00	2.37E-21 ± 0.00E+00	1.53E-110 ±8.20E-110
f3	2.16E-125 ± 1.02E-124	0.00E+00 ± 0.00E+00	7.44E-02 ± 2.63E-01	2.38E-11 ± 1.28E-10	0.00E+00 ± 0.00E+00	3.40E-07 ± 4.44E-07	2.16E-125 ± 0.00E+00	0.00E+00 ± 0.00E+00	7.44E-02 ± 0.00E+00	2.38E-11 ± 0.00E+00	4.27E-01 ±1.18E+00
f4	7.57E-60 ± 1.11E-59	0.00E+00 ± 0.00E+00	1.24E-77 ± 5.90E-77	3.89E-09 ± 1.97E-08	0.00E+00 ± 0.00E+00	5.09E-05 ± 6.48E-05	7.57E-60 ± 0.00E+00	0.00E+00 ± 0.00E+00	1.24E-77 ± 0.00E+00	3.89E-09 ± 0.00E+00	6.16E-01 ±2.33E+00
f5	7.71E+00 ± 1.20E+00	3.00E-01 ± 1.61E+00	7.59E+00 ± 6.96E-01	6.98E+00 ± 3.26E-01	8.89E+00 ± 2.74E-02	3.55E+01 ± 7.56E+01	7.71E+00 ± 0.00E+00	3.00E-01 ± 0.00E+00	7.59E+00 ± 0.00E+00	6.98E+00 ± 0.00E+00	5.64E+00 ±2.85E-01
f6	1.70E-02 ± 6.37E-02	2.02E+00 ± 3.49E-01	4.41E-02 ± 4.91E-02	2.71E-01 ± 1.31E-01	2.06E-01 ± 7.12E-02	1.61E-09 ± 5.70E-10	1.70E-02 ± 0.00E+00	2.02E+00 ± 0.00E+00	4.41E-02 ± 0.00E+00	2.71E-01 ± 0.00E+00	8.42E-06 ±3.64E-06
f7	2.31E-04 ± 1.44E-04	3.72E-05 ± 3.76E-05	1.17E-04 ± 8.06E-05	7.05E-04 ± 4.77E-04	1.70E-05 ± 1.38E-05	6.66E-03 ± 3.59E-03	2.31E-04 ± 0.00E+00	3.72E-05 ± 0.00E+00	1.17E–04 ± 0.00E+00	7.05E-04 ± 0.00E+00	1.14E-03 ±1.18E-03

Table 6. Mean and standard deviation of fitness values obtained in 30 independent simulations by meta-heuristic algorithms on multimodal functions.

	Proposed Mean ± Std. Dev.	IAOA Mean ± Std. Dev.	RSA Mean ± Std. Dev.	mGWOA Mean ± Std. Dev.	VWGWO	mGWO Mean ± Std. Dev.	GWO Mean ± Std. Dev.	SCA Mean ± Std. Dev.	JAYA Mean ± Std. Dev.	ALO Mean ± Std. Dev.	WOA Mean ± Std. Dev.
f8	−3.86E+01 ± 2.09E+00	−2.98E+01 ± 1.23E+00	−3.91E+01 ± 8.01E-01	−3.74E+01 ± 9.52E-01	−3.38E+01 ± 1.99E+00	−3.81E+01 ± 2.81E+00	−3.86E+01 ± 0.00E+00	−2.98E+01 ± 0.00E+00	−3.91E+01 ± 0.00E+00	−3.74E+01 ± 0.00E+00	-3.95E+01 ±5.07E-05
f9	0.00E+00 ± 0.00E+00	0.00E+00 ± 0.00E+00	1.97E+00 ± 5.51E+00	2.98E-01 ± 1.61E+00	0.00E+00 ± 0.00E+00	1.63E+01 ± 8.29E+00	0.00E+00 ± 0.00E+00	0.00E+00 ± 0.00E+00	1.97E+00 ± 0.00E+00	2.98E-01 ± 0.00E+00	0.00E+00 ±0.00E+00
f10	8.88E-16 ± 9.86E-32	8.88E-16 ± 9.86E-32	3.73E-15 ± 1.42E-15	4.56E-15 ± 6.37E-16	8.88E-16 ± 9.86E-32	2.64E-01 ± 5.38E-01	8.88E-16 ± 0.00E+00	8.88E-16 ± 0.00E+00	3.73E-15 ± 0.00E+00	4.56E-15 ± 0.00E+00	4.08E-15 ±2.12E-15
f11	0.00E+00 ± 0.00E+00	0.00E+00 ± 0.00E+00	1.62E-02 ± 7.31E-02	1.51E-02 ± 4.45E-02	0.00E+00 ± 0.00E+00	2.21E-01 ± 1.01E-01	0.00E+00 ± 0.00E+00	0.00E+00 ± 0.00E+00	1.62E-02 ± 0.00E+00	1.51E-02 ± 0.00E+00	3.08E-02 ±6.08E-02
f12	8.55E-04 ± 2.76E-03	5.54E-01 ± 2.33E-01	3.09E-02 ± 1.19E-01	5.67E-02 ± 2.37E-02	4.64E-02 ± 3.16E-02	5.69E-01 ± 8.68E-01	8.55E-04 ± 0.00E+00	5.54E-01 ± 0.00E+00	3.09E-02 ± 0.00E+00	5.67E-02 ± 0.00E+00	3.31E-04 ±1.69E-03
f13	2.63E-02 ± 5.62E-02	1.43E-31 ± 1.98E-31	6.12E-02 ± 4.90E-02	2.39E-01 ± 6.85E-02	1.38E-01 ± 4.48E-02	2.53E-03 ± 5.33E-03	2.63E-02 ± 0.00E+00	1.43E-31 ± 0.00E+00	6.12E-02 ± 0.00E+00	2.39E-01 ± 0.00E+00	8.13E-04 ±2.73E-03

Table 7. Mean and standard deviation of fitness values obtained in 30 independent simulations by meta-heuristic algorithms on fixed dimensional functions.

	Proposed Mean ± Std. Dev.	IAOA Mean ± Std. Dev.	RSA Mean ± Std. Dev.	mGWOA Mean ± Std. Dev.	VWGWO	mGWO Mean ± Std. Dev.	GWO Mean ± Std. Dev.	SCA Mean ± Std. Dev.	JAYA Mean ± Std. Dev.	ALO Mean ± Std. Dev.	WOA Mean ± Std. Dev.
f14	9.98E-01 ± 4.44E-16	2.96E+00 ± 2.18E+00	2.15E+00 ± 1.96E+00	1.13E+00 ± 4.95E-01	9.19E+00 ± 3.58E+00	1.36E+00 ± 7.00E-01	9.98E-01 ± 0.00E+00	2.96E+00 ± 0.00E+00	2.15E+00 ± 0.00E+00	1.13E+00 ± 0.00E+00	1.59E+00 ±1.83E+00
f15	6.03E-03 ± 9.16E-03	1.03E-03 ± 3.47E-04	1.14E-03 ± 3.93E-03	1.09E-03 ± 3.68E-04	2.21E-03 ± 2.39E-03	3.47E-03 ± 6.65E-03	6.03E-03 ± 0.00E+00	1.03E-03 ± 0.00E+00	1.14E-03 ± 0.00E+00	1.09E-03 ± 0.00E+00	7.71E-04 ±4.97E-04
f16	-1.03E+00 ± 7.02E-09	-1.03E+00 ± 1.35E-03	-1.03E+00 ± 1.67E-08	-1.03E+00 ± 9.84E-06	−9.60E-01 ± 6.27E-02	-1.03E+00 ± 0.00E+00	-1.03E+00 ± 0.00E+00	-1.03E+00 ± 0.00E+00	-1.03E+00 ± 0.00E+00	-1.03E+00 ± 0.00E+00	-1.03E+00 ±0.00E+00
f17	3.98E-01 ± 2.02E-05	4.08E-01 ± 2.62E-02	4.27E-01 ± 9.83E-02	3.98E-01 ± 4.76E-04	6.91E-01 ± 3.95E-01	3.98E-01 ± 1.11E-16	3.98E-01 ± 0.00E+00	4.08E-01 ± 0.00E+00	4.27E-01 ± 0.00E+00	3.98E-01 ± 0.00E+00	3.98E-01 ±1.96E-07
f18	3.00E+00 ± 5.49E-07	3.00E+00 ± 1.12E-04	5.70E+00 ± 8.10E+00	3.00E+00 ± 1.59E-05	1.10E+01 ± 1.02E+01	3.00E+00 ± 0.00E+00	3.00E+00 ± 0.00E+00	3.00E+00 ± 0.00E+00	5.70E+00 ± 0.00E+00	3.00E+00 ± 0.00E+00	3.00E+00 ±2.53E-06
f19	-3.86E+00 ± 1.07E-06	−3.84E+00 ± 1.76E-02	-3.86E+00 ± 4.95E-05	-3.86E+00 ± 2.44E-03	−3.65E+00 ± 1.87E-01	-3.86E+00 ± 2.22E-15	-3.86E+00 ± 0.00E+00	−3.84E+00 ± 0.00E+00	-3.86E+00 ± 0.00E+00	-3.86E+00 ± 0.00E+00	-3.86E+00 ±2.02E-03
F20	−3.25E+00 ± 5.91E-02	−2.86E+00 ± 3.19E-01	−3.28E+00 ± 5.49E-02	−3.05E+00 ± 1.06E-01	−2.42E+00 ± 3.96E-01	-3.29E+00 ± 5.26E-02	−3.25E+00 ± 0.00E+00	−2.86E+00 ± 0.00E+00	−3.28E+00 ± 0.00E+00	−3.05E+00 ± 0.00E+00	−3.22E+00 ±1.08E-01
f21	−7.60E+00 ± 2.55E+00	−5.06E+00 ± 3.64E-07	-8.93E+00 ± 2.14E+00	−3.10E+00 ± 1.99E+00	−4.10E+00 ± 5.93E-01	−7.62E+00 ± 2.76E+00	−7.60E+00 ± 0.00E+00	−5.06E+00 ± 0.00E+00	-8.93E+00 ± 0.00E+00	−3.10E+00 ± 0.00E+00	−1.02E+01 ±3.20E-03
f22	-8.28E+00 ± 2.60E+00	−5.09E+00 ± 7.31E-07	−7.51E+00 ± 2.94E+00	−4.32E+00 ± 2.06E+00	−3.72E+00 ± 7.73E-01	−8.20E+00 ± 2.94E+00	-8.28E+00 ± 0.00E+00	−5.09E+00 ± 0.00E+00	−7.51E+00 ± 0.00E+00	−4.32E+00 ± 0.00E+00	−1.00E+01 ±1.51E+00
f23	−8.55E+00 ± 2.61E+00	−5.13E+00 ± 1.44E-06	−8.06E+00 ± 3.01E+00	−5.12E+00 ± 1.19E+00	−3.86E+00 ± 7.89E-01	−6.83E+00 ± 3.12E+00	−8.55E+00 ± 0.00E+00	−5.13E+00 ± 0.00E+00	−8.06E+00 ± 0.00E+00	−5.12E+00 ± 0.00E+00	-9.30E+00 ±2.54E+00

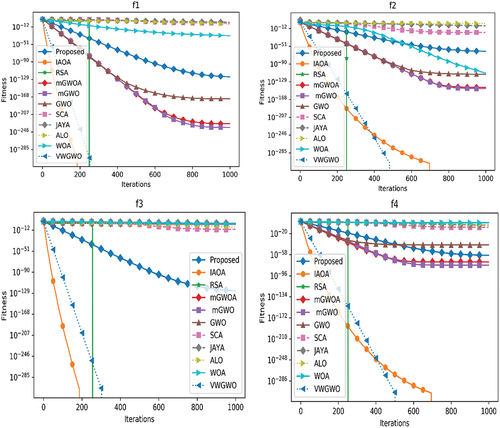
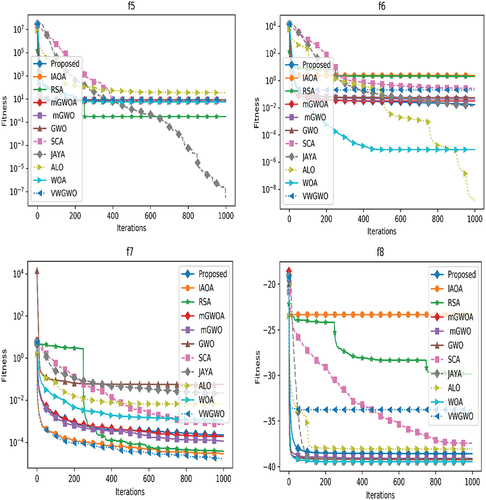
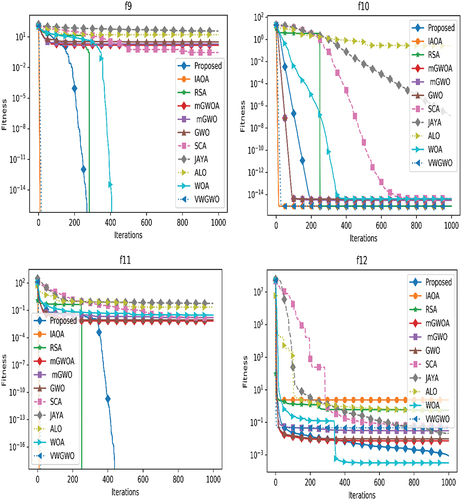
To determine both exploration and exploitation capability and convergence speed among stochastic algorithms, a set of unimodal benchmark functions are used as given in Table 5. The mean and standard deviation results of each algorithm is presented for seven unimodal functions. Additionally, to test the explorative behavior of all stochastic algorithms, our algorithm is tested for 16 multimodal test functions (f8-f23). These problems are again divided into two subgroups such as scalable multimodal functions (f8-f13) and multimodal fixed dimensional functions (f14-f23). The results obtained are presented in Table 6 that clearly shows that our proposed algorithm achieves the best performance in 3 benchmark functions among considered 6 functions such as in f9, f10 and f11. Similarly, it achieves the best performance in 5 number of fixed dimensional multimodal benchmark functions such as in f14, f16, f17, f18, f19 and f22. The mean and standard deviation results obtained over 23 benchmark functions suggest that the proposed algorithm has comparatively better explorative skill than the state-of-the-art meta-heuristic algorithms. Moreover, due to such explorative skill the proposed algorithm is able to avoid local convergence issue of the multimodal problems.

In order to compare the proposed algorithm with other algorithms, we have applied a non-parametric Wilcoxon signed-rank test with 95% confidence level on pairwise basis. The results after the test are shown by symbols “+,” “–” and “≈” in Table 8. The best and worst results with respect to our proposed algorithm are shown by the symbols “+” and “–” respectively. Similarly, the equivalent result is shown with symbol “≈” One can see from the table that the proposed algorithm achieves statistically better results in comparison to other comparative algorithms.

Table 8. Wilcoxon Signed-Rank test statistical results with + indicating superior (+), inferior (–) or statistically equivalent (≈) algorithm in comparison to our proposed algorithm on unimodal, scalable dimensions multimodal and fixed dimensions with multimodal functions.

function	IAOA	RSA	mGWOA	VWGWO	mGWO	GWO	SCA	JAYA	ALO	WOA
f1	+	+	+	+	+	+	̶	̶	̶	̶
f2	+	+	+	+	+	+	̶	̶	̶	̶
f3	+	+	̶	+	̶	̶	̶	̶	̶	̶
f4	+	+	+	+	+	̶	̶	̶	̶	̶
f5	̶	+	+	̶	≈	≈	≈	+	≈	̶
f6	̶	̶	̶	̶	̶	̶	̶	̶	+	̶
f7	+	+	≈	+	+	≈	̶	̶	̶	̶
f8	̶	̶	≈	̶	̶	≈	̶	+	≈	+
f9	≈	≈	≈	≈	≈	̶	≈	̶	̶	̶
f10	≈	≈	̶	≈	̶	̶	̶	̶	̶	̶
f11	≈	≈	≈	≈	≈	≈	̶	̶	̶	̶
f12	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
f13	̶	+	̶	̶	̶	̶	̶	+	+	̶
f14	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
f15	̶	≈	≈	≈	≈	≈	≈	̶	≈	̶
f16	̶	̶	≈	̶	≈	≈	̶	̶	+	̶
f17	̶	̶	+	̶	≈	≈	̶	̶	+	̶
f18	̶	̶	̶	̶	̶	̶	̶	̶	+	̶
f19	̶	̶	̶	̶	≈	̶	̶	+	+	̶
f20	̶	̶	≈	̶	≈	≈	̶	+	+	̶
f21	̶	≈	+	̶	≈	≈	̶	+	≈	̶
f22	̶	̶	≈	̶	̶	≈	̶	+	≈	̶
f23	̶	̶	̶	̶	̶	̶	̶	+	≈	̶
+ / ̶/ ≈	5/15/3	7/11/5	6/9/8	5/14/4	4/10/9	2/11/10	0/20/3	8/15/0	7/10/6	1/22/0

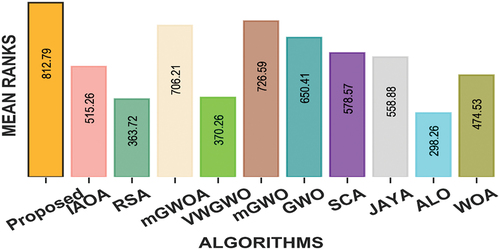
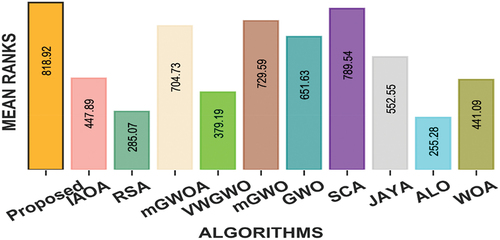
To make sure that the mean and standard deviation results obtained from the test are not just by chance, a non-parametric test is also conducted using Friedman and Nemenyi hypothesis test on the obtained results. The mean ranks obtained from the non-parametric test are presented in Figure 2. The results obtained for minimizing these functions are analyzed at p-value = .000 and critical distance (CD) = 3.1. It can be observed from the figure that the proposed algorithm is showing lowest mean rank (value = 128.60) among other algorithms while minimizing 23 benchmark test functions. Hence, the proposed algorithm is best among other algorithms considered in this study. It can also be observed that the mGWOA and mGWO are statistically equivalent (since mean rank difference is not greater than CD). Similarly, RSA, JAYA and ALO are statistically equivalent. It is also revealed from the test result that RSA and ALO are statistically equivalent.

Figure 2. Mean rank of meta-heuristic algorithms for 23 benchmark functions with P-value = .000 and Critical Distance = 3.1.

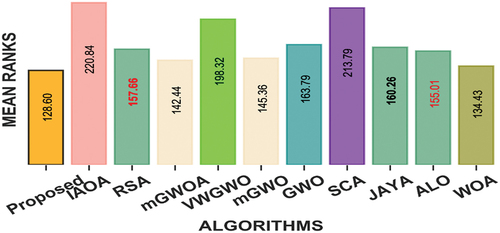
In comparison to unimodal functions, multimodal functions have more number of local optima and it also increases exponentially with the number of design variables. Therefore, this kind of test problems turns very useful to evaluate the exploration capability of an optimization algorithm. Hence, the results obtained over function f8-f23 (i.e. multimodal, scalable dimension multimodal and fixed dimensional multimodal test problems) indicate that our proposed enhanced GWO algorithm has very good explorative capability that avoids most of the local optimal solutions. In fact, our proposed algorithm is most efficient in most of the multimodal problems. This is due to the integration of differential perturbation operator and consideration of randomly chosen omega wolves into the steps of existing GWO algorithm.

For a better visual understanding of comparative performance of meta-heuristic algorithms, we have plotted the convergence curves. As the convergence curve changes in different simulation, we have taken the mean convergence curves of 30 independent simulations for each of the algorithms separately on each benchmark function and plotted which are shown in Figures 3, Figures 4 , 5 , Figure 6 , Figures 7 and 8.

Figure 3. The convergence curves for functions f1, f2, f3 and f4.

Figure 4. The convergence curves for functions f5, f6, f7 and f8.

Figure 5. The convergence curves for functions f9, f10, f11 and f12.

Figure 6. The convergence curves for functions f13, f14, f15 and f16.

Figure 7. The convergence curves for functions f17, f18, f19 and f20.

Figure 8. The convergence curves for functions f21, f22 and f23.

Performance Analysis of Our Proposed Enhanced GWO Algorithm on Benchmark Clustering Datasets

Experiment Setup

Dataset Description and Resource Characteristics

The experiment is conducted using 12 clustering problem datasets that are accessed from UCI machine learning repository (Dua and Graff 2017). The detailed descriptions of the datasets are presented in Table 9. The details about resource characteristics and simulation parameter setting are presented separately in Tables 10 and 11 respectively.

Table 9. Dataset Descriptions.

Dataset name	Number of Instances	Classes	Features	Characteristics of Features
WBDC	699	02	09	Real
Bupa	345	02	06	Real, Integer
Haberman’s Survival	306	02	03	Real
Hepatitis	155	02	19	Real, Integer Categorical
Indian Liver Patient	583	02	10	Real, Integer,
Ionosphere	351	02	34	Real, Integer
Iris	150	03	04	Real
Liver	345	02	06	Integer
Mammographic Mass	961	02	06	Integer
Seeds	210	03	07	Real
WDBC	569	02	30	Real
Zoo	101	07	16	Integer

Table 10. Resource Characteristics.

Software	Windows 10 Pro 64-bit, Jupyter 4.4.0, Conda 4.9.0, Python 3.6.5
Hardware	Intel(R) Core(TM) i3-6006U CPU @ 2.00GHz, 8 GB RAM

Table 11. Simulation Parameter Settings of Meta-heuristic Algorithms for Clustering Problems.

Maximum Iterations	1000
Max Independent Simulations	100
Population size	20

Evaluation Metrics

To access the performance of each algorithm we have used four performance metrics such as Accuracy, Precision, F-score and MCC. The detailed discussion and importance of each metric are described as follows.

Accuracy

Accuracy measure has been predominantly used in the literature to measure the performance of a classification and clustering algorithm. It computes its value by taking the ratio between the correctly classified instances and total number of instances. Mathematically, the accuracy performance is calculated as given in eq. (30)(30) $Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$(30) .

(30) $Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$(30)

Here, TP denotes true positive values, TN denotes true negative values, FP denotes false positive values and FN denotes false negative values.

Precision

With respect to information retrieval the positive samples and negative samples are termed as relevant and irrelevant instances respectively. Here, precision can be seen as the fraction of retrieved documents that are relevant. In classifier performance measure the pair precision and recall are more informative than sensitivity and specificity respectively, where recall is the fraction of relevant samples that are correctly retrieved. Mathematically, the precision can be obtained from the confusion matrix as given in eq. (31)(31) $Precision=\frac{TP}{TP+FP}$(31) .

(31) $Precision=\frac{TP}{TP+FP}$(31)

F-Score

With the context of information retrieval recall can be termed as relevant retrieved information which is the ratio between sums of relevant retrieved and total number of relevant items in the corpus whereas precision refers to the ratio between relevant retrieved documents and the total number of retrieved documents. Harmonic mean of both precision and recall is termed as F-score. Nowadays F1 − score is used in machine learning for both binary and multiclass scenarios. F-score has major drawback over MCC by giving incorrect score in the case of class swapping (if the positive class is renamed negative or vice-versa). However, F-score is equally invariant compared to MCC if micro/macro average F1 is used for class swapping problem. Second problem is F − score that it is independent from negative class being classified as positive. Despite of several flaws, F − score still remains the most widely spread performance matric among researchers. According to Cao et al., F-score and MCC estimate more realistic performance metrics for classification models (Cao, Chicco, and Hoffman 2020). Mathematically, the F-score performance measure is calculated as given in eq. (32)(32) $\mathrm{F}-\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=\frac{2\ast precision\ast recall}{precision+recall}$(32) .

(32) $\mathrm{F}-\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=\frac{2\ast precision\ast recall}{precision+recall}$(32)

MCC

In order to tackle the class imbalance problem, Matthew Correlation Coefficient (MCC) measure is used as an alternative. In this paper, some of the datasets are imbalanced, we have considered MCC to measure the performance of the models. MCC generates a high score if the binary classifier is producing high true positive instances and high true negative instances (Chicco and Jurman 2020).The extreme value of MCC lies in the range [−1, +1] where +1 represents perfect classification and −1 represents perfect misclassification and MCC = 0 value is considered as coin tossing classifier. Mathematically, the MCC for a classification problem can be obtained using eq. (33)(33) $MCC=\frac{TP\ast TN-FP\ast FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}$(33) .

(33) $MCC=\frac{TP\ast TN-FP\ast FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}$(33)

Result Analysis on Clustering Datasets

To access the performance of our proposed algorithm in clustering different datasets, the mean of 100 simulation results of all meta-heuristic algorithms are obtained. Table 12 shows the mean and standard deviation (Std. Dev.) of all the considered meta-heuristic algorithms for data clustering. This table contains the results for 12 different datasets separately employing 4 performance measures such as accuracy, precision, F-score and MCC. One can see that our proposed algorithm achieves the best mean results in 10 different datasets such as Bupa, Haberman’s Survival, Hepatitis, Indian Liver Patient, Iris, Liver, Mammographic Mass, Seeds, WDBC and Zoo datasets considering accuracy performance measure. Similarly, considering precision performance measure our proposed algorithm shows the best mean results for 6 different datasets such as Haberman’s Survival, Iris, Liver, Mammographic Mass, Seeds and WDBC. Considering F-score performance measure our algorithms shows the best mean result for 7 different datasets such as Habarman’s Survival, Indian Liver Patient, Iris, Mammographic, Seeds, WDBC and Zoo. Considering MCC performance measure our proposed algorithm shows the best mean results for 7 different datasets such as Bupa, Iris, Liver, Mammographic Mass, Seeds, WDBC and Zoo.

Table 12. Mean and standard deviation of Accuracy, Precision, F-Score and MCC for data clustering employing Meta-Heuristic Algorithms.

Dataset	Algorithms	Accuracy Mean ± Std. Dev.	Precision Mean ± Std. Dev.	F-Score Mean ± Std. Dev.	MCC Mean ± Std. Dev.
Breast Cancer	Proposed	97.5918 ±0.11769	0.9935±0.00197	0.9814 ± 0.00091	0.9479 ± 0.00247
	IAOA	97.4217 ±0.16960	0.9928±0.00300	0.9801 ± 0.00133	0.9443 ± 0.00363
	RSA	97.3842 ±0.16598	0.9926±0.00295	0.9798 ± 0.00130	0.9434 ± 0.00354
	mGWOA	97.6150 ±0.10584	0.9939±0.00194	0.9816 ± 0.00082	0.9484 ± 0.00229
	VWGWO	97.3437±0.21099	0.9933±0.00281	0.9795±0.00166b	0.9427±0.00449
	mGWO	97.6202 ±0.12330	0.9942±0.00190	0.9816 ± 0.00095	0.9485 ± 0.00261
	GWO	97.5933 ±0.12327	0.9936±0.00160	0.9814 ± 0.00096	0.9479 ± 0.00254
	SCA	98.0311 ±0.22855	0.9942±0.00313	0.9800 ± 0.00120	0.9610 ± 0.00235
	JAYA	97.0912 ±0.56940	0.9848±0.01231	0.9777 ± 0.00414	0.9364 ± 0.01309
	ALO	96.2070 ±0.66616	0.9702±0.01369	0.9711 ± 0.00488	0.9163 ± 0.01501
	WOA	97.2657 ±0.47796	0.9903±0.00940	0.9789 ± 0.00352	0.9407 ± 0.01093
Bupa	Proposed	69.8379±2.00649	0.7008±0.04928	0.5819 ± 0.04990	0.3717 ± 0.04369
	IAOA	64.1698 ± 2.93447	0.6151±0.06820	0.4993 ± 0.12074	0.2543 ± 0.06764
	RSA	62.2647 ± 2.96675	0.6515±0.13373	0.3906 ± 0.18075	0.2012 ± 0.07753
	mGWOA	68.4098 ± 2.66572	0.6757±0.05710	0.5637 ± 0.08190	0.3418 ± 0.05844
	VWGWO	66.0113±2.31326b	0.6634±0.07700	0.5048±0.08667	0.2902±0.05183
	mGWO	68.8043 ± 2.00491	0.6751±0.05014	0.5780 ± 0.04609	0.3504 ± 0.04137
	GWO	68.2017 ± 2.51987	0.6785±0.05828b	0.5556 ± 0.07253	0.3373 ± 0.05427
	SCA	66.8700±2.24381	0.7124±0.04985	0.6347±0.03247	0.3469±0.04813
	JAYA	65.7289 ± 3.71330	0.6191±0.07588	0.5553 ± 0.08907	0.2946 ± 0.07800
	ALO	60.6205 ± 3.18258	0.5439±0.08264	0.4795 ± 0.13998	0.1895 ± 0.07398
	WOA	64.0509 ± 4.22652	0.6246±0.10608	0.4987 ± 0.13120	0.2567 ± 0.08195
Haberman’s Survival	Proposed	77.4960±0.51020	0.7951±0.00637	0.8594±0.00308	0.3424±0.02054
	IAOA	75.8589±1.11948	0.7769±0.02083	0.8520±0.00495	0.2645±0.07312
	RSA	74.1608±0.49985	0.7448±0.01635	0.8491±0.00395	0.1335±0.05642
	mGWOA	76.8852±0.70874	0.7902±0.01129	0.8560±0.00385	0.3191±0.03687
	VWGWO	75.7188±1.12470	0.7803±0.02171	0.8499±0.00549	0.2659±0.07875
	mGWO	76.9599±0.65604	0.7913±0.00973	0.8563±0.00361	0.3230±0.03108
	GWO	76.4796±0.90963	0.7866±0.01332	0.8538±0.00507	0.3025±0.04566
	SCA	70.3667±1.97626	0.6894±0.02403	0.7146±0.03061	0.4112±0.03683
	JAYA	75.3922±2.51042	0.7902±0.02369	0.8438±0.02237	0.2879±0.07632
	ALO	72.6989±4.35163	0.7757±0.02802	0.8252±0.04059	0.2082±0.10012
	WOA	75.4638±1.79403	0.7780±0.01992	0.8484±0.01166	0.2606±0.07141
Hepatitis	Proposed	80.9557±1.21522	0.8434±0.17412	0.2124±0.17317	0.2452±0.10136
	IAOA	80.0646±0.48250	0.8963±0.19055	0.1019±0.10403	0.1711±0.05754
	RSA	80.0388±0.20158	0.9852±0.07425	0.0711±0.05572	0.1632±0.02750
	mGWOA	80.6917±0.95494	0.8223±0.18951	0.2028±0.16358	0.2325±0.08975
	VWGWO	80.3689±0.68887	0.8823±0.16843	0.1375±0.12055	0.1972±0.06477
	mGWO	80.5751±0.92186	0.8621±0.18407	0.1794±0.16694	0.2213±0.09114
	GWO	80.4207±0.64531	0.8528±0.18179	0.1585±0.13206	0.2071±0.06839
	SCA	68.0805±4.10206	0.6675±0.05397	0.6952±0.06033	0.3751±0.08398
	JAYA	78.6246±2.55288	0.5857±0.29418	0.1728±0.13618	0.1572±0.09032
	ALO	74.9220±3.81544	0.3001±0.07686	0.1798±0.11179	0.0767±0.07116
	WOA	79.2452±3.19805	0.7145±0.29399	0.1457±0.13746	0.1669±0.09614
Indian Liver Patient	Proposed	72.6172±0.64517	0.7432±0.01609	0.8309±0.00602	0.1966±0.05691
	IAOA	71.9443±0.50158	0.7337±0.02088	0.8293±0.00611	0.1430±0.07672
	RSA	71.7123±0.33981	0.7262±0.01948	0.8305±0.00586	0.1101±0.07048
	mGWOA	72.3618±0.53883	0.7434±0.01761	0.8288±0.00650	0.1900±0.05648
	VWGWO	72.0146±0.49718	0.7325±0.01933	0.8303±0.00608	0.1464±0.06843
	mGWO	72.3858±0.53659	0.7465±0.01871	0.8278±0.00723	0.1988±0.05634
	GWO	72.2233±0.51918	0.7436±0.01887	0.8275±0.00693	0.1857±0.06302
	SCA	70.3839±0.45127	0.7359±0.01229	0.6825±0.00736	0.4118±0.00958
	JAYA	69.8541±3.17733	0.7672±0.04887	0.7968±0.04185	0.2087±0.09301
	ALO	67.4394±3.93935	0.7829±0.05075	0.7663±0.05464	0.2213±0.08056
	WOA	68.7121±8.12732	0.7568±0.06118	0.7793±0.13169	0.1663±0.07454
Ionosphere	Proposed	81.7696±3.38525	0.8773±0.07145	0.6917±0.07141	0.5995±0.07715
	IAOA	72.1480±2.05223	0.6840±0.14136	0.5711±0.11357	0.4081±0.05068
	RSA	75.6917±4.10261	0.7681±0.15401	0.6081±0.09685	0.4779±0.08792
	mGWOA	81.8068±3.13072	0.8779±0.07827	0.6942±0.06424	0.6017±0.06926
	VWGWO	75.7345±2.97216	0.8550±0.11285	0.5439±0.08879	0.4641±0.07046
	mGWO	81.7555±3.49685	0.8835±0.07501	0.6892±0.07549	0.5998±0.08043
	GWO	78.1539±4.06346	0.8393±0.12058	0.6231±0.09481	0.5224±0.08849
	SCA	72.1079±4.56557	0.7643±0.08590	0.7021±0.06443	0.4557±0.08860
	JAYA	77.6664±4.42710	0.7957±0.11385	0.6275±0.10096	0.5072±0.09890
	ALO	70.5874±2.31209	0.6807±0.15141	0.5217±0.15119	0.3651±0.06507
	WOA	73.7260±4.02217	0.7623±0.14256	0.5419±0.15563	0.4188±0.10113
Iris	Proposed	98.4414±0.65855	0.9850±0.00626	0.9844±0.00659	0.9769±0.00969
	IAOA	96.9332±1.26730	0.9700±0.01235	0.9693±0.01270	0.9544±0.01883
	RSA	93.5529±1.91439	0.9391±0.01769	0.9352±0.01935	0.9053±0.02777
	mGWOA	97.6201±0.77178	0.9771±0.00751	0.9762±0.00775	0.9648±0.01143
	VWGWO	90.6869±4.45821	0.9213±0.02870	0.9043±0.05005	0.8682±0.05833
	mGWO	97.7137±1.02684b	0.9779±0.01000	0.9771±0.01029	0.9661±0.01523
	GWO	97.3674±1.10662	0.9744±0.01103	0.9737±0.01108	0.9609±0.01657
	SCA	98.2345±0.89638	0.9829±0.00882	0.9823±0.00897	0.9738±0.01335
	JAYA	97.3737±1.37963	0.9746±0.01340	0.9737±0.01384	0.9611±0.02045
	ALO	94.9136±2.07974	0.9522±0.01863	0.9489±0.02102	0.9255±0.02987
	WOA	96.0131±2.00831d	0.9617±0.01902	0.9600±0.02020	0.9411±0.02945
Liver	Proposed	69.7357±2.49735	0.7040±0.05621	0.5761±0.05874	0.3696±0.05497
	IAOA	63.8539±2.83225	0.6304±0.08371	0.4676±0.13761	0.2446±0.06743
	RSA	62.0792±2.62348	0.6429±0.13101	0.3857±0.18600	0.1939±0.07374
	mGWOA	67.9554±2.46542	0.6698±0.06159	0.5597±0.06149	0.3332±0.05248
	VWGWO	66.3013±2.56115	0.6571±0.05985	0.5135±0.08035	0.2934±0.05913
	mGWO	68.6330±2.24208	0.6713±0.04284	0.5733±0.04619	0.3444±0.04872
	GWO	68.0194±2.34249	0.6670±0.05204	0.5609±0.06273	0.3328±0.05123
	SCA	66.5975±2.70612	0.6831±0.05343	0.6560±0.03277	0.3384±0.05539
	JAYA	65.1556±3.41624	0.6154±0.06294	0.5370±0.10046	0.2799±0.07220
	ALO	61.0816±3.34142	0.5440±0.06291	0.4884±0.12312d	0.1946±0.07921
	WOA	64.0131±4.11443	0.5995±0.11359	0.5085±0.13724	0.2543±0.08487
Mammographic Mass	Proposed	80.9709±1.09880	0.8272±0.02329	0.8218±0.01267	0.6192±0.02147
	IAOA	71.3915±3.32175	0.7104±0.04490	0.7498±0.02568	0.4247±0.06756
	RSA	67.8632±1.78538	0.6989±0.03706	0.7046±0.03104f	0.3568±0.03762
	mGWOA	78.1339±3.49363	0.8159±0.04673	0.7896±0.04338	0.5690±0.06412
	VWGWO	69.3269±3.52510	0.7864±0.07154	0.6763±0.05715	0.4136±0.07202
	mGWO	79.1762±2.09917	0.8248±0.04132	0.8003±0.03168	0.5895±0.03400
	GWO	77.3475±3.73396	0.8082±0.06068	0.7841±0.03926	0.5543±0.07125
	SCA	80.4617±2.81795	0.8145±0.03373	0.8016±0.03027	0.6108±0.05552
	JAYA	77.8180±4.47165	0.8141±0.06917	0.7897±0.03601	0.5610±0.09139
	ALO	70.2940±3.28309f	0.7249±0.06464	0.7274±0.03473	0.4101±0.07018
	WOA	73.1590±5.13931	0.7543±0.08324	0.7547±0.05653	0.4734±0.09927
Seeds	Proposed	92.4090±0.54627	0.9255±0.00533	0.9237±0.00543	0.8871±0.00808
	IAOA	91.3949±0.80084	0.9171±0.00755	0.9138±0.00772	0.8727±0.01166
	RSA	89.6999±1.56320	0.9023±0.01245	0.8969±0.01518	0.8484±0.02151
	mGWOA	91.7562±0.59266	0.9199±0.00537	0.9173±0.00573	0.8778±0.00852
	VWGWO	85.4049±5.76350	0.8664±0.04610	0.8517±0.06122	0.7883±0.07955
	mGWO	91.9657±0.59300	0.9217±0.00524	0.9194±0.00574	0.8807±0.00850
	GWO	91.8321±0.61026	0.9202±0.00584	0.9182±0.00595	0.8786±0.00897
	SCA	91.7465±0.69675	0.9203 ±0.00686	0.9174±0.00690	0.8778±0.01030
	JAYA	91.6041±0.79939	0.9188±0.00725	0.9158±0.00800	0.8757±0.01150
	ALO	89.8570±1.06455	0.9030±0.00955	0.8982±0.01064	0.8504±0.01511
	WOA	90.8287±1.25614	0.9123±0.00928	0.9082±0.01214	0.8647±0.01687
WDBC	Proposed	92.9459±0.51816	0.9257±0.01478	0.9450±0.00362	0.8490±0.01055
	IAOA	91.6857±0.52365	0.9000±0.01246	0.9365±0.00346	0.8228±0.01076
	RSA	91.0772±0.34554	0.8933±0.00617	0.9320±0.00314	0.8098±0.00736
	mGWOA	92.1703±0.60441	0.9166±0.02192	0.9392±0.00423	0.8333±0.01269
	VWGWO	91.0506±0.37532	0.8936±0.00818	0.9317±0.00343	0.8093±0.00830
	mGWO	92.2386±0.63224	0.9159±0.02093	0.9399±0.00439	0.8347±0.01323
	GWO	91.8520±0.61351	0.9091±0.02059	0.9372±0.00408	0.8264±0.01260
	SCA	92.3462±0.72270	0.9238±0.01751	0.9234±0.00780	0.8476±0.01444
	JAYA	92.0316±0.80562	0.9077±0.01926	0.9388±0.00568	0.8304±0.01680
	ALO	90.4100±0.88946	0.8958±0.02303	0.9262±0.00746	0.7963±0.01732
	WOA	91.6658±0.90481	0.9044±0.02123	0.9360±0.00595	0.8226±0.01823
Zoo	Proposed	90.7732±0.85453	0.8677±0.02547	0.8487±0.01824	0.8435±0.01585
	IAOA	89.7436±0.82674	0.8534±0.02845	0.8253±0.01961	0.8230±0.01689
	RSA	88.7536±1.29364	0.8475±0.03239	0.8019±0.03126	0.8036±0.02681
	mGWOA	90.6841±0.66142	0.8637±0.02436	0.8460±0.01614	0.8408±0.01464
	VWGWO	89.1694±1.16732	0.8624±0.03951	0.8156±0.03002	0.8153±0.02656
	mGWO	90.7039±0.70208	0.8673±0.02706	0.8474±0.01699	0.8424±0.01483
	GWO	90.3871±0.79965	0.8677±0.02992	0.8426±0.02031	0.8389±0.01762
	SCA	69.8608±9.32141	0.7534±0.09929	0.6880±0.08530	0.6658±0.09882
	JAYA	89.4070±0.96979	0.8502±0.03128	0.8187±0.02199	0.8177±0.01923
	ALO	88.5952±0.84988	0.8395±0.02489	0.8034±0.01742	0.8042±0.01647
	WOA	89.4664±1.29364	0.8558±0.03259	0.8217±0.030340	0.8198±0.02653

To statistically verify the performance difference among all state-of-the-art meta-heuristic algorithms with respect to our proposed algorithm, we have applied the Wilcoxon signed-rank test and Friedman and Nemenyi hypothesis test on the obtained results considering 12 clustering problems. Here, the statistical nonparametric Wilcoxon signed-rank test is conducted at 95% confidence level on a pairwise basis on the obtained results. The test results are presented in Tables 13, 14 , Tables 15 and 16 for accuracy, precision, F-score and MCC performance measures respectively. One can observe from the tables that the proposed algorithm is showing statistically superior or equivalent performance than other alternative algorithms with respect to all performance measures.

Table 13. Wilcoxon Signed-Rank test statistical results with + indicating superior (+), inferior (–) or statistically equivalent (≈) algorithm in comparison to our proposed algorithm on clustering 12 benchmark datasets considering accuracy performance measures.

Accuracy	IAOA	RSA	mGWOA	VWGWO	mGWO	GWO	SCA	JAYA	ALO	WOA
WBDC	̶	̶	≈	̶	≈	≈	+	̶	̶	̶
Bupa	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Haberman’s Survival	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Hepatitis	̶	̶	≈	̶	̶	̶	̶	̶	̶	̶
Indian Liver Patient	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Ionosphere	̶	̶	≈	̶	≈	̶	̶	̶	̶	̶
Iris	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Liver	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Mammographic Mass	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Seeds	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
WDBC	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Zoo	̶	̶	≈	̶	≈	̶	̶	̶	̶	̶
+/̶/≈	0/12/0	0/12/0	0/8/4	0/12/0	0/9/3	0/11/0	1/9/2	0/12/0	0/12/0	0/12/0

Table 14. Wilcoxon Signed-Rank test statistical results with + indicating superior (+), inferior (–) or statistically equivalent (≈) algorithm in comparison to our proposed algorithm on clustering 12 benchmark datasets considering precision performance measures.

Precision	IAOA	RSA	mGWOA	VWGWO	mGWO	GWO	SCA	JAYA	ALO	WOA
WBDC	̶	̶	≈	≈	≈	≈	̶	+	+	̶
Bupa	̶	̶	≈	̶	≈	≈	≈	+	≈	̶
Haberman’s Survival	+	+	≈	̶	≈	≈	≈	̶	̶	≈
Hepatitis	̶	̶	≈	≈	≈	̶	≈	≈	≈	̶
Indian Liver Patient	+	+	≈	̶	̶	≈	≈	̶	̶	≈
Ionosphere	≈	≈	≈	≈	≈	̶	̶	̶	̶	̶
Iris	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Liver	̶	̶	≈	̶	≈	≈	≈	≈	≈	≈
Mammographic Mass	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Seeds	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
WDBC	+	+	≈	̶	≈	≈	≈	̶	≈	+
Zoo	̶	̶	≈	≈	≈	̶	̶	̶	̶	̶
+//≈	3/8/1	3/8/1	0/3/9	0/8/4	0/4/8	0/6/6	0/4/8	2/8/2	1/7/4	1/8/3

Table 15. Wilcoxon Signed-Rank test statistical results with + indicating superior (+), inferior (–) or statistically equivalent (≈) algorithm in comparison to our proposed algorithm on clustering 12 benchmark datasets considering F-score performance measures.

F-score	IAOA	RSA	mGWOA	VWGWO	mGWO	GWO	SCA	JAYA	ALO	WOA
WBDC	̶	̶	≈	̶	≈	≈	̶	̶	̶	̶
Bupa	̶	̶	≈	̶	≈	̶	+	≈	̶	̶
Haberman’s Survival	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Hepatitis	̶	̶	≈	̶	≈	̶	+	≈	≈	̶
Indian Liver Patient	≈	≈	̶	≈	̶	̶	̶	̶	̶	̶
Ionosphere	̶	̶	≈	̶	≈	̶	≈	̶	̶	̶
Iris	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Liver	̶	̶	̶	̶	≈	≈	+	̶	̶	̶
Mammographic Mass	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Seeds	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
WDBC	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Zoo	̶	̶	≈	̶	≈	≈	̶	̶	̶	̶
+/̶/≈	0/11/1	0/11/1	0/7/4	0/11/1	0/6/6	0/9/3	3/7/2	0/10/2	0/11/1	0/12/0

Table 16. Wilcoxon Signed-Rank test statistical results with + indicating superior (+), inferior (–) or statistically equivalent (≈) algorithm in comparison to our proposed algorithm on clustering 12 benchmark datasets considering MCC performance measures.

MCC	IAOA	RSA	mGWOA	VWGWO	mGWO	GWO	SCA	JAYA	ALO	WOA
WBDC	̶	̶	≈	̶	̶	≈	+	̶	̶	̶
Bupa	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Haberman’s Survival	̶	̶	̶	̶	̶	̶	+	̶	̶	̶
Hepatitis	̶	̶	≈	̶	≈	̶	+	̶	̶	̶
Indian Liver Patient	̶	̶	≈	̶	≈	≈	+	≈	+	̶
Ionosphere	̶	̶	≈	̶	≈	̶	̶	̶	̶	̶
Iris	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Liver	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
Mammographic Mass	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Seeds	̶	̶	̶	̶	̶	̶	̶	̶	̶	̶
WDBC	̶	̶	̶	̶	̶	̶	≈	̶	̶	̶
Zoo	̶	̶	≈	̶	≈	≈	̶	̶	̶	̶
+/̶/≈	0/12/0	0/12/0	0/7/5	0/12/0	0/8/4	0/9/3	4/5/3	0/11/1	1/11/0	0/12/0

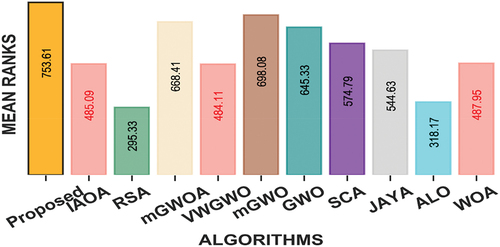
To rank each meta-heuristic algorithm, we have applied the Friedman and Nemenyi hypothesis test on the results obtained over 12 benchmark clustering problems. Since the performance measures are independent to each other, so we have conducted the test for the results obtained over all datasets on each performance measures separately. The statistical mean rank results for all the state-of-the-art meta-heuristic algorithms from the test are presented in Figures 9, Figures 10, 11 and Figure 12 for accuracy, precision, F-score and MCC performance measures respectively. The obtained p-value = .000 and critical distance (CD) = 4.4. From the figures, one can see that, our proposed enhanced GWO algorithm is showing the highest mean ranks (since maximization problem) in all performance measures that varies from all the other meta-heuristic algorithms by at least the critical distance. Therefore, the proposed algorithm is considered as the best algorithm for addressing the clustering problems. Furthermore, it can also be observed from Figure 10 that among all comparative algorithms, IAOA, VWGWO and WOA are tested statistically equivalent to each other in precision performance measure (since the mean rank differences are not greater than the critical distance).

Figure 9. Mean rank of meta-heuristic algorithms for clustering using 12 benchmark datasets on Accuracy performance measure with P-value = .000 and Critical Distance = 4.4.

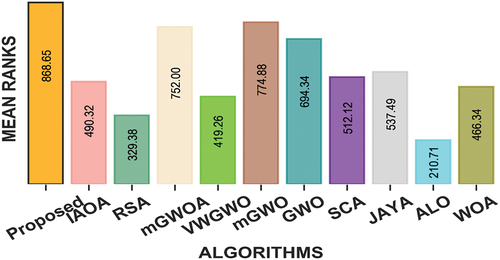
Figure 10. Mean rank of meta-heuristic algorithms for clustering using 12 benchmark datasets on Precision performance measure with P-value = .000 and Critical Distance = 4.4.

Figure 11. Mean rank of meta-heuristic algorithms for clustering using 12 benchmark datasets on F-Score performance measure with P-value = .000 and Critical Distance = 4.4.

Figure 12. Mean rank of meta-heuristic algorithms for clustering using 12 benchmark datasets on MCC performance measure with P-value = .000 and Critical Distance = 4.4.

Conclusion

In this paper, we have proposed a novel differential perturbation operator with help of three randomly selected omega wolves to improve the search capability of the existing GWO algorithm. Additionally, we have introduced similar values for parameters $A$ and $C$ for each leader wolf while updating the position of a single omega wolf to incorporate an element of exploration in the exploitation phase. Hence, it improves the explorative capability while managing a proper trade between exploration and exploitation behavior of the algorithm. It also has a great impact in avoiding the algorithm from trapping at local optimal solutions. In order to evaluate the performance of our proposed algorithm, a comparative performance analysis has been carried out using 3 variants of GWO algorithm and 7 other promising meta-heuristic algorithms from recent literature. The statistical analysis on the simulation results show the superiority of our proposed algorithm with respect to the state-of-the-art meta-heuristic algorithms considering 23 benchmark functions and 12 data clustering problems. The Wilcoxon signed-rank test was conducted on the obtained results, and it confirms the superiority of our proposed algorithm in both mathematical benchmark function and data clustering problems. It is also observed from the Friedman and Nemenyi hypothesis test on the results obtained from benchmark function (minimization problems) that our algorithm achieves lowest mean rank result (128.60) that varies from other comparative algorithm by at least the critical distance (CD) and rejects the null hypothesis at p-value =.000 and critical distance = 3.1. Additionally, the results obtained from the benchmark clustering problems (maximization problems) that our proposed algorithm shows highest mean results in 10 different clustering problems such as Bupa, Haberman’s Survival, Hepatitis, Indian Liver Patient, Iris, Liver, Mammographic Mass, Seeds, WDBC and Zoo datasets considering accuracy performance measures. In precision performance measure, our algorithm achieves highest mean results in 6 benchmark clustering problems such as Haberman’s Survival, Iris, Liver, Mammographic Mass, Seeds and WDBC benchmark datasets. Similarly, considering F-score performance measure our algorithms is performing superior in 7 different clustering problems such as in Habarman’s Survival, Indian Liver Patient, Iris, Mammographic, Seeds, WDBC and Zoo datasets. Considering MCC performance measure, our proposed algorithm achieves highest mean results in 7 different clustering problems such as Bupa, Iris, Liver, Mammographic Mass, Seeds, WDBC and Zoo datasets. It is also observed from the Friedman and Nemenyi hypothesis test that our proposed algorithm achieves highest mean rank results such as 868.65, 735.61, 812.79 and 818.92 for accuracy, precision, F-score and MCC performance measures respectively. It is evident from the test results that our proposed enhanced GWO algorithm is showing highest mean rank results that varies from all other meta-heuristic algorithms by at least the critical distance. The obtained p-value=.000 and CD = 4.4. Hence, with the evidence from statistical results, the proposed GWO algorithm is statistically superior to other considered meta-heuristic algorithms considered in this study. One can observe from Tables 9, 10 and Table 11 that our proposed algorithm is able to overcome the local convergence issue for maximum multimodal problems. The results also reveals that, for some unimodal problems, it is showing comparatively inferior performance than some of the meta-heuristic algorithms. However, the supremacy of our proposed algorithm is statistically verified for the results obtained from both mathematical benchmark functions and clustering problems. Therefore, it is concluded that the proposed algorithm is highly competitive in avoiding local convergence issues and can be applied to solve different multimodal optimization problems. The following are some of the future research directions and academic implications of our proposed algorithm.

• The GWO with differential perturbation operator enhances the diversities among the solution and hence enhances the balance between exploration and exploitation. Hence, it be applied to avoid local convergence issues of multimodal problems.

• The proposed enhanced GWO algorithm can be applied to address engineering design problems.

• Moreover, the proposed algorithm with better trade-off between exploration and exploitation can be modified to tackle the large-scale global optimization (LSGO) problems.

• The proposed GWO algorithm can be applied for parameter optimization and feature selection for complex real world problems.

• The proposed GWO algorithm can be applied to address multi-objective optimization problems such as path planning of multi-robots, vehicle ad-hoc network, clustering for wireless sensor networks and task scheduling for heterogeneous cloud environment etc.

• The proposed GWO algorithm can be used to define optimized fitness function for calculating weight values in artificial neural network.

• The proposed GWO algorithm can be integrated with gradient descent optimizer or independently applied for optimizing parameters and hyper-parameters of deep learning models.

Disclosure statement

No potential conflict of interest was reported by the authors.